冶金行业中双金属复层合金的制备、高分子聚合物的挤压成型、气动挤压塑料片、吹制玻璃等加工工艺中均会涉及到磁流体边界层内的流动问题[1, 2, 3].在这些领域中,导电流体被置于电磁场环境下,通过施加电磁力可以控制导电流体的运动状态[4, 5].此外,在机翼上合理布置电磁场及相关设备,可以有效改变绕流边界层的结构,从而达到减震、减阻等效果[6, 7].
导电流体在法向外置磁场的作用下,在贴近壁面处会形成速度梯度很大、厚度很薄的边界层,即哈特曼边界层[8, 9]. 哈特曼边界层的稳定性研究对电磁制动[10]、电磁搅拌[11]、晶体增长[12]、热核聚变反应冷却系统[13]等相关设备的设计和制造都有着十分重要的意义. Lundquist[14]最早提出了判断哈特曼边界层是否稳定(层流还是湍流)的参数------局部雷诺数$R$ $$ R = \dfrac{Re}{Ha} \tag{1}$$ 式中,$Re$为主流雷诺数,$Ha$为哈特曼数.Murgatroyd[15]对哈特曼边界层的稳定性进行了实验研究,发现局部临界雷诺数$R_{\rm c}$位于150$\sim $250的范围内,哈特曼边界层内流体开始从层流向紊流转捩.Moresco和Alboussiére[16]实验得到的临界雷诺数$R_{\rm c}$约为380,但是Lingwood和Alboussière[17]采用正则模态线性稳定性分析得到的临界雷诺数$R_{\rm c}$均明显高于实验结果.最近,Krasnov等[18]采用直接数值模拟的方法,通过在流场中施加随机背景噪声扰动来观测流场变化,得到了与实验值相近的结果,临界雷诺数$R_{\rm c}$约为350.基于直接数值模拟结果,他们提出了如下转捩过程假说:(1)流向漩涡和哈特曼层流流动相互作用形成流向条纹结构;(2)流向条纹结构失稳,进而过渡到湍流.
Gerard-Varet[19]通过非正则模态稳定性的分析方法对单一无限大平板上的哈特曼边界层进行研究,认为在壁面绝缘情况下,其最优扰动为流向漩涡,最优扰动增长倍数$G_{\max}$和局部雷诺数$R$呈平方关系,即$G_{\max} \approx 5.65\times 10^{-4}R^{2}$. Airiau和Castets[20]获得的结果与之类似.
Krasnov等[21]随后对大哈特曼数$Ha$下,导电流体在方形截面管道内的流动进行了直接数值模拟. 当哈特曼数$Ha$从0变化到400时,流动从湍流逐渐过渡到层流,哈特曼边界层厚度不断减小,上下两个哈特曼边界层之间的相互作用也逐渐减弱.
目前,对哈特曼边界层稳定性的研究主要针对较大哈特曼数$Ha$下的磁流体流动,对小哈特曼数$Ha$ ($Ha <10$)下流动的研究还不充分.本文对两块平行的无限大绝缘平板内导电流体流动的稳定性进行分析,重点考察初级扰动的增长情况,以及哈特曼数$Ha$和雷诺数$Re$的影响.平板流内上下两个哈特曼边界层之间可能存在着一定的相互作用,从而对整个流场的稳定性产生影响,这在以前的研究中并未引起足够的重视,本文将就此展开研究和讨论.
1 数值方法 1.1 物理模型本研究考察的物理模型为不可压缩导电流体在两块无限大的绝缘平行平板之间的流动,在垂直流场的方向施加一个均匀恒定的静态磁场. 其中,两平板的间距为$d$,磁场强度为$B$,层流流场中心线上的速度为$U$. 平板内的流体在压力作用下流动,其体积流量保持恒定.
1.2 控制方程组本文是对低磁雷诺数下导电流体展开的研究,即忽略了流场对外界磁场的影响,只考虑外界磁场对流场的影响[22]. 其无量纲控制方程组和边界条件为 $$ \left. \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \left( {u \cdot \nabla } \right)u = - \nabla p + \frac{1}{{Re}}{\nabla ^2}u + \\ \frac{{H{a^2}}}{{Re}}\left[ { - \nabla \phi \times e + \left( {u \times e} \right) \times e} \right]\\ \nabla \cdot u = 0\\ {\nabla ^2}\phi = \nabla \cdot \left( {u \times e} \right)\\ z = \pm 1,u = v = w = \frac{{\partial \phi }}{{\partial z}} = 0 \end{array} \right\} \tag{2}$$ 其中,${ e}=(0, 0, 1)$为单位矢量,$x$,$y$,$z$分别代表了流向,展向和法向方向. ${ u}$为速度矢量,$p$为压力,$\phi $为电势,$u$, $v$和$w$分别代表了流向、展向、法向速度.进行无量纲化时,特征速度取哈特曼层流流动中心线上的速度$U$,特征长度$L$取平板间距的一半,即$L=d/2$;磁场强度特征值取$B$,相应的电势特征值为$\sigma UB$,时间和压力的特征值分别为$L/U$和$\rho U^{2}$. 式(2)中出现了两个重要的无量纲参数,哈特曼数$Ha = BL\sqrt {\dfrac{\sigma }{\rho \upsilon }} $和主流雷诺数 $Re = \dfrac{LU}{\upsilon }$.
本文研究的基本流是哈特曼层流流动,流场中的任一物理量$\psi $可以分解为 $$ \psi = \varPsi (z, t) + \psi _p (x, y, z, t) \tag{3}$$ 其中,$\varPsi (z, t)$表示基本流场的物理量,$\psi_{p}(x, y, z, t)$表示扰动变量. 将式(3)代入式(2)中,减去基本流的控制方程组,并忽略关于扰动的高阶项,即可获得关于扰动的线性方程组.
$$ \left. \begin{array}{l} \frac{{\partial {u_p}}}{{\partial t}} + \left( {{u_p} \cdot \nabla } \right)U + (U \cdot \nabla ){u_p} = - \nabla {p_p} + \\ \frac{1}{{Re}}{\nabla ^2}{u_p} + \frac{{H{a^2}}}{{Re}}\left[ { - \nabla {\phi _p} \times e + \left( {{u_p} \times e} \right) \times e} \right]\\ \nabla \cdot {u_p} = 0\\ {\nabla ^2}{\phi _p} = \nabla \cdot \left( {{u_p} \times e} \right)\\ z = \pm 1,{u_p} = {v_p} = {w_p} = \frac{{\partial {\phi _p}}}{{\partial z}} = 0 \end{array} \right\} \tag{4}$$
本研究主要采用非正则模态稳定性分析方法[23, 24, 25, 26, 27],考察扰动的增长模式及其获得的最大峰值,为了对扰动的增长情况进行分析,将扰动项展开成如下形式 $$ \psi _p (x, y, z, t) = \hat {\psi }(z, t)\exp\left( { {\rm i}\alpha x + {\rm i}\beta y} \right) \tag{5}$$ 其中,$\alpha $ 为流向波数,$\beta $ 为展向波数. 为了定量的描述扰动的增长,选取变量$E(t)$代表扰动动能随时间的变化情况 $$ E(t) = \int \Big[\hat {u}\left( {z, t} \right)\hat {u}^\ast \left( {z, t} \right) + \hat {v}\left( {z, t} \right)\hat {v}^\ast \left( {z, t} \right) + \\ \hat {w}\left( {z, t} \right)\hat {w}^\ast \left( {z, t} \right) \Big] d z $$ 其中,上标"*"代表变量的共轭复数. 初始扰动的增长或者衰减可由下式表示 $$ G \equiv \dfrac{E(T)}{E(0)} \tag{6} $$ 式中,$T$是所要考察的时刻,0为初始时刻,$G$称为扰动增长倍数.
当哈特曼数$Ha$、局部雷诺数$R$、流向波数 $\alpha $、展向波数 $\beta $ 和时刻$T$分别取某一定值时,扰动的分布形式仍有若干种可能,这些扰动都是控制方程组的解,目的是要从中找到某一特定的扰动分布,在$T$时刻获得扰动增长倍数$G$的最大值. 这一特定的扰动分布被称之为最优扰动.
1.3 求解方法要获得$G$因子的最大值,数学上可以采用拉格朗日乘子法求解[28, 29].即引入扰动变量的伴随场,通过耦合求解关于扰动的原始控制方程组和相应的关于伴随场变量的控制方程组,来获取最优扰动的空间分布形式和增长倍数.为了求解$T$时刻对应的最优初始扰动$\hat{u} ( z, 0)$,可以采用循环迭代的数值算法[23],如图1所示. 图1中顶标"$\sim $"代表变量的伴随场,顶标"$ \hat{ }$ "代表变量的原始场.首先由初始时刻的扰动分布$\hat{u}(z, 0)$,在时间轴上正向迭代求解控制方程组,即可获得在$T$时刻的扰动分布$\hat{u}(z, T)$;该扰动分布经由适当变换可作为伴随场变量的初始值$\tilde u(z, T)$,然后在时间轴上逆向迭代求解伴随场变量满足的控制 方程组,可得$\tilde u(z, 0)$,并用该扰动分布去更新初始扰动$\hat{u}(z, 0)$. 如此循环迭代下去,直至$\tilde u(z, 0)$和$\hat{u}(z, 0)$满足一定的收敛标准,最后需要再次求解控制方程组,计算最优扰动$\hat{u}(z, 0)$在$T$时刻的扰动动能,并代入式(6)中求解扰动增长倍数$G$.
|
图1 数值求解中的循环迭代 Fig.1 The iteration loop of solving optimal problems |
本文采用了高精度的伪谱方法求解无量纲方程组,在法向方向上采用切比雪夫配置点布置方式.这种网格节点布置方式的特点是中间稀疏,两边密集,从而可以较好地求解近壁面边界层内的流动.当哈特曼数较小时,磁场效果不明显,哈特曼边界层厚度较大,采用较少的网格节点($N =64$)可以精确求解控制方程组.当哈特曼数较大时,哈特曼边界层厚度变薄,需要相应增加节点个数($N =128$)以满足计算精度要求.
对于一组确定的局部雷诺数$R$和哈特曼数$Ha$,某一初始扰动能够在某一流向波数 $\alpha $、展向波数 $\beta $ 和时刻$T$下,得到所有扰动增长倍数$G$的最大值,称为最优扰动增长倍数$G_{\max}$,对应的流向波数 $\alpha $、展向波数$\beta $和时刻$T$分别称为最优流向波数$\alpha_{\rm opt}$、最优展向波数$\beta_{\rm opt}$和最优时刻$t_{\rm opt}$. 对剪切流的研究发现,无论是平行平板流还是圆管中的流动,最优扰动的初始分布形式均为沿着流场方向的漩涡($\alpha =0$),并且通常为关于法向反对称或者对称的漩涡[26, 27, 30, 31]. 所以本文选取初始扰动为沿着流场方向的对称漩涡或者反对称漩涡两种情况进行分析,并设定流向波数 $\alpha =0$,只考虑了展向波数 $\beta $ 的变化情况.
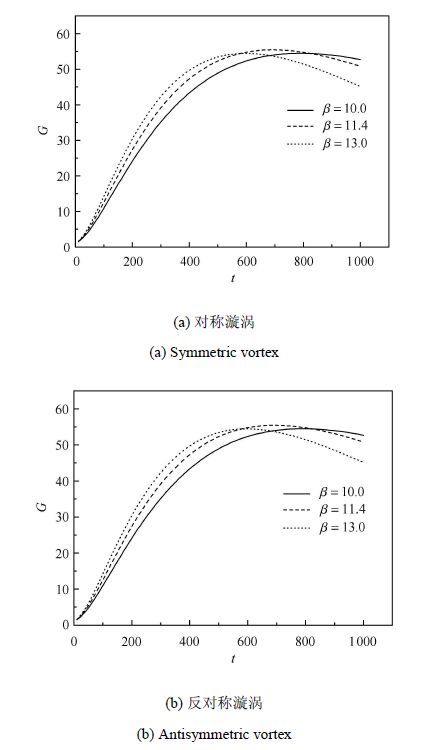
2 结果与讨论图2和图3分别表示局部雷诺数$R =300$,哈特曼数$Ha =5$和15时,不同展向波数 $\beta $ 下、不同扰动增长倍数$G$和时刻$t$之间的 关系. 当哈特曼数$Ha =5$时,相同的展向波数 $\beta $ 下,反对称漩涡在相应时刻的扰动增长倍数$G$均大于对称漩涡的扰动增长倍数$G$,即反对称漩涡获得了更大的扰动能量,但反对称漩涡达到最优扰动增长倍数$G_{\max}$的时刻大于对称漩涡. 在哈特曼数$Ha =15$时,相同的展向波数 $\beta $ 下,初始对称漩涡和反对称漩涡取得了相等的最优扰动增长倍数$G_{\max}$,说明在较大哈特曼数$Ha$时,两种不同结构的初始扰动其增长情况基本相同.

|
图2 $R =300$,$Ha =5$,不同 $\beta $ 时,$G$和$t$之间的关系 Fig.2 The amplification of perturbation $G$ as function of time $t$ at $R =300$, $Ha =5$ |
|
图3 $R=300$,$Ha =15$,不同 $\beta $ 时,$G$和$t$之间的关系 Fig.3 The amplification of perturbation $G$ as function of time $t$ at $R =300$, $Ha =15$ |
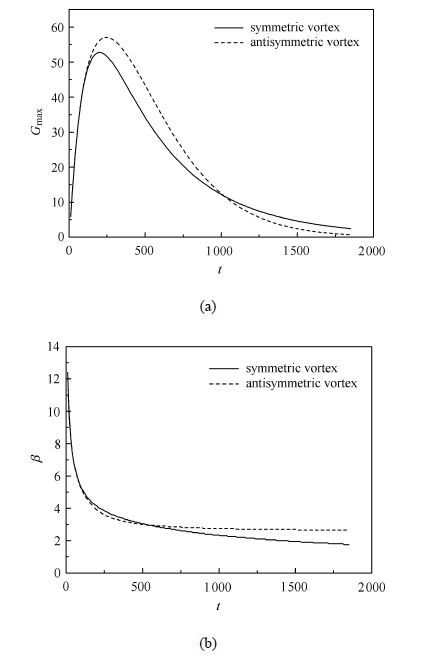
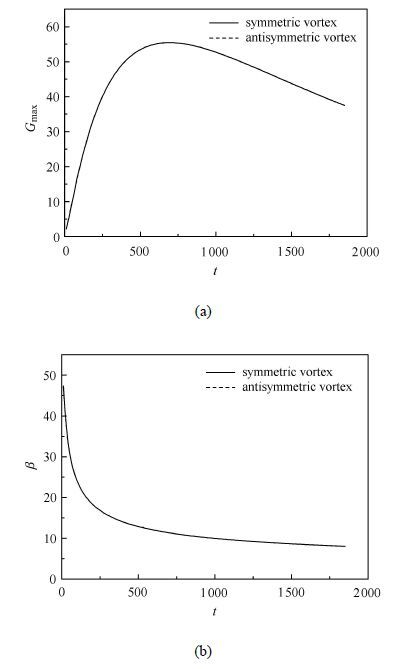
图4和图5分别表示局部雷诺数$R =300$,哈特曼数$Ha =5$和15时,最优扰动增长倍数$G_{\max}$和展向波数 $\beta $ 随时间的变化情况. 当哈特曼数$Ha =5$时,反对称漩涡扰动动能达到最大值的时刻要大于对称漩涡,展向波数 $\beta $ 要小于对称漩涡,这说明磁场对反对称漩涡的抑制效果更加明显.但是必须明确的是,反对称漩涡的最大扰动动能要大于对称漩涡. 汇总结果如表1所示. 当哈特曼数$Ha =15$时,磁场对两种漩涡的影响相同,其最优扰动增长倍数$G_{\max}$和展向波数 $\beta $随时间的变化基本相同,并在相同的时刻和展向波数 $\beta $ 下取得最优扰动. 两种情况下,随着展向波数 $\beta $ 和时间$t$的增加,扰动增长倍数$G$均逐渐增大,直到$G$因子在某一时刻$t$和某一展向波数 $\beta $ 下获取峰值,即$G_{\max}$,相应的取得最优展向波数 $\beta_{\rm opt}$和最优时刻$t_{\rm opt}$.
|
图4 $R =300$, $ Ha =5$ (a) $G_{\max}$和$ t$之间的关系; (b) $\beta $ 和$t$之间的关系 Fig.4 The optimal amplification of perturbation $G_{\max}$ (a) and spanwise wavenumber (b) as function of time $t$ for $R =300$, $Ha =5$ |
|
图5 $R =300$, $Ha =15$,(a) $G_{\max}$和$ t$之间的关系; (b) $\beta $ 和$t$之间的关系 Fig.5 The optimal amplification of perturbation $G_{\max}$ (a) and spanwise wavenumber (b) as function of time $t$ for $R =300$, $Ha =15$ |
| 表1 $R =300$,不同$Ha$和漩涡结构的最优扰动参数 Table 1 Parameters of optimal perturbation for different $Ha$ and vortex at $R =300$ |
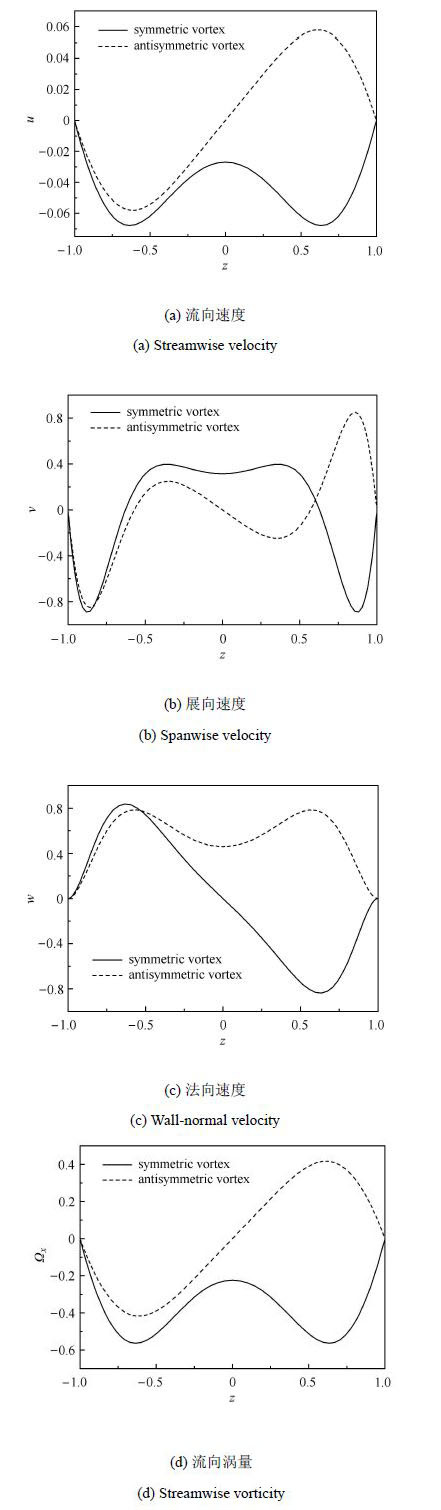
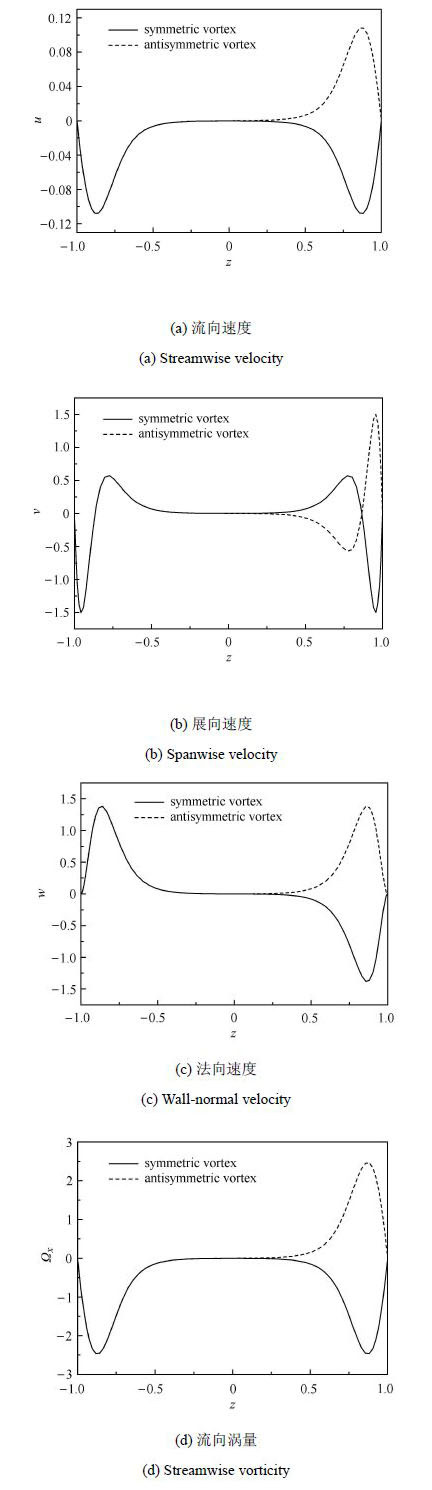
图6和图7分别显示局部雷诺数$R =300$,哈特曼数$Ha =5$和15时,最优初级扰动在初始时刻的空间分布.哈特曼数$Ha =5$时,对称漩涡和反对称漩涡扰动的幅值是不同的;而哈特曼数$Ha =15$时,对称漩涡和反对称漩涡的幅值相同,并且无论流向、展向还是法向速度,在流场中心区域均保持在零值上下,说明最优扰动主要分布在边界层附近,当哈特曼数越大($Ha =15$)时,这种趋势更加明显.从图中还可以看出,当哈特曼数$Ha$较小时,上下两块平板上的边界层之间有着一定程度的相互作用;而当哈特曼数较大时,两个边界层之间基本上不会互相影响.
|
图6 $R =300$, $Ha =5$时,最优初级扰动在初始时刻的空间分布 Fig.6 Distribution of optimal primary perturbation at initial time for $R =300$, $Ha =5$ |
|
图7 $R =300$, $Ha =15$时,最优初级扰动在初始时刻的空间分布 Fig.7 Distribution of optimal primary perturbation at initial time for $R =300$, $Ha =15$ |
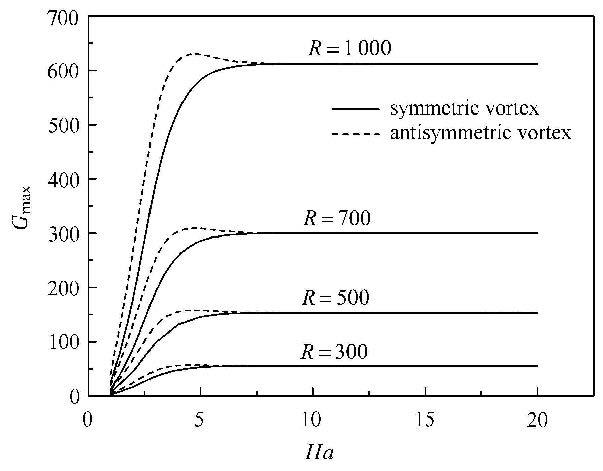
图8显示了初始扰动为对称漩涡和反对称漩涡两种情况下,局部雷诺数$R =300$, 500, 700, 1 000时,最优扰动增长倍数$G_{\max}$随哈特曼数$Ha$的变化规律.在局部雷诺数$R$取值不同时,最优扰动增长倍数$G_{\max}$随哈特曼数$Ha$的主要变化趋势都是相同的,即哈特曼数$Ha <8$时,最优扰动增长倍数$G_{\max}$随着哈特曼数$Ha$的增大而增大,当哈特曼数$Ha >8$时,最优扰动增长倍数$G_{\max}$基本不变.
|
图8 不同$R$、不同漩涡结构时,$G_{\max}$和$Ha$之间的关系 Fig.8 The optimal amplification of perturbation $G_{\max}$ as function of $Ha$ for different $R$ and vortex structures |
在局部雷诺数$R$相同,哈特曼数$Ha <8$情况下,反对称漩涡的最优扰动增长倍数$G_{\max}$均大于对称漩涡. 说明这种形式的扰动更为不稳定,而上下两个边界层之间的影响也是不可以忽略的. 在哈特曼数$Ha =5$附近,反对称漩涡的最优.最动扰动增长倍数$G_{\max}$出现了先增大后减小的特征. 这表明哈特曼数$Ha <5$时,磁场作用较弱,扰动增长主要受主流雷诺数的制约,即$G_{\max} \propto Re^{2}$;当哈特曼数$Ha =5$时,最优扰动增长倍数$G_{\max}$达到最大值;当哈特曼数$Ha >5$时,磁场强度的增加,扰动增长主要受局部雷诺数的制约,即$G_{\max} \propto R^{2}$.
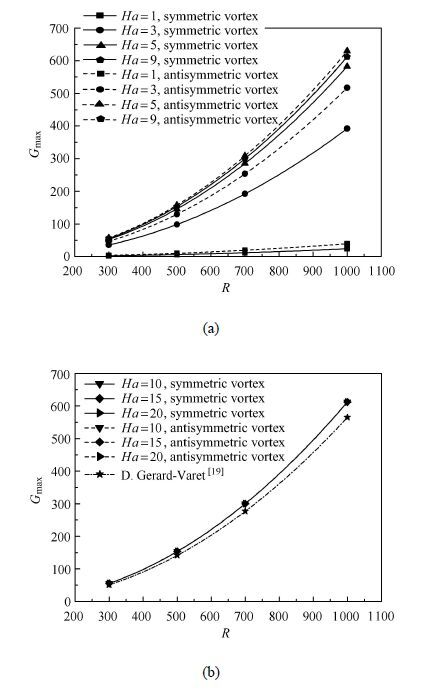
图9所示为不同哈特曼数$Ha$、不同漩涡结构时,最优扰动增长倍数$G_{\max}$和局部雷诺数$R$之间的关系,并与 Gerard-Varet[19]的结果进行了对比. 在哈特曼数$Ha =1$, 3, 5, 9时,对称和反对称漩涡的$G_{\max}$-$R$曲线出现了明显的差别,反对称漩涡的最优扰动增长倍数$G_{\max}$均大于对称漩涡的值.哈特曼数$Ha =10$, 15, 20时,对称和反对称漩涡的$G_{\max}$-$R$曲线全部重合,即不仅哈特曼数$Ha$的大小不影响最优扰动增长倍数$G_{\max}$ 的大小,漩涡结构对最优扰动增长倍数$G_{\max}$的影响也非常有限.本文研究表明,在壁面绝缘情况下,最优扰动增长倍数$G_{\max}$和局部雷诺数$R$呈平方关系,$G_{\max} \approx 6.12 \times 10^{ - 4}R^{2}$,该结果与Gerard-Varet[19]的结果$G_{\max} \approx 5.65\times 10^{ - 4}R^{2}$一致.因此,在哈特曼数$Ha$较大时,哈特曼边界层很薄,平行平板间的上、下两个边界层可以认为是相互独立的,不会互相影响.但是对于小哈特曼数,上下两平板间的哈特曼边界层距离较近,会互相影响.
|
图9 不同$Ha$、不同漩涡结构时,$G_{\max}$和$R$之间的关系 (a) $Ha <10$; (b) $Ha ≥ 10$ Fig.9 The optimal amplification of perturbation $G_{\max}$ as function of $R $ for different $Ha$ and vortex structures (a) $Ha <10$; (b) $Ha ≥ 10$ |
图10显示了不同漩涡结构时,最优展向波数 $\beta_{\rm opt}$和哈特曼数$Ha$之间的关系. 哈特曼数$Ha ≥ 10$时,最优展向波数 $\beta_{\rm opt}$和哈特曼数$Ha$呈线性增长关系;哈特曼数$Ha <10$时,最优展向波数 $\beta_{\rm opt}$和哈特曼数$Ha$呈指数增长关系. 哈特曼数$Ha <10$时,在相同的哈特曼数$Ha$下,反对称漩涡在更小的最优展向波数 $\beta_{\rm opt}$下达到了最优扰动增长倍数$G_{\max}$.

|
图10 不同漩涡结构时,$\beta_{\rm opt}$和$Ha$ 之间的关系 Fig.10 The optimal spanwise wavenumber $\beta_{\rm opt}$ as function of $Ha $ for different vortex structures |
图11表明不同局部雷诺数$R$、不同漩涡结构时,最优时刻$t_{\rm opt}$和哈特曼数$Ha$之间的关系. 哈 特曼数$Ha <10$时,最优时刻$t_{\rm opt}$和哈特曼数$Ha$二者增长关系不明显;哈特曼数$Ha ≥ 10$时,最优时刻$t_{\rm opt}$和哈特曼数$Ha$呈线性增长关系,且局部雷诺数$R$越大,斜率越大. 哈特曼数$Ha <10$时,反对称漩涡对磁场更加敏感,其最优时刻$t_{\rm opt}$大于对称漩涡的最优时刻$t_{\rm opt}$. 哈特曼数$Ha ≥ 10$时,磁场对两种漩涡的抑制效果相同.

|
图11 不同$R$、不同漩涡结构时,$t_{\rm opt}$和$Ha$之间的关系 Fig.11 The optimal time $t_{\rm opt}$ as function of $Ha$ for different $R$ and vortex structures |
(1) 当哈特曼数$Ha$较大时,磁场可以有效抑制扰动的增长,无论是对称漩涡还是反对称漩涡,其效果相同.在哈特曼数$Ha$较小的时候,对称漩涡和反对称漩涡对磁场的敏感性是不同的,反对称漩涡需更长的时间取得最优扰动增长倍数,说明磁场抑制了其增长速度,但是其取得了比对称漩涡更大的扰动增长倍数,即这种形式的扰动更为不稳定.
(2) 哈特曼数$Ha >10$时,最优扰动增长倍数$G_{\max}$与局部雷诺数$R$的平方成正比,与哈特曼数$Ha$大小无关,对应的最优展向 波数 $\beta_{\rm opt}$和最优时刻$t_{\rm opt}$均正比于哈特曼数$Ha$的一次方.
(3)哈特曼数$Ha>10$时,上下两边界层之间无相互影响;哈特曼数$Ha<10$时,上下两边界层存在一定的相互作用,并且对整个流场的稳定性产生一定的影响.
| 1 | Mukhopadhyay S, Layek GC, Samad SA. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. International Journal of Heat and Mass Transfer, 2005, 48(21):4460-4466 |
| 2 | Sharma R, Bhargava R, Bhargava P. A numerical solution of unsteady MHD convection heat and mass transfer past a semi-infinite vertical porous moving plate using element free Galerkin method. Computational Materials Science, 2010, 48(3):537-543 |
| 3 | Rao JS, Sankar H. Numerical simulation of MHD effects on convective heat transfer characteristics of flow of liquid metal in annular tube. Fusion Engineering and Design, 2011, 86(2):183-191 |
| 4 | Molokov S, Moreau R, Moffatt HK. Magnetohydrodynamics-Historical Evolution and Trends. New Yorker:Springer, 2007:231-233 |
| 5 | Moreau R. Magnetohydrodynamics. New York:Springer, 1990:1-4 |
| 6 | 周本谋, 范宝春, 陈志华等. 流体边界层上电磁力的控制效应研究. 力学学报, 2004, 36(4):472-478(Zhou Benmou, Fan Baochun, Chen Zhihua, et al. Flow control effects of electromagnetic force in the boundary layer. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(4):472-478(in Chinese)) |
| 7 | 陈耀慧, 范宝春, 周本谋等. 翼型绕流的电磁力控制. 力学学报, 2008, 40(1):121-127(Chen Yaohui, Fan Baochun, Zhou Benmou, et al. Electro-magnetic control of hydrofoil wake. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(1):121-127(in Chinese)) |
| 8 | Hartmann J. Hg-Dynamics I, Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. Kongelige Danske Videnskabernes Selskab, Matematisk-Fysiske Meddelelser, 1937, 15(6):1-28 |
| 9 | Hartmann J,Lazarus F. Hg-dynamics Ⅱ:Experimental investigation on the flow of mercury in a homogeneous magnetic field. Kongelige Danske Videnskabernes Selskab, Matematisk-Fysiske Meddelelser, 1937, 15(7):1-45 |
| 10 | Ha MY, Lee HG, Seong SH. Numerical simulation of threedimensional flow, heat transfer, and solidification of steel in continuous casting mold with electromagnetic brake. Journal of Materials Processing Technology, 2003, 133(3):322-339 |
| 11 | Fujisaki K. In-Mold electromagnetic stirring in continuous casting. IEEE Transactions on Industry Applications, 2001, 37(4):1098-1104 |
| 12 | Dold P, Benz KW. Rotating magnetic fields:Fluid flow and crystal growth applications. Progress in Crystal Growth and Characterization of Materials, 1999, 38(1):39-58 |
| 13 | Smolentsev S, Moreau R, Buhler L, et al. MHD thermofluid issues of liquid-metal blankets:Phenomena and advances. Fusion Engineering and Design, 2010, 85(7):1196-1205 |
| 14 | Lundquist S. Studies in magnetohydrodynamics. Arkiv für Fysik, 1952, 5(4):297-347 |
| 15 | Murgatroyd W. Experiments on magnetohydrodynamic channel flow. Philosophical Magazine, 1953, 44(359):1348-1354 |
| 16 | Moresco P, Alboussiére T. Experimental study of the instability of the Hartmann layer. Journal of Fluid Mechanics, 2004, 504(10):167-181 |
| 17 | Lingwood RJ, Alboussiére T. On the stability of the Hartmann layer. Physics of Fluids, 1999, 11(8):2058-2068 |
| 18 | Krasnov D, Zienicke E, Zikanov O, et al. Numerical study of the instability of the Hartmann layer. Journal of Fluid Mechanics, 2004, 504(10):183-211 |
| 19 | Gerard-Varet D. Amplification of small perturbations in a Hartmann layer. Physics of Fluids, 2002, 14(4):1458-1467 |
| 20 | Airiau C, Castets M. On the amplification of small disturbances in a channel flow with a normal magnetic field. Physics of Fluids, 2004, 16(8):2991-3005 |
| 21 | Krasnov D, Zikanov O, Boeck T. Numerical study of magnetohydrodynamic duct flow at high Reynolds and Hartmann numbers. Journal of Fluid Mechanics, 2012, 704(2):421-446 |
| 22 | Davidson PA. An Introduction to Magnetohydrodynamics. Cambridge:Cambridge University Press, 2001:117-119 |
| 23 | Dong S, Krasnov D, Boeck T. Secondary energy growth and turbulence suppression in conducting channel flow with streamwise magnetic field. Physics of Fluids, 2012, 24(7):074101 |
| 24 | 李春曦, 陈朋强, 叶学民. 含活性剂液滴在倾斜粗糙壁面上的铺展稳定性. 物理学报, 2015, 64(1):014702(Li Chunxi, Chen Pengqiang, Ye Xuemin. Stability of surfactant-laden droplet spreading over an inclined heterogeneous substrate. Acta Physica Sinica, 2015, 64(1):014702(in Chinese)) |
| 25 | Luchini P. Reynolds-number-independent instability of the boundary layer over a flat surface:optimal perturbations. Journal of Fluid Mechanics, 2000, 404(2):298-309 |
| 26 | Butler KM, Farrell BF. Three-dimensional optimal perturbations in viscous shear flow. Physics of Fluids A:Fluid Dynamics, 1992, 4(8):1637-1650 |
| 27 | Andersson P, Berggren M, Henningson DS. Optimal disturbances and bypass transition in boundary layers. Physics of Fluids, 1999, 11(1):134-150 |
| 28 | Schmid PJ, Henningson DS. Stability and Transition in Shear Flows. New Yorker:Springer, 2001:515-519 |
| 29 | Reddy SC, Schmid PJ, Baggett JS, et al. On stability of streamwise streaks and transition thresholds in plane channel flows. Journal of Fluid Mechanics, 1998, 365:269-303 |
| 30 | Zikanov O. On the instability of pipe Poiseuille flow. Physics of Fluids, 1996, 8(11):2923-2932 |
| 31 | Gustavsson LH. Energy growth of three-dimensional disturbances in plane Poiseuille flow. Journal of Fluid Mechanics, 1991, 224:241-260 |
 2016, Vol. 48
2016, Vol. 48