直长柱体是众多工程应用中常见的结构型式,如系泊缆绳,石油平台的立管,海洋工程中的各种管线,建筑物和悬索桥等.当来流绕过这种结 构之后会产生非定常尾迹和交替脱落的涡旋,对结构产生非定常流体载荷.结构受此流体载荷激励将发生振动,称之为涡激振动(VIV).特别是,当涡脱落频率接近结构的固有频率时,将发生频率锁定和共振现象.这时,结构振幅和相应的流体载荷也会快速增大,并导致结构发生疲劳破坏,进而威胁整体结构的完整性,甚至人员和生产的安全.因而近半个世纪以来,对钝体结构发生涡激振动的动力学特性进行了大量的研究.相关的综合性报告可以参考相关文献[1, 2, 3, 4].
为了最大程度地降低这种破坏作用或延长结构的使用寿命,近几十年来各国学者和研究人员提出了多种涡激振动的抑制措施或方法.其目的是期望能实现对钝体的尾迹流动或者涡脱落进行干扰,进而降低流体载荷,使柱体的振动频率远离共振频率范围.大多数抑制措施是通过对钝体绕流流动直接干扰的方式实现的,即被动式控制方法.例如,Owen等[5]提出的在柱体表面螺旋形布置鼓包,其减阻率达到了47%;且在特定的扰动强度(或波动强度,定义为扰动波形上波峰波谷间的波高$W$与扰动波长 $\lambda $ 之比,即$W/ \lambda $)下尾迹中检测不到脉动的涡脱落现象.但这种方法的质量阻尼系数较大.宋吉宁等[6]采用在柱体周边等间距布置控制杆,也能起到影响立管的横向振动响应的作用;但其效果会受到海洋生物附着的影响.Korkischko等[7]在结构绕流边界层中布置较细的旋转圆柱以延迟边界层的分离,其减阻率可达到60%.截至目前为止,一般认为在柱体上附加流线型导流罩[8]仍然具有相当优良的水动力特性.这是由于流线形外罩使得结构流线型化,从而延迟了流动分离.此外,分离平板也能有效延迟钝体两侧上下自由剪切层之间的相互作用以及涡脱落的形成[9].然而由于洋流方向是不确定的,因此导流罩和分离板通常都会安装可旋转的装置;这就引起新的动力稳定性问题和工程实用性问题.近年来也有采用在柱体表面刻上螺旋槽(helical grooves)[10]或采用通风裤(ventilated trouser)[11]来抑制结构的涡激振动.螺旋形列板是目前最常用的一种用于干扰展向涡脱落的均匀一致性的装置[12, 13].更多的涡激振动抑制装置可以参考相关的综述文献[14, 15, 16].
近年来,也有研究学者提出了另外一种涡激振动抑制措施,即引入三维几何扰动,如波动状迎风面[17]和整体波动柱体[18, 19, 20]. 这些方法的扰动主要是在流向展向平面内引入的,因而对于流动方向具有敏感性.为了克服这一问题,且避免对预先设计的柱体结构进行改造,借助伯努利方程和引入的几何扰动对流动的影响,人们又提出了一种新型涡激振动抑制措施------在径向展向平面内引入几何扰动,称之为径向扰动[21],如谐波型,圆球型,椭球型,圆锥型,类圆锥型等等.其中对于固定的谐波型扰动柱,前人也分别进行过尾迹测量实验和大涡模拟的数值计算[22, 23, 24],表明在一定的参数范围内谐波型扰动确实能够实现阻力和升力减小.
本文针对圆柱体上附加谐波型和(类)圆锥型两种扰动(相对于直圆柱,这两种柱体分别称之为谐波柱和圆锥柱,或统称为波动柱),分别进行了单摆结构的涡激振动实验研究和柱体结构绕流的水动力数值模拟计算. 探讨了这两种径向扰动的引入导致原先直柱体结构水动力特性发生变化的特点. 研究结果表明:这两种类型的扰动对引入扰动后的波动柱的振幅随来流速度的变化,水动力参数(如升、阻力系数和涡脱落频率)随波动强度、波长、雷诺数变化,及尾迹中的涡脱落模态变化等均表现出相似的规律. 在所研究的雷诺数范围内,能实现升力较大下降(最大升力减小率达到81%),且涡脱落频率随着$W / \lambda $ 增大而逐渐减小, 从而可有效地延迟共振现象的发生,即在结构固有频率不发生显著改变的情况下,只有继续增大来流速度,才可能使得涡脱落频率接近结构固有频率从而发生共振. 也就是说,波动柱导致结构有效避开了在原有共振流速下发生的共振,却在更高流速下才可能发生共振. 可见,本文不仅得到了两种波动柱的水动力学特性,而且提供了一种实用的避免涡激振动或实现涡激振动抑制的工程方法(其中谐波柱已获得国家发明专利).
1 涡激振动实验 1.1 实验装置本次实验的研究目的是为了初步验证所引入的径向扰动对结构发生涡激振动实现抑制这一措施的有效性.实验是在中国科学院力学研究所流固耦合系统力学重点实验室中流固土耦合力学实验系统的循环水槽中进行的.实验装置如图1所示,其中测试段长6 m,宽1 m. 实验测量时水深在0.65 m到0.7 m.通过双向电机控制流动,最大流速达到1 m/s.

|
图1 实验水槽 Fig.1 Circulating water channel |
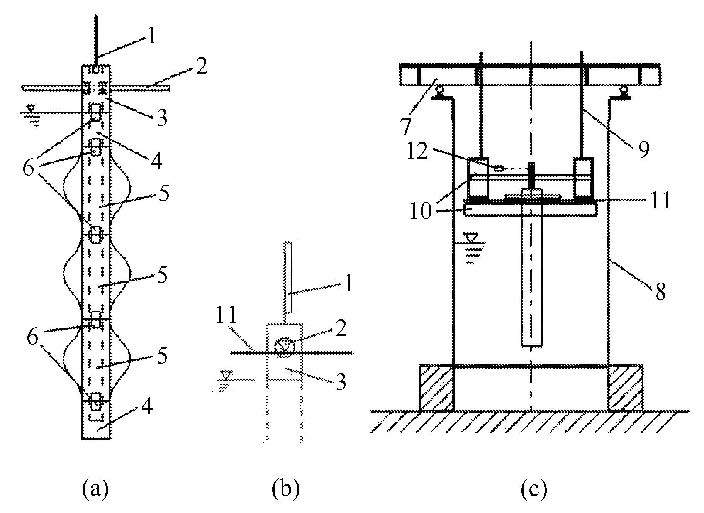
借鉴前人实验装置的设计[25],本次涡激振动实验测量装置如图2所示. 整个摆动系统主要由水下和水上两个部分构成.其中,水上部分包括用于接收由激光位移传感器所发射出激光束的指示臂,支撑实验柱体的等边三角形铁质支架和一段长100 mm的直柱体.支架随着摆动柱体一起旋转,如图2(b)所示. 固定在支架上的柱体将在与来流(与支架轴向平行)垂直的平面内发生摆动;回复力则来自于整个摆动系统的重力.对于水下部分,为了降低波动的自由面和水槽底部的影响,采用了两端均为长100 mm的直柱体.测试部分根据实验情况可调整为直柱体,或者不同扰动强度下的波动柱体;不同分段采用内置螺丝相互联接.来流速度通过放置于柱体前段5 m处的超声波多普勒测速仪进行测量.
|
图2 涡激振动实验装置示意图,(a) 实验用的整个摆动柱体的前视图,(b) 支架侧视图,(c)架设于水槽上方的实验平台,其中1为指示臂,2为等边三角支架,3和4 分别为水上和水下直柱体,5为三段直或波动柱体,6为内置螺丝,7为架于轨道上的横梁,8为水槽,9为长螺杆,10和11分别为水面上方的沉降室框架,12为激光位移传感器 Fig.2 Schematic diagrams of VIV experiments, (a) front view of whole oscillating cylinder in tests, (b)side view of support, (c) experimental platform mounted above the channel, where 1 is the indicating arm, 2 is the equilateral triangle support, 3 and 4 are straight cylinders over and under water respectively, 5 are three segments of straight or wavy cylinder for tests, 6 is the inner screw, 7 is the crossbeam supported on rails, 8 is the channel, 9 is the long screw, 10 and 11 are frames of settling chamber above water, 12 is the laser displacement sensor |
实验对两种不同扰动波型的柱体进行了测量,如图3所示,其中1#、2#、3#为谐波柱,4#、5#、6#为类似圆锥柱. 其中,波型表面上的波峰和波谷分别定义为柱体直径最大和最小处. 柱体材料为铝制.每个具有完整波型的柱体长均为120 mm;因而整个水下实验柱体长度为560 mm. 最小直径为20 mm.3个不同扰动强度分别为0.025,0.05和0.1. 由此得到最大外径分别为26 mm,32 mm和44 mm.值得注意的是,估算雷诺数时采用的是最小直径(以及下文数值模拟中应用的特征长度),是和直圆柱柱体直径$D$相同,而不能采用平均柱体直径;这是由于从工程应用的角度来看,一方面对于预先设计好的立管或者管道结构,这种抑制措施不改动原有结构尺寸或外形;另一方面避免了重新对结构进行设计,如采用平均直径导致直径较小的波谷处需要进行包括强度等的重新设计;因此是作为一种抑制罩的方式进行安装和使用的.测量得到的柱体质量比(整个柱体质量与直柱体排水质量之比)的变化范围从7到10之间.

|
图3 实验柱体,0# 直柱体,1#、 2#、 3# 谐波柱,4#、5#、6# 类似圆锥柱 Fig.3 Cylinders in tests, 0# straight cylinder, 1#, 2#, 3# harmonic cylinders, and 4#, 5#, 6# cone-like cylinders |
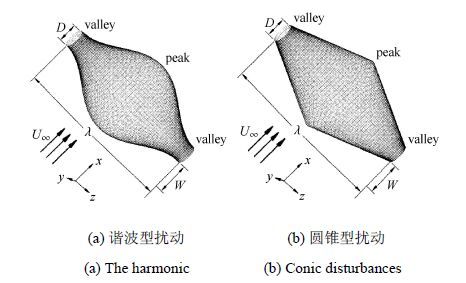
如图4所示,在惯性笛卡尔坐标系($x, y, z)$ (其中$x$向为沿着自由来流的方向,$z$向为沿着柱体轴向的方向,$y$向为垂直于自由来流和柱体轴向的方向)中,不可压缩流体绕过具有两种不同径向扰动的圆截面柱体的流动.由此,波动的几何外形就能采用波长 $\lambda $ 和波高$W$进行数学描述.无量纲的质量连续性方程和纳维-斯托克斯方程为 $$ \nabla \cdot { u} = 0 \tag{1}$$ $$\dfrac{\partial { u}}{\partial t} + ({ u} \cdot \nabla ) { u} = - \nabla p + \dfrac{1}{Re} \nabla ^2{ u} \tag{2}$$ 式中,${ u}=(u, v, w)$为速度矢量,$p$为静态压力,$t$为时间,$Re$为雷诺数,定义为$U_{\infty }D/ u $,其中$U_{\infty }$为自由来流速度,$D$为直圆柱的柱体直径,$ u $为流体运动黏性系数,$ \nabla $为梯度算子.
|
图4 圆截面波动柱体绕流示意图 Fig.4 Schematics of flows past a circular-section cylinder |
由于当$Re$较高时钝体结构尾迹中发生湍流转捩,因此除了$Re=100$时采用层流模型进行计算外,当$Re$高于100以上时均采用大涡模拟进行计算(其中子网格模型采用Smagorinsky-Lilly模型).
2.2 计算方法计算边界条件分别为:假设流动沿展向呈周期性,因而展向设置为周期性边界条件;计算域入口处为自由来流速度$U_{\infty }$; 出口处采用简单的无反射出流边界条件;计算域$y$向两侧采用自由滑移边界条件;柱体壁面采用无滑移速度边界条件.
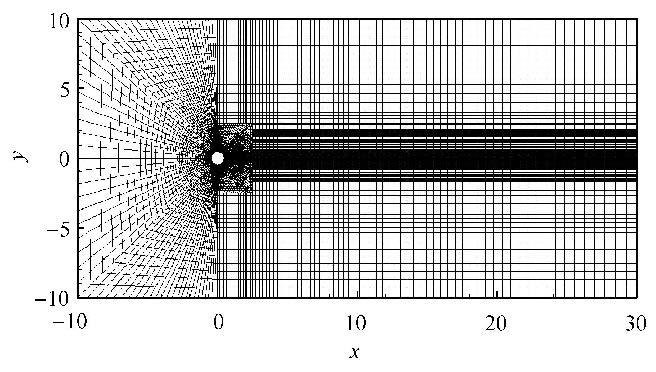
由于采用了六面体网格,因此本文只给出了在$(x, y)$平面内的计算域和网格布置,如图5所示. 无量纲计算域大小为 $40 \times 20 ( x\times y)$. 无量纲展向计算域大小为一个波长 $\lambda / D$.平面内网格布置总数大约为17 600个,主要在柱体壁面及尾迹中心平面附近比较密集,其他区域则逐渐稀疏.展向每单位长度内均匀布置5个网格,则网格总数为$5 \lambda / D$个.
|
图5 $(x, y)$平面内无量纲计算域大小和网格布置 Fig.5 Non-dimensional computational domain and grids in ($x, y)$ plane |
无量纲计算时间为0.01或0.005;非定常项采用二阶时间精度的离散格式;连续性方程收敛误差控制在10$^{-3}$以内.
计算采用Fluent软件;压力-速度耦合应用SIMPLEC算法;压力方程采用二阶空间离散格式,应用W型或柔性多重网格进行计算;动量方程采用有界中心差分格式 (bounded central differencing scheme).
为了检验计算方法的有效性,对直圆柱绕流在不同雷诺数和不同计算波长(4,6和8)下进行了数值模拟.如表1所示,对比了计 算得到的水动力学参数(如平均阻力系数$C_{\rm D\_M}$和无量纲涡脱落频率$St$)和实验值[14],表明两者结果吻合较好.
| 表1 直圆柱的数值计算得到的平均阻力系数和$St$和实验值的比较 Table 1 Comparison of the mean drag coefficient and Strouhal number between computations of the flow past a straight circular cylinder and experimental results |
由于展向网格数也涉及到计算精度和计算时间或代价,尤其是高雷诺数时,因此选取一个算例(圆锥柱$Re=10^{5}$,$\lambda /D=4$和$W / \lambda =0.05$)进行展向网格加密计算,即展向网格总数为$10 \lambda / D =40$个.模拟计算得到未加密网格平均阻力系数$C_{\rm D\_M}$和$St$数分别为1.192和0.162;加密后则分别变为1.138和0.173.这表明原有未加密的网格总数是足够的,能够获得较准确的水动力参数;而目前网格加密对结果的影响不大,说明起主要作用的仍然是低波数模态,而激发的高波数模态主要对瞬时值和剖面或局部流动起重要影响.因此可以采用当前未加密网格进行高雷诺数水动力参数的计算.
3 结果分析 3.1 涡激振动实验的水动力响应分析首先有必要对单摆结构的阻尼水平进行估算;分析得到整个系统的无量纲阻尼系数为7$\times $10$^{-4}$,说明阻尼非常小,或对实验结果影响非常小[21].
通过在静水中结构的自由振动实验,测量了结构的固有频率.结果表明:无论是直柱体还是波动柱体,在不同扰动强度的情况下,结构固有频率几乎保持不变,均为0.55$\sim $0.56 Hz.
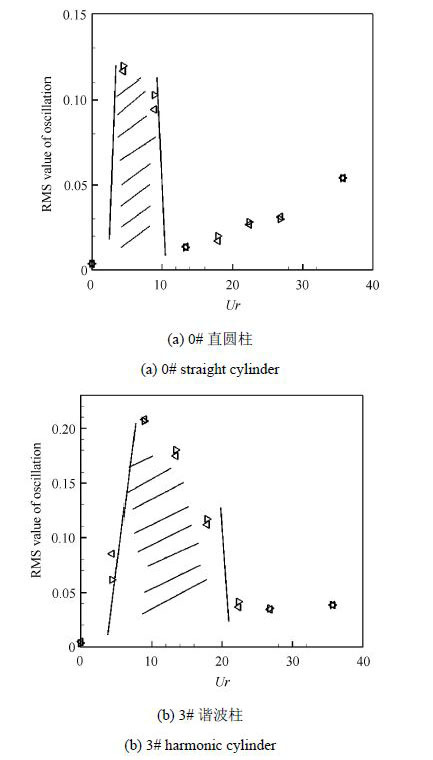
实验时,来流速度从5 cm/s逐渐增大到40 cm/s, 增大间距为5 cm/s;从而实验雷诺数是在1 000到8 000之间变化.当流速为5 cm/s时直圆柱的涡脱落频率恰好和结构固有频率相近,因此流速从5 cm/s开始结构就会发生涡激振动;此时直圆柱的共振振幅也达到极大值,如无量纲均方根值为0.12,如图6(a)所示.测量得到的波动柱体振幅随减缩速度$Ur$的变化,典型地如图6(b)所示.其中可以看出3点:(1)在直圆柱开始发生共振的流速下,即5 cm/s ($Ur =4.46$),扰动柱体的振幅确实显著下降,如图6(b)中均方根值为0.062到0.085;(2)在更高的流速下,结构共振振幅则显著增大,甚至超过直柱体的情况,如图6(b)中均方根值在10 cm/s ($Ur =8.93$)时达到极大值0.207;(3)扰动柱共振范围显著扩大,主要是向高速区域延拓.
|
图6 0#直圆柱和3#谐波柱脉动振幅均方根值随减缩速度的变化,其中阴影区域是所估计发生同步的区域,且$ \triangleright $和$ \triangleleft $分别表示减缩速度逐渐增大和减小 Fig.6 Variation of RMS amplitude of 0# straight circular cylinder and 3# harmonic cylinder with respect to the reduced velocity, where the shadow region denotes the estimation of occurrence of synchronization, and $ \triangleright $ and $ \triangleleft $ denote the increasing and decreasing reduced velocities |
通过频谱分析发现,在共振发生的流速范围内,结构振动频率只有一个,且随着减缩速度增大而逐渐增大.更多的结果,包括 其他柱体振幅的变化和频谱的小波分析,可以参见文献 [26].
然而,由于刚性的单摆结构毕竟和两端固定或一端呈悬链状态的柔性立管有本质上的区别,因此为了更好地了解这种新设计的涡激振动抑制罩的抑制效果,仍然有必要研究其水动力特性,因而对这种带有抑制罩的波动柱结构进行绕流数值模拟.
3.2 波动柱绕流数值模拟计算由于波动柱的几何外形主要由两个参数决定,即波长 $\lambda $ 和波高$W$,因此可以组成两个无量纲控制参数,即无量纲波长 $\lambda /D$和波动强度$W / \lambda $.因而控制波动柱体绕流的参数主要有3个:$Re$,$\lambda /D$和$W / \lambda $.选取如下一系列的计算参数进行研究:$Re=10^{2}$,$10^{3}$,$10^{4}$和$10^{5}$; $\lambda /D =4$,6和8;$W / \lambda =0.012 5$,0.025,0.05,0.1和0.2.具体计算中,分别保持特征速度和特征尺度不变,且改变计算的流体运动黏性系数,扰动波长和扰动波高. 另外,当$W/ \lambda =0$时,可以理解为相同直径和展向长度的直圆柱.
通过对谐波型和圆锥型两种波动柱在$Re=100$时进行了数值模拟,目的是研究这两种扰动在水动力特性上的相同点和不同点.如图7和图8所示,随$W / \lambda $ 和 $\lambda /D$的变化,谐波柱和圆锥柱的$C_{\rm D\_M}$,$C_{\rm L\_RMS}$ (脉动升力系数)和$St$ 总体变化趋势基本一致. 例如,$C_{\rm D\_M}$均随着波动强度的增大而增大,且在 $\lambda /D =6$和$W / \lambda =0.025$时均出现阻力系数极小值情况;$C_{\rm L\_RMS}$在波长为6和8时均是先快速减小,随后再缓慢增加,因而在$W / \lambda =0.025$和0.05达到局部极小值;$St$几乎都是随着波动强度增大而逐渐减小.
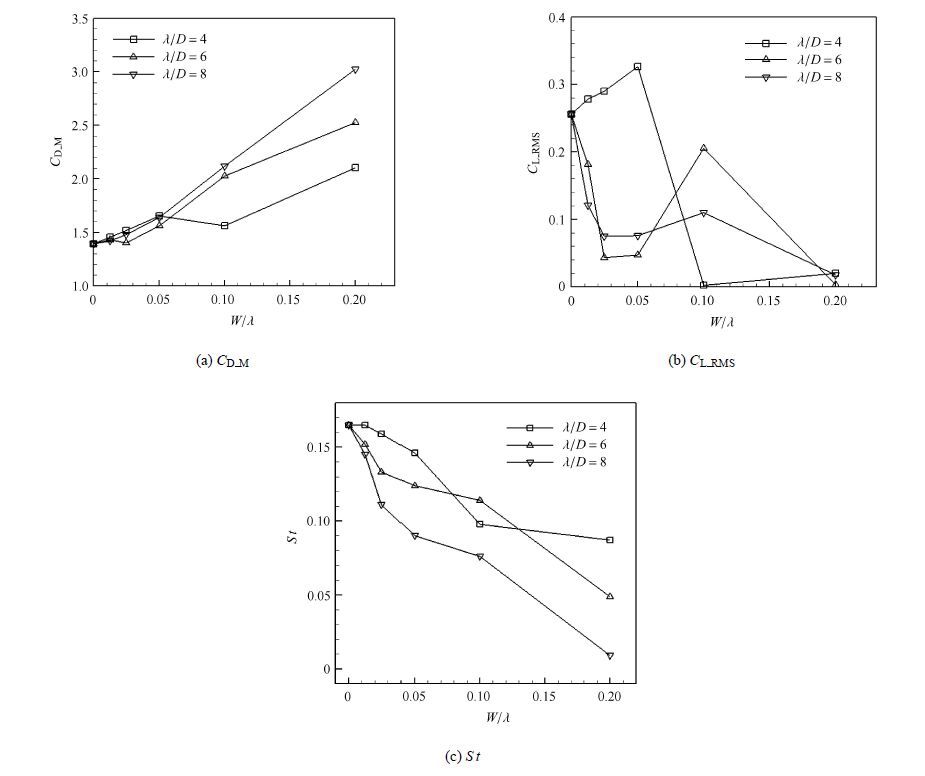
|
图7 $Re=100$时谐波柱的$C_{\rm D\_M}$,$C_{\rm L\_RMS}$和$St$随$W/\lambda $ 和 $\lambda /D$的变化 Fig.7 Variations of $C_{\rm D\_M}$, $C_{\rm L\_RMS}$ and $St$ for the harmonic cylinder with respect to $W/\lambda $ and $\lambda /D$ at $Re=100$ |
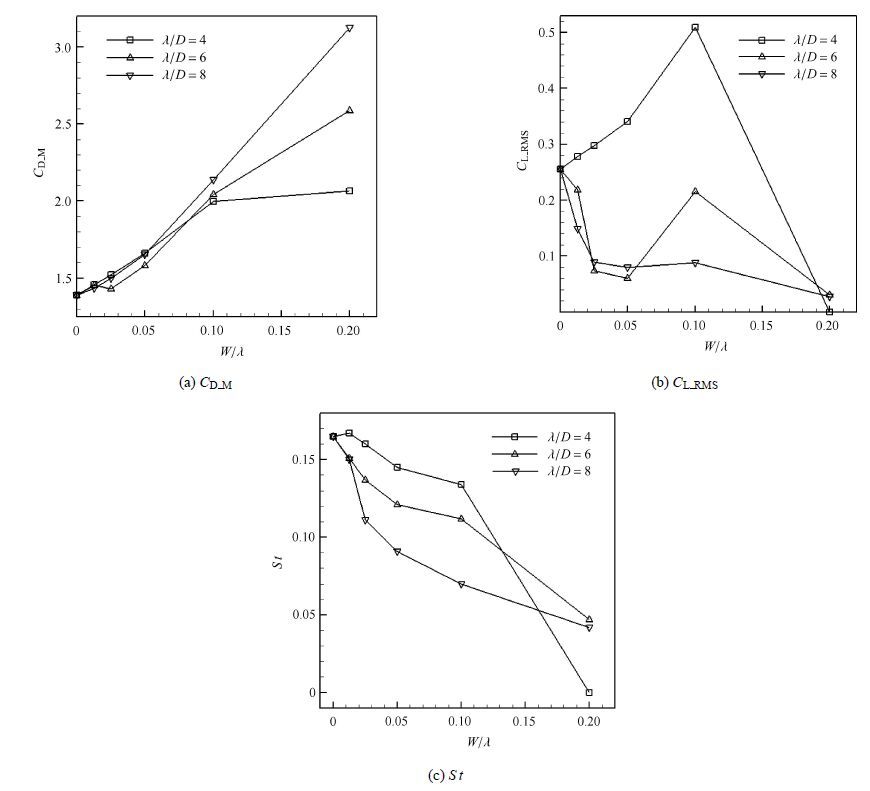
|
图8 $Re=100$时圆锥柱的$C_{\rm D\_M}$,$C_{\rm L\_RMS}$和$St$随$W/\lambda $和$\lambda /D$的变化 Fig.8 Variations of $C_{\rm D\_M}$, $C_{\rm L\_RMS}$ and $St$ for the conic cylinder with respect to $W/\lambda $ and $\lambda /D$ at $Re=100$ |
此外,通过对涡脱落模态的分析,将扰动柱尾迹中涡脱落模态分成3类:弱扰动(尾迹中仍然以交替脱落的展向涡为主,即对原有直圆柱体中经典的卡门涡脱落的影响程度较小,且出现沿下游快速衰减的流向和垂向涡量),中扰动(虽然尾迹中仍然存在交替脱落的展向涡,然而流向和垂向涡对显著增强,导致展向涡沿流向或展向出现显著的扭曲波动),和强扰动(尾迹中或者涡脱落完全受到抑制,或者涡脱落模态完全不同于原先的卡门涡,如云片状涡或$\Omega $ 型涡)[27]. 由此得到参数空间($W/\lambda $,$\lambda /D$)中流动特征性态归纳图[28] (修正了原图的一个错误),如图9所示.更多的其他流动相似特征,如表面涡量分布,柱体两侧剪切层的展向波动变化,表面压力系数变化等,请参考文献 [27, 29].
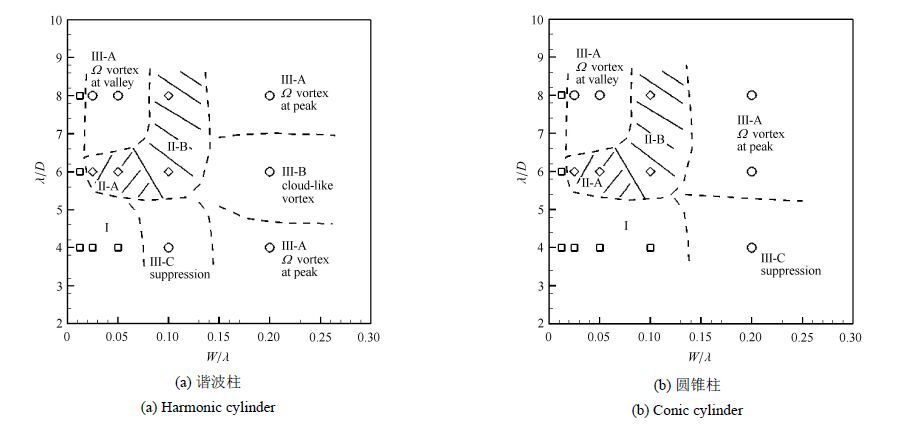
|
图9 $Re=100$时随$W/\lambda $和$\lambda /D$变化的谐波柱和圆锥柱绕流流动归纳图,其中$\square $为区域Ⅰ(弱扰动),◇为区域Ⅱ(中扰动)和$\bigcirc $为区域Ⅲ(强扰动) Fig.9 Summary of flows past the harmonic and conic cylinders varied with $W/\lambda $ and $\lambda /D$ at $Re=100$, where $\square $ denotes the region Ⅰ (weak disturbance), ◇ the region Ⅱ (moderate disturbance) and $\bigcirc $ the region Ⅲ (strong disturbance) |
根据上述分析说明谐波型扰动与圆锥型扰动对流动性态(如涡脱落模态)和水动力参数等的影响是相似的;因此考虑到工程实际应用时的简便性和可操作性,采用圆锥型结构更具有实用价值. 下面针对这种扰动型式作进一步的计算和分析.
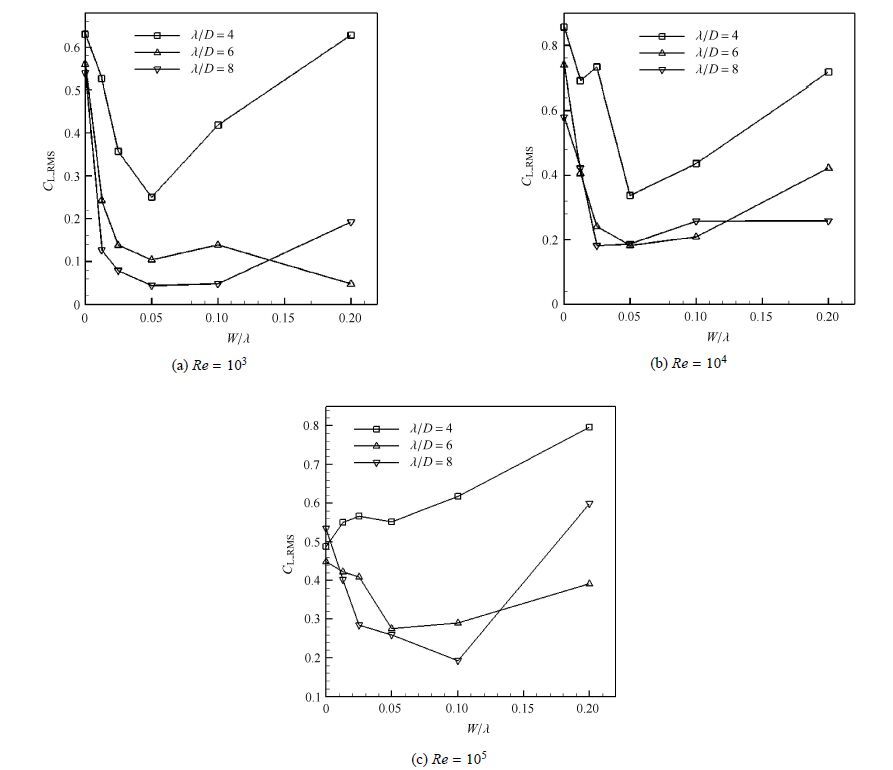
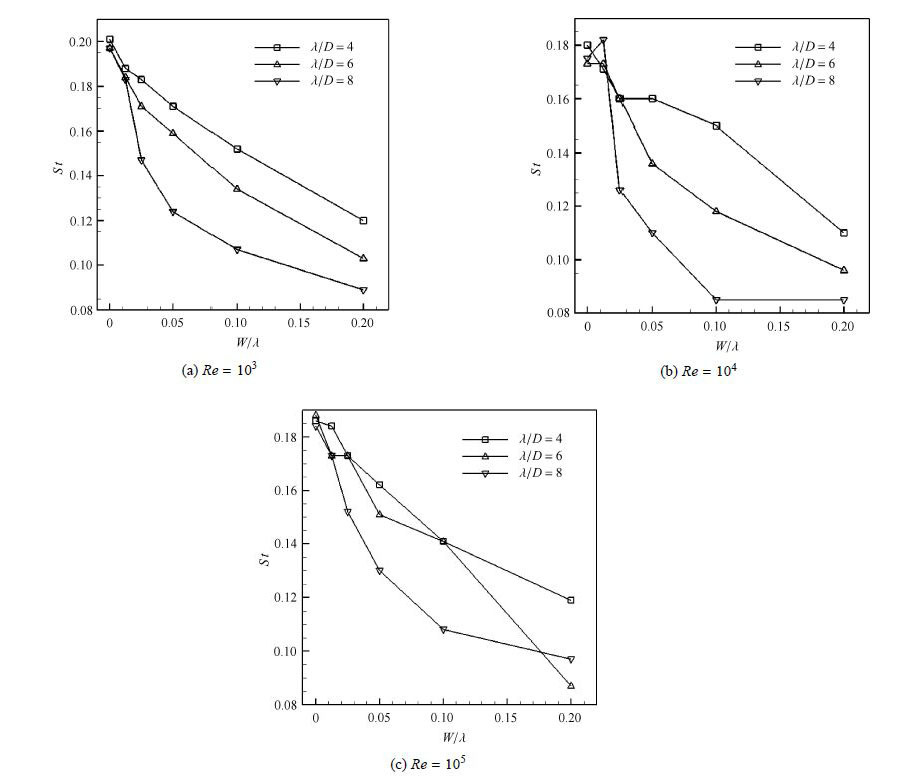
当$Re$为10$^{3}$,10$^{4}$和10$^{5}$时,圆锥柱的水动力参数,如平均阻力系数,脉动升力系数和涡脱落频率,随$\lambda / D$和$W/\lambda $变化分别如图10,图11和图12所示.结合图8的$Re=10^{2}$时的结果可以看出:(1)目前计算的$Re$下,一般阻力系数均是随着$W /\lambda $ 增大而逐渐增大;然而在较低的$W / \lambda $ 时($ ≤ 0.05$)均出现阻力局部极小值;(2)当$Re=10^{2}$和$10^{5}$且$\lambda / D=4$时脉动升力系数随着$W/\lambda $ 增大而逐渐增大,且都大于直圆柱时的情况;其他情况下,升力都是先是快速减小,达到极小值后再逐渐增大. 结合阻力的变化规律,可以得到当前$Re$范围内,参数$\lambda / D=6$和$W/ \lambda =0.025$或0.05时,阻力略有减小 (最大减阻率达到11%)或者有所增加(最大增阻率达到14%)的情况下,实现升力较大下降(最大升力减小率达到81%);(3)涡脱落频率也几乎都是随着$W/\lambda $增大而逐渐减小的;这一特点导致,在结构固有频率不发生显著改变的情况下,只有继续增大来流速度,才可能使得涡脱落频率接近结构固有频率从而发生共振;换句话说,波动柱导致结构有效避开了原有共振流速下发生共振,却在更高流速下可能发生共振;这一结论和先前单摆振动试验结论完全一致.
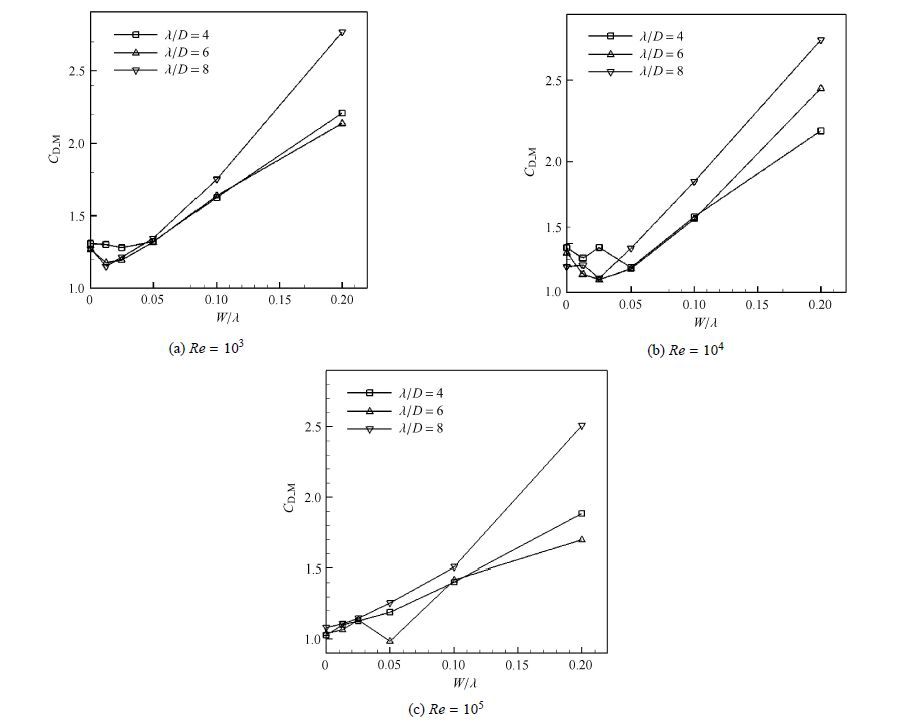
|
图10 不同$Re$下圆锥柱$C_{\rm D\_M}$随$\lambda / D$和$W/\lambda $变化 Fig.10 At different Reynolds numbers, $ C_{\rm D\_M}$ of the conic cylinder varies along $\lambda / D$ and $W/\lambda $ |
|
图11 不同$Re$下圆锥柱$C_{\rm L\_RMS}$随 $\lambda / D$和$W/\lambda $ 变化 Fig.11 At different Reynolds numbers, $C_{\rm L\_RMS}$ of the conic cylinder varies along $\lambda / D$ and $W/\lambda $ |
|
图12 不同$Re$下圆锥柱$St$随$\lambda / D$和$W/\lambda $变化 Fig.12 At different Reynolds numbers, $St$ of the conic cylinder varies along $\lambda / D$ and $W/\lambda $ |
本文通过模型试验和数值模拟计算,研究了用以实现涡激振动抑制、具有径向扰动的圆截面柱体的水动力特性. 其中,模型试验主要针对具有谐波型和类圆锥型两种扰动的波动柱进行单摆结构的涡激振动试验;数值模拟则针对一系列参数(如$Re$,$\lambda /D$和$W/\lambda $)的变化下带有谐波型和圆锥型扰动的柱体绕流进行了计算. 获得了如下的一些结论:
(1)单摆试验结果表明,无论谐波型还是类圆锥型扰动,都能在直柱体开始发生共振的流速下实现扰动柱的振幅相比直圆柱时的显著减小;然而随着流速增大,扰动柱的振幅则逐渐增大,并超过了直圆柱的情况;共振范围向较高流速扩展;单一的结构共振频率随着减缩速度增大而逐渐增大;
(2)在$Re=100$时,谐波柱和圆锥柱的绕流数值模拟结果表明,定性上来说,阻力、升力以及涡脱落频率随波动强度和波长的变化是一致的;从涡脱落模态来看,两者对流动的干扰也具有相似性;
(3)当$Re$从10$^{2}$逐步增大到10$^{5}$,圆锥柱的平均阻力系数一般随着波动强度增大而逐渐增大,而脉动升力系数多数情况下先是逐渐减小而后再增大(个别参数下脉动升力系数是逐渐增大的除外);
(4)引入扰动后,尾迹中涡脱落频率随着波动强度增大一般是逐渐减小的,这就导致结构可能在更高流速下发生共振;这一特点和单摆结构的涡激振动实验结论相符合.
结合工程实际应用情况,根据上述的研究结果,提出如下几点建议:(1)采用圆锥型扰动作为涡激振动抑制罩的型式;(2)在一定的扰动强度和波长参数范围内,阻力和升力均存在局部极小值现象,因而可以据此优化圆锥型结构,设计合适的几何控制参数;(3)由于扰动导致涡脱落频率减小,因此在结构固有频率不变的前提下,只有提高来流速度才可能使得涡脱落频率增大,从而接近结构固有频率并导致涡激振动的现象出现,因而工程设计时建议选取较高流速的来流工况.
在此研究基础之上,后期将开展相关的涡激振动实验,模拟柔性立管两端固定或者一端固定一端自由悬垂或悬链状态下,对增加圆锥型涡激振动抑制罩后的柔性结构进行水动力特性研究.
| 1 | Sarpkaya T. A critical review of the intrinsic nature of vortexinduced vibrations. J Fluids Struct, 2004, 19:389-447 |
| 2 | Williamson CHK, Govardhan R. Vortex-induced vibrations. Annu Rev Fluid Mech, 2004, 36:413-455 |
| 3 | Williamson CHK, Govardhan R. A brief review of recent results in vortex-induced vibrations. J Wind Eng Ind Aerodyn, 2008, 96:713-735 |
| 4 | Gabbai RD, Benaroya H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J Sound Vib, 2005, 282:575-616 |
| 5 | Owen JC, Bearman PW, Szewczyk AA. Passive control of VIV with drag reduction. J Fluids Struct, 2001, 15:597-605 |
| 6 | 宋吉宁,吕林,张建侨等. 三根附属控制杆对海洋立管涡激振动抑制作用实验研究. 海洋工程, 2009, 27(3):23-29(Song Jining, Lv Lin, Zhang Jianqiao, et al. Experimental investigation of suppression of vortex-induced vibration of marine risers by three control rods. Ocean Eng, 2009, 27(3):23-29(in Chinese)) |
| 7 | Korkischko I, Meneghini JR. Suppression of vortex-induced vibration using moving surface boundary-layer control. J Fluids Struct, 2012, 34:259-270 |
| 8 | Lee L, Allen DW. The dynamic stability of short fairlings. Offshore Tech. Conf. Houston, Texas, USA, 2005, OTC-17125 |
| 9 | Assi, GRS, Bearman PW, Kitney N. Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J Fluids Struct, 2009, 25:666-675 |
| 10 | Huang S. VIV suppression of a two-degree-of-freedom circular cylinder and drag reduction of a fixed circular cylinder by use of helical grooves. J Fluids Struct, 2011, 27:1124-1133 |
| 11 | King R, Brown A, Braaten H, et al. Suppressing full-scale riser VIV with the VT suppressor. ASME 2013, 32nd Int. Conf. Ocean, Offshore and Arctic Eng. OMAE 2013, Nantes, France, June 9-14, 2013, American Society of Mechanical Engineers. OMAE2013-11642 |
| 12 | Korkischko I, Meneghini JR. Experimental investigation of flowinduced vibration on isolated and tandem circular cylinders fitted with strakes. J Fluids Struct, 2010, 26:611-625 |
| 13 | 杨加栋,张晓灵,杜宝银等. 螺旋列板-深水立管涡激振动抑制装置. 海洋技术. 2010, 29(4):88-92(Yang Jiadong, Zhang Xiaoling, Du Baogen, et al. Helical strakes-vortex induced vibration suppression devices of deepwater risers. Ocean Technology, 2010, 29(4):88-92(in Chinese)) |
| 14 | Sarpkaya T, Isaacson M. Mechanics of Wave Forces on Offshore Structures. New York, USA:Van Nostrand Reinhold Company, 1981 |
| 15 | Kumar RA, Sohn CH, Gowda BHL. Passive control of vortexinduced vibrations:an overview. Recent Patents on echanical Engineering, 2008, 1:1-11 |
| 16 | 吴浩,孙大鹏. 深海立管涡激振动被动抑制措施的研究. 中国海洋平台, 2009, 24(4):1-8(Wu Hao, Sun Dapeng. Study of suppression measures for vortex-induced vibration of the deepwater riser. China Offshore Platform, 2009, 24(4):1-8(in Chinese)) |
| 17 | Bearman PW, Owen JC. Reduction of bluff-body drag and suppression of vortex shedding by the introduction of wavy separation lines. J Fluids Struct, 1998, 12:123-130 |
| 18 | Owen JC, Szewczyk AA, Bearman PW. Suppressing Kármán vortex shedding by use of sinuous circular cylinders. Bulletin of the American Physcial Society, 1999, 44:124 |
| 19 | Darekar RM, Sherwin SJ. Flow past a square-section cylinder with a wavy stagnation face. J Fluid Mech, 2001, 426:263-295 |
| 20 | Lin LM, Ling GC,Wu YX. Mechanism responsible for the complete suppression of Kármán vortex in flows past a wavy square-section cylinder. Chinese Physcis Letters, 2010, 27:034702 |
| 21 | Lin LM, Zhong XF, Wu YX. Experimental investigation of a new device in suppressing vortex-induced vibrations of a circular cylinder. Proc. 21st Int. Offshore and Polar Eng. Conf., Maui, Hawaii, USA, ISOPE2011, 2011:1283-1288 |
| 22 | Zhang W, Daichin, Lee SJ. PIV measurements of the near-wake behind a sinusoidal cylinder. Exp Fluids, 2005, 38:824-832 |
| 23 | Lam K, Lin YF. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number. Int J Heat Fluid Flow, 2008, 29:1071-1088 |
| 24 | Lam K, Lin YF. Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers. J Fluid Mech, 2009, 620:195-220 |
| 25 | Balasubramaian S, Skop RA, Haan J, et al. Vortex-excited vibrations of uniform pivoted cylinders in uniform and shear flow. J Fluid Struct, 2000, 14:65-85 |
| 26 | Lin LM, Zhong XF, Wu YX. Vortex-induced vibrations of a circular cylinder with different geometric disturbances. Proc. 22nd Int. Conf. Offshore and Polar Eng. Conf. Rhodes, Greece, ISOPE2012, 2012:623-629 |
| 27 | Lin LM, Zhong XF, Wu YX. Flow around a circular cylinder with radial disturbances at a low Reynolds number. Proc. 23rd Int. Off-shore and Polar Eng. Conf. Anchorage, Alaska, USA, ISOPE2013, 2013:387-394 |
| 28 | Lin LM, Zhong XF, Wu YX. The drag, lift and Strouhal number of a circular-section cylinder with a conic disturbance at subcritical Reynolds numbers. Proc. ASME 2014 33rd Int. Conf. Ocean, Off-shore and Arctic Eng. OMAE2014, San Francisco, California, USA, 2014, OMAE2014-23017 |
| 29 | Lin LM, Zhong XF, Wu YX. Characteristics for a flow past a circular cylinder with two types of radial disturbances at Re=100. Advanced Materials Research, 2014, 871:107-114 |
 2016, Vol. 48
2016, Vol. 48