2. 海军装备研究院, 北京 100161;
3. 中国船舶及海洋工程设计研究院, 上海 200011;
4. 高新船舶与深海开发装备协同创新中心, 上海 200240
流场作用在柔性立管来流方向(IL)上的阻力可分解为恒定阻力与零均值的周期性振荡阻力,此恒定阻力即为立管顺流向上的平均阻力.平均阻力会导致立管在顺流向上发生恒定弯曲变形,而周期性振荡阻力则会导致立管在顺流向上发生涡激振动(VIV)[1].涡激振动会对立管造成严重的疲劳损 伤[2, 3, 4, 5, 6, 7, 8, 9, 10, 11].平均阻力主导着立管的结构强度,在立管的强度设计与校核中,通常采用莫里森公式计算立管的平均阻力.在利用莫里森公式计算立管阻力时,阻力系数的选取对计算结果至关重要,当前各类规范中使用的阻力系数均是通过刚性圆柱体的水池拖曳试验获得的.然而近年来的研究表明,当柔性立管发生涡激振动时,涡激振动会对立管的阻力系数产生放大效应,使得柔性立管的阻力系数不再为一常数,并且大于1.2[12, 13, 14].因此研究涡激振动发生时柔性立管的阻力特性成为当前深水柔性立管结构设计中的一个重要问题.
目前用于研究涡激振动发生时柔性立管阻力特性的方法主要有计算流体力学方法以及水池模型试验.计算流体力学方法是研究涡激振动这 种复杂流固耦合问题的理想方法[15, 16].已有的研究表明,基于三维大涡模拟方法进行的模拟结果,可以很好地与水池模型试验结果相吻合[17].很多研究者采用计算流体力学方法对立管的涡激振动进行了研 究[18, 19, 20, 21, 22].然而计算流体力学方法对流场和结构的网格质量要求十分精细,其计算量特别巨大,即便是一个6 m长的试验立管,每个流速工况计算都需耗时数月[23],因而目前采用计算流体力学方法研究涡激振动发生时柔性立管的阻力特性是不太可能实现的.鉴于计算流体力学方法的局限性,研究者通常采用水池模型试验的方法研究柔性立管的阻力特性.然而在水池模型试验中,直接测量立管各横截面处的阻力存在很大困难.因此,研究者通常在立管模型的端部安装力传感器来获得立管模型的总阻力[13, 14, 24, 25].为了揭示阻力沿立管模型轴向的分布特性,有研究者对剪切流中竖直顶张力立管模型试验中测得的立管顺流向与横流向的应变信号进行二次积分,得到立管模型的位移信息后,利用有限元方法间接计算作用在立管上的流体力,包括顺流向上的阻力和横流向上的升力[26].
此外,在如何考虑涡激振动对阻力系数的放大效应方面,一些研究者通过模型试验的方法对此作了研究.文献[13]通过试验发现柔性立管的阻力系数与立管横流向涡激振动位移均方根存在非线性关系[13],而文献[27]则认为阻力系数与立管横流向涡激振动位移均方根存在简单的线性关系[27].此外,文献[14]基于阶梯流中柔性立管涡激振动试验的结果发现:阻力系数为立管横流向涡激振动位移标准差的2次函数[14].在上述各模型试验中,最大雷诺数不超过$3\times 10^4$,然而真实环境中立管的雷诺数在10$^{5}$量级或者更高.雷诺数的差异对涡激振动的放大效应到底有什么样的影响,如何在计及这些影响的前提下,去预报真实雷诺数下涡激振动发生时柔性立管的阻力系数,成为一个值得研究的问题.
本文通过旋转塔架带动立管模型在水池中旋转运动形成相对的剪切来流的方法,研究线性剪切流下涡激振动发生时柔性立管的阻力特性以及涡激振动对阻力系数的放大效应,试验中最大雷诺数达$1.2\times 10^5$.文中基于光纤光栅应变传感器测得的立管模型顺流向上应变信息,采用梁复杂弯曲理论计算立管的平均阻力,并根据莫里森公式计算立管模型在不同流速下的阻力系数,分析阻力系数随雷诺数的分布特性以及涡激振动对阻力系数的影响.最后基于本文试验结果提出适用于估算高雷诺数下涡激振动发生时柔性立管阻力系数的经验公式.
1 试验装置剪切来流的模拟采用T型塔架在水池中绕中心轴做圆周运动的方法来实现. 如图1所示:将试验立管安装在T型塔架上,利用塔架带动试验立管在水池中旋转,造出剪切的相对来流. 本文试验中,采用铰接的方式将立管的顶端与预张力施加装置相连,底端与旋转塔架的中心轴相连,立管与水面的夹角为16$^{\circ}$. 预张力施加装置通过驱动模块的控制箱来控制,可以给立管施加$0\sim 10$ kN的预张力. 试验中通过旋转塔架带动立管模型在水池中旋转运动,从而形成相对的剪切来流. 图2为本文试验装置图. 需要注意的是,在现场试验中,只采集立管模型绕中心轴运动的第一个周期内的数据,因此试验结果不会涉及到前一个运动周期的流场对后一个运动周期的流场的干扰问题.

|
图1 剪切流试验装置示意图 Fig.1 Sketch of test set-up in shear flow |

|
图2 剪切流试验装置 Fig.2 Set up for VIV test in shear current |
试验中所使用的立管模型为缩尺模型,模型的结构外径为30 mm,有效长度为6.75 m,细长比为225.为了保证立管模型表面的 光滑性,在模型的外表面覆盖有厚度为0.5 mm的热缩管.因此,实际试验中立管模型的水动力直径为31 mm. 立管模型具体参数见表1.
| 表1 立管模型基本参数 Table 1 Basic structural parameters of the riser models |
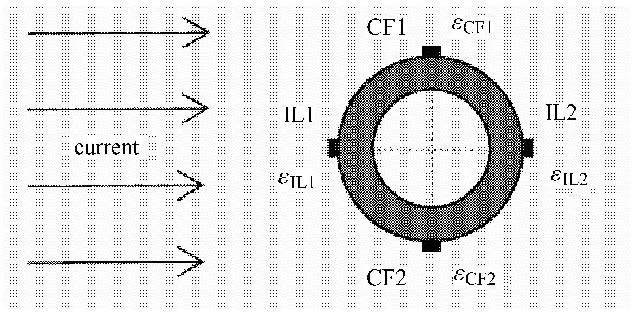
立管模型表面布置有88个光纤光栅应变传感器,分别布置于模型的CF1,CF2, IL1以及IL2四个方向,用于测量模型在此4个方向上的应变,即${\varepsilon _{{\rm{CF1}}}}$, ${\varepsilon _{{\rm{CF2}}}}$, ${\varepsilon _{{\rm{IL1}}}}$和${\varepsilon _{{\rm{IL2}}}}$, 如图3所示. 其中CF1和CF2方向上的传感器分别为19个,IL1和IL2方向上的传感器分别为25个. CF与IL方向上的传感器均均匀分布,相邻两测点的间距分别为0.34 m和0.255 m. 光纤光栅传感器的采样频率为250 Hz.
|
图3 立管模型表面光纤光栅传感器布置方式 Fig.3 Arrangement of strain gauges on the surface of the riser model |
当旋转塔架带动立管模型在水池中旋转运动时,相对剪切来流在立管模型顺流面产生的平均阻力会使得立管模型在其顺流面内发生恒定弯曲变形,从而使得立管模型偏离其原始位置,此恒定弯曲变形在本文中称为初始弯曲,立管模型发生初始弯曲后的位置称为初始位置. 立管模型初始弯曲示意图,如图4所示.图中坐标系的原点位于立管模型的顶端,坐标系的 $x$轴沿立管模型的轴向方向,坐标系的$oxy$面为立管模型的顺流面.

|
图4 立管模型初始弯曲 Fig.4 Initial bending of riser model |
由于试验中立管模型两端简支且承受预张力,因此立管模型的初始弯曲可以看作为梁复杂弯曲. 根据梁复杂弯曲理论,立管初始弯曲的控制方程如下[28] $$ EI\frac{{{\partial ^4}w(x)}}{{\partial {x^4}}} - \bar T\frac{{{\partial ^2}w(x)}}{{\partial {x^2}}} = {f_{\rm{d}}}(x)\tag{1}$$ 其中,$EI$为立管模型的弯曲刚度,$w(x)$为立管模型轴向$x$点处的初始弯曲位移,$f_{\rm d}(x)$为立管模型轴向$x$点处的平均阻力,$\bar T$为立管模型两端的平均张力.
根据梁弯曲理论,立管初始弯曲位移与初始弯曲应变有如下关系 $$ \frac{{{\partial ^2}w(x)}}{{\partial {x^2}}} = - \frac{{{\varepsilon _{\rm{B}}}(x)}}{R} \tag{2}$$ 其中,$R$为立管模型半径,${\varepsilon _{\rm{B}}}(x)$为立管模型外表面处由初始弯曲引起的弯曲应变,本文中称为初始弯曲应变.
由式(1)和式(2)可以得到用于计算立管模型平均阻力$f_{\rm d}(x)$的公式 $$ {F_{\rm{d}}}(x) = - \frac{{EI}}{R}\frac{{{\partial ^2}{\varepsilon _{\rm{B}}}(x)}}{{\partial {x^2}}} + \frac{{\bar T}}{R}{\varepsilon _{\rm{B}}}(x) \tag{3}$$
当由式(3)得到沿立管模型轴向分布的平均阻力$f_{\rm d}(x)$后,即可根据莫里森公式得到立管模型各横截面处的阻力系数$C_{\rm d}(x)$ $$ C_{\rm d}(x)=\dfrac{2f_{\rm d}(x)}{\rho DU (x) | U(x)|} \tag{4}$$ 其中,$\rho$为流体密度,$D$为立管模型的水动力直径,$U(x)$ 为管模型轴向$x$点处的来流速度,式中的$U(x)|U(x)|$项表示阻力和来流同向.
将立管模型的阻力系数$C_{\rm d}(x)$在整个立管上进行平均,可得到立管模型平均阻力系数$C_{\rm D}$ $$ C_{\rm D}=\dfrac 1L \int^L_0 C_{\rm d} (x) d x \tag{5}$$ 其中,$L$为立管模型的长度.
2.2 初始弯曲应变与涡激振动弯曲应变试验中通过布置在立管模型表面处上的光栅光纤应变片来测量模型顺流向上迎流面和背流面各测点处的应变$\varepsilon_{\rm IL1}$和$\varepsilon_{\rm IL2}$的时历信息. 应变$\varepsilon_{\rm IL1}$和$\varepsilon_{\rm IL2}$可以表示如下 $$ \left.\!\! \varepsilon_{\rm IL1} =\varepsilon_{\rm T}-\varepsilon_{\rm B}-\varepsilon_{\rm IL} \\ \varepsilon_{\rm IL2} =\varepsilon_{\rm T}+\varepsilon_{\rm B}+\varepsilon_{\rm IL} \!\! \right\} \tag{6}$$ 其中,$\varepsilon_{\rm B}$为初始弯曲引起的模型外表面处的初始弯曲应变,$\varepsilon_{\rm IL}$ 为涡激振动引起的弯曲应变,$\varepsilon_{\rm T}$为各测点处由轴向张力$T$ 引起的拉伸应变. 根据式(6)可以得到 $$ \varepsilon_{\rm B}+\varepsilon_{\rm IL} =(\varepsilon_{\rm IL2}-\varepsilon_{\rm IL1})/2 \tag{7}$$
由于立管模型顺流向的涡激振动为均值为零的周期性振动,因此各测点处由涡激振动引起的应变$\varepsilon_{\rm IL}$在时间上的平均值为0,即 $$ \bar \varepsilon_{\rm IL}=0 \tag{8}$$
此外由于初始弯曲为不随时间变化的恒定弯曲,故各测点处的应变$\varepsilon_{\rm B}$ 也不随时间变化 $$ \varepsilon_{\rm B}=\bar\varepsilon_{\rm B} \tag{9}$$
对式(7)在时间上进行平均,并结合式(8)和式(9)即可得到立管模型顺流向上各测点处的初始弯曲应变$\varepsilon_{\rm B}$、涡激振动引起的弯曲应变$\varepsilon_{\rm IL}$ $$\varepsilon_{\rm B}=\overline{(\varepsilon_{\rm IL2}-\varepsilon_{\rm IL1})}/2 \tag{10}$$ $$\varepsilon_{\rm IL} =[(\varepsilon_{\rm IL2}-\varepsilon_{\rm IL1})-\overline{(\varepsilon_{\rm IL2}-\varepsilon_{\rm IL1})}]/2 \tag{11}$$
由光纤光栅应变传感器测量的立管模型横流向各测点处的应变$\varepsilon_{\rm CF1}$和 $\varepsilon_{\rm CF2}$均包含两部分:轴向张力产生的拉伸应变$\varepsilon_{\rm T}$ 以及涡激振动产生的弯曲应变$\varepsilon_{\rm CF}$ $$ \left. \varepsilon_{\rm CF1}=\varepsilon_{\rm T}-\varepsilon_{\rm CF} \\ \varepsilon_{\rm CF2}=\varepsilon_{\rm T}+\varepsilon_{\rm CF} \right\} \tag{12}$$
对上式进行简单的变换,便可得到横流向由涡激振动引起的弯曲应变$\varepsilon_{\rm CF}$ $$ \varepsilon_{\rm CF}=(\varepsilon_{\rm CF2}-\varepsilon_{\rm CF1})/2 \tag{13}$$
在获得立管模型横流向与顺流向各测点处由涡激振动引起的弯曲应变$\varepsilon_{\rm CF}$ 和$\varepsilon_{\rm IL}$后,可采用模态分析法[29]求取立管横流向与顺流向的涡激振动位移响应.
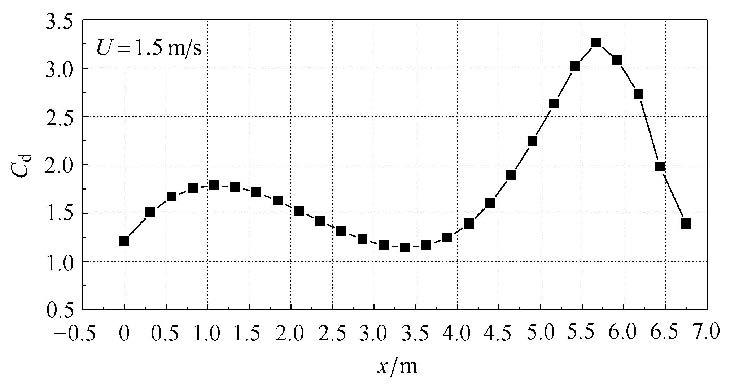
3 分析与讨论 3.1 阻力系数图5为立管模型顶端流速为1.5 m/s下立管模型阻力系数$C_{\rm d}$ 沿立管轴向分布,图中$x=0$ m表示立管模型的顶端.从图中可以看出,立管模型不同横截面处的阻力系数互不相同,且靠近立管模型顶端的阻力系数基本上小于靠近立管底端的阻力系数.这是因为立管模型所处的流场为剪切流,模型顶端流速最大,底端流速最小.各横截面处流速的不同导致各横截面处的雷诺数也不相同,顶端的雷诺数最大,底端的雷诺数最小.雷诺数的不同会导致阻力系数的不同,且阻力系数会随着雷诺数的增大而减 小[1].此外,立管模型的横流向会发生涡激振动,横流向的涡激振动也会使得顺流向的阻力系数分布不均匀[30].
|
图5 立管顶端流速1.5 m/s下立管模型阻力系数沿立管轴向分布 Fig.5 Axial distribution of drag coefficient along the riser attop current of 1.5 m/s |
从图5中还可以发现,立管模型的阻力系数基本上均大于亚临界雷诺数区间内静止刚性圆柱体的阻力系数1.2,最大的阻力系数高达3.2. 当立管模型顶端流速为1.5 m/s时,立管横流向涡激振动的主导频率为5.868 Hz,主导模态阶数为2阶,立管第2阶模态的固有频率为6.16 Hz (附加质量系数为1.0). 因此,立管模型的主导频率与其第2阶固有频率大致相等,这说明立管横流向的涡激振动发生了"锁频"现象,而当立管的涡激振动发生"锁频"现象时,涡激振动会对立管的阻力系数产生放大作用,这与文献[13]的发现是一致的.
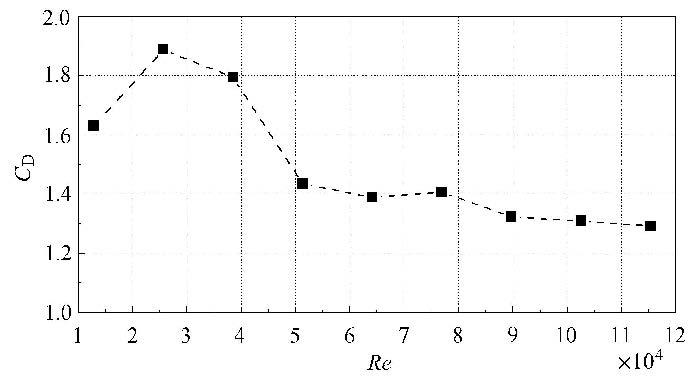
图6为立管模型的平均阻力系数$C_{\rm D}$ 随雷诺数的分布,其中雷诺数为立管模型顶端最大流速对应的值.如图6所示,平均阻力系数随着雷诺数的增大而减小.文献[13]指出在雷诺数小于2.2×10$^{4}$的均匀流中,当涡激振动发生"锁定"时,立管的阻力系数可以达到3 [13];文献[14]发现在雷诺数为2.8×10$^{3}$到2.8×10$^{4}$的阶梯流中,立管的阻力系数在1.6 到2.7 之间[14].从图6可以看出,在本文的模型试验中,当雷诺数在1.0×10$^{4}$到4×10$^{4}$之间时,立管模型的阻力系数在1.6到2.0之间,这与文献[13, 14]的发现一致. 从图6还可以发现,当雷诺数增大到8×10$^{4}$时,立管模型的阻力系数在1.4以上;当雷诺数进一步增大 到1.2×10$^{5}$时,立管模型阻力系数在1.3以上.这表明高雷诺数范围内,柔性立管发生涡激振动时的阻力系数仍大于亚临界雷诺数区间内静止刚性圆柱体的阻力系数1.2.
|
图6 平均阻力系数随雷诺数分布 Fig.6 Mean drag coefficient for different $Re$ values |
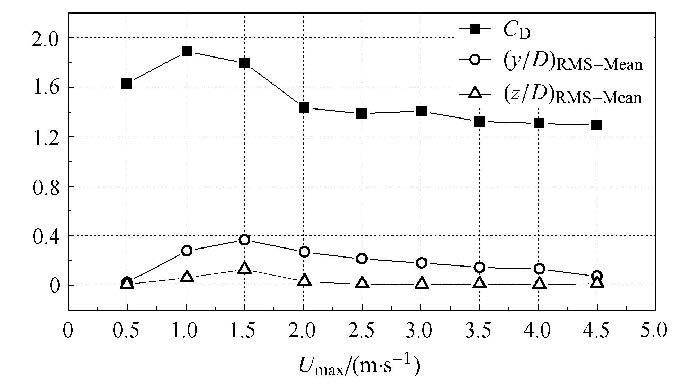
图7为立管模型的平均阻力系数$C_{\rm D}$ 以及横流向和顺流向上涡激振动无因次位移均方根的平均值($(y/D)_{\rm RMS-Mean}$ 和$(z/D)_{\rm RMS-Mean}$)随立管模型顶端流速的分布. 从图7中可以看出,立管的平均阻力系数与横流向的涡激振动位移均方根有相同的变化趋势:随着流速的增加,阻力系数和横流向涡激振动位移均方根均先增大后减小;而顺流向的涡激振动响应在顶端流速0.5 m/s到2.0 m/s先增大后减小,而当顶端流速大于2.0 m/s时,顺流向的涡激振动响应非常小.
|
图7 立管模型平均阻力系数及横流向和顺流向涡激振动无因次位移均方根均值随顶端流速的分布 Fig.7 Mean drag coefficient and mean value of non-dimensional root mean square of VIV displacement in the CF and IL directions at different top currents |
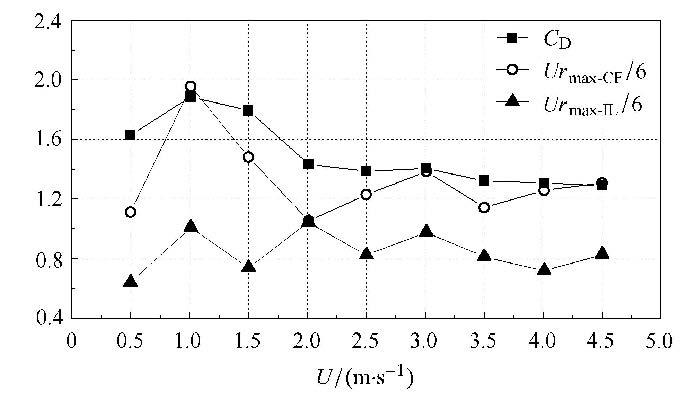
图8为立管模型平均阻力系数$C_{\rm D}$以及横流向和顺流向上的最大约化速度$Ur_{\max-{\rm CF}}$和$Ur_{\rm max-IL}$随顶端流速的 分布. 最大约化速度$Ur_{\max}$ 的定义如 式(14)$$ Ur_{\max}=\dfrac{U_{\max}}{f_{\rm ex}D} \tag{14}$$ 式中的$U_{\max}$为立管模型顶端的流速,也即为立管模型上的最大流速;$f_{\rm ex}$ 为立管模型横流向或顺流向涡激振动的主导频率(对涡激振动弯曲应变做快速傅里叶变换(FFT),求得涡激振动弯曲应变的频率谱,最大谱峰值对应的频率即为涡激振动"主导频率",具体求解过程可见参考文献[31]);$D$为立管模型的水动力直径.
|
图8 立管模型平均阻力系数及横流向和顺流向上最大约化速度随顶端流速的分布 Fig.8 Mean drag coefficient and Max reduced velocitiesin CF and IL directions at different top currents |
从图8可以看出,相比于顺流向而言,立管的平均阻力系数与横流向的最大约化速度相关:均随着流速的增加而先增大后减小.
从上面的分析可以看出,相比与顺流向而言,横流向的涡激振动对立管模型的阻力系数影响比较大. 这与文献[13, 14, 27]均认为横流向的涡激振动会对阻力系数产生影响的结论是一致的. 其可能的原因为:横流向上的涡激振动会影响立管在顺流向上的迎流面积,从而对立管顺流向的阻力(阻力系数)产生影响,而更深层次的原因需要利用计算流体力学方法作进一步的研究.
文献[13]基于试验结果给出了可估算涡激振动发生时柔性立管阻力系数的经验公式[13],如式(15)$$ C_{\rm d}(x)=C_{\rm d0}[1+1.043(2y_{\rm RMS}(x)/D)^{0.65}] \tag{15}$$ 式中,$ y_{\rm RMS}(x)$为横流向上涡激振动位移的均方根;$C_{\rm d0}$ 为静止刚性圆柱体的阻力系数,在亚临界雷诺数下,$C_{\rm d0}$取为1.2.
根据本文试验结果以及平均阻力系数与横流向涡激振动位移均方根、约化速度之间的关系,将立管模型横流向上涡激振动主导模态阶数(获得立管模型的涡激振动位移响应后,求取各阶模态的位移权重均方根值,最大均方根值对应的模态即为涡激振动的"主导模态",具体求解过程可见参考文献[31])、主导频率以及来流速度引入到式(15)中,得到了新的用于估算涡激振动发生时柔性立管阻力系数的公式,如下 $$ C_{\rm d}(x)=C_{\rm d0} \Big[1+\dfrac{0.16}{\sqrt{N_{\rm d}}}\dfrac{U(x)}{f_{\rm ex} D} (2y_{\rm RMS} (x)/D^{0.65}) \Big] \tag{16}$$ 其中,$U(x)$为立管横截面$x$处的来流速度;$N_{\rm d}$为立管横流向涡激振动主导模态阶数.
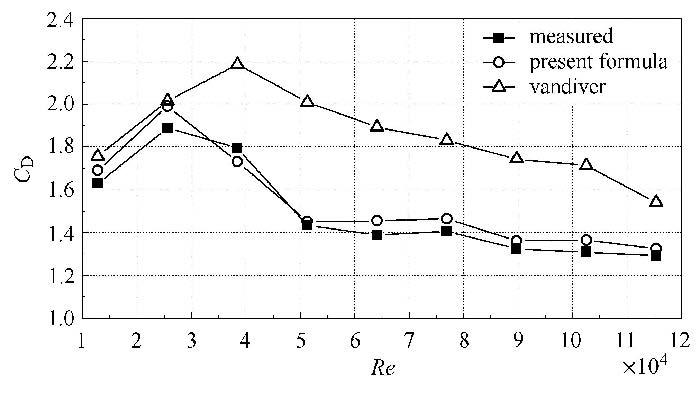
利用式(15)和式(16)计算不同顶端流速下立管模型的阻力系数$C_{\rm d}$ 后,根据式(5)得到立管模型的平均阻力系数$C_{\rm D}$,并与本文的试验结果进行比较. 图9给出了平均阻力$C_{\rm D}$随雷诺数的分布曲线(图中的雷诺数为立管模型顶端最大流速对应的值). 从图9中可以看出,当雷诺数小于$3.0 \times 10^4$ 时,通过 式(15)得到的阻力系数与试验结果大致吻合,而当雷诺数大于$3.0 \times 10^4$ 时,随着雷诺数的增大,二者的差距也增大. 其原因有可能是因为在建立式(15)的试验中,其最大雷诺数仅为$2.2 \times 10^4$,而本文试验中的雷诺数却高达 $1.2 \times 10^5$. 从图中可以看出,相比于式(15),经过横流向上涡激振动的主导模态阶数、主导频率以及来流速度修正后的式(16)计算得到的阻力系数与试验结果更加接近.因此,当柔性立管在高雷诺数下发生涡激振动时,可以用式(16)估算柔性立管的阻力系数.
|
图9 不同顶端流速下立管模型平均阻力系数的测量值与预测值 Fig.9 Measured and predicted value of mean drag coefficientat different top current |
本文对线性剪切流场中涡激振动发生时柔性立管的阻力特性进行了研究. 利用试验测得的立管模型顺流向上应变值,得到了不同流速下柔性立管模型的阻力系数,分析了涡激振动发生时柔性立管阻力系数的变化特性以及涡激振动对阻力系数的放大效应,同时基于本文试验结果得到了适用于计算高雷诺数下涡激振动发生时柔性立管阻力系数的经验公式. 本文的主要结论如下:
(1)剪切流下发生涡激振动的立管,其不同横截面处的阻力系数互不相同;涡激振动对阻力系数有放大效应,立管局部阻力系数可达3.2;
(2)雷诺数位于1.0×10$^{4}$到1.2×10$^{5}$区间的平均阻力系数在1.3到2.0之间,并随着雷诺数的增大而减小;
(3)本文提出的考虑横流向上涡激振动的主导模态、主导频率以及来流速度影响的阻力系数公式适用于估算高雷诺数下柔性立管发生涡激振动时的阻力系数.
| 1 | Sumer B, Fredsoe J. Hydrodynamics around Cylindrical Structures. Singapore:World Scientific, 2006. 2-70 |
| 2 | Fang SM, Niedxwecki JM, Fu S, et al. VIV response of a flexible cylinder with varied coverage bybuoyancy elements and helical strakes. Marine Structures, 2014, 39:70-89 |
| 3 | Niedxwecki JM, Fang SM. Suppression of flow-induced vibrations using ribbon fairings. International Journal of Computational Methods and Experimental Measurements, 2013, 1(4):395-405 |
| 4 | Fang SM. Structural response evaluation using non-uniform sensor arrays.[PhD Thesis]. Texas A & M University, 2013 |
| 5 | Fu S, Wang J, Baarholm R, et al. VIV of flexible cylinder in oscillatory flow. Proc. of the 32nd OMAE, Nantes, 2013. Paper No. 2013-10348 |
| 6 | Fu S, Wang J, Baarholm R, et al. Features of vortex-induced vibration in oscillatory flow. J Offshore Mech Arct Eng, 2013, 136(1):011801 |
| 7 | Wang J, Fu S, Baarholm R. Vortex-induced vibration of steel catenary riser under vessel motion. Proc. of the 33rd OMAE, San Francisco, 2014. Paper No. 2014-23584 |
| 8 | Gao Y, Fu S, Ma L, et al. Experimental investigation of the response performance of viv on a flexible riser with helical strakes. Ships Offshore Structures, 2014. http://dx.doi.org/10.1080/17445302.2014.962788 |
| 9 | Wang J, Fu S, Baarholm R, et al. Fatigue damage induced by vortexinduced vibrations in oscillatory flow. Marine Structures, 2015, 40:73-91 |
| 10 | Wang J, Fu S, Baarholm R, et al. Fatigue damage of a steel catenary riser from vortex-induced vibration caused by vessel motions. Marine Structures, 2014, 39:131-156 |
| 11 | 王俊高,付世晓,许玉旺等. 正弦振荡来流下柔性立管涡激振动发展过程. 力学学报, 2014, 46(2):173-182(Wang Jungao, Fu Shixiao, Xu Yuwang, et al. VIV developing process of a flexible cylinder under oscillatory flow. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2):173-182(in Chinese)) |
| 12 | De Wilde JJ, Huijsmans RH. Laboratory investigation of long riser VIV response. Proc. of the 14th International Offshore and Polar Conference, Toulon, France, 2004. 511-516 |
| 13 | Vandiver JK. Drag coefficients of long flexible cylinders. Proc. of the 15th Annual Offshore Technology Conference, Houston, 1983, TX. No. 4490 |
| 14 | Chaplin JR, Bearman PW, Huera-Huarte FJ, et al. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. Journal of Fluids and Structures, 2005, 21:3-24 |
| 15 | Kaiktsis L, Triantafyllou GS, Öxbas M. Excitation inertia, and drag forces on a cylinder vibrating transversely to a steady flow. Journal of Fluids and Structures, 2007, 23(1):1-21 |
| 16 | Sarpkaya T. A critical review of the intrinsic nature of vortexinduced vibrations. Journal of Fluids andStructures, 2004, 19:389-447 |
| 17 | Al-Jamal H, Dalton C. Vortex induced vibrations using large eddy simulation at a moderate Reynolds number. Journal of Fluids and Structures, 2004, 19(1):73-92 |
| 18 | Liu ZG, Liu YJ, Lu J. Numerical simulation of the fluid-structure interaction for an elasticcylinder subjected to tubular fluid flow. Computers & Fluids, 2012, 68:192-202 |
| 19 | Willden RHJ, Graham JMR. Numerical prediction of VIV on long flexible circular cylinders. Journal of Fluids and Structures, 2001, 15:659-669 |
| 20 | Yamamoto CT, Meneghini JR, Saltara F, et al. Numerical simulations ofvortex-induced vibration on flexible cylinders. Journal of Fluids and Structures, 2005, 19:467-489 |
| 21 | Guilmineau E, Queutey P. Numerical simulation of vortex-induced vibration of a circularcylinder with low mass-damping in a turbulent flow. Journal of Fluids and Structures, 2004, 19:449-466 |
| 22 | Wang J, Liu H, Jiang S, et al. Vortex-induced vibration on 2D circular riser using a high resolution numerical scheme. Proc. of the 9th International Conference on Hydrodynamics, October 11-15, 2010 Shanghai, China |
| 23 | Chen H, Huang K, Chen C, et al. CFD simulation of a riser VIV. Final Project Report, 2007 |
| 24 | Baarholm R, Kristiansen T, Lie H. Interaction and clashing between bare or straked risers:Analyses ofexperimental data. Proc. of the 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, USA, 2007, 3:803-812 |
| 25 | Fu S, Ren T, Li R, et al. Experimental investigation on VIV of the flexible model under full scale Re number. Proc. of the 30rd OMAE, Rotterdam, 2011. Paper No. 2011-49042 |
| 26 | Huera-Huarte FJ, Bearman PW, Chaplin JR. On the force distribution along theaxis of a flexible circular cylinder undergoing multimode vortex-induced vibrations. Journal of Fluids and Structures, 2006, 22:897-903 |
| 27 | Blevins RD. Flow-induced Vibration. New York:Van Nostrand Reinhold, 1990 |
| 28 | Chen T, Chen B. Structural Mechanics for Ships. Beijing:National Defence Industrial Press, 1984. 29-30 |
| 29 | Lie H, Kaasen KE. Modal analysis of measurements from a largescale vivmodel of a riser in linearly sheared flow. Journal of Fluids and Structures, 2006, 22:557-575 |
| 30 | Zhao P, Wang J. Numerical simulation of fluid-structural interaction for vortex-induced vibration of risers. Ocean Technology, 2010, 10(3):73-77 |
| 31 | 李琳. 带浮力块的柔性立管涡激振动特性研究. 上海:上海交通大学, 2012(Li Lin. Investigation on vortex-induced vibration of flexible riser with buoyancy modules. Shanghai:Shanghai Jiao Tong University, 2012(in Chinese)) |
2. Naval Academy of Armament, Beijing 100161, China;
3. Marine Design and Research Institute of China, Shanghai 200011, China;
4. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
 2016, Vol. 48
2016, Vol. 48