2. 中国空气动力研究与发展中心, 绵阳 621000;
3. 中国航天科工集团31研究所, 北京 100074
吸气式高超声速飞行器是一个复杂的多学科系统,涉及气动、推进、控制、材料/结构等诸多学科[1, 2, 3, 4, 5, 6, 7].在气动布局上,一般采用机体和推进系统一体化的设计方案,以有效减小飞行器的气动阻力,满足推阻匹配需求[8].进入21世纪以来,美国X-43A[9]和X-51A[10]演示验证飞行器的成功试飞,标志着上述关键技术已获得重大突破.近期美国所提出SR-72高超声速飞机及HSSW高速打击武器等一系列研究计划[11],进一步表明此领域已逐步开始细分并向实用化研究推进.本文工作主要针对高超声速飞机概念构型的气动特性研究.
高超声速飞机的研究最早可追溯至20世纪80年代的美国空天飞机(NASP)计划[12]. 自1987年黏性优化乘波体[13]提出之后,乘波体腹部进气布局开始获得关注. 这类构型同时利用了乘波体高升阻比和均匀压缩来流的两个优点,可兼顾飞行器和发动机的设计需求. 纵观整个腹部进气构型的研究历程,优化设计一直受到重视,并在20世纪90年代一度成为研究主流[14, 15, 16, 17],且在近期仍不断有研究成果发表[18, 19, 20, 21, 22].
由于标准乘波体较为扁平,容积率较低,已有研究大多采用加大尺寸的方法来保证内部容积,典型飞行器长度 为60 m $\sim$ 110 m[16, 17],但这导致飞行器及发动机设计难度均大幅增加. 此外,在乘波体腹部安装发动机还将诱生横向流动,破坏其乘波性能,导致飞行器阻力增加及升阻比降低. 针对上述问题,有学者[20]提出将飞行器上表面分为机体和机翼两部分独立设计,以进一步改善容积和升阻性能;也有学者[21]发展了一种发动机进气口完全依据激波面切割,整个飞行器下表面完全采用流线追踪的设计方法;还有学者[22]提出双乘波设计,把内乘波进气道和外乘波前体进行耦合设计,均可在一定程度上改善整机性能.
与腹部进气布局相比,旁侧进气布局将进气道入口设置于飞行器两侧或侧腹部,发动机内流道完全包裹于机体内部,典型如美国"FALCON"计划所提出的高超声速巡航飞行器(HCV) [23].国内亦有基于乘波前体与"Busemann"进气道一体化设计的旁侧进气性能研究工作发表[24].文献[25]提出了一种双乘波体旋转对拼的前体设计方法,在此基础上进一步考虑内部容积有效利用问题,采用翼身融合体的设计理念开展了整机概念构型设计方法研究,并初步分析了飞行器前缘型线对其气动性能的影响.文献[26]发展了这一方法,通过改进乘波前体形状并考虑发动机内流道设计,给出了一种具有实用化前景的整机构型.
本文以文献[26]给出的乘波体旁侧进气一体化构型为基准飞行器外形,以分析前缘形状对飞行器升阻力性能的影响为主要目标,采用自行发展的增量修正方法[27]进行前缘型线参数化设计,利用均匀实验设计方法[28]在设计空间内生成一系列具有不同前缘型线的飞行器构型并通过数值模拟获得其气动参数,最后基于计算结果对前缘形状与气动参数间的关系进行分析.结果表明,飞行器前缘形状对其升阻力参数的影响十分明显,设计空间内升力、阻力和升阻比的变化范围分别为21.3%, 31.8% 和10.63%. 相比之下,纵向压心的变化范围仅为3.87.结果还表明,飞行器俯视投影面积以及容积均对其气动参数呈较为明显的比例关系.
1 基准构型简介及性能评估 1.1 基准构型简介优化设计所用基准构型设计流程在文献[26]中已有细致阐述,此处不再重复,仅做简单描述.整机三维效果图及三视图如图1所示. 飞行器前体基于双乘波体旋转对拼生成,基准乘波体为设计马赫数为6的锥导乘波体,前缘线轴向投影为直线,以减小机体前端拼接距离,减弱前缘脱体激波影响. 乘波体两前缘线间的夹角为90°,每个乘波体向两侧分别偏转30°.乘波体间的拼接面逐点直线连接,以减小阻力. 动力系统采用两台轴对称形燃烧室的超燃冲压发动机配置.

|
图1 基准构型效果图(左)和三视图(右) Fig.1 The effect drawing (left) and the three-view (right) of the baseline vehicle |
整机设计采用翼身融合布局以减小阻力,机体中部均可用于装载载荷,两侧自然收缩形成飞翼布局.整机俯视形状为大后掠梯形,前缘侧视方向呈近似余弦分布,形成等效装配攻角,以保证飞行器小攻角飞行时兼顾发动机来流需求及整机气动性能.机体后部安装V形双垂尾. 整机主要轮廓参数如表1所示,其中,$L$为整机长度,$L_{\rm b}$为前体(乘波体)长度,$W$为翼展长度,$H$为整机尾部高度(不含垂尾),$H_{\rm b}$为边缘钝化厚度.
| 表1 基准构型主要尺寸参数 Table 1 Size parameters of the baseline vehicle |
在整机构型设计基础上,利用数值模拟对其气动性能进行了初步评估.计算网格采用非结构四面体网格,近壁面网格进行加密,总网格单元个数约1 065万,计算域及物面/对称面网格如图2所示. 计算中发动机流道给定为冷态通流状态.已有文献表明,如果物面网格尺度合理选择,采用层流模型可获得可以接受的气动参数[29],同时,考虑到后续优化过程中飞 行器湿润面积变化较小,故摩擦阻力变化相应较小.为缩减计算量,采用层流模型进行计算,控制方程的无黏项采用Roe格式进行通量分裂,黏性项采用二阶中心差分格式计算.

|
图2 基准构型数值模拟计算域及网格示意图 Fig.2 Illustration of the computational domain and meshes for aerodynamic performance evaluation of the baseline |
计算条件为飞行马赫数6、高度26 km、飞行攻角范围$0^\circ \sim 8^\circ$. 为细致分析,对整机进行了气动界面划分.将整机的升 阻力系数分为头部、发动机和机体3个部分来分别进行统计.界面划分方式如图3所示,此处给出半模内部剖视图以清晰描述:头部(head)包括两侧乘波压缩面及腹部/背部中间连接面; 发动机(engine)从内压段开始直至内流道尾部;其余部分包括机体上下壁面、底部端面以及垂尾等均归为机体(body).

|
图3 气动界面划分示意图 Fig.3 Control volume for force calculation |
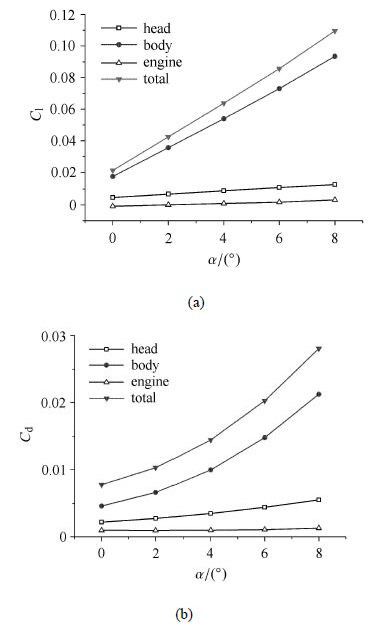
图4给出了上述3个部分及整机的升力系数$C_{\rm l}$和阻力系数$C_{\rm d}$随飞行攻角$\alpha $ 变化曲线.此处升阻力系数计算 以整机俯视投影面积为参考面积.计算结果表明整机升阻比最大值出现于4°飞行攻角状态,约为4.41 (含内流道及底部阻力).在此攻角条件下,飞行器各部件升力及阻力所占比例如图5所示.从图中可知,机体部分由于法向投影面积最大,故而其对飞行器升力和阻力的贡献均最大,其升力和阻力分 别约占整机的84.55%和67.4%.
|
图4 基准构型升阻力系数随攻角变化曲线 Fig.4 Variation of the lift and the drag coefficients with flight angle of attack |

|
图5 各主要部分升力(上)及阻力(下)比例(4°攻角) Fig.5 Proportions of the lift and the drag for each part (at 4° angle of attack) |
基于上述计算结果可以获得如下初步结论:采用翼身融合体的气动布局设计方案所获构型具有较好的气动性能,特别是具有较高的升阻比. 此外,头部及内流道的升阻力数值随飞行攻角变化较小,且对整机升阻力的贡献相对较小.由于机体部分是飞行器的主升力面,整机的气动性能的优劣基本由这一部分决定.基于上述结论并综合文献[25]中的结论,本文主要采用外形优化作为手段来分析机体前缘线对其性能的影响,以期对后续的实用化设计提供有力参考.
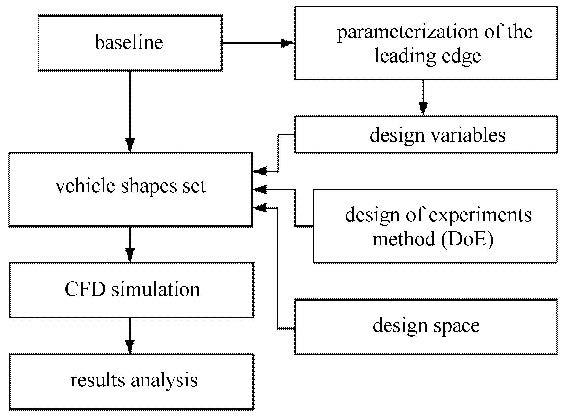
2 优化分析流程及方法 2.1 优化分析流程简介优化分析的主要流程如图6所示,简要解释如下:以基准构型为出发点,首先对机体前缘线俯视投影形状进行参数化描述,确定设计变量个数及含义;其次给定每个变量的上下扰动边界,选择合理的实验设计表生成设计变量集,并与基准构型相结合获得一系列典型飞行器外形;之后利用数值模拟对前述典型飞行器外形分别进行计算分析,获得其气动、容积等主要参数;最后通过结果统计和整理,分析和总结机体前缘线形状对飞行器主要性能参数的影响.
|
图6 优化分析主要流程 Fig.6 Flowchart of the optimization and analysis |
目前复杂曲面参数化设计方法种类较多,包括基向量方法、域单元逼近、基于多项式和样条曲线的方法、自由变形方法等[30],本文采用作者自行发展的基于增量修正的参数化设计方法.此方法曾在细长体吸气式飞行器上壁面优化中应用,并获得良好效果[27],本文中我们对其进行了进一步发展.该方法的主要思路如下:(1)以基准外形为基础,选定外形可变区域(控制域)划分结构化网格,并提取控制域内任意一点的直角坐标值; (2)在控制域内给定所有离散点的空间坐标增量值,其设定方式为分别给定3个空间坐标方向的最大增量值和增量分布函数(控制函数).由于采用分量表达,每个方向的控制函数均为一维函数;(3)在网格坐标系统下,将每个网格点上的三维增量修正值与基准外形的坐标值进行叠加,获得变形后的外形.由于这一方法是将外形参数化转化为其增量的参数化,因此称为基于增量修正的参数化设计方法.该方法的应用与基准构型复杂度无关,适合于复杂外形的参数化.通过控制函数的形式选择,不但可有效保持原有气动布局的设计特点,而且可缩减设计变量个数.该参数化设计方法可采用如下公式表达 $$ \left.\!\!\begin{array}{l} { r}^{i,j} = { r}_{0}^{i,j} + \Delta { r}^{i,j} \\ \Delta { r}^{i,j} = A_x C_x ({ p})^{i,j}{ x} + A_y C_y ({ p})^{i,j}{ y} + A_z C_z ({ p})^{i,j}{ z} \end{array} \!\!\right\} \tag{1}$$ 式中,$i$和$j$分别为控制域内的面网格点编号,${ r}_{0}^{i,j}$为控制域内基准外形网格点的三维空间坐标向量,$\Delta { r}^{i,j}$为该点坐标修正量向量,${ r}^{i,j}$为修正后的该点外形坐标值向量. $A_{x}$, $A_{y}$和$A_{z}$ 分别为3个空间坐标方向的最大增量值,$C_{x}$, $C_{y}$和$C_{z}$分别对应3个方向的控制函数,${ p}$为3个方向控制函数的参变量系数集,实际中作为设计变量使用.
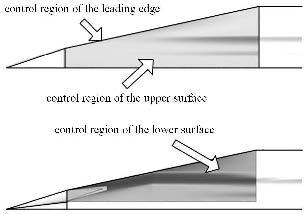
上述方法的具体实现过程如下所述. 控制域给定为机体前缘线及其附近上/下壁面的给定部分,共包含3个区域,如图7阴影部分所示.前缘线为前缘带状区域,始于前体末端(前体部分前缘线由乘波体外形确定),终于其与末端平直段的连接点(后部平直部分受翼展约束限制),是外形变化最明显的部分.上表面控制区域自前缘线沿展向至对称面,下表面控制区域自前缘线沿展向至侧乘波体边缘位置,同时去除进气道泄流槽附近部分区域,以免变形后与进气道内压缩面产生外形交错.
|
图7 参数化设计的控制区域 Fig.7 Control regions for parameterization |
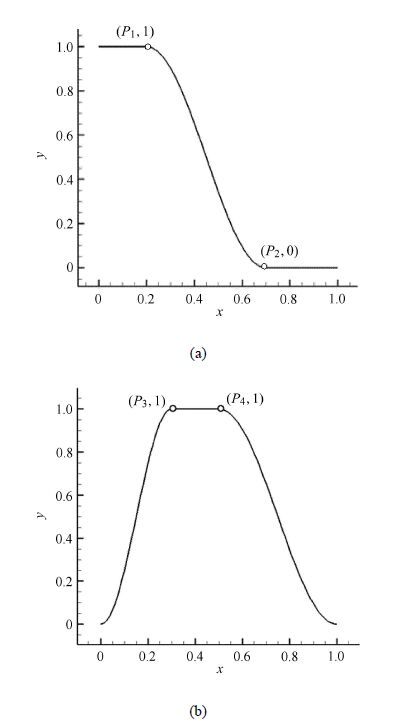
优化分析仅针对前缘线俯视型线,故垂直方向最大增量(式(1)中的$A_{z}$)为0,即飞行器最大厚度不变. 基准外形翼前缘俯视为斜线,$ x$和$y$方向的变量相关,这两个方向上只需任给定一个增量值,即采用一个变量表达,此处采用$x$方向增量值.由于垂直方向增量为0,故此方向无需给定控制函数.基于文献[25]的结果,前缘线的俯视形状呈余弦分布时相对较好,因此其余两个方向(展向及轴向)的控制函数分别采用归一化的半周期广义余弦分布函数和全周期广义余弦分布函数,采用上述控制函数形式还可以保证外形变化后拼接位置的光滑过渡.展向和轴向控制函数表达形式如式(2)和式(3)所示,对应的函数曲线如图8所示.
|
图8 展向(a)和轴向(b)控制函数曲线 Fig.8 Curves of control function at the wingspan (a) and the axial (b) directions |
$$ C_y (x) = \left\{ \!\!\begin{array}{ll} 1,& x \in [0,P_1 ) \\ \dfrac{1}{2}\left[{1 + \cos \left( {\dfrac{x - P_1 }{P_2 - P_1 }\pi } \right)} \right] ,& x \in [P_1 ,P_2 ) \\ 0 ,& x \in \left[{P_2 ,1} \right] \end{array} \!\! \right. \tag{2}$$
$$C_x (x) = \left\{ \!\!\begin{array}{ll} \dfrac{1}{2}\left[{1 + \cos \left( {\pi + \dfrac{x}{P_3 }\pi } \right)} \right] ,& x \in [0,P_3 ) \\ 1 ,& x \in [P_3 ,P_4 ) \\ \dfrac{1}{2}\left[{1 + \cos \left( {\dfrac{x - P_4 }{1 - P_4 }\pi } \right)} \right] ,& x \in [P_4 ,1] \end{array} \!\! \right. \tag{3}$$
为直观描述,图9给出了两个经参数化变形后的飞行器构型实例.可以看出,采用上述参数化方法可灵活调整机体前 缘线形状,呈现内凹或者外凸形状.通过给定上述控制域和控制函数,前缘线变化将连带翼根部分相应增厚,可避免大面积薄翼,保证其结构强度.此外,由于控制函数选择合理,经变形后构型的控制域内和边界光滑性与基准构型保持一致.

|
图9 变形后构型实例 Fig.9 Examples of deformed configurations |
经参数化设计后,共使用5个设计变量描述,即最大增量值$A$、展向控制函数参数$P_{1}$和$P_{2}$、以及轴向控制函数参数$P_{3}$和$P_{4}$. 由式(2)和式(3)所知,参数$P_{1}\sim P_{4}$均为无量纲参数.进一步将参数$A$以飞行器半展长($A_{\rm w})$为参考量进行无量纲化,以便后续处理.依据实际情况,给定各变量的上下界范围(设计空间),如表2所示. 其中,变量$A/A_{\rm w}$为负表示变形量为负,即前缘内凹,反之表现为前缘线外凸. 参数$P_{4}$取值与$P_{3}$相关联,以避免外形交错.
| 表2 设计变量取值范围 Table 2 Boundary values of design space |
为覆盖整个设计空间,以提高结果的广适性并减小工作量,本文采用实际中广泛使用的均匀实验设计方法作为优化分析方法. 该方法基于数轮理论在整个设计空间内构造合理的均匀设计表并获得样本集.具体中结合采用的好格子点法和方幂好格子点法,自行开发了均匀设计表构造程序. 该方法推导过程相对复杂,且在相关文献中已有细致介绍[28],此处不再赘述,仅简要给出程序流程.
第1步:输入试验次数$n$、设计变量个数$s$、设计空间$R^{s}$;
第2步:计算质数集$H_{n} = \{ h: h < n$,gcd($n ,h) =1 \}$及每个质数$h_{i}$对应的方幂次数$t_{i}$. 同时获取质数集的大小$m$、组合数$C^{s-1 }_{m-1}$、最高幂次数$T_{\max}=\max\{t_{1},t_{2},\cdots,t_{n}\}$;
第3步:判断是否可生成满足要求的均匀设计表. 当好格子点法产生的U 矩阵个数$C^{s-1 }_{m-1}$不大于1 000,且同时满足$s ≤ m$时,采用好格子点法,以改善设计表的均匀性,转第4步;若$C^{s-1 }_{m-1}>1 000$且$s<T_{\max}$时,采用方幂好格子点法生成均匀设计表并转第4步;当上述条件都不满足时,则程序终止,并提示错误;
第4步:生成U 矩阵,并选择中心化偏差最小的U 矩阵作为最终均匀设计表并输出.
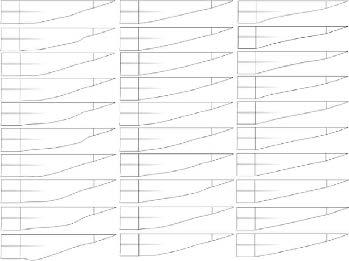
采用上述程序,在表2给出的设计空间内给定每个变量的水平值(即构型样本个数)为31. 图10给出了除基准构型外的所有30个样本俯视外形. 由于构型左右对称,这里仅给出半模的外形.
|
图10 构型样本集 Fig.10 Samples set of configurations |
如前所述,飞行器外形的变化仅影响机体中央部分,其余部分包括前体、发动机、底部及垂尾等均保持不变,故在优化计算中暂不包含上述部分. 为保证可比性,计算模型、网格尺度、格式等与前述基准构型计算中使用均保持一致. 发动机进气道入口给定无反射外推条件,计算域尾部截至飞行器尾缘,即计算结果不包含底部阻力. 计算条件仍设定为飞行马赫数6,飞行高度26 km. 参考基准构型的计算结果,飞行攻角设定为最大升阻比对应的状态,即4°攻角. 气动力系数计算时,参考面积仍采用飞行器俯视投影面积.
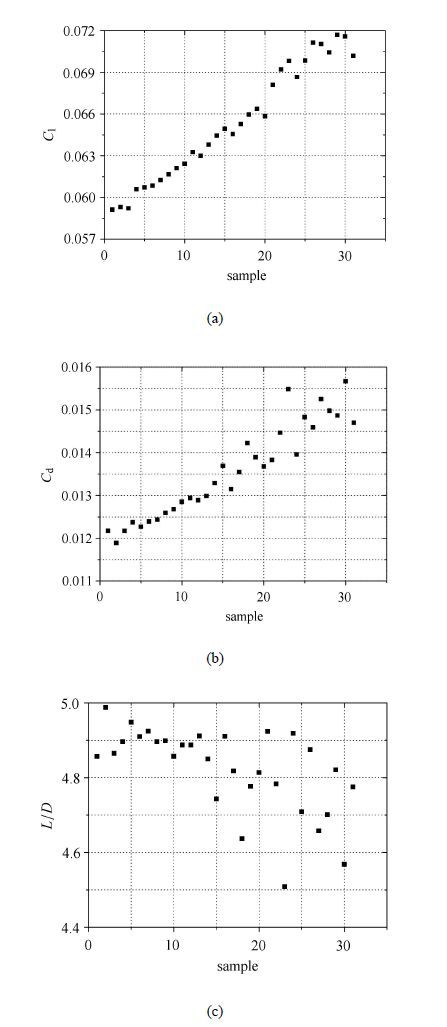
3.2 气动参数计算结果及分析图11给出了前述构型集中所有样本的升力系数$C_{\rm l}$、阻力系数$C_{\rm d}$及升阻比$L/D$分布图,分别如 图11(a) $\sim$图11(c)所示,图中横坐标为样本构型编号,按增量最大值$A$的数值排列.综合所有数据看,随着前缘线外形的变化,在不计内流道、垂尾和底部受力时,升力系数变化范围为0.059 12$\sim$0.071 69,相对变化量约为21.3%;阻力系数变化范围约为0.011 89$\sim$0.015 67,相对变化量约为31.8%;升阻比的变化范围为4.51$\sim$4.99,相对变化量约为10.6%. 显然,前缘线形状对飞行器气动参数的影响十分明显.
|
图11 样本构型气动参数比较图 Fig.11 Aerodynamic parameters comparison of all sample configurations |
从图11的结果还可看出,升力和阻力系数均随外形变化量的增加而增大,且在外形变化较小时(横坐标编号值小于15),沿增长方向的分布带较窄,几乎完全呈直线增长.而随外形变化量的增加,升力和阻力系数的分布带逐渐变宽,且对于阻力系数而言,这一特点更为明显.由此可见,在外形增量较大时,前缘型线的影响开始体现,并随外形增量的增加而逐渐增大.相比之下,升阻比变化规律并不明显,但从其上包络线看,升阻比基本随外形增量的增大呈非线性下降趋势.
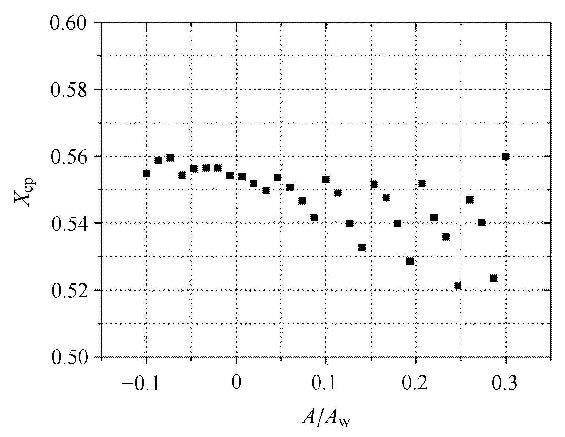
通过分析前述5个设计变量与纵向相对压心系数$X_{\rm cp}$的关系,发现最大增量值$A$对$X_{\rm cp}$的影响最为明显,故此处 仅给出二者的关系曲线,如图12所示. 图中横坐标采用相对增量表达,$A_{\rm w}$表示飞行器半翼展长度. 由此图可知,当$A/A_{\rm w}$较小时,$X_{\rm cp}$几乎不变,伴随$A/A_{\rm w}$增加,$X_{\rm cp}$的变化范围逐渐增加. 但在整个设计空间内,$X_{\rm cp}$的变化范围仅为3.87%.也就是说,前缘线形状变化对$X_{\rm cp}$的影响相对较小.
|
图12 纵向压心系数随相对增量值变化 Fig.12 Variation of longitudinal pressure center coefficients with dimensionless increments |
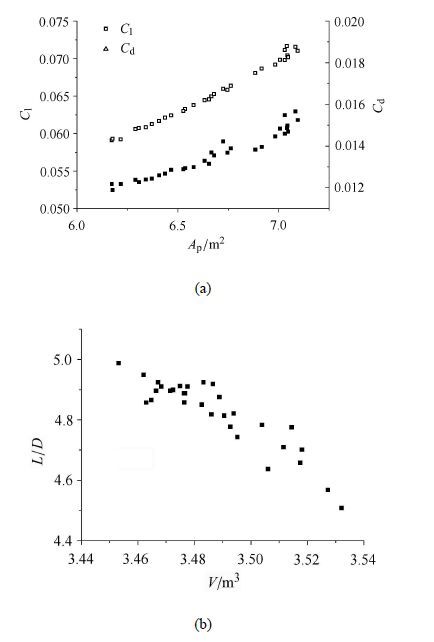
前缘外形变化后,飞行器的几何参数亦随之变化,图13(a)给出了俯视投影面积$A_{\rm p}$与升/阻力系数关系,图13 (b)给出了 容积$V$随升阻比变化趋势. 从图13(a)中可以看出,升力和阻力系数均与$A_{\rm p}$基本呈正比关系.但同时也可看出,在$A_{\rm p}$较小时,升力和阻力系数随$A_{\rm p}$增加的线性度在整个设计空间内均较好,而在$A_{\rm p}$较大时,升阻力系数变化相对分散,即$A_{\rm p}$相同时,气动参数值可能有较大差别,且阻力系数表现更为明显. 其主要原因在于前缘线的形状不同. 由于的$A_{\rm p}$变化主要由外形增量$A/A_{\rm w}$决定,故此结果进一步验证了前述分析.从图13(b)中可以看出,容积与升阻比之间则呈现明显的反比关系,即升阻比的提升一般需以减小容积为代价.
|
图13 关键几何参数与气动参数的关系 Fig.13 Relationship between geometrical and aerodynamic parameters of configurations |
为进一步对前述结果进行分析,我们从构型样本集中选取了3个典型构型,主要气动参数值如表3所示.3种构型分别为最大升力构型(a)、 最大升阻比构型(b),在本文算例中同时也是最小阻力构型)和基准构型(c).以基准的气动参数值为基准量,其余两种构型的升阻比相对变化量分别为1.84%和$-1.26%$,升力系数相对变化量分别为$-5.74%$和13.96%,阻力系数相对变化量分别为$-7.40%$和15.81%.从上述数据可知,通过调整前缘线形状可在较大范围内调节升力和阻力系数,同时保证飞行器升阻比变化较小.
| 表3 3种典型构型气动参数 Table 3 Values of aerodynamic parameters of three typical configurations |
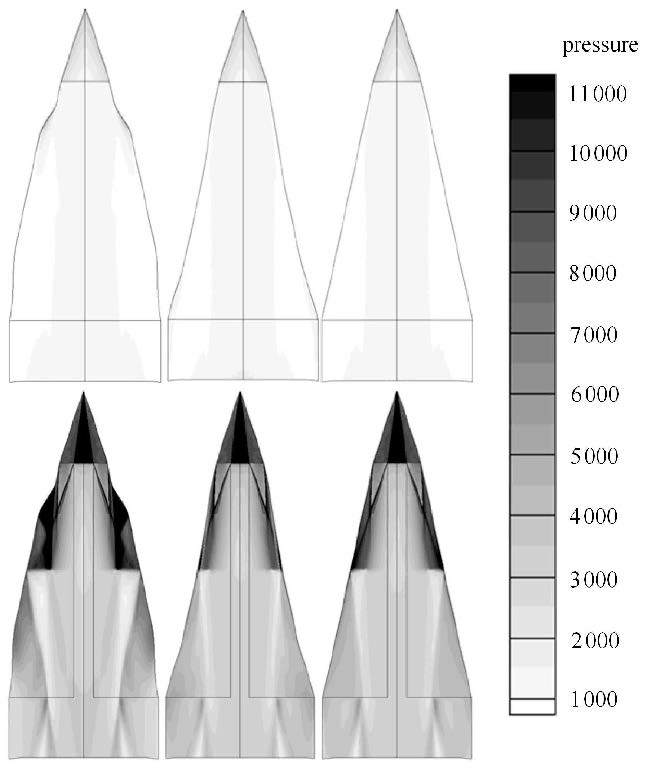
图14给出了上述3个典型构型的上下表面压力分布比较. 从图中可知,尽管前缘线外形存在明显差别,但上表面压力分布差别较小.对下表面而言,最大升阻比构型与基准构型相比腹部两侧向内收缩,侧壁对来流压缩减弱,迎流面积减小,因此阻力明显减小.此外前缘线后掠增加也对减阻有利. 但同时由于升力面积减小导致升力产生明显下降.反之,最大升力构型由于腹部两侧向外膨胀及翼前部厚度增加,气流经这一区域后先压缩后膨胀,导致阻力明显增加.但同时翼前部对来流压缩增强,亦可获得升力的增加.此外,从图中还可看出,侧壁压缩产生的高压区部分作用于机翼,是整机升力提高的重要因素.这一结果与文献[21]的相关结果相符,且特征更为明显.
|
图14 3个典型构型的物面压力分布 Fig.14 Wall pressure distribution of three typical configurations |
此外,从图中还可较为直观地看出,前缘形状的变化主要影响机体部分,前缘型线的外凸同时导致整个机翼部分的压力升高,在前半部分,压力升高较为明显,但俯视投影面积相对较小.而在后半部分,尽管压力升高值相对较小,但俯视投影面积较大,因而综合导致整机压心偏移量相对较小.
4 结 论本文基于一种翼身融合布局的高超声速飞机构型,以机体前缘线为设计变量并采用增量修正方法对其进行参数化描述,结合使用实验设计方法和计算流体力学分析为主要分析工具,分析了机体前缘线变化对飞行器主要气动性能参数及几何参数的影响. 增量修正参数化方法具有设计变量少及灵活方便的特点,通过合理给定控制区域分布函数可保证拼接面的光滑连接,适用于复杂外形的优化设计. 均匀实验设计方法进行取样可保证样本的代表性,并具有较好的结果可分析性.
计算结果表明,采用大后掠前缘形状具有较好的减阻效果,并可有效改善升阻比,但同时导致升力减小. 在俯视投影面积相同的条件下,升力面较大时采用不同的前缘形状可使飞行器的升阻性能产生较大变化. 当前缘线选择合理时,可部分利用机体侧壁压缩产生的高压改善飞行器的升力. 此外,本文结果还表明飞行器前缘形状的改变同时改变了机体投影面形状以及物面压力分布,综合来看对纵向压心的影响相对较小.
本文工作仅针对于高超声速飞行的巡航状态进行分析和优化,尚未涉及水平起降及加速阶段. 从现有构型来看,大后掠的翼身设计可能难以在低速飞行条件下产生足够的升力. 因而,在现有工作基础上,开展多设计点下的多目标优化设计将是未来重点考虑的问题.
| 1 | 崔尔杰. 近空间飞行器研究发展现状及关键技术问题. 力学进展,2009,39(6):658-673(Cui Erjie. Research statutes, development trends and key technical problems of near space flying vehicles. Advances in Mechanics,2009,39(6):658-673(in Chinese)) |
| 2 | 叶友达. 近空间高速飞行器气动特性研究与布局设计优化. 力学进展,2009,39(6):683-694(Ye Youda. Study on aerodynamic characteristic and design of optimization for high speed near space vehicles. Advances in Mechanics,2009,39(6):683-694(in Chinese)) |
| 3 | Steelant J, Langener T, Hannemann K, et al. Conceptual design of the high-speed propelled experimental flight test vehicle HEXAFLY. 2015,AIAA Paper 2015-3539 |
| 4 | Sippel M. Spaceliner technical progress and mission definition. 2015,AIAA Paper 2015-3582 |
| 5 | Preller D,Smart M. Scramjets for reusable launch of small satellites. 2015,AIAA Paper 2015-3586 |
| 6 | Villace VF,Steelant J. The thermal paradox of hypersonic cruisers. 2015,AIAA Paper 2015-3643 |
| 7 | Huang W, Li SB, Liu J, et al. Investigation on high angle of attack characteristics of hypersonic space vehicle. Science China Technological Sciences,2012, 55(5):1437-1442 |
| 8 | 吴颖川,贺元元,贺伟等. 吸气式高超声速飞行器机体推进一体化技术研究进展. 航空学报,2015,36(1):245-260(Wu Yingchuan, He Yuanyuan, He Wei, et al. Progress in airframepropulsion integration technology of air-breathing hypersonic vehicle. Acta Aeronautica et Astronautica Sinica,2015,36(1):245-260(in Chinese)) |
| 9 | McClinton CR, Rausch VL, Shaw RJ, et al. Hyper-X:Foundation for future hypersonic launch vehicles. Acta Astronautica,2005,57:614-622 |
| 10 | Hank JM, Murphy JS, Mutzman RC. The X-51A scramjet engine flight demonstration program. 2008,AIAA Paper 2008-2540 |
| 11 | 刘鹏,宁国栋,王晓峰等. 从SR-72 项目看美国高超声速平台研究现状. 飞航导弹,2013,12:1-9(Liu Peng, Ning Guodong,Wang Xiaofeng, et al. Status of hypersonic research platform in the Unite States of America on the basis of the SR-72 program. Aerodynamic Missile Journal,2013,12:1-9(in Chinese)) |
| 12 | Mehta UB. Strategy for developing air-breathing aerospace planes. Journal of Aircraft,1996,33(2):377-385 |
| 13 | Bowcutt KG,Anderson JD,Diego C. Viscous optimized hypersonic waveriders. 1987,AIAA Paper 87-0272 |
| 14 | Lewis MJ,Takashima N. Wedge-cone waverider configuration for engine-airframe integration. Journal of Spacecraft and Rockets, 1995,32(5):1142-1144 |
| 15 | Takashima N,Lewis MJ. Engine-airframe integration on osculating cone waverider-based vehicle designs. 1995,AIAA Paper 1995-2551 |
| 16 | Takashima N,Lewis MJ. Optimization of waverider-based hypersonic cruise vehicles with off-design considerations. Journal of Aircraft, 1999,36(1):235-245 |
| 17 | Lobbia MA, Suzuki K. Numerical investigation of waveriderderived hypersonic transport configurations. 2003,AIAA Paper 2003-3804 |
| 18 | Lobbia MA, Suzuki K. Multidisciplinary design optimization of hypersonic transport configurations using waveriders. 2014,AIAA Paper 2014-2359 |
| 19 | Marcus L,Kojiro S. Multidisciplinary design optimization of hypersonic transport configurations using waveriders. 2014,AIAA Paper 2014-2359 |
| 20 | Cui K,Yang GW. Conceptual design of hypersonic vehicles with large capacity and high aerodynamic performance. 2009,AIAA Paper 2009-7400 |
| 21 | Ding F,Liu J,Shen CB, et al. Novel inlet-airframe integration methodology for hypersonic waverider vehicles. Acta Astronautica,2015,111:178-197 |
| 22 | Li YQ, An P, Pan CJ, et al. Integration methodology for waveriderderived hypersonic inlet and vehicle forebody. 2014,AIAA Paper 2014-3229 |
| 23 | Walker S, Tang M, Morris S, et al. Falcon HTV-3X-a reusable hypersonic test bed. 2008,AIAA Paper 2008-2544 |
| 24 | 南向军, 张堃元, 金志光. 乘波前体两侧高超声速内收缩进气道一体化设计. 航空学报,2012,33(8):1417-1426(Nan Xiangjun, Zhang Kunyuan,Jin Zhiguang. Integrated design of waverider forebody and lateral hypersonic inward turning inlets. Acta Aeronautica et Astronautica Sinica,2012,33(8):1417-1426(in Chinese)) |
| 25 | Cui K, Hu SC, Li GL, et al. Conceptual design and aerodynamic evaluation of hypersonic airplane with double flanking air inlets. Science China Technology Science,2013,56(8):1980-1988 |
| 26 | Cui K,Hu SC,Li GL,et al. A conceptual design of next generation hypersonic air-breathing airplanes with dual waveriders forebody//Proc. of 2015 AIAA International Conference on Spaceplanes, Hypersonic Systems and Technologies,Glasgow,2015-7-6-9 |
| 27 | 高太元,崔凯,胡守超等. 高超声速飞行器上壁面多目标优化及性能分析. 力学学报,2013,45(2):193-201(Gao Taiyuan, Cui Kai, Hu Shouchao, et al. Multi-objective optimization and aerodynamic performance analysis of the upper surface for hypersonic vehicles. Chinese Journal of Theoretical and Applied Mechanics, 2013,45(2):193-201(in Chinese)) |
| 28 | 方开泰,刘民千,周永道. 试验设计与建模. 北京:高等教育出版社,2011(Fang Kaitai,Liu Minqian,Zhou Yongdao. Design and Modeling of Experiments. Beijing:Higher Education Press, 2011(in Chinese)) |
| 29 | Cui K, Yang GW. Shape optimization for hypersonic arc-wing missiles. Journal of Spacecraft and Rockets,2010,47(4):694-700 |
| 30 | Samareh JA. A survey of shape parameterization techniques. 1999,NASA/CP-1999-209136:333-343 |
2. China Aerodynamic Research and Development Center, Mianyang 621000, China;
3. The 31th Research Institute of CASIC, Beijing 100074, China
 2016, Vol. 48
2016, Vol. 48