吸气式高超声速飞行器高速飞行时将产生剧烈的气动加热效应，气动加热使飞行器结构温度升高且产生温度梯度，升温将使得材料性能的下降，温度梯度则会产生热应力，这将改变结构的刚度和固有频率，进而影响飞行器的气动弹性特性，因此，近年来，高超声速热气动弹性的研究成为一个热点问题^{[1, 2, 3, 4, 5]}. 国内外对热气动弹性展开了大量的研究.Culler和McNamara^[6]通过采用三阶活塞理论计算气动力，采用Eckert参考焓法计算气动热，建立了双向耦合的热气动弹性方法，并分别对高超声速飞行器舵面和壁板进行了热气动弹性研究. Lamorte和Friedmann^[7]研究了真实气体效应，湍流转棙位置对热气动弹性的影响，研究发现转棙位置和热应力以非线性形式对舵面的热气动弹性分析产生明显的影响. Crowel^[8],Falkiewicz和Cesnik^[9]等研究了高超声速热气动弹性中的降阶模型，基于POD方法建立计算瞬态热传导的降阶模型. Crowell和McNamara^[8]分别基于Kriging方法和POD方法建立了高超声速热气动弹性中气动热的降阶模型，结果表明降阶模型极大的增加了计算效率，并且降阶模型得到的舵面热流分布误差在5%以内.杨超等^[10]对通过气动热-气动弹性双向耦合的方法对高超声速曲面壁板进行颤振分析，结果表明：与传统的只考虑气动热-气动弹性单向耦合的分析结果进行对比，基于气动热和气动弹性双向耦合的壁板颤振分析结果更危险.吴志刚等^[11]等分析比较了高超声速全动舵面和小展弦比根部固支翼面的热颤振特性，表明热效应会影响结构动力特性和颤振特性.张伟伟等^[12]等采用不同的温度和结构支持方式，基于CFD的当地流活塞理论，在时域内对高超声速小展弦比大后掠翼进行了热气动弹性仿真.

高超声速流动中的真实气体效应、化学反应、黏性干扰使得其流动特征十分复杂，准确预测气动热依然是一个十分具有挑战的问题^{[13, 14, 15, 16]}.Bose和Brown^[13]详细介绍了高超声速气动热预测能力的不确定性.目前，高超声速气动热的研究主要有以下3种方法：(1)风洞试验代价较高，以现有条件，较难建立针对高超声速，同时满足高速、高焓的风洞^[13]，由于模型存在误差且测量设备在精度和灵敏度上的某些局限，其结果有时也会具有一定程度上的不确定性，Shigeru^[14]对风洞实验中气动热的不确定性进行了研究.(2)气动热工程计算方法，比较常用的有参考温度和参考焓法，计算效率高，但是忽略了实际当中的很多影响因素；(3)求解NS方程得到气动热，计算代价较高，且受网格、湍流模型、计算格式、以及真实气体效应等诸多因素的影响，计算结果也是具有一定的不确定性^{[15, 16]}.Weaver等^[15], Hosder等^[16]研究发现，实际高超声速飞行过程中，来流速度，黏性系数，来流密度等来流参数的不确定性也将明显影响气动热的计算结果.因此，事实上，一方面，通过风洞实验和数值模拟得到的气动热结果都具有一定程度上的不确定性，另一方面，来流参数的波动也会造成气动热计算结果的不确定性.

对于热气动弹性分析而言，气动热是进行热传导分析的基础，气动热的不确定性必将影响热传导后结构的温度分布的不确定性，进而影响热气动弹性的分析的可靠性.因此，研究气动热的不确定性对热气动弹性的影响是一个非常有意义的问题.关于气动弹性中的不确定性分析方面的研究，Lamorte 等^[17]针对二维高超声速菱形翼，研究了俯仰模态和沉浮模态的不确定性对气动弹性的影响，并研究了转棙位置和热流的不确定性对高超声速二维壁板热气动弹性的影响. Danowsky等^[18]研究了马赫数，高度，结构参数的不确定性对机翼颤振特性的影响. 国内文献大多在均匀温度分布的假设下，分析温度对气动弹性的影响^{[11, 12]}，分析方法简单、快速，但与实际中结构的温度分布相差很大，影响分析结果的可靠性，并且在给定的几种温度下，只能得出较定性的结论. 据笔者查找的国内外文献，还没有发现有关研究气动热的不确定性对三维结构热气动弹性影响的论文.

热气动弹性问题本身就是一个复杂多学科的耦合问题，很难对其进行完全求解^{[1, 2, 3, 4, 5]}，直接研究气动热的不确定性对三维结构热气动弹性影响求解过程将极其复杂且计算量巨大.因此，本文将气动热不确定性导致的结果近似为热传导后温度分布的不确定性，在此基础上开展不确定性研究，提出一种温度分布参数化模型，基于此模型，分别采用传统MSC方法和一种高效的SGNI方法进行不确定性和全局灵敏度分析.

不确定性分析和全局灵敏度分析需要计算大量的样本，而结构热传导分析过程耗时较长，因此，计算量会非常大，并且本文对两种情况进行了分析对比，由于高超声速舵面结构一般较薄，热传导分析稳定后的结构温度分布与气动热分析中物面的温度分布规律较相似，因此，为了降低计算量和易于分析，本文将气动热不确定性导致的结果近似为温度分布的不确定性，在此基础上开展不确定性研究是合理的.

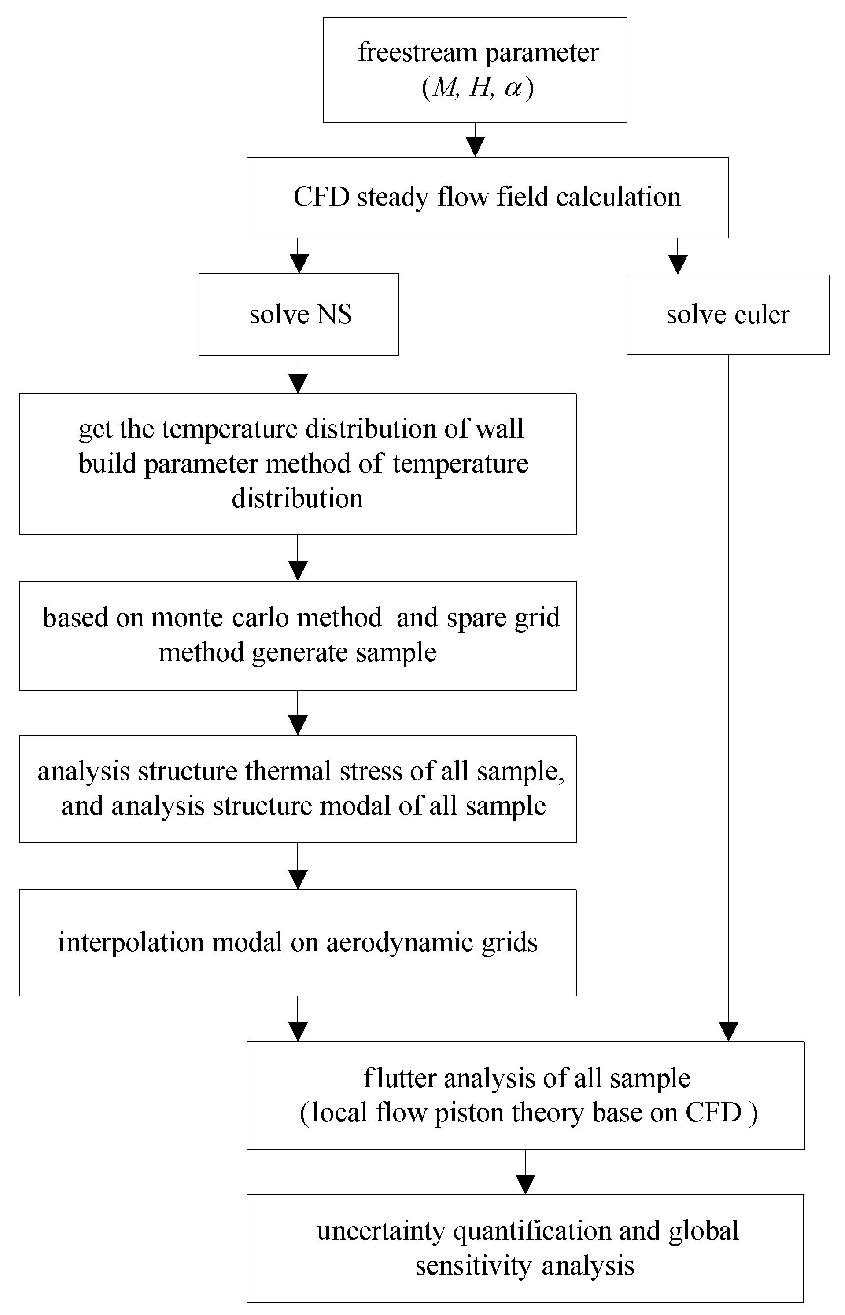
本文研究舵面热气动弹性中气动热不确定性和全局灵敏度的分析思路如下.

(1) 求解NS方程得到舵面的温度分布，其中物面边界条件采用辐射热平衡边界.

(2)对此温度分布进行参数化，确定不确定参数，采用MSC方法和SGNI方法生成不确定性分析所需的参数样本.

(3) 在任意参数确定的温度分布条件下，对结构进行热应力分析和模态分析.

(4) 将结构振型插值到气动网格上.

(5)求解Euler方程得到舵面的流动参数，基于CFD的当地流活塞理论，在状态空间中对舵面进行了气动弹性分析.

(6) 分别采用MSC方法和SGNI方法对结果进行不确定性和全局灵敏度分析.

具体流程如图1所示.

图1(Fig.1)

图1 分析思路 Fig.1 Analysis method

如图2所示，本文的计算模型为一个三维全动舵面，由于高超声速流动中，热流与前缘半径成反比例关系，因此，高超声速飞行器及部件通常采用钝头外形设计思路，为了便于分析，本文舵面剖面翼型选用前缘钝头的NACA0005.舵面根部连接一根舵轴，结构有限元分析约束条件为：舵轴根部平面固定支撑，舵面采用实心结构，材料采用TIMETAL834，密度为4 550 kg/m$^{3}$，泊松比为0.3，比热为525 J/(kg$\cdot $K)，导热系数为7.06 W/(m$\cdot $K)，材料属性随温度的变化如表1所示.其中$C_{\exp}$表示热膨胀系数，$E$为弹性模量，部分材料属性通过线性插值得到.

图2(Fig.2)

图2 有限元网格 Fig.2 Mesh of model

表1(Table 1)

表1 TIMETAL834热膨胀系数和弹性模量Table 1 Coefficient of thermal expansion and elasticity of TIMETAL834 $T$/℃ $C_{\exp}$/10$^{-6}$K$^{-1}$ $E$/GPa 20 10.3 115 200 10.6 96.4 800 10.9 38.2 1 000 10.9 26.2 1 200 10.9 62.2 1 500 10.9 50.2

表1 TIMETAL834热膨胀系数和弹性模量 Table 1 Coefficient of thermal expansion and elasticity of TIMETAL834

为了研究温度分布的不确定性对热气动弹性的影响，首先应该设计一种描述温度分布的参数化模型，Crowell等在文献^[8]中采用二次完全多项式描述物面温度分布，如式(1)所示，需要6个参数对函数进行控制，但是，如采用此温度分布函数模型进行不确定性研究，有如下两个不足之处：(1)参数较多，进行不确定性分析时，采用蒙特卡洛方法需要计算大量的样本才能保证不确定分析结果的精度，(2)二次多项式中的6个参数对于刻画函数温度分布的意义不明确，其中，$b_1 $控制函数上下平移；$b_2 \sim b_6 $都不同程度地控制函数斜率，很难区别相互之间的意义. 如采用这6个参数进行不确定性分析，很难得出明确的结论.

$$ T_s \left( {x,y,t} \right) = b_1 \left( t \right) + b_2 \left( t \right)x + b_3 \left( t \right)y + b_4 \left( t \right)x^2 + \\ b_5 \left( t \right)xy + b_6 \left( t \right)y^2 \tag{1}$$

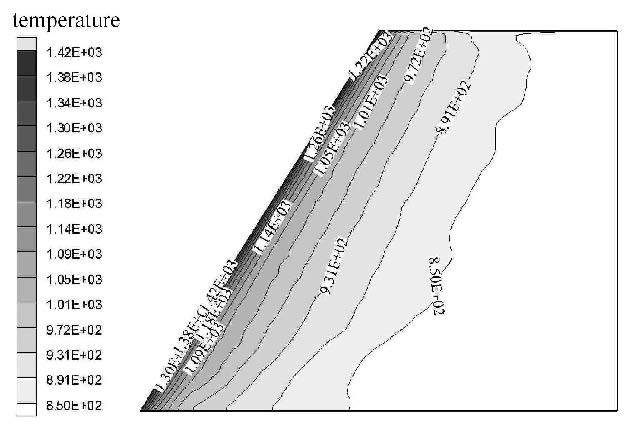
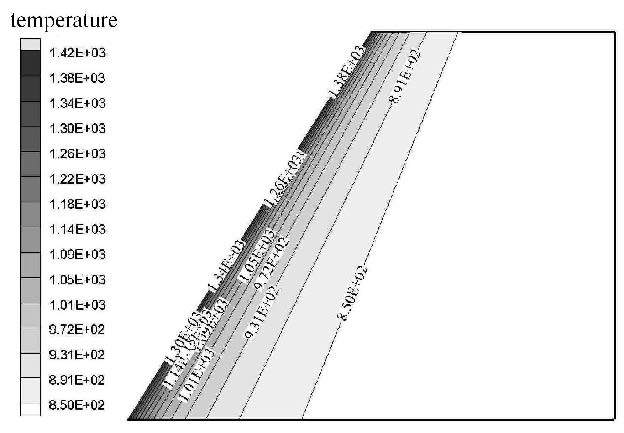
对于本文的舵面模型，由于舵面采用对称翼型，并且来流迎角为0°，因此，气动热的分布也是对称的.如图3和图4所示，给出 了舵面在$M =6$，$H =15$ km下的温度分布云图以及舵面展向上3个剖面的温度分布($x$轴为弦向方向，$z$轴为展向方向).从图3和4中可以看出，各剖面温度分布变化规律基本一致，前缘驻点温度非常接近，各剖面温度分布曲线形状也非常类似，因此，对根部剖面上温度分布进行函数拟合，然后根据展向位置对展向其他剖面进行归一化，由此就得到整个舵面上的温度分布.图5即为通过函数拟合得到的温度分布，可以看出，图5与图3是比较接近的，说明本参数化方法的思路的是可行的.

图3(Fig.3)

图3 舵面温度分布云图 Fig.3 Temperature distribution

图4(Fig.4)

图4 剖面温度分布曲线 Fig.4 Temperature distribution of sections

图5(Fig.5)

图5 参数化后物面温度分布 Fig.5 Temperature distribution of parameterized

拟合函数为 $$ f(X) = (p_1 X + p_2 ) / (X + p_3 ) \tag{2}$$

归一化的转换函数为 $$ X(x,z) = (x - az) / (1 - az) \tag{3}$$

最终函数表达式即为 $$ f(x,z) = [p_1 (x - ax) / (1 - az) + p_2] / \\ [(x - ax)/ (1 - az) + p_3] \tag{4}$$

从气动热的角度讲，采用不同方式得到热流或温度分布趋势类似，主要是分布曲线的斜率和驻点温度存在分散性.从结构的角 度讲，温度影响材料属性，温度梯度(对应曲线斜率)影响热应力，而材料属性和热应力影响结构刚度.因此，基于以上两方面分析，本文通过如下两种方式对$f(x,z)$进行扰动以提取不确定性分析参数.(1)对$f(x,z)$进行上下平移；(2)保证驻点温度不变的条件下，改变$f(x,z)$的斜率. 经分析，函数$f(x,z)$中的参数$p_1 $可以很好地控制函数的斜率，且发现$p_2 $，$p_3 $都不能很好地控制函数的上下平移，因此，引入一个新的参数$q_1 $，将$f(x,z)$加$q_1 $减$b$.

$$ f(x,z) = [p_1 (x - ax) / (1 - az) + p_2] / \\ [(x - ax) / (1 - az) + p_3] + q_1 - b \tag{5}$$ 其中，$q_1 = b$，通过$q_1 $即可以很好地对函数进行上下平移，$b$取为前缘驻点温度.

因此，本文提取$p_1 $和$q_1 $作为不确定性参数以控制温度分布，其中$p_1 $控制温度分布曲线斜率，$q_1 $控制温度分布中驻 点的温度，进而研究温度场的不确定性对热气动弹性的影响. 图6(a)为对$p_1 $进行正负20%的扰动，图6(b)为对$q_1 $进行正负10%的扰动.

图6(Fig.6)

图6 不确定参数扰动图 Fig.6 Disturbance of uncertainty parameters

首先采用广泛应用于不确定性分析中的蒙特卡罗(Monte Carlo simulation,MCS)方法对本文问题进行研究^[19]，同时采用近年来一种高效不确定性分析方法------稀疏网格数值积 分(spare grid numerical integration, SGNI)方法.

近年来，以Smolyak 准则为基础的SGNI方法受到了越来越广泛的应用，其基本思想是用合适的一维求积公式的张量积组合来构建多维求积公式^{[20, 21, 22]}.相比于直接的张量积组合方法，SGNI方法的模型计算量以及计算精度不再以指数形式依赖于输入变量的维数.下面给出SGNI方法的基本理论.

设$U_1^{ij} $和$w_1^{i_j } $表示第$j$个变量一维空间中的积分点和权重，则$n$维空间中$k$水平精度下所有的稀疏网格积 分点的集合$U_n^k $由以下Smolyak 准则选取 $$ U_n^k = \bigcup\limits_{k+1 ≤ | i | ≤ q} U_1^{i_1 } \otimes U_2^{i_2 } \otimes \cdots \otimes U_d^{i_n } \tag{6}$$ 其中，$ \otimes $表示张量积计算，$q = k + n$，$\left| i \right| = i_1 + i_2 + \cdots + i_n $为多维指标之和.为了从全网格中剔除那些对计算精度贡献较小的网格点，可以限制$k + 1 ≤ \left| i \right| ≤ q$，依据Smolyak 准则，集合$U_n^k $中相应于第$l$个积分 点${ \xi }_l = \left[{\xi _{j_{i_1 } }^{i_1 } ,\xi _{j_{i_2 } }^{i_2 } ,\cdots ,\xi _{j_{in} }^{i_n } } \right]$的权重$w_l $为 $$ w_l = ( - 1)^{q - \left| i \right|}\left( \!\!\begin{array}{l} n - 1 \\ q - \left| i \right| \end{array}\!\! \right) (w_{j_{i_1 } }^{i_1 } \cdots w_{j_{in} }^{i_n } ) \tag{7}$$

则对含有$n$维基本变量${ x} = (x_1 ,x_2 ,\cdots ,x_n )$的非线性函数$g({ x})$的积分可由式(8)中的稀疏网格积分公式求得，并且能够达到$2k+1$阶多项式的精度 $$ \int_{ - \infty }^{ + \infty } g({ x}) f({ x})d{ x} \approx \sum_{l = 1}^{N_n^k } w_l g[T^{ - 1}({ \xi}_l )] = \sum_{l = 1}^{N_n^k } w_l g({ x}_l ) \tag{8}$$ 其中，$N_n^k $表示在集合$U_n^k $中积分点的个数，$f({ x})$为${ x}$的联合概率密度函数. ${ \xi}_l $和$w_l $分别为 依据稀疏网格选点技术得到的$n$维空间中的积分点以及相应的权重，$T^{ - 1}({ \xi}_l )$为任意分布的变量${ x}$向积分点空间变换函数的反函数，在第$l$个积分点${ \xi }_l $处的${ x}$的值${ x}_l $.

稀疏网格积分法求解模型$y = g({ x})$输出均值和方差的积分可以表示为如下形式公式求得，并且能够达到$2k+1$阶多项式精度

$$ E_Y = \int_{ - \infty }^{ + \infty } g({ x}) f({ x})d{ x} \approx \sum_{l = 1}^{N_n^k } w_l g[T^{ - 1}( { \xi }_l )] = \sum_{l = 1}^{N_n^k } w_l g({ x}_l ) \tag{9}$$ $$V_Y = \int_{ - \infty }^{ + \infty } [g({ x}) - E_Y]^2f({ x}) d{ x} \approx$$ $$ \sum_{l = 1}^{N_n^k } w_l [g(T^{ - 1}({ \xi}_l )) - E_Y]^2=\sum_{l = 1}^{N_n^k } w_l (g({ x}_l ) - E_Y )^2 \tag{10}$$

基于Smolyak准则的SGNI方法能够在一定程度上克服传统数值积分计算量随变量维数呈指数级增长，对高维积分问题具有很好的适用性.其实现过程简单灵活，采用不同类型一维积分点可适用不同输入分布，通过调整精度水平$k$可以很方便地提高积分的精度.

全局灵敏度分析(global sensitivity analysis)，又称重要性测度，研究模型中输入变量的不确定性对模型输出不确定性的贡献程度，以其能够综合考虑基本变量在其整个取值范围内变化时对输出不确定性的影响而在工程设计及概率安全评估中应用广泛.基于方差的全局灵敏度分析方法能够简单有效地反映基本变量对输出不确定性的影响，该方法究输入参数对输出参数波动的重要性影响，同时考察参数的交叉耦合作用，本文采用该方法进行全局灵敏度的计算.

由Sobol 降维分析^[19]，总方差可以由下式表示 $$ V(Y) = \sum_i {V_i } + \sum_i {\sum_{j > i} {V_{ij} } } + \cdots + V_{12 \cdots k} \tag{11}$$ 其中$V_i = V[E(Y\left| {X_i } \right.)],V_{ij} = V[E(Y\left| {X_i } \right.,X_j )],\cdots $，式(11)两边除以$V(Y)$，得到下式 $$ \sum_i {S_i } + \sum_i {\sum_j {S_{ij} } } + \sum_i {\sum_{j > i} {\sum_{l > j} {S_{ijl} } } } + \cdots + S_{123\ldots k} = 1 \tag{12}$$ 其中，$S_i $是主灵敏度指标，$S_{ij} ,S_{ijl} ,\cdots ,S_{123\ldots k} $体现交叉影响. 主要灵敏度指标可以表示为单个输入变量条件下输出响应条件期望的方差与总方差之比 $$ S_i = \dfrac{V[E(Y\left| {X_i } \right.)]}{V(Y)} \tag{13}$$

非线性函数$f(x_1 ,x_2 ) = x_1 \times x_2 $，其中$x_1 $，$x_2 $服从如下正态分布$\mu _1 = 1,\mu _2 = 2,\sigma _1 = 3,\sigma _2 = 2$，采用6阶精度的SGNI方法对$f(x_1 ,x_2 )$进行不确定性和全局灵敏度分析，结果如表2所示.

表2(Table 2)

表2 SGNI方法分析结果对比Table 2 Comparison of result of SGNI method SGNI Analytic solution mean 2.000 0 2.000 variance 76.000 76.000 $S_{x_1 } $ 0.473 7 9/19 $S_{x_2 } $ 0.052 6 1/19 $S_{x_1 ,x_2 } $ 0.473 7 9/19

表2 SGNI方法分析结果对比 Table 2 Comparison of result of SGNI method

控制方程采用积分形式的N-S方程和Euler方程，求解N-S方程得到气动热，求解Euler方程得到壁面当地流动参数，其统一形式如下 $$ \dfrac{\partial }{\partial t}\iint\limits_V { Q} \cdot d v + \int\limits_{\partial V} { { F} \cdot { n} d s} = 0 \tag{14}$$ 其中，${ Q} = [\rho ,\rho u,\rho v,\rho w,e]^{\rm T}$，$\rho ,u,v,w,e$分别为空气密度、$x,y,z$方向的速度分量和单位体积的总内能，${ n}$为积分边界的单位法向向量，$V$为流场积分域，$\partial V$为积分域的边界，${ F}$为通量项，它包括无黏项${ F}_{\rm E} $和黏性项${ F}_{\rm v} $两部分 $$ { F} = { F}_{\rm E }+ { F}_{\rm v } \tag{15}$$

空间离散采用AUSM+格式，采用SST湍流模型，湍流模型采用中心格式，时间推进采用LU-SGS格式，令${ F}_{\rm v }={\bf 0}$，则方程变为Euler方程.通过求解N-S方程来计算舵面上的温度分布，其中物面的边界条件采用辐射热平衡，热辐射采用Stefan-Boltzmann定律修正公式进行计算 $$ q_{\rm rad} = \sigma \varepsilon (T_{\rm w}^4 - T_\infty ^4 ) \tag{16}$$ 其中，$\varepsilon $为物体辐射发射率，本文取0.8，$\sigma $为斯坦福常数为$5.669 7\times 10^{ - 8}$ W/(m$^2$K$^4$).

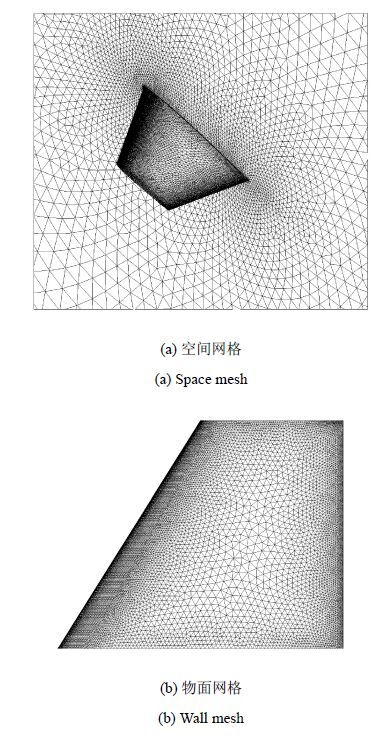
空间及物面网格划分如图7所示.

图7(Fig.7)

图7 舵面模型网格 Fig.7 Mesh of control surface

热应力广义虎克定律${ \sigma} = { D}\left( {{ \varepsilon} -{ \varepsilon}_{\rm T} } \right)$，其中 $$D = \dfrac{E}{1 - u - 2 u ^2} \cdot$$ $$\left[\!\!\begin{array}{cccccc} {1 - u } & u & u & 0 & 0 & 0 \\ u & {1 - u } & u & 0 & 0 & 0 \\ u & u & {1 - u } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\dfrac{1 - 2 u }{2}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\dfrac{1 - 2 u }{2}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\dfrac{1 - 2 u }{2}} \end{array}\!\!\right] \tag{17}$$ $${ \varepsilon}_{\rm T} = (\alpha \Delta T,\alpha \Delta T,\alpha \Delta T,0,0,0)^{\rm T} $$ 其中，${ \sigma }$是考虑变温度影响的弹性应力，称为热应力；${ \varepsilon } $为总应变；${ \varepsilon}_{\rm T} $是由温度改变而引起的热应变.${ D}$为弹性矩阵，$E$为弹性模量，$u $为泊松比. 将${ \sigma} ={ D}\left( {{ \varepsilon }-{ \varepsilon}_{\rm T} } \right)$变形，可得${ \varepsilon} = { D}^{-1}{ \sigma} + { \varepsilon}_{\rm T} $.

令${ \varepsilon }_{\rm E} = { D}^{-1}{ \sigma} $; ${ S} = { D}^{-1}$，则有${ \varepsilon} ={ S}{ \sigma}+ { \varepsilon}_{\rm T} = { \varepsilon}_{\rm E} + { \varepsilon}_{\rm T} $

因此，可将总应变为两部分之和：一部分是由应力引起的弹性应变${ \varepsilon }_{\rm E} $；另一部分是由温度变化引起的热应变${ \varepsilon}_{\rm T} $.

考虑温度效应并忽略阻尼的结构自由振动方程如下所示 $$ { M}\ddot{ u} + \left( {{ K}_{\rm s} (T) + { K}_\sigma (T)} \right) { u }= {\bf 0} \tag{18}$$ 其中，${ M}$为质量阵，${ K}_{\rm s} (T)$为传统的结构刚度矩阵，考虑到结构材料属性随温度变化，故而为温度的函数；${ K}_\sigma (T)$为热应力引起的附加几何刚度矩阵. 当结构发生简谐振动，即${ u} = { U}\sin (\omega t)$时，方程为 $$ \left( {{ K}_{\rm s} (T) + { K}_\sigma (T) - \omega _i^2 { M}} \right)\phi _i = {\bf 0} \tag{19}$$

通过求解上述特征方程可以得到结构的前$i$阶固有圆频率$\omega _i $和模态$\phi _i $. 结构温度为300 K时，结构前四阶固有频率计算结果如表3所示.

表3(Table 3)

表3 结构固有频率Table 3 Natural frequency of structure Mode 1 Mode 2 Mode 3 Mode 4 Freq/Hz 17.262 32.913 153.96 198.2

表3 结构固有频率 Table 3 Natural frequency of structure

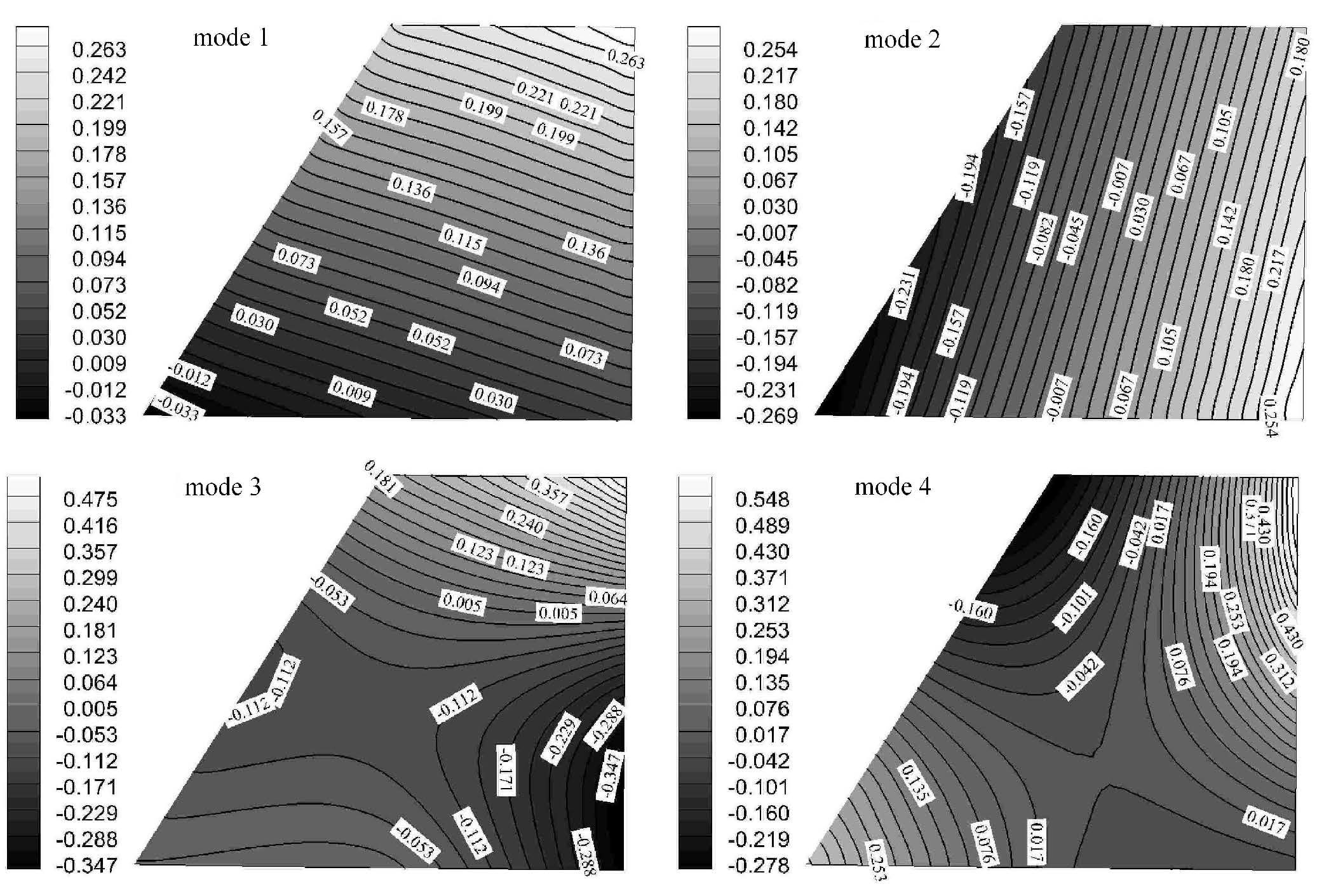
采用径向基函数方法(radial basis function,RBF)，将模态插值到气动网格上，图8为前四阶模态云图.

图8(Fig.8)

图8 前四阶阵型 Fig.8 First four order modal

非定常气动力计算采用文献^[23]基于CFD技术的当地流活塞理论，其基于模态坐标的气动力为 $$ { Q} = \dfrac{\rho _\infty V_\infty ^2 }{M_\infty }{ A}{\xi} + \dfrac{\rho _\infty V_\infty } {M_\infty }{ B}\dot {\xi } \tag{20}$$ 其中

$${ A}_{ij} = \iint\limits_{\rm wing} \Bigg\{ \sqrt {D_\rho D_p } \left[{D_a D_M \cdot ({ n}_0 - { n}_j^0 )} \right]\cdot \Big[( - { n}_0 ) \cdot { z}{ x}_i \Big]\Bigg\} d s \tag{21}$$

$${ B}_{ij} = \iint\limits_{wing} {\left\{ {\sqrt {D_\rho D_p } \left[{{ z}{ x}_j \cdot { n}_0 } \right]\left[{( - { n}_0 ) \cdot { z}{ x}_i } \right]} \right\}d s} \tag{22}$$

$$D_p = \dfrac{p_{\rm l} }{p_\infty } \tag{23a}$$

$$ D_\rho = \dfrac{\rho _{\rm l} }{\rho _\infty } \tag{23b}$$

$$D_a = \dfrac{a_{\rm l} }{a_\infty } \tag{23c}$$

$$D_M = \dfrac{M_{\rm l} }{M_\infty } \tag{23d}$$ 其中，$\rho _\infty $,$V_\infty $,$M_\infty $,$p_\infty $和 $a_\infty $表示来流密度、速度、马赫数、压强和声速；$\rho _{\rm l} $,$V_{\rm l} $,$M_{\rm l} $,$p_{\rm l} $和$a_{\rm l} $表示当地密度、速度、马赫数、压强和声速；${ n}_0 $为物面变形前的外法线单位矢量，${ n}_j^0 $为第$j$阶模态单位变形后的物面外法线单位矢量，${ z}{ x}_i $为对应点的第$j$阶振型，${ \xi} $为广义坐标.

对于一个特定计算状态，用Euler方程得到定常流场后，即可确定${ A}$和${ B}$，进而得到了气动力关于广义位移的表达式.

应用拉格朗日方程，基于模态坐标的的运动方程可以写为 $$ { M}\ddot { \xi } + { G}\dot { \xi } + { K}{ \xi} = { Q} \tag{24}$$ 其中，${ M}$为质量矩阵，${ G}$为结构阻尼矩阵，${ K}$为刚度矩阵，${ Q}$为广义气动力. 实验测定${ G}$很困难，这里令${ G}$为0. 将式(20)代入式(24)得 $$ { M}\ddot{ \xi } + { K}{ \xi }= \dfrac{\rho _\infty V_\infty ^2 }{M_\infty }{ A}{ \xi }+ \dfrac{\rho _\infty V_\infty }{M_\infty }{ B}\dot{ \xi } \tag{25}$$ 令${ x}_{\rm s} = \left[{\xi _1 ,\xi _2 ,\cdots ,\xi _N ,\dot {\xi }_1 ,\dot {\xi }_2 ,\cdots ,\dot {\xi }_N } \right]^{\rm T}$，则颤振方程可写为 $$ \dot{ x}_{\rm s} = { C} \cdot { x}_{\rm s} \tag{26}$$ 其中 $$ { C} = \left[\!\!\begin{array}{cc} {\bf 0} & { I} \\ { M}^{ - 1}\left( {\dfrac{\rho _\infty V_\infty ^2 }{M_\infty }{ A} -{ K}} \right) & \dfrac{\rho _\infty V_\infty }{M_\infty }{ M}^{ - 1}{ B} \end{array} \!\! \right] \tag{27}$$

给定$M_\infty $,$V_\infty $和$\rho _\infty $，则${ C}$为一实矩阵，这样气动弹性系统的稳定性分析就转化为求解状态方程中矩阵${ C}$的特征值问题了.当某一特征值的根轨迹穿越虚轴时，系统的稳定性将发生变化，该根的虚部表示颤振的频率.详细推导过程以及验证算例参考文献^[23].

针对本文的全动舵面模型，分别在$M =5$，$H =15$ km，$\alpha=0^\circ$ 和$M=6$，$H=15$ km，$\alpha=0^\circ$两种飞行状态，对热气动弹性中气动热的不确定性影响进行分析.

来流参数为：$M =5$，$H =15$ km，$\alpha=0^\circ$，温度分布函数中各参数值如下 $$ p_1 = 625.5 ,p_2 = 74.86 ,p_3 = 0.074 83 \\ q_1 = 1 010 ,a = 0.625 ,b = 1 010 $$

不确定参数$p_1 $和$q_1 $的统计特征如表4所示，本文取$p_1 $的变异系数为0.2，而$q_1 $的变异系数为0.1，其原因为：此条件下，两参数对温度的最大扰动均为101 K，在进行全局灵敏度分析时，$p_1 $和$q_1 $时可以近 似认为对函数处于同一程度的影响，状态二与此类似.

表4(Table 4)

表4 不确定参数统计特征Table 4 Static property of the uncertainty parameters Distribution Mean Standard deviation Variation coefficient $p_1 $ normal 625.50 125.10 0.20 $q_1 $ normal 1 010.00 101.00 0.10

表4 不确定参数统计特征 Table 4 Static property of the uncertainty parameters

分别采用MCS方法和SGNI方法对上述问题进行不确定性及灵敏度分析，为了使得分析尽量准确，MCS方法中样本数为20 000；SGNI方法采用10阶精度，其中做不确定性分析积分点数为381，做全局灵敏度分析积分点数为200.

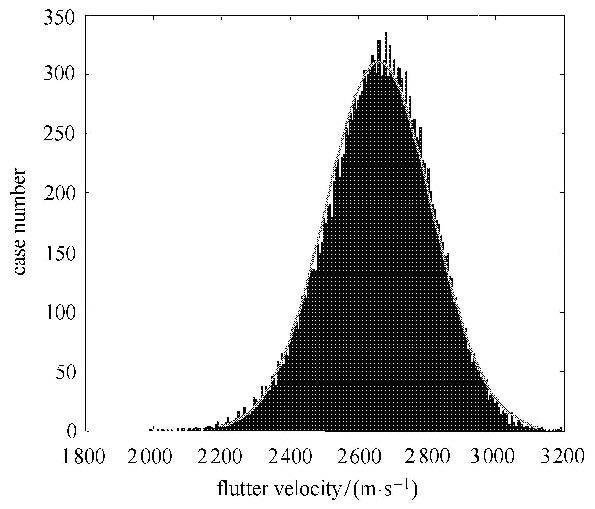
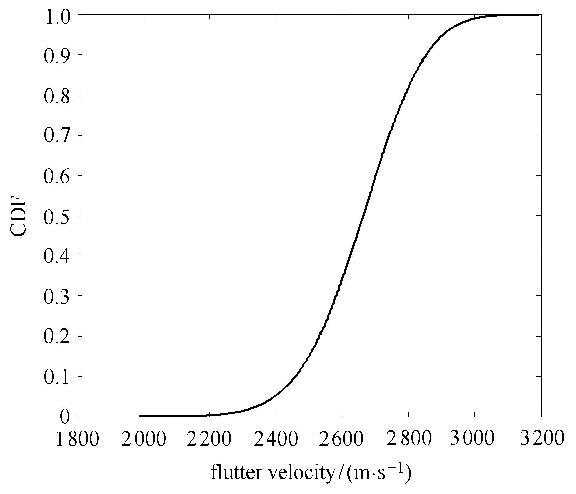
图9和图10分别为MCS方法得到的颤振速度概率密度分布和累计概率密度分布，表5和表6分别为采用MCS方法和SGNI方法分析得到的热气动弹性不确定性以及全局灵敏度结果，可以看出两种方法分析的结果非常接近，但是，SGNI方法所需计算的样本数量远低于MCS方法，从分析结果看，舵面结构的一阶频率、二阶频率、一阶频率和二阶频率的间距以及颤振速度和频率的变异系数都非常接近，都在5.82%附近. 说明对本文模型而言，温度分布的不确定性对结构刚度和颤振分析的影响规律是一致的.其中参数$p_1 $的灵敏度为0.535，参数$q_1 $的全局灵敏度为0.464，说明在上述不确定参数分布下，$p_1 $和$q_1 $的不确定性对颤振结果的影响接近，$p_1 $略高于$q_1 $，$p_1 $和$q_1 $耦合作用的全局灵敏度为0.000 3，非常小，说明耦合作用几乎可忽略.

图9(Fig.9)

图9 颤振速度概率密度 Fig.9 Probability density of flutter velocity

图10(Fig.10)

图10 颤振速度累计概率密度 Fig.10 Cumulative probability density of flutter velocity

表5(Table 5)

表5 MCS方法不确定性以及全局灵敏度分析结果 Table 5 Uncertainty and global sensitivity analysis results of MCS method First order frequency/Hz Secondorder frequency/Hz Frequency space/Hz Flutter velocity/(m·s-1) Flutter frequency/Hz mean 13.650 00 26.176 50 12.524 20 2 658.930 20.202 50 standard deviation 0.794 240 1.523 856 0.729 612 154.818 3 1.175 972 variation coefficient 0.058 186 0.058 215 0.058 256 0.058 226 0.058 209 $S_{p_1 } $ 0.535 522 0.533 532 0.531 452 0.537 561 0.537 217 $S_{q_1 } $ 0.464 160 0.462 959 0.461 866 0.461 689 0.462 682 $S_{p_1 - q_1 } $ 0.000 318 0.003 509 0.006 682 0.000 750 0.000 101

表5 MCS方法不确定性以及全局灵敏度分析结果 Table 5 Uncertainty and global sensitivity analysis results of MCS method

表6(Table 6)

表6 SGNI方法不确定性以及全局灵敏度分析结果 Table 6 Uncertainty and global sensitivity analysis results of SGNI method First order frequency/Hz Secondorder frequency/Hz Frequency space/Hz Flutter velocity/(m·s-1) Flutter frequency/Hz mean 13.137 31 13.652 12 12.526 56 2 659.630 20.205 69 standard deviation 0.766 750 0.795 296 0.730 689 154.909 0 1.172 990 variation coefficient 0.058 364 0.058 254 0.058 331 0.058 243 0.058 052 $S_{p_1 } $ 0.535 402 0.533 328 0.535 956 0.536 674 0.541 039 $S_{q_1 } $ 0.459 848 0.461 853 0.459 511 0.460 673 0.456 359 $S_{p_1 - q_1 } $ 0.004 750 0.004 819 0.004 533 0.002 653 0.002 602

表6 SGNI方法不确定性以及全局灵敏度分析结果 Table 6 Uncertainty and global sensitivity analysis results of SGNI method

对状态二进行不确定性分析，状态二的来流参数为：$M =6$，$H =15$km，$\alpha=0^\circ$，温度分布函数中各参数值如下 $$ p_1 = 758.3 ,p_2 = 84.92 ,p_3 = 0.061 38 \\ q_1 = 1421 ,a = 0.625 ,b = 1421 $$ 其中，不确定参数$p_1 $和$q_1 $的统计特征如表7所示.

表7(Table 7)

表7 不确定参数统计特征Table 7 Statistic property of uncertainty parameters Distribution Mean Standard deviation Variation coefficient $p_1 $ normal 758.30 151.66 0.20 $q_1 $ normal 1 421.00 142.10 0.10

表7 不确定参数统计特征 Table 7 Statistic property of uncertainty parameters

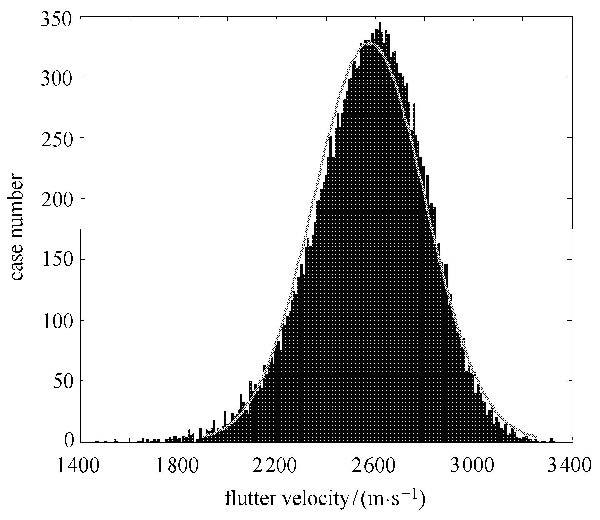
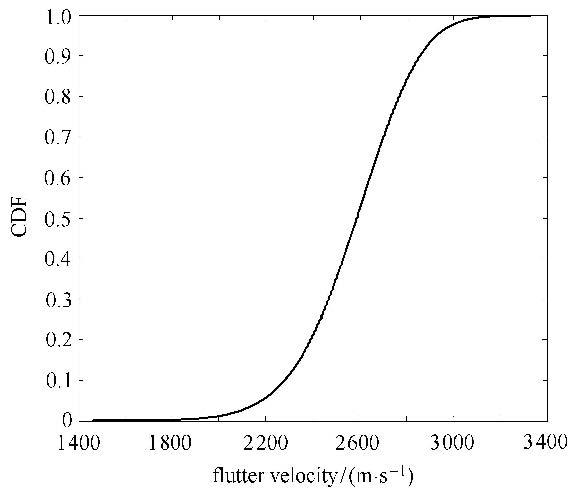
图11和图12，分别为MCS方法得到的颤振速度概率密度分布和累计概率密度分布，表8和表9分别为采用MCS方法和SGNI方法分析得到的热气动弹性不确定性以及全局灵敏度结果，从分析结果看，舵面结构的一阶频率、二阶频率、频率间距以及颤振速度和频率的变异系数非常接近，都在8.83%附近.此时，气动热的不确定性对结构频率和颤振特性有着明显的影响，因此，结构设计时应对气动热的不确定性产生的影响应加以考虑.

图11(Fig.11)

图11 颤振速度概率密度图 Fig.11 Probability density of flutter velocity

图12(Fig.12)

图12 颤振速度累计概率密度 Fig.12 Cumulative probability density of flutter velocity

表8(Table 8)

表8 MCS方法不确定性以及全局灵敏度分析结果Table 8 Uncertainty and global sensitivity analysis results of MCS method First order frequency/Hz Secondorder frequency/Hz Frequency space/Hz Flutter velocity/(m·s-1) Flutter frequency/Hz mean 12.779 78 24.511 19 11.729 58 2 576.520 18.647 78 standard deviation 1.130 163 2.167 413 1.037 249 227.600 0 1.647 405 variation coefficient 0.088 434 0.088 425 0.088 430 0.088 338 0.088 343 $S_{p_1 } $ 0.472 670 0.473 719 0.474 567 0.472 425 0.472 719 $S_{q_1 } $ 0.525 122 0.524 199 0.523 115 0.525 686 0.525 614 $S_{p_1 - q_1 } $ 0.002 208 0.002 082 0.002 318 0.001 889 0.001 667

表8 MCS方法不确定性以及全局灵敏度分析结果 Table 8 Uncertainty and global sensitivity analysis results of MCS method

表9(Table 9)

表9 SGNI方法不确定性以及全局灵敏度分析结果Table 9 Uncertainty and global sensitivity analysis results of SGNI method First order frequency/Hz Secondorder frequency/Hz Frequency space/Hz Flutter velocity/(m·s-1) Flutter frequency/Hz mean 12.771 03 24.516 50 11.728 90 2 576.470 18.648 17 standard deviation 1.132 696 2.171 439 1.037 261 227.930 0 1.648 742 variation coefficient 0.088 692 0.088 570 0.088 435 0.088 465 0.088 413 $S_{p_1 } $ 0.469 838 0.471 876 0.474 481 0.471 181 0.471 815 $S_{q_1 } $ 0.522 871 0.522 641 0.523 545 0.524 165 0.524 318 $S_{p_1 - q_1 } $ 0.007 291 0.005 483 0.001 974 0.004 654 0.003 867

表9 SGNI方法不确定性以及全局灵敏度分析结果 Table 9 Uncertainty and global sensitivity analysis results of SGNI method

相比于状态一，当不确定参数的变异程度一样时，状态二中结构频率和颤振分析结果的变异程度都要高于状态一. 参数$p_1 $的灵敏度为0.472 6，参数$q_1 $的灵敏度为0.525，相比于状态一，$p_1 $的全局灵敏度略有下降，$q_1 $的全局灵敏度略有上升，$p_1 $和$q_1 $耦合作用的全局灵敏度依然很小为0.002.

表10为分别采用MCS和SGNI方法进行不确定性及全局灵敏度分析时的效率对比，表中的CPU时间数据均为单个CPU下的结果，实际操作中，本文将分析方法中所有流程通过程序实现自动调用，利用现有计算资源：两台四核(CPU主频为4.00 GHz)计算机，两个状态的计算时间约为11天. 其中主要的时间花费在MCS方法上.虽然本文的MCS方法计算样本较多，但是，在两个不确定性参数条件下，10阶精度SGNI方法的计算结果与MCS方法非常接近，且效率比MCS方法的提高了50倍左右，说明SGNI方法是一种高效的不确定分析方法.

表10(Table 10)

表10 MCS方法和SGNI方法效率对比Table 10 Efficiency between MCS method and SGNI method Uncertainty analysis Global sensitivity analysis Number of sample CPU time/h Number of sample CPU time/h MCS 20 000 220 30 000 330 SGNI 381 4.19 200 2.20

表10 MCS方法和SGNI方法效率对比 Table 10 Efficiency between MCS method and SGNI method

本文关于高超声速热气动弹性中气动热不确定性的影响研究有以下结果：

(1)提出了一种适合本文舵面的温度分布参数化模型，该模型参数数量少，仅有两个，且可以描述温度分布的两种重要扰动形式.

(2)分别在两种飞行状态下，采用MCS方法和SGNI方法对温度分布问题进行不确定性和全局灵敏度分析，结果表明：在本文的给定的不确定参数下，① $M =5$，$H =15$ km，结构固有频率和颤振分析结果的变异系数为5.83%. ② $M= 6$，$H =15$ km，结构固有频率和颤振分析结果的变异系数为8.84%，这表明气动热的不确定性对结构频率和颤振特性有着明显的影响，结构设计时应加以考虑.

(3)两种飞行状态下，本文设计的两个不确定参数的全局灵敏度都在50%左右，两者耦合作用很小.

(4) MCS方法和SGNI方法的计算结果非常接近，SGNI方法的效率远高于MCS方法.

Ye Kun, Ye Zhengyin, Qu Zhan, Wu Xiaojin, Zhang Weiwei