2. 西安交通大学航天航空学院, 机械结构强度与振动国家重点实验室, 西安 710049
潜艇具有隐蔽性好、突袭力强等特点,是海战中的重要威慑力量,各国海军对其发展极为重视[1]. 但是,伴随着声纳技术的不 断发展,潜艇的隐蔽性已经成为了其最重要的性能之一,也是潜艇技术需要优先考虑的发展方向[2]. 潜艇的辐射噪声每降低6$\sim$10 dB,敌方被动声纳的作用距离就可降低约50%,而己方被动声纳的作用距离可提高1倍左 右[3]. 在潜艇壳体表面覆盖消声层是提高潜艇声隐身性能最常用的方法. 消声层既能吸收敌方声纳探测声波的能量,减少其反射,又可减少潜艇内部机械振动产生的噪声辐射,同时还可改善艇体表面的流体动力特性,减小阻力[4]. 因此,针对水下消声结构声学性能开展研究,对提高潜艇的声隐身效果起着至关重要的作用.
水下消声结构得到了各海洋军事大国的重视,并被广泛运用于潜艇结构降噪[5]. 在诸多材料中,高分子黏弹性材料在消声结构中的应用最广,包括共振式、阻抗渐变式、夹芯层式、微粒复合式和压电复合式结构等典型结构[6],主要消声机理有[4, 7]:黏弹性损耗吸声、波型转换吸声、周期散射吸声、低频谐振吸声等.
针对包含有颗粒夹杂物的消声层,有学者从理论上求解了颗粒复合材料的等效参数[8]. 赵敏兰 等[9]基于文献[8]的理论,求解了含球形孔腔弹性体的等效参数,研究了这种消声层的消声性能. 有人进一步研究了背衬对含球形夹杂物消声层的影响,指出背衬在低频段的影响较明显,当背衬质量增加时,吸声峰值向低频方向移动[10]. 还有人利用波导法研究了含多重柔性管栅的黏弹性消声层的声学特性[11, 12];朱锡等[13]提出了夹芯复合材料在消声层中的应用,指出这种结构具有结构承载和声隐身一体化的优点,避免了传统消声层容易脱落的问题. 另外,文献[14]提出了一种名为声子玻璃(phononic glass)的材料结构,这是一种在传统的具有网络状结构的泡沫铝中填充聚氨酯材料的结构,其在很高的水压下还能保持较宽的消声频带.
目前,在众多类别的消声结构中,内部含有渐变孔腔的开孔型消声层运用最广. 由于消声层孔腔的尺寸沿厚度方向变化,故消声层内的声学参数也沿厚度方向变化. 理论分析时,有必要把开孔型消声层等效为多层均质结构,然后利用传递函数法开展研究. 例如,有学者从理论上推导出了由固体层和液体层组成的多层系统在声波入射下的传递矩阵[15];杨雪等[16]运用三维传递矩阵的数学模型,计算了多层复合结构的吸声系数,发现外层材料的性能参数变化对吸声性能的影响更为明显;还有学者对多层黏弹性结构的声波反射和透射性能进行了综合分析与计算[17, 18];有人针对声波的斜入射问题,对多层结构进行了研究[19]. 此外,何世平等[20]通过解析计算,给出了含变截面圆柱形孔腔消声层的二维近似解;文献[21]运用有限元法,以阿尔贝里西(Alberich)型开孔消声层为例,分析了双重周期结构的消声层的声学性能;陶猛等[22]则研究了阿尔贝里西消声层的低频消声特性及其与内部孔腔共振之间的关系. 在相同穿孔率的情况下,有人对消声层内孔腔的形状进行了分析比较,发现含圆台型空腔优于含圆柱型空腔[23];有人从理论和实验两个方面对含有方形截面和圆形截面孔腔的消声层进行了声学性能的分析与比较[24];还有人运用马尔可夫链蒙特卡尔理论(MCMC)对消声层进行了优化分析,比较了不同孔腔截面形状对消声性能的影响[25];文献[26]则主要通过有限元法,研究了含圆柱形孔腔的消声层的声学性能.
上述研究大多是针对消声层自身的研究,未考虑潜艇壳体与消声层的耦合振动对整个壁面结构的影响. 针对覆盖有消声层的平板,在平板受到激振力时,有学者采用弹性理论研究了整个结构的声学性能[27];针对开孔型消声层与潜艇壳体相连的潜艇壁面结构,文献[28]研究了当艇壳受到激振力时壁面结构的振动与声学性能,指出整个结构的减振降噪效果来自于消声层对结构振动的削弱作用,并非平板自身振动的减弱.
在文献[28]工作基础上,本文进一步考虑潜艇壁面结构两侧流体负载对水下消声覆盖层声学性能的影响. 本文考虑潜艇的外壁面结构,可以是潜艇中人员生活工作的舱室或放置艇用设备器械的舱室,其壁面结构的内侧介质为空气,外侧介质为水;也可以是控制潜艇升降、平衡的水舱,其壁面结构的内外侧介质均为水. 因此,本文在壁面结构两侧均考虑流体负载,相比文献[28]只考虑外侧水介质的工况更符合实际. 另外,在相同的激振力作用下,本文还比较了相同的壁面结构应用于不同的介质工况(内侧介质为空气或水)时,结构振动与声学性能的异同,而这在其它文献中很少涉及.
下文将选取由艇壳和开孔型消声层两部分组成的潜艇壁面结构为研究对象,建立其消声理论模型,应用传递函数法进行解析求解. 随后,根据具体的材料、介质参数,利用理论模型进行数值计算,讨论内侧介质、艇壳厚度、消声层厚度和孔腔形状等因素对潜艇壁面结构振动与声学性能的影响.
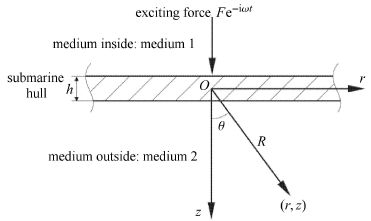
1 理论分析 1.1 无消声层时潜艇壳体的声学性能如图 1所示,由于艇壳的曲率较小,且其厚度远小于壁面尺寸,为简化分析将其考虑为无曲率的无限大薄板,其厚度为$h$, 内侧介 质记为介质1,外侧介质记为介质2. 假设潜艇内部传给艇壳的振动为点激振力$F{\rm e}^{-{\rm i}\omega t}$. 有鉴于结构的轴对称性,采用圆柱 坐标系,$Or$平面位于艇壳的中面,$Oz$轴位于激振力的作用线上,方向指向潜艇外部. 介质2中任意一点$\left( {r,z} \right)$离原点$O$的距离为$R$,原点与该点连成的向量与$Oz$轴的夹角为$\theta $.
|
图 1 无消声层时潜艇壁结构示意图 Fig.1 Schematic of submarine wall structure without sound anechoic layer |
基于薄板理论,艇壳的振动方程为
| $D\left( {\nabla ^4 - k_{\rm f}^4 } \right)w_{\rm w} \left( r \right) = p_1 \left( {r,0} \right) - p_2 \left( {r,0} \right) + \dfrac{F\delta \left( r \right)}{2π r} $ | (1) |
式中,$w_{\rm w} \left( r \right)$为艇壳上各点在其法向上的位移,$p_1 \left( {r,0} \right)$与$p_2 \left( {r,0} \right)$分别为介质1与介质2中艇壳处的声压值,$D = E{h^3}/\left[ {12\left( {1 - {\nu ^2}} \right)} \right]$为艇壳的抗弯刚度,其中$E$和$\nu $分别为其母体材料的杨氏模量、泊松比. $k_{\rm f} = \left[{{12\omega ^2} /{\left( {c_{\rm p}^2 h^2} \right)}} \right]^{1/4}$为艇壳中的弯曲波波数,$\omega $为圆频率,$c_{\rm p} = \sqrt {E /{\left[{\left( {1 - \nu ^2} \right)\rho _{\rm w} } \right]}} $为艇壳中的压缩波波速,$\rho _{\rm w} $为艇壳的密度.
介质1和2中的声波控制方程为[29]
| $\left( {\nabla _r^2 + \dfrac{\partial ^2}{\partial z^2} + k_1^2 } \right)p_1 \left( {r,z} \right) = 0 $ | (2) |
| $ \left( {\nabla _r^2 + \dfrac{\partial ^2}{\partial z^2} + k_2^2 } \right)p_2 \left( {r,z} \right) = 0 $ | (3) |
式中,$p_1 \left( {r,z} \right)$和$p_2 \left( {r,z} \right)$分别为介质1和2中的声压,$k_1 = \omega / {c_1 }$和$k_2 = \omega /{c_2 }$分别为介质1和2中的声波波数,$c_1 $和$c_2 $分别为介质1和2中的声速.
利用汉克尔变换,可分别把式(1) $\sim$式(3)变换到波数域中
| $D\left( {\gamma ^4 - k_{\rm f}^4 } \right)\tilde {w}_{\rm w} (\gamma) = \tilde {p}_1 \left( {\gamma ,0} \right) - \tilde {p}_2 \left( {\gamma ,0} \right) + \dfrac{F}{2π } $ | (4) |
| $\left[{\dfrac{\partial ^2}{\partial z^2} + \left( {k_1^2 - \gamma ^2} \right)} \right]\tilde {p}_1 \left( {\gamma ,z} \right) = 0 $ | (5) |
| $\left[{\dfrac{\partial ^2}{\partial z^2} + \left( {k_2^2 - \gamma ^2} \right)} \right]\tilde {p}_2 \left( {\gamma ,z} \right) = 0 $ | (6) |
式中,$\gamma $为波数,$\tilde {w}_{\rm w} $,$\tilde {p}_1 $和$\tilde {p}_2 $分别为$w_{\rm w} $,$p_1 $和$p_2 $在波数域中的值. 下文中,若把某一物理量$X$记为$\tilde {X}$,则$\tilde {X}$为$X$在波数域中的值.
联立求解式(4) $\sim$式(6),可得在波数域中,艇壳位移和介质1和2中的声压分别为
| $\tilde {w}_{\rm w} (\gamma) = \dfrac{{\rm i}F}{2π \omega } \cdot \dfrac{1}{\tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_1 ( \gamma ) + \tilde {Z}_2 (\gamma)} $ | (7) |
| $\tilde {p}_1 \left( {\gamma ,z} \right) = {\rm i} \omega \tilde {Z}_1 ( \gamma )\tilde {w}_{\rm w} (\gamma){\rm e}^{{\rm i}z\sqrt {k_1^2 - \gamma ^2} } $ | (8) |
| $\tilde {p}_2 \left( {\gamma ,z} \right) = - {\rm i}\omega \tilde {Z}_2 \left( \gamma \right)\tilde {w}_{\rm w} (\gamma){\rm e}^{{\rm i}z\sqrt {k_2^2 - \gamma^2} } $ | (9) |
式中,$\tilde {Z}_{\rm w} (\gamma)$,$\tilde {Z}_1 \left( \gamma \right)$ 和$\tilde {Z}_2 \left( \gamma \right)$分别为波数域中艇壳的机械阻抗、介质1的声阻抗、介质2的声阻抗,其表达式分别为
| $\tilde {Z}_{\rm w} (\gamma) = - {\rm i}\omega \rho _{\rm w} h\left( {1 - \dfrac{\gamma ^4}{k_{\rm f}^4 }} \right) $ | (10) |
| $\tilde {Z}_1 (\gamma) = \dfrac{\rho _1 \omega }{\sqrt {k_1^2 - \gamma ^2} } $ | (11) |
| $\tilde {Z}_2 (\gamma) = \dfrac{\rho _2 \omega }{\sqrt {k_2^2 - \gamma ^2} } $ | (12) |
式中,$\rho _1 $和$\rho _2 $分别为介质1和2的密度.
对式(7) $\sim$式(9)分别进行反汉克尔变换可得波数域中,艇壳位移和介质1和2中声压的如下无穷积分形式
| $ \begin{array}{l} {w_{\rm{w}}}\left( r \right) = \frac{{{\rm{i}}F}}{{4\pi \omega }}\int_{ - \infty }^{ + \infty } {\frac{1}{{{{\tilde Z}_{\rm{w}}}(\gamma ) + {{\tilde Z}_1}\left( \gamma \right) + {{\tilde Z}_2}(\gamma )}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J_0^{(1)}\left( {\gamma r} \right)\gamma d\gamma \end{array} $ | (13) |
| $ \begin{array}{l} {p_1}\left( {r,z} \right) = \frac{F}{{4\pi }}\int_{ - \infty }^{ + \infty } {\frac{{{{\tilde Z}_1}(\gamma )}}{{{{\tilde Z}_{\rm{w}}}(\gamma ) + {{\tilde Z}_1}(\gamma ) + {{\tilde Z}_2}(\gamma )}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e^{iz\sqrt {k_1^2 - {\gamma ^2}} }}J_0^{(1)}(\gamma r)\gamma d\gamma \end{array} $ | (14) |
| $ \begin{array}{l} {p_2}\left( {r,z} \right) = \frac{F}{{4\pi }}\int_{ - \infty }^{ + \infty } {\frac{{{{\tilde Z}_2}(\gamma )}}{{{{\tilde Z}_{\rm{w}}}\left( \gamma \right) + {{\tilde Z}_1}(\gamma ) + {{\tilde Z}_2}\left( \gamma \right)}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{e}}^{{\rm{i}}z\sqrt {k_2^2 - {\gamma ^2}} }}J_0^{\left( 1 \right)}\left( {\gamma r} \right)\gamma d\gamma \end{array} $ | (15) |
对式(13) $\sim$式(15),其无穷积分可变换为在复平面中的周线积分,然后运用稳相法可得介质2中在原始坐标系下的远场声压为
| $ p_2 \left( {R,\theta } \right) =\\ \qquad - \dfrac{{\rm i}\omega \rho _2 F{\rm e}^{{\rm i}k_2 R}}{2π R}\dfrac{1}{\tilde {Z}_{\rm w} \left( {\gamma _{\rm s} } \right) + \tilde {Z}_1 \left( {\gamma _{\rm s} } \right) + \tilde {Z}_2 \left( {\gamma _{\rm s} } \right)} $ | (16) |
式中,$\gamma _{\rm s} = k_2 \sin \theta $为稳相点处$\gamma $的值.
有消声层时,潜艇壁面结构由潜艇壳体和消声层组成,如图 2所示. 考虑基于黏弹性高分子材料(橡胶)的开孔型消声层,其内的孔腔周期 性排列,孔腔的横截面沿其轴向渐变. 声波传入时,材料中的高分子链产生形变与相互之间的内摩擦,从而声能转化为热能而被损耗. 另外,由于流体介质只能传播纵波,而固体介质可以传播纵波与横波,故在基底材料靠近孔腔表面的区域内,由孔腔内流体部分传来的 纵波会部分转换为横波. 由于横波剪切变形比纵波体积变形更易使黏弹性高分子材料产生热能损耗,故开孔后产生的这种波形转换作用可以增强消声层对声能的 损耗[4, 7].

|
图 2 有消声层时潜艇壁面结构 Fig.2 Schematic of submarine wall structure with sound anechoic layer |
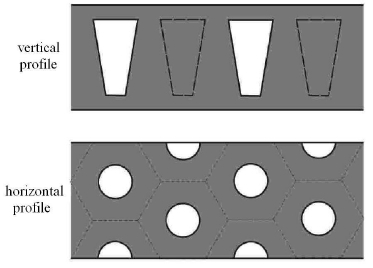
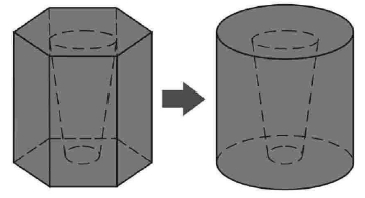
如图 3所示,由于开孔型消声层中的孔腔呈周期性分布,建模计算时可仅分析含单个孔腔的胞元(单元胞). 简便起见,考虑正六棱柱胞 元并将其近似为圆柱胞元,如图 4所示,近似的原则是孔腔在胞元中所占的体积分数不变. 该近似已被证明足够精确[30].
|
图 3 消声层的剖面图 Fig.3 Profile of anechoic layer |
|
图 4 消声层胞元 Fig.4 Unit cell in anechoic layer |
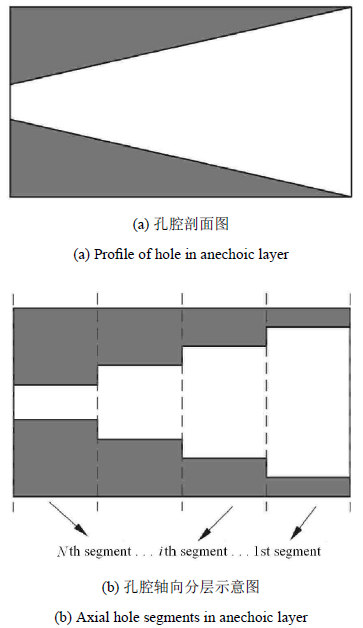
考虑单元中孔腔的横截面大小沿其轴向渐变,如图 5(a)所示. 该渐变孔腔可简化为如图 5(b)所示的多层等间距声学圆管结构,邻近层 界面满足声压连续和质点振速连续的条件[20,31].
|
图 5 消声层胞元剖面 Fig.5 Cross-section of unit cell in anechoic layer |
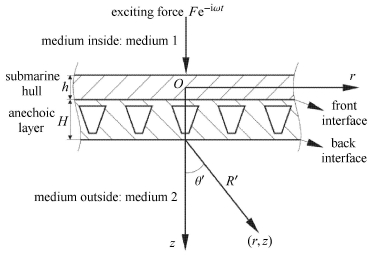
有消声层覆盖时的潜艇壁面结构如图 6所示. 与图 1所示的无消声层潜艇壁结构相比,内外部的介质依然分别记为介质1、介质2,激 振力不变,坐标系的选取不变. 艇壳的厚度为$h$,消声层的厚度记为$H$. 消声层与艇壳间的界面记为消声层前界面,而消声层与介质2间的界面记为消声层后界面. 介质2中任意一点$\left( {r,z} \right)$离$Oz$轴与消声层后界面的交点的距离为${R}'$,$Oz$轴与消声层后界面的交点与该点连成的向量和$Oz$轴的夹角为${\theta }'$.
|
图 6 有消声层时潜艇壁面结构 Fig.6 Schematic of submarine wall structure with sound anechoic layer |
潜艇壁结构的总阻抗$\tilde {Z}_{\rm t} (\gamma)$为
| $ \tilde {Z}_{\rm t} (\gamma) = \tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_{\rm r} (\gamma) + \tilde {Z}_1 (\gamma) $ | (17) |
其中输入阻抗$\tilde {Z}_{\rm r} \left( \gamma \right)$为消声层与介质2之合的等效无限厚介质总阻抗,等于消声层前界面上的阻抗. 根据声学中阻抗的物理含义,消声层前界面上的阻抗应等于该界面上的声压与该界面上的振速之比,即
| $ \tilde {Z}_{\rm r} (\gamma) = \dfrac{\tilde {p}^{\rm ( f )}(\gamma)}{\tilde {v}^{\rm (f)}\left( \gamma \right)} $ | (18) |
式中,$\tilde {p}$为声压,$\tilde {v}$为振速,上标 (f) 代表该物理量是消声层前界面上的相应物理量. 与此类似,上标 (b) 代表该物理量是消声层后界面上的相应物理量.
根据声振耦合原理,有消声层时艇壳的法向位移为
| $ \tilde {w}^{(f)}(\gamma) = \dfrac{{\rm i}F}{2π \omega } \cdot \dfrac{1}{\tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_{\rm r} \left( \gamma \right) + \tilde {Z}_1 (\gamma)} $ | (19) |
与式(7)相比,上式只是在等号右边用输入阻抗$\tilde {Z}_{\rm r} \left( \gamma \right)$代替了介质2的声阻抗$\tilde {Z}_2 (\gamma)$.
采用与前文类似的推导,利用汉克尔变换,可得介质2中的声压${\tilde {p}}'_2 \left( {\gamma ,z} \right)$与消声层后界面处的法向位移$\tilde {w}^{\left( b \right)}(\gamma)$的如下关系式
| $ \tilde {p}'_2 \left( {\gamma ,z} \right) = -{\rm i}\omega \tilde {Z}_2 \left( \gamma \right)\tilde {w}^{\rm ( b )}(\gamma){\rm e}^{{\rm i}\left( {z - H} \right)\sqrt {k_2^2 - \gamma ^2} } $ | (20) |
根据传递函数法,消声层前后界面的声压和振速的传递方程为
| $ \left\{ \!\! \begin{array}{c} {\tilde {p}^{\rm (f)}(\gamma)} \\ {\tilde {v}^{\rm (f)}(\gamma)} \end{array} \!\! \right\} = {\pmb T}(\gamma) \left\{ \!\! \begin{array}{c} {\tilde {p}^{\rm (b)}(\gamma)} \\ {\tilde {v}^{\rm (b)}(\gamma)} \end{array} \!\! \right\} $ | (21) |
式中,$ {\pmb T}(\gamma) $为消声层的总传递矩阵,即
| $ {\pmb T} (\gamma) _{2\times 2} = \left[\!\! \begin{array}{cc} {T_{11} (\gamma)} & {T_{12} (\gamma)} \\ {T_{21} (\gamma)} & {T_{22} (\gamma)} \end{array} \!\! \right] $ | (22) |
如图 5(b)所示,本文将消声层近似为$N$个分层. 根据传递矩阵的性质,消声层的总传递矩阵$ {\pmb T}(\gamma) $可表示为各分层传递矩 阵的乘积,即
| $ {\pmb T} (\gamma) = \prod\limits_{i = 1}^N {\pmb T}_i (\gamma) $ | (23) |
式中,${\pmb T}_i (\gamma) $为第$i$个分层的传递矩阵. 消声层的每一分层均可用等效参数法表征为均质材料[20,31],由此 可得第$i$分层的传递矩阵为
| $ {\pmb T}_i (\gamma) = \left[\!\! \begin{array}{cc} {\cos \left( {\xi _i h_i } \right)} & { - {\rm i}\tilde {Z}_i \sin \left( {\xi _i h_i } \right)} \\ { - {\rm i}\dfrac{\sin \left( {\xi _i h_i } \right)}{\tilde {Z}_i }} & {\cos \left( {\xi _i h_i } \right)} \end{array} \!\! \right] $ | (24) |
其中$h_i $为第$i$层厚度,$\xi _i $和$\tilde {Z}_i $分别为
| $ \xi _i = \sqrt {k_i^2 - \gamma ^2} $ | (25) |
| $ \tilde {Z}_i = \dfrac{\rho _i \omega }{\sqrt {k_i^2 - \gamma ^2} } $ | (26) |
其中,$k_i $为第$i$层等效复波数,$\rho _i $为第$i$层等效密度.
由于黏弹性对声波产生的能量损耗,对黏弹性材料进行声学分析时,常常把与之相关的物理量表示为复数形式,用复数的虚部来 刻画能量的耗散[32]. 消声层中的声速$c$可表示为如下复数形式
| $ c = c_{\rm r} \left( {1 - {\rm i}\eta _{\rm c} } \right) $ | (27) |
式中,$c_{\rm r} $为复声速$c$的实部,$\eta _{\rm c} $为声速的损耗因子.
将式(22)代入式(21)可得
| $ \tilde {p}^{\rm (f)}(\gamma) = T_{11} \left( \gamma \right)\tilde {p}^{\rm (b)}(\gamma) + T_{12} \left( \gamma \right)\tilde {v}^{\rm (b)}(\gamma) $ | (28) |
| $ \tilde {v}^{\rm (f)}(\gamma) = T_{21} \left( \gamma \right)\tilde {p}^{\rm (b)}(\gamma) + T_{22} \left( \gamma \right)\tilde {v}^{\rm (b)}(\gamma) $ | (29) |
| $ \dfrac{\tilde {p}^{\rm (f)}(\gamma)}{\tilde {v}^{\rm ( f)}(\gamma)} = \dfrac{T_{11} \left( \gamma \right)\dfrac{\tilde {p}^{\rm (b)}(\gamma)}{\tilde {v}^{\rm (b)}(\gamma)} + T_{12} \left( \gamma \right)}{T_{21} (\gamma)\dfrac{\tilde {p}^{\rm ( b )}(\gamma)}{\tilde {v}^{\rm (b)}\left( \gamma \right)} + T_{22} (\gamma)} $ | (30) |
消声层后界面是消声层与介质2间的界面,由于介质2为半无限厚,因此界面上的表面阻抗等于介质2的特性阻抗,即
| $ \tilde {Z}_2 (\gamma) = \dfrac{\tilde {p}^{\rm ( b )}(\gamma)}{\tilde {v}^{\rm (b)}\left( \gamma \right)} $ | (31) |
把式(18)与式(31)代入式(30)可得
| $ \tilde {Z}_{\rm r} (\gamma) = \dfrac{T_{11} (\gamma) \tilde {Z}_2 (\gamma) + T_{12} \left( \gamma \right)}{T_{21} (\gamma) \tilde {Z}_2 \left( \gamma \right) + T_{22} (\gamma)} $ | (32) |
对式(28),在等号两边同时除以$\tilde {p}^{\rm (b)}\left( \gamma \right)$后,再代入式(31),可得消声层前后界面上的声压之比为
| $ \dfrac{\tilde {p}^{\rm (f)}(\gamma)}{\tilde {p}^{\rm ( b )}(\gamma)} = T_{11} (\gamma) + \dfrac{T_{12} (\gamma)}{\tilde {Z}_2 (\gamma)} $ | (33) |
同样地,对式(29),在等号两边同时除以${{\tilde v}^{({\rm{b}})}}\left( \gamma \right)$,再代入式(31),可得消声层前后界面上的振速之比为
| $\dfrac{\tilde {v}^{\rm (f)}(\gamma)}{\tilde {v}^{\rm ( b )}(\gamma)} = T_{21} (\gamma)\tilde {Z}_2 (\gamma) + T_{22} (\gamma) $ | (34) |
由于$\dfrac{\tilde {w}^{\rm (f)}(\gamma)}{\tilde {w}^{\rm (b)}(\gamma)} = \dfrac{\tilde {v}^{\rm ( f )}(\gamma)}{\tilde {v}^{\rm (b)}\left( \gamma \right)}$,结合式(34),可得
| $ \tilde {w}^{\rm (b)}(\gamma) = \tilde {w}^{\rm ( f )}(\gamma) \cdot \dfrac{1}{T_{21} \left( \gamma \right)\tilde {Z}_2 (\gamma) + T_{22} (\gamma)} $ | (35) |
把式(19)代入式(35)后可得
| $ \tilde {w}^{\rm (b)}(\gamma) = \dfrac{{\rm i}F}{2π \omega } \cdot \dfrac{1}{\tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_{\rm r} \left( \gamma \right) + \tilde {Z}_1 (\gamma)} \cdot \\ \qquad \dfrac{1}{T_{21} (\gamma)\tilde {Z}_2 (\gamma) + T_{22} (\gamma)} $ | (36) |
再把式(36)代入式(20)可得
| $ {\tilde {p}}'_2 \left( {\gamma ,z} \right) = \dfrac{F}{2π } \cdot \dfrac{\tilde {Z}_2 (\gamma)}{T_{21} (\gamma)\tilde {Z}_2 (\gamma) + T_{22} (\gamma)} \cdot \\ \qquad \dfrac{1}{\tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_{\rm r} (\gamma) + \tilde {Z}_1 (\gamma)} \cdot {\rm e}^{{\rm i}\left( {z - H} \right)\sqrt {k_2^2 - \gamma ^2} } $ | (37) |
最后,在原始的坐标系中,由反汉克尔变换和稳相法可得介质2中的远场声压为
| $ {p}'_2 \left( {{R}',{\theta }'} \right) = - \dfrac{{\rm i}\omega \rho _2 F{\rm e}^{{\rm i}k_2 {R}'}}{2π {R}'} \Bigg\{ \left[{T_{11} \left( {{\gamma }'_{\rm s} } \right)\tilde {Z}_2 \left( {{\gamma }'_{\rm s} } \right) + } \right. \\ \qquad \left. {T_{12} \left( {{\gamma }'_{\rm s}} \right)} \right] + \left[{\tilde {Z}_1 \left( {{\gamma }'_{\rm s} } \right) + \tilde {Z}_{\rm w} \left( {{\gamma }'_{\rm s} } \right)} \right] \cdot \\ \qquad \left[{T_{21} \left( {{\gamma }'_{\rm s} } \right)\tilde {Z}_2 \left( {{\gamma }'_{\rm s} } \right) + T_{22} \left( {{\gamma }'_{\rm s} } \right)} \right]\Bigg\} ^{ - 1} $ | (38) |
式中,${\gamma }'_{\rm s} = k_2 \sin {\theta }'$为稳相点处$\gamma $坐标的值.
1.3 有/无消声层时潜艇壁面结构的声学性能比较有/无消声层两种情况下,前文分别给出了潜艇壁面结构声学性能表达式,主要由介质2中的远场声压评估. 无消声层时,介质2中 的远场声压$p_2$由式(16)给出;有消声层时,介质2中的远场声压${p}'_2 $由式(38)给出. 因此,对比两种情况下介质2中的远场声压,可以量化消声层对结构声学性能的影响. 在远场处,$z \gg H$,故${R}' \approx R$,${\theta }' \approx \theta $,${\gamma }'_{\rm s} \approx \gamma _{\rm s} $.
式(38)除以式(16),可得
| $ \dfrac{{p}'_2 \left( {{R}',{\theta }'} \right)}{p_2 \left( {R,\theta } \right)} = \left[{\tilde {Z}_{\rm w} \left( {\gamma _{\rm s} } \right) + \tilde {Z}_1 \left( {\gamma _{\rm s} } \right) + \tilde {Z}_2 \left( {\gamma _{\rm s} } \right)} \right] \cdot \\ \qquad \Bigg\{ \left[{T_{11} \left( {{\gamma }'_{\rm s} } \right)\tilde {Z}_2 \left( {{\gamma }'_{\rm s} } \right) + T_{12} \left( {{\gamma }'_{\rm s} } \right)} \right] + \left[{\tilde {Z}_1 \left( {{\gamma }'_{\rm s} } \right) + }\right. \\ \qquad \left.{ \tilde {Z}_{\rm w} \left( {{\gamma }'_{\rm s} } \right)} \right] \cdot \left[{T_{21} \left( {{\gamma }'_{\rm s} } \right)\tilde {Z}_2 \left( {{\gamma }'_{\rm s} } \right) + T_{22} \left( {{\gamma }'_{\rm s} } \right)} \right] \Bigg \}^{ - 1} $ | (39) |
声压插入损失$IL_{\rm p} $为有消声层和无消声层时的远场声压比值,以分贝的形式表示为
| $ IL_{\rm p} = 20\lg \left| {\dfrac{{p}'_2 \left( {{R}',{\theta }'} \right)}{p_2 \left( {R,\theta } \right)}} \right| $ | (40) |
据式(20)和式(9),可得
| $ \dfrac{\tilde {{p}'}_2 \left( {\gamma ,z} \right)}{\tilde {p}_2 \left( {\gamma ,z} \right)} = \dfrac{\tilde {w}^{\rm (b)}\left( \gamma \right)}{\tilde {w}_{\rm w }(\gamma)} = \dfrac{\tilde {w}^{\rm ( f )}(\gamma)}{\tilde {w}_{\rm w }(\gamma)} \cdot \dfrac{\tilde {w}^{\rm (b)}(\gamma)}{\tilde {w}^{\rm ( f )}(\gamma)} $ | (41) |
故声压插入损失也可表达为
| $ IL_{\rm p} = 20\lg \left| {\dfrac{\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s } } \right)}{\tilde {w}_{\rm w } \left( {\gamma _{\rm s } } \right)}} \right| + 20\lg \left| {\dfrac{\tilde {w}^{\rm (b)}\left( {{\gamma }'_{\rm s } } \right)}{\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s } } \right)}} \right| $ | (42) |
式(42)中,$\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)$是消声层前界面上的法向位移,$\tilde {w}_{\rm w} \left( {\gamma _{\rm s} } \right)$是无消声层时艇壳的法向位移;由于消声层与艇壳紧密相连,$\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)$也是有消声层时艇壳的法向位移. 因此,位移比 ${\tilde {w}^{\rm ( f )}\left( {{\gamma }'_{\rm s} } \right)} /\tilde {w}_{\rm w} \left( {\gamma _{\rm s} } \right)$代表消声层加入前后艇壳的振动变化,位移比${\tilde {w}^{\rm ( b )}\left( {{\gamma }'_{\rm s} } \right)} / {\tilde {w}^{\rm ( f )}}\left( {{\gamma }'_{\rm s} } \right)$则是消声层后界面位移与其前界面位移之比,代表消声层对结构振动的削弱程度.
由式(19)与式(7)可得
| $ \dfrac{\tilde {w}^{\rm (f)}(\gamma)}{\tilde {w}_{\rm w} (\gamma)} = \dfrac{\tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_1 (\gamma) + \tilde {Z}_2 (\gamma)}{\tilde {Z}_{\rm w} (\gamma) + \tilde {Z}_{\rm r} (\gamma) + \tilde {Z}_1 (\gamma)} $ | (43) |
由式(35)可得
| $ \dfrac{\tilde {w}^{\rm (b)}(\gamma)}{\tilde {w}^{\rm ( f )}(\gamma)} = \dfrac{1}{T_{21} \tilde {Z}_2 \left( \gamma \right) + T_{22} } $ | (44) |
将式(43)和式(44)代入式(42)中,可得
| $ \left.\!\! 20\lg \left| {\dfrac{\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)}{\tilde {w}_{\rm w} \left( {\gamma _{\rm s} } \right)}} \right| = 20\lg \left| {\dfrac{\tilde {Z}_{\rm w} \left( {\gamma _{\rm s} } \right) + \tilde {Z}_1 \left( {\gamma _{\rm s} } \right) + \tilde {Z}_2 \left( {\gamma _{\rm s} } \right)}{\tilde {Z}_{\rm w} \left( {{\gamma }'_{\rm s} } \right) + \tilde {Z}_r \left( {{\gamma }'_{\rm s} } \right) + \tilde {Z}_1 \left( {{\gamma }'_{\rm s} } \right)}} \right| \\ 20\lg \left| {\dfrac{\tilde {w}^{\rm (b)}\left( {{\gamma }'_{\rm s} } \right)}{\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)}} \right| = 20\lg \left| {\dfrac{1}{T_{21} \left( {{\gamma }'_{\rm s} } \right)\tilde {Z}_2 \left( {{\gamma }'_{\rm s} } \right) + T_{22} \left( {{\gamma }'_{\rm s} } \right)}} \right| \!\!\right\} $ | (45) |
在下文的计算分析中,选取声学中常用的法向,即统一的方位角$\theta = {\theta }' = 0$来比较不同参数对潜艇壁面结构声学性能的影响,此时$\gamma _{\rm s} = {\gamma }'_{\rm s} = 0$. 另外,把${\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)}/ \tilde {w}_{\rm w} \left( {\gamma _{\rm s} } \right)$与${\tilde {w}^{\rm ( b )}\left( {{\gamma }'_{\rm s} } \right)}/ {\tilde {w}^{\rm ( f )}}\left( {{\gamma }'_{\rm s} } \right)$分别简记为$W^{FW}$与$W^{\rm BF}$,$20\lg \left| {\dfrac{\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)}{\tilde {w}_{\rm w} \left( {\gamma _{\rm s} } \right)}} \right|$与$20\lg \left| {\dfrac{\tilde {w}^{\rm ( b )}\left( {{\gamma }'_{\rm s} } \right)}{\tilde {w}^{\rm (f)}\left( {{\gamma }'_{\rm s} } \right)}} \right|$分别简记为$d BW^{\rm FW}$与$d BW^{\rm BF}$.
至此,利用声压插入损失$IL_{\rm p} $可以刻画消声层的加入对潜艇壁面结构声学性能的影响,其值可由式(39)与式(40)求得. $IL_{\rm p} $自身可表示为两个 位移比$d BW^{\rm FW}$与$d {\rm B}W^{\rm BF}$的叠加,其计算式为式(45).
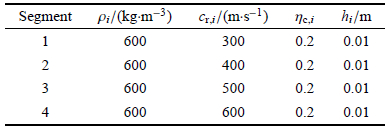
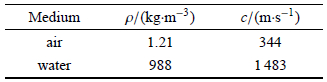
2 数值计算与结果分析本节的数值计算讨论了相关系统参数对潜艇壁面结构振动与声学性能的影响,具体包括不同的介质1、艇壳厚度、消声层厚度和孔腔形状. 计算时,艇壳考虑为钢材(密度$\rho _{\rm w} = 7 800$ kg/m$^3$),厚度$h = 0.02 $m. 如图 5(b)所示,将消声层近似为4层,从前界面到后界面依次记为第1到第4层,各层均等效为均质材料,其等效密度$\rho _i $、等效复声速实部$c_{{\rm r},i} $、损耗因子$\eta _{{\rm c},i} $以及厚度$h_i $列入表 1. 此外,空气介质和水介质的物理参数均取20${^\circ}$C (室温)时的值,如 表 2.
| 表 1 消声层各分层的材料参数 Table 1 Material parameters of different anechoic layer segments |
| 表 2 流体介质参数 Table 2 Medium parameters |
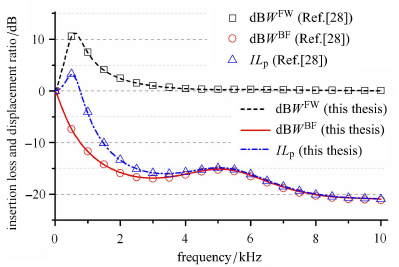
为检验理论模型,把本文中考虑的潜艇壁面结构所处的工况退化为文献 [28]中潜艇壁面结构所处的工况,即不考虑内侧介质的存在(可认为$\rho_1 = 0$),外侧介质考虑为水,所用物理参数见表 2. 在0到10 kHz频率范围内,声压插入损失$IL_{\rm p}$以及位移比$d {\rm B}W^{\rm FW}$和$d {\rm B}W^{\rm BF}$的变化曲线,如图 7所示;计算时所取的结构以及材料参数与文献 [28]给出的一致.
|
图 7 介质1 不存在时潜艇壁面结构的声振性能 Fig.7 Vibro-acoustic properties of submarine wall structure in the absence of medium 1 |
图 7结果表明,本文计算结果与文献 28]结果吻合良好,这检验了本文理论模型的合理性.
2.2 不同介质1时的潜艇壁面结构声学性能本文考虑的潜艇壁面结构可以是潜艇中人员生活工作的舱室或放置艇用设备器械的舱室,此时壁面结构的内侧介质为空气,外侧介质为水;也可以是控制潜艇升降、平衡的水舱,此时壁面结构的内外侧介质均为水.
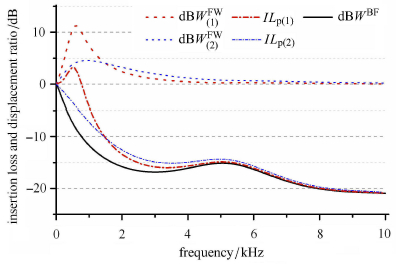
针对壁面结构用于不同的舱室时所处的不同工况,本小节把介质1(内侧介质)考虑为空气或水,分析比较这两种工况下壁面结构的声学性能,如图 8所示. 其中,介质1为空气时的声学参量,$IL_{\rm p}$和$ d{\rm B}W^{\rm FW}$,用下标(1)标出,介质1为水时的相应参量用下标(2)标出. 据式(45),位移比$d {\rm B}W^{\rm BF}$与介质1的性质无关,故介质1不同时,$d {\rm B}W^{\rm BF}$不变,图 8以一条曲线(黑色实线)标出其值. 从图 8可以看出,随着频率增大,$d {\rm B}W^{\rm BF}$呈现负向增大的趋势,表明消声层的引入削弱了艇壳的振动,且随着频率的增大,削弱程度逐渐增大.
|
图 8 介质1 对潜艇壁面结构声振性能的影响 Fig.8 Influence of medium 1 on vibro-acoustic properties of submarine wall structure |
从图 8可以看出,当介质1为空气时,$d {\rm B}W_{(1)}^{\rm FW} $始终为正值,且在频率约为0.6 kHz时存在峰值,这说明,在低频段,消声层的加入增强了艇壳的振动,在约0.6 kHz时最为明显. 在高频段,$d {\rm B}W_{(1)}^{\rm FW} $随频率增大而递减,直至逐渐趋于0,换言之,消声层对艇壳振动的增强作用逐渐减小,最终趋于0. 另外,在低频时,声压插入损失$IL_{\rm p\left( 1 \right)} $为较小的正值;在中高频段,$IL_{\rm p\left( 1 \right)} $随频率增大而负向增大. 声压插入损失$IL_{\rm p} $是两个位移比$d {\rm B}W^{\rm FW}$与$d {\rm B}W^{\rm BF}$的叠加. 低频时,$\left| {d {\rm B}W_{(1)}^{\rm FW} } \right| > \left| { d {\rm B}W^{\rm BF}} \right|$,故声压插入损失为正值,即消声层的加入加强了潜艇壁面结构的振动,中高频时,$\left| { d {\rm B}W_{(1)}^{\rm FW} } \right| < \left| { d {\rm B}W^{\rm BF}} \right|$,因此声压插入损失为负值,即消声层的加入使潜艇壁面结构的振动减弱. 由此说明,当介质为1空气时,消声层在中高频段能起到不错的减振降噪效果.
当介质1为水时,$IL_{\rm p(2)} $曲线在全频段均为负值,且随着频率的增大负向增大,这说明在该工况下,壁面结构在全频段均有不错的减振降噪效果,且频率越高,效果越好. 这主要是因为,相较于介质1为空气时的$d {\rm B}W_{(1)}^{\rm FW} $曲线,介质1为水时的$d {\rm B}W_{(2)}^{\rm FW} $曲线有类似的变化趋势,但低频段的峰值大幅降低,故声压插入损失$IL_{\rm p(2)} $始终为负值.
因此,与介质1为空气的工况相比较,本文考虑的潜艇壁面结构用于介质1为水的工况时在低频段的减振降噪效果更好,在高频段的区别则不大.
2.3 艇壳厚度的影响以下分析艇壳厚度对潜艇壁面结构声学性能的影响. 其它材料、介质参数保持不变(表 1和表 2),仅改变艇壳厚度$h$,分别 取$h = 0.01$ m,0.02 m和0.04 m,结果如图 9所示. 其中,图 9(a)是介质1为空气时各声学参量随$h$变化的对比示意图,3种艇壳厚度从小到大所对应的声学参量依次用下标(1), (2)和(3)标出;图 9(b)是介质1为水时,各声学参量随$h$变化的对比示意图,艇壳厚度从小到大所对应的声学参量依次用下标(1), (2)和(3)标出.

|
图 9 艇壳厚度对潜艇壁面结构声振性能的影响 Fig.9 Influence of submarine hull thickness on vibro-acoustic properties |
从图 9可以看出,艇壳厚度越大,$d {\rm B}W^{\rm FW}$的值越小,即由于消声层加入引起的艇壳振动增强作用越小;与此同时,声压插入损失$IL_{\rm p}$随厚度的增大而负向增大,即壁面结构的减振降噪性能随艇壳厚度的增大而增大.
据式(10),艇壳厚度的增大反映的是其机械阻抗的增大. 结合上述分析,可得如下结论:增加艇壳厚度增大了其机 械阻抗,有利于潜艇壁面结构的减振降噪.
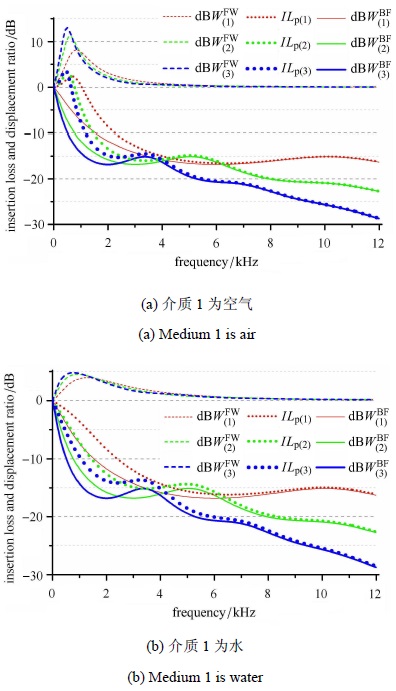
2.4 消声层厚度的影响本小节分析消声层厚度对潜艇壁面结构声学性能的影响. 相关材料、介质参数不变(表 1和表 2),依然把消声层分为4个分层,选 取各分层的厚度均为0.005 m,均为0.01 m,和均为0.015 m 3种情况,计算结果如图 10所示. 其中,图 10(a)是介质1为空气时,各声学参量随消声层厚度变化的对比示意图,消声层分层的厚度从小到大所对应的各声学参量 依次用下标(1),(2)和(3)标出;图 10(b)对应介质1为水时工况, 消声层分层的厚度从小到大所对应的各声学参量依次用下标(1),(2)和(3)标出.
|
图 10 消声层厚度对潜艇壁面结构声振性能的影响 Fig.10 Influence of anechoic layer thickness on vibro-acoustic properties of submarine wall structure |
图 10结果表明,随着消声层厚度的增大,$d {\rm B}W^{\rm FW}$在低频段的峰值逐渐增大且逐渐向低频方向移动,即消声层对艇壳振动的增强作用增大. 此外,伴随着消声层厚度的增大,$d {\rm B}W^{\rm BF}$和$IL_{\rm p}$曲线向低频偏移,$d {\rm B}W^{\rm BF}$和$IL_{\rm p}$在低频与高频段负向增大,在中频段有波动但也呈负向增大趋势,即潜艇壁面结构的减振降噪性能随消声层厚度的增大而增大.
综合上述分析,增大消声层厚度总体上有利于改善潜艇壁面结构的声振性能,且在高频段可显著增强减振降噪效果.
2.5 孔腔形状的影响本文考虑的消声层被近似为4个分层,各层均等效为均质材料,每一分层的孔腔内径大小可采用该层的等效复声速的实部进行表征. 根据参数等效的原理,孔径越大,则该层的等效复声速的实部越小,反之亦然[31]. 在上文中,从前界面至后界面,消声层各分层等效复声速的实部依次取为300 m/s,400 m/s,500 m/s和600 m/s (即孔径逐渐减小). 以下将这4个分层进行不同顺序的排列(其它材料、介质参数保持不变),以探讨不同排列顺序(即孔腔形状)对潜艇壁面结构的振动和声 学性能的影响.
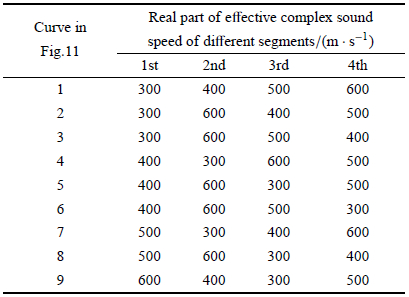
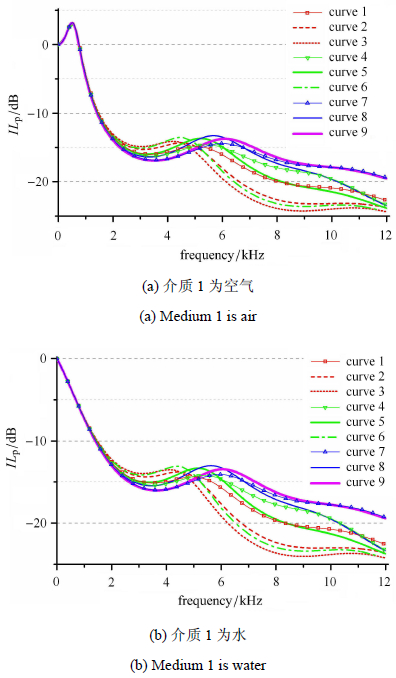
就含4个分层的消声层而言,共有$4! = 24$种不同排列顺序. 比较所有24种排列顺序所对应的声压插入损失$IL_{\rm p} $后,选 取其中典型的9条曲线分析其规律,如图 11所示. 其中,图 11(a)和图 11(b)分别是介质1为空气和水时,不同空腔排布顺序对应的声压插入损失比较,图中曲线1$\sim$9所代表的孔腔形状 的各层声速如表 3.
|
图 11 不同孔腔形状对插入损失的影响 Fig.11 Influence of hole topology on vibro-acoustic properties of submarine wall structure |
| 表 3 不同孔腔形状的声速分布 Table 3 Sound speed distribution for different hole topologies |
比较图 11(a)和图 11(b)可发现,低频时,随各分层排布顺序变化,声压插入损失的变化很小,中高频段时,随各分层排布顺序变化,声压插入损失发生明显变化:其中,2$\sim $5 kHz左右的中频与5 kHz以上的高频,曲线变化规律正好相反. 接下来以5 kHz以上的高频段为例,分析孔腔形状的声速分布规律;2$\sim $5 kHz左右的中频段规律与之相反.
图 11中,同一颜色的曲线代表其第1层的等效复声速具有相同的实部. 比较图中的9条曲线可以发现,无论对空气或水介质,第1层的等效复 声速实部越小,对应的曲线在高频段越低,即潜艇壁面结构的减振降噪效果越好:比较24种不同排列顺序,结果呈同样趋势. 第1层相同的情况下,比较曲线1, 2和3,或比较曲线4,5和6,或比较曲线7和8,发现第2层的等效复声速实部相对于第1层的增量较大时,曲线在高频段较低,而其负增量较大时,曲线在高频段较高. 对曲线9而言,其第1层的等效复声速实部较大,第2层相对于第1层的负增量也较大,故在9条曲线中,其在高频段具有最高值. 进一步比较曲线2和3,或比较曲线5和6,发现在第2层的等效复声速实部比第1层的值的增加量较大的基础上,第2$\sim$4层的等效复声速实部依次减小的排列顺序可以使曲线在高频段更低.
最后,将等效复声速实部对应为孔径,即可得如下结论:沿前界面至后界面方向,当消声层中孔腔的内径在第1层中较大,在第2层中相对于 第1层的减小量较大,在第2$\sim$4层中依次增大时,潜艇壁面结构的减振降噪效果在高频段更佳.
3 结 论针对潜艇的减振降噪问题,本文选取由潜艇壳体和开孔型消声层组成的潜艇壁面结构为研究对象,考虑结构两侧的流体负载,建立了消声 理论模型,然后开展解析分析,应用传递函数法导出了3个重要的声学参量(声压插入损失$IL_{\rm p} $、位移比$d {\rm B} W^{\rm FW}$以及$d {\rm B} W^{\rm BF}$)的计算表达式. 随后,根据具体的材料和介质参数,利用该模型进行了数值计算,讨论分析了介质1、艇壳厚度、消声层厚度和孔腔形状对潜艇壁面结构 振动与声学性能的影响,主要结论如下.
(1)介质1为空气时,在低频段,消声层对结构振动的削弱量小于消声层加入后艇壳振动的增强量,故消声层的加入反而使潜艇壁面结构 的振动增大;而当介质1为水时,在低频段,覆盖消声层后,壁面结构的振动则明显减小. 在高频段,介质1为空气或者水这两种情况的区别不大,均比低频段的减振降噪效果更好.
(2)增加艇壳的厚度有利于潜艇壁面结构的减振降噪.
(3)增加消声层的厚度总体有利于潜艇壁面结构的减振降噪效果,尤其是在高频段.
(4)当消声层孔腔的内径分布沿前界面至后界面方向先减小再增大时,潜艇壁面结构的减振降噪效果在高频段最好,中频段的规律则与之相反.
| 1 | 胡家雄, 伏同先. 21 世纪常规潜艇声隐身技术发展动态. 舰船科 学技术, 2001, 4: 2-5,14 (Hu Jiaxiong, Fu Tongxian. Progress of the acoustic stealth technology of conventional submarine in the 21st century. Ship Science and Technology, 2001, 4: 2-5,14 (in Chinese)) |
| 2 | Easton M. Future submarines. Rusi Defence Systems, 2006, Autumn:44-46 |
| 3 | 王磊, 常书刚. 潜艇噪声与综合降噪技术的应用. 航海技术, 2007,2: 44-48 (Wang Lei, Chang Shugang. Application of submarine noise and synthetical noise reduction technology. Marine Technology,2007, 2: 44-48 (in Chinese)) |
| 4 | 石云霞, 奚正平, 汤慧萍等. 水下吸声材料的研究进展. 材料导 报, 2010, 24(1): 49-52 (Shi Yunxia, Xi Zhengping, Tang Huiping, et al. Progress of underwater sound-absorbing materials. Materials Review, 2010, 24(1): 49-52 (in Chinese)) |
| 5 | 张文毓. 国外消声瓦的研究与应用进展. 船舶, 2010, 6: 1-4 (Zhang Wenyu. Overseas research and application of the silence tile. Ship & Boat, 2010, 6: 1-4 (in Chinese)) |
| 6 | 余超, 熊伟, 文庆珍等. 高分子水声吸声材料的研究进展. 工 程塑料应用, 2011, 39(5): 103-105 (Yu Chao, Xiong Wei, Wen Qingzhen, et al. Progress of underwater acoustic absorbing polymer materials. Engineering Plastics Application, 2011, 39(5): 103-105 (in Chinese)) |
| 7 | 罗忠, 朱锡, 林志驼等. 水下吸声覆盖层结构及吸声机理研究进 展. 舰船科学技术, 2009, 31(8): 23-30 (Luo Zhong, Zhu Xi, Lin Zhituo, et al. A review of underwater anechoic coating structure and absorption theories. Ship Science and Technology, 2009, 31(8):23-30 (in Chinese)) |
| 8 | Gaunaurd GC, Ü berall H. Resonance e ects and the ultrasonic e ective properties of particulate composites. Journal of the Acoustical Society of America, 1983, 74(1): 305-313 |
| 9 | 赵敏兰, 朱蓓丽. 用等效参数法研究含球形空腔弹性体的吸声 性能. 噪声与振动控制, 1996, 5: 11-14 (Zhao Minlan, Zhu Beili. Study of sound absorption properties of elastomer containing spherical cavities using e ective parameter method. Noise and Vibration Control, 1996, 5: 11-14 (in Chinese)) |
| 10 | Zhao HG, Wen JH, Yang HB, et al. Backing e ects on the underwater acoustic absorption of a viscoelastic slab with locally resonant scatterers. Applied Acoustics, 2014, 76: 48-51 |
| 11 | Radlinski RP, Simon MM. Scattering by multiple gratings of compliant tubes. Journal of the Acoustical Society of America, 1982,72(2): 607-614 |
| 12 | Radlinski RP. Scattering from multiple gratings of compliant tubes in a viscoelastic layer. Journal of the Acoustical Society of America,1989, 85(6): 2301-2310 |
| 13 | 朱锡, 石勇, 梅志远. 夹芯复合材料在潜艇声隐身结构中的应用 及其相关技术研究. 中国舰船研究, 2007, 2(3): 34-39 (Zhu Xi, Shi Yong, Mei Zhiyuan. Laminated compound material and technologies in the development of acoustic stealth structure in submarine. Chinese Journal of Ship Research, 2007, 2(3): 34-39 (in Chinese)) |
| 14 | Jiang H, Wang YR. Phononic glass: A robust acoustic-absorption material. Journal of the Acoustical Society of America, 2012,132(2): 694-699 |
| 15 | Cervenka P, Challande P. A new e cient algorithm to compute the exact reflection and transmission factors for plane waves in layered absorbing media (liquids and solids). Journal of the Acoustical Society of America, 1991, 89(4): 1579-1589 |
| 16 | 杨雪, 王源升, 余红伟. 多层高分子复合结构斜入射声波吸声性 能. 复合材料学报, 2006, 23(6): 21-28 (Yang Xue, Wang Yuansheng, Yu Hongwei. Sound absorption properties of multilayered polymer composites for oblique incidence. Acta Materiae Compositae Sinica, 2006, 23(6): 21-28 (in Chinese)) |
| 17 | Stepanishen PR, Strozeski B. Reflection and transmission of acoustic wideband plane waves by layered viscoelastic media. Journal of the Acoustical Society of America, 1982, 71(1): 9-21 |
| 18 | 李海涛, 朱锡, 石勇等. 层状结构水下声学特性研究. 噪声与振动 控制, 2005, 3: 54-57 (Li Haitao, Zhu Xi, Shi Yong, et al. Investigation of sound field in multiple-layer structure in water. Noise and Vibration Control, 2005, 3: 54-57 (in Chinese)) |
| 19 | Liang GL, Pang FB. Acoustic characteristics of underwater composite materials at oblique incidence of sound wave. Noise & Vibration Worldwide, 2013, 44(5): 12-17 |
| 20 | 何世平, 汤渭霖, 何琳等. 变截面圆柱形空腔覆盖层吸声系数的 二维近似解. 船舶力学, 2006, 10(1): 120-127 (He Shiping, Tang Weilin, He Lin, et al. Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity. Journal of Ship Mechanics, 2006, 10(1): 120-127 (in Chinese)) |
| 21 | Hladky-Hennio AC, Decarpigny JN. Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method: Application to Alberich anechoic coatings. Journal of the Acoustical Society of America, 1991, 90(6): 3356-3367 |
| 22 | 陶猛, 汤渭霖. Alberich 型吸声覆盖层的低频吸声机理分析. 振动 与冲击, 2011, 30(1): 56-60 (Tao Meng, Tang Weilin. Mechanism analysis of Alberich sound-absorption coating at low-frequency. Journal of Vibration and Shock, 2011, 30(1): 56-60 (in Chinese)) |
| 23 | Shang C, Zhang JZ, Wei YJ. Absorption characteristics of anechoic coating embedding frustum-of-a-cone cavities. Journal of Ship Mechanics,2010, 14(12): 1425-1431 |
| 24 | Sgard FC, Olny X, Atalla N, et al. On the use of perforations to improve the sound absorption of porous materials. Applied Acoustics,2005, 66: 625-651 |
| 25 | Ivansson SM. Markov-chain Monte Carlo identification of favorable design choices with application to anechoic coatings. Journal of the Acoustical Society of America, 2014, 135(6): 3338-3351 |
| 26 | Langlet P, Hladky-Hennio AC, Decarpigny JN. Analysis of the propagation of plane acoustic waves in passive periodic materials us ing the finite element method. Journal of the Acoustical Society of America, 1995, 98(5): 2792-2800 |
| 27 | Ko SH. Reduction of structure-borne noise using an air-voided elastomer. Journal of the Acoustical Society of America, 1997, 101(6):3306-3312 |
| 28 | Tao M, Tang WL, Hua HX. Noise reduction analysis of an underwater decoupling layer. Journal of Vibration and Acoustics, 2010,132(6): 061006(1-7) |
| 29 | Junger MC, Feit D. Sound, Structures, and Their Interaction. Cambridge: The MIT Press, 1986: 28-29 |
| 30 | 陶猛, 卓琳凯. 基于ANSYS 的吸声覆盖层声学性能计算与分析. 振动与冲击, 2011, 30(1): 87-90 (Tao Meng, Zhuo Linkai. Simulation and analysis for acoustic performance of a sound absorption coating using ANSYS software. Journal of Vibration and Shock,2011, 30(1): 87-90 (in Chinese)) |
| 31 | 朱蓓丽, 任克明. 等效参数法研究带圆柱通道橡胶体的声学性 能. 上海交通大学学报, 1997, 31(7): 20-25 (Zhu Beili, Ren Keming. Acoustic properties analysis of elastomer with cylindrical bores using equivalent parametric method. Journal of Shanghai Jiaotong University, 1997, 31(7): 20-25 (in Chinese)) |
| 32 | 王荣津. 水声材料手册. 北京: 科学出版社, 1983: 6-9 (Wang Rongjin. Underwater Acoustic Material. Beijing: Science Press,1983: 6-9 (in Chinese)) |
2. State Key Laboratory for Mechanical Strength and Vibration, School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, China
 2016, Vol. 48
2016, Vol. 48