近年来,以空间机器人为代表的复杂多体系统得到日益广泛的应用,其自由度数目大,结构复杂,对其动力学解算会消耗大量 的时间和资源;因此,寻求多体系统动力学高效算法始终是众多学者的研究兴趣. 安德森和段[1, 2]在1999年提出了直接迭代混合算法(hybrid direct-iterative algorithm),该方法将大型多体系统分割为多个子系统以便充分利用计算机中的各个处理器,之后通过并行和迭代法求解 各子系统动力学输出,并将其代入系统级方程从而解算出 分割处的约束力. 然而由于解算过程中的迭代步骤,该算法的实际时间复杂度高于其理论值. 克里奇利和安德森[3]于2004年提出了占用时间和内存资源都更少的递归坐标削减并行算法(recursive coordinate reduction parallelism),该方法可以使用少于$N$个处理器进行并行计算而使时间复杂度降低至对数阶,但无法解算奇异构型下的动力学 输出,因此需要在模型中对系统的奇异构型加以鉴别和避免,难以应用于一般的多体系统. 此外,比较有代表性的多体系统高效算法还有1999年费瑟斯通给出的利用$N$个处理器进行并行计算、具有渐进于$O(\log N)$时间复杂度的分治算法(divide and conquer algorithm,DCA)[4, 5]. 由于该方法适用范围较广,因此后续产生了许多基于该方法的其它高效算法,例如一些日本学者于2002年提出的装配拆解算 法(assembly disassembly algorithm)[6]、穆克吉等[7]于2007年提出的基于正交补的分治算法(orthogonal-complement based DCA)、克里奇利[8, 9]于2005年提出并且于2009年实现的高效分治算法(efficient DCA)、夏鸿建等[10]于2009年给出的子系统求解算法、巴里奥等[11]于2012年综合了分治算法和铰 链体算法(articulated body algorithm, ABA)而提出的分治铰链体方法[12]以及鲍尔斯纳[13]于2013年给出的广义分治算法(generalized DCA)等;穆克吉和安德森[14]还将分治算法拓展至多柔体系统,解决了多柔体系统动力学解算的问题. 此外,各类动力学递推算 法[15, 16, 17, 18]使得利用单个处理器进行计算而达到O(N)的时间复杂度成为现实. 如果以高效解算任意多体系统正动力学输出为目的,各类串行、并行计算方法以及递推算法已经发展得比较成熟了. 但从关节结构强度设计和控制器设计的角度考虑,除得到系统正动力学的输出外,还需要同时求解约束力并给出显式动力学方程,上述各种方法难以同时满足这两方面设计工作的需求. 而费吉尼等[19]于1995年提出的约束力算法(constraint force algorithm, CFA)能够同时满足以上两项任务,并且其方程形式简单,适合使用计算机进行编程解算,可在串行和并行化后进行高效计算.
约束力算法串行化后的时间复杂度为O(N),并且其首次实现了利用N个处理器的并行计算,并行化后时间复杂度 为O(log N). 但该方法仅适用于固定基座的链状系统. 费吉尼等[20]通过分析单个漂浮体动力学,将约束力算法拓展至自由漂浮的链状系统,实现其在空间机器人领域的应用. 之后,费瑟斯通和费吉尼[21]提出了基变换方法,改进了对漂浮体的处理------将之等效为``六自由度连接''. 至此,约束力算法已适用于单主链(single main chain,指除分支结构外,系统仅有唯一的链状结构)或主链上仅带有短分支结构(short branches,指该分支结构上不再有节点和新的分支)的多体系统,但仍不能应用于任意树形多体系统的解算.
本文为提高约束力算法的普适性,通过对树形系统中任意节点刚体的动力学进行分析,将其拓展至任意树形系统;之后给出该 算法的``串行化''方法,以提高计算效率. 最后,通过数值仿真验证了所提约束力算法的准确性和高效性.
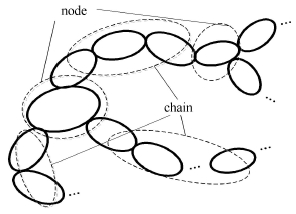
1 树形多体系统的描述研究图 1所示任意树形多体系统,其由单链结构(chain)和节点(node)组成.
|
图 1 树形多体系统的拓扑结构 Fig.1 Topology of tree-like multibody system |
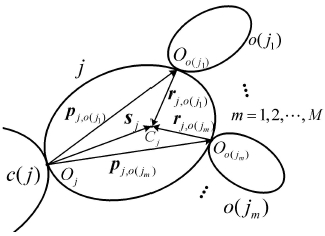
称仅有一个外接体的刚体为单链刚体、有多于一个外接体的刚体为节点刚体,系统中的任意刚体j可表示为图 2所示形式, 图中除体j外共(M + 1)个刚体(M∈N+),其中体c(j)为体j的内接体,体 o(j1)、体o(j2)…… 体o(jM)均为体j的外接体.
|
图 2 树形系统中的任意刚体 Fig.2 Arbitrary rigid-body in tree-like system |
称刚体j与其内接体c(j)的连接点为点Oj ,并在该点处定义体j的附体坐标系ej;体o(jM与体j连接于点O
如图 2,sj 为体j的质心Cj 在坐标系ej 中的矢 径,rj,o( jm) 为质心Cj 相对点Oo(jm) 的矢径,pj,o(jm) 为 点Oo(jm) 在坐标系ej 中的矢径. 定义描述体c( j) 和 体j 间连接关系的自由度投影矩阵Hj∈R6×Nj 和约 束投影矩阵Wj∈R6×(6-Nj) (其中Nj 为体j 与内接体 间的自由度数量),二者互为正交补矩阵,即满足
$ \begin{array}{l} H_j^T \cdot {H_j} = {U^{{N_j} \times {N_j}}}{\mkern 1mu} ,\;W_j^T \cdot {W_j} = {U^{(6 - {N_j}) \times (6 - {N_j})}}\\ W_j^T \cdot {H_j} = {{\bf{0}}^{(6 - {N_j}) \times {N_j}}}{\mkern 1mu} ,\;H_j^T \cdot {W_j} = {{\bf{0}}^{{N_j} \times (6 - {N_j})}} \end{array} $
其中U和0分别表示单位矩阵和零矩阵.
当体c(j)和体j间无约束时,其自由度投影矩阵Hj为6×6的单位矩阵,约束投影矩阵Wj 退化为6×0的零矩阵. 树形系统中的任意刚体均可采用以上方法进行坐标系和参数定义.
对系统中的任意位置矢量p,定义与其对应的变换矩阵
| $\widehat P = \left[ \begin{array}{l} U{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array} \right.\left. \begin{array}{l} \widetilde P\\ U \end{array} \right] \in {R^{6 \times 6}} $ | (1) |
其中 $ \tilde{\pmb p} $ 表示矢量阵列 $ {\pmb p} = \left[\begin{array}{ccc} {p_1 } & {p_2 } & {p_3 } \end{array} \right]^{\rm T} $ 的叉乘矩阵,即
| $ \widetilde P = \left[ \begin{array}{l} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {p_3}{\kern 1pt} {\kern 1pt} \\ {p_3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\\ - {p_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {p_1}{\kern 1pt} \end{array} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. \begin{array}{l} {p_2}\\ - {p_1}\\ 0 \end{array} \right] $ | (2) |
则刚体位置矢量的加减关系 $ {\pmb p}_{j,o(j_m )} + {\pmb r}_{j,o(j_m )} = {\pmb s}_j $ ,可转化为矩阵乘法$ \hat{\pmb P}_{j,o(j_m )} \cdot \hat {\pmb R}_{j,o(j_m )} = \hat {\pmb S}_j. $ 记体j的质量为mj,相对质心的惯性矩为JCj,定义其相对质心的质量矩阵为
| $ {I_{Cj}} = \left[ \begin{array}{l} {J_{Cj}}\\ {\bf{0}} \end{array} \right.\left. \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bf{0}}\\ {m_j}U \end{array} \right] \in {R^{6 \times 6}} $ | (3) |
其相对点Oj的质量矩阵 $ {\pmb I}_{Oj }= \hat {\pmb S}_j \cdot {\pmb I}_{C j} \cdot \hat {\pmb S}_j^{\rm T}. $
将作用在点Oj处的力fj和力矩nj记为 $ {F_j} = {[n_j^T,f_j^T]^T} $ ,则将其等效至点Oo(jm), 有 $ {\pmb F}_{o(j_m )} = \hat {\pmb P}_{j,o(j_m )} \cdot {\pmb F}_j $ ;若刚体j上点Oj处加速度为 $ \dot{\pmb V}_j = [\dot {\pmb\omega }_j^{\rm T} , \dot{\pmb v}_j^{\rm T}]^{\rm T} $ ,点Oo(jm)处加速度为 $ \dot{\pmb V}_{o(j_m )} = [\dot {\pmb\omega}_{o(j_m )} ^{\rm T},\dot{\pmb v}_{o(j_m )} ^{\rm T}]^{\rm T} $ ,则同一刚体上两点间加速度的关系可表示为 $ \dot {\pmb V}_j = (\hat {\pmb P}_{j,o(j_m )} )^{\rm T} \cdot \dot{\pmb V}_{o(j_m )} . $
2 任意树形系统约束力算法的一般形式 2.1 铰链处受力分解基于耦合模型[22, 23, 24]的多体系统动力学方程最终均可化为如下形式
| $ {\pmb M}\dot {\pmb x} + {\pmb b}(\theta ,{\pmb Q},{\pmb F}_{\rm E} ) = {\pmb T} $ | (4) |
其中M为系统质量阵,x为系统广义速率, $ {\pmb b}(\theta ,{\pmb Q},{\pmb F}_{\rm E} ) $ 为由于各体间运 动耦合产生的力的非线性项,${\pmb T}$为输入系统的控制力. 令${\pmb F}_{\rm T} = {\pmb T} - {\pmb b}(\theta ,{\pmb Q},{\pmb F}_{\rm E} )$,则$\dot{\pmb x} = {\pmb M}^{ - 1} \cdot {\pmb F}_{\rm T} $,可以看出系统的广义加速度$\dot{\pmb x}$完全“依赖”于${\pmb F}_{\rm T} $,因此称${\pmb F}_{\rm T} $为等效控制力,其包含了真实系统所受控制力与所有非线性项,可使各体间的受力“解耦”.
定义任意刚体j上点Oj处的等效受力为${\pmb F}_j = [{\pmb n}_j^{\rm T},{\pmb f}_j ^{\rm T}]^{\rm T}$. ${\pmb F}_j $有两个来源,一是作用在点Oj处、存在于关节自由度方向上的等效控制力${\pmb F}_{{\rm T}j} $,因此${\pmb F}_j $所表达的并非是系统的真实受力情况;另一部分是存在于非自由度方向上的约束力${\pmb F}_{{\rm S}j} $,则${\pmb F}_j $可分解为
| $ {\pmb F}_j = {\pmb H}_j \cdot {\pmb F}_{{\rm T}j} + {\pmb W}_j \cdot {\pmb F}_{{\rm S}j} $ | (5) |
当体j与其内接体间无约束时,${\pmb F}_j $可以分解为
| $ {\pmb F}_j = {\pmb H}_j \cdot {\pmb F}_{{\rm T}j} $ | (6) |
由于推导上述关系时未对刚体种类进行限定,因此无论刚体j属于单链结构还是节点,${\pmb F}_j $均可通过式(5) 或式(6)进行分解.
2.2 运动学与动力学递推关系对于系统中的某一刚体j,其与相邻刚体间的运动学和动力学递推关系可写为
| $ \left. {\begin{array}{*{20}{l}} {{{\mathop V\limits^. }_j} = \widehat P_{c(j)}^{\rm{T}}{{\mathop V\limits^. }_{c(j)}} + {H_j}{{\mathop Q\limits^. }_j}{\rm{ }}{F_j} = {I_j}{{\mathop V\limits^. }_j} + {\rm{ }}\sum\limits_{m = 1}^M {{{\widehat P}_{j,o({j_m})}}{F_{o({j_m})}}} } \end{array}} \right\} $ | (7) |
其中$\dot{\pmb V}_j $定义为刚体j上点$O_j $处绝对加速度中满足线性递推关系的部分,其仅与内接体的对应项$\dot{\pmb V}_{c(j)} $以及自身关节处的相对加速度$\dot{\pmb Q}_j $有关,去掉了绝对加速度中的非线性部分. 由此写出式(7) 中的第1式以描述刚体j与内接体$c(j)$间的运动学递推关系.
将式(7)中第2式写为
| $ {F_j} + {\rm{ }}\sum\limits_{m = 1}^M {{{\widehat P}_{j,o({j_m})}}} \cdot ( - {F_{o({j_m})}}) + ( - {I_j}{\mathop V\limits^. _j}) = 0 $ | (8) |
其中${\pmb F}_j $以及${\pmb F}_{o(j_m )} \ (m = 1,2,\cdots ,M)$除包含系统所受的真实主动力和约束力外,还包含 了各体间运动耦合产生的力的非线性项;这些非线性项补偿了$ - {\pmb I}_j \dot{\pmb V}_j $一项中由于$\dot{\pmb V}_j $的定义所造成的系统惯性力的缺失. 因此根据达朗贝尔原理,该式成立,从而可用式(7)中的第2式描述刚体j与外接体$o(j_m ) \ (m = 1,2,\cdots , M)$间的动力学递推关系.
式(7)通过 $\dot{\pmb V}_j $和${\pmb F}_j $对系统运动学和动力学进行了描述,其目的是使得系统运动学和动力学 方程的形式较为简单,方便后续对递推关系进行组集.
2.3 系统递推关系的组集 2.3.1 单链结构的递推关系组集对于包含$n$个刚体和$N$个自由度的单链结构,式(7)可写为
| $ \left. \begin{array}{l} {F_j} = {I_j}{\mathop V\limits^. _j} + {\widehat P_{j,o({j_m})}}{F_{o(j)}}\\ {\mathop V\limits^. _j} = {\widehat P^T}_{c(j)} + {H_j}{\mathop Q\limits^. _j} \end{array} \right\}$ | (9) |
定义以下组集形式的矩阵,下标i依次取$n,n - 1,\cdots,1$ (${\rm col}\{ {\pmb a}_i \}$表示矩阵${\pmb a}$下标i依次取值进行排列所组成的分块列矩阵)
| $ {P_{{\rm{chain}}}} = \left[ \begin{array}{l} U\\ - {\widehat P_{n - 1}}\\ \\ \\ \end{array} \right.\begin{array}{*{20}{c}} {}\\ U\\ { - {{\widehat P}_{n - 2}}}\\ \begin{array}{l} \\ \end{array} \end{array}\begin{array}{*{20}{c}} {}\\ {}\\ U\\ \begin{array}{l} \ddots \\ \end{array} \end{array}\begin{array}{*{20}{c}} {}\\ {}\\ {}\\ \begin{array}{l} \ddots \\ - {\widehat P_1} \end{array} \end{array}\left. \begin{array}{l} \\ \\ \\ \\ U \end{array} \right] \in {R^{6n \times 6n}} $ | (10) |
| $ \left. \!\! \begin{array}{l} {H }= {\rm diag}\{{\pmb H}_i \} \in {\pmb R}^{6n\times N} \cr { W }= {\rm diag}\{{\pmb W}_i \} \in {\pmb R}^{6n\times (6n - N)}\cr { I} = {\rm diag}\{{\pmb I}_i \} \in {\pmb R}^{6n\times 6n}\cr { F} = {\rm col}\{{\pmb F}_i \} \in {\pmb R}^{6n} \cr { F}_{\rm T}= {\rm col}\{{\pmb F}_{{\rm T}i} \} \in {\pmb R}^N \cr { F}_{\rm S} = {\rm col}\{{\pmb F}_{{\rm S}i} \} \in {\pmb R}^{(6n - N)} \cr \dot { V} = {\rm col}\{\dot{\pmb V}_i \} \in {\pmb R}^{6n}\cr \dot { Q} = {\rm col}\{ \dot{\pmb Q}_i \} \in {\pmb R}^N \end{array}\!\! \right\} $ | (11) |
基于式(9) $\sim $式(11),整个单链结构的递推关系可表示为矩阵形式
| $ \left. {\begin{array}{*{20}{l}} \begin{array}{l} {P_{{\rm{chain}}}}F = I\mathop V\limits^. \\ P_{{\rm{chain}}}^{\rm{T}}\mathop V\limits^. = H\mathop Q\limits^. \end{array} \end{array}} \right\}$ | (12) |
对外接了$ M $个刚体的节点,其递推关系也可用式(7)表示.
定义矩阵
| $ { P}_{\rm node } = \left[\begin{array}{ccc|c} {P}_{o(j_1 )} & & & \\ & \ddots & & {\bf 0} \\ & & { P}_{o(j_ M )} & \\ \hline { P}_{{\rm n}j,o(j_1 )} & \cdots & { P}_{{\rm n}j,o(j_ M )} & { P}_{{\rm n}j} \end{array} \right] =\\ \qquad \left[\begin{array}{ccc|c} {\pmb U} & & & \\ & \ddots & & {\bf 0} \\ & & {\pmb U} & \\ \hline -\hat{\pmb P}_{j,o(j_1 )} & \cdots &- \hat {\pmb P}_{j,o(j_ M )} & {\pmb U} \end{array} \right] $ | (13) |
与单链结构的${ P}_{\rm chain} $相比,该矩阵的分块主对角线同样均为单位矩阵,但由于假设节点的外接结构均为单个刚体,故分块主对角线下方为零矩阵(符合只包含一个刚体的单链结构的${ P}_{\rm chain} $定义方式);此外,多个外接体与刚体j间均有耦合,因此在${ P}_{\rm node} $的最后一行补充$ M $个对应分块对角线上${ P}_{o(j_m )} $的非零矩阵$ - \hat{\pmb P}_{j,o(j_m )} $. 之后定义其他组集矩阵,其中下标i按照${ P}_{\rm node} $分块对角线上 矩阵${ P}_{o(j_m )} $下标的排列顺序依次取值
| $ \left. \!\! \begin{array}{l} { H }= {\rm diag}\{{\pmb H}_i \} \in {\pmb R}^{6( M + 1)\times N} \\ { W }= {\rm diag}\{{\pmb W}_i \} \in {\pmb R}^{6( M + 1)\times (6( M + 1) - N)} \\ { I }= {\rm diag}\{{\pmb I}_i \} \in {\pmb R}^{6( M + 1)\times 6( M + 1)} \\ { F} = {\rm col}\{{\pmb F }_i \} \in {\pmb R}^{6( M + 1)} \\ { F}_{\rm T} = {\rm col}\{{\pmb F }_{{\rm T} i} \} \in {\pmb R}^N \\ { F}_{\rm S} = {\rm col}\{{\pmb F }_{{\rm S} i} \} \in {\pmb R }^{(6( M + 1) - N)} \\ \dot{ V} = {\rm col}\{\dot{\pmb V}_i \} \in {\pmb R }^{6( M + 1)} \\ \dot{ Q} = {\rm col}\{ \dot{\pmb Q}_i \} \in {\pmb R}^N \end{array}\!\! \right\} $ | (14) |
则对单个节点,其对应的递推关系可表示为
| $ \left.\!\! \begin{array}{l} { P}_{\rm node}{ F} ={ I}\dot{ V} \\ { P}_{\rm node}^{\rm T} \dot { V} = { H}\dot { Q} \\ \end{array} \right \} $ | (15) |
注意到该式与式(12)形式相似,因此单链结构和节点处的动力学和运动学的组集形式得到统一.
2.3.3 系统级递推关系组集任意一个树形系统均可由不同的单链结构和节点结构首尾相接而成,因此可以通过借助式(10)、式(11)以及式(13)、式(14)的定义 方法,写出整个系统的矩阵${ P}$和其它各个对应的组集矩阵,使得系统递推关系仍满足以下方程
| $ \left. \!\! \begin{array}{l} { P}{ F} = { I}\dot{ V} \\ { P}^{\rm T} \dot{ V} = { H}\dot{ Q} \\ \end{array} \!\! \right \} $ | (16) |
下面对树形系统的动力学组集方法进行讨论.
首先,考虑图 3所示系统,一个节点外接$ M $条单链结构,单链$m$包含$n_{{\rm c}m} $个刚体和$N_{{\rm c}m} $个自由度,对式(13)中的矩阵进行扩充,得到
| $ { P }= \left[\begin{array}{ccc|c} { P}_{{\rm ch}o(j_1 )} & {\bf 0} & {\bf 0} & {\bf 0} \\ {\bf 0} & \cdots & {\bf 0} & \cdots\\ {\bf 0} & {\bf 0} & {{ P}_{{\rm ch}o(j_ M )} } & {\bf 0} \\ \hline {{ P}_{{\rm n }j,{\rm ch} o(j_1 )} } & \cdots & {{ P}_{{\rm n }j,{\rm ch}o(j_ M )} } & {{ P}_{{\rm n }j} } \end{array} \right] $ | (17) |

|
图 3 节点外接单链结构 Fig.3 Node with outboard chains |
其中${ P}_{{\rm ch} o(j_m )} $按照式(10)中的${ P}_{\rm chain} $进行定义,各项为
| $ { P}_{{\rm ch }o(j_m )} = \left[\!\! \begin{array}{ccccc} {\pmb U} & {\bf 0} & {\bf 0} & \cdots & {\bf 0} \\ { - \hat{\pmb P}^{{\rm chain }m}_{n_{ cm } - 1} } & {\pmb U} & {\bf 0} & \cdots & {\bf 0} \\ {\bf 0} & { - \hat{\pmb P}^{{\rm chain }m}_{n_{ cm } - 2} } & {\pmb U} & \cdots & {\bf 0} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ {\bf 0} & {\bf 0} & \cdots & - \hat{\pmb P}^{{\rm chain }m}_1 & {\pmb U} \end{array} \!\! \right] $ | (18) |
并且依旧有${ P}_{{\rm n }j} = {\pmb U}$.
由于多个外接体与刚体j间存在耦合,并且考虑到式(17)中对角线上的矩阵的维度变化,所补充的最后一行的矩阵 ${ P}_{{\rm n}j,{\rm ch}o(j_m )} $中各项应写为
| ${ P}_{{\rm n }j,{\rm ch}o(j_m )} = \left[ {\bf 0} \ \ \cdots \ \ {\bf 0} \ \ - \hat {\pmb P}_{j,o(j_m )} \right] \in {\pmb R}^{6\times 6n_{{\rm c}m} } $ | (19) |
其余矩阵仍按照式(14)进行定义,从而得到了节点外接单链结构时的各个组集矩阵,使图 3所示系统的递推关系依然满足式(16). 当节点外接复杂结构时,仍可按照式(17)的形式写出整个系统的矩阵${ P}$,然后细化其中各个非零阵并按照式(14)定义其它组集矩阵,即可得到组集后的递推关系式(16).
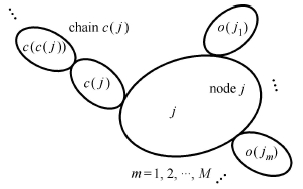
其次,考虑图 4所示的单链结构外接节点的情况,矩阵${ P}$的形式为
| $ { P} = \left[\begin{array}{cc} { P}_{{\rm node }j} & {\bf 0} \\ { P}_{{\rm ch }c (j),{\rm node }j} & { P}_{{\rm ch }c(j)} \end{array} \right] =\\ \left[\begin{array}{ccc|c|c} { P}_{o(j_1 )} & {\bf 0} & {\bf 0} & {\bf 0} & {\bf 0} \\ {\bf 0} & \ddots & {\bf 0} & \vdots & \vdots \\ {\bf 0} & {\bf 0} & { P}_{o(j_ M )} & {\bf 0} & {\bf 0} \\ \hline { P}_{{\rm n }j,o(j_{1} )} & \cdots & { P}_{{\rm n }j,o(j_ M )} & { P}_{{\rm n }j} & {\bf 0} \\ \hline {\bf 0} & \cdots & {\bf 0} & { P}_{{\rm ch} c(j),{\rm n}j} & { P}_{{\rm ch}c(j)} \end{array} \right] $ | (20) |
|
图 4 单链结构外接节点 Fig.4 Chain with outboard node |
对于外接$ M $个结构的节点j,可按照式(17)写出矩阵${ P}_{{\rm node }j} $,在节点刚体j所在行的对应位置上同样补充由耦合产生的矩阵${ P}_{{\rm n }j,o(j_m )} $;而对于其内接的单链结构,矩阵${ P}_{{\rm ch }c (j)} $按照式(10)中的${ P}_{\rm chain} $进行定义;除了将${ P}_{{\rm node }j} $,${ P}_{{\rm ch }c(j)} $在 对角线上进行排列外,在刚体j所在列的位置上补充了分块列矩阵${ P}_{{\rm ch} c(j),{\rm n}j} $,其行数与${ P}_{{\rm ch }c(j)} $相同,有
| $ { P}_{{\rm ch} c(j),{\rm n}j} = [-\hat {\pmb P }^{\rm T}_{c(j),j} \ \ {\bf 0} \ \ \cdots \ \ {\bf 0} ]^{\rm T} $ | (21) |
补充该矩阵实质上是将节点刚体j等效为其所内接的单链结构${\rm chain }c(j)$名义上的“最后”一个刚体. 其余组集矩阵依旧按照式(14)进行定义,从而可以使图 4所示系统的递推关系同样满足式(16).
由以上分析可得组集任意树形系统动力学递推关系式的方法:
(1)由内到外逐层分辨出节点与单链结构,并将每个部分的各自的矩阵${ P}_{{\rm ch }x} $与${ P}_{{\rm n }y} $由外到内排列,作为整个矩阵${ P}$的对角线:其中${ P}_{{\rm ch }x} $按照式(10)进行定义,而${ P}_{{\rm n }y} = {\pmb U}$;
(2)在每个节点刚体所在行和列的对应位置补充由于耦合所产生的矩阵,并将所补充的矩阵具体化,得到整个系统的矩阵${ P}$:所补充的矩阵${ P}_{{\rm n }y,{\rm ch }x} $为分块行矩阵,其列数与矩阵${ P}_{{\rm ch }x} $的维度相同,且其中唯一非零项为$ - \hat{\pmb P}_{{\rm n }y,{\rm ch }x} $,位于最后一列;所补充的矩阵${ P}_{{\rm ch }x,{\rm n }y} $为分块列矩阵,其行数与矩阵${ P}_{{\rm ch }x} $的维度相同,且其中唯一的非零项为$ - \hat{\pmb P}_{{\rm ch }x,{\rm n }y} $,位于第一行;
(3)按照式(14)以及矩阵${ P}$中分块对角线上的矩阵下标顺序,定义余下8个组集矩阵;
(4)系统的动力学递推关系组集为式(16).
2.4 约束力算法的一般形式各个关节处的受力分解关系式(5)可组集为
| $ { F} = { H} \cdot { F}_{\rm T} + { W} \cdot { F}_{\rm S} $ | (22) |
由式(16)可得
| $ \dot { Q} = { H}^{\rm T}{ P}^{\rm T}\dot{ V} $ | (23) |
| $ { W}^{\rm T}{ P}^{\rm T}{ I}^{ - 1}{ P}{ F }= {\bf 0} $ | (24) |
则将关节受力分解关系式(22)代入上式,得到
| $ { W}^{\rm T}{ P}^{\rm T}{ I}^{ - 1}{ P}{ W} \cdot { F}_{\rm S} = - { W}^{\rm T}{ P}^{\rm T}{ I}^{ - 1}{ P}{ H} \cdot { F}_{\rm T} $ | (25) |
进行如下定义
| $ \left.\begin{array}{l} { A}={ W}^{\rm T}{ P}^{\rm T}{ I}^{ - 1}{ P W} \\ { B}={ W}^{\rm T}{ P}^{\rm T}{ I}^{ - 1}{ P H} \\ { C }= { H}^{\rm T}{ P}^{\rm T}{ I}^{ - 1}{ P H } \end{array} \right \} $ | (26) |
则由式(25),可得
| $ { A F}_{\rm S} = - { B F}_{\rm T} $ | (27) |
并且有
| $ \dot{ Q} = { C} \cdot { F}_{\rm T} - { B}^{\rm T}{ A}^{ - 1}{ B} \cdot { F}_{\rm T} =\\ \qquad { H}^{\rm T}{ P}^{\rm T}({ I}^{ - 1}{ P}{ H }\cdot { F}_{\rm T} + { I}^{ - 1}{ P}{ W} \cdot { F}_{\rm S} ) $ | (28) |
由式(27)有${ A}^{ - 1} { B}{ F}_{\rm T} = - { F}_{\rm S} $,因此具体计算过程中可先根据式(27)解算出${ F}_{\rm S} = - { A}^{ - 1}{ B}{ F}_{\rm T} $,再依照式(28)计算出$\dot{ Q}$,从而在动力学解算过程中得到系统中的约束力. 由于矩阵与矢量相乘的计算效率显然高于矩阵与矩阵相乘,因而无需计算矩阵${ B}$和${ C}$的显式形式. 由此,对任意树形多体系统的动力学解算问题转化为对系数矩阵为稀疏正定矩阵${ A}$的线性方程组的求解,即
| $ { A} \cdot { F}_{\rm S} =\dot{ X} $ | (29) |
其中$\dot{ X} ={\rm col} \{\dot { X}_i \} = - { B}{ F}_{\rm T}= - { W}^{\rm T}{ P}^{\rm T}{ I}^{-1}{ P}{ H} \cdot { F}_{\rm T}$,可由一系列的矩阵与矢量相乘求得.
由此推导出了约束力算法的一般形式,可总结为以下3个主要步骤直接进行应用:
(1)计算系统的等效控制力${ F}_{\rm T} $;
(2)解方程(29),得到系统约束力${ F}_{\rm S} $;
(3)根据公式(28)得到动力学解算结果.
3 任意树形系统约束力算法的串行化前文推导了适用于任意树形系统的约束力算法的一般形式,并给出直接应用的方法,但实际上其效率较低:主要计算量集中在求解式(29)时对系数矩阵${ A}$的求逆,该步计算量与矩阵${ A}$的维度$N_{\rm S} $成三次方关系. 因此要提高计算效率,应从解决该问题入手.
在费吉尼等所给出的串行化的约束力算法[19]中,采取了对矩阵${ A}$进行${\rm LDL}^{\rm T}$分解[25]后再求解方程(29)的方法,将时间复杂度降至$O(N)$,这是由于链状系统所对应 的矩阵${ A}$(即式(30))为分块三对角矩阵;而本文的研究对象是任意树形系统,其对应的矩阵${ A}$除在分块三对角线上非零外,还存在一些有规律分布的非零矩阵,因此若依旧采用原方法,其时间复杂度将不再是$O(N)$,而是$O(N^3)$. 此外,费吉尼等[19]给出的并行约束力算法对矩阵${ A}$使用了具有二分特性的奇偶消元法[26],从而使得链状系统的并行约束力算法在并行计算的条件下时间复杂度降至$O (\log N)$,并指出该并行约束力算法用于串行计算的时间复杂度为$O (N \cdot \log N)$,仍低于一般的动力学解算方法. 受此启发,本文在所给出的串行化约束力算法中采用奇偶消元法,以降低待求逆的稠密矩阵的阶数,从而提高计算效率.
3.1 关于矩阵${ A}$及方程组解法的讨论对于单链结构,矩阵${ A}$为分块三对角矩阵
| $ { A} = \left[\begin{array}{ccccc} {\pmb A}_n & {\pmb B}_{n - 1}^{\rm T} & & & \\ {\pmb B}_{n - 1} & {\pmb A}_{n - 1} & {\pmb B}_{n - 2}^{\rm T} & & \\ & {\pmb B}_{n - 2} & {\pmb A}_{n - 2} &{\pmb B}_{n - 3}^{\rm T} & \\ & & \cdots & \cdots & \cdots \\ & & & {\pmb B}_1 & {\pmb A}_1 \end{array} \right] $ | (30) |
其中
| $ \left.\begin{array}{l} {\pmb A}_i = {\pmb W}_i^{\rm T} ({\pmb I}_i^{ - 1} + \hat {\pmb P}_{i - 1}^{\rm T} {\pmb I}_{i - 1}^{ - 1} \hat {\pmb P }_{i - 1} ){\pmb W}_i {\rm }\\ \qquad i = n,n - 1,\cdots,1 \\ {\pmb B}_i = - {\pmb W}_i^{\rm T} {\pmb I}_i^{ - 1} \hat {\pmb P}_i {\pmb W}_{i + 1} \\ \qquad i = n -1,n- 2,\cdots,1 \end{array} \right\} $ | (31) |
式(31)中,${\pmb A}_i $包括两部分,一部分是${\pmb W}_i^{\rm T} {\pmb I}_i^{ - 1} {\pmb W}_i $,由于${\pmb I}_i^{ - 1} $定义在刚体i的附体坐标系${\pmb e}_i $下,所以其为定值;另一部分中 $^{i - 1}\hat{\pmb P}_{i - 1}^{\rm T} \cdot (^{i - 1}{\pmb I}_{i - 1} )^{ - 1} \cdot ^{i - 1}\hat{\pmb P}_{i - 1} = ^{i - 1}{\pmb I }_{i - 1,O_i }^{ - 1} $,$^{i - 1}{\pmb I}_{i - 1,O_i }^{ - 1} $在坐标系${\pmb e}_{i - 1} $下为定值,在计算中通过转换矩阵${\pmb C}(i,i - 1)$转换到坐标系${\pmb e}_i $下即可,从而${\pmb A}_i $和${\pmb B}_i $可通过下式计算
| $ \left.\begin{array}{l} {\pmb A}_i = {\pmb W}_i^{\rm T} \cdot ({\pmb I}_i^{ - 1} + {\pmb I}_{i - 1,O_i }^{ - 1} ) \cdot {\pmb W}_i \quad i = n,n-1,\cdots,1 \\ {\pmb B}_i = - {\pmb W}_i^{\rm T} \cdot {\pmb I}_i ^{ - 1} \cdot \hat{\pmb P}_i \cdot {\pmb W}_{i + 1} \quad i = n- 1,n- 2,\cdots,1 \end{array} \right\} $ | (32) |
由于单链系统矩阵${ A}$的分块三对角形式,在后续对算法进行串行化或并行化处理时可以采取很多针对三对角线 性方程组的处理方法[27, 28, 29].
对于树形系统,除了在3条分块对角线上存在对应的${\pmb A}$,${\pmb B}$外,节点的存在使矩阵${ A}$ 3条分 块对角线外产生了一些非零耦合项(本质原因是矩阵${ P}$中补充了非零耦合项),使得分块${\rm LDL}^{\rm T}$方法不再适用. 但这些非零耦合项的计算方式以及分布都有很强的规律性,总共有4类,以有$ M $个外接结构的节点j为例,说明其分布、物理含义和计算方法:
(1) ${\pmb A}_j^{\rm t} $:位于矩阵${\pmb A}_j $处,代表节点j与其内接体$c(j)$间的耦合对节点j的影响,有
| $ {\pmb A}_j^{\rm t} = {\pmb W}_j^{\rm T} {\pmb I}_{c(j),O_j }^{ - 1} {\pmb W}_j $ | (33) |
(2) ${\pmb B}_{c(j)}^{\rm t} $和 $({\pmb B}_{c(j)}^{\rm t} )^{\rm T}$:分别位于矩阵${\pmb A}_j $的下方和右方,表达了节点j与其内接体$c(j)$间的耦合对内接体$c(j)$的影响,有
| $ {\pmb B}_{c(j)}^{\rm t} = - {\pmb W}_{c(j)}^{\rm T} {\pmb I}_{c(j)}^{ - 1} \hat{\pmb P}_{c(j)} {\pmb W}_j $ | (34) |
(3) ${\pmb D}_{j,o(j_m )}^{\rm t} $和$({\pmb D}_{j,o(j_m )}^{\rm t} )^{{\rm T}}$:分别位于矩阵${\pmb A}_j $所在行与矩阵${\pmb A}_{o(j_m )} $所在列的交点处和其转置的位置($m = 1,2,\cdots ,M $),表达了节点j与其各个外接体o(jM间的耦合,且
| $ {\pmb D}_{j,o(j_m )}^{\rm t} = - {\pmb W}_j^{\rm T} {\pmb I}_j^{ - 1} \cdot \hat{\pmb P}_{j,o(j_m )} {\pmb W}_{o(j_m )} $ | (35) |
(4) ${\pmb b}_{o(j_a ),o(j_b )}^{\rm t}$:位于节点j任意两个外接体$o(j_a )$和$o(j_b )$所对应的矩阵${\pmb A}_{o(j_a )} $所在行和矩阵${\pmb A}_{o(j_b )} $所在列的耦合项($a$和$b$遍历$1,2,\cdots ,M $中任选两数的所有数对),表达了节点j的各个外接结构之间的耦合,且
| $ {\pmb b }_{o(j_a ),o(j_b )}^{\rm t} = {\pmb W}_{o(j_a )}^{\rm T} \hat{\pmb P}_{j,o(j_a )}^{\rm T} {\pmb I}_j^{ - 1} \hat{\pmb P }_{j,o(j_b )} {\pmb W}_{o(j_b )} $ | (36) |
上述4类非零耦合项中,${\pmb A }_j^{\rm t} $,${\pmb B }_{c(j)}^{\rm t} $和$({\pmb B }_{c(j)}^{\rm t} )^{\rm T}$位于矩阵${ A}$的3条分块对角线上,不妨更新节点j对应的矩阵${\pmb A }_j $为
| $ {\pmb A }_j = {\pmb W}_j^{\rm T} {\pmb I}_j^{ - 1} {\pmb W }_j + {\pmb A }_j^{\rm t} $ | (37) |
以及补充定义
| ${\pmb B }_{c(j)} = {\pmb B }_{c(j)}^{\rm t} $ | (38) |
则实际上对矩阵${ A}$形式有影响的仅为${\pmb D}_{j,o(j_m )}^{\rm t} $,$({\pmb D}_{j,o(j_m )}^{\rm t} )^{{\rm T}}$和${\pmb b}_{o(j_a ),o(j_b )}^{\rm t} $,并且均分布在节点刚体及其外接体对应的矩阵${\pmb A}$所在的行和列上. 若对矩阵${ A}$进行初等变换,则新的耦合项将同样满足这一分布规律. 而奇偶消元法实质上就是通过对方程组系数矩阵进行行变换实现的,因此对方程(29)使用奇偶消元法后,最终系 数矩阵${ A}^{(K)}$中的耦合项分布范围不变,而矩阵${ A}^{(K)}$中除去与节点刚体及其外接体有关的行和列外,已经 成为一个分块对角矩阵,消元次数${ K}$为大于等于$\log_2 [\max (n_{{\rm chain }m} )]$的最小整数.
对于刚体i的第j轮消元,首先按照以下两式计算两个参数
| $ \left.\!\!\begin{array}{l} {\pmb E}_i^{(j)} = {\pmb B}_i^{(j - 1)} \cdot ({\pmb A}_{i + 2^{j - 1}}^{(j - 1)} )^{ - 1} \\ {\pmb G}_i^{(j)} = ({\pmb B}_{i - 2^{j - 1}}^{(j - 1)} )^{\rm T} \cdot ({\pmb A}_{i - 2^{j - 1}}^{(j - 1)} )^{ - 1} \end{array} \right \} $ | (39) |
再计算各个矩阵
| $ \left.\!\!\begin{array}{l} {\pmb A}_i^{(j)} = {\pmb A}_i^{(j - 1)} - {\pmb E}_i^{(j)} \cdot ({\pmb B}_i^{(j - 1)} )^{\rm T} - {\pmb G}_i^{(j)} \cdot {\pmb B}_{i - 2^{j - 1}}^{(j - 1)} \\ {\pmb B}_i^{(j)} = - {\pmb E}_i^{(j)} \cdot {\pmb B}_{i + 2^{j - 1}}^{(j - 1)} \\ {\pmb D}_{i,o(i_m )}^{(j)} = {\pmb D}_{i,o(i_m )}^{(j - 1)} - {\pmb D}_{i - 2^{j - 1},o(i_m )}^{(j - 1)} \cdot {\pmb G}_i^{(j){\rm T}} \\ {\pmb b}_{i,i_b }^{(j)} = {\pmb b}_{i,i_b }^{(j - 1)} - {\pmb b}_{i - 2^{j - 1},i_b }^{(j - 1)} \cdot {\pmb G}_i^{(j){\rm T}} \\ \dot {\pmb X}_i^{(j)} = \dot {\pmb X}_i^{(j - 1)} - {\pmb E}_i^{(j)} \cdot \dot {\pmb X}_{i + 2^{j - 1}}^{(j - 1)} - {\pmb G}_i^{(j)} \cdot \dot {\pmb X}_{i - 2^{j - 1}}^{(j - 1)} \end{array} \right\} $ | (40) |
完成${K}$轮消元后,考虑适当调整方程组${ A}^{(K)} { F}_{\rm S} = \dot { X}^{(K)}$中方程的排列次序(即对方程组${ A}^{(K)} { F}_{\rm S} = \dot { X}^{(K)}$进行换法初等变换),将系数矩阵${ A}^{(K)}$中与节点和其外接体有关的行和列集中,即将所 有耦合项集中至右下方$N_{\rm S}^{\rm node} $阶的稠密矩阵和右上方$N_{\rm S}^{\rm chain} \times N_{\rm S}^{\rm node} $阶的耦合矩阵中,使变换后方程$\bar { A}\bar { F}_S = \bar {\dot { X}}$的系数矩阵可以进行如下二阶分块:左上方为$N_{\rm S}^{\rm chain} $阶的分块对角矩阵,该矩阵是与节点结构无关的项,记为$\bar { A}_{\rm chain} $;左下方为$N_{\rm S}^{\rm node} \times N_{\rm S}^{\rm chain} $阶零矩阵;右下方的$N_{\rm S}^{\rm node} $阶矩阵是全部与节点结构有关的项,记为$\bar { A}_{\rm node} $;右上方的矩阵表达了节点与单链结构之间的耦合关系,记为$\bar { A}_{{\rm chain\_node}} $.
即有
| $ \bar { A} = \left[\begin{array}{cc} {\bar { A}_{\rm chain} } & {\bar { A}_{{\rm chain\_node}} } \\ {\bf 0} & {\bar { A}_{\rm node} } \end{array} \right] $ | (41) |
| $ \bar {\dot { X}} = \left[\begin{array}{l} \bar {\dot { X}}_{\rm chain} \\ \bar {\dot { X}}_{\rm node} \end{array} \right] $ | (42) |
则原待求解方程(29)转化为
| $ \left[\begin{array}{cc} {\bar { A}_{\rm chain} } & {\bar { A}_{{\rm chain\_node}} } \\ {\bf 0} & {\bar { A}_{\rm node} } \end{array} \right]\left[\begin{array}{l} { F}_{{\rm S} {\rm chain}} \\ { F}_{{\rm S} {\rm node}} \end{array} \right] = \left[\begin{array}{l} \bar {\dot { X}}_{\rm chain} \\ \bar {\dot { X}}_{\rm node} \end{array} \right] $ | (43) |
从而可以依次求解以下两个方程,对原方程组进行求解
| $ \left. \begin{array}{l} \bar { A}_{\rm node}{ F}_{{\rm S} \rm node} = \bar {\dot { X}}_{\rm node} \\ \bar { A}_{\rm chain} { F}_{{\rm S} \rm chain} = \bar {\dot { X}}_{\rm chain} - \bar { A}_{{\rm chain\_node}} \cdot { F}_{{\rm S} \rm node} \end{array} \right \} $ | (44) |
新的方程组中,两个系数矩阵$\bar { A}_{\rm chain} $和$\bar { A}_{\rm node} $分别为低阶的稠密矩阵和分块对角矩阵;虽然无论采取串行还是并行计算方式,对矩阵$\bar { A}_{\rm node}$求逆的过程依然与其阶数成三次方,但其阶数已由$N_{\rm S}$下降为$N_{\rm S}^{\rm node} $,因此计算效率得到了提高;而在求解第二个方程的过程中,由于$\bar { A}_{\rm chain} $为分块对角矩阵,因此其时间复杂度得到了更大程度的降低. 由此,通过对原方程组先利用奇偶消元法进行消元,再进行换法初等变换的方法,得到了提高解算效率的串行化约束力算法.
由于相同维度的矩阵之间相乘的效率低于矩阵与矢量相乘,故将约束力算法一般形式中的矩阵乘法转化为串行形式,依次对各 体的数据(也就是原矩阵的各行)计算,符合串行计算的特点,在一定程度上可以提高算法的效率.此外,上节讨论了矩阵${ A}$形式及其处理方法,将约束力算法第2步中系数矩阵为高阶的稠密矩阵的待求解方程(29),转化为系 数矩阵分别为低阶稠密矩阵和低阶分块对角矩阵的两个方程(44):其中第1个方程采取直接求解的方法;第2个方程可以以串行 的方式依次计算各体对应的解,时间复杂度得以降低.
约束力算法串行化应用的具体步骤如下:
(1)以串行方式计算单个刚体的等效控制力${\pmb F }_{{\rm T }i} $;
(2)解方程${ A} \cdot { F}_{\rm S} = \dot { X}$,得到各约束力${\pmb F }_{{\rm S }i} $:
① 以串行方式依次计算各体的$\dot {\pmb X}_i $和矩阵${ A}$中各项;
② 按照式(39)和式(40),以串行方式对方程${ A} \cdot { F}_{\rm S} = \dot { X}$中各单链部分进行${K}$轮分块奇偶消元(${K}$为大于等于$\log _2 [\max (n_{{\rm chain }m} )]$的最小整数),得到方程组${ A}^{(K)} { F}_{\rm S} = \dot { X}^{(K)}$;
③ 对线性方程组${ A}^{(K)} { F}_{\rm S} = \dot { X}^{(K)}$进行换法变换,得到符合要求的$\bar { A}$,$\bar { F}_{\rm S} $和$\bar {\dot { X}}$;
④ 解方程$\bar { A}_{\rm node} { F}_{{\rm S} \rm node} = \bar {\dot { X}}_{\rm node} $得到约束力${ F}_{{\rm S} \rm node} $,并带入方程$\bar { A}_{\rm chain} { F}_{{\rm S} \rm chain} = \bar {\dot { X}}_{\rm chain} - \bar { A}_{{\rm chain\_node}} \cdot { F}_{{\rm S} \rm node} $,以串行方式求解各单链刚体的约束力${\pmb F}_{{\rm S }i} $;
(3) 根据式(28),以串行方式计算得到动力学解算结果.
需要指出,基于以上推导,约束力算法同样可并行化求解,进一步提高计算效率,但对技术和硬件要求较高,因此约束力算 法并行化仅作为后续研究内容.
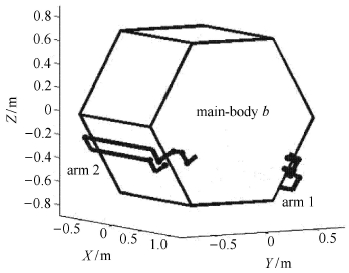
4 仿真算例及结果研究图 5所示的刚性空间 机器人,该系统为空间漂浮系统,且含有节点结构.
|
图 5 空间机器人结构和尺寸 Fig.5 Structure and size of space robot |
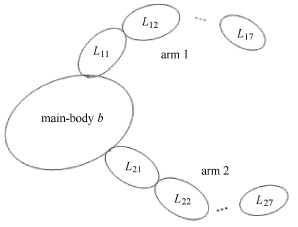
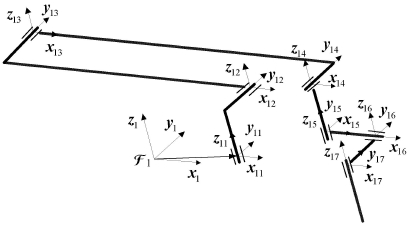
该机器人有两部结构相同的机械臂,机械臂1和机械臂2均可在力矩的驱动下运动,其拓扑结构如图 6所示. 机器人本体为长1.2 m、底面边长0.8 m的六棱柱,在质心处建立其附体坐标系;机械臂的结 构和零状态下的构 型如图 7 (以机械臂1为例).
|
图 6 算例的拓扑结构 Fig.6 Topology of example |
|
图 7 机械臂1 结构 Fig.7 Structure of arm 1 |
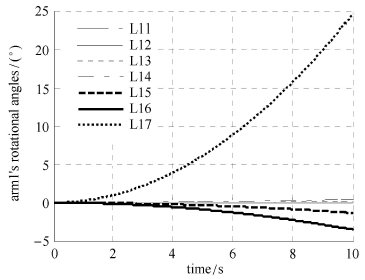
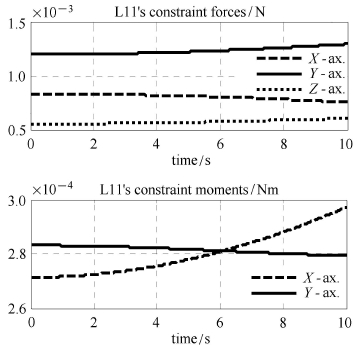
为验证本文算法的正确性,同时利用递推算 法[30]和约束力算法的一般形式建立了该算例的动力学模型,并对两模型输 入相同激励,进行了10 s仿真. 图 8 ~图 10分别给出了约束力算法模型所得到的本体姿态角响应、机械臂1关节转角响应以及臂杆L11与其内接体相连处的约束力.

|
图 8 本体姿态角 Fig.8 Main-body’s attitude angles |
|
图 9 机械臂1 各转角 Fig.9 Arm1’s rotational angles |
|
图 10 臂杆L11 约束力 Fig.10 L11’s constraint forces & moments |
约束力算法模型与递推算法模型的解算结果之差如图 11和图 12所示. 两模型相对误差小于$10^{ - 12}$,可以认为两组结果 互相吻合,从而证明了推广到任意树形系统下的约束力算法的准确性.

|
图 11 本体姿态角误差 Fig.11 Errors of main-body’s attitude angles |

|
图 12 机械臂1 各转角误差 Fig.12 Errors of arm1’s rotational angles |
除使用递推算法和约束力算法的一般形式对算例进行建模外,本节还采用常规的凯恩方法[31]和串行化约束力算法对该系 统进行了建模. 为比较4种方法的解算效率,对系统进行10 s的仿真,仿真步长为0.002 s. 利用同一计算机在相同工作状态下各仿真5次后,得到依据4种方法建立的模型中,动力学模块的处理器运行时间及其平均值见表 1.
| 表 1 4 种模型动力学模块的处理器运行时间 Table 1 CPU time for 4 kinds of dynamics models |
可以看出,常规凯恩方法用时最长、递推方法用时最短,两种约束力算法的用时居于二者之间,且串行化的约束力算法用时较短.
首先,常规凯恩方法和直接应用的约束力算法的时间复杂度分别与系统的自由度数量和约束数量成三次方关系;常规凯恩方程实质上是一种耦合模型,在推导数学模型时需要从耦合的动力学中得出各体的动力学方程,最终得到单体的动力学方程极为复杂,并且该方法并未对系统的所有方程进行组集,导致实际得到的模型过于庞大,求解效率低;而约束力算法则利用系统的递推关系,单体的显式方程形式简单,并且将整个系统方程组集为矩阵形式,更加适合计算机解算.
其次,递推算法的时间复杂度与系统中的自由度数量呈线性关系,而约束力算法两种应用的复杂度均高于递推算法,因此递推算 法用时较短是合理的;虽然从仿真用时角度看,约束力算法不及递推算法,但其可以在解算过程中解出系统约束力,这是递推算法[30]所不具备的.
第三,应用两种约束力算法所建立的模型相比,串行化算法的模型的用时较短,这一结果证实了串行化应用对约束力算法效 率的提升;并且该算法后续还可以通过并行化应用,达到更低的时间复杂度,在解算效率上获得更大的优势.
综上所述,通过本文推广后的约束力算法仍具有方程形式简单、适合计算机编程解算的特点;经串行化应用后,约束力算法的计 算效率得到了一定提高,虽然尚未达到递推算法的效率,但其具有可解算系统约束力的 优势. 此外,约束力算法还可以通过并行化使效率进一步提升,故其具有一定的应用前景.
5 结论与展望本文针对任意树形构型多体系统,分析任意节点处的动力学、运动学递推关系,得出系统递推关系的组集方法,对约束力 算法进行了推广,并给出了其串行化应用方法. 推广后的约束力算法普适性更强,能够适用于任意树形多体系统. 与其他多体动力学解算方法相比,可直接解算系统约束力,并具有显式动力学方程. 所提算法保持了约束力算法形式简单、适合计算机编程解算的特点,并且串行化后效率得到了相应提高. 通过对空间机器人的 仿真,验证了算法的正确性和串行化后的高效性. 后续将对该算法进行并行化处理和应用.
| 1 | Ma J, Qian L, Chen G, et al. Dynamics analysis of mechanical systems with planar revolute joints with clearance. Mechanism and Machine Theory, 2015, (94): 148-164 |
| 2 | 陈思雨,唐进元. 间隙对含摩擦和时变刚度的齿轮系统动力学响 应的影响. 机械工程学报,2009, 46(8): 119-124 (Chen Siyu, Tang Jinyuan. E ect of backlash on dynamics of spur gear pair system with friction and time-varying sti ness. Journal of Mechanical Engineering,2009, 46(8): 119-124 (in Chinese)) |
| 3 | Liu X, Li X, Chen Y, et al. Dynamics and control of space robot considering joint friction. Acta Astronautica, 2015, 111: 1-18 |
| 4 | Burns SJ, Piiroinen PT. A hybrid scheme for simulation of planar rigid bodies with impacts and friction using impact mappings. International Journal of Non-linear Mechanics, 2015, 77: 312-324 |
| 5 | Adly S. Attractivity theory for second order non-smooth dynamical systems with application to dry friction. Journal of Mathematical Analysis and Applications, 2006, 332(2): 1055-1070 |
| 6 | Theodossiades S, Natsiavas S. Non-linear dynamics of gear-pair systems with periodic sti ness and backlash. Journal of Sound and Vibration,2000, 229(2): 287-310 |
| 7 | Duncan M,Wassgren C, Krousgrill C. The damping performance of a single particle impact damper. Journal of Sound and Vibration,2005, 286(1): 123-144 |
| 8 | Mehmood A, Hajj M, Nayfeh A, et al. E ectiveness of nonlinear energy sink (nes) in suppressing vortex-induced vibrations of a circular cylinder. In: Proc. of Structures, Structural Dynamics, and Materials and Co-located Conferences, April 2013, Boston, Massachusetts |
| 9 | Bichiou Y, Hajj MR, Nayfeh AH. Investigation on the e ectiveness of a nonlinear energy sink on an aeroelastic system. In: Proc. of 55th AIAA/ASMe/ASCE/AHS/SC Structures, Structural Dynamics, and Materials Conference, January 2014, National Harbor, Maryland |
| 10 | Parseh M, Dardel M, Ghasemi MH. Investigating the robustness of nonlinear energy sink in steady dynamics of linear beams with different boundary conditions. Communications in Nonlinear Science and Numerical Simulation, 2015, 29(1-3): 50-71 |
| 11 | Gourc E, Seguy S, Michon G, et al. Quenching chatter instability in tuning process with a vibro-impact nonlinear energy sink. Journal of Sound and Vibration, 2015, 355: 392-406 |
| 12 | Yu M, Chen Q, Gao X. Theoretical and experimental investigation of molecular spring isolator. Microsystem Technology, 2015,10.1007/s00542-0140240107 |
| 13 | 余慕春,陈前,高雪等. 分子弹簧的隔振机理与力学性能研究. 力学学报, 2014, 46(4): 553-560 (Yu Muchun, Chen Qian, Gao Xue, et al. Investigation of molecular spring on vibration isolation mechanism and mechaanical properties. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 553-560 (in Chinese)) |
| 14 | Deshpande S, Mehta S, Jazar GN. Optimization of secondary suspension of piecewise linear vibration isolation systems. International Journal of Mechanical Sciences, 2006, 48(4): 341-377 |
| 15 | Gao X, Chen Q. Static and dynamic analysis of a high static and low dynamic sti ness vibration isolator utilising the solid and liquid mixture. Engineering Structures, 2015, 99: 205-213 |
| 16 | Jazar GN, Mahinfalah M, Deshpande S. Design of a piecewise linear vibration isolator for jump avoidance. Journal of Multi-body Dynamics, 2007, 221(3): 441-449 |
| 17 | 胡海岩. 隔振系统限位器的非线性动力学设计. 航空学报, 1996,17(5): 529-533 (Hu Haiyan. Design elastic constraints in a vibration isolation system from the view of nonlinear dynamics. Acta Aeronautica et Astronautica Sinica, 1996, 17(5): 529-533 (in Chinese)) |
| 18 | Vasconcellos R, Abdelkefi A. Phenomena and characterization of grazing-sliding bifurcations in aeroelastic systems with discontinuous impact e ects. Journal of Sound and Vibration, 2015, 358:315-323 |
| 19 | Shen J, Li Y, Du Z. Subharmonic and grazing bifurcations for a simple bilinear oscillator. International Journal of Nonlinear Mechanics,2014, 60: 70-82 |
| 20 | Humphries N, Piiroinen PT. A discontinuity-geometry view of the relationship between saddle-node and grazing bifurcations. Physica D: Nonlinear Phenomena, 2012, 241(22): 1911-1918 |
| 21 | Roy RV. Noise perturbations of a non-linear system with multiple steady states. International Journal of Non-linear Mechanics, 1994,29(5): 755-773 |
| 22 | Roy RV. Asymptotic analysis of first-passage problems. International Journal of Non-llinear Mechanics, 1997, 32(1): 173-186 |
| 23 | Wiggins S, Golubitsky M. Introduction to applied nonlinear dynamical systems and chaos. New York: Springer, 1990 |
| 24 | 张伟,胡海岩. 非线性动力学理论与应用的新进展. 北京:科学 出版社, 2009 (Zhang Wei, Hu Haiyan. Advance in nonlinear dynamics theory and applications. Beijinig: Science Press, 2009 (in Chinese)) |
| 25 | Gao X, Chen Q. Nonlinear frequency response analysis and dynamics design of a solid and liquid mixture nonlinear vibration isolator. Journal of Vibration and Control, 2014, 20(15): 2389-2400 |
| 26 | Shaw SW, Holmes P. A periodically forced piecewise linear oscillator. Journal of Sound and Vibration, 1983, 90(1): 129-155 |
| 27 | 刘先斌. 随机力学系统的分叉行为与变分方法研究. [博士论文]. 成都: 西南交通大学, 1995 (Liu Xianbin. On the bifurcation behaviours and the variational methods of stochastic mechanical systems. [PhD Thesis]. Chengdu: Southwest Jiaotong University, 1995 (in Chinese)) |
| 28 | Roy RV, Nauman E. Noise-induced e ects on a non-linear oscillator. Journal of Sound and Vibration, 1995, 183(2): 269-295 |
| 29 | 皇甫玉高, 李群宏. 一类单侧碰撞悬臂振动系统的擦边分岔分析. 力学学报, 2008, 40(6): 812-819 (Huangpu Yugao, Li Qunhong. Grazing bifurcation of a cantilever vibrating system with one-sided impact. Chinese Journal of Theoretical and Applied Mechani, 2008,40(6): 812-819 (in Chinese)) |
| 30 | Bernardo MD, Champneys AR, Budd CJ. Piecewise-smooth Dynamical Systems: Theory and Applications. London: Springer,2008 |
 2016, Vol. 48
2016, Vol. 48
