由于诸如间隙[1, 2]、约束、摩擦[3, 4, 5]等非光滑因素广泛存在于振动工程中,因此诸多振动研究对象均可抽象为非光滑动力学系统[6, 7, 8, 9, 10, 11].分段光滑隔振系统的基本特征是具备分段光滑刚度或阻尼,利用分段光滑的刚度或阻尼特性能够实现隔振系统的特定动力学性能及提升隔振性能.如,在分子弹簧隔振系统中[12, 13],分段光滑刚度方便地实现了高静态低动态的刚度特性,从而解决了低频隔振中高承载能力与小静变形无法兼顾的矛盾;在分段汽车悬挂系统中,分段刚度和阻尼降低了响应的最大幅值,使得悬挂系统具有更为优越的缓冲性能[14, 15, 16];含弹性约束的隔振系统亦是一类具备分段刚度和阻尼的分段光滑系统,合理的弹性约束设计能够限制隔振系统的变形,从而保证其稳定性[17].然而,分段光滑隔振系统的非光滑非线性特性[18, 19, 20]亦会给隔振系统的动力学行为带来诸多不利影响.在主共振区,当动力装置变速经过主共振区时,鞍结分岔及擦边分岔的出现都将导致幅值跳跃现象的发生,而这种幅值突变会给隔振机械带来不利冲击;而在隔振段内,尽管激励频率远高于共振频率,但仍有可能发生倍周期分岔及亚谐共振等影响隔振性能的动力学行为;对于隔振有效区内的多稳态运动,随机扰动会使得系统出现随机离出现象[21, 22],破坏系统的可靠性.以上动力学现象普遍存在于分段光滑隔振系统中,对隔振系统的安全性与可靠性有着切实影响.例如,在某型空地导弹的红外线稳瞄系统研制攻关中发现,设计不妥的弹性限位器在振动实验中不仅未能限制隔振器的位移,反而诱发了亚谐共振致使红外线稳瞄系统受损[17].因此,非线性动力学设计是分段光滑隔振系统设计环节中的重要研究内容之一.
分段光滑隔振系统本质上属非光滑动力学系统,除具有传统光滑隔振系统的动力学特性外(如主共振幅值跳跃),还具备特有的非光滑动力学行为 (如擦边失稳),因此其动力学行为的理论分析较为复杂,且已得到广泛关注;而在工程角度上,人们更为关心的问题是,如何利用这些非线性动力学行为来提升隔振性能以及如何屏蔽不利动力学现象的影响. 因此,本文从非线性动力学角度出发,系统地研究分段光滑隔振系统的动力学设计方法,以期在利用非光滑非线性实现优越隔振性能的同时摒除不利动力学行为.
本文以分段双线性刚度的分段光滑隔振系统为理论模型,研究分段光滑隔振系统的非线性动力学设计方法,该理论模型抽象于波纹管液固混合介质隔振系统,亦可代表带弹性约束的隔振系统等.本文安排如下:首先,利用平均法与奇异性理论完整刻划主共振频响曲线的分岔情形,并提出避免主共振跳跃的设计方法;其次,建立了周期轨道的庞加莱映射,通过特征值分析给出避免倍周期分岔发生的条件;继而通过数值仿真研究噪声对多稳态运动的影响.
1 主共振区的动力学设计 1.1 主共振分岔分析分段双线性刚度的分段光滑隔振系统的动力学方程为
| $M\ddot {x} + C\dot {x} + F_{\rm k} (x) = F\cos \omega t$ | (1) |
其中,弹性恢复力和位移的关系
| $ {F_{\rm{k}}}(x) = \left\{ \begin{array}{l} {K_1}x{\mkern 1mu} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \ge {a_{\rm{c}}}{\kern 1pt} \\ {K_2}x + ({K_1} - {K_2}){a_{\rm{c}}}{\mkern 1mu} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x < {a_{\rm{c}}} \end{array} \right. $ | (2) |
为了标度系统的非线性因素,引入符号C,ε∈[0,1],ε越大,系统非线性越强,ε=0则说明系统为线性的.为了采用平均法[23]进行主共振分析,重新标度阻尼、激振力项,如 $C / M = 2\xi _1 \omega _0 = 2\varepsilon \xi \omega _0$ , $F/M = {F_1} = \varepsilon {F_0}$ ,其中 $K_1 / M = \omega _0^2$ ,σ为主共振调谐参数.设方程的一阶解为x=a cos (ωt-φ0),利用平均法得到幅频方程为
| $ \begin{array}{l} {[ - (\sin {\varphi _0}\cos {\varphi _0} + {\varphi _0} + \frac{2}{\beta }\sin {\varphi _0} - \pi )\frac{\varepsilon }{\pi } + (\lambda _\omega ^2 - 1)]^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {(2{\xi _1}{\lambda _\omega })^2} = \frac{{F_1^2}}{{{\beta ^2}a_{\rm{c}}^2\omega _0^4}} \end{array} $ | (3) |
(3)其中,λω=ω/ω0,β=|a/ac|.需要注意的是,以上只是针对稳定振幅会超过临界位移时的频响方程;而对于稳定振幅不会超过临界位移的情况,系统则体现出典型的线性频响特性.
在不同参数组合下,隔振系统可能体现出完全不同的主共振频率响应特性.因此,下文利用奇异性理论对主共振的分岔进行系统分析,目的在于对隔振系统在主共振区的动力学响应特性有全面的了解,从而保证共振区动力学设计的完整性.令
$\begin{array}{l} Y = 1/\beta {\mkern 1mu} ,\;\;\cos {\varphi _0} = - 1/\beta = - Y\\ \sin {\varphi _0} = \sqrt {1 - 1/{\beta ^2}} = 1 - \frac{1}{2}{Y^2} + O({Y^3})\\ {\varphi _0} = \arccos ( - 1/\beta ) = \pi /2 + Y + {Y^3}/6 + O({Y^4}) \end{array}$
主共振频响方程(3)可改写为
| $ G(Y ,\mu; \alpha _1 ,\alpha _2 ) = \left[ { \Big (\dfrac{1}{3}Y^3 - 2Y \Big) + \mu } \right]^2 + \alpha _1 - \alpha _2 Y^2 = 0 $ | (4) |
其中, $ {\alpha _1} = {(2\frac{\pi }{\varepsilon }{\xi _1}{\lambda _\omega })^2} = {(2\frac{\pi }{\varepsilon }{\xi _1})^2} $ , $ {\alpha _2} = \frac{{{\pi ^2}F_1^2}}{{{\varepsilon ^2}a_{\rm{c}}^2\omega _0^4}} $ , $ \mu = [\frac{\pi }{2} + \frac{\pi }{\varepsilon }(\lambda _\omega ^2 - 1)] . $ 这里μ可视为分岔参数,α1 和α2可视作开折参数,它们和系统物理参数密切相关.
以下利用奇异性理论对参数空间进行分类[24]: 分岔集B1:由G=GY=Gμ=0,得α1=α2=0; 滞后集H:由G=GY=GYY=0,得
$ \alpha _2 = - \dfrac{(Y^2 - 2)^3}{Y^2 + 2}\,, \ \ \alpha _1 = \alpha _2 Y^2 - \left( {\dfrac{\alpha _2 Y}{Y^2 - 2}} \right)^2\,; $
双极限点集合:空集. 此外,特殊地,对于非光滑系统,在分段点处还有分岔集B2:由 $ {\left. {\frac{{d\mu }}{{dY}}} \right|_{Y = 1}} = 0. $ 它表明图μ-Y在Y=1 处(即临界位移分界面)有垂直切线.而结合下文图 2 可以更为清晰地理解到,该分岔集B2为界定系统在临界位移分界面处发生鞍结分岔或擦边分岔的分界线.
|
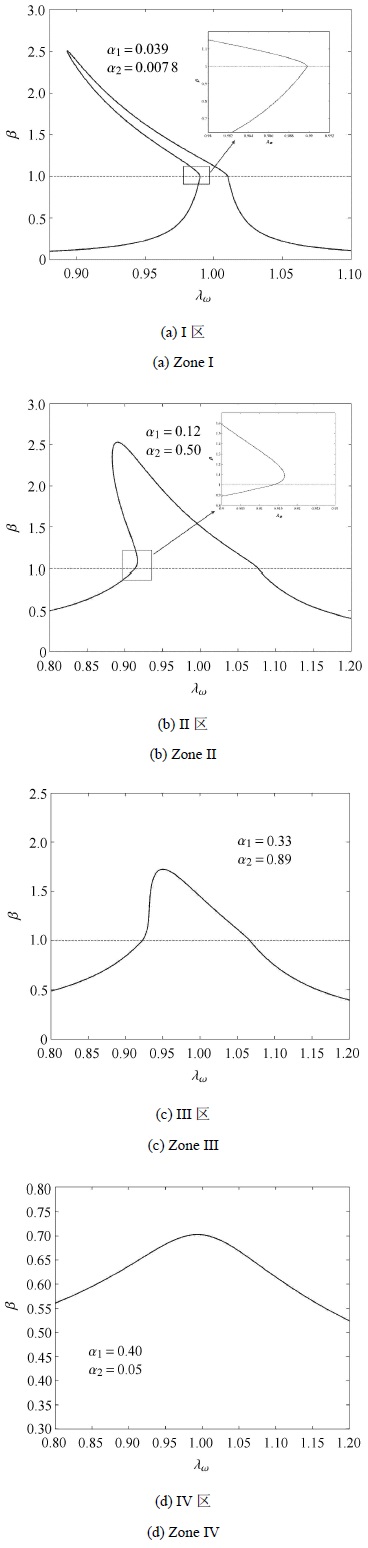
图 2 典型的主共振曲线 Fig.2 Different frequency responses of primary resonance |
由式(4)解出
| $ \mu = - (\frac{1}{3}{Y^3} - 2Y) \pm \sqrt { - ({\alpha _1} - {\alpha _2}{Y^2})} {\rm{ }} $ | (5) |
所以
| $ \frac{{d\mu }}{{dY}} = - ({Y^2} - 2) \pm ({\alpha _2}Y){[ - ({\alpha _1} - {\alpha _2}{Y^2})]^{ - 1/2}} $ | (6) |
进而根据$ {\left. {\frac{{d\mu }}{{dY}}} \right|_{Y = 1}} = 0 $ 得到
| $ \alpha _1 = \alpha _2 - 4\alpha _2^2 $ | (7) |
因此,式(7)所确定的参数分界线区分了系统是否发生了擦边分岔.
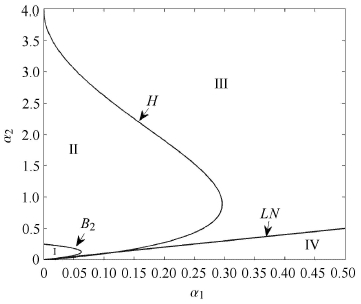
注意到上述讨论仅是针对振动位移可超过刚度转折点(β≥ 1)的非线性情形,因此还需对系统是否为非线性系统进行界定,其划分边界标记为LN,可令线性系统响应振幅等于1简单确定.归纳以上参数空间的划分,如图 1所示.
|
图 1 主共振的参数划分 Fig.1 Parameter zone of primary resonance response with different topology characteristics |
图中,Ⅰ区和Ⅱ区由分岔集B2划分,这两区域参数所对应的幅频曲线的区别在于主共振曲线β > 1 部分存在的垂直切线个数不同.并且在Ⅰ区,分岔发生在转折点β=1处即转折边界上,见图 2(a).这意味着在正向扫频过程中,当系统响应振幅增大至β=1时(对应于轨线与分界面相切情形)随后立即跳跃至更大的共振响应解支上,此处所发生的分岔并非鞍结分岔而是非光滑动力学系统特有的擦边分岔.而由于分段刚度隔振系统的频响函数曲线由线性部分和非线性部分拼接而成,因此在β=1处形成了尖角.而在II处,分岔发生在β > 1,为典型鞍结分岔,如图 2(b)所示.不难看出,Ⅰ区和Ⅱ区频响曲线均发生了跳跃现象.而Ⅲ区所对应的系统为分段刚度系统,且幅频曲线未发生跳跃现象,见图 2(c).Ⅳ 区对应于典型线性系统,其频响曲线如图 2(d)所示. 因此,主共振区幅频特性曲线的特征可归结为以下 3类:线性振动,存在幅值跳跃的非线性振动以及不存在幅值跳跃的非线性振动.除此之外,并不存在其他更为复杂的主共振分岔曲线.
总结来看,鞍结分岔和擦边分岔均可以导致跳跃的发生.而根据图 2(b)可以看出,若跳跃现象由鞍结分岔导致,则在频响函数曲线β > 1部分上一般存在两个点使得dλω/dβ=0,即该点具有铅垂切线; 若β > 1区域,在频响函数曲线上只存在一点满足 dλω/dβ=0,则跳跃即是由擦边分岔所导致的;若频响函数曲线上不存在具有铅垂切线的点,则跳跃不会发生.而从工程意义来看,鞍结分岔和擦边分岔导致的幅值跳跃均具危害性,并无区别.
前述分析对主共振幅频特性曲线拓扑结构进行了分类,除一次跳跃外并无更为复杂的动力学现象出现,因此在主共振区则仅需防治跳跃现象的出现. 尽管这里的分析为近似分析,但并不影响对主共振幅频特性的分类.但对于参数设计,则需基于更为精确的幅频方程,下一节将基于修正平均法所得到的频响方程研究避免跳跃发生的设计方法.
1.2 避免跳跃发生的条件注意到本文所研究的系统(1)为非对称的分段光滑系统,在对称简谐激励作用下系统响应也为非对称(显然这里并不考虑更为复杂的多周期及混沌等运动),而在平均法的求解过程中,试探解仅为一阶近似.所以这里在原试探解的基础上添加一直流项,如x=d+a cos (ωt-φ0)和 $ \dot x = - a\omega \sin (\omega t - {\varphi _0} $ ,再根据平均法得到频响方程为
| $ \begin{array}{l} [ - (\sin {\varphi _0}\cos {\varphi _0} + {\varphi _0} + \frac{2}{\beta }\sin {\varphi _0} - \frac{{2{d_\lambda }}}{\beta }\sin {\varphi _0} - \pi )\frac{\varepsilon }{\pi } + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\lambda _\omega ^2 - 1){]^2} + {(2{\xi _1}{\lambda _\omega })^2} = \frac{{F_1^2}}{{{\beta ^2}a_{\rm{c}}^2\omega _0^4}} \end{array} $ | (8) |
其中,dλ=d/ac,但该项却是未知的,具体求解可参见文献[25].
根据上文的讨论,若跳跃现象由鞍结分岔导致,则在频响函数曲线β > 1部分一般存在两点使得dλω/dβ=0.若频响函数曲线上任何一点都不满足 dλω/dβ=0,则系统不会产生跳跃现象.所以跳跃现象产生的临界条件为,在频响曲线上仅存在一点使得dλω=dβ=0.
由式(8)可得到关于$ \lambda _\omega ^2 $ 频响方程的一对实根,如
| $ \lambda _\omega ^2 = - (Z_1 + 2\xi _1^2 )\pm \sqrt {4Z_1 \xi _1^2 + 4\xi _1^4 + Z_2 } $ | (9) |
其中
$ \begin{array}{l} {Z_1} = [ - (1 - 2{d_\lambda })\frac{1}{\beta }\sqrt {\frac{{{\beta ^2} - 1}}{{{\beta ^2}}}} - \arccos ( - \frac{1}{\beta }) + \pi ]\frac{\varepsilon }{\pi } - 1\\ {Z_2} = \frac{{F_1^2}}{{{\beta ^2}a_{\rm{c}}^2\omega _0^4}} \end{array} $
取其幅值较小的解支,两边对β求导,得到
| $ \frac{{d{\lambda _\omega }}}{{d\beta }} = \frac{1}{{2{\lambda _\omega }}}( - \frac{{d{Z_1}}}{{d\beta }} - \frac{{4\xi _1^2\frac{{d{Z_1}}}{{d\beta }} + \frac{{d{Z_2}}}{{d\beta }}}}{{2\sqrt {4{Z_1}\xi _1^2 + 4\xi _1^4 + {Z_2}} }}) $ | (10) |
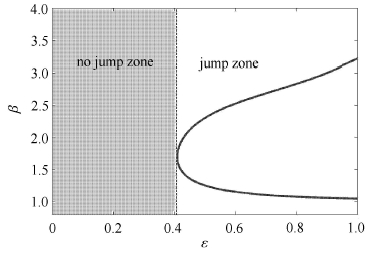
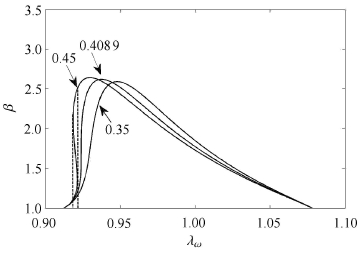
进而令式(10)等于0,即可得出跳跃现象发生的临界条件.给定系统参数为 $ (\omega _0^2 = 2{\mkern 1mu} 670,{\xi _1} = 0.036{\mkern 1mu} 7,{F_1} = 4,{a_{\rm{c}}} = - 0.008{\mkern 1mu} 3) $ ,按照上述步骤确定出临界条件,如图 3所示.从图 3中拾取刚度非线性因子的临界值为0.408 9.在非线性因子小于0.408 9 区域,不存在满足条件的解,因此该区域对应非跳跃区;而在非线性因子大于0.408 9区域,则不难看出存在两个解,亦即频响曲线上存在两点使得满足 dλω/dβ=0,系统则将产生跳跃现象.图 4对应地给出了这3种情况下的频响曲线.可以观察到,当非线性因子取值小于临界值0.408、,9时,系统频响曲线没有发现跳跃现象;而当非线性因子取值大于临界值0.408 9时,确实存在多解区间,即图中虚线之间区域.
|
图 3 跳跃发生的临界条件 Fig.3 Critical condition for jump avoidance |
|
图 4 临界频响函数 Fig.4 Critical frequency response |
周期运动的倍周期分岔指的是当非线性动力系统的控制参数发生很小的变化时,其原周期运动将转迁为本质不同的运动状态.而从设计角度来看,分岔点很有可能就是参数是否符合设计需求的阀值.倍周期分岔往往发生在远离主共振频率的倍频附近,正处于隔振有效区内,而倍周期运动会恶化该频段内的隔振性能,因此倍周期分岔是隔振设计需要规避的非线性动力学行为.
本小节将采用庞加莱映射方法分析周期运动的稳定性[23],寻找避免倍周期运动发生的条件.首先将系统转化为状态方程
| $ \left. \begin{array}{l} \dot x = {f_1}(t,x){\mkern 1mu} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \in {S_1}\\ \dot x = {f_2}(t,x){\mkern 1mu} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \in {S_2}{\kern 1pt} {\kern 1pt} \end{array} \right\} $ | (11) |
式中 $ x = (x,\dot x) $ 为状态变量,f1(t;x)和f2(t;x)分别为 T=2π/ω的周期函数.系统分界面定义为
| $ \{ \Sigma |h(x) = x - {a_0} = 0\} $ | (12) |
分界面将整个相空间分为两个子空间{S1|h(x) < 0}和{S2|h(x) > 0}.而对于分段光滑系统,除采用定相位面为庞加莱截面,还可取分界面作为庞加莱映射的截面[24],如
| $ {\Sigma _{x,1}} = \{ (x,\dot x,t)|x = {a_{\rm{c}}},\dot x > 0\} $ | (13) |
在分段构造庞加莱映射过程中,需在分界面处定义一辅助截面
| $ {\Sigma }_{x,2} = \{ (x,\dot x, t) | x = a_{\rm c} , \dot {x} < 0\} $ | (14) |
因此完整的庞加莱映射由两个子映射 $ {P_1}:{\Sigma _x} \to {{\bar \Sigma }_x} $ 和 $ {P_2}:{{\bar \Sigma }_x} \to {\Sigma _x} $ 复合而成.如下
| $ P = {P_2}^\circ {P_1} $ | (15) |
相应地,雅可比矩阵为
| $ DP = D{P_2}^\circ D{P_1} $ | (16) |
其中,DP1和DP2分别为子映射P1和P2的雅可比矩阵.
以下介绍雅可比矩阵的求解步骤.首先考虑映射$ {P_1}:{\Sigma _x} \to {{\bar \Sigma }_x}:({v_0},{t_0}) \to ({v_1},{t_1}) $ 考虑到状态变量 (v1;t1)由初始条件(v0;t0)决定,因此
| $ D{P_1} = \frac{{\partial ({v_1}({v_0},{t_0}),{t_1}({v_0},{t_0}))}}{{\partial ({v_0},{t_0})}} = \left[ \begin{array}{l} \frac{{\partial {v_1}}}{{\partial {v_0}}}\\ \frac{{\partial {t_1}}}{{\partial {v_0}}} \end{array} \right.\left. \begin{array}{l} \frac{{\partial {v_1}}}{{\partial {t_0}}}\\ \frac{{\partial {t_1}}}{{\partial {t_0}}} \end{array} \right] $ | (17) |
以下分别计算式(17)矩阵中的各项.在t0时刻,原始轨道的位移和速度分别为
| $ a_{\rm c} = x_1 (t_0 ) \ \ \hbox{和} \ \ v_0 = \dot {x}_1 (t_0 ) $ | (18) |
这里x1(t)和$ \dot {x}_1 (t) $ 为系统在S1子空间内的位移和速度时域响应,由常微分方程理论直接得到,其中包含两个依赖于初始条件的积分常数A1(v0;t0),B1(v0;t0),它们可由式(18)中的两个代数方程直接求得,进而便可得到$ \frac{{\partial {A_1}}}{{\partial {v_0}}},\frac{{\partial {A_1}}}{{\partial {t_0}}},\frac{{\partial {B_1}}}{{\partial {v_0}}} $ 和 $ \dfrac{\partial B_1 }{\partial t_0 } $ .
在t1时刻,位移和速度分别为
| $ a_{\rm c} = x_1 (t_1 (v_0 ,t_0 );v_0 ,t_0 ,A_1 (v_0 ,t_0 ),B_1 (v_0 ,t_0 )) $ | (19) |
| $ v_1 (v_0 ,t_0 ) = \dot {x}_1 (t_1 (v_0 ,t_0 );v_0 ,t_0 ,A_1 (v_0 ,t_0 ), B_1 (v_0 ,t_0 )) $ | (20) |
对式(19)和式(20)两边求t0偏导,分别得到
| $0 \equiv \dfrac{\partial a_{\rm c} }{\partial t_0 } = \dfrac{\partial x_1 }{\partial A_1 } \dfrac{\partial A_1 }{\partial t_0 } + \dfrac{\partial x_1 }{\partial B_1 }\dfrac{\partial B_1 } {\partial t_0 } + \dfrac{\partial x_1 }{\partial t_1 }\dfrac{\partial t_1 }{\partial t_0 } + \dfrac{\partial x_1 }{\partial t_0 } $ | (21) |
| $ \dfrac{\partial v_1 }{\partial t_0 } = \dfrac{\partial \dot {x}_1 }{\partial A_1 }\dfrac{\partial A_1 }{\partial t_0 } + \dfrac{\partial \dot {x}_1 }{\partial B_1 }\dfrac{\partial B_1 }{\partial t_0 } + \dfrac{\partial \dot {x}_1 }{\partial t_1 }\dfrac{\partial t_1 }{\partial t_0 } + \dfrac{\partial \dot {x}_1 }{\partial t_0 } $ | (22) |
式中 $ \frac{{\partial {x_1}}}{{\partial {A_1}}},\frac{{\partial {x_1}}}{{\partial {B_1}}},\frac{{\partial {{\dot x}_1}}}{{\partial {A_1}}} $ 和 $ \dfrac{\partial \dot {x}_1 }{\partial B_1 } $ 以及 $ \frac{{\partial {x_1}}}{{\partial {t_1}}},\frac{{\partial {x_1}}}{{\partial {t_0}}},\frac{{\partial {{\dot x}_1}}}{{\partial {t_1}}} $ 和 $ \dfrac{\partial \dot {x}_1 }{\partial t_0 } $ 可由其响应表达式直接得出.因此 $ \dfrac{\partial t_1 }{\partial t_0 } $ 和 $ \dfrac{\partial v_1 }{\partial t_0 } $ 可由式(21)和式(22)的方程组得到.
然后,对式(19)和式(20)两边求v0偏导,得到
| $ 0 \equiv \dfrac{\partial a_{\rm c} }{\partial v_0 } = \dfrac{\partial x_1 }{\partial A_1 }\dfrac{\partial A_1 }{\partial v_0 } + \dfrac{\partial x_1 }{\partial B_1 }\dfrac{\partial B_1 }{\partial v_0 } + \dfrac{\partial x_1 }{\partial t_1 }\dfrac{\partial t_1 }{\partial v_0 } + \dfrac{\partial x_1 }{\partial v_0 } $ | (23) |
| $ \dfrac{\partial v_1 }{\partial v_0 } = \dfrac{\partial \dot {x}_1 }{\partial A_1 }\dfrac{\partial A_1 }{\partial v_0 } + \dfrac{\partial \dot {x}_1 }{\partial B_1 }\dfrac{\partial B_1 }{\partial v_0 } + \dfrac{\partial \dot {x}_1 }{\partial t_1 }\dfrac{\partial t_1 }{\partial v_0 } + \dfrac{\partial \dot {x}_1 }{\partial v_0 } $ | (24) |
由式(23)和式(24)不难得到 $ \dfrac{\partial t_1 }{\partial v_0 } $ 和 $ \dfrac{\partial v_1 }{\partial v_0 } $.
而映射 $ {P_2},{{\bar \Sigma }_x} \to {\Sigma _x}:({v_1},{t_1}) \to ({v_2},{t_2}) $ 的雅可比矩阵亦可根据相同方法求得,只需将上述计算各符号中的下标"1"替换成"2",而"0"替换为"1"即可. 如下
| $ D{P_2} = \frac{{\partial ({v_2}({v_1},{t_1}),{t_2}({v_1},{t_1}))}}{{\partial ({v_1},{t_1})}} = \left[ \begin{array}{l} \frac{{\partial {v_2}}}{{\partial {v_1}}}\\ \frac{{\partial {t_2}}}{{\partial {v_1}}} \end{array} \right.\left. \begin{array}{l} \frac{{\partial {v_2}}}{{\partial {t_1}}}\\ \frac{{\partial {t_2}}}{{\partial {t_1}}} \end{array} \right] $ | (25) |
若雅可比矩阵的迹为T,而行列式值为D,则其特征值为
| $ \lambda _{1,2} = \dfrac{1}{2}(T\pm \sqrt {T^2 - 4D} ) $ | (26) |
其中
$ \begin{array}{l} D = {{\rm{e}}^{ - {\textstyle{{2\pi c} \over \omega }}}}{\mkern 1mu} ,\quad T = {{\rm{e}}^{ - {\textstyle{{\pi c} \over \omega }}}}\left[ { - {s_ + }{s_ - }(\frac{{\omega _2^2 + \omega _1^2}}{{{\omega _1}{\omega _2}}}) + 2{c_ + }{c_ - }} \right]\\ {\omega _2} = \sqrt {{k_2} - \xi _1^2} {\mkern 1mu} ,\;\;{\omega _1} = \sqrt {{k_1} - \xi _1^2} \\ {s_ + } = \sin [{\omega _2}({t_2} - {t_1})]{\mkern 1mu} ,\;{s_ - } = \sin [{\omega _1}({t_1} - {t_0})]\\ {c_ + } = \cos [{\omega _2}({t_2} - {t_1})]{\mkern 1mu} ,\;\;{c_ - } = \cos [{\omega _1}({t_1} - {t_0})] \end{array} $
若其中一个特征值为-1,则发生二倍周期分岔.
假设 $ {t_2} - {t_1} = \frac{{\pi {\Omega _n}}}{{\omega {\omega _2}}},{t_1} - {t_0} = \frac{{\pi {\Omega _n}}}{{\omega {\omega _1}}} $ [26],所以 $ {s_ + } = {s_ - } = \sin (\frac{{\pi {\Omega _n}}}{\omega })\mathop {{\rm{ }} = }\limits^{{\rm{def}}} s,{c_ + } = {c_ - } = \cos (\frac{{\pi {\Omega _n}}}{\omega })\mathop {{\rm{ }} = }\limits^{{\rm{def}}} c $ 其中 $ {\Omega _n} = \frac{{2{\omega _1}{\omega _2}}}{{{\omega _1} + {\omega _2}}} $ .令式(26)等于-1,则可推导出
| $ {{\rm{e}}^{{\textstyle{{ - 4\pi {\xi _1}} \over \omega }}}} + 2{{\rm{e}}^{{\textstyle{{ - 2\pi {\xi _1}} \over \omega }}}}( - \frac{1}{2}\frac{{\omega _1^2 + \omega _2^2}}{{{\omega _1}{\omega _2}}}{s^2} + {c^2}) + 1 = 0 $ | (27) |
上式是关于 $ {{\rm{e}}^{{\textstyle{{ - 2\pi {\xi _1}} \over \omega }}}} $ 的二次方程,且$ 0 < {{\rm{e}}^{{\textstyle{{ - 2\pi {\xi _1}} \over \omega }}}} < 1 $ .所以为了保证上式有解且至少存在一个根.
在0与1之间,所以其必要条件为
| $ \Big( - \dfrac{1}{2}\dfrac{\omega _1^2 + \omega _2^2 }{\omega _1 \omega _2 }s^2 + c^2) < - 1 $ | (28) |
根据式(27)可得到
| $ \begin{array}{l} \frac{{{\xi _1}}}{\omega } + \frac{1}{{2\pi }}\ln [(\frac{1}{2}\frac{{\omega _1^2 + \omega _2^2}}{{{\omega _1}{\omega _2}}}{s^2} - {c^2}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{{(\frac{1}{2}\frac{{\omega _1^2 + \omega _2^2}}{{{\omega _1}{\omega _2}}}{s^2} - {c^2})}^2} - 1} {\mkern 1mu} ] = 0 \end{array} $ | (29) |
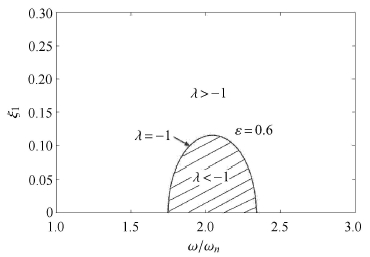
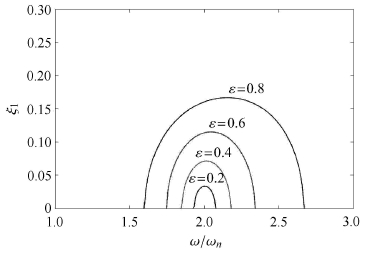
明显地,式(29)包含了式(28),因此式(29)即为发生倍周期分岔的临界条件,如图 5.其中阴影区周期1轨道的特征值λ < -1,也就是说系统周期1运动失稳,但其周期2运动稳定;平面其余区域(不包括曲线上的点)内的参数组合则不会导致系统发生倍周期运动的产生,这部分为可选区域.由该图可以看出,当激励频率(ω/ωn)一定时,较大的线性阻尼比ξ11可以抑制倍周期分岔的发生.图 6还给出了不同"时倍周期发生的临界条件曲线.可以看到,随着非线性因子的增大,发生倍周期分岔的可能性也随之增加.
|
图 5 亚谐分岔发生的临界条件( $ \omega _0^2 = 1{\mkern 1mu} 833,\varepsilon = 0.6 $) Fig.5 Critical condition for occurrence of period-doubling bifurcation ( $ \omega _0^2 = 1{\mkern 1mu} 833,\varepsilon = 0.6 $ ) |
|
图 6 不同非线性因子ε所对应的倍周期分岔发生的临界条件 Fig.6 Critical conditions for occurrence of period-doubling bifurcation under different nonlinear factorsε |
事实上,亚谐共振响应也是倍周期运动,1/n亚谐共振就是n倍周期运动.亚谐共振可由倍周期分岔导致,亦可体现为是一种多稳态运动共存的现象,包含了非共振的周期1运动与共振的周期n运动.以下将继续探讨随机扰动对多稳态运动的影响.
2.2 多稳态运动随机扰动对于动力系统的长期形态往往有着决定性的影响.尽管这时相应的确定性系统具有渐近稳定的稳态解,但随机扰动的影响足以使系统的样本轨线具有从稳态解的吸引域中离出的可能性,随着事态的发展轨线将会以概率1离开吸引域并最终导致系统响应在多个稳态解之间不断转移[27, 28].即使对于一个非常小的随机扰动,其长期作用的累积效应同样会使轨线具有概率1的离出机率.所以,在非线性隔振设计中,需要避免系统出现多稳态运动.
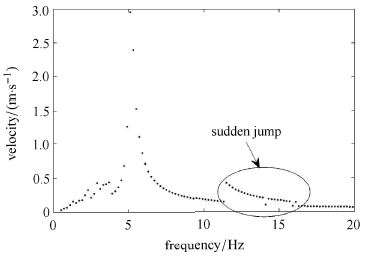
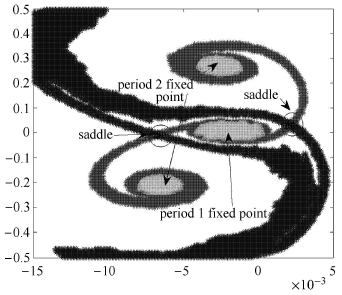
受随机扰动影响的分段光滑隔振系统的激励项则变为F1 cosωt+η(t).这里η(t)为高斯白噪声,自相关函数为 < η(t)η(t+τ) > =2Dδ(τ).对于未受扰的分段光滑隔振系统 $ (\omega _0^2 = 2{\mkern 1mu} 670,\varepsilon = 0.8,{\xi _1} = 0.018{\mkern 1mu} 4,{F_1} = 4,{a_c} = - 0.001) $ ,图 7给出了频响特性曲线的数值结果.可以看出,尽管主共振区不存在跳跃现象,隔振有效区内没有出现倍周期分岔,但仍在约2倍频率处,出现了幅值突变,经进一步数值分析得知在幅值突变是由于系统存在多稳态运动所导致,分别为周期1和周期2运动,如图 8所示.该图由图胞映射所得,可以看出,分段光滑隔振系统存在一个周期 1不动点和一个周期2不动点,二者由鞍点的不稳定性流形连接.
|
图 7 速度频率响应 Fig.7 Velocity frequency response |
|
图 8 定相位庞加莱截面上的不动点(12 Hz) Fig.8 Fixed points on fixed phase Poincar′e section (12 Hz) |
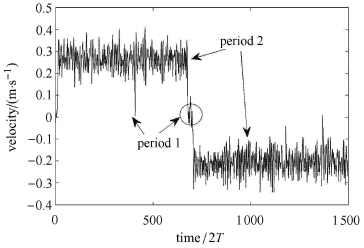
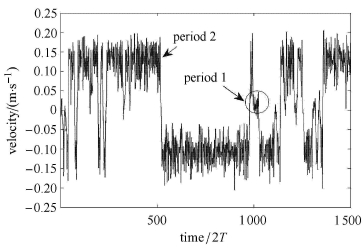
以下考察随机扰动对分段光滑隔振系统动力学行为的影响,设激励中含有一定强度(D=0:075)的白噪声,庞加莱截面上的速度时间序列由图 9给出. 注意这里的时间序列为间隔为周期两倍周期(2T)的离散数据,并非传统意义上的时域响应.可以看到尽管系统以周期2运动为主,但仍存在短时的周期1 运动.直观地解释,这是由于周期2运动的吸引域更大,所以响应更长时间停留在周期2运动状态.而随着激励频率的改变,周期1的吸引域随之会变大,停留在周期1运动时间会随之增长,如图 10.
|
图 9 庞加莱截面上位移状态的时间序列(12 Hz) Fig.9 Time series on fixed phase Poincar′e section (12 Hz) |
|
图 10 庞加莱截面上位移状态的时间序列(14 Hz) Fig.10 Time series on fixed phase Poincar′e section (14 Hz) |
由于分段光滑隔振系统的多稳态分析较为复杂,尚未形成简洁有效解析方法进行反问题设计.此外,由于隔振系统的分段光滑非线性所带来的复杂性,除上述动力学现象外,在设计过程中仍有一些问题需要留心,例如擦边分岔.在一定参数条件下,系统的周期1运动经与分界面擦边会失稳,致使出现其他周期运动,如周期2运动,甚至混沌运动[29, 30]. 理论研究发现,擦边分岔的规范型为二维含3/2次非线性的分段映射,通过对该分段映射分岔的研究可将参数平面进行划分,从而获知所需要的设计参数,但目前对这类分段非线性映射的理论分析不够成熟.因此,在实际设计中,在完成跳跃与倍周期分岔的防治设计后,建议将采取数值仿真全面校验系统的动力学行为以排除诸如多稳态运动、擦边分岔等不利影响.
3 总 结本文从非线性动力学角度研究了一类分段光滑隔振系统的动力学反问题设计方法.本文的主要研究工作与结论如下:
(1)采用平均法研究了主共振的幅频特性曲线,并利用奇异性理论分析了主共振的分岔,进而基于修正后的频响方程给出了避免由鞍结分岔诱导的跳跃现象发生的动力学设计方法.
(2)隔振有效区内的倍周期分岔主要由周期1运动的特征值穿越-1(穿出)所导致,增大阻尼可以抑制倍周期分岔的发生,但在被动隔振技术中,增大线性阻尼却会削弱隔振有效区的隔振效果.
(3)数值仿真研究证实,在噪声影响下,分段光滑隔振系统的响应会在不同稳态间跃迁,非常不利于隔振.因此,在完成跳跃与倍周期分岔的防治设计后,应采用数值仿真校验系统是否存在多稳态运动.
此外,擦边分岔对分段光滑隔振系统的影响较为复杂,在一定参数条件下,系统的周期1运动经与分界面擦边会失稳,致使出现其他周期运动,如周期2运动甚至混沌运动.因此,擦边分岔的反问题设计仍需进一步的深入研究.
| 1 | Lam KY, Ng TY. Dynamic stability of cylindrical shells subjected to conservative periodic axial loads using different shells theories.Journal of Sound and Vibration, 1997, 207(4): 497-520 |
| 2 | Ng TY, Lam KY, Liew KM, et al. Dynamic stability analysis of functionally graded cylindrical shells under periodic axial loading. International Journal of Solids and Structures, 2001, 38: 1295-1309 |
| 3 | Darabi M, Darvizeh M, Darvizeh A. Non-linear analysis of dynamic stability for functionally graded cylindrical shells under periodic axial loading. Composite Structures, 2008, 83: 201-211 |
| 4 | 周承倜, 王列东. 复合材料叠层圆柱壳的非线性动力稳定性分析. 大连大学学报, 1993, 01: 1-15 (Zhou Chengti, Wang Liedong. Nonlinear analysis of dynamic stability for laminated composite cylindrical shells. Journal of Dalian University, 1993, 01: 1-15 (in Chinese)) |
| 5 | 曾潇, 卓曙君. 有随机初始缺陷的轴压圆柱薄壳的动力稳定性分 析. 昆明理工大学学报, 1996, 21(3): 59-63 (Zeng Xiao, Zhuo Shujun. Dynamic stability analysis of axially compressed cylindrical shell with random initial geometric imperfections. Journal of Kunming University of Science and Technology, 1996, 21(3): 59-63 (in Chinese)) |
| 6 | 张善元, 张涛. 圆柱壳的轴向动力屈曲、参数共振与混沌运动. 振 动与冲击, 2010, 29(12): 34-38, 66 (Zhang Shanyuan, Zhang Tao. Axial dynamic buckling parametric resonance and chaotic motion of a closed cylindrical shell. Journal of Vibration and Shock, 2010,29(12): 34-38, 66 (in Chinese)) |
| 7 | 赵晶瑞, 唐友刚, 王文杰. 传统 Spar 平台参数激励 Mathieu 不稳定 性的研究. 工程力学, 2010, 27(3): 222-227 (Zhao Jingrui, Tang Yougang, Wang Wenjie. Study on the parametrically excited Mathieu instability of a classic Spar platform. Engineering Mechanics,2010, 27(3): 222-227 (in Chinese)) |
| 8 | 徐万海, 吴应湘, 钟兴福等. 海洋细长结构参数激励不稳定区的确 定方法. 振动与冲击, 2011, 30(9): 79-83 (Xu Wanhai, Wu Yingxiang, Zhong Xingfu, et al. Methods for parametric excitation instability analysis of slender flexible cylindrical structures in offshore engineering. Journal of Vibration and Shock, 2011, 30(9): 79-83 (in Chinese)) |
| 9 | 王俊荣, 谢彬. 深水半潜式平台Mathieu不稳定问题研究. 工程力 学, 2012, 29(10): 347-353 (Wang Junrong, Xie Bin. Mathieu instability study of a deepwater semi-submersible platform. Engineering Mechanics, 2012, 29(10): 347-353 (in Chinese)) |
| 10 | 吴学敏, 黄维平, 滕文刚. 深水顶张式立管参数振动与涡激振动耦 合振动分析方法研究. 中国海上油气, 2014, 04: 100-105 (Wu Xuemin, Huang Weiping, Teng Wengang. Study on analysis method for coupled vibration of parameter excited vibration and vortexinduce vibration on deep water top-tensed riser. China Offshore Oil and Gas, 2014, 04: 100-105 (in Chinese)) |
| 11 | Zhang J, Tang YG. Mathieu instability analysis of deep-water toptensioned Risers. Journal of Ship Mechanics, 2014, 09: 1142-1150 |
| 12 | 桑松, 石晓, 李长东等. 深海SPAR平台垂荡-纵摇耦合运动Mathieu 稳定性分析. 中国海洋平台, 2014, 04: 34-40 (Sang Song, Shi Xiao, |
| 13 | Li Changdong, et al. Study on Mathieu stability of heave-pitch coupled motions of SPAR platform in deep sea. China Offshore Platform, 2014, 04: 34-40 (in Chinese)) 李为洲. 斜拉索面内参数振动数值分析及其控制. [硕士论文]. 长 沙: 湖南大学, 2013 (Li Weizhou. Numerical analysis of in-plane parametric vibration and the controlling measures for stay cables. [Master Thesis]. Changsha: Hunan University, 2013 (in Chinese)) |
| 14 | 孙超. 大跨度铁路斜拉桥拉索参数振动研究. [硕士论文]. 成都: 西 南交通大学, 2014 (Sun Chao. Parametric vibration of cables for long-span railway cable-stayed bridges. [Master Thesis]. Chengdu: Southwest Jiaotong University, 2014 (in Chinese)) |
| 15 | 李周. 大跨度悬索桥悬吊体系参数振动研究. [博士论文]. 广州: 华 南理工大学, 2013 (Li Zhou. The research on parametric vibration of suspended system of large-span suspension bridge. [PhD Thesis]. Guangzhou: South China University of Technology, 2013 (in Chinese)) |
| 16 | 杨咏漪, 陈克坚. 大跨度铁路斜拉桥斜拉索参数振动分析. 铁道工 程学报, 2013, 10: 60-65 (Yang Yongyi, Chen Kejian. Research on parametric oscillation of cables for long span railway cable-stayed Bridge. Journal of Railway Engineering Society, 2013, 10: 60-65 (in Chinese)) |
| 17 | 张晓湘. 竖向周期荷载作用下单层钢框架的动力稳定性分析. [硕 士论文]. 长沙: 中南大学, 2013 (Zhang Xiaoxiang. Dynamic stability analysis of single-story steel frames under vertical cyclic load. [Master Thesis]. Changsha: Central South Univerdity, 2013 (in Chinese)) |
| 18 | 邱良. 径向均布周期荷载作用下拱的动力稳定性能研究. [硕士论 文]. 长沙: 中南大学, 2013 (Qiu Liang. Dynamic stability research of arch under radial uniform cyclic loading. [Master Thesis]. Changsha: Central South Univerdity, 2013 (in Chinese)) |
| 19 | Ruzzene M. Dynamic buckling of periodically stiffened shells: appli- cation to supercavitating vehicles. International Journal of Solids and Structures, 2004, 41: 1039-1059 |
| 20 | Ruzzene M. Non-axisymmetric buckling of stiffened supercavitating shells: static and dynamic analysis. Computers and Structures,2004, 82: 257-269 |
| 21 | Ahn SS, Ruzzene M. Optimal design of cylindrical shells for enhanced buckling stability: Application to supercavitation underwater vehicles. Finite Elements in Analysis and Design, 2006, 42: 967-976 |
| 22 | Choi JY, Ruzzene M. Stability analysis of supercavitating underwater vehicles with adaptive cavitator. International Journal of Mechanical Sciences, 2006, 48: 1360-1370 |
| 23 | 施连会, 王安稳. 轴向载荷下超空泡航行体动力稳定性的数值研 究. 振动与冲击, 2011, 30(2): 55-59 (Shi Lianhui, Wang Anwen. Numerical study on dynamic stability of supercavitating vehicles subjected to axial loads. Journal of Vibration and Shock, 2011,30(2): 55-59 (in Chinese)) |
| 24 | 麻震宇. 超空泡航行体结构动力学仿真研究. [博士论文]. 长沙: 国 防科学技术大学, 2012 (Ma Zhenyu. Numerical research on dynamics of structures for supercavitating vehicles. [PhD Thesis]. Changsha: National University of Defense Technology, 2012 (in Chinese)) |
| 25 | 麻震宇, 胡凡, 陈广南等. 超空泡航行体双层壳结构动力稳定性分 析. 国防科技大学学报, 2011, 33(4): 43-47 (Ma Zhenyu, Hu Fan, Chen Guangnan, et al. Dynamic stability analysis of supercavitating double shells. Journal of National University of Defense Technology,2011, 33(4): 43-47 (in Chinese)) |
| 26 | 宋向华, 安伟光, 刘明. 轴向周期载荷下超空泡射弹的动力稳定性 分析. 哈尔滨工程大学学报, 2012, 33(10): 1238-1243 (Song Xi- anghua, An Weiguang, Liu Ming. Dynamic stability analysis of supercavitating projectile subjected to axial periodic load. Journal of Harbin Engineering University, 2012, 33(10): 1238-1243 (in Chinese)) |
| 27 | 宋向华, 安伟光, 蒋运华. 超空泡射弹动力稳定性的非概率可靠性 分析. 兵工学报, 2012, 33(8): 997-1003 (Song Xianghua, An Weiguang, Jiang Yunhua. Non-probabilistic reliability analysis for supercavitating projectile based on dynamic stability. Acta Armamentarii,2012, 33(8): 997-1003 (in Chinese)) |
| 28 | 刘明, 安伟光, 宋向华. 随机载荷下随机参数超空泡射弹的动力稳 定性. 计算机仿真, 2012, 10: 55-58 (Liu Ming, An Weiguang, Song Xianghua. Dynamic stability of supercaviting projectile with stochastic parameters subject to random load. Computer Simulation,2012, 10: 55-58 (in Chinese)) |
| 29 | 刘明, 安伟光, 宋向华29 . 随机参数超空泡射弹的动力稳定性和可靠 性. 爆炸与冲击, 2013, 33(5): 525-530 (Liu Ming, An Weiguang, Song Xianghua. Dynamic stability and reliability of a supercavitating projectile with stochastic parameters. Explosion and Shock Waves, 2013, 33(5): 525-530 (in Chinese)) |
| 30 | 王杰方, 安伟光, 宋向华. 超空泡运动体圆柱薄壳动力屈曲及可靠 性分析. 振动与冲击, 2014, 33(8): 22-28 (Wang Jiefang, An Weiguang, Song Xianghua. Dynamic buckling and reliability analysis of a cylindrical thin shell for supercavitating vehicles. Journal of Vibration and Shock, 2014, 33(8): 22-28 (in Chinese)) |
| 31 | 符华, 鲍洛金. 弹性体系的动力稳定性. 北京: 高等教育出版社,1960: 124-125 (Bolotin VV. Dynamic Stability of Elastic Systems. Beijing: Higher Education Press, 1960: 124-125 (in Chinese)) |
| 32 | 何芝仙, 崔建华. 材料力学. 武汉: 武汉大学出版社, 2013 (He Zhixian, Cui Jianhua. Mechanics of Materials. Wuhan: Wuhan University Press, 2013 (in Chinese)) |
 2016, Vol. 48
2016, Vol. 48