2. 南昌工程学院 土木与建筑工程学院, 南昌 330099
对于细长超空泡运动体 (长细比约为10 ~ 22) 而言,仅在头部和尾部与水接触,由于工作环境特殊 (气、液两项介质) 且航行速度很高,超空泡运动体比常规武器 (单一介质) 对结构的动力稳定性能更加敏感,特别是轴向周期载荷作用下的参数失稳问题 (轴向载荷作用下横向振动的共振). 只有在特定的情况下,即在横向振动频率、激发系数及外载荷频率等满足一定关系的参数平面内,参数共振才会被激发出来,但参数共振一旦被激发,其振动振幅会迅速地增长. 因此,对于高速甚至超高速运动的细长体而言,参数共振是一种突发的、危险的、隐蔽的值得引起重视的失效模式.
国内外对参数振动的研究有:文献[1, 2, 3] 利用弗吕格、桑德尔、拉甫、唐奈尔方程建立了在轴向力作用下的圆柱壳的微分方程,并转化为马奇耶方程分析了圆柱壳的动力稳定性问题. 周承倜等 [4] 用汉密尔顿原理导出了复合材料叠层圆柱壳的非线性动力稳定性微分方程. 曾潇等 [5] 对受轴向压缩的有随机初始缺陷的圆柱壳进行了动力稳定性及其可靠性分析. 张善元等 [6] 对圆柱壳在轴向周期载荷作用下的参数振动进行了研究. 以上的文献都是以圆柱壳作为研究对象的. 实际上,参数振动有广泛的工程背景,例如,赵晶瑞等 [7] 对一种新型的深海顺应式采油平台 (“Spar”平台) 的纵摇运动进行了分析,得到了具有三次非线性项的有阻尼马奇耶方程. 徐万海等 [8] 研究了张力腿、立管等海洋细长结构参数振动的动力不稳定区域. 王俊荣等 [9] 研究了深水半潜式平台的纵摇和横摇的参数共振,给出了半潜式平台的马奇耶方程,分析了平台失稳的参数条件. 吴学敏等 [10] 开展了深水顶张式立管参数振动与涡激振动耦合振动分析方法研究. 文献[11] 研究了参数激励作用下立管的动力稳定性问题. 桑松等 [12] 用希尔无穷行列式法推导得到了纵摇响应的马奇耶稳定性图谱,并用数值方法分析了平台纵摇马奇耶不稳定运动的发生过程. 除了以上海洋工程结构以外,大跨度斜拉桥的斜拉索参数振动研究也十分热门 [13, 14, 15, 16]. 另外,张晓湘 [17] 分析了钢框架结构承受周期载荷时的动力稳定性. 邱良 [18] 研究了径向均布周期载荷作用下拱结构的动力稳定性.
目前,国内外关于超空泡航行体参数共振研究公开发表的文献很少. 国外,佐治亚理工学院在超空泡航行体的参数共振方面做了一些工作:文献[19, 20] 根据汉密尔顿原理建立超空泡航行体结构壳体运动方程,通过有限元离散求解航行体结构动力屈曲问题,采用鲍洛金方法得到超空泡航行体模型的失稳区域. 文献[21] 采用有限元方法对超空泡航行体普通、加肋和渐缩壳体结构进行静力和动力屈曲研究. 文献[22] 引入自适应空化器概念,采用考虑剪切变形的梁单元建立超空泡航行体有限元模型,对航行体结构进行动力屈曲分析. 国内,施连会等 [23] 基于弹性壳体的一般理论,利用鲍洛金方法对航行体的动力屈曲问题进行了数值研究. 麻震宇等 [24, 25] 基于更新拉格朗日格式的超空泡航行体结构有限元模型,将结构动力屈曲理论与非线性有限元方法相结合,开展了超空泡航行体双层壳结构动力屈曲研究. 宋向华等 [26, 27] 建立了超空泡射弹截锥形结构的动力微分方程,利用鲍洛金方法进行动力稳定性分析,求解出动力不稳定区域边界; 随后,给出射弹结构动力稳定性的安全余量方程,计算了结构的动力稳定性的非概率可靠度. 刘明等 [28, 29] 在超空泡射弹动力稳定性分析的基础上,采用随机因子法求出随机参数射弹结构的动力不稳定区域边界,并对结构的可靠性进行了分析. 王杰方等 [30] 将超空泡运动体模拟成受动态轴向载荷作用的圆柱薄壳,推导了结构的动力稳定性微分方程,计算了舱段动力屈曲的可靠性指标.
从现有的文献来看,基于参数共振的高速航行体圆柱薄壳结构非线性动力失稳问题的研究文献较少. 较大的运动体横向变形,会直接破坏原有的空泡稳定性,而空泡的稳定性决定了高速航行体的运动稳定性. 线性的参数共振理论只适用于小变形的情况,随着横向振幅的增长,非线性因素的影响开始显露出来,成为不可忽略的必要因素. 因此,本文将从非线性的角度开展基于参数振动的失稳研究.
文中将线应变和剪应变中计入非线性因素,建立圆柱薄壳横向振动的非线性微分方程; 采用伽辽金变分法和鲍洛金方法,将非线性微分方程转化为具有周期性系数和非线性项的马奇耶方程; 求解非线性马奇耶方程,得到考虑非线性因素细长圆柱薄壳的第一、第二阶不稳定区域内的定态振动的振幅解析表达式,进而对影响圆柱薄壳的非线性参数共振曲线的因素进行分析.
1 圆柱薄壳的非线性动力屈曲微分方程将超空泡运动体模拟成受轴向周期载荷作用的细长圆柱薄壳. 对于圆柱薄壳,采用未变形前的曲线坐标系 ($\alpha ,\beta ,z$) 来描述有限变形的几何位置,$\alpha ,\beta$ 为壳体中面的主曲率线.
在扭转变形 ($ \kappa _{12} $) 的几何关系中计入切向位移 ($u,v$) 的影响,在线应变 (${\varepsilon _1},{\varepsilon _2}$) 和剪应变 (${\gamma _{12}}$) 中计入非线性项,细长圆柱薄壳的非线性几何方程为
| \begin{equation} \left. \begin{aligned} & {\varepsilon _1} = \displaystyle\frac{1}{R}\frac{{\partial u}}{{\partial \alpha }} \,{\rm{ + }} \,\frac{{\rm{1}}}{{{\rm{2}}{R^2}}}{\left( {\frac{{\partial w}}{{\partial \alpha }}} \right)^2}\\ & {\varepsilon _2} = \displaystyle\frac{1}{R}\left( {\frac{{\partial v}}{{\partial \beta }} + w} \right) \,{\rm{ + }} \,\frac{{\rm{1}}}{{{\rm{2}}{R^2}}}{\left( {\frac{{\partial w}}{{\partial \beta }}} \right)^2}\\ & {\gamma _{12}} = \displaystyle\frac{1}{R}\left( {\frac{{\partial v}}{{\partial \alpha }} + \frac{{\partial u}}{{\partial \beta }}} \right) \,{\rm{ + }} \,\frac{{\rm{1}}}{{{R^2}}}\frac{{\partial w}}{{\partial \alpha }} \cdot \frac{{\partial w}}{{\partial \beta }}\\ & {\kappa _1} = - \,\displaystyle\frac{1}{{{R^2}}}\frac{{{\partial ^2}w}}{{\partial {\alpha ^2}}}\\ & {\kappa _2} = - \,\displaystyle\frac{1}{{{R^2}}}\left( {\frac{{{\partial ^2}w}}{{\partial {\beta ^2}}} + w} \right)\\ & {\kappa _{12}} = \displaystyle - \,\frac{1}{{2{R^2}}}\left( {\frac{{\partial u}}{{\partial \beta }} - \frac{{\partial v}}{{\partial \alpha }} + 2\frac{{{\partial ^2}w}}{{\partial \alpha \partial \beta }}} \right) \end{aligned} \right\} \end{equation} | (1) |
式中,($u,v,w$) 为轴向、周向和径向位移,$R$ 为圆柱薄壳的半径,${\varepsilon _1},{\varepsilon _2}$ 为中面内的线应变,${\gamma _{12}}$ 为中面内的剪切变形,$\kappa _1,\kappa _2$ 为弯曲变形,$\kappa _{12}$ 为扭转变形.
物理方程中,中面力 (${N_1},{N_2},{N_{12}},{N_{21}}$) 中计入弯曲变形 ($\kappa _1,\kappa _2,\kappa _{12}$) 的影响,中面外的力 ${M_1}$ 中计入中面应变 (${\varepsilon _1},{\varepsilon _2}$) 的影响,即
| \begin{equation} \left. {\begin{aligned} & {{N_1} = \displaystyle\frac{{Eh}}{{1 - {\nu ^2}}}\left( {{\varepsilon _1} + \nu {\varepsilon _2} + \frac{{{h^2}}}{{12R}}{\kappa _1}} \right)}\\ & {{N_2} = \displaystyle\frac{{Eh}}{{1 - {\nu ^2}}}\left( {{\varepsilon _2} + \nu {\varepsilon _1} - \frac{{{h^2}}}{{12R}}{\kappa _2}} \right)}\\ & {{N_{12}} = \displaystyle\frac{{Eh}}{{2\left( {1 + \nu } \right)}}\left( {{\gamma _{12}} + \frac{{{h^2}}}{{12R}}{\kappa _{12}}} \right)}\\ & {{N_{21}} = \displaystyle\frac{{Eh}}{{2\left( {1 + \nu } \right)}}\left( {{\gamma _{12}} - \frac{{{h^2}}}{{12R}}{\kappa _{12}}} \right)}\\ & {{M_1} = - \,\displaystyle\frac{{E{h^3}}}{{12\left( {1 - {\nu ^2}} \right)}}\left[{{\kappa _1} + \nu {\kappa _2} + \frac{1}{R}\left( {{\varepsilon _1} + \nu {\varepsilon _2}} \right)} \right]}\\ & {{M_2} = - \,\displaystyle\frac{{E{h^3}}}{{12\left( {1 - {\nu ^2}} \right)}}\left( {{\kappa _2} + \nu {\kappa _1}} \right)}\\ & {{M_{12}} = \displaystyle\frac{{E{h^3}}}{{24\left( {1 + \nu } \right)}}\left( {2{\kappa _{12}} + \frac{1}{R}{\gamma _{12}}} \right)}\\ & {{M_{21}} = \displaystyle\frac{{E{h^3}}}{{12\left( {1 + \nu } \right)}}{\kappa _{12}}} \end{aligned}} \right\} \end{equation} | (2) |
式中,$E$ 为材料弹性模量,$h$ 为薄壳厚度,$v$ 为泊松比,${N_1},{N_2},{N_{12}},{N_{21}}$ 是中面内的法向力和剪力,${M_1},{M_2},{M_{12}},{M_{21}}$ 是中面外的弯矩和扭矩.
平衡方程中,在圆周切线方向 (周向) 考虑横向剪切力 ${Q_2}$ 的影响,即
| \begin{equation} \left. \begin{aligned} && \displaystyle\frac{{\partial {N_1}}}{{\partial \alpha }} + \frac{{\partial {N_{21}}}}{{\partial \beta }} \,{\rm{ + }} \,RX = 0\\ && \displaystyle\frac{{\partial {N_{12}}}}{{\partial \alpha }} + \frac{{\partial {N_2}}}{{\partial \beta }} + {Q_2}\,{\rm{ + }}\,RY = 0\\ && \displaystyle\frac{{\partial {Q_1}}}{{\partial \alpha }} + \frac{{\partial {Q_2}}}{{\partial \beta }} - {N_2} \,{\rm{ + }} \,RZ = 0\\ && {Q_1} = \displaystyle\frac{1}{R}\left( {\frac{{\partial {M_{21}}}}{{\partial \beta }} - \frac{{\partial {M_1}}}{{\partial \alpha }}} \right)\\ && {Q_2} = \displaystyle\frac{1}{R}\left( {\frac{{\partial {M_{12}}}}{{\partial \alpha }} - \frac{{\partial {M_2}}}{{\partial \beta }}} \right) \end{aligned} \right\} \end{equation} | (3) |
式中,$ X $ 为沿圆柱薄壳轴向的表面力,$ Y $ 为沿周向的表面力,$ Z $ 为沿法向的表面力,$ {Q_1},{Q_2} $ 为横向剪切力.
综合以上 3 个方程,得到细长圆柱薄壳的非线性微分方程组为
| \begin{equation} \left. {\begin{aligned} & {{L_{11}}\left( u \right) + {L_{12}}\left( v \right) + {L_{13}}\left( w \right) + {\varDelta _1} + \displaystyle\frac{{{R^2}\left( {1 - {\nu ^2}} \right)}}{{Eh}}X = 0}\\ & {{L_{21}}\left( u \right) + {L_{22}}\left( v \right) + {L_{23}}\left( w \right) + {\varDelta _2} + \displaystyle\frac{{{R^2}\left( {1 - {\nu ^2}} \right)}}{{Eh}}Y = 0}\\ & {{L_{31}}\left( u \right) + {L_{32}}\left( v \right) + {L_{33}}\left( w \right) + {\varDelta _3} - \displaystyle\frac{{{R^2}\left( {1 - {\nu ^2}} \right)}}{{Eh}}Z = 0} \end{aligned}} \right\} \end{equation} | (4) |
方程组 (4) 是关于位移 $u,v,w$ 的 3 个微分方程组,相关微小项已省略,${\varDelta_1},{\varDelta_2},{\varDelta_3}$ 为非线性项,仅与位移 $ w $ 有关,式中
| \begin{equation} \left. \begin{aligned} & \displaystyle{L_{11}} = \frac{{{\partial ^2}}}{{\partial {\alpha ^2}}} + \frac{{1 - \nu }}{2}\frac{{{\partial ^2}}}{{\partial {\beta ^2}}} \\ & {L_{12}} = \displaystyle \frac{{1 + \nu }}{2}\frac{{{\partial ^2}}}{{\partial \alpha \partial \beta }}\\ & {L_{13}} = \displaystyle \nu \frac{\partial }{{\partial \alpha }} - {c^2}\frac{{{\partial ^3}}}{{\partial {\alpha ^3}}} + \frac{{1 - \nu }}{2}{c^2}\frac{{{\partial ^3}}}{{\partial \alpha \partial {\beta ^2}}} \end{aligned} \right\} \end{equation} | (5) |
| \begin{equation} \left. \begin{aligned} & \displaystyle{L_{21}} = \frac{{1 + \nu }}{2}\frac{{{\partial ^2}}}{{\partial \alpha \partial \beta }} \\ & {L_{22}} = \displaystyle \frac{{1 - \nu }}{2}\frac{{{\partial ^2}}}{{\partial {\alpha ^2}}} + \frac{{{\partial ^2}v}}{{\partial {\beta ^2}}}\\ & {L_{23}} =\displaystyle \frac{\partial }{{\partial \beta }} - \frac{{3 - \nu }}{2}{c^2}\frac{{{\partial ^3}}}{{\partial {\alpha ^2}\partial \beta }} \end{aligned} \right\} \end{equation} | (6) |
| \begin{equation} \left. \begin{aligned} & {L_{31}} = \displaystyle \nu \frac{\partial }{{\partial \alpha }} - {c^2}\left( {\frac{{{\partial ^3}}}{{\partial {\alpha ^3}}} - \frac{{1 - \nu }}{2}\frac{{{\partial ^3}}}{{\partial \alpha \partial {\beta ^2}}}} \right)\\ & {L_{32}} =\displaystyle \frac{\partial }{{\partial \beta }} - {c^2}\frac{{3 - \nu }}{2}\frac{{{\partial ^3}}}{{\partial {\alpha ^2}\partial \beta }}\\ & {L_{33}} = \displaystyle {c^2}\left( {{\nabla ^2}{\nabla ^2} + 2\frac{{{\partial ^2}}}{{\partial {\beta ^2}}} + 1} \right) + 1 \end{aligned} \right\} \end{equation} | (7) |
式中
| \begin{equation} {\nabla ^2}{\nabla ^2} = \frac{{{\partial ^4}}}{{\partial {\alpha ^4}}} + 2\frac{{{\partial ^4}}}{{\partial {\alpha ^2}\partial {\beta ^2}}} + \frac{{{\partial ^4}}}{{\partial {\beta ^4}}} \end{equation} | (8) |
| \begin{equation} {c^2} = \frac{{{h^2}}}{{12{R^2}}} \end{equation} | (9) |
为了求得方程组 (4) 的近似解,在轴向周期载荷作用下的圆柱薄壳,设其横向振动的弯曲形式为
| \begin{equation} w\left( {\alpha ,\beta ,t} \right) = f(t)\sin (n\alpha) \cos (k\beta) \end{equation} | (10) |
式中,$ n = i\pi R/L $,圆柱薄壳两端没有法向位移,$ i,k $ 为轴向和周向的半波数,取整数值,$ L $ 为圆柱薄壳的长度. 式 (10) 给出了在均布轴向载荷作用下的圆柱薄壳线性问题的精确解,将其代入 ${\varDelta _1},{\varDelta _2},{\varDelta _3}$ 中得
| \begin{align} {\varDelta _1} = & \,\left( {\nu {k^2} - {n^2}} \right)\displaystyle\frac{{n{f^2}}}{{2R}}\sin (2n\alpha) \; {\cos ^2}(k\beta) \,- \notag \quad\quad\quad \\ & \displaystyle\frac{{\left( {1 + \nu } \right){k^2}}}{2}\frac{{n{f^2}}}{{2R}}\sin (2n\alpha) \cos (2k\beta) \end{align} | (11) |
| \begin{align} {\varDelta _2} = & \,\left( {{k^2} - \nu {n^2}} \right)\frac{{k{f^2}}}{{2R}}\sin (2k\beta) \; {\sin ^2}(n\alpha) \,- \quad\quad\quad\,\,\,\notag \\ & \frac{{\left( {1 + \nu } \right){n^2}}}{2}\frac{{k{f^2}}}{{2R}}\sin (2k\beta) \cos (2n\alpha) \end{align} | (12) |
| \begin{align} {\varDelta _3} = & \,\frac{{{c^2}{n^2}{f^2}}}{R}\cos (2n\alpha) \Big[{{n^2}{{\cos }^2}(k\beta) } - {k^2}{\sin ^2}(k\beta) \,+ \notag \\ & { \frac{{\left( {1 - \nu } \right){k^2}}}{2}} \Big] + \frac{{{f^2}{k^2}}}{{{\rm{2}}R}}{\sin ^2}(n\alpha) \; {\sin ^2}(k\beta) \,+ \notag \\ & \frac{{\nu {n^2}{f^2}}}{{{\rm{2}}R}}{\cos ^2}(n\alpha) \; {\cos ^2}(k\beta) \end{align} | (13) |
设方程组 (4) 中前两式的解的形式为
| \begin{equation} \left. \begin{aligned} u = & \,{A_1}\sin (2n\alpha) \; {\cos ^2}(k\beta) + {B_1}\sin (2n\alpha) \cos (2k\beta) + {u_0}\\ v = & \,{A_2}\sin (2k\beta) \; {\sin ^2}(n\alpha) + {B_2}\sin (2k\beta) \cos (2n\alpha) + {v_0}\\ w = & \,{w_0} = f(t)\sin (n\alpha) \cos (k\beta) \end{aligned} \right\} \end{equation} | (14) |
式中,$ {u_0},{v_0},{w_0} $ 满足线性方程组
| \begin{equation} \left. \begin{aligned} {L_{11}}\left( u \right) + {L_{12}}\left( v \right) + {L_{13}}\left( w \right) = 0\\ {L_{21}}\left( u \right) + {L_{22}}\left( v \right) + {L_{23}}\left( w \right) = 0 \end{aligned} \right\} \end{equation} | (15) |
且应该满足边界条件. 将式 (14) 代入式 (4) 的前两式 (略去切向表面力,$ X = Y = 0 $),得到系数 $ {A_1},{B_1},{A_2},{B_2} $ 的表达式为
| \begin{equation} \left. \begin{aligned} {A_1} = & \,\displaystyle\frac{{{f^2}\left( {\nu {k^2} - {n^2}} \right)}}{{8nR}},\,\,\,{B_1} = - \frac{{\nu {k^2}{f^2}}}{{16nR}}\\ {A_2} = & \,\displaystyle\frac{{{f^2}\left( {{k^2} - \nu {n^2}} \right)}}{{8kR}},\,\,\,{B_2} = - \frac{{\nu {n^2}{f^2}}}{{16kR}} \end{aligned} \right\} \end{equation} | (16) |
联立几何方程式 (1)、物理方程式 (2)、式 (14) 和式 (16),得到轴向力 $ {N_1} $ 和周向力 $ {N_2} $ 为
| \begin{equation} \left. \begin{aligned} {N_1} = & \,\displaystyle\frac{{Eh\nu {k^2}{f^2}}}{{8\left( {1 - {\nu ^2}} \right){R^2}}} \! \left[{1 + \frac{{{n^2}}}{{\nu {k^2}}} + \frac{{\left( {1 - {\nu ^2}} \right){n^2}}}{{\nu {k^2}}}\cos (2k\beta) } \! \right] + N_1^0\\ {N_2} = & \,\displaystyle\frac{{Eh\nu {n^2}{f^2}}}{{8\left( {1 - {\nu ^2}} \right){R^2}}} \! \left[{1 + \frac{{{k^2}}}{{\nu {n^2}}} - \frac{{\left( {1 - {\nu ^2}} \right){k^2}}}{{\nu {n^2}}}\cos (2n\alpha) } \! \right] + N_2^0 \end{aligned} \right\} \end{equation} | (17) |
式中
| \begin{equation} \left. \begin{aligned} N_1^0 = \displaystyle\frac{{Eh}}{{\left( {1 - {\nu ^2}} \right)R}}\left[{\frac{{\partial {u_0}}}{{\partial \alpha }} + \nu \frac{{\partial {v_0}}}{{\partial \beta }} + \left( {\nu + {c^2}{n^2}} \right){w_0}} \right]\\ N_2^0 = \displaystyle\frac{{Eh}}{{\left( {1 - {\nu ^2}} \right)R}}\left[{\nu \frac{{\partial {u_0}}}{{\partial \alpha }} + \frac{{\partial {v_0}}}{{\partial \beta }} + \left( {1 - {k^2}{c^2}} \right){w_0}} \right] \end{aligned} \right\} \end{equation} | (18) |
设 $ {u_0},{v_0},{w_0} $ 的表达式为
| \begin{equation} \left. {\begin{aligned} & {{u_0}\left( {\alpha ,\beta ,t} \right) = U\cos (n\beta) \cos (k\beta) }\\ & {{v_0}\left( {\alpha ,\beta ,t} \right) = V\sin (n\alpha) \sin (k\beta) }\\ & {{w_0}\left( {\alpha ,\beta ,t} \right) = f\sin (n\alpha) \cos (k\beta) } \end{aligned}} \right\} \end{equation} | (19) |
既可以满足边界条件 (径向和周向位移为 0,轴向不为 0),又可以满足方程组 (15). 将式 (19) 代入式 (15) 中得
| \begin{equation} \left. {\begin{aligned} U = & \,\displaystyle\frac{{n \left[{\nu {n^2} - {k^2} + {c^2}\left( {{n^4} - {k^4}} \right)} \right]f}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}}\\ V = & \,\displaystyle - \frac{{k \left[{\left( {\nu + 2} \right){n^2} + {k^2} + 2{c^2}{n^2}\left( {{n^2} + {k^2}} \right)} \right]f}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}} \end{aligned}} \right\} \end{equation} | (20) |
对于受轴向周期载荷 ${P_0} + {P_t}\cos (\theta t)$ 作用的圆柱薄壳,其轴向的平衡条件为
| \begin{equation} \int_0^{2{\pi} } {{N_1}} \left( {\alpha ,\,\beta } \right){\rm{d}}\beta = - \frac{{{P_0} + {P_t}\cos (\theta t)}}{R} \end{equation} | (21) |
式中,$ {P_0} $ 为不随时间变化的部分,$ {P_t} $ 为随时间变化的部分,$ \theta $ 为动载荷的角频率.
联立式 (17)~式 (21),求得内力 $ {N_1},{N_2} $ 为
| \begin{equation} {\left. \begin{aligned} {N_1} = & - \frac{{{P_0} + {P_t}\cos (\theta t)}}{{2{\pi} R}} + \frac{{Eh{f^2}}}{{8{R^2}}}{n^2}\cos (2k\beta) \,+ \\ & \frac{{Eh{n^2}{k^2}}}{{\left( {1 - {\nu ^2}} \right)R}} \left[{\frac{{\left( {1 - \nu } \right)\left( {1 + \nu + 2{c^2}{k^2} + 2{c^2}{n^2}} \right)}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}}} \right] \cdot \\ & f\sin (n\alpha) \cos (k\beta) \\ {N_2} = & \,\frac{{Eh\left( {\nu {n^2} + {k^2}} \right){f^2}}}{{8\left( {1 - {\nu ^2}} \right){R^2}}} - \frac{{Eh{f^2}}}{{8{R^2}}}{k^2}\cos (2n\alpha) \,+ \\ & \frac{{Eh}}{{\left( {1 - {\nu ^2}} \right)R}}\left[{\frac{{\left( {1 - {\nu ^2}} \right){n^4} + \left( {\nu - 4} \right){c^2}{n^2}{k^4}}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}} \,- } \right.\\ & \left. { \displaystyle\frac{{{c^2}\nu {n^6} + 3{c^2}{n^4}{k^2} + {c^2}{k^6}}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}}} \right]f\sin (n\alpha) \cos (k\beta) \end{aligned} \right\} } \end{equation} | (22) |
横向振动微分方程组 (4) 的第 3 式中,沿圆柱薄壳法向的表面力为 [31]
| \begin{equation} Z = \frac{1}{{{R^2}}}\left[{{N_1}\frac{{{\partial ^2}w}}{{\partial {\alpha ^2}}} + {N_2}\left( {\frac{{{\partial ^2}w}}{{\partial {\beta ^2}}} + w} \right)} \right] - m\frac{{{\partial ^2}w}}{{\partial {t^2}}} \end{equation} | (23) |
式中,$ m $ 是圆柱薄壳中面内单位面积的质量,$ m = \rho h $.
综合式 (4) 中的第 3 式、式 (13)、式 (14)、式 (16)、式 (19)、式 (20)、式 (22)和式 (23),得到圆柱薄壳的非线性横向振动微分方程式,即
| \begin{align} & \displaystyle\bigg[{f'' + {{ {{{\omega '}_{n,k}}} }^2}f - {n^2}\frac{ {{P_0} + {P_t}\cos (\theta t)} }{{2\pi m{R^3}}}f} \bigg]\sin (n\alpha) \cos (k\beta) \,+ \notag \\ & \quad\quad \displaystyle\frac{{EhB}}{{m{R^2}\left( {1 - {\nu ^2}} \right)}}{f^2} + \left[{\frac{{\left( {1 - {\nu ^2}} \right){n^4}}}{{8{R^2}}}\cos (2k\beta) \,+ } \right.\notag \\ & \quad\quad \displaystyle\left. {\frac{{\left( {1 - {\nu ^2}} \right){k^2}\left( {1 - {k^2}} \right)}}{{8{R^2}}}\cos (2n\alpha) - \frac{{\left( {1 - {k^2}} \right)\left( {\nu {n^2} + {k^2}} \right)}}{{8{R^2}}}} \right] \cdot \notag \\ & \quad\quad \displaystyle{f^3}\sin (n\alpha) \cos (k\beta) = 0 \end{align} | (24) |
式中
| \begin{align} B = & \displaystyle\frac{{{\nu ^2}{k^2}}}{{8R}}\cos (2n\alpha) + \frac{{{k^2}}}{{4R}}{\sin ^2}(n\alpha) + \frac{{\nu {n^2}}}{{8R}} \,{\rm{ + }} \,\frac{{{n^2}}}{R} \cdot \notag \\ & \displaystyle\frac{{\left( {1 - \nu } \right){n^2}{k^2}\left( {1 + \nu + 2{c^2}{k^2} + 2{c^2}{n^2}} \right)}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}} {\sin ^2}(n\alpha) \; {\cos ^2}(k\beta) \,- \notag \\ & \displaystyle\frac{{\left( {1 - {\nu ^2}} \right){n^4} - {c^2}\nu {n^6} + \left( {\nu - 4} \right){c^2}{n^2}{k^4} - 3{c^2}{n^4}{k^2} - {c^2}{k^6}}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}} \cdot \notag \\ & \displaystyle\frac{{\left( {1 - {k^2}} \right)}}{R} {\sin ^2}(n\alpha) \; {\cos ^2}(k\beta) \end{align} | (25) |
${\omega '_{n,\,k}}$ 是振型为 ($ n,\,k $) 时圆柱薄壳的自由振动固有频率
| \begin{equation} {\omega '_{n,k}}^2 = \frac{{Eh{c^2}g'\left( {n,k} \right)}}{{m{R^2}\left( {1 - {\nu ^2}} \right)}} \end{equation} | (26) |
式中
| \begin{align} g'\left( {n,k} \right) = & \,\displaystyle\frac{{{{\left( {{n^2} + {k^2} - 1} \right)}^2}{{\left( {{n^2} + {k^2}} \right)}^2}}}{{{{\left( {{n^2} + {k^2}} \right)}^2}}} \,{\rm{ + }} \notag \\ & \displaystyle\frac{\Big[{2\left( {1 - \nu } \right)\left( {{n^6} - {n^2}{k^4}} \right) + \displaystyle\frac{{1 - {\nu ^2}}}{{{c^2}}}{n^4}}\Big]}{{{{\left( {{n^2} + {k^2}} \right)}^2}}} \end{align} | (27) |
$g'\left( {n,\,k} \right) $ 与文献[30] 中的表达式完全一致,经验证,文献[30] 中的线性问题得到的自由振动固有频率 ${\omega _{n,k}}$ 与非线性问题中 ${\omega '_{n,k}} $ 的表达式一致,这说明非线性微分方程式 (24) 中的线性部分与文献[30] 中的线性微分方程式是一致的,也进一步验证了圆柱薄壳非线性横向振动微分方程式 (24) 的正确性.
对圆柱薄壳的非线性横向振动微分方程式 (24) 进行伽辽金变分,得到非线性横向振动微分方程为
| \begin{align} \displaystyle f'' + & { {{{\omega '}_{n,k}}} ^2}f - {n^2}\frac{{ {{P_0} + {P_t}\cos (\theta t)} }}{{2\pi m{R^3}}}f \,{\rm{ + }} \notag \\ & \displaystyle \frac{{\left[{{n^4} + {k^2}\left( {{k^2} - 1} \right) - 2\left( {1 - {k^2}} \right)\left( {\nu {n^2} + {k^2}} \right)} \right]Eh}}{{16m{R^4}}}{f^3} = 0 \end{align} | (28) |
引入临界载荷的记号 $ {P_*} $,令
| \begin{equation} {P_{*n,k}} = \frac{{2\pi m{R^3}{{\omega '}_{n,k}}^2}}{{{n^2}}} = \frac{{2\pi Dg'\left( {n,\,k} \right)}}{{{n^2}R}} \end{equation} | (29) |
这一记号形如文献[30] 中的临界载荷 $ {p^*} $. 另外,引入非线性系数的记号 $ {\gamma _{n,k}}$,令
| \begin{equation} {\gamma _{n,k}} = \frac{{\left[{{n^4} + {k^2}\left( {{k^2} - 1} \right) - 2\left( {1 - {k^2}} \right)\left( {\nu {n^2} + {k^2}} \right)} \right]Eh}}{{16m{R^4}}} \end{equation} | (30) |
于是,横向振动微分方程写成下面的形式,即
| \begin{equation} f'' + { {{{\omega '}_{n,k}}} ^2}\left[{1 - \frac{{{P_0} + {P_t}\cos (\theta t)}}{{{P_{*n,k}}}}} \right]f + {\gamma _{n,k}}\,{f^3} = 0 \end{equation} | (31) |
式 (31) 的微分方程是带有周期性系数和非线性项的二阶齐次微分方程,用于描述细长圆柱薄壳在轴向周期载荷作用下的参数振动问题. 按照鲍洛金方法,将式 (31) 写成马奇耶方程的形式
| \begin{equation} f'' + \varOmega _{n,k}^2\left[{1 - 2{\mu _{n,k}}\cos (\theta t)} \right]f + {\gamma _{n,k}}\,{f^3} = 0 \end{equation} | (32) |
式中,$ {\varOmega _{n,k}} $ 为在轴向力的定值分量 $ {P_0} $ 作用下的横向振动的固有频率,$ {\mu _{n,k}} $ 为激发系数,即
| \begin{equation} {\varOmega _{n,k}} = {\omega '_{n,k}}\sqrt {1 - \frac{{{P_0}}}{{{P_{*n,k}}}}} ,\quad {\mu _{n,k}} = \frac{{{P_t}}}{{2\left( {{P_{*n,k}} - {P_0}} \right)}} \end{equation} | (33) |
采用鲍洛金方法确定圆柱薄壳在动力不稳定区域内的定态振动振幅.
2.1 第一阶不稳定区域内的定态振动振幅为了确定第一阶不稳定区域内的定态振动振幅,取
| \begin{equation} f\left( t \right) = {a_1}\sin \frac{{\theta t}}{2} + {b_1}\cos \frac{{\theta t}}{2} \end{equation} | (34) |
将式 (34) 代入式 (32),得到包含系数 $ {a_1} $ 和 $ {b_1} $ 的方程组
| \begin{equation} \left. \begin{aligned} \left[{\varOmega _{n,k}^2\left( {1 + {\mu _{n,k}}} \right) - \displaystyle\frac{{{\theta ^2}}}{4}} \right]{a_1} + {\varPhi _1} = 0\\ \left[{\varOmega _{n,k}^2\left( {1 + {\mu _{n,k}}} \right) - \displaystyle\frac{{{\theta ^2}}}{4}} \right]{b_1} + {\varPsi _1} = 0 \end{aligned} \right\} \end{equation} | (35) |
式中,系数 $ {\varPhi _k} $ 和 $ {\varPsi _k} $ 的表达式为
| \begin{equation} \left. {\begin{aligned} {{\varPhi _k} = \displaystyle\frac{\theta }{{2{\pi} }}\int_0^{\textstyle \frac{{4{\pi} }}{\theta }} {{\gamma _{n,k}}{f^3}\sin \frac{{k\theta t}}{2}{\rm{d}}t} }\\ {{\varPsi _k} = \displaystyle\frac{\theta }{{2{\pi} }}\int_0^{\textstyle \frac{{4{\pi} }}{\theta }}{{\gamma _{n,k}}{f^3}\cos \frac{{k\theta t}}{2}{\rm{d}}t} } \end{aligned} \left( {k = 1,2,3,\cdots } \right)} \right\} \end{equation} | (36) |
将式 (34) 中的解代入式 (36) 中,忽略谐波项,获得式 (35) 中的两个非线性项 $ {\varPhi _1} $ 和 $ {\varPsi _1} $ 的表达式,并将式 (35) 变换为
| \begin{equation} \left. \begin{aligned} \left( 1 + {\mu _{n,k}} - \displaystyle\frac{{{\theta ^2}}}{{4\varOmega _{n,k}^2}} \right) {a_1} + \displaystyle\frac{{3{\gamma _{n,k}}A_1^2}}{{4\varOmega _{n,k}^2}}{a_1} = 0 \\ \left( 1 - {\mu _{n,k}} - \displaystyle\frac{{{\theta ^2}}}{{4\varOmega _{n,k}^2}} \right) {b_1} + \displaystyle\frac{{3{\gamma _{n,k}}A_1^2}}{{4\varOmega _{n,k}^2}}{b_1} = 0 \end{aligned} \right\} \end{equation} | (37) |
式中,$ {A\!_1} = \sqrt {a_1^2 + b_1^2} $ 表示第一共振区内的定态振幅. 显然,$ {a_1} = {b_1} = {A\!_1} = 0$时,方程组 (37) 是成立的,相当于受轴压作用的圆柱薄壳没有横向振动的情况.
为了获得方程组 (37) 的非零解,将其视为 $ {a_1} $ 和 $ {b_1} $ 的线性齐次方程组,只有当未知数的系数组成的行列式等于零时,$ {a_1} $ 和 $ {b_1} $ 才有非零解,即
| \begin{equation} {\begin{vmatrix} {1 + \mu \! - \! \displaystyle{{\left(\frac{\theta }{{2{\varOmega _{n,k}}}} \right)}^2} \!\! + \frac{{3\gamma A_1^2}}{{4\varOmega _{n,k}^2}}} \!\!\! & \!\! 0\\ 0 \!\! & \!\! {1 \! - \mu - \displaystyle{{\left( {\frac{\theta }{{2{\varOmega _{n,k}}}}} \right)}^2} \!\! + \frac{{3\gamma A_1^2}}{{4\varOmega _{n,k}^2}}} \end{vmatrix}} = \! 0 \! \end{equation} | (38) |
解出第一阶不稳定区域内的定态振幅 $ {A_1} $ 为
| \begin{equation} \left. {\begin{aligned} & {{A_{1{\rm{1}}}} = \displaystyle\frac{{2{\varOmega _{n,k}}}}{{\sqrt {3\gamma } }}\sqrt {{{\left( {\frac{\theta }{{2{\varOmega _{n,k}}}}} \right)}^2} - 1 \,{\rm{ + }} \,\mu } }\\ & {{A_{1{\rm{2}}}} = \displaystyle\frac{{2{\varOmega _{n,k}}}}{{\sqrt {3\gamma } }}\sqrt {{{\left( {\frac{\theta }{{2{\varOmega _{n,k}}}}} \right)}^2} - 1 - \mu } } \end{aligned}} \right\} \end{equation} | (39) |
马奇耶方程具有以下性质 [31]:不稳定区域和稳定区域被周期为 $ T $ 和 $ 2T $ 的周期解隔开了,也就是说,周期相同的两个解包围着不稳定区域,周期不同的两个解包围着稳定区域. 因此,第一阶不稳定区域由振幅为 $ {A_{11}} $ 和 $ {A_{12}} $、周期为 $ 2T $ 的两个周期解所包围.
2.2 第二阶不稳定区域内的定态振动振幅为了确定第二阶不稳定区域内的定态振幅,取
| \begin{equation} f\left( t \right) = {b_0} + {a_2}\sin (\theta t) + {b_2}\cos (\theta t) \end{equation} | (40) |
将式 (40) 代入式 (32),得到包含系数 $ {a_2} $ 和 $ {b_0} $,$ {b_2} $ 的方程组
| \begin{equation} \left. {\begin{aligned} & \ {\varOmega _{n,k}^2\left( {{b_0} - {\mu _{n,k}}{b_2}} \right) + {\varPsi _0} = 0}\\ & {\left( {\varOmega _{n,k}^2 - {\theta ^2}} \right){a_2} + {\varPhi _2} = 0}\\ & {\left( {\varOmega _{n,k}^2 - {\theta ^2}} \right){b_2} - 2{\mu _{n,k}}\varOmega _{n,k}^2{b_0} + {\varPsi _2} = 0} \end{aligned}} \right\} \end{equation} | (41) |
式中,$ {\varPhi _2} $ 和 $ {\varPsi _2} $ 按式 (36) 计算,系数 $ {\varPsi _0} $ 为
| \begin{equation} {\varPsi _0} = \frac{\theta }{{4{\pi} }}\int_0^{\textstyle \frac{{4{\pi} }}{\theta }} {{\gamma _{n,k}}\,{f^3}{\rm{d}}t} \end{equation} | (42) |
将式 (40) 代入式 (36) 和式 (42) 中,忽略各项谐波,获得式 (41) 中的 3 个非线性项 $ {\varPsi _0} $,$ {\varPhi _2} $ 和 $ {\varPsi _2} $,并将式 (41) 变化为
| \begin{equation} \left. {\begin{aligned} & {\left( {{b_0} - {\mu _{n,k}}{b_2}} \right) + \frac{{3{\gamma _{n,k}}{b_0}}}{{\varOmega _{n,k}^2}}\left( {\frac{2}{3}{b_0}^2 + {A_2}^2} \right) = 0}\\ & {\left( {1 - \frac{{{\theta ^2}}}{{\varOmega _{n,k}^2}}} \right){a_2} + \frac{{3{\gamma _{n,k}}{a_2}}}{{4\varOmega _{n,k}^2}}\left( {\frac{1}{4}{b_0}^2 + {A_2}^2} \right) = 0}\\ & {\left( {1 - \frac{{{\theta ^2}}}{{4\varOmega _{n,k}^2}}} \right){b_2} - 2{\mu _{n,k}}{b_0} + \frac{{3{\gamma _{n,k}}{b_2}}}{{4\varOmega _{n,k}^2}}\left( {\frac{1}{4}{b_0}^2 + {A_2}^2} \right) = 0} \end{aligned}} \right\} \end{equation} | (43) |
式中,$ {A_2} = \sqrt {a_2^2 + b_2^2} $ 为第二共振区附近的定态振幅. 为获得方程组 (43) 非零解,将其视为 $ {a_2},\;{b_0} $ 和 $ {b_2} $ 的线性齐次方程组,只有当未知数的系数组成的行列式等于零时,$ {a_2},\,{b_0} $ 和 $ {b_2} $ 才有非零解 (由于$b_0^2 \ll A_2^2 $,故略去式 (43) 中的微小项 [31]),将行列式等式变换为
| \begin{align} & \left( {1 - \displaystyle\frac{{{\theta ^2}}}{{\varOmega _{n,k}^2}} + \frac{{3{\gamma _{n,k}}}}{{4\varOmega _{n,k}^2}}{A_2}^2} \right) \cdot \notag \\ & \quad\quad {\begin{vmatrix} {1 + \displaystyle\frac{{3{\gamma _{n,k}}}}{{\varOmega _{n,k}^2}}{A_2}^2} & { - {\mu _{n,k}}} \\ { - 2{\mu _{n,k}}} & {1 - \displaystyle\frac{{{\theta ^2}}}{{\varOmega _{n,k}^2}} + \frac{{3{\gamma _{n,k}}}}{{4\varOmega _{n,k}^2}}{A_2}^2} \end{vmatrix}} = {\bf 0} \end{align} | (44) |
解出第二阶不稳定区域内的定态振幅的解为
| \begin{equation} \left. {\begin{aligned} & {{A_{2{\rm{1}}}} = \frac{{2{\varOmega _{n,k}}}}{{\sqrt {3{\gamma _{n,k}}} }}\sqrt {{{\left( {\frac{\theta }{{{\varOmega _{n,k}}}}} \right)}^2} - 1} }\\ & {{A_{22}} = \frac{{{\varOmega _{n,k}}}}{{\sqrt {6{\gamma _{n,k}}} }}\sqrt {\frac{{4{\theta ^2}}}{{\varOmega _{n,k}^2}} - 5 \,{\rm{ + }}\sqrt {{{\left( {\frac{{4{\theta ^2}}}{{\varOmega _{n,k}^2}} - 3} \right)}^2} + 32\mu _{n,k}^2} } }\\ & {{A_{23}} = \frac{{{\varOmega _{n,k}}}}{{\sqrt {6{\gamma _{n,k}}} }}\sqrt {\frac{{4{\theta ^2}}}{{\varOmega _{n,k}^2}} - 5 - \sqrt {{{\left( {\frac{{4{\theta ^2}}}{{\varOmega _{n,k}^2}} - 3} \right)}^2} + 32\mu _{n,k}^2} } } \end{aligned}} \right\} \end{equation} | (45) |
计算表明,在不稳定区域内,式 (45) 中的 $ {A_{23}} $ 始终为虚数,因此,第二阶不稳定区域内的定态振动振幅为 $ {A_{21}} $ 和 $ {A_{22}} $. 因此,第二阶不稳定区域由振幅为 $ {A_{21}} $ 和 $ {A_{22}} $、周期为 $ T $ 的两个周期解所包围.
由式 (39) 和式 (45) 可知,在考虑几何非线性因素的圆柱薄壳非线性动力屈曲问题中,动力不稳定区域边界上周期解的定态振动振幅 $ {A_{ij}} $ 会随着外载荷频率 $ \theta $ 变化而变化,而在线性问题中,认为动力不稳定区域边界上为无限增长的解 [31]. 因此,动力屈曲的非线性分析能定量地给出超空泡运动体在不同外载荷频率下的参数振动振幅,进而为运动体尾部的浸水深度和沾湿面积的确定以及水动力分析打基础.
3 超空泡运动体圆柱薄壳舱段的数值算例超空泡运动体航行深度 $ H $ = 10 m,流场密度 $ {\rho _w} = 1\; 000\;{\mathop{\rm kg}\nolimits} /{\rm{m^3}} $,对于自然超空泡,空泡内的饱和蒸汽压 $ {p_c} = 2\;350\;{\rm Pa}\;(20{\rm{^\circ }}{\rm C}) $ ,标准大气压 $ p = 101\; 325\; {\rm Pa}$. 圆柱薄壳舱段的几何参数:半径 $ R = 0.2\; {\rm m} $,长度 $ L = 4\;{\rm m} $,厚度 $ h = 3\;{\rm mm} $,空化器直径 $ {d_n} = 0.12\;{\rm m} $. 材料物理参数 [32]:弹性模量 $ E = 209\;{\rm GPa} $,材料密度 $ \rho = 7\;850\;{\rm{kg/}}{{\rm{m}}^{\rm{3}}} $,泊松比 $ \mu = 0.3 $.
3.1 超空泡运动体受力分析对于超空泡运动体水平向前运动时的动力屈曲分析,其受力可以简化为轴向的均布载荷,即头部阻力和尾部推力,二者大小相等,作用在头部空化器的阻力 [21] 为
| \begin{equation} {F_D} = \frac{1}{2}{\rho _w}{A_c}{C_x}{V^2} \end{equation} | (46) |
式中,$ {\rho _w} $ 为流体密度,$ {A_c} $ 是空化器的横截面积,$ {C_x} $ 是空化器的阻力系数,$ V $ 是航行体的运动速度. 零攻角时,圆盘空化器的阻力系数为
| \begin{equation} {C_x} = {C_{x0}}\left( {1 + \sigma } \right) \end{equation} | (47) |
| \begin{equation} {C_{x0}} = 0.5 + 1.81( \varphi /360 - 0.25) - 2{( \varphi /360 - 0.25)^2} \end{equation} | (48) |
| \begin{equation} \sigma = \frac{{2\left( {{p_\infty } - {p_c}} \right)}}{{{\rho _w}{V^2}}} \end{equation} | (49) |
式中,$ \varphi $ 为空化器锥角,圆盘空化器的锥角为180°,$ \sigma $ 为空化数,$ {p_c} $ 为空泡内压力,$ {p_\infty } $ 为环境压力,其表达式为
| \begin{equation} {p_\infty } = {\rho _w}gH + p \end{equation} | (50) |
式中,$ H $ 为航行深度,$ p $ 为标准大气压.
运动体在高速航行过程中,空泡形状和尺寸的不稳定性会导致轴压幅值 $ {p_0} $ 随时间变化,本文将这一动态的轴向载荷简化为 [19]
| \begin{equation} p\left( t \right) = {P_0} + {P_t} = {p_0}\left[{1 + \delta \cos (\theta t)} \right] \end{equation} | (51) |
| \begin{equation} {P_0} = {F_D} = \frac{\pi{\rho _w}{C_x}d_n^2{V^2}}{8} \qquad \qquad \end{equation} | (52) |
式中,$ \delta $ 为扰动载荷的比例系数,$ {d_n} $ 为圆盘空化器的直径.
3.2 圆柱薄壳舱段非线性动力屈曲计算结果及分析综合第 2 节和第 3 节中的内容可知,动力不稳定区域附近的定态振幅 $ {A_1}({A_2}) $ 不仅与横向振动的振型 $ n,\,k $ 有关,与轴向载荷频率 $ \theta $ (或 $ \theta /(2\varOmega) $) 有关,还与载荷比例系数 $ \delta $ 和航行速度 $ V $ 有关. 因此,下文将分析这些因素对非线性参数共振曲线的影响.
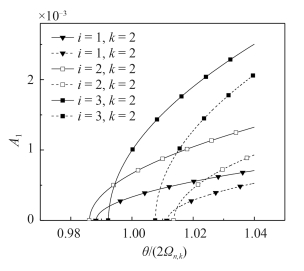
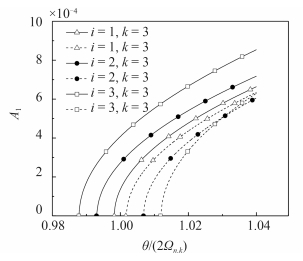
3.2.1 给定速度和载荷比例系数时,不同振型下的非线性参数共振曲线图 1 、图 2和图 3 给出了一定速度 ($ V = 400\;{\rm m/s} $) 和载荷比例系数 ($ \delta $ = 0.4) 时,不同振型下,考虑几何非线性因素的第一阶非线性参数共振曲线图,其中虚线表示的是不稳定解. 从式 (39) 可知,若$ {A_1} = 0$,则 ${\theta _{1上}}/\left( {2{\Omega _{n,k}}} \right) = \sqrt {1 + \mu } ,{\theta _{1下}}/\left( {2{\Omega _{n,k}}} \right) = \sqrt {1 - \mu } ,$ 以振型 $ i =\,1 $,$ k = 1 $ 为例,${\theta _{1上}}/\left( {2{\Omega _{n,k}}} \right)$ 对应于图 1 中的 $ G $ 点,${\theta _{1下}}/\left( {2{\Omega _{n,k}}} \right)$ 对应于图 1 中的 $ C $ 点. 所以,某一振型对应的两条曲线 (一条实线和一条虚线) 所夹的横坐标上的区域即为这一振型下的激发区.

|
图 1 第一阶参数共振曲线图(a) Fig.1 The first order parametric resonance curves (a) |
|
图 2 第一阶参数共振曲线图(b) Fig.2 The first order parametric resonance curves (b) |
|
图 3 第一阶参数共振曲线图(c) Fig.3 The first order parametric resonance curves (c) |
从以上 3 幅图中可以得出以下结论:
(1) 当圆柱薄壳所受的外载荷的频率处于激发区以外且在小于激发区一侧 (图 1 中的 $ BC $ 段) 时,圆柱薄壳没有横向振动.
(2) 考虑几何非线性的圆柱薄壳舱段,其各阶参数共振曲线都向大于激发区频率的一侧倾斜. 因此,
① 外载荷频率从小于激发下界的一侧开始逐渐增大 (图 1 中的路线为 $ BCGF $) 时,圆柱薄壳的横向振动振幅沿着 $ BCHD $ 增大.
② 外载荷频率从大于激发上界的一侧开始逐渐减小 (路线为 $ FGCB $) 时:
若从 F 到 G 点没有外界干扰或者干扰不足以使壳体的横向振动越过不稳定解 ( $ EG $ 曲线) 到达稳定解 ( $ DH $ 曲线) 上去,则壳体的横向振动振幅依然为 0,直到频率到达 $ G $ 点时,壳体才会发生“突变”的、振幅位于 $ H $ 点的横向振动.
若从 F 到 G 点时,存在干扰使得壳体的横向振动越过不稳定解 ( $ EG $ 曲线) 到达稳定解 ( $ DH $ 曲线) 上去,横向振动的振幅由零突然增大到 $ DH $ 曲线,这使得 $ GF $ 段成为潜在的激发区域,导致危险的激发区域扩大.
(3) 对比图 1、图 2和图 3 的纵坐标可知,当 $ k $ = 2 或 $ k $ = 3 时,不稳定区域内的定态振动振幅与壳体的厚度 ($ h $ = 3 mm) 是同一个数量级的,但当 $ k $ = 1 时,不稳定区域内的定态动振幅比 $ k $ = 2 或 $ k $ = 3 时高出两个数量级.
以振型 $ i $ = 1,$ k $ = 1 为例,对比参数振动的线性和非线性理论,可知:
(1) 在参数振动的线性理论中,不存在参数共振曲线的“倾斜”问题,激发区域只有图 1 中的 $ CG $ 段,但在考虑几何非线性的参数振动非线性理论中,由于参数共振曲线向大于激发区频率一侧“倾斜”,导致激发区不仅有 $ CG $ 段,还包括 $ GF $ 段. 因此,考虑几何非线性后,激发区的扩大会导致外载荷安全频率范围的缩小和结构动力稳定可靠性的降低.
(2) 参数振动的线性理论认为激发区域内振动的振幅是无限大的,这不符合工程实际. 考虑几何非线性,激发区域内的振动振幅实际上为有限振幅. 对于超空泡运动体而言,结构的变形量直接影响其沾湿面积,而沾湿面积决定了空泡的稳定性,这是一个典型的流固耦合问题. 因此,考虑非线性因素,准确地获得激发区域内的参数振动振幅,是进行流固耦合分析的必要前提.
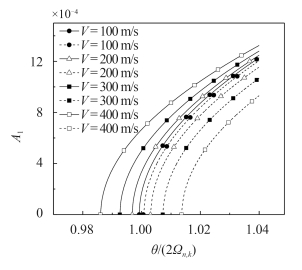
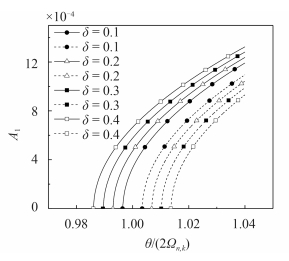
3.2.2 给定的振型 ($ i $ = 2,$ k $ = 2) 时,速度和载荷比例系数对非线性参数共振曲线的影响图 4 给出了载荷比例系数 $ \delta $ = 0.4 时,不同航行速度 $ V $ 下的第一阶非线性参数共振曲线图. 图 5 给出了航行速度 $ V $ = 400 m/s 时,不同载荷比例系数 $ \delta $ 下的第一阶非线性参数共振曲线图.
|
图 4 不同航行速度下的第一阶参数共振曲线图 Fig.4 The first order parametric resonance curves with different speed |
|
图 5 不同载荷比例系数下的第一阶参数共振曲线图 Fig.5 The first order parametric resonance curves with different proportional coefficient of load |
由图 4 和图 5 可以得出以下结论:
(1) 激发区的范围随着超空泡运动体的航行速度 $ V $ 和载荷比例系数 $ \delta $ 增大而增大; 激发区内的定态振动的振幅随着超空泡运动体的航行速度 $ V $ 和载荷比例系数 $ \delta $ 增大而增大.
(2) 结论“(1)”与线性理论的结论相同 [30],事实上,从式 (38) 和文献[31] 中的线性临界频率方程式的对比中可知,若令式 (38) 中的 $ {A_1} $ = 0,那么,式 (38) 和线性临界频率方程式是一致的,也就是说,图 1 中的 $ CG $ 段的激发区域在线性理论和非线性理论中是相同的. 不同之处在于,非线性理论中要将 $ GF $ 段也计入激发区域范围内,使激发区比线性理论中给出的激发区扩大.
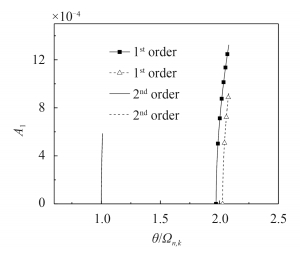
通过对第二阶非线性参数共振的共振曲线进行分析,也能得出与第一阶相同的结论. 图 6 给出了第一阶和第二阶非线性共振曲线的对比图 ($ \delta $ = 0.4,$ V $ = 400 m/s).
|
图 6 第一阶和第二阶非线性参数共振曲线对比图 Fig.6 The comparison chart of the nonlinear resonance between the firstand the second-order. |
由图 6 可知,第二阶非线性共振曲线与第一阶的形状相似,都向较大频率的一侧倾斜; 第二阶不稳定区域内的定态振动的振幅远小于第一阶的定态振动的振幅,这也说明了在圆柱薄壳的横向参数振动中,第一阶不稳定区域不仅激发区远大于第二阶,考虑非线性因素后,第一阶激发区内的振动振幅也远大于第二阶.
4 结论本文建立了圆柱薄壳的非线性动力屈曲计算模型,并给出了超空泡运动体的圆柱薄壳舱段的分析算例,得到以下结论:
(1) 考虑几何非线性因素后,参数共振曲线向大于激发区频率的一侧倾斜,使得激发区的范围变大,从而导致外载荷安全频率范围的缩小和结构动力稳定可靠性的降低.
(2) 考虑非线性因素,能准确地获得激发区域内的参数振动振幅,是进行超空泡运动体流固耦合分析的基础.
(3) 激发区的范围随着超空泡运动体的航行速度 $ V $ 和载荷比例系数 $ \delta $ 增大而增大; 激发区内的定态振动的振幅随着超空泡运动体的航行速度 V 和载荷比例系数 δ 增大而增大.
(4) 当 k = 2 或 k = 3 时,不稳定区域内的定态振动振幅与壳体的厚度 (h = 3 mm) 是同一个数量级的,但当 $ k $ = 1 时,不稳定区域内的定态振动振幅比 $ k $ = 2 或 $ k $ = 3 时高出两个数量级.
| 1 | Lam KY, Ng TY. Dynamic stability of cylindrical shells subjected to conservative periodic axial loads using different shells theories.Journal of Sound and Vibration, 1997, 207(4): 497-520 |
| 2 | Ng TY, Lam KY, Liew KM, et al. Dynamic stability analysis of functionally graded cylindrical shells under periodic axial loading. International Journal of Solids and Structures, 2001, 38: 1295-1309 |
| 3 | Darabi M, Darvizeh M, Darvizeh A. Non-linear analysis of dynamic stability for functionally graded cylindrical shells under periodic axial loading. Composite Structures, 2008, 83: 201-211 |
| 4 | 周承倜,王列东.复合材料叠层圆柱壳的非线性动力稳定性分析.大连大学学报, 1993, 01: 1-15 (Zhou Chengti, Wang Liedong. Nonlinear analysis of dynamic stability for laminated composite cylindrical shells. Journal of Dalian University, 1993, 01: 1-15 (in Chinese)) |
| 5 | 曾潇,卓曙君.有随机初始缺陷的轴压圆柱薄壳的动力稳定性分析.昆明理工大学学报, 1996, 21(3): 59-63 (Zeng Xiao, Zhuo Shujun. Dynamic stability analysis of axially compressed cylindrical shell with random initial geometric imperfections. Journal of Kunming University of Science and Technology, 1996, 21(3): 59-63 (in Chinese)) |
| 6 | 张善元,张涛.圆柱壳的轴向动力屈曲、参数共振与混沌运动.振动与冲击, 2010, 29(12): 34-38, 66 (Zhang Shanyuan, Zhang Tao. Axial dynamic buckling parametric resonance and chaotic motion of a closed cylindrical shell. Journal of Vibration and Shock, 2010,29(12): 34-38, 66 (in Chinese)) |
| 7 | 赵晶瑞,唐友刚,王文杰.传统 Spar平台参数激励 Mathieu不稳定性的研究.工程力学, 2010, 27(3): 222-227 (Zhao Jingrui, Tang Yougang, Wang Wenjie. Study on the parametrically excited Mathieu instability of a classic Spar platform. Engineering Mechanics,2010, 27(3): 222-227 (in Chinese)) |
| 8 | 徐万海,吴应湘,钟兴福等.海洋细长结构参数激励不稳定区的确定方法.振动与冲击, 2011, 30(9): 79-83 (Xu Wanhai, Wu Yingxiang, Zhong Xingfu, et al. Methods for parametric excitation instability analysis of slender flexible cylindrical structures in offshore engineering. Journal of Vibration and Shock, 2011, 30(9): 79-83 (in Chinese)) |
| 9 | 王俊荣,谢彬.深水半潜式平台Mathieu不稳定问题研究.工程力学, 2012, 29(10): 347-353 (Wang Junrong, Xie Bin. Mathieu instability study of a deepwater semi-submersible platform. Engineering Mechanics, 2012, 29(10): 347-353 (in Chinese)) |
| 10 | 吴学敏,黄维平,滕文刚.深水顶张式立管参数振动与涡激振动耦合振动分析方法研究.中国海上油气, 2014, 04: 100-105 (Wu Xuemin, Huang Weiping, Teng Wengang. Study on analysis method for coupled vibration of parameter excited vibration and vortexinduce vibration on deep water top-tensed riser. China Offshore Oil and Gas, 2014, 04: 100-105 (in Chinese)) |
| 11 | Zhang J, Tang YG. Mathieu instability analysis of deep-water toptensioned Risers. Journal of Ship Mechanics, 2014, 09: 1142-1150 |
| 12 | 桑松,石晓,李长东等.深海SPAR平台垂荡-纵摇耦合运动Mathieu稳定性分析.中国海洋平台, 2014, 04: 34-40 (Sang Song, Shi Xiao, Li Changdong, et al. Study on Mathieu stability of heave-pitch coupled motions of SPAR platform in deep sea. China Offshore Platform, 2014, 04: 34-40 (in Chinese)) |
| 13 | 李为洲.斜拉索面内参数振动数值分析及其控制. [硕士论文].长沙:湖南大学, 2013 (Li Weizhou. Numerical analysis of in-plane parametric vibration and the controlling measures for stay cables. [Master Thesis]. Changsha: Hunan University, 2013 (in Chinese)) |
| 14 | 孙超.大跨度铁路斜拉桥拉索参数振动研究. [硕士论文].成都:西南交通大学, 2014 (Sun Chao. Parametric vibration of cables for long-span railway cable-stayed bridges. [Master Thesis]. Chengdu: Southwest Jiaotong University, 2014 (in Chinese)) |
| 15 | 李周.大跨度悬索桥悬吊体系参数振动研究. [博士论文].广州:华南理工大学, 2013 (Li Zhou. The research on parametric vibration of suspended system of large-span suspension bridge. [PhD Thesis]. Guangzhou: South China University of Technology, 2013 (in Chinese)) |
| 16 | 杨咏漪,陈克坚.大跨度铁路斜拉桥斜拉索参数振动分析.铁道工程学报, 2013, 10: 60-65 (Yang Yongyi, Chen Kejian. Research on parametric oscillation of cables for long span railway cable-stayed Bridge. Journal of Railway Engineering Society, 2013, 10: 60-65 (in Chinese)) |
| 17 | 张晓湘.竖向周期荷载作用下单层钢框架的动力稳定性分析. [硕士论文].长沙:中南大学, 2013 (Zhang Xiaoxiang. Dynamic stability analysis of single-story steel frames under vertical cyclic load. [Master Thesis]. Changsha: Central South Univerdity, 2013 (in Chinese)) |
| 18 | 邱良.径向均布周期荷载作用下拱的动力稳定性能研究. [硕士论文].长沙:中南大学, 2013 (Qiu Liang. Dynamic stability research of arch under radial uniform cyclic loading. [Master Thesis]. Changsha: Central South Univerdity, 2013 (in Chinese)) |
| 19 | Ruzzene M. Dynamic buckling of periodically stiffened shells: appli- cation to supercavitating vehicles. International Journal of Solids and Structures, 2004, 41: 1039-1059 |
| 20 | Ruzzene M. Non-axisymmetric buckling of stiffened supercavitating shells: static and dynamic analysis. Computers and Structures,2004, 82: 257-269 |
| 21 | Ahn SS, Ruzzene M. Optimal design of cylindrical shells for enhanced buckling stability: Application to supercavitation underwater vehicles. Finite Elements in Analysis and Design, 2006, 42: 967-976 |
| 22 | Choi JY, Ruzzene M. Stability analysis of supercavitating underwater vehicles with adaptive cavitator. International Journal of Mechanical Sciences, 2006, 48: 1360-1370 |
| 23 | 施连会,王安稳.轴向载荷下超空泡航行体动力稳定性的数值研究.振动与冲击, 2011, 30(2): 55-59 (Shi Lianhui, Wang Anwen. Numerical study on dynamic stability of supercavitating vehicles subjected to axial loads. Journal of Vibration and Shock, 2011,30(2): 55-59 (in Chinese)) |
| 24 | 麻震宇.超空泡航行体结构动力学仿真研究. [博士论文].长沙:国防科学技术大学, 2012 (Ma Zhenyu. Numerical research on dynamics of structures for supercavitating vehicles. [PhD Thesis]. Changsha: National University of Defense Technology, 2012 (in Chinese)) |
| 25 | 麻震宇,胡凡,陈广南等.超空泡航行体双层壳结构动力稳定性分析.国防科技大学学报, 2011, 33(4): 43-47 (Ma Zhenyu, Hu Fan, Chen Guangnan, et al. Dynamic stability analysis of supercavitating double shells. Journal of National University of Defense Technology,2011, 33(4): 43-47 (in Chinese)) |
| 26 | 宋向华,安伟光,刘明.轴向周期载荷下超空泡射弹的动力稳定性分析.哈尔滨工程大学学报, 2012, 33(10): 1238-1243 (Song Xi- anghua, An Weiguang, Liu Ming. Dynamic stability analysis of supercavitating projectile subjected to axial periodic load. Journal of Harbin Engineering University, 2012, 33(10): 1238-1243 (in Chinese)) |
| 27 | 宋向华,安伟光,蒋运华.超空泡射弹动力稳定性的非概率可靠性分析.兵工学报, 2012, 33(8): 997-1003 (Song Xianghua, An Weiguang, Jiang Yunhua. Non-probabilistic reliability analysis for supercavitating projectile based on dynamic stability. Acta Armamentarii,2012, 33(8): 997-1003 (in Chinese)) |
| 28 | 刘明,安伟光,宋向华.随机载荷下随机参数超空泡射弹的动力稳定性.计算机仿真, 2012, 10: 55-58 (Liu Ming, An Weiguang, Song Xianghua. Dynamic stability of supercaviting projectile with stochastic parameters subject to random load. Computer Simulation,2012, 10: 55-58 (in Chinese)) |
| 29 | 刘明,安伟光,宋向华29 .随机参数超空泡射弹的动力稳定性和可靠性.爆炸与冲击, 2013, 33(5): 525-530 (Liu Ming, An Weiguang, Song Xianghua. Dynamic stability and reliability of a supercavitating projectile with stochastic parameters. Explosion and Shock Waves, 2013, 33(5): 525-530 (in Chinese)) |
| 30 | 王杰方,安伟光,宋向华.超空泡运动体圆柱薄壳动力屈曲及可靠性分析.振动与冲击, 2014, 33(8): 22-28 (Wang Jiefang, An Weiguang, Song Xianghua. Dynamic buckling and reliability analysis of a cylindrical thin shell for supercavitating vehicles. Journal of Vibration and Shock, 2014, 33(8): 22-28 (in Chinese)) |
| 31 | 符华,鲍洛金.弹性体系的动力稳定性.北京:高等教育出版社,1960: 124-125 (Bolotin VV. Dynamic Stability of Elastic Systems. Beijing: Higher Education Press, 1960: 124-125 (in Chinese)) |
| 32 | 何芝仙,崔建华.材料力学.武汉:武汉大学出版社, 2013 (He Zhixian, Cui Jianhua. Mechanics of Materials. Wuhan: Wuhan University Press, 2013 (in Chinese)) |
2. Department of Civil and Architecture Engineering, Nanchang Institute of Technology, Nanchang 330099, China
 2016, Vol. 48
2016, Vol. 48