由于设计或者制造误差的原因,动力机械内部各个零部件之间或者零部件与边界之间常常存在一定的间隙,这往往导致零部件之间或者零部件与边界之间存在碰撞以及往复振动现象,这种现象称为碰撞振动.由于碰撞的存在,碰撞振动系统是强非线性系统.研究碰撞振动系统的动力学行为对于机械系统的优化设计和噪声控制具有重要意义,因此,碰撞振动系统的动力学行为的复杂性引起了国内外学者们的极大关注.随着非线性动力系统理论[1, 2, 3, 4, 5]、动态测试技术和计算机技术的迅速发展,碰撞振动系统的研究进入了全新的阶段[6, 7].早期关于碰撞振动系统的研究主要针对单自由度系统,研究内容包括周期运动的存在性及其稳定性、以及分岔和混沌行为[8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18].对于多自由度碰撞振动系统,属于高维强非线性动力系统,在一个分岔临界点处可能同时存在两种或两种以上的分岔形式,这些共存的分岔将会相互作用,给碰撞振动系统的动力学带来更为复杂而深刻的影响.有学者通过应用中心流形-范式理论以及计算机数值分析,较为系统地研究了多自由度碰撞振动系统的各种余维二分岔,包括霍普 夫倍化(Hopf-flip)分岔、霍普夫-霍普夫(Hopf-Hopf)分岔,以及各种共振的情况[19, 20, 21, 22, 23, 24]. 其余关于碰撞振动系统动力学的研究参见文献[25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35].
基于中心流形-范式理论,结合对称性质,文献[36]推导了内伊马克沙克-音叉分岔点处的庞加莱映射的范式,并通过数值模拟揭示了内伊马克沙克-音叉分岔如何发生.然而,此文尚未进一步探讨在内伊马克沙克-音叉分岔点处存在的各种复杂动力学行为.%}有人基于庞加莱映射直接运用中心流形-范式理论,并讨论了对称周期运动的霍普夫音叉(Hopf-pitchfork)分岔(即对称不动点的内伊马克沙克-音叉分岔)[37, 38],然而并未引入系统内在的对称性质来研究系统动力学.而碰撞振动系统的对称性会对局部分岔行为产生本质影响[33],因此一些由于对称性导致的动力学现象可能还未被揭示.
本文引入对称性研究了一类三自由度碰撞振动系统在内伊马克沙克-音叉分岔点处的局部两参数动力学,是文献[36]的工作的延 续和深化. 基于对称性质可以导出庞加莱映射${\pmb P}$是另外一个隐式虚拟映射${\pmb Q}$的二次迭代. 基于映射${\pmb Q}$,讨论了内伊马克沙克-音叉分岔点处的两参数开折.数值模拟得到了内伊马克沙克-音叉分岔点附近在投影的庞加莱截面上的各种可能的局部两参数动力学行为.研究表明内伊马克沙克-分岔和音叉分岔互相作用可能得到新的结果,而这正是由于系统内在的对称性作用所决定的.
1 力学模型以及对称周期运动一个受简谐激励的具有对称刚性约束的三自由度碰撞振动系统如图 1所示[36]. 系统有3个质量 块$M_1 $,$M_2$,$M_3 $. 质量块$M_2 $上对称放置左右两个刚性约束. 假定$C_1 $,$C_2 $,$C_3 $为比例阻尼,$K_1 $,$K_2 $,$K_3$是线性弹簧. 当激励振幅很小时,系统做简单的振动,是一个 线性系统. 当激励振幅增加到一定值时,$M_3$将会依次与左右两个刚性约束碰撞,此时系统成为强非线性系统. 瞬时碰撞过程以恢复系数$R$描述.
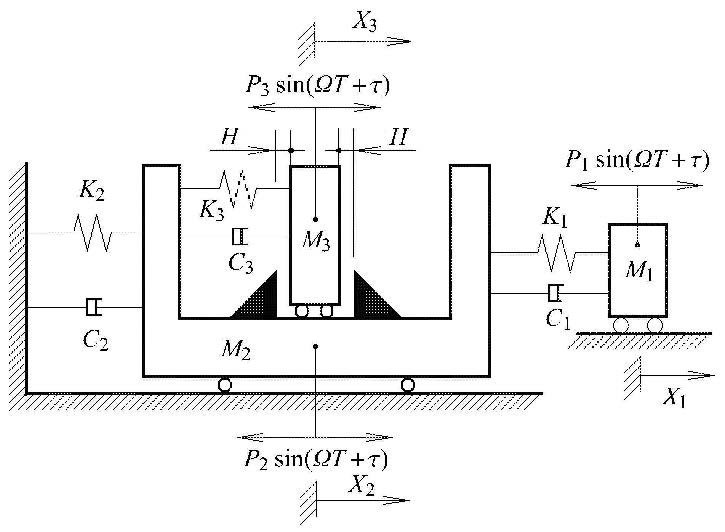
|
图 1 具有对称刚性约束的三自由度碰撞振动系统 Fig. 1 Three-degree-of-freedom vibro-impact system with symmetric rigid constraints |
在任意两次连续碰撞之间,无量纲化的运动微分方程为
| $ {\pmb U}_m \ddot {\pmb x} + 2\zeta {\pmb U}_c \dot {\pmb x} + {\pmb U }_k {\pmb x} = {\pmb U}_f f\sin (\omega t + \tau ) $ | (1) |
式中,${\pmb x} = [x_1 ,x_2 ,x_3]^{\rm T }$,${\pmb U}_m ={\rm diag}[u_{m_1 } ,u_{m_2 } ,u_{m_3 }]$,${\pmb U}_f ={\rm diag} [u_{f_1 } ,u_{f_2 } ,u_{f_3 }]$,${\pmb U}_c $和${\pmb U}_k$分别表示无量纲的阻尼矩阵和刚度矩阵,见文献[36]. 无量纲的参数和变量为
| $ t= T\sqrt {\dfrac{K_3 }{M_3 }} ,\zeta = \dfrac{C_3 }{2\sqrt {K_3 M_3 } } ,\omega =\varOmega \sqrt {\dfrac{M_3 }{K_3 }} \\ f = \dfrac{P_3 }{P_0 } ,u_{m_i } = \dfrac{M_i }{M_3 } ,u_{k_i } = \dfrac{K_i }{K_3 } \\ u_{c_i } = \dfrac{C_i }{C_3 } ,u_{f_i } = \dfrac{P_i }{P_3 } ,x_i = \dfrac{X_i K_3 }{P_0 } $ |
其中$P_0 = \sum\limits_i^3 { {\left| {P_i } \right|} }$,$i = 1$,2,3.
在碰撞之后,根据碰撞定理以及动量守恒定律,质量块$M_2 $和$M_3 $的速率为
| $ y_{2 + } = \delta _{11} y_{2 - } + \delta _{12} y_{3 - } ,y_{3 + } = \delta _{21} y_{2 - } + \delta _{22} y_{3 - } $ | (2) |
式中
| $ \delta _{11} = \dfrac{u_{m_2 } - R}{1 + u_{m_2 } } ,\delta _{12} =\dfrac{1 + R}{1 + u_{m_2 } } \\ \delta _{21} = \dfrac{u_{m_2 } (1 + R)}{1 + u_{m_2 } } ,\delta _{22} = \dfrac{1 - u_{m_2 } R}{1 + u_{m_2 } } $ |
$y_{i - } = \dot {x}_{i - } $,$y_{i + } = \dot {x}_{i + } $分别表示$M_2 $和$M_3$在碰撞之前和碰撞之后的无量纲化瞬时速度.
当$M_3 $与$M_2 $上的左右两块刚性约束碰撞时,两质量块的无量纲位移满足$\left| {x_2 - x_3 } \right| = h$,其中$h={K_1 H}/{P_0 }$. 设方程(1)的特征频率为$\omega _1 $,$\omega _2 $,$\omega _3 $,且$ {\pmb \psi}$为正则振型矩阵. 做变量代换$\left[{x_1 ,x_2 ,x_3 } \right]^{\rm T} = {\pmb \psi }\xi $,方程(1)成为
| $ {\pmb I}\ddot {\xi } + {\pmb C}\dot {\xi } + {\pmb \varLambda}\xi = {\pmb \psi }^{\rm T}{\pmb U}_f f \sin(\omega t + \tau ) $ | (3) |
式中${\pmb \varLambda } ={\rm diag} [\omega _1^2 ,\omega _2^2 ,\omega _3^2]$,${\pmb C} = 2\zeta {\pmb \varLambda }$. 令$\phi _{ij} $代表矩阵${\pmb \psi }$中的元素,方程(1)的解为
| $ x_i (t) = \sum\limits_i^3 { } \phi _{ij} \Big \{ {\rm e}^{ - \eta _j t}[a_j \cos(\omega _{dj} t) + b_j \sin (\omega _{dj} t)] + \\ \qquad A_j \sin (\omega t + \tau ) + B_j \cos (\omega t + \tau ) \Big\} $ | (4) |
式中,$\eta _j = \zeta \omega _j^2 $,$\omega _{dj} = \sqrt {\omega _j^2 - \eta _j^2 } $. $a_j $,$b_j $为积分常数,$A_j $ 和$B_j $ 为振幅常数.
碰撞振动系统的对称性允许"对称周期运动"在适当的参数条件下存在.以符号$n$-$p$来表示碰撞系统的周期运动,其中$n$为激励的 周期数,$p$为碰撞次数.采用"对称周期$n-2$运动"来表示每$n$ ($n$为奇数)个激励周期发生左右两次对称碰撞的运动,即对称周期运动.
对于碰撞振动系统的对称周期$n-2$运动,在经过半个激励力周期发生碰撞后,碰撞过程并没有改变周期解的形式,只是改变了周期解 的积分常数.则对称周期解可表示为
| $ x_i (t) = \left\{ \!\!\begin{array}{l} \sum\limits_i^3 { } \phi _{ij} [{\rm e}^{ - \eta _j t}(a_{ji} \cos(\omega _{dj} t) + \\ \qquad b_{ji} \sin (\omega _{dj} t)) + A_j \sin (\omega t + \tau _0 ) + \\ \qquad B_j \cos (\omega t + \tau _0 )] ,t \in [0,t_1] \\ \sum\limits_i^3 { } \phi _{ij} \Big\{ {\rm e}^{ - \eta _j (t - t_1 )} [a_{ji} \cos (\omega _{dj} (t - t_1 )) + \\ \qquad b_{ji} \sin (\omega _{dj}(t - t_1 ))] + A_j \sin (\omega t + \tau _0 ) + \\ \qquad B_j \cos (\omega t + \tau _0 )\Big\} ,t \in [t_1 ,t_2] \end{array} \!\!\right. (i = 1,2,3) $ | (5) |
式中$a_{jk} \ (j = 1,2,3; k = 1,2)$是由初始条件所决定的积分常数.
2 庞加莱映射以及对称不动点的稳定性及分岔在任意两次碰撞之间,方程(1)可写为
| $ \dot{\pmb X} = {\pmb F}({\pmb X},t) $ | (6) |
式中,${\pmb X} = (x_1 ,y_1 ,x_2 ,y_2 ,x_3 ,y_3 )^{\rm T}$,且$x_i $和$y_i =\dot {x}_i $分别表示第$i$个质量块在$t$时刻的位移和速度. 显然,方程(6)同时满足
| $ {\pmb F} \Big({\pmb X},t + \dfrac{2n\pi }{\omega }\Big) = {\pmb F}({\pmb X},t) $ | (7) |
和
| $ {\pmb F}( - {\pmb X},t + \dfrac{n\pi }{\omega }) = - {\pmb F}({\pmb X},t) $ | (8) |
式中$n$为奇数. 另外,由于在左右刚性约束的碰撞恢复系数相等,因此把这样的系统称为对称碰撞振动系统.
碰撞振动系统的相空间为
| $ {\pmb R}^6\times {\pmb S}^1 = \{ x_1 ,y_1 ,x_2 ,y_2 ,x_3 ,y_3 , \\ \qquad t |(x_1 ,y_1 ,x_2 ,y_2,x_3 ,y_3 ) \in {\pmb R}^6 ,\ t \in {\pmb S}^1 \} $ | (9) |
式中${\pmb S}^1$是频率为$ {2\pi }/{\omega }$的圆. 把庞加莱截面${\pmb \varPi }_0 $取在与左边约束碰撞的瞬时
| $ {\pmb \varPi }_0 = \{ (x_1 ,y_1 ,x_2 ,y_2 ,x_3 ,y_3 ,t) \in \\ \qquad {\pmb R}^6\times {\pmb S}^1\big | x_2 - x_3 = h,y_i = \dot {x}_{i + } \} $ | (10) |
当在右边约束处碰撞时,定义截面${\pmb \varPi }_1 $为
| $ {\pmb \varPi }_1 = \{ (x_1 ,y_1 ,x_2 ,y_2 ,x_3 ,y_3 ,t) \in \\ \qquad {\pmb R}^6\times {\pmb S }^1\big |x_2 - x_1 = - h,y_i = \dot {x}_{i + } \} $ | (11) |
并定义一个变换${\pmb R}$
| $ {\pmb R}:(x_1 ,y_1 ,x_2 ,y_2 ,x_3 ,y_3 ,t) \mapsto \\ \qquad \Big( - x_1 ,- y_1 ,- x_2 ,- y_2 ,- x_3 ,- y_3 ,t + \dfrac{n\pi }{\omega } \Big) $ | (12) |
因为$t \in {\pmb S}^1$,显然
| $ {\pmb R}^2={\pmb I} $ | (13) |
根据 式(8)和 式(12),有
| $ {\pmb R \pmb F}({\pmb X}) = {\pmb F}({\pmb R \pmb X}) $ | (14) |
庞加莱映射在一个激励力周期以内可以分为4个连续的子映射:(1)质量块$M_3$与左边约束碰撞后运动到与右边约束碰撞前的阶段(${\pmb P }_1 )$;(2)质量块$M_3 $与右边约束碰撞的阶段(${\pmb P}_2 )$;(3)质量块$M_3 $与右边约束碰撞后运动到左边约束碰撞前的 阶段(${\pmb P }_3 )$;(4)质量块$M_3$与左边约束碰撞的阶段(${\pmb P }_4 )$. 则庞加莱映射可表示为
| $ {\pmb P } = {\pmb P }_4 \circ {\pmb P }_3 \circ {\pmb P }_2\circ {\pmb P }_1 $ | (15) |
庞加莱映射在不动点${\pmb X}_0 $处的雅可比矩阵可按下式计算
| $ {\pmb D\pmb P} = {\pmb D\pmb P }_4 ({\pmb P }_3 \circ {\pmb P }_2 \circ {\pmb P }_1({\pmb X }_0 )) \cdot {\pmb D\pmb P }_3 ({\pmb P }_2 \circ {\pmb P }_1 ({\pmb X }_0 )) \cdot \qquad {\pmb D\pmb P }_2 ({\pmb P }_1 ({\pmb X }_0 )) \cdot {\pmb D\pmb P }_1 ({\pmb X }_0 ) $ | (16) |
令
| $ {\pmb Q } = {\pmb R }^{ - 1} \circ {\pmb Q }_u $ | (17) |
式中${\pmb Q}_u = {\pmb P}_2 \circ {\pmb P}_1 $.
则庞加莱映射可表示为[33]
| $ {\pmb P } = {\pmb Q }^2 $ | (18) |
即,庞加莱映射${\pmb P}$是映射${\pmb Q}$的二次迭代,${\pmb Q}$是一个虚拟的隐式映射. 式(18)隐含了庞加莱映射的${\pmb P }$的对称性.
如果相点${\pmb X }_0 \in {\pmb \varPi }_0 $满足${\pmb P }({\pmb X }_0 ) = {\pmb X }_0 $,则${\pmb X }_0 $是庞加莱映射${\pmb P }$的不动点,对应于系统相应的周期运动.
定义1 (对称不动点) 如果不动点${\pmb X }_0 $进一步满足
| $ {\pmb X }_0 = {\pmb Q }({\pmb X }_0 ) $ | (19) |
则${\pmb X}_0 $叫做"对称不动点",对应于碰撞振动系统相应的对称周期$n$-2运动.
定义2 (共轭不动点) 如果${\pmb X }_\alpha $是庞加莱映射${\pmb P }$的不动点(即满足${\pmb P }({\pmb X }_\alpha ) = {\pmb X }_\alpha )$,并且进一步满足
| $ {\pmb Q }({\pmb X }_\alpha ) = {\pmb X }_\beta \ne {\pmb X }_\alpha $ | (20) |
则把${\pmb X}_\alpha $和${\pmb X}_\beta$叫做一对共轭(或反对称)不动点,对应于碰撞振动系统的一对共轭(或反对称)周期$n$-2 运动.
根据式(19)可以得到对称不动点的存在性条件
引理3 (对称不动点的存在性) 如果存在初始条件$\tau (0) = \tau _0$,$x_i (0) = x_{i0} $,$\dot {x}_{i + } (0) = y_{i0} $,使方程(1)在区间$t\in \Big[0,\dfrac{n\pi }{\omega }\Big]$上的解满足
| $ x_i \Big(\dfrac{n\pi }{\omega }\Big) = - x_i (0) ,\quad\dot {x}_{i + }\Big (\dfrac{n\pi }{\omega } \Big) = - \dot {x}_{i + } (0) $ | (21a) |
| $ x_2 (0) - x_1 (0) = h ,x_2 \Big (\dfrac{n\pi }{\omega }\Big) - x_1 \Big (\dfrac{n\pi }{\omega }\Big) = - h $ | (21b) |
则碰撞振动系统的庞加莱映射${\pmb P }$存在对称不动点${\pmb X }_0$,对应于相应的对称周期运动.
将式(4)代入式(21),可以解得初相位角$\tau _0 $以及积分常数$a_j $,$b_j $.
| $ \tau _0 = 2\tan ^{ - 1} \Big (\dfrac{V_c \pm \sqrt {V_c^2 + U_c^2 - h^2} }{U_c + h} \Big ) $ | (22) |
| $ a_j = E_{aj} \cos \tau _0 + F_{aj} \sin \tau _0 $ | (23) |
| $ b_j = I_{bj} a_1 + J_{bj} a_2 + K_{bj} a_3 $ | (24) |
式中,$V_c $,$U_c $,$E_{aj} $,$F_{aj} $,$I_{bj} $,$J_{bj} $,$K_{bj}$的表达式略去,并省略冗长的推导过程. 把$\tau _0 $,$a_j $,$b_j $和$t = 0$带回式(4),得到对称不动点的解析解${\pmb X }_0 = (x_{10}$,$y_{10}$,$x_{20}$,$y_{20}$,$x_{30}$,$\tau _0 )$(略).
在一定的参数条件下,令碰撞振动系统在映射${\pmb P }$的情况下线性化矩阵的特征值为$\lambda = e^{\pm {\rm i}\theta }$,而在映射$ {\pmb Q }$的情况下线性化矩阵的特征值为$\tilde {\lambda } = {\rm e}^{\pm {\rm i}\tilde{\theta }}$,$\theta $ 和$\tilde {\theta }$分别表示$\lambda $和$\tilde {\lambda}$穿越单位圆的位置(以角度表示). 因为${\pmb P } = {\pmb Q }^2$,则$\lambda = \tilde {\lambda }^2$,即:$\theta= 2\tilde {\theta }$. 现作以下讨论:(1)当映射${\pmb Q }$有一对共轭复特征值穿越单位圆时,映射${\pmb P}$必然也有一对共轭复特征值穿越单位圆. 因此在一般的情况下(是指两映射均满足非共振条件),映射${\pmb Q}$发生余维一的内伊马克沙克-分岔对应于映射${\pmb P }$发生余维一的内伊马克沙克-分岔.(2)映射${\pmb Q }$有一个特征值从($ - 1$,0)处($\tilde {\theta } = \pi )$穿越单位圆对应于映射${\pmb P}$有一个特征值从($ + 1$,0)处($\theta = 2\pi )$穿越单位圆. 因此映射$ {\pmb Q}$发生余维一的周期倍化分岔对应于映射${\pmb P }$发生余维一的音叉分岔. (3) 当映射${\pmb Q}$有一个$-1$的实特征值和一对共轭复特征值同时穿越单位圆时,映射${\pmb P}$必然有有一个$+1$的实特征值和一对共轭复特征值同时穿越单位圆. 因此,映射$ {\pmb Q}$发生内伊马克沙克-倍化分岔对应于映射${\pmb P }$发生内伊马克沙克-音叉分岔.(4)映射${\pmb P }$不可能发生内伊马克沙克-倍化分岔(证明过程与文献[33]中列举的方法类似).
3 根据映射${\pmb Q}$确定映射 ${\pmb P}$在内伊马克沙克-音叉分岔点附近的范式表达首先考虑映射${\pmb Q }$的内伊马克沙克-倍化分岔的范式映射. 在临界值$ {\pmb \mu } = {\pmb \mu }_c$处,${\pmb D \pmb Q}({\pmb \mu })$满足下列假设:
C1. ${\pmb D\pmb Q}({\pmb \mu })$有一对共轭复特征值以及一个$-1$的实特征值同时位于单位圆上:$\lambda _{1,2}= \tilde {\lambda },\bar {\tilde {\lambda }} = {\rm e}^{\pm {\rm i}\tilde {\theta}}$,$\lambda _3 =-1$;其余特征值在单位圆内.
C2. $\dfrac{\partial \tilde {\lambda }({\pmb \mu }_c )}{\partial \mu _1 } \ne 0$,以及 $\dfrac{\partial \tilde {\lambda }({\pmb \mu }_c )}{\partial \mu _2 } \ne 0$,这是映射${\pmb Q }$的两参数簇的穿越条件;
C3. 非共振条件:$\tilde {\lambda }_{1,2}^n \ne 1$,$n = 1$,2,$\cdots$,6;且$\tilde {\lambda }_{1,2}^n \ne - 1$,$n = 4$,5.
则根据中心流形-范式理论,可以得到映射${\pmb Q}$在内伊马克沙克-倍化分岔点附近的范式表达[24]
| $ {u}' = - u + \tilde {a}_1 u^3 + \tilde {a}_2 uz\bar {z} + O((\left| u\right| + \left| z \right|)^5) $ | (25a) |
| $ {z}' = {\lambda }'_0 z + \tilde {b}_1 u^2z + \tilde {b}_2 z^2\bar {z} +O((\left| u \right| + \left| z \right|)^5) $ | (25b) |
式中系数$\tilde {a}_1 $,$\tilde {a}_2 $,$\tilde {b}_1 $,$\tilde {b}_2$的表达式以及推导过程见文献[24],且$u \in {\pmb R }^1$,$z \in {\pmb C }^1$.
根据${\pmb P } = {\pmb Q }^2$,把式(25)进行迭代,即得到映射${\pmb P }$的范式表达
| $ {u}' = u + a_1 u^3 + a_2 uz\bar {z} + O((\left| u \right| + \left| z\right|)^5) $ | (26a) |
| $ {z}' = \lambda _0 z + b_1 u^2z + b_2 z^2\bar {z} + O((\left| u \right| +\left| z \right|)^5) $ | (26b) |
式中$a_1 = - 2\tilde {a}_1 $,$a_2 = - \tilde {a}_2 (1 + \tilde {\lambda}\bar {\tilde {\lambda }})$,$b_1 = 2\tilde {b}_1 \tilde {\lambda }$,$b_2 =\tilde {b}_2 \tilde {\lambda }(1 + \tilde {\lambda }\bar {\tilde {\lambda}})$.
4 在内伊马克沙克-音叉分岔点附近的两参数范式开折当二维控制参数${\pmb \mu } = \left[{\mu _1 } {\mu _2 } \right]^{\rm T}$在临界参数值${\pmb \mu }_c $的邻域内变化时,映射${\pmb Q }$的内伊马克沙克-倍化分岔(即周期运动的霍普夫倍化分岔)含参数的范式映射为[24]
| $ {\pmb F }:{\pmb R }\times {\pmb C } \to {\pmb R }\times {\pmb C } \\ \left( \!\! \begin{array}{c} {u}' \\ {z}' \end{array}\!\! \right) = \left[\!\! \begin{array}{cc} { - 1} & 0 \\ 0 & \tilde {\lambda } \end{array}\!\! \right]\left(\!\! \begin{array}{c} u \\ z \end{array}\!\! \right) + \\ \qquad \left(\!\! \begin{array}{c} { - \varepsilon _1 u + \tilde {a}_1 u^3 + \tilde {a}_2 u\left| z \right|^2+ O\left[{(\left| u \right| + \left| z \right|)^5} \right]} \\ {\tilde {\lambda }(\bar {\varepsilon }_2 z + \bar {b}_1 u^2z + \bar {b}_2z\left| z \right|^2 + O\left[{(\left| u \right| + \left| z \right|)^5}\right]} \end{array}\!\! \right) $ | (27) |
式中
| $ \varepsilon _1 = \varepsilon _1 ({\pmb \mu }) = - \lambda _3 ({\pmb \mu }) - 1 = \\ \qquad - \dfrac{\partial \tilde {\lambda }_3 (\mu _1 ,\mu _2)}{\partial \mu _1 }\mu _1 - \dfrac{\partial \tilde {\lambda }_3 (\mu _1 ,\mu_2 )}{\partial \mu _2 }\mu _2 \\ \bar {\varepsilon }_2 = \bar {\varepsilon }_2 ({\pmb \mu }) = \tilde{\lambda }({\pmb \mu })\bar {\tilde {\lambda }}({\pmb \mu }) - 1 = \\ \qquad\bar {\tilde {\lambda }}\dfrac{\partial \tilde {\lambda }(\mu _1 ,\mu _2)}{\partial \mu _1 }\mu _1 + \bar {\tilde {\lambda }}\dfrac{\partial \tilde{\lambda }(\mu _1 ,\mu _2 )}{\partial u_2 }\mu _2 \\ \bar {b}_1 \approx \dfrac{b_1 }{\tilde {\lambda }} ,\quad\bar {b}_2 \approx \dfrac{b_2 }{\tilde {\lambda }} $ |
令$z = r {\rm e}^{{\rm i}\tilde {\theta }' }$,可转化为含参数的极坐标映射形式:$ \tilde {\pmb F}_\varepsilon : {\pmb R }^2\times {\pmb S }^1 \to{\pmb R }^2\times {\pmb S }^1$
| $ \left( \!\! \begin{array}{c} {x}' \\ {r}' \\ {\tilde {\theta }}'\end{array} \!\! \right) = \left(\!\! \begin{array}{c} {X(x,r,\tilde {\theta },\varepsilon )} \\ {R(x,y,\tilde {\theta },\varepsilon )} \\ {\varTheta (x,y,\tilde {\theta },\varepsilon )}\end{array} \!\! \right) = \\ \qquad \left(\!\! \begin{array}{c} { - x - \varepsilon _1 x + a_1 x^3 + a_2 xr^2 + h.o.t.} \\ {r + \varepsilon _2 r + \beta _1 x^2r + \beta _2 r^3 + h.o.t.} \\ {\tilde {\theta } + \arg \tilde {\lambda }_0 + \varepsilon _3 + \gamma _1x^2 + \gamma _2 r^2 + h.o.t.} \end{array} \!\! \right) $ | (28) |
式中,$\varepsilon _2 = \left| {1 + \bar {\varepsilon }_2 } \right| - 1$,$\varepsilon _3={\rm arg} (\bar \varepsilon_2)$,$\beta _1 ={\rm Re}(\bar {b}_1 )$,$\beta _2 = {\rm Re}(\bar {b}_2 )$,$\gamma _1 = {\rm Im}(\bar {b}_1 )$,$\gamma _2 = {\rm Im}(\bar {b}_2 )$.
根据${\pmb P } = {\pmb Q }^2$,考虑映射$ \tilde {\pmb F }_\varepsilon $的二次复合映射 ${\pmb F }_\varepsilon= \tilde {\pmb F }_\varepsilon ^2 $,并略去高阶项以及旋转方向的坐标,得到一个平面映射:${\pmb F }_\varepsilon: {\pmb R }^2 \to {\pmb R }^2$
| $ \left( \begin{array}{c} {x}' \\ {r}' \end{array} \right) = \left( \begin{array}{l} (1 + 2\varepsilon _1 )x - 2a_1 (1 + 2\varepsilon _1 )x^3 - \\ \qquad 2a_2 (1 +\varepsilon _1 + \varepsilon _2 )xr^2 \\ (1 + 2\varepsilon _2 )r + 2\beta _1 (1 + \varepsilon _1 + \varepsilon _2)x^2r + \\ \qquad 2\beta _2 (1 + 2\varepsilon _2 )r^3\end{array} \right) $ | (29) |
则映射(29)就是映射${\pmb P}$的内伊马克沙克-音叉分岔的范式映射的极坐标形式(略去高阶项以及旋转方向的坐标).
若不考虑不动点位置坐标的高阶项,则可以解得映射(29)的4个不动点,这4个不动点在映射${\pmb P}$和映射${\pmb Q}$的情 况下对应的类型列于表 1中.
| 表 1 映射(29) 的不动点以及P 和Q 所对应的吸引子类型比较 Table 1 The fixed points of (29) and the corresponded attractors of P and Q |
当$a_1 > 0$,$\beta _2 < 0$时,简化映射的局部分岔行为如图 2所示. 其它可能的符号选择与此类似. 图中
| $ L_1 :a_2 \varepsilon _2 + \beta _2 \varepsilon _1 = 0 hbox{或} \ a_1 \varepsilon _2 + \beta _1\varepsilon _1 = 0 \\ L_2 :a_1 \varepsilon _2 + \beta _1 \varepsilon _1 = 0 hbox{或} \ a_2 \varepsilon_2 + \beta _2 \varepsilon _1 = 0 $ |
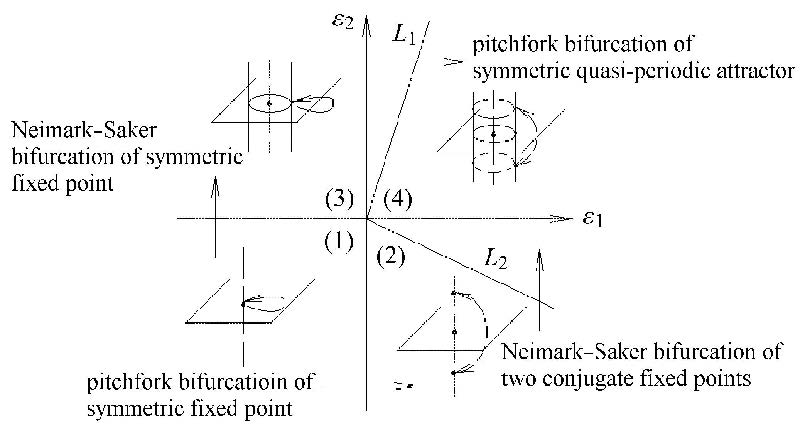
|
图 2 映射P 在内伊马克沙克-音叉分岔点附近的范式局部 两参数开折 Fig. 2 The local two-parameter unfolding near Neimark-Saker-pitchfork point the of the map P |
图 2中分为(1),(2),(3),(4) 4个区域,对于映射${\pmb P}$而言,吸引子类型分别为:对称不动点、共轭周期1点、对称拟周期吸引子(对称$ {\pmb T}^1$环面)、共轭拟周期吸引子(反对称${\pmb T}^1$环面).从区域(1)到区域(2)发生对称不动点的音叉分岔,从区域(1)到区域(3)发生对称不动点的内伊马克沙克-分岔,从区域(2)到区域(4)发生反对称不动点的内伊马克沙克-分岔,从区域(3)到区域(4)发生对称拟周期运动的音岔分岔. 对于映射${\pmb Q}$而言,这4种分岔分别为不动点的周期倍化分岔、不动点的内伊马克沙克-分岔、周期2点的内 伊马克沙克-分岔、环面倍化分岔.
5 在内伊马克沙克-音叉分岔点附近的局部两参数动力学数值分析考虑系统参数:$n =1$,$\zeta =0.008$,$R =0.85$,$h =0.08$,$u_{m1} =5$,$u_{m2} =2$,$u_{m3} = 1$,$u_{k1} =0.8$,$u_{k2} =1$,$u_{k3} =1$,$u_{f1} =0.49$,$u_{f3} = 1$. 取$\omega $和$u_{f2} $为系统控制参数:${\pmb \mu } = [\omega ,u_{f2}]^{\rm T}$. 当$ {\pmb \mu }_c = [\omega _c ,u_{f2c}]^{\rm T} = [1.143 880,0.378 724 003 6]^{\rm T}$时,庞加莱映射${\pmb P}$的雅可比矩阵${\pmb D \pmb P}({\pmb X}_0,{\pmb \mu }_c)$同时有一对复共轭特征值以及一个$+1$的实特征值位于单位圆上,其余特征值位于单位圆内,此时${\pmb \mu } =[\omega _c ,u_{f2c}]^{\rm T}$是映射${\pmb P}$的内伊马克沙克-音叉分岔临界参数值.对应的映射${\pmb Q }$的雅可比矩阵${\pmb D\pmb Q }({\pmb X }_0,{\pmb \mu }_c)$同时有一对复共轭特征值以及一个$-1$的实特征值位于单位圆上,因此${\pmb \mu } = [\omega _c ,u_{f2c}]^{\rm T}$又是映射${\pmb Q}$的内伊马克沙克-倍化分岔临界参数值. 取${\pmb \mu } = {\pmb \mu }_c + \Delta {\pmb \mu } = [\omega _c + \Delta \omega ,u_c + \Delta u_{f2}]^{\rm T}$,根据$\Delta {\pmb \mu } = [\Delta \omega ,\Delta u_{f2}]^{\rm T}$的取值讨论碰撞振动系统的庞加莱映射${\pmb P }$在内伊马克沙克-音叉分岔点处的各种复杂的局部动力学行为.
当$\Delta {\pmb \mu } = [0.006 618,0.02]^{\rm T}$时,根据系统参数计算出在图 2中落入区域(3),则碰撞振动系统的庞加莱映 射${\pmb P}$的对称不动点${\pmb X}_0$发生音叉分岔,得到庞加莱截面上的一对反对称不动点 (对于运动轨迹的相空间而言,为反对称周期吸运动),如图 3所示.此时,对于庞加莱映射${\pmb P}$而言,在不动点${\pmb X}_0 $上加上某个微小的初始扰动$\Delta {\pmb X}_0$进行迭代,迭代最终的收敛结果都将是两个反对称不动点${\pmb X}_\alpha $和${\pmb X}_\beta $其中之一.而对于映射${\pmb Q}$而言,不动点${\pmb X}_0 $发生倍化分岔,即:在不动点${\pmb X}_0 $上加微小的初始扰动$\Delta{\pmb X}_0 $进行迭代,偶数次迭代将会收敛于${\pmb X}_\alpha $,奇数次迭代收敛于${\pmb X}_\beta $(或相反).当$\Delta {\pmb \mu } = [0.006 616,0.02]^{\rm T}$时,根据系统参数计算出在图 2中落入区域(2),则对称不动点${\pmb X}_0$发生内伊马克沙克-分岔,得到庞加莱截面上的对称拟周期吸引子,如图 4所示.

|
图 3 庞加莱截面投影图:音叉分岔 Fig. 3 The projected Poncar′e section: pitchfork bifurcation |

|
图 4 庞加莱截面投影图:内伊马克沙克-分岔 Fig. 4 The projected Poncar′e section: Neimark-Saker bifurcation |
当$\Delta {\pmb \mu } = [0.006 617 25,0.02]^{\rm T}$时,根据系统参数计算出在图 2中落入区域(4),则对称不动点${\pmb X}_0 $发生内伊马克沙克-音叉分岔,得到庞加莱截面上的对称拟周期吸引子(对于运动轨迹的相空间而言,为对称${\pmb T}_1 $环面),如图 5所示. 此时的分岔序列是:不稳定的对称不动点${\pmb X}_0 \to $一对不稳定的共轭不动点${\pmb X}_\alpha $和${\pmb X}_\beta \to$一个对称的拟周期吸引子. 即: ${\pmb X}_0 $首 先经过音叉分岔收敛到共轭不动点${\pmb X}_\alpha $和${\pmb X}_\beta $,${\pmb X}_\alpha $和${\pmb X}_\beta$再分别经过内伊马克沙克-分岔收敛到两个拟周期吸引子上,而这两个拟周期吸引子在对称性的作用下刚好重合为一个对称拟周期吸引子. 以$\omega _{ P} ({\pmb X})$和$\omega _{ Q } ({\pmb X })$表示分别相点${\pmb X}$在映射${\pmb P}$和${\pmb Q}$的迭代下产生的$\omega $ 极限集. 如果$\omega _{ P } ({\pmb X }) = \omega _{ P} ({\pmb Q }({\pmb X }))$,则$\omega _{ P } ({\pmb X })$被定义为对称的$\omega $ 极限集. 即:如果$\omega $极限集等于其共轭极限集,则它是对称极限集. 显然,图 5中所示的拟周期吸引子满足上述关于对称极限集的定义.
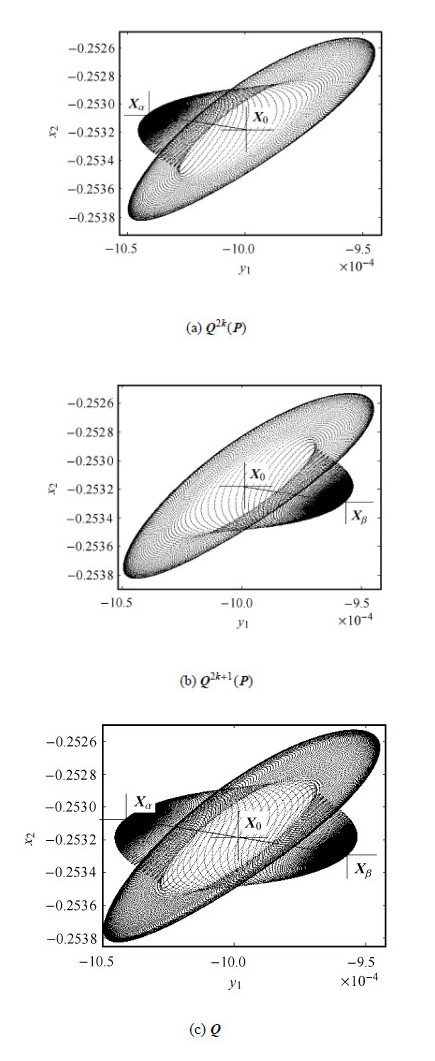
|
图 5 两个共轭不动点和一个对称的拟周期吸引子: 内伊马克沙克-音叉分岔 Fig. 5 Two conjugate fixed points and a single symmetric quasi-periodic attractor: Neimark-Saker-pitchfork bifurcation |
当$\Delta {\pmb \mu } = [-0.000 12,-0.000 8]^{\rm T}$时,根据系统参数计算出在图 2中落入区域(4),则对称不动点${\pmb X}_0 $发生内伊马克沙克-音叉分岔. 值得注意的是,此时映射的相图呈现出两个反对称${\pmb T}^2$环面,仍为两个共轭拟周期吸引子,如图 6所示.
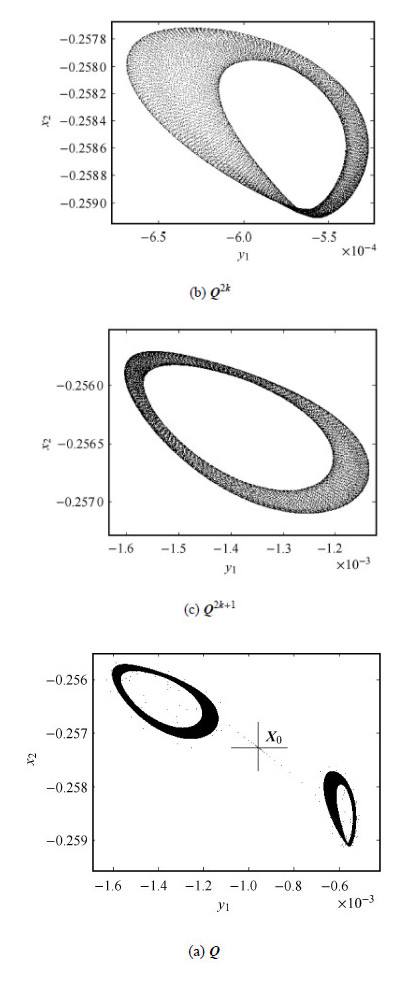
|
图 6 通过内伊马克沙克-音叉分岔产生两个共轭的拟周期吸引子: 一对共轭的T2 环面 Fig. 6 Two conjugated quasi-periodic attractors induced by Neimark-Saker-pitchfork bifurcation: a pair of conjugate T2 tori |
如果碰撞振动系统的庞加莱映射${\pmb P}$的雅可比矩阵同时有一对复共轭特征值以及一个+1的实特征值穿越单位圆,其余特征值位于 单位圆内,映射${\pmb P}$的对称不动点将会发生内伊马克沙克-音叉分岔,对应于映射${\pmb Q}$发生内伊马克沙克-倍化分岔. 利用隐式虚拟映射${\pmb Q}$,通过对范式作两参数开折分析,并结合数值模拟,详细讨论了映射${\pmb P}$在内伊马克沙克-音叉分岔点附近的复杂局部两参数动力学行为.
在内伊马克沙克-音叉分岔点附近,碰撞振动系统的局部动力学行为可能表现为庞加莱截面上的一个对称不动点、一对共轭不动点、一对共轭的拟周期吸引子或者单个的对称拟周期吸引子.当内伊马克沙克-音叉分岔发生时,一个对称不动点可能分岔出一对共轭的拟周期吸引子或者单个的对称拟周期吸引子.共轭的拟周期吸引子不仅可能以${\pmb T}^1$环面的形式出现,还可能以${\pmb T}^2$环面的形式出现.
虽然映射${\pmb P}$的内伊马克沙克-音叉分岔对应于映射${\pmb Q}$的内伊马克沙克-倍化分岔,内伊马克沙克-分岔和音叉分岔互相作用将会产生新的结果,而这正是碰撞振动系统的内在对称性质的表现.在图 5所示的情况下,最后的分岔结果是单个的拟周期吸引子,而不是一对共轭的拟周期吸引子,分岔序列为对称不动点(不稳定)$\to $两个共轭不动点(不稳定)$ \to $单个对称的拟周期吸引子(稳定).
| 1 | Guckenheimer J, Holmes P. Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields. New York: Springer, 1990 |
| 2 | 陆启韶.分岔与奇异性.上海:上海科技教育出版社, 1995 (Lu Qishao. Bifurcation and Singularity. Shanghai: Science, Technology and Education Press, 1995 (in Chinese)) |
| 3 | Kuznetsov YA. Elements of Applied Bifurcation Theory, The Second Edition. New York: Springer-Verlag, 1998 |
| 4 | Parker TS, Chua LO. Practical Numerical Algorithms for Chaotic Systems. Springer-Verlag, 1989 |
| 5 | 陈予恕,唐云.非线性动力学中的现代分析方法.北京:科学出版社, 2000 (Chen Yushu, Tang Yun. Modern Analysis Methods of Nonlinear Dynamics. Beijing: Science Press, 2000 (in Chinese)) |
| 6 | 罗冠炜,谢建华.碰撞振动系统的周期运动和分岔.北京:科学出版社, 2004 (Luo Guanwei, Xie Jianhua. The Periodic Motion and Bifurcations of Vibro-impact Systems. Beijing: Science Press, 2004 (in Chinese)) |
| 7 | 金栋平,胡海岩.碰撞振动与控制.北京:科学出版社, 2005 (Jin Dongping, Hu haiyan. Vibration and Control of Collision. Beijing: Science Press, 2005 (in Chinese)) |
| 8 | Holmes PJ. The dynamics of repeated impacts with a sinusoidally vibrating table. Journal of Sound and Vibration, 1982, 84 (2): 173-189 |
| 9 | Shaw SW, Holmes PJ. Periodically forced linear oscillator with impacts: Chaos and long-period motions. Physical Review Letters,1983, 51 (8): 623-626 |
| 10 | Shaw SW. A periodically forced piecewise linear oscillator. Journal of Sound and Vibration, 1983, 90(1): 129-155 |
| 11 | Shaw SW. The dynamics of a harmonically excited system having rigid amplitude constraints, Part 1: Subharmonic motion and local bifurcation. Journal of Applied Mechanics, 1985, 52: 453-458 |
| 12 | Shaw SW. The dynamics of a harmonically excited system having rigid amplitude constraints, Part 2: Chaotic motions and global bifurcations. Journal of Applied Mechanics, 1985, 52: 459-464 |
| 13 | Shaw SW. Forced vibrations of a beam with one-sided amplitude constraint: Theory and experiment. Journal of Sound and Vibration,1985, 92(2): 199-212 |
| 14 | Whiston GS. Global dynamics of a vibro-impacting linear oscillator. Journal of Sound and Vibration, 1987, 115(2): 303-319 |
| 15 | Bapat CN, Sankar S. Single unit impact damper in free and forced vibration. Journal of Sound and Vibration, 1985, 99 (1): 85-94 |
| 16 | Thompson JMT, Gha ari R. Chaos after period-doubling bifurcations in the resonance of an impact oscillator. Physics Letters A,1982, 91(1): 5-8 |
| 17 | Jin L, Lu QS, Twizell EH. A method for calculating the spectrum of Lyapunov exponents by local maps in non-smooth impacting systems. Journal of Sound and Vibration, 2006, 298: 1019-1033 |
| 18 | 金俐,陆启韶,王琪.双自由度非定点斜碰撞振动系统的动力学分析.应用数学和力学, 2005, 26(7): 810-818 (Jin Li, Lu Qishao, Wang Qi. Dynamic analysis of two-degree-of-freedom oblique impact system with non-fixed impact positions. Applied Mathematics and Mechanics, 2005, 26(7): 810-818 (in Chinese)) |
| 19 | Luo GW, Xie JH. Hopf bifurcation of a two-degree-of-freedom vibro-impact system. Journal of Sound and Vibration, 1998, 213(3):391-408 |
| 20 | Luo GW, Xie JH. Bifurcation and chaos in a system with impacts. Physica D, 2001, 148: 183-200 |
| 21 | Luo GW, Xie JH. Hopf bifurcation and chaos of a two-degree-offreedom vibro-impact system in two strong resonance cases. International Journal of Non-Linear Mechanics, 2002, 37(1): 19-34 |
| 22 | Xie JH, Ding WC. Hopf-Hopf bifurcation and invariant torus T2 of a vibro-impact system. International Journal of Non-Linear Mechanics,2005, 40: 531-543 |
| 23 | Ding WC, Xie JH. Torus T2 and its routes to chaos of a vibro-impact system. Physics Letters A, 2006, 349: 324-330 |
| 24 | Ding WC, Xie JH. Dynamical analysis of a two-parameter family for a vibro-impact system in resonance cases. Journal of Sound and Vibration, 2005, 287: 101-115 |
| 25 | Gan CB, Lei H. Stochastic dynamic analysis of a kind of vibroimpact system under multiple harmonic and random excitations. Journal of Sound and Vibrations, 2011, 330: 2174-2184 |
| 26 | Zhai HM, Ding Q. Stability and nonlinear dynamics of a vibration system with oblique collisions. Journal of Sound and Vibrations,2013, 332: 3015-3031 |
| 27 | Zhang YX, Luo GW. Torus-doubling bifurcations and strange nonchaotic attractors in a vibro-impact system. Journal of Sound and Vibrations, 2013, 332: 5462-5475 |
| 28 | Ding WC, Li GF, Luo GW, et al. Torus T2 and its locking, doubling, chaos of a vibro-impact system. Journal of the Franklin Institute,2012, 349: 337-348 |
| 29 | Kryzhevich S,Wiercigroch M. Topology of vibro-impact systems in the neighborhood of grazing. Physical D, 2012, 241: 1919-1931 |
| 30 | Du ZD, Li YR, Shen J, et al. Impact oscillators with homoclinic orbit tangent to the wall. Physical D, 2013, 245: 19-33 |
| 31 | Xu HD, Wen GL, Qin QX, et al. New explicit critical criterion of Hopf-Hopf bifurcation in a general discrete time system. Communication in Nolinear Science and Numerical Simulation, 2013, 18:2120-2128 |
| 32 | 冯进钤,徐伟.碰撞振动系统中周期轨擦边诱导的混沌激变.力学学报. 2013, 45(1):30-36 (Feng Jinqian, Xu Wei. Grazing-induced chaostic crisis for periodic orbits in vibro-impact systems. Chinese Journal of theoretic and applied mechanics, 2013, 45(1):30-36 (in Chinese)) |
| 33 | Yue Y, Xie JH. Symmetry of the Poncaré map and its influence on bifurcations in a vibro-impact system. Journal of Sound and Vibration,2009, 323: 292-312 |
| 34 | Yue Y, Xie JH. Lyapunov exponents and coexistense of attractors in vibro-impact systems with symmetric two-sided constraints. Physics Letters A, 2009, 373: 2041-2046 |
| 35 | Yue Y, Xie JH. Capturing the symmetry of attractors and the transition to symmetric chaos in a vibro-impact system. International Journal of Bifurcation and Chaos, 2012, 5(22): 1250109 |
| 36 | Yue Y, Xie JH. Neimark-Sacker-pitchfork bifurcation of the symmetric period fixed point of the Poncaré map in a three-degree-offreedom vibro-impact system. International Journal of Nonlinear Mechanics, 2013, 48: 51-58 |
| 37 | Luo GW, Zhang YL, Zhang JG. Dynamical behavior of a class of vibratory systems with symmetrical rigid stops near the point of codimension two bifurcation. Journal of Sound and Vibration, 2006,297: 17-36 |
| 38 | Luo GW, Zhang YL, Chu YD, et al. Codimension two bifurcations of fixed points in a class of vibratory systems with symmetrical rigid stops. Nonlinear Analysis: RealWorld Applications, 2007, 8: 1272-1292 |
 2016, Vol. 48
2016, Vol. 48
