2. 军械工程学院车辆与电气工程系, 石家庄 050003;
3. 军械工程学院基础部, 石家庄 050003;
4. 中国人民解放军78638部队, 什邡 618400
通过在基体材料中添加颗粒物形成复合材料是改良材料性能的常用方法.但由于颗粒物的加入,材料细观结构变得复杂,颗粒的相互 作用使材料有效性能、强度、韧性等性能预报变得相对困难.如果将材料中异性颗粒、微裂纹、孔洞等都视为夹杂,则颗粒复合材料问题可统称为夹杂问题.对于夹杂物问题,具有重要开创性意义的研究是1957年艾雪比(Eshelby)[1]证明了椭球夹杂中应力应变场均匀,并提出了等效夹杂理论.基于此,发展了多种材料性能预报方法,如自洽法[2, 3]、基于背应力的自洽法(Mori-Tanaka法)[4]、有效自洽法[5]及其相互作用直推估 计[6]等,精度和适应性不断提高.实际材料中,由于夹杂并非规则的椭球形,夹杂与基体的结合性能也有多种情况,因此,自艾雪比之后,围绕夹杂理论解的研究不断深入,近年来,单一夹杂物问题的应力应变场的理论解研究,逐渐发展到异形夹杂[7, 8, 9, 10, 11],边界滑移[12, 13, 14, 15],多层界面[16, 17]等条件下的解析解研究.
由于夹杂和基体材料性能的差异,夹杂边缘基体通常存在较强的应力集中效应,这种应力集中通常造成夹杂与基体的界面脱粘,界面裂纹扩展最终造成材料的破坏,因此,在夹杂材料的失效分析中应重点关注界面裂纹问题. 围绕材料脱粘的研究也有很多,主要致力于两方面:一是研究无穷大基体中单个夹杂产生界面脱粘时应力应变场的精确解如文献[18, 19, 20, 21, 22]等的研究,这类结果虽然理论作用明显,但当夹杂含量较高时(夹杂间平均距离小于夹杂直径),夹杂间相互作用强烈,上述单一夹杂的理论解直接用在实际材料性能分析中可能产生较大的误差;二是研究多夹杂条件下颗粒脱粘后的材料性能和损伤失效研究,由于多夹杂相互作用的复杂性,这类研究主要是采用有限元等数值方法[23, 24, 25]. 有限元等数值方法虽然在解决复杂结构问题方面能够绕开复杂的理论问题,具有突出的优势,对于特定的分析能够得到合理的结果,但是通常建模过程复杂,计算量大,且难以得到规律性的结论. 因此,多夹杂材料的细观力学分析仍是很有必要的,特别是将脱粘研究的两个方面有效结合起来的方法.
实际材料中,颗粒添加量一般较高,因此,夹杂间相互作用比较强烈,相互作用下要获得夹杂和基体中应力应变场的精确解是非常困难甚至是不可能的,目前相互作用问题简化成双夹杂问题[26, 27, 28, 29]进行研究. 多夹杂相互影响下,通常需要对实际材料进行结构简化和理论近似,建立一些等效结构和方法,胞元模型法结构模型简单,既能反映细观结构,又能代表宏观性能,并得到了不少解析解,是一种简单直观的等效方法,因此运用较多,而如何建立等效关系对模型的可靠性具有重要影响.
为在失效分析中运用胞元模型,同时又要尽量减小胞元模型中平均效应带来的偏差,通常的处理方法一种是将局部界面脱粘处理为整体界面脱粘,粒子或界面[30]平均刚度弱化,另一种是假设脱粘都是夹杂整个脱粘,但是只有部分夹杂脱粘[31],这两种处理方式都是用平均效果代替局部效果,便于直接运用均匀规则椭球的艾雪比张量. 还有是认为夹杂全部脱粘,但根据不同加载条件(拉、压)区别对待[32]. 鉴于上述处理经验,本文提出一种基于胞元模型平均作用下的局部场模型,对夹杂界面裂纹开裂进行分析. 在夹杂含量较高的多夹杂材料中,相互作用直推估计法(the interaction direct derivativeestimate,IDD)[6]是目前为止在有效性能预测方面精度最好且简单直观的理论模型,但在局部场方面有一定的局限性. 本文以精度较高的相互作用直推估计法为基础,计算残余应力和外载应力共同作用下含界面裂纹夹杂中平均应力,然后将夹杂置于无限大基体介质中,计算此时夹杂中达到同样应力状态时所需加载的远场应力,将此远场应力作为等效加载条件,在此等效加载条件下分析夹杂界面裂纹开裂情况,建立一种研究夹杂、界面裂纹相互作用平均效果下的界面裂纹等效胞元模型.
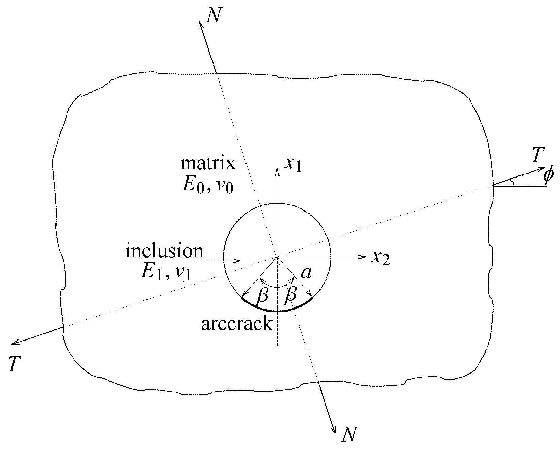
1 相互作用直推估下的等效加载应力场相互作用直推估计法是目前为止精度最高并且形式简洁的有效性能估计方法,含界面裂纹的相互作用直推估计法胞元结构模型如下:首先在含界面裂纹的夹杂周围取合适体积分数的基体材料氛围组成三相胞元,然后将三相胞元看作等效夹杂置于有效介质中,如图 1所示.有效介质具有复合材料的平均力学性能,而三相胞元具有几何位置的随机性,复合材料由三相胞元随机分布构成.

|
图 1 含随机三相胞元的四相模型 Fig. 1 The four phase model with random three-phase-cell |
根据相互作用直推估计法,假设材料受${\pmb \sigma}_\infty $应力作用,则胞元中夹杂周围基体介质和夹杂中应力分别为${\pmb \sigma}_0 $和${\pmb \sigma}_i $
| $ {\pmb \sigma}_0 = ({\pmb I}-{\pmb \varOmega}_{i} {\pmb H})^{- 1}{\pmb \sigma}_\infty $ | (1) |
| $ {\pmb \sigma}_i = \left( {{\pmb I}+{\pmb \varOmega}_i {\pmb H}_i } \right)^{ - 1}{\pmb \sigma}_0 $ | (2) |
其中
| $ {\pmb H }= \Big({\pmb I} - \sum {\pmb \varOmega}_{i} {\pmb H}_{i}^{\rm d} \Big )^{ - 1}{\pmb H}^{\rm d} $ | (3) |
| $ {\pmb H}_{i}^{\rm d} = \sum f_{i} ({\pmb H}_{i}^{ - 1}+ {\pmb \varOmega}_{i} )^{ - 1} $ | (4) |
| $ {\pmb H}^{\rm d} = \sum {\pmb H}_i^{\rm d} $ | (5) |
而含夹杂材料的等效刚度为
| $ {\pmb C} = ( {\pmb S}_0 +{\pmb H})^{-1} $ | (6) |
其中,所有的下标$i$表示第$i$类夹杂,下标0表示基体,${\pmb \varOmega}_i ={\pmb C}_{0} ({\pmb I}-{\pmb M}_{i} )$为夹杂的本征刚度,${\pmb H}_i = {\pmb S}_i - {\pmb S}_0$为夹杂相对基体的柔度波动,${\pmb I}$为单位张量,${\pmb C}_i $和${\pmb S}_i $为夹杂刚度矩阵和柔度矩阵,${\pmb S}_0 = {\pmb C}_0^{ - 1}$为基体柔度矩阵,${\pmb M}_{i}$为基体${\pmb C}_0$中夹杂相对应的艾雪比张量,可参考文献[33],$f_{i} $为颗粒体积含量.
根据相互作用直推估计法,如果基体中仅含颗粒(下标1)和界面裂纹(下标2)两类夹杂,则颗粒夹杂中平均残余应力为
| $ {\pmb \sigma}_1^{\rm t} = - {\pmb \varOmega}_1 \left( {{\pmb I} + {\pmb \varOmega}_1{\pmb H}_1 } \right)^{ - 1}{\pmb \varepsilon }_{10}^{\rm t} + \left( {{\pmb I} + {\pmb \varOmega}_1 {\pmb H}_1 } \right)^{ - 1}{\pmb \sigma}_0 $ | (7) |
| $ {\pmb \sigma}_0 ={\pmb \varOmega} \left( {{\pmb I} - {\pmb \varOmega} {\pmb H}}\right)^{-1}{\pmb \varepsilon } $ | (8) |
| $ {\pmb \varepsilon} = \left[{\pmb I } + \left( f_1 {\pmb \omega}_1 + f_2 {\pmb \omega}_2 \right) \left( {{\pmb I} - {\pmb \varOmega} {\pmb H}} \right)^{ - 1} \right]^{ - 1} \cdot \left( {f_1 {\pmb \omega}_1 {\pmb \varepsilon}_{10}^{\rm t} + f_2 {\pmb \omega}_2 {\pmb \varepsilon}_{20}^{\rm t} } \right) $ | (9) |
其中,${\pmb \varepsilon}_{{i}0}^{\rm t} = (T_0 - T_{\rm M} )( {\pmb \alpha}_{i}^{\rm t} - {\pmb \alpha }_0^{\rm t} )$为温度从$T_{\rm M} $变为$T_0 $时第$i$类夹杂与基体的失配热应变,${\pmb \alpha} _{i}^{\rm t}$为对应的热膨胀系数. 由于界面裂纹刚度为0,有${\pmb \omega}_2 = \left( {{\pmb I} + {\pmb \varOmega}_2 {\pmb H}_2 } \right)^{ - 1} = 0$,则式(9)为
| $ {\pmb \varepsilon} = \left[{{\pmb I} + f_1 {\pmb \omega}_1 \left( {{\pmb I} -{\pmb \varOmega} {\pmb H}} \right)^{ - 1}} \right]^{-1}f_1 {\pmb \omega}_1{\pmb \varepsilon}_{10}^{\rm t} $ | (10) |
考虑多夹杂相互作用时(界面裂纹也视为一类夹杂),运用相互作用直推估计法计算得到夹杂中平均应力应变场,以夹杂中平均应力应变场代表相互作用下夹杂中以及夹杂附近实际场,基于这个应力应变场研究界面裂纹的开裂情况.
根据相互作用直推估计法,对于无限大基体中椭球形夹杂,当夹杂中应力为${\pmb \sigma} _i$时,相当于在此夹杂周围无限大基体边界施加应力场
| $ {\pmb \sigma }'_\infty = {\pmb \omega }_1^{ - 1} {\pmb \sigma}_{i} = ({\pmb I} - {\pmb \varOmega}_i{\pmb H})^{-1 }{\pmb \sigma}_\infty $ | (11) |
正如Zheng等[5]所指出的那样,可以运用这个等效平均应力研究夹杂局部现象.
同理,仅存在残余应力${\pmb \sigma}_1^{\rm t} $时,${\pmb \sigma}_1^{\rm t}$相当于将夹杂置于边界条件为${\pmb \sigma}_\infty ^{\rm t} $的无限大基体中产生的应力,且
| $ {\pmb \sigma}_\infty ^{\rm t} = {\pmb \omega}_1^{ - 1} {\pmb \sigma}_1^{\rm t} $ | (12) |
因此,同时考虑外载应力和残余应力条件下,含界面裂纹夹杂相当于在等效应力边界条件${\pmb \sigma }_{\rm eff}^\infty $作用下的置于无限大基体中的单夹杂问题.
| $ {\pmb \sigma}_{\rm eff}^\infty = {\pmb \sigma }'_\infty + {\pmb \sigma}_\infty ^{\rm t} $ | (13) |
这样,就可以分别在${\pmb \sigma}_{\rm eff}^\infty $作用下,求得颗粒界面裂纹的应力强度因子,进而研究界面裂纹的开裂情况.
从上述过程可以看出,这种求夹杂附近基体中局部应力场的方法并非精确,实际上是在局部分析中将多夹杂相互作用的平均效应考虑了进去,对模型进行了适当的修正,使之更接近于实际情况.
2 界面裂纹开裂分析根据文献[18]中的推导,无限大平面基体中圆形颗粒夹杂界面裂纹尖端应力强度因子用复数形式表示如下
| $ K = K_{\rm I} - {\rm i}K_{\rm II} = \dfrac{1}{2}\sqrt {\dfrac{\pi}{a\sin \beta }} {\rm e}^{ - \lambda \beta }{\rm e}^{ -{\rm i}(\psi + \tfrac{\beta }{2})} \cdot \\ \qquad \left( { - {\rm i}a {\rm e}^{{\rm i}\beta }P_1 + P_0 +\dfrac{{\rm i}P_{ - 1} }{a{\rm e}^{ - {\rm i}\beta }} - \dfrac{P_{ - 2}}{a^2{\rm e}^{2{\rm i}\beta }}} \right) $ | (14) |
其中
| $ P_1 = P_{\rm 1r} + {\rm i}P_{\rm 1m} \\ P_{\rm 1r} = \dfrac{m(1 + \alpha )}{ 1 + m }\dfrac{(N + T)(1 + m) - (N - T)F\cos 2\phi }{\alpha (1 + 2m) - {\rm e}^{ - 2\lambda \beta }(\cos \beta +2\lambda \sin \beta )} \\ P_{\rm 1m} = - \dfrac{N - T}{1 + m}\dfrac{m(1 + \alpha )F\sin2\phi }{\alpha +{\rm e}^{- 2\lambda \beta }(\cos \beta + 2\lambda \sin \beta )} \\ F =(\cos \beta - 2\lambda \sin \beta )^2 + 2\lambda \sin 2\beta -\\ \qquad \lambda ^2(1 -\cos 2\beta ) - \dfrac{1 + 3\cos 2\beta }{4} \\ P_0 = {\rm i}aP_1 (\cos \beta + 2\lambda\sin \beta ) \\ P_{ - 2} = {\rm i}ma^3{\rm e}^{2\lambda \beta }\dfrac{1 + \alpha }{1 +m}(N - T){\rm e}^{2{\rm i}\phi } \\ P_{ - 1} = \dfrac{{\rm i}P_{ - 2} }{a}(\cos \beta -2\lambda \sin \beta ) \\ \alpha = \dfrac{E_0 + E_1 \kappa _0 }{E_1 + E_0 \kappa _1 } ,\ \ \lambda = \dfrac{ - \ln \alpha }{2\pi } \\ m = \dfrac{E_0 (1 + \kappa _1 )}{E_1 (1+ \kappa _0 )} ,\ \ \psi = \lambda \ln (2a\sin \beta ) \\ \kappa _0 = \dfrac{3 - v_0}{1 + v_0 } ,\ \ \kappa _1 = \dfrac{3 - v_1 }{1 + v_1 } \ \ \hbox{(平面应力)} \\ \kappa_0 = 3 - 4v_0 ,\ \ \kappa _1 = 3 - 4v_1 \ \ \hbox{ (平面应变)} $ |
式中,$E_0,E_1$,$v_0$,$v_1$分别为基体和夹杂的弹性模量和泊松比,$a$为夹杂的半径,$2\beta$为界面裂纹弧长在夹杂圆上对应的圆心角,$N$和$T$为正交的外载主应力,$\phi$为应力主轴和主坐标的夹角,如图 2所示.
如果是双向拉伸,即假设$T = N$,则
| $ K = N\sqrt { \pi a\sin \beta } P $ | (15) |
| $ P = \dfrac{(1 + \alpha )m(1 + 2{\rm i}\lambda ){\rm e}^{ - \lambda \beta }{\rm e}^{ - {\rm i}(\psi + \tfrac{\beta }{2})}}{\alpha (1 + 2m) - {\rm e}^{ - 2\lambda \beta}(\cos \beta + 2\lambda \sin \beta )} $ | (16) |
如果是单向拉伸,即$T = 0$且$\phi = 0$时
| $ K_{\rm I} = N\sqrt {\pi a\sin \beta } Q $ | (17) |
| $ Q = \dfrac{1}{2}\left [(D-1)\cos \dfrac{\beta }{2} +{\rm i} (D+1)\sin \dfrac{\beta }{2} \right] $ | (18) |
其中,$D = \dfrac{4 - \sin ^2\beta }{4[1 + \sin ^2(\beta / 2)]} + 2\cos \beta $.如果等效外载应力${\sigma }'_\infty $和等效残余应力$\sigma _\infty ^{\rm t}$产生的应力强度因子分别为$K_\infty = K_{{\rm I}\infty } - {\rm i}K_{{\rm II}\infty } $,$K_{\rm t} = K_{\rm It} - {\rm i}K_{ \rm II t} $,则界面裂纹尖端应力强度因子应当为
| $ K = K_\infty + K_{\rm t} $ | (19) |
下面以$y$方向的简单拉伸为例研究界面裂纹开裂引起复合材料失效的极限外载应力. 为便于应力强度因子公式的运用,将外载应力和残余应力的等效外载应力${\pmb \sigma }'_\infty $和${\pmb \sigma}_\infty ^{\rm t}$叠加后分解为双向等值部分和单向拉伸部分进行计算,平面条件下假设${\pmb \sigma}_{\rm r} = (\sigma _{\rm r11},\sigma _{\rm r22} ,0)^{\rm T}$为等效外载应力的叠加,即
| $ {\pmb \sigma}_{\rm r} = {\pmb \sigma}'_\infty + {\pmb \sigma} _\infty ^{\rm t} = {\pmb L}{\pmb \sigma}_\infty +{\pmb \sigma}_\infty ^{\rm t} $ | (20) |
其中${\pmb L}= ({\pmb I }- {\pmb \varOmega}_i {\pmb H})^{-1}$. 若材料受竖直方向(设为1方向)大小为${\pmb \sigma}_\infty $的简单拉伸,即
| $ {\pmb \sigma}_\infty = (\sigma _\infty ,0,0)^{\rm T} $ | (21) |
则
| $ \left.\begin{array}{l} \sigma _{\rm r11} = L_{11} \sigma _\infty + \sigma _{\infty 11}^{\rm t} \\ \sigma _{\rm r22} = L_{21} \sigma _\infty + \sigma _{\infty 22}^{\rm t} \end{array} \right \} $ | (22) |
令$\sigma _{\rm R} = \sigma _{\rm r11} $表示双向拉伸应力大小,$\sigma _{\rm T}= \sigma _{\rm r22} - \sigma _{\rm r11} $表示单向拉伸应力大小,则
| $ \left. \begin{array}{l} {\sigma _{\rm{R}}} = {\sigma _{{\rm{r22}}}} = {L_{21}}{\sigma _\infty } + \sigma _{\infty 22}^{\rm{t}}\\ {\sigma _{\rm{T}}} = ({L_{11}} - {L_{21}}){\sigma _\infty } + (\sigma _{\infty 11}^{\rm{t}} - \sigma _{\infty 22}^{\rm{t}}) \end{array} \right\} $ | (23) |
等效外载应力的应力强度因子可记为
| $ K = \sigma _{\rm R} P\sqrt { \pi a\sin \beta } + \sigma _{\rm T}Q\sqrt {\pi a\sin \beta } $ | (24) |
界面裂纹扩展的能量释放率由下式确定
| $ G = \dfrac{(b_0 + b_1 )K\bar {K}}{16\cosh ^2 (\pi \lambda) } $ | (25) |
式中,$b_0 = \dfrac{1 + \kappa _0 }{U_0 }$,$b_1 = \dfrac{1 + \kappa _1 }{U_1 }$,$U_0 $,$U_1$分别为基体和夹杂的剪切模量,$\bar {K}$为复相应力强度因子的共轭. 设$G_{\rm c} $为界面极限能量释放率,$G_{\rm c} = (1 - \upsilon _0^2 )K_{\rm Ic }^2 / E_0 $,令$G = G_{\rm c} $,将式(24)代入式(25),得到
| $ G_{\rm c} = \dfrac{(b_0 + b_1 ) \pi a\sin \beta }{16\cosh ^2 \pi \lambda } \cdot \\ \qquad \left[{\sigma _{\rm R}^2 P\bar {P} + \sigma _{\rm R} \sigma_{\rm T} (P\bar {Q} + \bar {P}Q) + \sigma _{\rm T}^2 Q\bar {Q}} \right] $ | (26) |
解上述方程即可得到由于界面裂纹开裂的极限外载应力$\sigma _{\rm c }$. 显然,上式为外载应力$\sigma _\infty $的一元二次方程,将上述方程改写为
| $ g_1 \sigma _\infty ^2 + g_2 \sigma _\infty + g_3 = 0 $ | (27) |
其中
| $ g_1 = P\bar {P}L_{21}^2 + (P\bar {Q} + \bar {P}Q)L_{21} (L_{11} - L_{21} ) + \\ \qquad Q\bar {Q}(L_{11} - L_{21} )^2 \\ g_2 = (P\bar {Q} + \bar {P}Q)[(L_{11} - L_{21} )\sigma _{\infty 22}^{\rm t} +L_{21} (\sigma _{\infty 11}^{\rm t} - \sigma _{\infty 22}^{\rm t} )] + \\ \qquad 2P\bar {P}L_{21} + 2Q\bar{Q}(L_{11} - L_{21} )(\sigma _{\infty 11}^{\rm t} - \sigma _{\infty 22}^{\rm t} ) \\ g_3 = P\bar {P}(\sigma _{\infty 22}^{\rm t} )^2 + (P\bar {Q} + \bar {P}Q)\sigma_{\infty 11}^{\rm t} (\sigma _{\infty 11}^{\rm t} - \sigma _{\infty 22}^{\rm t} ) + \\ \qquad (\sigma_{\infty 11}^{\rm t} - \sigma _{\infty 22}^{\rm t} )^2 - \dfrac{16[\cosh (\pi \lambda )]^2G_{\rm c} }{(b_0+ b_1 ) \pi a\sin \beta } $ |
解方程(27)得到界面裂纹开裂的极限外载应力$\sigma _{\rm c} $.
| $ \sigma _{\rm c} = \dfrac{\sqrt {g_2^2 - 4g_1 g_3 } - g_2 }{2g_1 } $ | (28) |
首先验证上述方法的有效性,这里通过对比本文方法计算和有限元模拟一定脱粘角度下的界面裂纹的能量释放率大小进行验证.在《ABAQUS》软件中建立含界面裂纹夹杂材料有限元结构模型如图 3(a)所示,其中图 3为双向拉伸下的材料模型,图 3(b)为界面裂纹张开后的情况,模型中安排了3行3列相同的含界面裂纹的夹杂,界面裂纹位于夹杂顶部.基体和夹杂刚度分别为$E_0 = 200$ GPa,$E_1 = 5E_0 $,$2\beta = 20^ \circ$,取夹杂半径为0.4 mm,夹杂面积比为0.126,材料单元选八结点四次平面应变四边形单元(CPE8).双向拉伸时得到界面裂纹尖端能量释放率为9.93 kPa$\cdot $mm,本文方法计算值为11.0 kPa$\cdot$mm,而取单个夹杂计算为12.4 kPa$\cdot $mm,单向拉伸下3个数据分别为10.1 kPa$\cdot $mm,10.8 kPa$\cdot$mm,11.8 kPa$\cdot $mm.可见本文的方法计算值介于有限元和单夹杂计算结果之间,更加接近实际结果,是一种有效的近似,夹杂刚度小于基体时也有相似的结果.

|
图 3 有限元材料模型和裂纹张开情况 Fig. 3 FEM model of material and its opening interface crack |
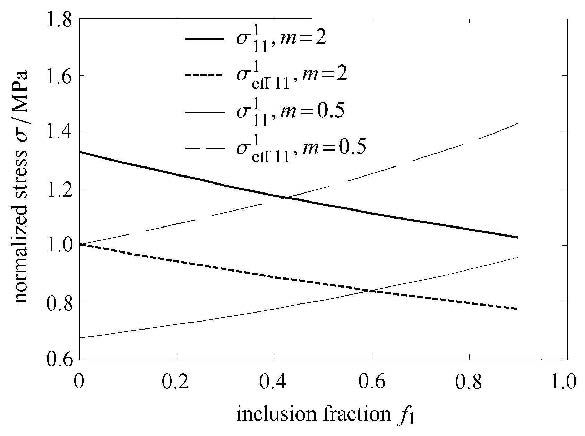
夹杂刚度、含量以及缺陷含量变化导致材料中应力重新分布. 假设基体弹性模量$E_0 =200$ GPa,夹杂弹性模量为$E_1 = mE_0 $,泊松比$v_0 = v_1 =0.25$,夹杂含量和界面裂纹含量变化时,基体中平均应力变化如图 4和图 5所示.
|
图 4 不同刚度夹杂中平均应力和等效外载应力 Fig. 4 Average stress in inclusion and effective applied loading with different inclusion stiffness |
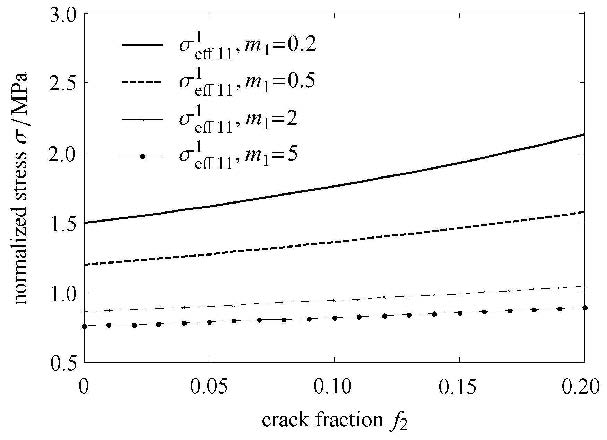
|
图 5 等效外载应力随界面裂纹含量增加而增大 Fig. 5 Effective applied loading increased with interface crack volume fraction |
图 4中可见,当夹杂刚度大于基体时,等效外载应力小于夹杂中平均应力,且随着夹杂含量增大而减小;而夹杂刚度小于基体时,等效外载应力大于夹杂中平均应力,并且随夹杂含量增加而增加.图 5中可见,当界面裂纹含量增加时,无论是刚性夹杂还是柔性夹杂,基体中等效应力都会随着界面裂纹含量增加而增加,原因在于,缺陷含量增加时,相当于造成了等效基体刚度的降低,夹杂中分担更多应力,造成等效外载应力增加.由于等效外载应力与界面裂纹尖端应力强度因子和能量释放率直接相关,相同的裂纹长度下,等效外载应力的增加将导致裂尖应力强度因子增加,因此,在此种失效形式下,增加刚性夹杂的加入量有利于降低裂纹尖端能量释放率,从而有利于提高 材料强度,而裂纹含量增加有相反的效果.
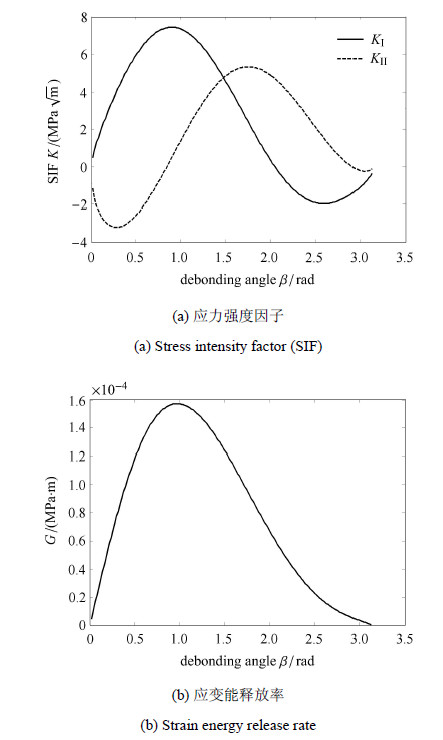
取夹杂直径为100 $\mu $m,假设界面裂纹沿夹杂界面扩展,取夹杂含量和界面裂纹含量分别为$f_1 = 0.4$,$f_2 = 0.001$,在$\sigma _\infty = 500$ N的单向拉伸作用下,应力强度因子随扩展角变化规律如图 6.
|
图 6 简单拉伸下应力强度因子和应变能释放率随脱粘角的 变化规律 Fig. 6 Variation of stress intensity factor (SIF) and strain energy release rate with crack angle β under simple tension |
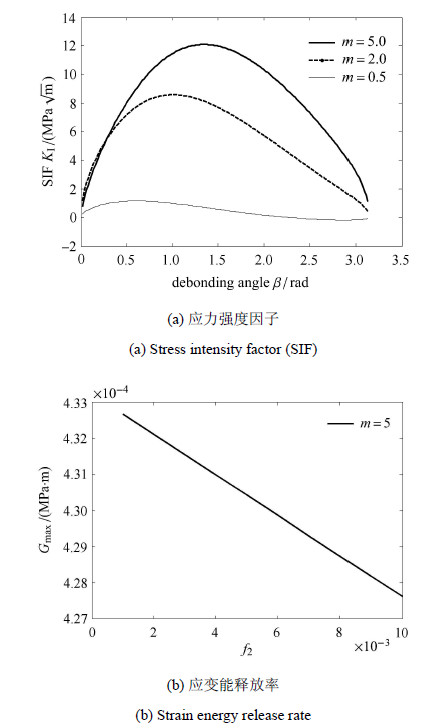
如图 6中所示,单向拉伸应力作用下,假设界面裂纹能一直沿着界面扩展直到夹杂完全脱粘,I型应力强度因子随着裂纹随着扩展角度的增加先增加后减小,在扩展角 $\beta \approx 1$ rad ($ < \pi/2$)时达到最大,之后逐渐降低,当角度扩大到一定程度($\beta \approx 2$ rad)后直至夹杂完全脱粘,应力强度因子甚至变为负值;II型应 力强度因子在$\beta \approx \pi /2$ rad达到最大,之后逐渐减小反向,能量释放率在扩展角接近于1 rad时达到最大值.
夹杂刚度对材料基体和夹杂中平均应力场的分布具有重要影响,假设夹杂弹性模量$E_1= mE_0 $,分别取不同的$m$值时,I型应力强度因子和最大能量释放率变化如图 7所示.

|
图 7 不同刚度夹杂在简单拉伸下应力强度因子和应变能释放率变化规律 Fig. 7 Variation of stress intensity factor (SIF) and strain energy release rate under simple tension of different inclusion stiffness |
如图 7所示,随着夹杂刚度的增加,I型应力强度因子逐渐减小,但裂纹尖端的最大能量释放率$G_{\max}$ (不同 $\beta $值下$G$的最大值)却是先增加再降低,在$m=0.7$附近达到最大值.因此,在此失效形式下,不考虑残余应力影响时,刚度略小于基体的夹杂最容易造成界面裂纹脱粘开裂,相对于基体刚度,柔性夹杂或刚性夹杂都有利于降低最大能量释放率,从而提高此失效模式下的材料强度.但是如图 7(b)所示,在残余应力影响下最大能量释放率却随着夹杂刚度增加单调增加,说明这种条件下高刚度夹杂有利于提高强度.
脆性材料夹杂和基体的刚度都比较大,制备反应温度较高,材料中残余应力一般比较大,界面裂纹开裂通常会释放一定的残余应力势能,使残余应力降低,界面裂纹造成的材料等效刚度下降同样会降低残余应力,因此,界面裂纹含量增加时,残余应力通常会减小,图 8中可以看出,最大能量释放率随裂纹含量增加而降低.
|
图 8 残余应力下应力强度因子和应变能释放率随 脱粘角的变化规律 Fig. 8 Variation of stress intensity factor (SIF) and strain energy release rate with crack angle β under residual stress |
从图 6 $\sim$图 8中可见,无论是简单拉伸还是残余应力作用下,裂纹扩展的能量释放率并不是随着裂纹扩展角增加而一直增大,因此,夹杂并不会发生完全脱粘.如果夹杂和基体热膨胀系数差别较大,夹杂和基体间存在较大的残余应力,夹杂界面初始裂纹长度大于某个值时,使得残余应力在界面裂纹尖端产生的应力强度因子大于界面开裂韧性,则在残余应力作用下此裂纹即可扩展开裂,因此对于弱界面,夹杂界面裂纹长度可能要么小于某个值,要么大于某个值,在这之间的初始界面裂纹在残余应力下自动扩展至一个较大的角度停止.
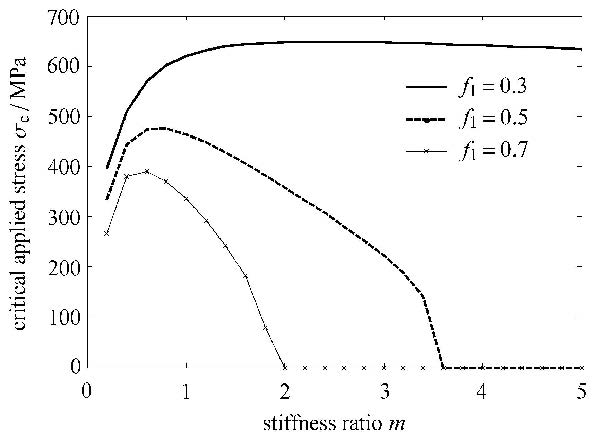
假设热膨胀系数$\alpha _{0}^{\rm t} = 5\times 10^{ - 6}$,$\alpha _{1}^{\rm t} = 10\times 10^{ -6}$,温度变化为$T_0 - T_{\rm M} = - 1 500{^\circ}$C. 基体韧性(界面韧性)$K_{\rm Ic} =10$ MPa$\cdot $ $\sqrt{\rm m}$,取夹杂含量和缺陷含量分别为$f_1 = 0.4$,$f_2 = 0.001$,取夹杂半径$a =100 \mu$m,设材料失效的极限外载应力为界面裂纹在能量释放率达到最大值时所需的外载应力,则极限外载应力随夹杂刚度变化关系如图 9所示.
|
图 9 不同刚度夹杂材料的界面裂纹开裂极限应力 Fig. 9 Critical applied stress for interface cracking in different inclusion stiffness |
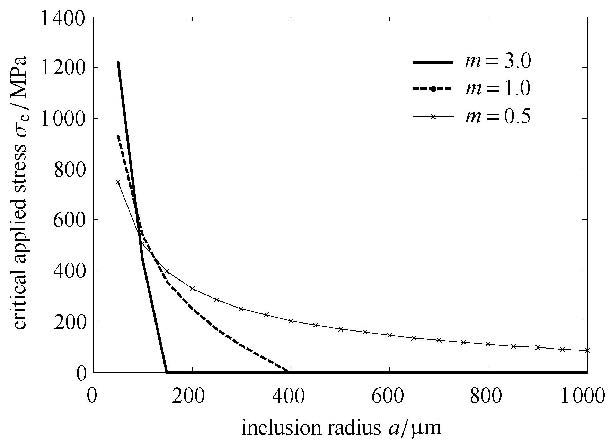
图 9中可以看出,存在残余拉应力的条件下,随着夹杂刚度增加,极限外载应力在夹杂刚度接近于基体刚度时达到最大值,当夹杂刚度较大时,极限外载应力甚至变为零,表明由于残余应力的作用,界面裂纹无需外加应力也会发生开裂.夹杂体积含量越高,强度越低,主要是夹杂含量增加时基体中残余应力增加的缘故.界面裂纹开裂极限应力与夹杂半径的平方根成反比,如图 10所示.
|
图 10 界面裂纹开裂极限应力随夹杂直径的变化规律 Fig. 10 Critical applied stress for interface cracking variation with inclusion diameter |
图 10中可看出,夹杂半径较小时(在本文设置的参数条件下半径$ < 100 \mu$m),较小刚度夹杂更容易造成界面裂纹开裂,而夹杂半径较大时($>100 \mu$m),刚度较大的夹杂半径较大时更易开裂. 因此,夹杂刚度越大,减小其半径就越有利于提高材料强度. 图 10中还显示,当夹杂尺寸增加到一定程度时,由于残余应力存在,有可能在没有外载应力情况下就发生裂纹开裂.
5 结 论基于相互作用直推估计法和等效夹杂理论,以夹杂中平均场作为标准求解多夹杂相互作用下等效加载条件,依据无限大圆形夹杂界面裂纹问题的理论解得到相互作用下界面裂纹开裂的极限外载应力,建立起一种考虑界面裂纹以及夹杂相互作用的界面裂纹开裂模型,并分析了不同参数对裂纹开裂条件的影响. 结果表明,在残余应力较小时,降低柔性夹杂刚度或者增大刚性夹杂刚度都有利于提高材料强度;残余应力较大时,夹杂刚度对强度影响比较复杂,但夹杂刚度较大时能明显提高界面开裂应力,夹杂尺寸的扩大对于材料强度提高是不利的.
| 1 | Eshelby JD. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc Royal Soc, 1957, A241: 376-396 |
| 2 | Hill R. A self-consistent mechanics of composite materials. J Mech Phys Solids, 1965, 13: 213-222 |
| 3 | Budiansky B. On the elastic modules of some heterogeneous materials. J Mech Phys Solids, 1965, 13: 223-227 |
| 4 | Mori T, Tanaka K. Average stress in matrix and average energy of materials with misfitting inclusion. Act Metal, 1973, 21: 571-574 |
| 5 | Zheng QS, Du DX. An explicit and universally applicable estimate for the e ective properties of multiphase composites which accounts for inclusion distribution. J Mech Phys Solids, 2001, 49(11): 2765-2788 |
| 6 | Du DX, Zheng QS. A further exploitation on the e ective selfconsistent scheme and IDD estimate for the e ective properties of multiphase composites which accounts for inclusion distribution. Acta Mech, 2001, 157(1-4): 61 |
| 7 | Kang H, Milton GW. Solutions to the Pólya-Szegö conjecture and the weak Eshelby conjecture. Archive for Rational Mechanics and Analysis, 2008, 188(1): 93-116 |
| 8 | Liu LP. Solutions to the Eshelby conjectures. Proceedings of the Royal Society of London A, 2008, 464: 573-594 |
| 9 | Zou WN, He QC, Huang MJ, et al. Eshelby's problem of nonelliptical inclusions. Journal of the Mechanics and Physics of Solids,2010, 58: 346-372 |
| 10 | Huang MJ, Wu P, Guan GY, et al. Explicit expressions of the Eshelby tensor for an arbitrary 3D weakly non-spherical inclusion. Acta Mech, 2011, 217: 17-38 |
| 11 | Xu BX,Wang MZ. Special properties of Eshelby tensor for a regular polygonal inclusion. Acta Mech Sinica, 2005, 21: 267-271 |
| 12 | Shodja HM. Shokrolahi-Zadeh B. Ellipsoidal domains: piecewise nonuniform and impotent eigenstrain fields. J Elasticity, 2007, 86:1-18 |
| 13 | Jasiuk I, Tsuchida E, Mura T. The sliding inclusion under shear. Int J Solids Struct, 1987, 23(10): 1373-1385 |
| 14 | Mura T, Jasiuk I, Tsuchida B. The stress field of a sliding inclusion. Int J Solids Struct, 1985, 21(12): 1165-1179 |
| 15 | Xu BX, Mueller R, Wang MZ. The Eshelby property of sliding inclusions. Arch Appl Mech, 2011, 81: 19-35 |
| 16 | Bonfoh N, Hounkpati V, Sabar H. New micromechanical approach of the coated inclusion problem: Exact solution and applications. Computational Materials Science, 2012, 62: 175-183 |
| 17 | Duan HL, Wang J, Huang ZP, et al. Eshelby formalism for nanoinhomogeneities. Mathematical, Physical and Engineering Sciences,2005, 461(2062): 3335-3353 |
| 18 | Prasad PBN, Simha KRY. Interface crack around circular inclusion: SIF, kinking, debonding energetics. Engineering Fracture Mechanics,2003, 70: 285-307 |
| 19 | Toya M. A crack along the interface of a circular inclusion embedded in an infinite solid. J Mech Phys Solids, 1974, 22: 325-348 |
| 20 | Chao R, Laws N. Closure of an arc crack in an isotropic homogeneous material due to uniaxial loading. Q Jl Mech Appl Math, 1992,45: 629-640 |
| 21 | Chen YZ, Chen RS. Interaction between curved crack and elastic inclusion in an infinite plate. Archive of Applied Mechanics, 1997, 67:566-575 |
| 22 | Chen JK,Wang GT, Yu ZZ, et al. Critical particle size for interfacial debonding in polymer/nanoparticle composites. Composites Science and Technology, 2010, 70: 861-872 |
| 23 | Moorthy S, Ghosh S. A Voronoi cell finite element model for particle cracking in elastic-plastic composite materials. Comput Methods Appl Mech Engrg, 1998, 151: 377-400 |
| 24 | Caballero A, López CM, Carol I. 3D meso-structural analysis of concrete specimens under uniaxial tension. Comput. Methods Appl Mech Engrg, 2006, (195): 7182-7195 |
| 25 | Wang D, Zhao J, Zhou Yonghui, et al. Extended finite element modeling of crack propagation in ceramic tool materials by considering the microstructural features. Computational Materials Science,2013, 77: 236-244 |
| 26 | England AH. An arc crack around a circular elastic inclusion. J Appl Mech, 1966, 32: 637-640 |
| 27 | 郭荣鑫, Lormand G, 李俊昌. 夹杂物问题应力场的数值计算. 昆明理工大学学报(理工版), 2004, 29(3): 51-55 (Guo Rongxin, Lormand G, Li Junchang. Numerical calculation of the stress field for the inclusion problem. Journal of Kunming University of Science and Technology(Science and Technology), 2004, 29(3): 51-55 (in Chinese)) |
| 28 | Shodja HM, Rad IZ, Soheilifard R. Interacting cracks and ellipsoidal inhomogeneities by the equivalent inclusion method. Journal of the Mechanics and Physics of Solids, 2003, 51: 945-960 |
| 29 | Li ZH, Yang LH. The application of the Eshelby equivalent inclusion method for unifying modulus and transformation toughening. International Journal of Solids and Structures, 2002, 39: 5225-5240 |
| 30 | Othmani Y, Delannay L, Doghri I. Equivalent inclusion solution adapted to particle debonding with a non-linear cohesive law. International Journal of Solids and Structures, 2011, 48: 3326-3335 |
| 31 | Lee HK, Pyo SH. Multi-level modeling of e ective elastic behavior and progressive weakened interface in particulate composites. Composites Science and Technology, 2008, 68: 387-397 |
| 32 | Hong T. Sti ness properties of particulate composites containing debonded particles. International Journal of Solids and Structures,2010, 47: 2191-2200 |
| 33 | Mura T. Micromechanics of Defects in Solids. 2nd edn. Martinus Nijho Publishers, 1987 |
2. Department of Vehicle and Electric Engineering, Ordnance Engineering College, Shijiazhuang 050003, China;
3. Department of Basic Course, Ordnance Engineering College, Shijiazhuang 050003, China;
4. Unit No.78638 of PLA, Shifang 618400, China
 2016, Vol. 48
2016, Vol. 48