热冲压成形技术,是将硼钢钢板(初始强度为500$\sim$600 MPa)加热至奥氏体化状态,快速转移到模具中高速冲压成形,在保证一定压力的情况下,制件在模具中以大于27℃/s的冷却速度进行淬火处理,保压淬火一段时间,以获得具有均匀马氏体组织的超高强钢零件的成形方式.
硼钢在热冲压过程中,材料内部存在的细观结构缺陷(如微裂纹、微孔洞等)会引起材料的损伤,这种由塑性变形导致的材料损伤会逐渐发展,最终引发材料的韧性断裂[1]. 目前对于损伤模型的研究有唯象法、微观-细观-宏观法等. 不同材料及不同的损伤过程的细观机制非常复杂,难以在力学模型上对其力学机制进行描述. 有人引入了"损伤因子"的概念[2],有人在研究金属蠕变 断裂时,首次引入"连续性因子"和"有效应力"的概念[3]. 在耦合型损伤模型中,损伤变量会对成形零件的机械性能产生影响,即材料的损伤与材料的性能相互影响. 有学者提出了多孔塑性模型[4, 5, 6, 7],材料的屈服表面取决于材料的密度. 损伤累积的过程表现为密度损失,反映了失效断裂前的初始阶段.
成形极限是冲压成形过程中一个非常重要的表征参数,它反映了冲压加工过程中,板料在塑性失稳前所能取得的最大变形程度,是各种不同成形工序能否顺利成形的重要依据. 文献[8, 9]分别用实验方法建立了成形极限图,广泛应用于生产实践,成为金属塑性成形工艺分析和模具设计的重要依据. 很多学者开展了广泛深入的实验研究,但是这不仅需要繁杂的实验,而且也受到实验条件(如模具的形状、尺寸、温度)和测量方法的影响,获得的实验数据一般比较分散,在一定程度上限制了该方法的推广应用. 随着损伤力学的不断完善,发现大多数金属材料的失稳和断裂与内部空洞在大塑性变形条件下的形核、长大及聚集过程密切相关[10],一些研究者开始用损伤的思想和方法来研究金属板料的失稳和断裂过程,并计算成形极限曲线. 有学者以热力学为基础提出了各向同性的三维塑性损伤模型并将其用于拉深工艺的成形极限分析[11]. 在以损伤力学为基础的成形极限研究中,如何建立更加符合实际的空洞生长模型和选择什么样的力学参数作为断裂判据成为关键问题.
本文将韧性损伤模型与有限元数值模拟技术结合 预测硼钢高温成形极限. 在原有的屈服函数和相关流动法则的基础上计算每一步的应力、应变场,采用与材料属性耦合的勒迈特韧性损伤模型,利用优化后的损伤因子准确预测板料成形过程的断裂现象. 根据硼钢热冲压成形的特点,选取裂纹出现作为成形极限的判断标准[12]. 本文在连续体损伤力学基础上,建立了考虑有效应力和等效塑性应变对微孔损伤影响的勒迈特韧性损伤模型演化方程. 为了准确反映硼钢在奥氏体状态下的成形特性,通过增加损伤变量$\alpha$,对经典的勒迈特耗散势函数进行了修正,结合硼钢高温成形特点,寻求一种简单准确的计算韧性损伤准则中材料损伤因子的方法,将本文建立的韧性损伤模型引入到硼钢板热冲压有限元数值模拟中,对硼钢高温凸模胀形实验的成形极限进行预测,并和实验结果相比较,进而评估所提出来的韧性损伤模型预测板料成形极限的可靠性.
1 勒迈特损伤模型 1.1 损伤变量从热力学角度看,损伤变量是表征材料微观结构改变状态的一种内变量,其物理含义是衡量材料损伤的程度[13]. 在变形体内任取一个损伤单元,该表面的单位法向量为$n$,则该处的损伤变量表示为
| $ D_n = \dfrac{S - \tilde {S}}{S} $ | (1) |
其中,$S$为损伤单元的截面积,$\tilde {S}$为材料损伤后损伤单元的有效承载截面积.
1.2 有效应力柯西应力表达式为$\sigma =F /S$,其中$F$为作用在截面上的力,$S$为截面面积. 在勒迈特损伤理论中,由于材料受到损伤,使有效承载面积变小,因此有效应力表示为
| $ \tilde {\sigma } = \dfrac{F}{\tilde {S}} $ | (2) |
其中,$\tilde {\sigma }$为有效应力,利用损伤变量和截面面积之间的关系式$\tilde {S} =S(1 -D)$,将损伤变量$D$引入到式(2)中得到新的表达式
| $ \tilde {\sigma } = \dfrac{F}{S(1 - D)} $ | (3) |
| $ E = E_0 \left( {1 - D} \right) $ | (4) |
其中,$ E_0 $为初始杨氏模量. 损伤变量$0 \leqslant D \leqslant 1$,当$D = 0$时表示材料尚未发生损伤,当$D =1$时表示材料断裂.
1.3 损伤演化方程通过严谨的热力学和细观力学分析,勒迈特提出了等效损伤应力概念[11]
| $ \sigma^{\rm D} = \sigma_{\rm eq } R_{\rm v}^{1/2} $ | (5) |
| $ R_{\rm v} = \dfrac{2}{3}\left( {1 + \nu } \right) + 3\left( {1 - 2\nu }\right){\left( {\dfrac{\sigma_{\rm m} }{\sigma_{{\rm eq}} }} \right)}^2 $ | (6) |
其中,$\sigma^{\rm D} $为等效损伤应力,$\sigma_{\rm eq} = \sqrt {\dfrac{3}{2} {\pmb s}:{\pmb s}} $为米塞斯(Mises)等效应力,${\pmb s}$是偏应力,$\sigma_{\rm m} $为静水压力,$\nu $为泊松比.式(5)由于引入了应力三轴度函数$R_{\rm v}$,从而表达出了损伤过程的物理机制:损伤受控于静水应力或应力三轴度,而且受主控塑性变形的等效应力和主控弹性体积变化的泊松比的影响[14].
损伤的不可逆耗散功率$Y$与损伤变量$D$关联[11]
| $ - Y = \dfrac{\sigma_{\rm eq}^2 }{2E{\left( {1 - D} \right)}^2 }\left[{\dfrac{2}{3}\left( {1 + \nu } \right) + 3\left( {1 - 2\nu } \right)\left( {\dfrac{\sigma_{\rm m}}{\sigma_{{\rm eq}} }} \right)^2 } \right] $ | (7) |
研究发现损伤耗散势函数不仅受不可逆耗散功率$Y$的影响,也由塑性应变所影响,因此耗散势函数是不可逆耗散功率$Y$和塑性应变的函数. 各向同性强化的前提下,耗散势函数包括两部分组成
| $ F = F_1 \left( {\sigma_{ij} ,R,D}\right) + F_{\rm D} \left( { - Y,p,D} \right) $ | (8) |
其中,$F_1 $是与材料屈服相关的塑性势,$F_{\rm D }$是与损伤有关的函数,$R$是与累积塑性应变$p$相关的强化应力.弹(黏)塑性 与损伤相耦合,采用米塞斯屈服准则,累积塑性应变$p$定义为等效塑性应变
| $p = \varepsilon _{{\rm{eq}}}^{\rm{p}} = \int {_0^t} \dot \varepsilon _{{\rm{eq}}}^{\rm{p}}{\rm{ d}}t $ | (9) |
从而获得等效塑性应变率
| $ \dot {\varepsilon }_{{\rm eq}}^{\rm p} = \sqrt {\dfrac{2}{3}\dot {\varepsilon }_{ ij }^{\rm p} \dot{\varepsilon }_{ ij }^{\rm p} } $ | (10) |
$\dot {\varepsilon }_{{\rm eq}}^{\rm p}$是等效塑性应变率,$\dot {\varepsilon }_{ ij }^{\rm p}$是应变率张量的塑性部分. 对于满足米塞斯屈服准则的材料,$F_1$ 表示为
| $ F_1 = \dfrac{\sigma_{{\rm eq}} - R}{1 - D} - \sigma_{\rm 0} = \sigma_{{\rm eq}}^{\rm \ast } - \sigma_{\rm y} $ | (11) |
其中,$\sigma_{\rm 0} $是初始屈服极限,$\sigma_{\rm y} $是当前屈服应力,表达为
| $ \sigma_{\rm y} = \dfrac{R}{1 - D} + \sigma_{\rm 0} $ | (12) |
根据塑性流动法则,获得本构方程和损伤演化规律
| $ \dot {\varepsilon }_{ ij }^{\rm p} = \dot {\lambda }\dfrac{\partial F_1 }{\partial\sigma_{ij} } = \dfrac{\dot {\lambda }}{1 - D}\dfrac{3{\sigma }'_{ij} }{2\sigma_{{\rm eq}} } $ | (13) |
| $ \dot {p} = \dot {\lambda }\dfrac{\partial F_1 }{\partial \left( { - R} \right)} =\dfrac{\dot {\lambda }}{1 - D} $ | (14) |
| $ \dot {D} = \dot {\lambda }\dfrac{\partial F_{\rm D} }{\partial \left( { - Y} \right)} $ | (15) |
由式(9)和(14)得知
| $ \dot {\lambda } = \left( {1 - D} \right)\dot {\varepsilon}_{{\rm eq}}^{\rm p} $ | (16) |
式(8)中的$F_{\rm D}$是勒迈特提出的与损伤有关的耗散势,并认为在塑性和损伤均为各向同性的情况下,其为$- Y$的非线性函数,$\dot {\varepsilon }_{{\rm eq}}^{\rm p}$(式(16))
| $ F_{\rm D} = \dfrac{S_0 }{\left( {b + 1} \right)}\dfrac{1}{\left( {1 - D} \right)}{\left( {\dfrac{ - Y}{ S_0}} \right)}^{b + 1} $ | (17) |
结合式(15),由此得到损伤演化方程为
| $ \dot {D} = {\left( { - \dfrac{Y}{S_0 }} \right)}^b \dot {\varepsilon}_{{\rm eq}}^{\rm p} = {\left( { - \dfrac{Y}{S_0 }} \right)}^b \dfrac{\dot {\lambda }}{1 - D} $ | (18) |
其中$S_0 $和$b$属于材料的损伤参数,其值与应变速率及温度大小有关,且当$\dot{\varepsilon }_{{\rm eq}}^{\rm p} { \geqslant \varepsilon }_{\rm D} $.
当等效塑性应变率小于阈值$\varepsilon_{\rm D} $时,$\dot{D} = 0$. 为了表征宏观断裂,引入损伤临界值$D_{\rm c}$,当损伤值$D = D_{\rm c} $时,令$D = 1$,模拟材料发生断裂.
在热冲压工艺中,硼钢22MnB5基本是处于奥氏体状态下成形的,因此在高温下具有优良的成形性能. 大量的"GLEEBLE"热模拟拉伸实验结果表明,在较高温度下进行拉伸实验获得的力-位移曲线变化更为平缓,表明材料有更好的塑性变形能力,材料的断裂随着塑性应变能力的增加而延迟. 如果采用式(17)的损伤相关耗散势无法准确描述材料的损伤演化规律. 为了准确反映硼钢在奥氏体状态下的成形特性,对经典的勒迈特损伤模型进行修正,通过增加损伤变量$\alpha $,对勒迈特耗散势函数进行修正
| $ F_{\rm D} = \dfrac{S_0 }{\left( {b + 1} \right)\left( {1 - D} \right)} {\left( {\dfrac{ - Y}{S_0 }} \right)}^{b + 1} {\left( {\dfrac{1}{\bar {\varepsilon }_{\rm p} }} \right)}^\alpha $ | (19) |
由此
| $ \dot {D} = \dot {\lambda }\dfrac{\partial F_{\rm D} }{\partial Y} = {\left( { - \dfrac{Y}{S_0 }}\right)}^b \dfrac{\dot {\lambda }}{1 - D}{\left({\dfrac{1}{\bar {\varepsilon }_{\rm p} }} \right)}^\alpha $ | (20) |
杨氏模量及泊松比与温度相关[15]. 在勒迈特损伤模型中,需要确定的参数有$\varepsilon_{\rm D} $,$S_0 $,$b$,$\alpha $和$D_{\rm c} $. 本文将采用优化算法确定参数的数值.
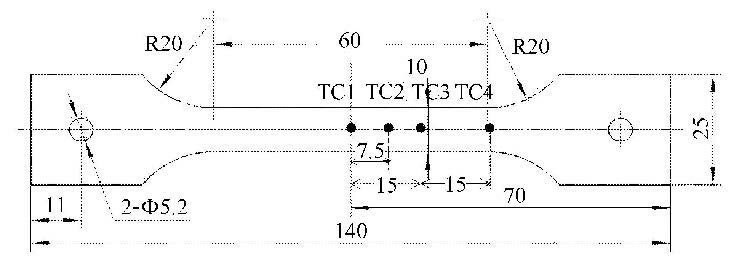
2 损伤模型优化 2.1 "GLEEBLE"热模拟拉伸试验利用"GLEEBLE"热模拟实验机获得拉伸试样在一定条件下的力-位移关系曲线,据此优化勒迈特损伤模型.试样形状如图 1所示. 试样材料为带 铝-硅镀层的硼钢22MnB5,材料成分见表 1 [16].实验在"GLEEBLE-1500"热模拟试验机上进行加热、拉伸及冷却.温度的测控采用K型镍/铬-镍热电偶,应变的测量采用"ARAMIS"光学应变测量系统.如图 1所示,为了记录温度沿试样长度方向的分布规律,4个热电偶按图示的位置焊接好.
|
图 1 试样形状及尺寸 Fig. 1 Schematic sketch and dimensions of tensile specimen |
| 表 1 22MnB5 试样成分 Table 1 Composition analysis of 22MnB5 steels (mass fraction) |
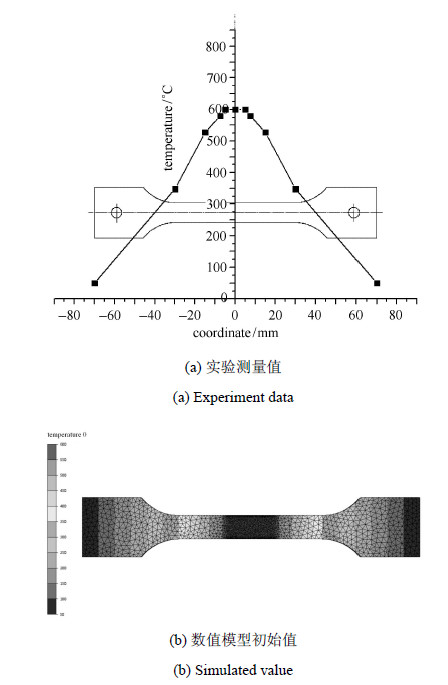
图 2为沿试样长度方向热电偶记录的温度分布曲线,可见在试样中央15 mm范围之内可以保障温度均匀分布.
|
图 2 试样在热拉伸前的温度分布 Fig. 2 Temperature distribution before tensile test |
为了准确描述硼钢在高温下塑性流动规律,采用汉森-斯皮特尔本构模型[17]来描述应力-应变关系曲线.
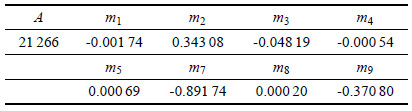
| $ \sigma = A {\rm e}^{m_1 T} \varepsilon^{m_2 } \dot {\varepsilon }^{m_3 } {\rm e}^{m_4/\varepsilon} {\left( {1 + \varepsilon } \right)}^{m_5 T} \cdot \\ \qquad {\rm e}^{m_7 \varepsilon }\dot {\varepsilon }^{m_8 T} T^{m_9 } $ | (21) |
其中,$\sigma $是流动应力,$\varepsilon $是等效应变,$\dot {\varepsilon }$是等效应变速率.利用非线性回归算法,根据热拉伸实验数据获得汉森-斯皮特尔模型各参数值如表 2所示.
| 表 2 汉森-斯皮特尔模型各参数值 Table 2 Values of Hensel-Spittel constitutive parameters |
图 3显示汉森-斯皮特尔模型与实验结果.

|
图 3 汉森-斯皮特尔模型与实验结果对比 Fig. 3 Comparison between the 22MnB5 experimental data and fitted ones through the Hensel-Spittel model |
采用反向分析法,将数值模拟结果与实验结果进行比对,同时修改各损伤变量值,直至比对结果满足要求. 具体优化步骤:
(1)定义损伤变量$\varepsilon_{\rm D} $,$S_0 $,$b$,$\alpha $和$D_{\rm c} $;
(2)选取优化算法-基于遗传算法的多目标优化算法NSGA-II [18];
(3)有限元分析软件《FORGE$^{\rm TM}$》模拟;
(4)执行实验和模拟获得的力-位移曲线比较程序;
(5)评估实验数据与模拟结果的相似度;
(6)修改损伤变量值返回步骤(2)直至(5)获得满足.
优化目标函数$\varphi $采用式(22),表示实验值与模拟值的差别
| $ \varphi = \dfrac{\sum\limits_i { {\left[{{\left( {y_i^{\exp } - y_i^{\rm num} } \right)}^2 \left( {x_i - x_{i - 1} } \right)}\right]}} }{\sum\limits_i { {\left[{{\left( {y_i^{\exp } } \right)}^2 \left( {x_i -x_{i - 1} } \right)} \right]} } } $ | (22) |
其中,$y$表示拉深力,$x$表示拉深方向的位移,$i$表示第$i$个数据点,$ y^{\exp } $为实验测定拉深力值,$y^{\rm num} $是模拟计算拉深力值.
当优化过程结束后,获得所需的损伤变量值,如表 3所示,其中损伤发生的阈值$\varepsilon_{\rm D} $取值0.01.
| 表 3 优化后的损伤值 Table 3 Values of damage parameters after optimization |
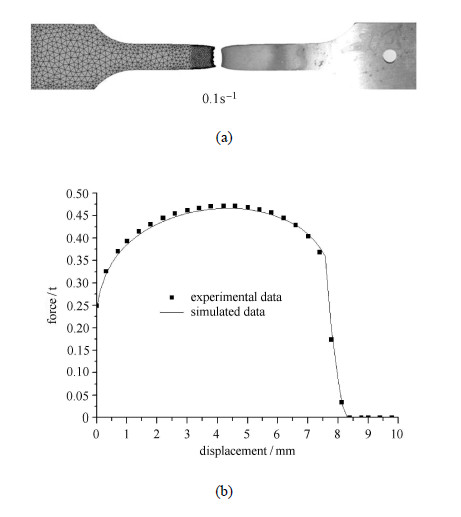
图 4(a)显示的是采用优化的损伤模型有限元模拟获得的试样断面与实验结果的对比,断面的几何形状吻合,符合韧性断裂特征.图 4(b)为两种情况下的位移-力曲线对比,可见模拟结果与实验结果高度吻合,较为真实地反映了试样拉伸过程由于损伤演化引起试样局部颈缩而导致的力曲线急剧下降过程.
|
图 4 有限元模拟结果与实验结果的比对 Fig. 4 Comparison between the experimental data and the simulation results |
为了测得硼钢在高温状态下的成形极限,在凸模胀形实验中需要将实验模具(包括凸模、凹模、压边圈)加热到指定温度,每种情况反复三次实验,费时费力.本节采用优化后的勒迈特损伤模型来预测硼钢热冲压成形极限,并与实验结果进行了比对.
3.1 高温凸模胀形试验图 5为开发的高温凸模胀形试验装置,实验过程:

|
图 5 凸模胀形试验装置 Fig. 5 Nakazima test experimental apparatus |
(1)利用电阻式加热棒将模具(包括凸模、凹模、压边圈)加热至指定温度,并在整个实验过程中保持恒温. 本实验选取实验温度为600℃为例说明;
(2)利用感性线圈将硼钢试样加热至900℃,并保温2$\sim$3 min至充分奥氏体化;
(3)利用安装在凹模面上的高压喷嘴将加热的硼钢试样快速($>50{^\circ}$C)冷却至600℃,确保冷却过程没有相变发生(奥氏体状态)[19];
(4)凸模以10 mm/s的速度进行拉深涨形,直至硼钢试样发生开裂(拉深力突然下降,停机).
3.2 高温凸模胀形实验成形极限曲线预测根据实验装置及实验步骤,建立了数值仿真模型. 试样被离散为四结点四面体单元,为了保证损伤模型的可靠性,变形区最小单元的尺寸与模型优化时的单轴拉伸模拟一样(0.4 mm). 其他刚性区的单元边长取较大值(4 mm)以提高计算效率,过渡区单元的尺寸取中间值(1 mm). 为了计算凸模与硼钢试样之间的传热,凸模认为是可变形体,并用9 981个4结点四面体单元进行离散. 凹模及压边圈不考虑与硼钢试样的传热及自身的变形,近似认为是刚体,因而采用三角形面单元进行离散. 整个成形过程模具的单元网格大小不变,而硼钢试样的网格则采用自适应网格重划分技术[20].
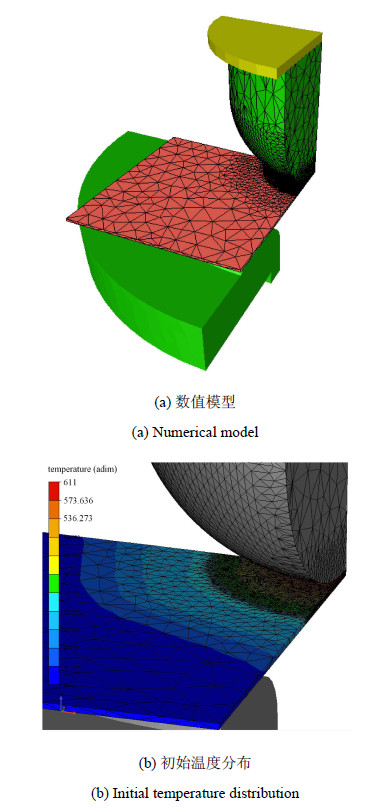
以200$\times $200双向等拉试样为例,由于模型的对称性,取1/4部分为研究对象,如图 6(a)所示.试样被离散为32 714个四 面体单元,并分别在$X$轴和$Y$轴施加对称约束.为了保证计算精度的前提下提高计算效率,变形区的单元最小边长为0.4 mm,压边圈周围的刚性区单元边长最小为4 mm,过渡区单元的大小为1 mm. 通过红外热成像系统测量拉伸试样的感应加热过程加热温度及拉伸之前试样初始温度分布情况.测量获得的温度分布导入数值仿真模型最为初始边界条件,如图 6(b)所示.
|
图 6 高温凸模双向等拉实验(1/4 部分) Fig. 6 Nakazima test in case of biaxial tensile experiment (one quarter) |
硼钢所采用汉森-斯皮特尔本构模型中各参数的取值见表 2,损伤模型中各参数的取值见表 3.
图 7所示为试样拉裂后的有限元模型(利用后处理镜像功能获得其他3/4部分).数值模拟过程显示,裂纹起始于凸模圆角区域,然后沿环向迅速扩展,待裂纹汇合后沿垂直于环向的方向扩展直至凸模停止运动.

|
图 7 高温凸模双向等拉实验拉裂后的数值模型 Fig. 7 Numerical fracture site of Nakazima test in case of biaxial tensile experiment |
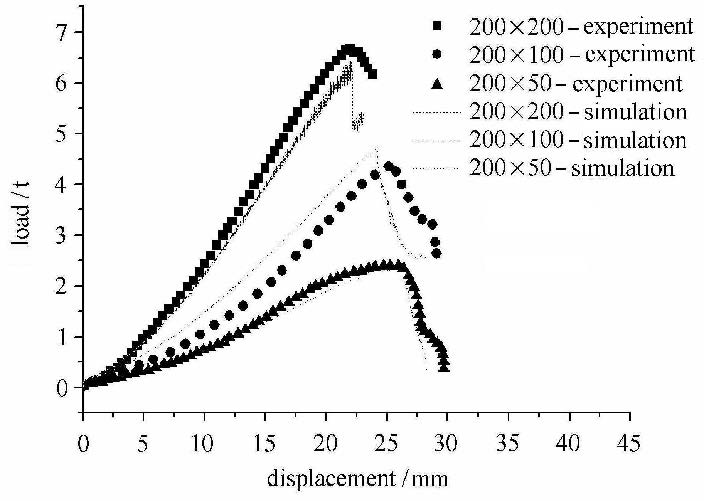
图 8为3.1节中高温凸模双向等拉实验获得的等拉实验样件,可见与压边圈贴合的部位没有变形,与球形凸模接触的区域变形剧烈,验证了高温凸模胀形数值模型中初始网格分布的合理性. 图 7中模拟的裂纹扩展路径与图 8试样断裂结果高度吻合.为了进一步验证所采用勒迈特损伤模型的可靠性,将模拟和实验获得的力-位移曲线进行比较,如图 9所示.采用优化后的损伤因子,勒迈特损伤模型可以较为准确地预测高温凸模胀形实验中力-位移变化规律,尤其是损伤断裂阶段力的急剧下降过程,吻合较好.由此可见,本文采用的勒迈特损伤模型能够较为准确地描述硼钢在高温条件下的变形规律,预测成性缺陷及损伤断裂过程.

|
图 8 高温凸模双向等拉实验拉裂试样 Fig. 8 Experimental fracture site of Nakazima test in case of biaxial tensile experiment |
|
图 9 凸模胀形试验中力-位移曲线对比 Fig. 9 Comparison between experimental and numerical load-displacement curves in Nakazima test |
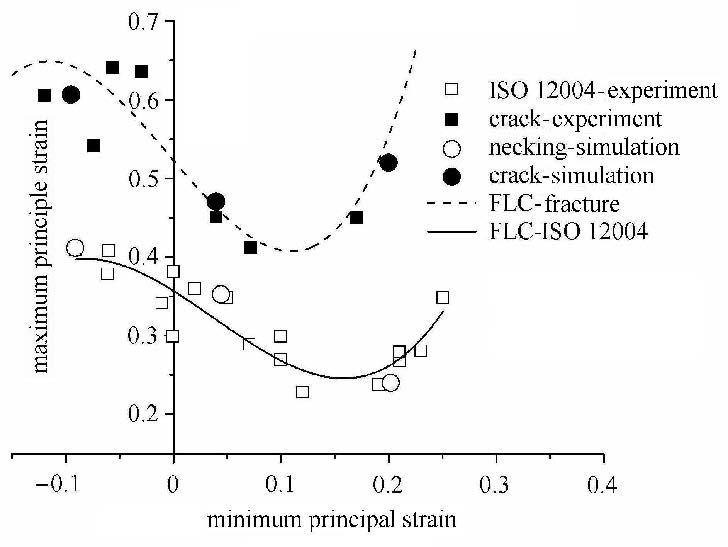
据此,可以根据数值模拟结果来获取硼钢热冲压成形的成形极限图(FLD).图 10所示为高温凸模胀形实验及采用数值方法获得的成形 极限图. 其中依据金属薄板材和带材成形极限曲线的测定标准ISO12004[21]测定的实验数据作为硼钢高温屈服判定依据.在数值模拟中,针对3个不同尺寸试样,当某单元的等效应力达到该温度及应变速率下的屈服应力时,获取到该单元的最大主应变和最小主应变,如图 10中的空心圆圈所示,从而获得高温屈服极限图(标记为FLD-ISO 12004).同理,当某单元的损伤值$D$达到临界损伤值(0.773)时,获取到该单元的最大主应变和最小主应变,如图 10中的实心圆圈所示,从而获得高温断裂极限图(标记为FLD-断裂).从获得的两种成形极限图分别与高温凸模胀形实验结果(实心和空心方格)对比可见,通过数值模拟方法,利用优化的勒迈特损伤模型 可以获得较为理想的成形极限图预测,为预测硼钢在高温状态下成形极限提供有益参考.
|
图 10 模拟与实验获得的成形极限曲线 Fig. 10 Comparison between experimental and numerically predicted FLCs at necking and fracture |
(1)推导了勒迈特韧性损伤模型的损伤演化方程,为了准确反映硼钢在奥氏体状态下的成形特性,通过增加损伤变量$\alpha $,对经典的勒迈特耗散势函数进行了修正. 提出在勒迈特损伤模型中,需要确定的参数有$\varepsilon_{\rm D} $,$S_0 $,$b$,$\alpha $和$D_{\rm c} $.
(2)提出了将韧性损伤模型与有限元数值模拟技术结合起来确定勒迈特损伤模型. 依据"GLEEBLE"热模拟拉伸实验获得的数据,利用优化算法获得与损伤有关的各参数$\varepsilon_{\rm D} $,$S_0 $,$b$,$\alpha $和$D_{\rm c}$的值. 并利用汉森-斯皮特尔本构模型准确描述了硼钢在高温下塑性流动规律.
(3)在数值模型中采用优化后的损伤变量,发现勒迈特损伤模型可以较为准确地预测高温凸模胀形实验中力-位移变化规律,尤其是损伤断裂阶段力的急剧下降过程,能够较为准确地描述硼钢在高温条件下的变形规律,预测成性缺陷及损伤断裂过程. 通过数值模拟结果与高温凸模胀形实验数据的对比可知,利用优化的勒迈特损伤模型可以获得较为理想的成形极限预测图,为预测硼钢在高温状态下成形极限提供有益参考.
致谢 感谢意大利帕多瓦大学提供《Transvalor FORGETM》软件模拟支持和实验支持.感谢国家留学基金委的项目支持.| 1 | 余寿文, 冯西桥. 损伤力学. 北京: 清华大学出版社, 1997: 1-6 (Yu Shouwen, Feng Xiqiao. Damage Mechanics. Beijing: Tsinghua University Press, 1997: 1-6 (in Chinese)) |
| 2 | Rabotnov YN. On the equations of state for creep. Progress in Applied Mechanics, 1963, 12: 307-315 |
| 3 | Kachanov LM. Introduction to Continuum Damage Mechanics. Netherlands: Martinus Nijho Publishers, 1986 |
| 4 | Kuhn HA, Downey CL. Deformation characteristic and plasticity theory of sintered powder materials. International Journal of Powder Metallurgy, 1971, 7(15): 78-88 |
| 5 | Tvergaard V. Influence of voids on shear bands instabilities under plane strain conditions. International Journal of Fracture, 1981,17: 389-407 |
| 6 | Tvergaard V. On localization in ductile materials containing spherical voids. International Journal of Fracture, 1982, 18: 157-169 |
| 7 | Tvergaard V, Needleman A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metallurgica, 1984, 32: 157-169 |
| 8 | Keeler P. Circular grid system—A valuable aid for evaluating sheet metal formability. SAE Transactions, 1968, (680092): 371-379 |
| 9 | Goodwin M. Application of strain analysis to sheet metal forming problems in the press shop. SAE Transactions, 1968, (680093): 380-387 |
| 10 | Gelin JC. Modeling of damage in metal forming processes. Journal of Materials Processing Technology, 1998, 80-81: 24-32 |
| 11 | Lemaitre J. A Course on Damage Mechanics. 3rd edn. New York: Springer-Verlag, 1998 |
| 12 | Tang CY, Chow CL. Development of a damage-based criterion for ductile fracture predictive in sheet metal forming. Journal of Materials Processing Technology, 1999, 91: 270-277 |
| 13 | 周筑宝, 卢楚芬. 连续损伤力学的几个基本问题. 湘潭大学自然科学学报, 1989, 11(4): 23-33 (Zhou Zhubao, Lu Chufen. Some basic problems in continuous damage mechanics. Natural Science Journal of Xiangtan University, 1998, 11(4): 23-33 (in Chinese)) |
| 14 | 马鑫, 钱乙余, Yoshida F. 相对损伤应力——Lemaitre等效损伤应力概念的修正及其在温度循环载荷下的应用. 自然科学进展,2001, 11(1): 86-89 (Ma Xin, Qian Yiyu, Yoshida F. Relative damage stress: Modification of Lemaitre e ective stress and its application in case of cycling temperature load. Progress in Natural Science,2001, 11(1): 86-89 (in Chinese)) |
| 15 | Lechler J, Merklein M, Geiger M. Determination of thermal and mechanical material properties of ultra high strength steels for hot stamping. Steel Research International, 2008, 2: 98-104 |
| 16 | Tang BT, Yuan ZJ, Cheng G, et al. Experimental verification of tailor welded joining partners for hot stamping and analytical modeling of TWBs rheological constitutive in austenitic state. Materials Science & Engineering A, 2013, 585(15): 304-318 |
| 17 | Hensel A, Spittel T. Kraft-und Arbeitsbedarf Bildsomer Formgeburgs Verfahren. Lipsk: VEB Deutscher Verlang für Grundsto ndustrie,1979 |
| 18 | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6: 182-197 |
| 19 | Turetta A, Bruschi S, Ghiotti A. Investigation of 22MnB5 formability in hot stamping operations. Journal of Materials Processing Technology, 2006, 177: 396-400 |
| 20 | Tang BT, Bruschi S, Ghiotti A, et al. Numerical modelling of the tailored tempering process applied to 22MnB5 sheets. Finite Elements in Analysis and Design, 2014, 81: 69-81 |
| 21 | ISO 12004-1:2008 金属材料薄板和薄带成形极限曲线的测定(第1部分): 冲压车间成形极限图的测量及应用, 2008 (ISO 12004-1:2008 Measurement and application of forming limit diagram in press shop (in Chinese)) |
 2016, Vol. 48
2016, Vol. 48