帘线增强橡胶基复合材料是由帘线增强相和橡胶基体经过有效复合而形成的一种柔性复合材料,广泛应用于轮胎、充气弹簧和传动带. 典型的子午线轮胎结构如图 1所示,胎体层主要由橡胶基体和钢丝帘线组成. 其基体是超弹性,可以大变形;帘线方向的拉伸模量远大于其他方向的拉伸模量而呈各向异性[1]. 发展一种合适的本构模型来准确表征轮胎在服役条件下的大变形、非线性、各向异性和高应变率等力学特性具有重要的理论意义和工程 应用价值.
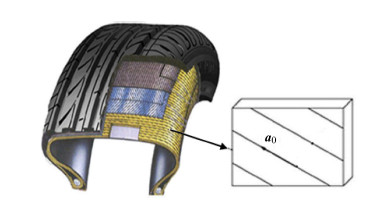
|
图 1 典型的子午线轮胎结构[1]:单层带束层帘线方向为${\pmb a}_0 $ Fig.1 Typical radial tire construction[1]:${\pmb a}_0 $ represents the direction of a single belt cord |
尽管在这一领域已经有很多研究成果,但都具有各自的局限性. 传统的线弹性理论不适用于大变形情况,无法解决材料非线性、几何非线性和边界非线性等多重耦合问题[1- 3]. 基于微观力学理论的哈尔平-蔡(Halpin-Tsai)方程虽然可以预测沿帘线方向的力学性能,但不能有效预测垂直帘 线方向的力学性能和面内剪切性能[4, 5, 6]. 加强筋模型[7, 8, 9]和横观各向同性超弹性模型[10, 11, 12, 13]忽略了帘线和橡胶基体间的相互作用,无法追踪帘线 角度变化下的力学行为. 考虑帘线和橡胶基体间相互作用的各向异性超弹性模型不能描述轮胎在服役工况下的冲击和高应变率效应[14, 15, 16, 17]. 近年来,一些学者分别针对帘线、橡胶及其复合材料进行了大量的实验研究,有利于理解其在大变形和高速冲击下的力学行为, 但没有进一步对其进行本构化建模[18, 19, 20]. 目前存在的黏-超弹性模型[21, 22, 23]在每一组应变率条件下都需要测定相应 的黏性系数,模型复杂导致参数确定困难,不具有普适性.
本文在作者前期提出的帘线/橡胶复合材料各向异性超弹性本构模型[1]的基础上,考虑轮胎在服役条件下的大变形、非线性和高应 变率等工况特点,建立一种能表征应变率效应的帘线/橡胶复合材料各向异性黏-超弹性本构模型.
1 各向异性黏--超弹性本构模型 1.1 本构模型的一般形式基于连续介质力学理论,对于黏性基体的纤维增强复合材料,应变能函数可以分解为超弹性应变能和黏性应变能两部分[24, 25, 26]
| $W\left( {C,\dot C,{a_0}} \right) = {W^{\rm{e}}}\left( {C,{a_0}} \right) + {\psi ^{\rm{v}}}\left( {C,\dot C,{a_0}} \right){\rm{ }}$ | (1) |
式中,${ C}$为右柯西-格林(Cauchy-Green)应变张量,$\mathop C\limits^. $为右柯西-格林应变率张量,${ a}_0 $为纤维的初始单位方向向量.
超弹性应变能$W^{\rm e}$可以表示为应变张量不变量$I_i$ $ \left( {i = 1,2,3,4,5} \right)$的标量函数,即
| ${W^{\rm{e}}}\left( {C,{a_0}} \right) = {W^{\rm{e}}}\left( {{I_1},{I_2},{I_3},{I_4},{I_5}} \right)$ | (2) |
右柯西-格林应变张量不变量分别为
| $ \left. \begin{array}{l} {I_1} = I:C = {\rm{tr}}\left( C \right)\\ {I_2} = \frac{1}{2}\left[{{{\left( {{\rm{tr}}C} \right)}^2} - tr{{\left( C \right)}^2}} \right]\\ {I_3} = \det \left( C \right)\\ {I_4} = {A_0}:C = {a_0} \cdot C \cdot {a_0} = \lambda _{\rm{a}}^2\\ {I_5} = {A_0}:{C^2} = {a_0} \cdot {C^2} \cdot {a_0} \end{array} \right\}$ | (3) |
式中,$I$为二阶单位张量,结构张量 ${A_0} = {a_0} \otimes {a_0}$.
黏性应变能$\psi^{\rm v}$也可以表示为应变率张量不变量$J_i \ \left( {i = 1,2,3,4,5} \right)$的标量函数,即
| $W\left( {{ C},\dot{ C},{ a}_0 } \right) = \psi^{\rm v}\left( {J_1 ,J_2 ,J_3 ,J_4 ,J_5 } \right)$ | (4) |
右柯西-格林应变率张量不变量分别为
| $\left. \begin{array}{l} {J_1} = I:\dot C = {\rm{tr}}\left( {\dot C} \right)\\ {J_2} = \frac{1}{2}\left( {I:{{\dot C}^2}} \right) = \frac{1}{2}{\rm{tr}}\left( {{{\dot C}^2}} \right)\\ {J_3} = \det \left( {\dot C} \right)\\ {J_4} = {A_0}:\dot C = {a_0} \cdot \dot C \cdot {a_0}\\ {J_5} = {A_0}:{{\dot C}^2} = {a_0} \cdot {{\dot C}^2} \cdot {a_0} \end{array} \right\}$ | (5) |
式中,$\lambda _{\rm a}$代表纤维(帘线)的拉伸比
.第二皮奥拉-基尔霍夫(Piola-Kirchhoff)应力张量${ S}$由超弹性应力张量${ S}^{\rm e}$和黏性应力张量${ S}^{\rm v}$两部分组成
| $\begin{array}{l} S = {S^{\rm{e}}} + {S^{\rm{v}}} = 2\left[{\frac{{\partial {W^{\rm{e}}}}}{{\partial C}} + \frac{{\partial {\psi ^{\rm{v}}}}}{{\partial \dot C}}} \right] = \\ \qquad 2\left[{\sum\limits_{i = 1}^5 {\left( {\frac{{\partial {W^{\rm{e}}}}}{{\partial {I_i}}}\frac{{\partial {I_i}}}{{\partial C}}} \right)} + \sum\limits_{j = 1}^5 {\left( {\frac{{\partial {\psi ^{\rm{v}}}}}{{\partial {J_j}}}\frac{{\partial {J_j}}}{{\partial \dot C}}} \right)} } \right] \end{array}$ | (6) |
超弹性应变能$W^{\rm e}$可以解耦为便于参数识别的基体等容变形能$W_{\rm m}^{\rm e} $、帘线拉伸应变能$W_{\rm f}^{\rm e} $和剪切应变能$W_{\rm shear} $三部分[14, 27]
| ${W^{\rm{e}}} = W_{\rm{m}}^{\rm{e}} + W_{\rm{f}}^{\rm{e}} + {W_{{\rm{shear}}}} = {V_{\rm{m}}}{W_{\rm{m}}} + {V_{\rm{f}}}{W_{\rm{f}}} + {W_{{\rm{shear}}}}$ | (7) |
式中,$V_{\rm m} $,$V_{\rm f} $分别为橡胶和帘线的体积百分比.
1.2.1 基体等容变形能函数假设基体为不可压缩材料,结合约(Yeoh)模型[28]和穆尼-里夫林(Mooney-Rivlin)模型[29],在不可压缩的假设下,纯橡胶基体等容变形能选用多项式函数
| ${W_{\rm{m}}} = {\rm{ }}\sum\limits_{i = 1}^2 {{C_{i0}}{{\left( {{I_1} - 3} \right)}^i}} + \sum\limits_{j = 1}^2 {{D_{j0}}{{\left( {{I_2} - 3} \right)}^j}} $ | (8) |
式中,基体材料参数$C_{i0} $和$D_{j0} $的单位均为MPa.
1.2.2 帘线拉伸应变能函数帘线的应变能与其拉伸有关,忽略其压缩应变能,则帘线拉伸应变能选用多项式函数[30]
| ${W_{\rm{f}}} = \left\{ \begin{array}{l} \sum\limits_{i = 2}^4 {{C_i}{{\left( {{I_4} - 1} \right)}^i}} ,\;{I_4}1\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;{I_4} \le 1\; \end{array} \right.\;$ | (9) |
式中,材料参数$C_i \ \left( {i = 2,3,4} \right)$的单位均为MPa.
1.2.3 帘线--橡胶剪切应变能函数忽略帘线和橡胶基体间的正剪切作用[17],角剪切应变能$W_{\rm shear} $可以表示为帘线和基体夹角变化$\varphi $的大小有关的函数[14],即
| ${W_{{\rm{shear}}}} = {W_{{\rm{shear}}}}({I_4},\chi ) = f({I_4})(a{\chi ^2} + b\chi ){\rm{ }}$ | (10) |
式中,$\chi = \tan ^2\varphi = \dfrac{I_4 }{I_3 }\left( {I_5 - I_1 I_4 + I_2 } \right)-1$[14]. 剪切性能参数$a$和$b$的单位均为MPa. 基于实验数据,剪切影响因子$f(I_4 )$可以表示为
| $f({I_4}) = \exp \left[{{c_1}\left( {{I_4} - 1} \right)} \right]{\rm{ }}$ | (11) |
式中,$c_1 $为无量纲参数.
1.3 黏性应变能函数的推导由帘线在不同应变率下的单向拉伸实验数据可知[18],帘线的应变率效应不明显,所以忽略其影响,只考虑基体黏性,则黏性应变能函数可表示为应变张量不变量和应变率张量不变量的函数,即
| ${\psi ^{\rm{v}}} = {\psi ^{\rm{v}}}\left( {{I_1},{J_1}} \right) = g\left( {{J_1}} \right){\rm{ }}\sum\limits_{i = 0}^2 {{\eta _i}{{\left( {{I_1} - 3} \right)}^i}} {\rm{ }}$ | (12) |
式中,$\sum\limits_{i = 0}^2 {{\eta _i}{{\left( {{I_1} - 3} \right)}^i}} $反映基体变形,黏性系数$\eta _0 $,$\eta _1 $和$\eta _2 $的单位均为MPa. 黏性影响因子$g\left( {J_1 } \right)$表征与率相关,为了满足准静态条件下$J_1 =0$时,$g\left( {J_1 } \right) = 0$的边界条件,构造了如下对数函数形式
| $g\left( {{J_1}} \right) = \ln \left( {{c_2}{J_1} + 1} \right){\rm{ }}$ | (13) |
式中,材料参数$c_2 $的单位为s.
1.4 帘线/橡胶黏--超弹性本构模型已经分别确定了基体等容变形能、帘线拉伸变 形能、剪切应变能和黏性应变能的函数形式,而且每一部分能量的物理意义都非常明确. 将式(7)$\sim $(13)代入式(6), 并令$W_i^{\rm e} = \dfrac{\partial W^{\rm e}}{\partial I_i }$,则得到超弹性应力张量${\pmb S}^{\rm e}$和黏性应力量${\pmb S}^{\rm v}$分别为
| $\begin{array}{l} {S^{\rm{e}}} = 2[\left( {W_1^{\rm{e}} + {I_1}W_2^{\rm{e}}} \right)I - W_2^{\rm{e}}C + W_4^{\rm{e}}{a_0} \otimes {a_0} + \\ \qquad W_5^{\rm{e}}\left( {{a_0} \otimes C \cdot {a_0} + {a_0} \cdot C \otimes {a_0}} \right)] \end{array}$ | (14) |
| ${S^{\rm{v}}} = 2{c_2}\ln \left( {{c_2}{J_1} + 1} \right)\left( {\sum\limits_{i = 0}^2 {{\eta _i}{{\left( {{I_1} - 1} \right)}^i}} } \right)$ | (15) |
通过最小二乘法拟合单轴拉伸和偏轴拉伸实验数据,可以确定本构模型参数,下面给出模型参数的确定方法:
(1) 拟合纯橡胶的准静态单轴拉伸实验数据得到橡胶的材料参数$C_{i0} $和$D_{j0} $.
(2) 拟合纯帘线的准静态单轴拉伸实验数据得到帘线的材料参数${C_i}{\rm{ }}\left( {i = 2,3,4} \right)$.
(3) 由(1)和(2)两步得到$C_i $,$C_{i0} $和$D_{i0} $后,拟合 准静态偏轴拉伸实验数据得到角剪切应变能密度函数$W_{\rm shear} $的参数$a$,$b$和$c_1 $.
(4) 根据前面3步得到的材料参数,拟合高应变率拉伸条件下的实验数据得到与率相关的黏性系数$\eta _0$,$\eta _1$和$\eta _2$ 和材料参数$c_2$.
2 本构模型的参数确定 2.1 模型应用于单轴拉伸对于不同帘线角度的单轴拉伸,如图 2所示,假设变形前帘线的单位方向向量为
| ${a_0} = \left[{\cos \alpha \;\;\sin \alpha \;\;0} \right]{\rm{ }}$ | (16) |
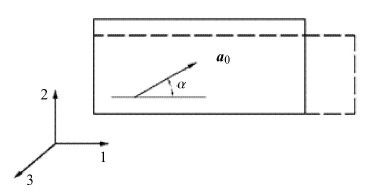
|
图 2 单层帘线/橡胶复合材料单轴拉伸变形 Fig.2 Uniaxial tensile deformation of one family of cord reinforced composites |
变形梯度张量${ F}$、格林应变张量${ C}$和应变率张量$\dot { C}$分别为
| $\left. \begin{array}{l} F = {\rm{dig}}\left[{{\lambda _1}\;\;{\lambda _2}\;\;{\lambda _3}} \right]\\ C = {F^{\rm{T}}} \cdot F = {\rm{dig}}\left[{\lambda _1^2\;\;\lambda _2^2\;\;\lambda _3^2} \right]\\ \dot C = {{\dot F}^{\rm{T}}} \cdot F + {F^{\rm{T}}} \cdot \dot F = {\rm{dig}}\left[{2{\lambda _1}{{\dot \lambda }_1}\;\;2{\lambda _2}{{\dot \lambda }_2}\;\;2{\lambda _3}{{\dot \lambda }_3}} \right] \end{array} \right\}$ | (17) |
式中,$\lambda _i $表示第$i$个主方向的拉伸比;不变量$I_1 $,$I_2 $,$I_3 $,$I_4 $,$I_5 $和$J_1 $的表达式为
| $\left. \begin{array}{l} {I_1} = \lambda _1^2 + \lambda _2^2 + \lambda _3^2\\ {I_2} = \lambda _1^2\lambda _2^2 + \lambda _2^2\lambda _3^2 + \lambda _1^2\lambda _3^2\\ {I_3} = \lambda _1^2\lambda _2^2\lambda _3^2\\ {I_4} = \lambda _1^2{\cos ^2}\alpha + \lambda _2^2{\sin ^2}\alpha \\ {I_5} = \lambda _1^4{\cos ^2}\alpha + \lambda _2^4{\sin ^2}\alpha \\ {J_1} = 2\left( {{\lambda _1}{{\dot \lambda }_1} + {\lambda _2}{{\dot \lambda }_2} + {\lambda _3}{{\dot \lambda }_3}} \right) \end{array} \right\}$ | (18) |
对于近似不可压缩材料的单轴拉伸变形,可将$I_5 - I_4 ^2$看作$\chi $的主要部分[14],即$\chi \approx I_5 - I_4 ^2$. 则沿拉伸方向的第二皮奥拉-基尔霍夫应力
| $\begin{array}{l} S_{11}^{\rm{e}} = 2[W_1^{\rm{e}}I + W_2^{\rm{e}}\left( {{I_1} - \lambda _1^2} \right) + \\ \qquad \left( {W_4^{\rm{e}} + 2W_5^{\rm{e}}\lambda _1^2} \right){\cos ^2}\alpha] \end{array}$ | (19) |
| $ S_{11}^{\rm{v}} = 2{c_2}\ln \left( {{c_2}{J_1} + 1} \right)\sum\limits_{i = 0}^2 {{\eta _i}{{\left( {{I_1} - 3} \right)}^i}} $ | (20) |
将第二皮奥拉-基尔霍夫(Piola-Kirchhoff)应力${ S}$转化为工程应力${ P}$
| $P = S \cdot {F^{\rm{T}}}$ | (21) |
由于缺少纯橡胶的单轴拉伸实验数据,因此忽略帘线与基体正剪切作用[14, 17],拟合与帘线方向垂直的准静态单轴拉伸实验数据[18],如图 3所示,可得到橡胶基体材料参数
| $\left. \begin{array}{l} {C_{10}} = 7.2449{\rm{MPa}},\quad {C_{20}} = 2.1952{\rm{MPa}}\\ {D_{10}} = - 3.6129{\rm{MPa}},\quad {D_{20}} = - 1.9871{\rm{MPa}} \end{array} \right\}$ | (22) |

|
图 3 横向单轴拉伸应力-应变曲线 Fig.3 Stress-strain curve of transverse tension |
拟合纯帘线准静态单轴拉伸实验数据[18],如图 4所示,可得到帘线材料参数
| ${C_2} = 12434{\rm{MPa}},\;{C_3} = 148{\rm{MPa}},\;{C_4} = 3{\rm{MPa }}$ | (23) |

|
图 4 帘线单轴拉伸应力-应变曲线 Fig.4 Uniaxial tensile stress-strain curve of pure cord |
得到基体材料参数$C_{i0} $和$D_{i0} $,帘线材料参数$C_i $以后,在体积百分比$V_{\rm m} = 0.8$和$V_{\rm f} = 0.2$的条件 下[18],将应变率为0.0033s$^{-1}$假设为准静态拉伸,拟合该应变率下与帘线成$45^\circ $夹角的 偏轴拉伸实验数据[18],如图 5所示,得到剪切性能参数
| $ a = 0.2743{\rm{MPa}},\;b = 0.3882{\rm{MPa}},\;{c_1} = - 0.6601{\rm{ }}$ | (24) |

|
图 5 应变率为0.0033s$^{-1}$和26s$^{-1}$的偏轴拉伸应力-应变曲线 Fig.5 Stress-strain curve of 45$^\circ$ off-axis tension under strain rate 0.0033s$^{-1}$ and 26s$^{-1}$ |
得到基体材料参数、帘线材料参数和剪切性能参数后,拟合应变率为26s$^{-1}$与帘线成$45^ \circ $夹角的偏轴拉伸实验数据[18],如图 5所示,得到与率相关的黏性应变能参数
| $\left. \begin{array}{l} {\eta _0} = 0.0157{\rm{MPa}},\;\;{\eta _1} = 0.0138{\rm{MPa}}\\ {\eta _2} = - 0.0038{\rm{MPa}},\;\;{c_2} = 5.2368{\rm{s}} \end{array} \right\}$ | (25) |
分别对应变率为1.2s$^{-1}$和 131s$^{-1}$和$g\left( {J_1 } \right) = 0$条件下对帘线呈$45^ \circ $角的偏轴拉伸进行预测,并将预测值与实验值[18]进行对比.
如图 6所示,应变率为1.2s$^{-1}$和131s$^{-1}$时,考虑黏性和不考虑黏性预测结果相差很大,且考虑黏性的预测结果与实验结果吻合度很好,不考虑黏性的预测结果与准静态下实验数据一致,因此证明了该帘线/橡胶复合材料各向异性黏-超弹性本构模型的准确性和有效性.
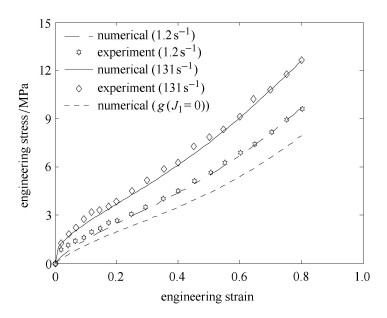
|
图 6 不同应变率下的偏轴拉伸应力-应变曲线 Fig.6 Stress-strain curve of 45$^\circ$ off-axis tension under different strain rates |
(1) 基于连续介质力学理论,提出了一种帘线/橡胶复合材料各向异性黏-超弹性本构模型来描述轮胎胎体层在服役条件下的大变形、非线性和高应变率力学行为.
(2) 单位体积的应变能被解耦为便于参数识别的基体等容变形能、帘线拉伸应变能、剪切应变能 和黏性应变能四部分,给出了模型参数的确定方法.
(3) 拟合出了本构模型参数,并验证了模型的准确性和有效性. 这一本构模型具有简单实用、材料参数容易确定的优点,为整体轮胎的动力学有限 元分析奠定了基础.
| 1 | 郭国栋, 彭雄奇, 赵宁. 一种考虑剪切作用的各向异性超弹性本 构模型. 力学学报, 2013, 45(3): 451-455 (Guo Guodong, Peng Xiongqi, Zhao Ning. An anisotropic hyperelastic constitutive model with shear interaction for cord-rubber tire composites. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3): 451-455 (in Chinese)) |
| 2 | Akasaka T, Kabe K, Sako K. Bending sti ness of a tire-belt structure with steel cords. Composites Science and Technology, 1985, 24(3):215-230 |
| 3 | Clark SK. Theory of the elastic net applied to cord-rubber composites. Rubber Chemistry and Technology, 1983, 56(2): 372-389 |
| 4 | A dl J, Kardos J. The Halpin-Tsai equations: A review. Polymer Engineering & Science, 1976, 16(5): 344-352 |
| 5 | Mansor M, Sapuan S, Zainudin E, et al. Rigidity analysis of kenaf thermoplastic composites using Halpin-Tsai equation. In: Proc. of Conference of in Applied Mechanics and Materials, 2014: 29-33 |
| 6 | Giner E, Vercher A, Marco M, et al. Estimation of the reinforcement factor for calculating E2 with the Halpin-Tsai equations using the finite element method. Composite Structures, 2015, 124: 402-408 |
| 7 | Helnwein P, Liu CH, Meschke G, et al. A new 3-D finite element model for cord-reinforced rubber composites—application to analysis of automobile tires. Finite Elements in Analysis and Design,1993, 14(1): 1-16 |
| 8 | Meschke G, Helnwein P. Large-strain 3D-analysis of fibrereinforced composites using rebar elements: Hyperelastic formulations for cords. Computational Mechanics, 1994, 13(4): 241-254 |
| 9 | Yanjin G, Guoqun Z, Gang C. 3-dimensional non-linear FEM modeling and analysis of steady-rolling of radial tires. Journal of Reinforced Plastics and Composites, 2011, 30(3): 229-240 |
| 10 | Itskov M, Aksel N. A class of orthotropic and transversely isotropic hyperelastic constitutive models based on a polyconvex strain energy function. International Journal of Solids and Structures, 2004,41(14): 3833-3848 |
| 11 | Brown LW, Smith LM. A simple transversely isotropic hyperelastic constitutive model suitable for finite element analysis of fiber reinforced elastomers. Journal of Engineering Materials and Technology,2011, 133(2): 021021 |
| 12 | Ciarletta P, Izzo I, Micera S, et al. Sti ening by fiber reinforcement in soft materials: A hyperelastic theory at large strains and its application. Journal of the Mechanical Behavior of Biomedical Materials, 2011, 4(7): 1359-1368 |
| 13 | 王友善, 王锋, 王浩. 超弹性本构模型在轮胎有限元分析中的应 用. 轮胎工业, 2009, 29(5): 277-282 (Wang Youshan, Wang Feng, Wang Hao. Application of hyperelastic constitutive models in finite element analysis on tires. Tire Industry, 2009, 29(5): 277-282 (in Chinese)) |
| 14 | Peng X, Guo Z, Moran B. An anisotropic hyperelastic constitutive model with fiber-matrix shear interaction for the human annulus fibrosus. Journal of Applied Mechanics, 2006, 73(5): 815-824 |
| 15 | Brieu M, Diani J, Bhatnagar N. A new biaxial tension test fixture for uniaxial testing machine-A validation for hyperelastic behavior of rubber-like materials. Journal of Testing and Evaluation, 2007,35(4): 364 |
| 16 | Aboshio A, Green S, Ye J. New constitutive model for anisotropic hyperelastic biased woven fibre reinforced composite. Plastics, Rubber and Composites, 2014, 43(7): 225-234 |
| 17 | Guerin HL, Elliott DM. Quantifying the contributions of structure to annulus fibrosus mechanical function using a nonlinear, anisotropic, hyperelastic model. Journal of Orthopaedic Research, 2007, 25(4):508-516 |
| 18 | Eiamnipon N, Nimdum P, Renard J, et al. Experimental investigation on high strain rate tensile behaviors of steel cord-rubber composite. Composite Structures, 2013, 99: 1-7 |
| 19 | Choi SS, Kim OB. Influence of specimen directions on recovery behaviors from circular deformation of polyester cord-inserted rubber composites. Journal of Industrial and Engineering Chemistry, 2014,20(1): 202-207 |
| 20 | Rao S, Daniel IM, Gdoutos EE. Mechanical properties and failure behavior of cord/rubber composites. Applied Composite Materials,2004, 11(6): 353-375 |
| 21 | Zhang F, Kuang Z, Wan Z, et al. Viscoelastic constitutive model of cord-rubber composite. Journal of Reinforced Plastics and Composites,2005, 24(12): 1311-1320 |
| 22 | Shim V, Yang L, Lim C, et al. A visco-hyperelastic constitutive model to characterize both tensile and compressive behavior of rubber. Journal of Applied Polymer Science, 2004, 92(1): 523-531 |
| 23 | Anani Y, Alizadeh Y. Visco-hyperelastic constitutive law for modeling of foam's behavior. Materials & Design, 2011, 32(5): 2940-2948 |
| 24 | Zhurov AI, Evans SL, Holt CA, et al. A nonlinear compressible transversely-Isotropic viscohyperelastic constitutive model of the periodontal ligament. In: Proc. of ASME 2008 International Mechanical Engineering Congress and Exposition, 2008: 707-719 |
| 25 | Spencer AJM. Continuum Theory of the Mechanics of Fibrereinforced Composites. New York: Springer, 1984 |
| 26 | Jiang Y, Wang Y, Peng X. A visco-hyperelastic constitutive model for human spine ligaments. Cell Biochemistry and Biophysics, 2015,71(2): 1147-1156 |
| 27 | 彭雄奇, 王宇. 腰椎椎间植骨融合有限元分析. 力学学报, 2011,43(2): 381-389 (Peng Xiongqi, Wang Yu. Finite elment analysis on lumbar interbody fusion. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3): 451-455 (in Chinese)) |
| 28 | Yeoh O. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chemistry and Technology, 1990,63(5): 792-805 |
| 29 | Holzapfel GA, Gasser TC. A viscoelastic model for fiber-reinforced composites at finite strains: continuum basis, computational aspects and applications. Computer Methods in Applied Mechanics and Engineering,2001, 190(34): 4379-4403 |
| 30 | Peng X, Guo Z, Du T, et al. A simple anisotropic hyperelastic constitutive model for textile fabrics with application to forming simulation. Composites Part B: Engineering, 2013, 52: 275-281 |
 2016, Vol. 48
2016, Vol. 48