2. 大连理工大学工业装备结构分析国家重点实验室/工程力学系, 大连 116023
将多孔固体近似为具有等效宏观材料常数的经典连续介质是研究多孔固体力学性能的主要方 法[1, 2]. 多孔固体结构通常由大量的微/细观子结构组成,基于工程需求,直接分析每一子结构细节既不现实也没有必要. 对于有序的多孔固体,如格栅材料、点阵材料等,利用其周期性特点,通过对代表性胞元分析获得等效连续介质的性质,在此基 础上得到多孔固体的宏观力学响应则较为经济. 目前,在经典连续介质力学理论的范围内,这一工作已较为成熟. 需要注意的是,等效经典连续介质力学模型的成功基于一个前提,即宏观结构的尺寸远大于多孔固体的单胞结构尺寸.
当多孔固体宏观结构的尺寸和单胞结构尺寸量级相近时,多孔固体的等效性能会随着试件或者结构的尺寸变化而产生变化,这一现 象称为尺寸效 应[3, 4]. 例如,数值计算发现,对于尺寸一定的层合多孔固体类梁或者类板结构,当梁/板的高度与多孔固体单胞尺寸相近时,等效的抗弯刚度会随着单胞尺寸的减小而产生变化并最终收敛于某一稳定值[5, 6, 7, 8, 9]. 这一现象也得到了实验支持[10]. 不仅如此,国内外学者对多孔固体等效性能分析的系列工作表明,不仅多孔固体的等效弯曲性能具有尺寸效应,等效面内/外剪切性能、自振性能、声波及电磁波吸收性能等方面均会表现出尺寸效应[11, 12, 13, 14, 15, 16, 17, 18, 19].
考虑尺寸效应的一个主要方法是采用广义经典连续介质理论来描述多孔固体的等效性能. 对多孔固体结构的所有单胞结构进行 完全的离散化也可以准确模拟尺寸效应,但是由于高昂的计算成本而很难推广,通常,完全离散模型的结果多用来作为标准解以检验其他方法的准确性. 广义连续介质理论从不同的角度对经典连续介质理论进行修正,目前应用最广的主要包括:考虑变形非局部化特征的应变梯度理论,考虑转动平衡的微极理论,以及在这两类理论基础上衍生的其他理论. 关于广义连续介质理论更深入的介绍,可查阅文献 [20, 21, 22]. 若在应变梯度理论中仅考虑转角的梯度,或者在微极理论中假定宏观转角和微观转角相等,便得到了偶应力理论[17, 23],偶应力理论是最简单的广义连续介质理论. 广义连续介质理论在描述由于材料的微/细观结构非均匀性所引起的尺寸效应方面的作用已经获得了认可[24, 25, 26, 27, 28].
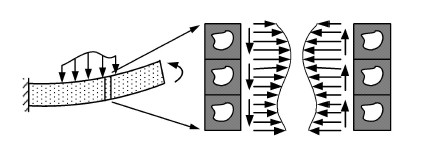
作为最简单的广义连续介质理论,偶应力理论是考虑多孔固体结构等效性能尺寸效应的重要工具. 将具有微结构的材料等效为偶应力连 续介质,可以有效地模拟其等效弯曲性能随单胞尺寸的变化关系. 图 1给出了一多孔固体类梁结构的变形示意图,因梁的高度与材料单胞的尺寸相近,相邻单胞之间的应力梯度效应变得不可忽略. 该应力梯度发生于单胞尺度之内,等效经典连续介质模型并未考虑,因此无法给出准确的计算结果;而等效偶应力连续介质模型则在经典模 型均匀单胞应力的基础上通过叠加一偶应力,较好地模拟了单胞尺度内的应力梯度. 文献[17]比较了偶应力理论和一般微极理论对平面非规则蜂窝材料的尺寸效应描述,发现在等效性能的表征方面,偶应力模型的效果优 于一般微极理论.
|
图 1 多孔固体类梁结构变形示意图 Fig.1 Sketch of the deformation of a cellular solid beam-like structure |
考虑到多孔固体结构或部件的实际工作环境,多孔固体的宏观等效动力学性能的研究更为重要. 然而,与静力学行为相比,多孔固体 的动力学行为的研究却远远不够,尤其是对等效动力学行为的尺寸效应的讨论. 对于一维多孔固体结构,即类梁结构,等效动力学弯曲行为下的尺寸效应表现得非常突出. 目前,为数不多的研究表明,当多孔固体单胞尺寸和梁的高度尺寸处于同一量级时,忽略单胞的尺寸大小将无法准确获得梁的自振频率、振型以及与此相关的其他力学响应[14, 15].
我们前期也开展了一些相关工作,将多孔固体均质化为具有等效力学性能的偶应力连续介质,并借助于剪切梁理论[29]以及有限元方法求解了等效介质的自振频率,发现:类梁结构的横向自振频率结果依赖于单胞结构的尺寸,而纵向振动则没有明显的尺寸效应;当类梁结构的高度与等效介质的特征长度之比高于20时,等效偶应力模型和等效经典连续介质模型的结果非常接近;随着梁高度方向单胞数量的减小,振动变形的边界效应愈发显著,并影响到频率计算的精度[16]. 但是,限于剪切梁忽略转动惯量的局限性,前期工作仅求解了前4阶的弯曲振动频率,且未研究等效模型对多孔固体类梁结构的振型描述.
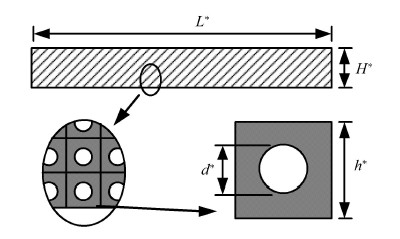
基于前期工作,本文将从频率和振型两方面系统研究多孔固体类梁结构的等效偶应力连续介质动力学模型. 在计算多孔固体等效偶应力介 质材料常数的基础上,将材料常数应用于连续介质梁理论建立等效的偶应力介质梁模型,分析多孔固体结构的自由振动特性. 研究对象限定为具有如图 2所示的单胞构型的一类典型多孔固体材料,这类材料具有显著的偶应力特性[30];将研究单胞尺寸、 孔径相对大小等参数对等效模型精度的影响;为了弥补剪切梁理论的不足,将采用具有更高精度的铁木辛柯 梁[29, 31]模型,并讨 论类梁结构的长高比对等效梁模型有效性的影响;考虑到等效经典模型和偶应力模型在类梁结构纵向振动描述方面结果一致的特点,将只研究类梁结构的横向弯曲振动.
|
图 2 一类多孔固体类梁结构及单胞构型 Fig.2 A typical cellular solid beam-like structure and its unit cell |
偶应力连续介质理论[23]引入了附加的转动自由度,因此描述变形的量除了传统介质的应变之外,还存在微曲率. 不妨以平面 应力问题为例,应变 $\varepsilon_{x}$,$\varepsilon _{y}$,$\gamma_{xy}$和微曲率$\kappa_{xz}$, $\kappa_{yz}$分别定义为
| $\left. \begin{align} & {{\varepsilon }_{x}}=\partial u/\partial x,\quad {{\varepsilon }_{y}}=\partial v/\partial y,\quad {{\gamma }_{xy}}=\partial u/\partial y+\partial v/\partial x \\ & {{\kappa }_{xz}}=\partial \phi /\partial x,\quad {{\kappa }_{yz}}=\partial \phi /\partial y \\ \end{align} \right\}$ | (1) |
其中,$u$,$v$,$\phi $分别表示面内的位移和转角.
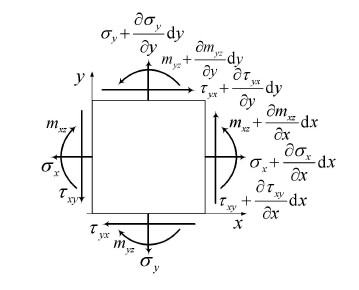
相应的,在单元体上也存在和微曲率对应的偶应力分量(图 3). 若不计体力和体力偶,应力$\sigma_{x}$,$\sigma_{y}$, $\tau_{xy}$,$\tau_{yx}$和偶应力$m_{xz}$,$m_{yz}$之间的需要满足的动力学微分方程为
| $\left. \begin{align} & \frac{\partial {{\sigma }_{x}}}{\partial x}+\frac{\partial {{\tau }_{yx}}}{\partial y}=\rho \frac{{{\partial }^{2}}u}{\partial {{t}^{2}}} \\ & \frac{\partial {{\tau }_{xy}}}{\partial x}\ +\frac{\partial {{\sigma }_{y}}}{\partial y}=\rho \frac{{{\partial }^{2}}v}{\partial {{t}^{2}}} \\ & \frac{\partial {{m}_{xz}}}{\partial x}+\frac{\partial {{m}_{yz}}}{\partial y}+{{\tau }_{xy}}-{{\tau }_{yx}}=\Theta \frac{{{\partial }^{2}}\phi }{\partial {{t}^{2}}} \\ \end{align} \right\}$ | (2) |
|
图 3 平面问题的应力和偶应力分量 Fig.3 Components of stress and couple-stress in a planar problem |
式中,$\rho $和 $\Theta $分别表示偶应力介质的密度和微转动惯量. 由方程可见,在偶应力连续介质理论中, 剪应力互等定理并不成立.
对于正交各向异性材料,材料的本构关系为
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\sigma _x}\\ {\sigma _y}\\ {\tau _S} \end{array} \end{array}} \right\} = \left[ \begin{array}{l} {C_{11}}\;\;{C_{12}}\;\;\;0\\ {C_{12}}\;\;{C_{22}}\;\;\;0\\ 0\;\;\;\;\;\;0\;\;\;{C_{66}} \end{array} \right]\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\varepsilon _x}\\ {\varepsilon _y}\\ {\gamma _{xy}} \end{array} \end{array}} \right\}\\ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {m_{xz}}\\ {m_{yz}} \end{array} \end{array}} \right\} = \left[ \begin{array}{l} {D_{11}}\;\;\;0\\ 0\;\;\;\;\;{D_{22}} \end{array} \right]\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\kappa _{xz}}\\ {\kappa _{yz}} \end{array} \end{array}} \right\} \end{array} \end{array}} \right\}$ | (3) |
也可写为如下的紧凑形式
| $\sigma =C\varepsilon ,m=D\kappa $ | (4) |
若材料的单胞结构具有中心对称的几何性质,则会展现正交各向异性的力学性质. 注意式(3)中,$\tau _S = {\left( {\tau _{xy} + \tau _{yx} } \right)} /2$表示剪应力的对称部分,通常认为,剪应力的对称部分产生经典的剪应变而反对称部分则对材料的变形不产生贡献[23]. 材料的本构矩阵${\pmb D}$的各元素依赖于材料的微结构尺寸. ${\pmb D}$的元素与传统本构矩阵${\pmb C}$的元素作比,并开平方,可以获得以长度为量纲的量,基于此,可以为偶应力介质定义不同的特征长度参数,以表征材料的尺度影响[6, 22-23]. 例如,正交各向异性偶应力介质的常用的特征长度有4个[16, 32],分别定义为
| $\left. \begin{align} & {{l}_{G1}}=\sqrt{{{B}_{11}}/G},\ {{l}_{E1}}=\sqrt{2\left( 1+{{\mu }_{21}} \right){{B}_{11}}/{{E}_{11}}} \\ & {{l}_{G2}}=\sqrt{{{B}_{22}}/G},\ {{l}_{E2}}=\sqrt{2\left( 1+{{\mu }_{12}} \right){{B}_{22}}/{{E}_{22}}} \\ \end{align} \right\}$ | (5) |
其中各工程常数为
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{E}_{11}}={{C}_{11}}\left( 1-{{\mu }_{12}}{{\mu }_{21}} \right) \\ & {{E}_{22}}={{C}_{22}}\left( 1-{{\mu }_{12}}{{\mu }_{21}} \right),G={{C}_{66}} \\ & {{\mu }_{12}}={{C}_{12}}/{{C}_{11}},{{\mu }_{21}}={{C}_{21}}/{{C}_{22}} \\ & {{B}_{11}}={{D}_{11}}/4,{{B}_{22}}={{D}_{22}}/4 \\ \end{align} \\ \end{array} \right\}$ | (6) |
建立多孔固体的等效连续介质模型,其任务就是确定式(3)中的本构参数$C_{11}\sim C_{66}$及$D_{11}\sim D_{22}$,以及式(2)中的惯性参数 $\rho $ 及 $\Theta$. 该工作在作者相关前期工作中[6, 7, 16]已经进行了介绍,这里仅简述其主要思想.
选定一个完整单胞作为代表体元,并将代表体元等效为具有相同尺寸的均质单元. 在应变能等价的意义下确定等效本构参数,即通过对均质单元施加特定的变形场,计算其应变能,该应变能是等效本构参数的函数,同时由均质单元的变形场返求实际单胞结构的位移场,并获得其应变能. 由实际单胞结构和等效均质单元的应变能相等即可获得相应的本构参数. 确定不同的本构参数需要设计几组不同的变形场. 需要说明的是上述过程中,设计等效均质单元的变形场需要考虑单元的变形协调条件.
惯性参数中的等效密度$\rho $即传统几何意义下的平均密度,等效微转动惯量$\Theta $需要在代表体元动能等价的意义下定义. 使等效均质单元以一定的角速度绕其形心进行面内转动,其动能包含两部分:一部分源于几何平均意义下的转动惯量,而另一部分则源于等效微转动惯量 $\Theta $. 实际单胞结构的动能可根据单胞结构的几何构型计算获得,由实际单胞结构和均质单元的动能相等即可获得等效偶应力介质的微转动惯量$\Theta $.
2 偶应力介质的铁木辛柯梁动力学模型相对于忽略了杆件截面转动惯量以及剪切变形的欧拉$\!$-$\!$-$\!$伯努利梁理论,铁木辛柯梁模型则在弯曲变形的基础上补充考虑了这两部分因素的影响,因此更精确. 经典连续介质的铁木辛柯梁理论的研究目前已较完备,偶应力介质因为材料自身既具有弯曲模量也具有微转动惯量,因此,需要重新推导求解. 以下,采用文献[29]的无量纲化技巧,并约定以带"$^{\ast }$"上标的字母表示原始物理量,以不带上标的字母表示相应的无量纲化物理量.
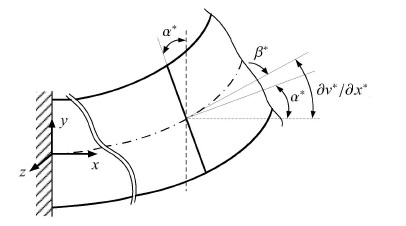
2.1 梁的横向振动微分方程考虑如图 4所示的梁,其中$x$轴与轴线相切,$z$轴与梁横截面的中性轴重合. 梁任意截面的横向位移满足下面关系
| $\frac{\partial {{v}^{*}}}{\partial {{x}^{*}}}={{\alpha }^{*}}+{{\beta }^{*}}\text{ }$ | (7) |
|
图 4 悬臂梁的横向挠度与横截面转角 Fig.4 Transverse deflection and angle of rotation of the cross-section of a cantilever beam |
其中,$v^{\ast }$表示梁的横向挠度,$\alpha^{\ast }$表示由弯曲变形产生的横截面转角,$\beta^{\ast }$表示由于剪切变 形而产生的轴线的转角.
不考虑梁的轴线伸长,并忽略材料的泊松效 应[29],梁横截面任意点的位移表示为
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{u}^{*}}\left( {{x}^{*}},{{y}^{*}} \right)=-{{y}^{*}}{{\alpha }^{*}}\left( {{x}^{*}} \right) \\ & {{v}^{*}}\left( {{x}^{*}},{{y}^{*}} \right)={{v}^{*}}\left( {{x}^{*}} \right) \\ & {{\phi }^{*}}\left( {{x}^{*}},{{y}^{*}} \right)={{\alpha }^{*}}\left( {{x}^{*}} \right) \\ \end{align} \\ \end{array} \right\}$ | (8) |
将上述位移代入式(1),可得应变及微曲率为
| $\left. \begin{array}{*{35}{l}} \begin{align} & \varepsilon _{x}^{*}=-{{y}^{*}}\frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}},\varepsilon _{y}^{*}=0,\gamma _{xy}^{*}=\frac{\partial {{v}^{*}}}{\partial {{x}^{*}}}-{{\alpha }^{*}} \\ & \kappa _{xz}^{*}=\frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}},\kappa _{yz}^{*}=0 \\ \end{align} \\ \end{array} \right\}$ | (9) |
不计外力,梁结构的势能为
| $\begin{align} & {{V}^{*}}=\frac{1}{2}\int{_{{{V}^{*}}}}{{\sigma }^{*\text{T}}}{{\varepsilon }^{*}}d{{V}^{*}}+\frac{1}{2}\int{_{{{V}^{*}}}}{{m}^{*\text{T}}}{{\kappa }^{*}}d{{V}^{*}}= \\ & \qquad \frac{1}{2}\int{_{{{V}^{*}}}}\left( \sigma _{x}^{*}\varepsilon _{x}^{*}+\tau _{S}^{*}\gamma _{xy}^{*} \right)\text{d}{{V}^{*}}+\frac{1}{2}\int{_{{{V}^{*}}}}m_{xz}^{*}\kappa _{xz}^{*}d{{V}^{*}}= \\ & \qquad \frac{1}{2}\int{_{{{V}^{*}}}}\left( E_{11}^{*}\varepsilon _{x}^{*2}+{{G}^{*}}\gamma _{xy}^{*2} \right)d{{V}^{*}}+\frac{1}{2}\int{_{{{V}^{*}}}}D_{11}^{*}\kappa _{xz}^{*2}\text{d}{{V}^{*}}= \\ & \qquad \frac{1}{2}\int{_{{{V}^{*}}}}\left[E_{11}^{*}{{\left( -{{y}^{*}}\frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}} \right)}^{2}}+{{G}^{*}}{{\left( \frac{\partial {{v}^{*}}}{\partial {{x}^{*}}}-{{\alpha }^{*}} \right)}^{2}} \right]\text{d}{{V}^{*}}+ \\ & \qquad \frac{1}{2}\int{_{{{V}^{*}}}}D_{11}^{*}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}} \right)}^{2}}d{{V}^{*}}= \\ & \qquad \frac{1}{2}\int{_{{{L}^{*}}}}\left[E_{11}^{*}{{I}^{*}}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}} \right)}^{2}}+{{G}^{*}}{{A}^{*}}{{\left( \frac{\partial {{v}^{*}}}{\partial {{x}^{*}}}-{{\alpha }^{*}} \right)}^{2}} \right]d{{x}^{*}}+ \\ & \qquad \frac{1}{2}\int{_{{{L}^{*}}}}D_{11}^{*}{{A}^{*}}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}} \right)}^{2}}d{{x}^{*}} \\ \end{align}$ | (10) |
其中,$E_{11}^{\ast } $为$x$方向的杨氏模量,$I^\ast $为梁横截面对中性轴的惯性矩,$G^{\ast }$为剪切模量,$A^{\ast }$为横截面面积.
引入剪切系数$k'$以修正剪应力在梁横截面的非均匀分布,并将式(10)进一步整理,梁的势能$V^{\ast }$可理解为由两部分构成,弯曲势能和剪切势能
| $\begin{align} & {{V}^{*}}=\frac{1}{2}\int_{0}^{L*}{\left( E_{11}^{*}{{I}^{*}}+D_{11}^{*}{{A}^{*}} \right)}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}} \right)}^{2}}d{{x}^{*}}+ \\ & \qquad \frac{1}{2}\int_{0}^{L*}{{k}'{{G}^{*}}{{A}^{*}}}{{\left( \frac{\partial {{v}^{*}}}{\partial {{x}^{*}}}-{{\alpha }^{*}} \right)}^{2}}\text{d}{{x}^{*}} \\ \end{align}$ | (11) |
其中,弯曲势能的第2项$V_{c}^{*}=\frac{1}{2}\int_{0}^{L*}{D_{11}^{*}{{A}^{*}}}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{x}^{*}}} \right)}^{2}}d{{x}^{*}} $即为偶应力介质所特有的弯曲势能,对于经典连续介质,因$D_{11}^\ast = 0$,故该项也为零; 剪切系数$k'$与梁横截面的形状及材料性质有关,目前仍无统一的定义方法. 本文采用如下方式[29]
| $ {k}'=\frac{10\left( 1+\mu \right)}{12+11\mu }\text{ }$ | (12) |
其中$\mu $为泊松比.
采用如下无量纲化操作
| $\left. \begin{array}{*{35}{l}} \begin{align} & x={{x}^{*}}/{{L}^{*}} \\ & v={{v}^{*}}/{{L}^{*}} \\ & A={{A}^{*}}/{{L}^{*2}} \\ & G={{G}^{*}}{{L}^{*4}}/\left( E_{11}^{*}{{I}^{*}}+D_{11}^{*}{{A}^{*}} \right) \\ & V={{V}^{*}}{{L}^{*}}/\left( E_{11}^{*}{{I}^{*}}+D_{11}^{*}{{A}^{*}} \right) \\ \end{align} \\ \end{array} \right\}$ | (13) |
则势能简化为
| $ V=\frac{1}{2}\int_{0}^{1}{{{\left( \frac{\partial \alpha }{\partial x} \right)}^{2}}}\text{ d}x+\frac{1}{2}\int_{0}^{1}{{k}'GA}{{\left( \frac{\partial v}{\partial x}-\alpha \right)}^{2}}\text{ d}x\text{ }$ | (14) |
梁的动能$T^{\ast }$也包含两部分,平动动能及转动动能
| $\begin{align} & {{T}^{*}}=\frac{1}{2}\int_{0}^{L*}{{{\rho }^{*}}{{A}^{*}}}{{\left( \frac{\partial {{v}^{*}}}{\partial {{t}^{*}}} \right)}^{2}}d{{x}^{*}}+ \\ & \qquad \frac{1}{2}\int_{0}^{L*}{\left( {{\rho }^{*}}{{I}^{*}}+{{\Theta }^{*}}{{A}^{*}} \right)}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{t}^{*}}} \right)}^{2}}d{{x}^{*}} \\ \end{align}$ | (15) |
其中,转动动能的第2项$T_{\text{c}}^{*}=\frac{1}{2}\int_{0}^{L*}{{{\Theta }^{*}}{{A}^{*}}}{{\left( \frac{\partial {{\alpha }^{*}}}{\partial {{t}^{*}}} \right)}^{2}}\text{ d}{{x}^{*}} $为偶应力介质所特有的转动动能,对经典连续介质,该项因$\Theta ^\ast = 0$而消失.
相应地,采用如下无量纲化操作
| $\left. \begin{array}{*{35}{l}} \begin{align} & t={{t}^{*}}\omega _{1}^{*} \\ & \rho ={{\rho }^{*}}{{L}^{*6}}\omega _{1}^{*2}/\left( E_{11}^{*}{{I}^{*}}+D_{11}^{*}{{A}^{*}} \right) \\ & \Theta ={{\Theta }^{*}}{{L}^{*4}}\omega _{1}^{*2}/\left( E_{11}^{*}{{I}^{*}}+D_{11}^{*}{{A}^{*}} \right) \\ & T={{T}^{*}}{{L}^{*}}/\left( E_{11}^{*}{{I}^{*}}+D_{11}^{*}{{A}^{*}} \right) \\ \end{align} \\ \end{array} \right\}$ | (16) |
其中,$\omega _1^\ast $表示梁的一阶自振圆频率.
则动能简化为
| $\begin{align} & T=\frac{1}{2}\int_{0}^{1}{\rho A}{{\left( \frac{\partial v}{\partial t} \right)}^{2}}dx+ \\ & \qquad \frac{1}{2}\int_{0}^{1}{\left( \rho I+\Theta A \right)}{{\left( \frac{\partial \alpha }{\partial t} \right)}^{2}}dx \\ \end{align}$ | (17) |
忽略非保守力做功,由哈密顿(Hamilton)原理,须满足
| $\delta \text{ }\int_{{{t}_{1}}}^{{{t}_{2}}}{\left( T-V \right)}\text{ d}t=0$ | (18) |
经过变分运算,即可得到偶应力介质的铁木辛柯梁的振动微分方程(19). 表面上看,该无量纲化的方程似乎并不依赖于偶应力介质的 材料常数${\pmb D}$,实际上,方程对${\pmb D}$的依赖关系已经通过无量纲化过程式(13)及式(16)隐含于其中.
| $\left. \begin{array}{*{35}{l}} \begin{align} & \rho A\frac{{{\partial }^{2}}v}{\partial {{t}^{2}}}-{k}'GA\left( \frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}-\frac{\partial \alpha }{\partial x} \right)=0 \\ & \left( \rho I+\Theta A \right)\frac{{{\partial }^{2}}\alpha }{\partial {{t}^{2}}}-\frac{{{\partial }^{2}}\alpha }{\partial {{t}^{2}}}-{k}'GA\left( \frac{\partial v}{\partial x}-\alpha \right)=0 \\ \end{align} \\ \end{array} \right\}$ | (19) |
遵循一般的分离变量法步骤,可求出梁的自振频率及振型函数. 需要注意的是,铁木辛柯梁总是存在一个临界频率$\omega_{\rm c}$,梁的振型函数取决于频率和$\omega_{\rm c}$的大小关系. 对于偶应力介质,该临界频率为
| ${{\omega }_{\text{c}}}=\sqrt{{k}'GA/\left( \rho I+\Theta A \right)}$ | (20) |
当$\omega < \omega_{\rm c}$时,振型函数为
| $\left. \begin{align} & W\left( x \right)={{C}_{1}}\sin ax+{{C}_{2}}\cos ax+ \\ & \qquad {{C}_{3}}\sinh bx+{{C}_{4}}\cosh bx \\ & \Psi \left( x \right)={{D}_{1}}\sin ax+{{D}_{2}}\cos ax+ \\ & \qquad {{D}_{3}}\sinh bx+{{D}_{4}}\cosh bx \\ \end{align} \right\}$ | (21) |
其中$W(x)$和$\varPsi (x)$分别与$v$和$\alpha $对应.
当$\omega >\omega_{\rm c}$时,振型函数为
| $\left. \begin{align} & W\left( x \right)={{{\tilde{C}}}_{1}}\sin ax+{{{\tilde{C}}}_{2}}\cos ax+ \\ & {{{\tilde{C}}}_{3}}\sin \tilde{b}x+{{{\tilde{C}}}_{4}}\cos \tilde{b}x \\ & \Psi \left( x \right)={{{\tilde{D}}}_{1}}\sin ax+{{{\tilde{D}}}_{2}}\cos ax+ \\ & \qquad {{{\tilde{D}}}_{3}}\sin \tilde{b}x+{{{\tilde{D}}}_{4}}\cos \tilde{b}x \\ \end{align} \right\}$ | (22) |
参数$a$,$b$或$\tilde{b}$通过梁的边界条件所确定的方程求解特征值方程得到,详细过程可参考文献 [29],但须注意偶应力 介质和经典连续介质梁振动方程的区别. 本文不妨以悬臂梁为例进行分析.
在固定端,须满足
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{\left. W\left( x \right) \right|}_{x=0}}=0 \\ & {{\left. \Psi \left( x \right) \right|}_{x=0}}=0 \\ \end{align} \\ \end{array} \right\}$ | (23) |
在自由端,须满足
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{\left. \frac{\text{d}\Psi \left( x \right)}{dx} \right|}_{x=1}}=0 \\ & {{\left. \left[\frac{dW\left( x \right)}{dx}-\Psi \left( x \right) \right] \right|}_{x=1}}=0 \\ \end{align} \\ \end{array} \right\}$ | (24) |
因铁木辛柯梁的频率方程具有强非线性特点,因此需要通过数值方法求解. 获得参数$a$,$b$或$\widetilde{b}$后,便相应获得 了频率及振型函数表达式.
3 模型准确性验证将多孔固体类梁结构的等效偶应力连续介质的铁木辛柯梁模型所获得的频率和振型结果与有限元直接离散结果进行对比, 可以验证模型的准确性. 其中,有限元计算结果是指将多孔固体结构进行传统的有限元离散计算,并获得结构的频率及振型. 有限元离散计算采用平面四节点四边形等参元,依据单胞相对孔径的大小,将结构的每一单胞均离散化为150$\sim $200个单元,采用分块兰索斯(Lanczos)方法计算结构的特征值,计算过程采用有限元商业软件"Ansys"实现. 此离散解视为结构振动的精确解.
频率结果的验证可直接比较两套模型所得到的数值,而振型结果的比较则要相对繁琐. 因为振型仅仅代表了结构在某一频率下振动时各点的相对位移,而并非绝对的位移响应,因此直接比较位移的数值没有意义. 这里采用模态分析领域常用的模态置信准则(modal assurance criterion,MAC)矩阵[33]来进行评价. 模态置信矩阵的元素通过下式计算获得
| $ {MAC}_{ij} = \dfrac{\left| {\left( {{ X}_i^{\rm e} } \right)^{\rm T}{ X}_j^{\rm d} } \right|^2}{\left[{\left( {{ X}_i^{\rm e} } \right)^ {\rm T}{ X}_i^{\rm e} } \right]\left[{\left( {{ X}_j^{\rm d} } \right)^ {\rm T}{ X}_j^{\rm d} } \right]}\,,\ \ \ i,j = 1,2,\cdots,r$ | (25) |
式中,$X_{i}^{\text{e}}$表示等效模型的第"$i$"阶振型,同理,${ X}_j^{\rm d} $表示离散模型的第"$j$"阶振型;$r$表示需要分析的振型阶数,故模态置信矩阵为$r\times r$方阵.
在模态置信矩阵中,对角线各元素代表了两个模型的同阶振型之间的相关性,而非对角线元素则代表了两个模型的不同阶振型之 间的相关性. 若两个振型完全相同,则矩阵的相应元素为1;反之,若两个振型完全不相关,则矩阵的相应元素为0. 由此,考虑到结构振型的正交性特点,理想精度的等效模型所产生的模态置信矩阵应为对角线元素为1的单位矩阵. 为直观显示振型的相关性,经常用灰度图表示模态置信矩阵的各元素.
梁模型并未直接给出任意点的纵向位移,为客观比较振型的准确性,需要先通过铁木辛柯梁的变形假设式(8)求解其纵向位移.
4 算例及分析对于图 2所示的多孔固体类梁结构,本节将分别讨论尺寸为$L^{\ast } =50$,$H^{\ast } =10$的短梁结构,$L^{\ast } =100$,$H^{\ast } =10$的中梁结构以及$L^{\ast } =200$,$H^{\ast } =10$的长梁 结构的自振行为,从频率和振型两方面讨论等效偶应力连续介质梁模型的计算精度. 梁的宽度尺寸均为1. 不失一般性,本文约定,结构的长度单位均为mm. 梁结构的边界条件为一端固定,一端自由(悬臂梁). 理论上,铁木辛柯梁模型对于长梁结构及短梁结构均应具有较高的精度.
对每一尺寸的梁,均讨论了梁结构高度与材料单胞边长之比$H^{\ast }/h^{\ast } =1 \sim 5$五种情况. 这是因为,根据我们前期的工作[16],当梁结构的高度与等效介质的特征长度之比超过20时,梁振动行为的尺寸效应不再显著,等效偶应力连续介质模型和等效经典连续介质模型的差异不再明显. 对于本文所研究的多孔固体,$H^{\ast }/h^{\ast } \geqslant 5$可以保证梁的高度与等效介质特征长度之比大于20.
在每一尺寸下,分别考虑了单胞结构中孔径相对大小$d^{\ast }/h^{\ast } $为0.3,0.5,0.7及0.9四种情况. 孔径的相对大小不仅反映多孔固体相对密度的大小,更重要的,会影响到等效偶应力介质材料常数的大小.
考虑到结构的前几阶振动对结构的振动分析影响较大,讨论了前16阶弯曲振动,因为结构在弯曲振动之外尚存在纵向振动,更高阶的振动在结构的整体振动中往往超过了20阶,因此我们认为分析前16阶是充分的.
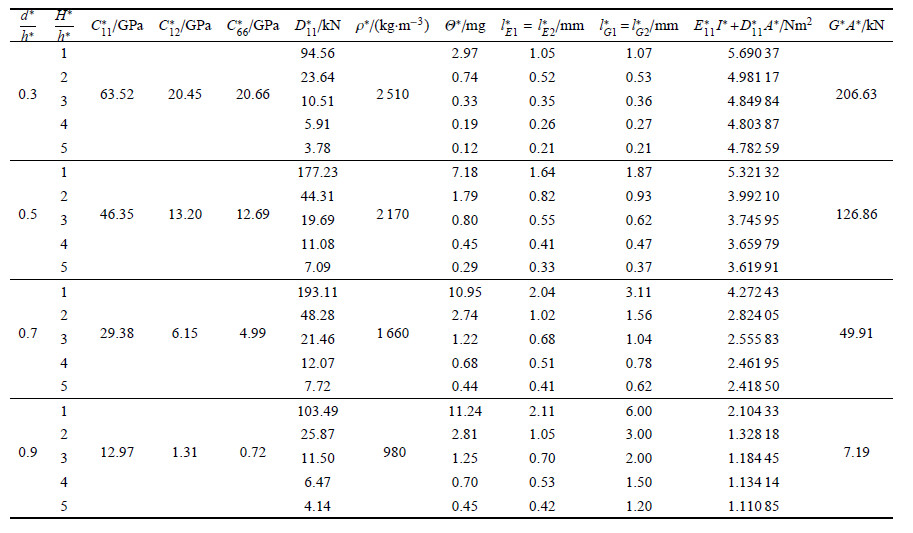
以下所有算例,多孔固体的基体材料均为各向同性材料,杨氏模量为69GPa,泊松比为0.3,密度为2.7$\times $10$^{3}$kg/m$^{3}$. 不同单胞尺寸及不同相对孔径下,等效偶应力介质的材料常数及相应的连续梁模型的等效刚度均列入表 1. 考虑到单胞结构的对称性,材料常数满足$C_{11}^\ast = C_{22}^\ast $,$D_{11}^\ast = D_{22}^\ast $.
| 表 1 不同单胞尺寸的等效偶应力介质材料常数及梁模型的刚度 Table 1 Effective couple-stress continuum mechanical constants and the rigidities of the beam models with different cell sizes |
图 5给出了多孔固体短梁结构在不同的单胞孔径相对大小$d^{\ast }/h^{\ast }$以及不同的单胞尺寸绝对大小下,等效偶应力介质铁木辛柯梁模型的横向振动频 率计算结果. 各阶频率分别由真实结构相应频率的 离散解进行归一化处理. 为了便于比较,每幅图中均包含两条虚线,对应归一化频率值为1.05及0.95,在此之间的频率值,误差低于5%,即工程上认可的较高精度.

|
图 5 不同的单胞孔径相对大小以及不同的单胞绝对尺寸下,多孔固体短梁结构($L^{\ast } =50$,$H^{\ast } =10$)的等效偶应力 介质铁木辛柯梁的计算频率. 各图中两条虚线分别对应0.95及1.05(下同) Fig.5 Frequencies of cellular solid short ($L^{\ast } =50$, $H^{\ast } =10$) beam-like structures with different relative sizes of void diameter and different absolute sizes of unit cells from the effective couple-stress continuum Timoshenko beam model. The two dotted lines denote the values of 0.95 and 1.05 (similarly hereinafter) |
随着单胞尺寸的减小($H^{\ast }/h^{\ast }$增大),等效梁模型自振频率的精度均由震荡而逐渐趋于稳定. 当 $H^{\ast }/h^{\ast } =1$时,单胞尺寸最大,等效梁模型的频率计算精度较差,且随着阶数的增加,频率精度逐渐产生波动,并偏 离精确解. 随着单胞尺寸的减小,等效梁模型的频率计算精度逐渐收敛于定值. 对于收敛后的结果,频率的计算精度随着阶数的增加并 无明显的变化.
随着孔径相对大小$d^{\ast }/h^{\ast }$的增大,等效梁模型所获得频率解精度呈逐渐降低的趋势. 当$d^{\ast }/h^{\ast } =0.3$时,结构只需${{H}^{*}}/{{h}^{*}}\ge 2$便具有前16阶频率的较高计算精度;而当$d^{\ast }/h^{\ast } =0.9$时,只有${{H}^{*}}/{{h}^{*}}\ge 4$的结构才具有较高的频率计算精度,且基频的精度较差,而基频对结构的振动分析至关重要.
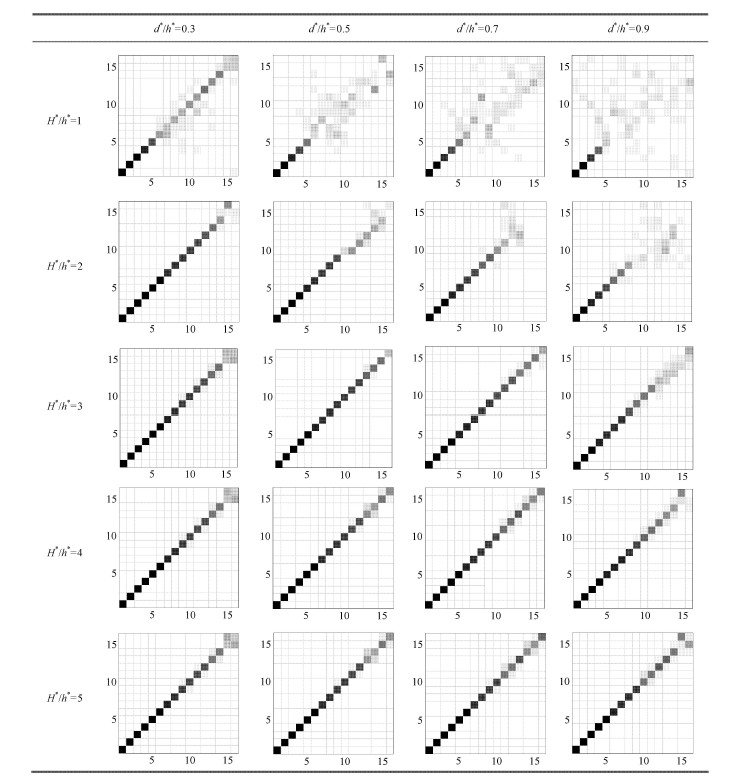
表 2给出了在不同的相对孔径以及不同的单胞绝对尺寸比下,等效梁模型与实际结构离散解的振型对比模态置信矩阵. 等效模 型的振型计算精度与频率计算精度具有相同的趋势:随着孔径相对大小$d^{\ast }/h^{\ast }$的增大,等效梁模型所获得振型结果精度逐渐降低;随着单胞结构绝对尺寸的减小,等效梁模型的振型计算精度逐渐提高. 特别的,当${{H}^{*}}/{{h}^{*}}\le 2$且${{d}^{*}}/{{h}^{*}}\ge 0.5$时,模态置信矩阵的高维部分元素呈现发散状态,表明在此范围内,实际多孔固体类梁结构由于局部刚度过低,其高阶振型 已经失去了整体类梁变形模式,而是产生了横纵混合振型或者局部振型,采用等效梁模型进行振动分析已经不再可靠. 正是因为 此时梁模型无法准确模拟结构的振动变形形态,故所求得的频率结果并不可信,表现为频率计算结果出现了较明显的震荡,计 算频率与实际结构的频率产生了很大的差异.
| 表 2 不同的单胞孔径相对大小以及不同的单胞绝对尺寸下,多孔固体短梁结构($L^{\ast } =50$,$H^{\ast }=10$)振型的等效偶应力介质铁木辛柯梁模型解与离散解的模态置信矩阵灰度演示 Table 2 MAC presentations between two sets of the mode shapes as calculated by the effective couple-stress continuum Timoshenko beam model and the discrete method of the cellular solid short ($L^{\ast } =50$,$H^{\ast } =10$) beam-like structures with different relative sizes of void diameter and different absolute sizes of unit cells |
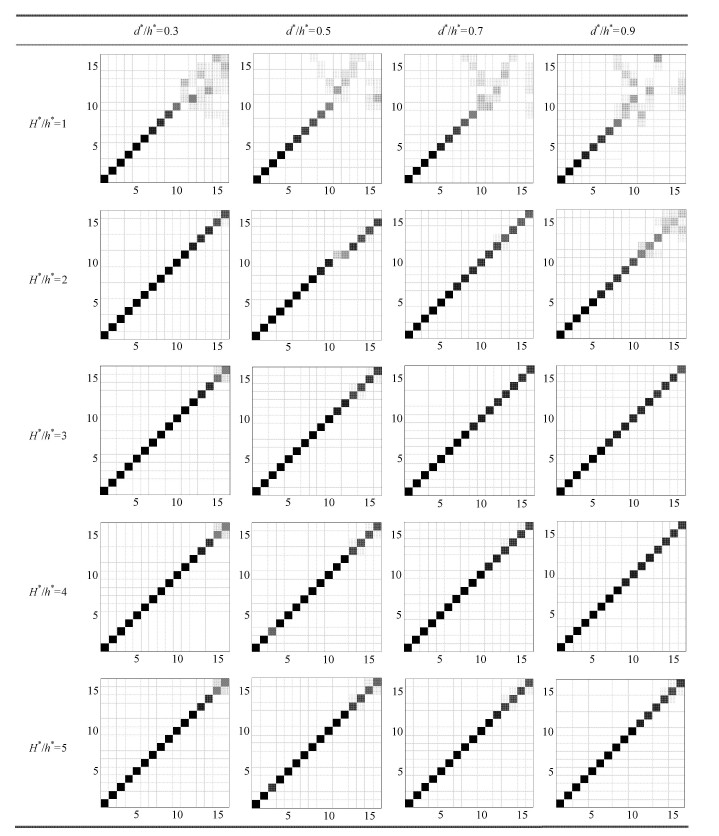
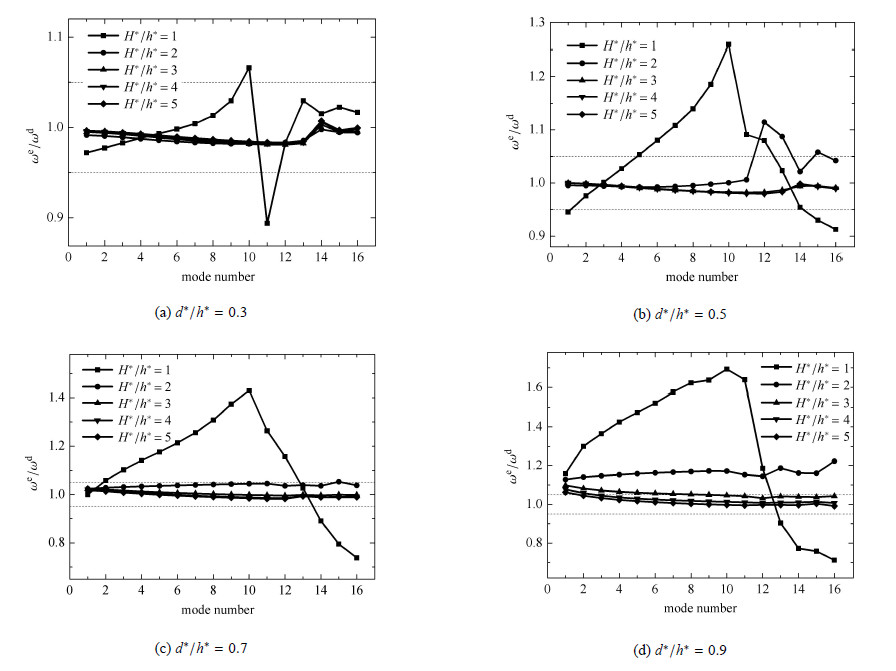
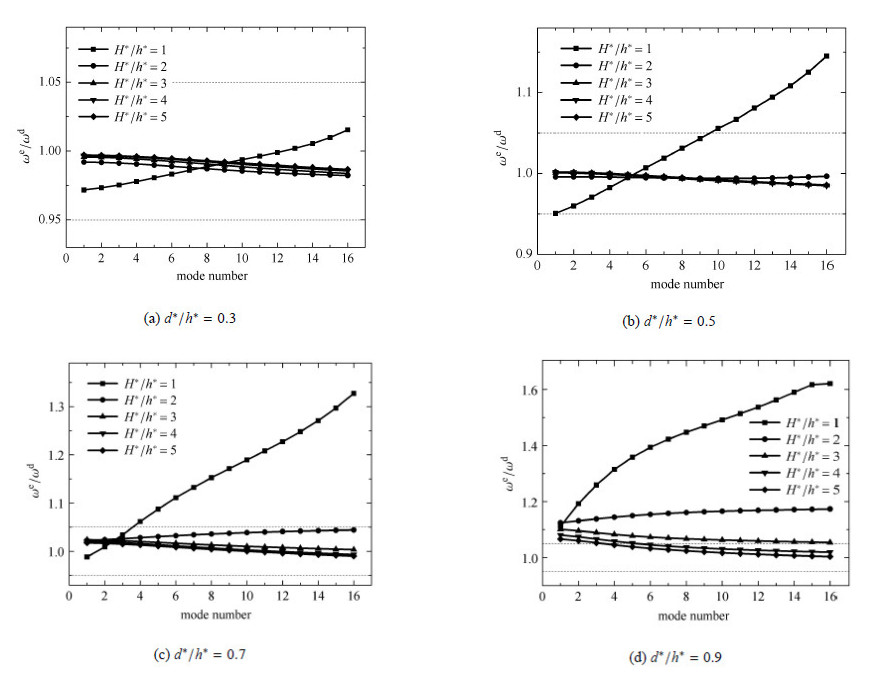
图 6 $\sim $图 7,表 3 $\sim $表 4分别给出了多孔固体中梁及长梁结构的等效梁模型的频率及振型计算结果与相应的离散解的对比. 和短梁相比,等效梁模型用于中 梁和长梁结构计算的结果趋势是一致的,但是随着多孔固体类梁结构长高比的增加,等效梁模型所获得的频率和振型在精度上均有较大 幅度的提高. 尤其是对于多孔固体长梁结构,在频率方面,当${{H}^{*}}/{{h}^{*}}\ge 2$且${{d}^{*}}/{{h}^{*}}\le 0.7$时,等效梁模型能够较准确地获得至少前16阶横向振动频率,即使$H^{\ast }/h^{\ast } =1$,只要${{d}^{*}}/{{h}^{*}}\le 0.5$,仍然能够较准确地获得至少前9阶频率(图 7(a),7(b));在振型方面,等效模型和离散模型的各模态置信矩阵均近似为单位矩阵, 表明此时类梁结构的实际横向振动确实为整体弯曲梁变形模式,采用等效梁模型是可行的.
| 表 3 不同的单胞孔径相对大小以及不同的单胞绝对尺寸下,多孔固体中梁结构($L^{\ast} =100$,$H^{\ast }=10$)振型的等效偶应力介质铁木辛柯梁模型解与离散解的模态置信矩阵灰度演示 Table 3 MAC presentations between two sets of the mode shapes as calculated by the effective couple-stress continuum Timoshenko beam model and the discrete method of the cellular solid middle long ($L^{\ast } =100$,$H^{\ast } =10$) beam-like structures with different relative sizes of void diameter and different absolute sizes of unit cells |
| 表 4 不同的单胞孔径相对大小以及不同的单胞绝对尺寸下,多孔固体长梁结构($L^{\ast} =200$,$H^{\ast } =10$)振型的等效偶应力介质铁木辛柯梁模型解与离散解的模态置信矩阵灰度演示 Table 4 MAC presentations between two sets of the mode shapes as calculated by the effective couple-stress continuum Timoshenko beam model and the discrete method of the cellular solid long ($L^{\ast } =200$,$H^{\ast } =10$) beam-like structures with different relative sizes of void diameter and different absolute sizes of unit cells |
|
图 6 不同的单胞孔径相对大小以及不同的单胞绝对尺寸下,多孔固体中梁结构($L^{\ast } =100$,$H^{\ast } =10$)的等效偶应力介质 铁木辛柯梁的计算频率 Fig.6 Frequencies of cellular solid middle long ($L^{\ast } =100$, $H^{\ast } =10$) beam-like structures with different relative sizes of void diameter and different absolute sizes of unit cells from the effective couple-stress continuum Timoshenko beam model |
|
图 7 不同的单胞孔径相对大小以及不同的单胞绝对尺寸下,多孔固体长梁结构($L^{\ast} =200$,$H^{\ast } =10$)的等效偶应力介质铁木辛柯梁的计算频率 Fig.7 Frequencies of cellular solid long ($L^{\ast } =200$, $H^{\ast } =10$) beam-like structures with different relative sizes of void diameter and different absolute sizes of unit cells from the effective couple-stress continuum Timoshenko beam model |
多孔固体类梁结构自振性能分析的等效连续介质梁模型的准确性主要受3个尺寸比的影响:梁高度与材料单胞尺寸的比值$H^{\ast }/h^{\ast }$,单胞结构的相对孔径$d^{\ast }/h^{\ast }$以及类梁结构的长高比$L^{\ast }/H^{\ast }$.
$H^{\ast }/h^{\ast }$实际上反映了宏观结构的关键尺寸与材料微结构的尺寸比,决定了多孔固体的等效连续介质模型应当基于经典连续介质理论或者广 义连续介质理论. 根据我们早期的工作,当宏观结构的关键尺寸与组成结构的材料特征长度尺寸比小于20时,结构横向振动行为存在尺寸 效应,需采用等效偶应力连续介质力学模型. 偶应力介质的特征长度可通过偶应力介质的材料常数计算获得[6, 23],其数值与材料的单胞尺寸大致成正比. 对于本文所述的多孔固体,将特征长度折算为单胞尺寸后,大致上,$H^{\ast }/h^{\ast }$值低于5的结构应采用偶应力模型.
$d^{\ast }/h^{\ast }$体现了材料的单胞结构的几何特征,其意义体现在两个方面:(1)决定了类梁结构的局部变形强弱程度,$d^{\ast }/h^{\ast }$越大,单胞的局部刚度越小,振动中的局部变形模式越容易出现;(2)在一定程度上决定等效介质高阶性能的强弱,即,在宏微观结 构尺寸比相差不大的情况下,$d^{\ast }/h^{\ast }$越大,越容易产生等效性能的尺寸效应. 由于采用了等效偶应力连续介质模型,第2方面影响已经可以忽略不计. 前文算例表明,$d^{\ast }/h^{\ast } =0.9$ 时,单胞层面的局部变形严重影响了等效梁模型的适用性.
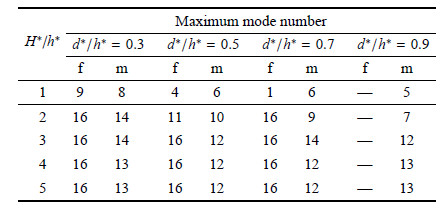
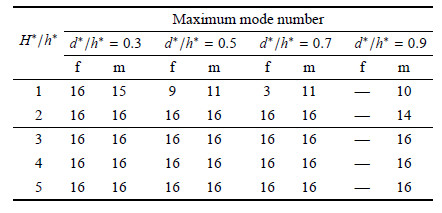
长高比$L^{\ast }/H^{\ast }$决定了类梁结构的振型是否符合梁模型的变形模式,即,是否可以采用等效梁理论模 型. 显然,长高比越大,梁理论的基本假设符合得越充分,等效梁模型的计算结果精度就越高. 前文算例中,等效梁模型对长梁结构的计算结果明显优于短梁,并不意外. 为了进一步比较上述3个尺寸比对梁模型准确性的影响,将不同尺寸比下等效偶应力介质铁木辛柯梁模型在频率和振型两方面所能够准 确获得的最高阶数列入表 5 $\sim $表 7. 其中,仿照频率的讨论,同样约定振型的MAC矩阵中若对角元元素的值高于0.95, 则认为该阶振型的具有较高精度.
| 表 5 等效梁模型对短梁($L^{\ast } =50$,$H^{\ast} =10$)结构自振所能准确描述的最高阶数 Table 5 Maximum mode number of the effective beam model for the short ($L^{\ast } =50$, $H^{\ast } =10$)beam-like structure to get the accurate solutions |
| 表 6 等效梁模型对中梁($L^{\ast } =100$,$H^{\ast} =10$)结构自振所能准确描述的最高阶数 Table 6 Maximum mode number of the effective beam model for the middle long ($L^{\ast } =100$, $H^{\ast }=10$) beam-like structure to get the accurate solutions |
| 表 7 等效梁模型对长梁($L^{\ast } =200$,$H^{\ast} =10$)结构自振所能准确描述的最高阶数 Table 7 Maximum mode number of the effective beam model for the long ($L^{\ast } =200$, $H^{\ast } =10$)beam-like structure to get the accurate solutions |
对比发现,对不同尺寸的梁结构,等效介质梁模型的精度总是随着结构长高比的增大而提高. 对 于$H^{\ast }/h^{\ast } \geqslant 2$,且$d^{\ast }/h^{\ast } \leqslant 0.7$的类梁结构,等效偶应力介质铁木辛柯梁模型所获得的准确频率的最高阶数总是要高于振型阶数. 评价等效介质梁模 型的准确与否应综合频率和振型两方面因素,因此,对于上述范围内的类梁结构,本文等效介质梁模型所能够准确 获得的最高计算阶数分别为:短梁7阶左右,中梁10阶以上,长梁16阶以上.
除了上述3个尺寸比,等效介质梁模型振动分析精度有时也会受到结构振动中常见的重特征值现象的影响. 当结构在某一频率下存在不同的振型时,根据振型的正交性理论,两个不同振型的任意线性组合均为该频率下的可能发生的振型. 故此时,利用模态置信矩阵比较等效梁的振型和实际结构的振型没有意义. 不仅如此,若与重特征值对应的两个振型分别为结构的纵向振动和横向振动,则有可能导致结构产生多余的横向振型,使两个模型的横向振动频率阶数发生错位,从而影响到频率计算结果的准确度. 上述算例中,中梁结构$d^{\ast }/h^{\ast } =0.5$,$H^{\ast }/h^{\ast } =4$及$H^{\ast }/h^{\ast } =5$的第3阶振型均发生了重特征值现象.
实际上,从力学模型的本质上考虑,对等效梁模型适用性起主导作用的因素是梁的平截面假定是否能够得到满足. 只有实际结构的变形满足了铁木辛柯梁模型的平截面假定,才可以采用等效梁模型来进行振动分析. 对于前面的算例, 在振型比较中,若忽略结构的纵向变形而仅比较横向位移,会发现等效梁模型的振型计算的精度有所提高.
其他的工程梁理论(如欧拉-伯努利梁、瑞利梁、剪切梁)由于引入的假定更强,因此其精度均不如铁木辛柯梁. 其中,欧拉-伯努利梁由于 形式简单而广泛采用,因此以下也简略讨论该模型在多孔固体类梁结构振动行为描述方面的准确性. 我们的重点并不是系统地探讨欧拉-伯努利梁模型的适用性,而是定性地观察其与铁木辛柯梁的差别. 为此,仅考虑高度为10,长高比$L^{\ast }/H^{\ast } $ 分别为20,50及100的3种长梁结构,且宏微观尺寸比选择有临界意义的$H^{\ast }/h^{\ast } =2$, 孔径相对大小只选择$d^{\ast }/h^{\ast } $为0.3,0.5及0.7三种情况.
为了排除尺寸效应的影响,同样先将多孔固体等效为具有等效材料常数的偶应力连续介质,在此基础上建立等效欧拉$\!$-$\!$-$\!$伯努 利梁模型. 该梁模型的振动微分方程的求解过程较简单,可参考文献 [29],只是需要将梁的抗弯刚度由$E_{11}^\ast I^\ast $替换为$\left( {E_{11}^\ast I^\ast + D_{11}^\ast A^\ast } \right)$. 图 8给出了相应的计算结果.

|
图 8 不同结构尺寸及单胞尺寸下,多孔固体梁结构的等效偶应力介质欧拉-伯努利梁模型的振动分析结果 Fig.8 Results for the vibration analysis of cellular solid beam-like structures with different structural size and cell size from the effective couple-stress continuum Euler-Bernoulli beam model |
结果表明,在多孔固体自由振动分析中,若计算要求为前10阶特征频率,等效偶应力介质欧拉-伯努利梁模型的计算效果较差,只有当类梁结构足够细长(如$L^{\ast }/H^{\ast } \geqslant 100$),且多孔固体单胞的相对孔径低于0.5时,才能够获得较高的计算精度. 但是,对于工程中最为关心的低频振动频率,如基频,当$L^{\ast }/H^{\ast } \geqslant 20$时,已经能够获得可以接受的计算精度. 值得一提的是,该梁模型对于多孔固体类梁结构的静力学行为描述,则具有较好的效果. 我们前期工作表明,当$L^{\ast }/H^{\ast } \geqslant 20$时,等效模型已经获得了非常高的弯曲变形计算精度[6, 7].
5 结论对于单胞含有圆形孔洞的一类典型的多孔固体类梁结构,本文基于偶应力理论,给出了计算其横向自由振动频率和振型的等效介质铁木辛柯梁模型. 分别对具有不同的类梁结构长高比、单胞孔径相对大小以及宏观结构与单胞结构尺寸比的大量结构进行了数值计算,并与实际结构的有限元完全离散模型结果进行了对比. 结果表明,本文所给出的梁模型在频率和振型两个方面均能够较好地描述多孔固体类梁结构的振动行为.
针对本文的计算结果,对于该类多孔固体的振动分析,若计算要求为前10阶特征频率,偏保守地,给出如下粗略建议:
(1)若多孔固体类梁结构的高度尺寸与单胞尺寸的比值为1,或者多孔固体单胞孔径相对大小大于0.7,建议采用直接离散模型.
(2)若多孔固体类梁结构的高度尺寸与单胞尺寸的比值介于2与5之间,且多孔固体单胞孔径相对大小小于0.7,建议采用等效偶应力连续介质的铁木辛柯梁模型.
(3)若多孔固体类梁结构的高度尺寸与单胞尺寸的比值大于5,且多孔固体单胞孔径相对大小小于0.7,建议采用等效经典连续介质的铁木辛柯梁模型.
(4)长高比低于5的短梁不建议采用等效梁模型,因短梁所能够获得准确振型阶数较低.
(5)等效的欧拉-伯努利梁模型,建议只用来计算低频振动,如一阶振动,因其对大多数梁的高阶振动计算结果较差.
| 1 | Gibson LJ, Ashby MF. Cellular Solids: Structure and Properties. Cambridge: Cambidge University Press, 1997 |
| 2 | Ashby MF, Evans AG, Fleck NA, et al. Metal Foams: A Design Guide. Boston: Butterworth-Heinemann, 2000 |
| 3 | Onck PR, Andrews EW, Gibson LJ. Size e ects in ductile cellular solids. Part I: Modeling. International Journal of Mechanical Sciences,2001, 43(3): 681-699 |
| 4 | Andrews EW, Gioux G, Onck P, et al. Size e ects in ductile cellular solids. Part II: Experimental results. International Journal of Mechanical Sciences, 2001, 43(3): 701-713 |
| 5 | Dai GM, Zhang WH. Size e ects of basic cell in static analysis of sandwich beams. International Journal of Solids and Structures,2008, 45(9): 2512-2533 |
| 6 | Liu S, Su W. E ective couple-stress continuum model of cellular solids and size e ects analysis. International Journal of Solids and Structures, 2009, 46(14-15): 2787-2799 |
| 7 | 苏文政, 刘书田. 基于偶应力理论的格栅材料等效介质模型. 力学学报, 2008, 40(6): 776-785 (Su Wenzheng, Liu Shutian. E ective continuum model of grid material based on couple-stress theory. Chinese Journal of Theoretical and Applied Mechanics, 2008,40 (6):776-785 (in Chinese)) |
| 8 | 蔡园武, 徐亮, 程耿东. 正六角形单胞周期性蜂窝板等效刚度研究. 大连理工大学学报, 2014, 54(4): 377-383 (Cai Yuanwu, Xu Liang, Cheng Gengdong. Study of e ective sti ness of periodic honeycomb plate with regular hexagonal unit cell. Journal of Dalian University of Technology, 2014, 54(4): 377-383 (in Chinese)) |
| 9 | Yi S, Xu L, Cheng G, et al. FEM formulation of homogenization method for e ective properties of periodic heterogeneous beam and size e ect of basic cell in thickness direction. Computers & Structures,2015, 156: 1-11 |
| 10 | Burgueno R, Quagliata MJ, Mohanty AK, et al. Hierarchical cellular designs for load-bearing biocomposite beams and plates. Materials Science and Engineering A, 2005, 390(1-2): 178-187 |
| 11 | 邱克鹏, 吴晨, 张卫红. 蜂窝夹芯结构吸波性能的有限元计算分析. 中国科学:物理学力学天文学, 2013, 43(9): 1057-1064 (Qiu Kepeng, Wu Chen, Zhang Weihong. Numerical analysis of absorbing property for structural absorbing material (SAM) with honeycomb cores. Scientia Sinica Physica, Mechanica & Astronomica,2013, 43(9): 1057-1064 (in Chinese)) |
| 12 | 张卫红, 段文东, 许英杰等. 六边形蜂窝等效面外剪切模量预测及其尺寸效应. 力学学报, 2013, 45(2): 288-292 (Zhang Weihong, Duan Wendong, Xu Yingjie, et al. Predictions of e ective out-plane shear modulus and size e ect of hexagonal honeycomb. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45 (2): 288-292 (in Chinese)) |
| 13 | 张卫红, 骆金威, 戴高明等. 周期性多孔材料等效剪切模量与尺寸效应研究. 力学学报, 2011, 43(1): 144-153 (Zhang Weihong, Luo Jinwei, Dai Gaoming, et al. Numerical predictions of e ective shear modulus and size e ect for periodic cellular materials. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43 (1):144-153 (in Chinese)) |
| 14 | Dai G, Zhang W. Cell size e ects for vibration analysis and design of sandwich beams. Acta Mechanica Sinica, 2009, 25(3): 353-365 |
| 15 | Banerjee S, Bhaskar A. The applicability of the e ective medium theory to the dynamics of cellular beams. International Journal of Mechanical Sciences, 2009, 51(8): 598-608 |
| 16 | Su W, Liu S. Vibration analysis of periodic cellular solids based on an e ective couple-stress continuum model. International Journal of Solids and Structures, 2014, 51(14): 2676-2686 |
| 17 | Tekoglu C, Onck PR. Size e ects in two-dimensional Voronoi foams: A comparison between generalized continua and discrete models. Journal of the Mechanics and Physics of Solids, 2008,56(12): 3541-3564 |
| 18 | 孟晗, 辛锋先, 卢天健. 多孔纤维吸声材料填充蜂窝结构的声学性能. 中国科学: 物理学力学天文学, 2014, 44(6): 599-609 (Meng Han, Xin Fengxian, Lu Tianjian. A coustical properties of honeycomb structures filled with fibrous absorptive materials. Scientia Sinica Physica, Mechanica & Astronomica. 2014, 44 (6): 599-609 (in Chinese)) |
| 19 | Yan J, Hu WB, Wang ZH, et al. Size e ect of lattice material and minimum weight design. Acta Mechanica Sinica, 2014, 30(2): 191-197 |
| 20 | 虞吉林. 考虑微结构的固体力学的进展和若干应用. 力学进展,1985, 15(1): 82-89 (Yu Jilin. Progress and applications of solid mechanics considering microstructure. Advances in Mechanics, 1985,15 (1): 82-89 (in Chinese)) |
| 21 | Eringen AC. Microcontinuum Field Theories. New York Springer,1999 |
| 22 | 胡更开, 刘晓宁, 荀飞. 非均匀微极介质的有效性质分析. 力学进展, 2004, 34(2): 195-214 (Hu Gengkai, Liu Xiaoning, Xun Fei. Micromechanics of heterogeneous micropolar mediums. Advances in Mechanics, 2004, 34(2): 195-214(in Chinese)) |
| 23 | Mindlin RD. Influence of couple-stresses on stress concentrations. Experimental Mechanics, 1963, 3(1): 1-7 |
| 24 | 任树伟, 辛锋先, 卢天健. 考虑尺度效应的微平板声振耦合特性研究. 中国科学: 技术科学, 2014, 44(2): 201-208 (Ren Shuwei, Xin Fengxian, Lu Tianjian. Vibroacoustic characteristics of micro-plates considering scale e ect. Science China: Technological Sciences,2014, 44(2): 201-208 |
| 25 | 王晓明, 王飞, 赵学增等. 基于Cosserat 理论的四边简支自由振动微平板尺度效应研究. 固体力学学报, 2012, 33(1): 63-68 (Wang Xiaoming, Wang Fei, Zhao Xuezeng, et al. On the size e ects in a freely-vibrating micro-plate with the four edges simply-supported based on the Cosserat theroy. Chinese Journal of Solid Mechanics,2012, 33(1): 63-68 (in Chinese)) |
| 26 | Asghari M, Kahrobaiyan MH, Rahaeifard M, et al. Investigation of the size e ects in Timoshenko beams based on the couple stress theory. Archive of Applied Mechanics, 2011, 81(7): 863-874 |
| 27 | 李莉, 陈万吉, 郑楠. 修正偶应力理论层合薄板稳定性模型及尺度效应. 工程力学, 2013, 30(5): 1-7 (Li Li, Chen Wanji, Zheng Nan. Model of composite laminated thin plate based on modified couple stress theory and buckling analysis of scale e ects. Engineering Mechanics,2013, 30 (5): 1-7 (in Chinese)) |
| 28 | Lakes R, Drugan WJ. Bending of a cosserat elastic bar of square cross section: theory and experiment. Journal of Applied Mechanics,2015, 82(9): 091002 |
| 29 | Han SM, Benaroya H, Wei T. Dynamics of transversely vibrating beams using four engineering theories. Journal of Sound and Vibration,1999, 225(5): 935-988 |
| 30 | Bigoni D, Drugan WJ. Analytical derivation of cosserat moduli via homogenization of heterogeneous elastic materials. Journal of Applied Mechanics, Transactions ASME, 2007, 74(4): 741-753 |
| 31 | 夏桂云, 曾庆元. 深梁理论的研究现状与工程应用. 力学与实践,2015, 37(3): 302-316 (Xia Guiyun, Zeng Qingyuan. Timoshenko beam theory and its applications. Mechanics in Engineering, 2015,37(3): 302-316 (in Chinese)) |
| 32 | Bouyge F, Jasiuk I, Boccara S, et al. A micromechanically based couple-stress model of an elastic orthotropic two-phase composite. European Journal of Mechanics, A/Solids, 2002, 21(3): 465-481 |
| 33 | Ewins DJ. Modal Testing: Theory, Practice and Application. Baldock: Research Studies Press, 2000 |
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian 116023, China
 2016, Vol. 48
2016, Vol. 48