激波风洞是航空航天领域极具代表性的地面实验设备,具有运行状态参数高、经济性好等优点. 作为典型的脉冲设备,激 波风洞试验时间很短,通常为2$\sim$30ms,即使世界最先进的激波风洞JF12[1]的试验时间也只有130$\sim$220ms. 在如此短暂的试验时间内,准确测量飞行器模型的气动力,是极具挑战性的课题. 常规风洞试验时间可以达到分钟量级,远大于测力系统(包括支承结构、测力元件和飞行器模型)的振动周期,振动过程呈现出明 显的衰减趋势,飞行器气动力测量过程类似于静态测量,精度较高. 与常规风洞不同,激波风洞的试验时间内仅能包含1个或几个振动周期,测力系统的结构振动不能及时衰减,测力实际上是对一 个"动态过程"的测量,其测量的精度和难度明显区别于常规风洞测力,从根本上决定了气动力测量技术在激波风洞发展中的核 心地位.
根据达朗贝尔原理,在上述动态测量过程中,测力天平所感知的信号是作用在模型上的气动力与振动对应的惯性力之间的差值. 测力天平是激波风洞气动力测量的核心元件,按照结构形式、测力原理等可以有多种分类. 目前,在激波风洞上应用较为典型的是应变天平[2]、压电天平[3]、应力波天 平[4, 5],也有关于磁悬 挂天平[6, 7]的讨论. 几十年来,天平的定义是,通过直接或者间接形式测量风洞中作用于模型上的气动力(包括力矩). 但实际上,激波风洞以及其他脉冲风洞的天平感知的是模型与支承结构之间的相对运动或相对运动趋势形成的内力,即前面所说 的气动力与惯性力之间的差值,这与模型所承受的气动力并不等价. 换言之,传统意义上的气动力测量在激波风洞中存在理论上的缺陷.
激波风洞实验过程中测力系统的振动是由起动过程形成的冲击载荷引起,最终在气动力平衡位置附近形成的周期性运动. 天平的 测量结果可以理解为真实气动力和振动干扰造成的影响量的叠加,目前处理方法大致分为两类. 第1类是提高测力系统固有频率,使得天平信号在有效的实验时间中出现更多振动周期,这对于小型风洞效果明显,但大型风洞 尾撑式测力系统尺寸庞大、结构复杂,其一阶振动频率可能仅为10$\sim$30Hz,大幅度提高其自振频率几乎难以实现. 第2类方法包括采用加速度计测力技术、惯性自补偿测力技术以及传统的加速度惯性补偿测力技术等. 加速度计天平测力[8]适用于极短脉冲型风洞(试验时间约几毫秒)测力,对于大型激波风洞不适用. 惯性自补偿测力技术通过比对天平信号中的与振动特性类似的信号(频率一致或接近),并将该类似信号从天平信号中"补偿"掉, 缺乏振动干扰的具体分析,可能将有效信号"补偿"掉,或对无效信号"未补偿". 此外,国内外学者采用惯性补偿测力天平技术[9, 10, 11],在天平测力的同时测量测力元件的加速度,但是其主要制约 在于如何选取合适的位置安装加速度计. 此外还有模型自由飞测力技术[12, 13]以及采用应力波天平测力的技术,由于这几类方法自身特点限制或技术有待 改进,在大型激波风洞中使用存在较大难度. 模型自由飞测力技术排除(或降低)了支承结构的干扰,但测量系统复杂、昂贵,并且对于大尺度模型难以适用;郭大华 等[14]采用支撑系统不约束天平全部自由度的方法,减少支撑系统的干扰. 这一方法的天平结构较为复杂,且并未能完全消除天平本身振动的干扰. 对于应力波天平,由于其校准技术、数据处理方法不同于常规应变天 平[15],需要进一步研究. 虽然上述两类处理方法取得了一定的效果,但在很大程度上依靠实验者的经验,导致精度受到较多制约,并且难以获得理论支持.
中国科学院力学研究所成功研制复现高超声速飞行条件激波风洞(JF12),可以复现25$\sim$40km高空、马赫数5$\sim$9飞行 条件,喷管出口直径可达2.5m,试验段直径3.5m,最大可进行长度 为6$\sim$8m 的飞行器气动实验. 对于类似的大型激波风洞,国内外都尚未形成解决振动干扰气动力测量的方法,实验研究更是缺乏理论的指导和支持. 本文针对JF12激波风洞的尾撑式测力系统,将飞行器模型、内式应变天平、模型支杆简化为等截面悬臂梁,采用理论分析的 方法,研究测力系统振动对气动力测量的影响. 需要说明的是,由于实际的尾撑式测力结构较为复杂,简化为等截面悬臂梁相当于对实际结构刚度以及质量分布的不均匀性作了简化. 这两种因素的改变将显著影响结构的自振频率,因此对于自振频率的定性分析不能采用等截面悬臂梁模型. 但是对于各阶振型来讲,由于尾撑式测力支撑的结构形式特点,其基本构型为悬臂梁,整体振动特性(如振型基本形状、振型节点数量等)与等截面悬臂梁类似. 不同截面处位移是由各阶振型叠加得到. 再进一步,俯仰力矩干扰量以及法向力干扰量是由位移函数对空间位置$x$求偏导数得到,因而实际结构气动力干扰量分布规律可通过对悬臂梁简化模型的分析来进行定性说明,从而得到具有一定普适性规律的结论.
本文首先讨论了自由振动情形下各振型对气动力各分量的干扰形式和规律;进一步假设不同类型的冲击载荷,求解系统对应的振动特性;结合振型分析,考察单个振型对气动力各分量的干扰规律,并依此分析强迫振动情形下不同振型对气动力各分量的干扰形式和规律,比较不同振型对气动力测量干扰的相对大小.
1 测力系统简化模型建立及研究方法JF12激波风洞测力系统由弯刀机构、模型支杆、内式应变天平、飞行器模型组成. 考虑到实际情形,弯刀机构刚度远大于其他部分,理论分析中可将弯刀与模型支杆相接处视作固定端,将测力系统的飞行器模型、内式应变天平、模型支杆简化为等截面悬臂梁,天平简化为梁上的某一截面. 不同实验对应不同长度和重量的模型,因此在简化模型中以天平测力截面相对于根部处于不同位置进行对应. 由于振动干扰对法向力以及俯仰力矩测量影响更为突出,本文主要对悬臂梁的横向振动进行了讨论. JF12激波风洞支承机构设计标准为承受5t冲击载荷,假定系统振动及受力产生的变形分析均在线 弹性范围内;由于实验时间较短,与振动周期可比,可以忽略振幅衰减和阻尼项;系统结构振动的振幅为小量,不影响实验模型姿态,忽略流动和结构变形的耦合作用;系统的实际结构长细比大于5,采用伯努利$\!$-$\!$-$\!$欧拉梁模型进行分析.
坐标系定义为悬臂梁轴向为$x$方向,$y(x,t)$表示振动对应的位移,选取基本参考量为特征长度$L$,特征弹性 模量$E_{\rm c}$,特征密度$\rho_{\rm c}$,无量纲化后等截面梁横向自由振动方程为
| $\bar{E}\bar{I}\frac{{{\partial }^{4}}\bar{y}\left( \bar{x},\bar{t} \right)}{\partial {{{\bar{x}}}^{4}}}+\bar{\rho }\bar{A}\frac{{{\partial }^{2}}\bar{y}\left( \bar{x},\bar{t} \right)}{\partial {{{\bar{t}}}^{2}}}=0$ | (1) |
相关的无量纲参数$\bar {x} = x /L$,$\bar {y} = y / L$,$\bar {\rho } = \rho /{\rho _{\rm c} }$,$\bar {E} = E /{E_{\rm c} }$,截面积$\bar {A} = A /{L^2}$,抗弯刚度$\bar {I} = I /{L^4}$,时间$\bar {t} = t /{T_{\rm c} }$,其中$T_{\rm c} = \sqrt {{\rho _{\rm c} L^2} /{E_{\rm c} }} $.
本文后续分析中将统一省去各物理量上的横线. 自由振动方程(1)的通解[16]为
| $y(x,t)=Y(x)T(t)\text{ }$ | (2) |
其中
$$\begin{align} & {{Y}_{i}}\left( x \right)={{C}_{i}}\{\cos \left( {{\beta }_{i}}x \right)-\text{ch}\left( {{\beta }_{i}}x \right)+\qquad \\ & \ \ \ \ \ \ \ \ {{r}_{i}}\left[\sin \left( {{\beta }_{i}}x \right)-\text{sh}\left( {{\beta }_{i}}x \right) \right]\} \\ & \ \ \ T\left( t \right)=b\sin (\omega t+\varphi ) \\ \end{align}$$对于梁横向强迫振动,选取同样的基本参考量,得到无量纲振动方程
| $EJ\frac{{{\partial }^{4}}y(x,t)}{\partial {{x}^{4}}}+\rho A\frac{{{\partial }^{2}}y(x,t)}{\partial {{t}^{2}}}=P(x,t)\delta (x-l)\text{ }$ | (3) |
其中无量纲参数与自由振动选取一致,载荷的特征量取为$E_{\rm c} L^2$,$\delta \left( { {x} - l} \right)$表示载荷相对作用位置.
振动方程(3)的解[16] 为
| $y\left( x,t \right)=\text{ }\sum\limits_{i=1}^{\infty }{\frac{{{Y}_{i}}\left( x \right)}{{{\omega }_{i}}}}\int_{0}^{t}{{{q}_{i}}\left( \tau \right)\sin \left[{{\omega }_{i}}\left( t-\tau \right) \right]\text{d}\tau }$ | (4) |
其中,广义力
$${{q}_{i}}\left( t \right)=\int_{0}^{1}{P\left( x,t \right)\delta \left( x-l \right){{Y}_{i}}\left( x \right)\text{ d}x}\text{ }$$俯仰力矩干扰量及法向力干扰量可以由位移表达式通过微分形式写为
| $$M\left( x,t \right)=EI\frac{{{\partial }^{2}}y\left( x,t \right)}{\partial {{x}^{2}}}$$ | (5) |
| $Q\left( {x,t} \right) = EI\dfrac{\partial ^3y\left( {x,t} \right)}{\partial x^3}$ | (6) |
以此上述理论公式为基础进行后续的分析和讨论. 比较自由振动和强迫振动的解式(2)和式(4)的形式,俯仰力矩干扰量、法向力干扰量均可采用级数形式描述为
| $M\left( x,t \right)=\sum\limits_{i=1}^{\infty }{{{A}_{Mi}}\left( x \right)}\sin \left( {{\omega }_{i}}t+{{\varphi }_{i}} \right)$ | (7) |
| $Q\left( x,t \right)=\text{ }\sum\limits_{i=1}^{\infty }{{{A}_{Qi}}\left( x \right)}\sin \left( {{\omega }_{i}}t\text{ + }{{\varphi }_{i}} \right)$ | (8) |
各振型对俯仰力矩干扰量的影响规律可以通过自由振动特性分析得到. 结合式(7)俯仰力矩干扰量级数形式,各振型俯仰力矩干扰量幅值为
| $\begin{align} & {{A}_{Mi}}\left( x \right)=EI{{b}_{i}}{{C}_{i}}\beta _{i}^{2}\{-\cos \left( {{\beta }_{i}}x \right)-\text{cosh}\left( {{\beta }_{i}}x \right)- \\ & \ \ \ \ \ \ \ {{r}_{i}}\left[\sin \left( {{\beta }_{i}}x \right)+\text{sinh}\left( {{\beta }_{i}}x \right) \right]\} \\ \end{align}$ | (9) |
干扰量幅值代表了振动对气动力测量的干扰程度,其幅值大小与振型阶数$i$以及截面位置$x$有关. 自由振动情形下,各振型对应的$EIb_i C_i \beta _i ^2$分别为不同常数,暂不作讨论,令
| $m_i \left( x \right) = - \cos \left( {\beta _i x} \right)-{\rm cosh} \left( {\beta _i x} \right) - r_i \left[ {\sin \left( {\beta _i x} \right) + {\rm sinh}\left( {\beta _i x} \right)} \right]$ | (10) |
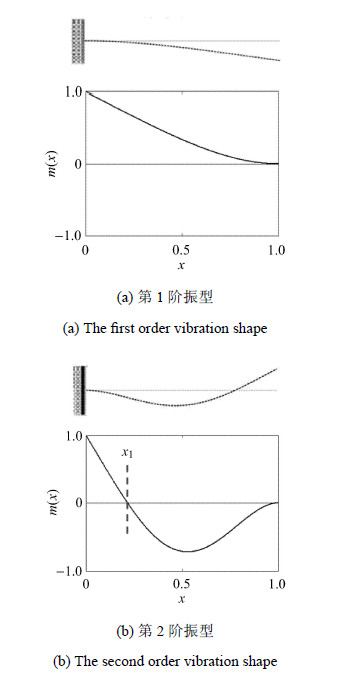
可采用$m_{i}(x)$对各阶振型干扰量幅值展开讨论,以第1、2阶振型对应的$m_{i}(x)$分布为例,并对其分布进行归一化处理,以固定端$m_{i} \ (0)=1$,分别如图 1所示. 经分析可得到:
|
图 1 测力结构自由振动振型及对应的$m_{i}(x)$分布 Fig.1 The free vibration shapes of force measurement structure and corresponding $m_{i}(x)$ distribution |
(1) 在$x=1$位置附近,各阶振型对应的俯仰力矩干扰量幅值较小. 此时对应于实际中飞行器模型长度或质量较小的情形,天平的相对位置接近$x=1$,振动对俯仰力矩干扰较小.
(2) 在第$i$阶振型($i\ge 2$),总存在$i-1$个"零点位置"($x \ne 1$),如图 1(b)中的$x=x_{1}$位置,在这些位置振型对应的俯仰力矩干扰量幅值为0,也就是说当天平处于该振型的零点位置时,则该振型对应的振动对俯仰力矩的测量无影响.
(3) 传统加速度惯性补偿存在理论上的缺陷. 进一步分析振型对应的加速度,其表达式可以由位移$y$对时间$t$求二次偏导数求得,各阶振型对应的加速度幅值可以表示为
| $a_i \left( x \right) = \cos \left( {\beta _i x} \right)-{\rm cosh}\left( {\beta _i x} \right) + r_i \left[ {\sin \left( {\beta _i x} \right)-{\rm sinh} \left( {\beta _i x} \right)} \right] $ | (11) |
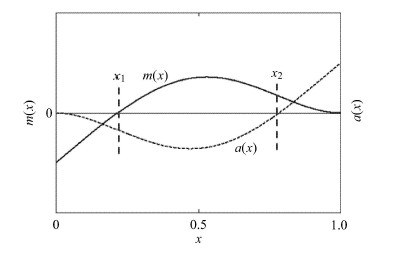
以第2阶振型为例,对应的$m_{2}(x)$和$a_{2}(x)$及其分布如图 2所示,振型对俯仰力矩的干扰及其分布与其对应的加速 度分布规律并不一致,尤其是理论上$m_{i}(x)$与$a_{i}(x)$各自的"零点位置"不重合. 在传统的加速度惯性补偿中,这可能会造成误补偿或零补偿. 以第2阶振型为例,在$x=x_{1}$位置处,第2阶振型对俯仰力矩的影响量幅值为0,但其对应的加速度信号幅值却不为0, 若天平处于该位置时,以加速度信号补偿俯仰力矩的测量结果是不可行的;另外,在$x=x_{2}$位置,第2阶振型对应的加速 度幅值为0,而振型对俯仰力矩的干扰量幅值却不为0,若天平处于该位置时,却无法采集加速度对应的信号对俯仰力矩进行补偿.
|
图 2 第2阶振型对应的俯仰力矩幅值$m(x)$和加速度幅值$a(x)$分布 Fig.2 The distribution of pitching moment amplitude $m(x)$ and acceleration amplitude $a(x)$ of the second vibration shape |
与俯仰力矩干扰量类似,各振型对法向力干扰量的影响规律亦可以通过自由振动特性分析得到. 结合式(8)法向力干扰量级数形式,各振型法向力干扰量幅值为
| $\begin{align} & {{A}_{Qi}}\left( x \right)=EJ{{b}_{i}}{{C}_{i}}\beta _{i}^{3}[\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)-\qquad \\ & \ \ \ \ \ \ \ {{r}_{i}}(\cos ({{\beta }_{i}}x)+\text{cosh}({{\beta }_{i}}x))] \\ \end{align}$ | (12) |
同样,法向力各阶干扰量幅值代表了振动对气动力测量的干扰程度,其大小与振动阶数$i$以及截面位置$x$有关. 自由振动情形下,各振型对应的$EJb_i C_i \beta _i ^3$分别为不同常数,暂不做讨论,令
| $\begin{align} & {{q}_{i}}(x)=\sin \left( {{\beta }_{i}}x \right)-\text{sinh}\left( {{\beta }_{i}}x \right)- \\ & \ \ \ \ \ \ \ \ \ {{r}_{i}}\left[\cos \left( {{\beta }_{i}}x \right)+\text{cosh}\left( {{\beta }_{i}}x \right) \right] \\ \end{align}$ | (13) |
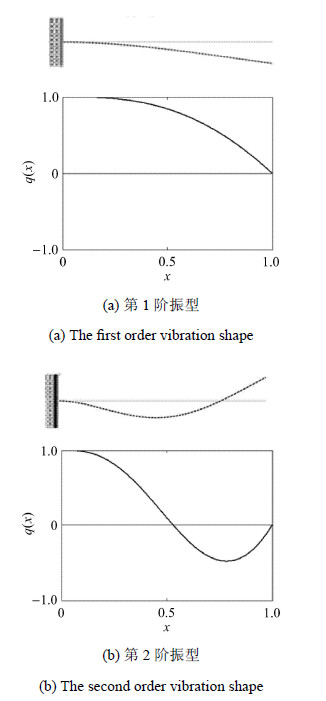
可采用$q_{i}(x)$对各阶振型干扰量幅值展开讨论,以第1、2阶振型对应的$q_{i}(x)$分布为例,并以固定端 $q_{i} (0)=1$对其分布进行归一化处理,分别如图 3(a)和图 3(b)所示,可以获得与2.1中类似的结论.
|
图 3 测力系统自由振动振型及对应的$q_{i}(x)$分布图像 Fig.3 The free vibration shape of force measurement structure and corresponding $q_{i}(x)$ distribution |
(1) 在$x =1$位置附近,各阶振型对法向力干扰量幅值较小. 即若实验中飞行器模型长度或质量较小,天平的相对位置接近$x =1$,振动对法向力及俯仰力矩干扰较小.
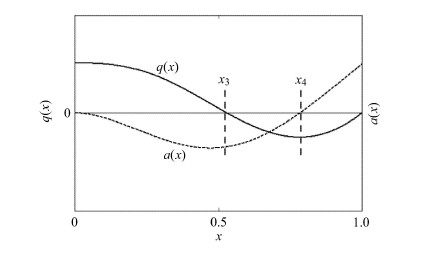
(2) 在第$i$阶振型($i\ge 2$),$q_{i}(x)$总存在$i -1$个"零点位置"($x \ne 1$),如图 4中的$x=x_{3}$位置,在这些位置振型对应的法向力干扰量幅值为0,也就是说当天平处于该振型所对应 的$q_{i}(x)$零点位置时,则该振型对应的振动对法向力的测量无影响.
|
图 4 第2阶振型对应的法向力幅值$q(x)$和加速度幅值$a(x)$分布 Fig.4 The distribution of normal force amplitude $q(x)$ and acceleration amplitude $a(x)$ of the second order vibration shape |
(3) 传统加速度惯性补偿理论上存在的缺陷在对法向力干扰补偿中仍有所体现. 与俯仰力矩干扰量类似,$ q_{i}(x)$与$a_{i}(x)$各自 的"零点位置"不重合,以如图 4所示第二阶振动为例,$q_{2}(x)$与$a_{2}(x)$的零点分别位于$x=x_{3}$及$x=x_{4}$两处不同的 位置,导致对法向力补偿中也可能存在误补偿或零补偿.
3 不同冲击载荷作用下振动对气动力干扰量影响规律振型之间气动力干扰量分析可以通过强迫振动特性分析得到. 强迫振动中载荷形式主要研究了以下3种可能与实际情况相接近的 载荷形式:简谐载荷、单个矩形脉冲载荷以及抛物线载荷,如图 5所示. 简谐载荷因其构造的特殊性,可以组合形成其他载荷;单个矩形脉冲载荷则类似于天平的动态校准过程[10]中力的施加过程; 抛物线载荷是考虑简单外形飞行器模型周围流场建立过程中,气动力加载过程可能是与时间的平方有关.
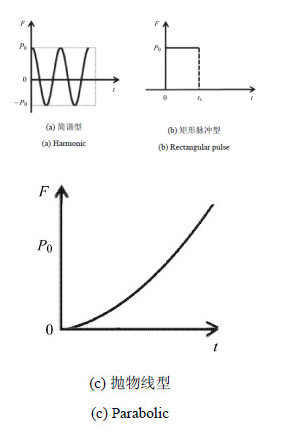
|
图 5 3种不同加载形式示意图 Fig.5 Schematics of three different loads |
对于简谐载荷,$P(x,t) = P_0 \delta (x - 1)\cos \omega t$,简谐载荷频率 $\omega ={{\omega }_{1}}+\Delta ({{\omega }_{2}}-{{\omega }_{1}})$,$\Delta $取0.2,0.5,0.8,其中,$\omega_1$,$\omega_{2}$为梁横向振动第1, 2阶频率.
位移解
| $\begin{align} & y(x,t)=\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)}{{{\omega }^{2}}-\omega _{i}^{2}}}\{\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+ \\ & \ \ \ \ \ \ \ \ \ \ \ {{r}_{i}}[\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\}(\cos {{\omega }_{i}}t-\cos \omega t) \\ \end{align}$ | (14) |
振动对俯仰力矩的干扰量
| $\begin{align} & M(x,t)=\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)\beta _{i}^{2}}{{{\omega }^{2}}-\omega _{i}^{2}}}\{-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+ \\ & \ \ \ \ \ \ \ {{r}_{i}}[-\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\}[\cos ({{\omega }_{i}}t)-\cos (\omega t)] \\ \end{align}$ | (15) |
振动对法向力干扰量
| $\begin{align} & Q(x,t)=\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)\beta _{i}^{3}}{{{\omega }^{2}}-\omega _{i}^{2}}}\{\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)+ \\ & \ \ \ \ \ \ {{r}_{i}}[-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)]\}[\cos ({{\omega }_{i}}t)-\cos (\omega t)] \\ \end{align}$ | (16) |
为进一步说明理论推导结果的可靠性,将式(14)推导得到的结果有量纲化后与数值计算结果进行比较,两者吻合较好,如图 6所示. 采 用《ANSYS》有限元分析软件进行数值计算,计算模型为等截面悬臂梁模型,后续计算中的方法以及模型与此相同,不再赘述. 取等截面悬臂梁长度为1m,矩形截面尺寸为0.1m$\times $0.1m,弹性模量200GPa,密度为7850kg/m$^{3}$,外载荷频率为450rad/s,$P_{0}=10000$N,载荷作用时间0.02s.
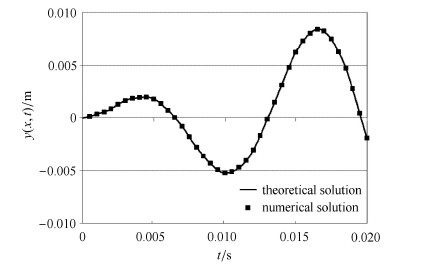
|
图 6 简谐载荷作用下位移$y(x,t)$理论解和数值解 Fig.6 Theoretical and numerical solution of the displacement $y(x,t)$ under the harmonic load |
对于单个矩形脉冲载荷,其中$P(x,t) = P(t)\delta (x - 1)$,其中$P(t)=\left\{ \begin{array}{*{35}{l}} {{P}_{0}},& 0\le t\le {{t}_{\text{s}}} \\ 0,& \text{else} \\ \end{array} \right.$.
位移解
| $y(x,t)=\left\{ \begin{align} & \begin{array}{*{35}{l}} \sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{Y}_{i}}(1){{P}_{0}}}{\omega _{i}^{2}}}\{\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+\text{ } \\ \end{array} \\ & \ \ \ \ \ \ \ \ \ {{r}_{i}}[\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\}[1-\cos ({{\omega }_{i}}t)],\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0\le t\le {{t}_{\text{s}}} \\ & \text{ }\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{Y}_{i}}(1){{P}_{0}}}{\omega _{i}^{2}}}{{W}_{i}}(x)\{[1-\cos ({{\omega }_{i}}{{t}_{\text{s}}})]\cos [{{\omega }_{i}}(t-{{t}_{\text{s}}})]+ \\ & \ \ \ \ \ \ \ \ \sin ({{\omega }_{i}}{{t}_{\text{s}}})\sin [{{\omega }_{i}}(t-{{t}_{\text{s}}})]\},\ \ \ \ \ \text{ }t>{{t}_{\text{s}}} \\ \end{align} \right.$ | (17) |
仅考虑$0\le t\le {{t}_{\text{s}}}$时间段内振动,有
振动对俯仰力矩的干扰量
| $\begin{align} & M(x,t)=\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{Y}_{i}}(1){{P}_{0}}\beta _{i}^{2}}{\omega _{i}^{2}}}\{-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+\qquad \\ & \ \ \ \ \ \ \ \ {{r}_{i}}[-\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\}[1-\cos ({{\omega }_{i}}t)] \\ \end{align}$ | (18) |
振动对法向力的干扰量
| $ \begin{align} & Q(x,t)=\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{Y}_{i}}(1){{P}_{0}}\beta _{i}^{3}}{\omega _{i}^{2}}}\{\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)+\qquad \\ & \ \ \ \ \ \ \ \ \ {{r}_{i}}[-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)]\}[1-\cos ({{\omega }_{i}}t)] \\ \end{align}$ | (19) |
为进一步说明理论推导结果的可靠性,将式(17)推导得到的结果有量纲化后与数值计算结果进行比较,两者吻合较好,如图 7所示. 等截面悬臂梁长度为1m,矩形截面尺寸为0.1m$\times $0.1m,弹性模量200GPa,密度为7850kg/m$^{3}$,$P_{0} =10000$N.
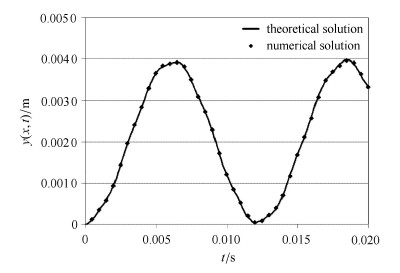
|
图 7 单个矩形脉冲载荷作用下位移$y(x, t)$理论解和数值解 Fig.7 Theoretical and numerical solution of the displacement $y(x, t)$ under a rectangular pulse load |
对于抛物线载荷,$P\left( {x,t} \right) = P_0 t^2\delta \left( {x - 1} \right)$,位移解
| $\begin{align} & y(x,t)\ =\ \sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)}{\omega _{i}^{2}}}\{\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+\qquad \\ & \ \ \ \ \ {{r}_{i}}[\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\}\left[{{t}^{2}}-\frac{2}{\omega _{i}^{2}}+\frac{2}{\omega _{i}^{2}}\cos ({{\omega }_{i}}t) \right] \\ \end{align}$ | (20) |
振动对俯仰力矩的干扰量
| $\begin{align} & M(x,t)=EI\sum\limits_{i=1}^{\infty }{\frac{{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)}{\omega _{i}^{2}}}\beta _{i}^{2}\{-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+\qquad \\ & \ \ \ \ \ \ \ {{r}_{i}}[-\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\}\left[{{t}^{2}}-\frac{2}{\omega _{i}^{2}}+\frac{2}{\omega _{i}^{2}}\cos ({{\omega }_{i}}t) \right] \\ \end{align}$ | (21) |
振动对法向力的干扰量
| $\begin{align} & Q(x,t)=\sum\limits_{i=1}^{\infty }{\frac{EI{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)}{\omega _{i}^{2}}}\beta _{i}^{3}\{\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)+\qquad \\ & \ \ \ \ \ \ \ \ {{r}_{i}}[-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)]\}\left[{{t}^{2}}-\frac{2}{\omega _{i}^{2}}+\frac{2}{\omega _{i}^{2}}\cos ({{\omega }_{i}}t) \right] \\ \end{align}$ | (22) |
为进一步说明理论推导结果的可靠性,将式(20)推导得到的结果有量纲化后与数值计算结果进行比较,两者吻合较好,如图 8所示. 等截面悬臂梁长度为1m,截面尺寸为0.1m$\times $0.1m,弹性模量200GPa,密度为7850kg/m$^{3}$,$P_{0} =10000$N.
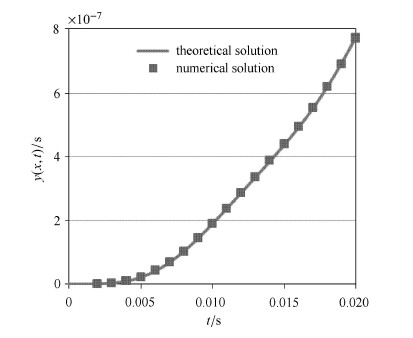
|
图 8 抛物线载荷作用下位移$y (x,t)$理论解和数值解 Fig.8 Theoretical and numerical solution of the displacement $y(x,t)$ under a parabolic load |
在强迫振动下,总干扰量是由各阶干扰量叠加得到. 与单个振型干扰量大小讨论方式相同,这里着重关注振动对俯仰力矩干扰量幅值$A_{Mi} ( x )$,其对应为式(15),(18)和式(21) 中不包含时间$t$的项. 例如式(21)中,对于抛物线载荷,俯仰力矩干扰量幅值
| $\begin{align} & {{A}_{Mi}}(x)=\frac{EI{{C}_{i}}{{P}_{0}}{{Y}_{i}}(1)}{\omega _{i}^{2}}\beta _{i}^{3}\{\sin ({{\beta }_{i}}x)- \\ & \ \ \ \ \ \ \ \text{sinh}({{\beta }_{i}}x)+{{r}_{i}}[-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)]\} \\ \end{align}$ | (23) |
令
| ${{\eta }_{i}}\left( x \right)=\left| {{A}_{Mi}}\left( x \right) \right|/\sum\limits_{i=1}^{\infty }{\left| {{A}_{Mi}}\left( x \right) \right|\text{ }}$ | (24) |
该参数代表同一位置处各阶振动干扰量幅值与幅值总和的百分比. 总体上来讲,13阶之后振动干扰量幅值小于被激发振型幅值的1%,因此选取前12阶振动进行分析. 经分析可得在强迫振动过程中,振型间干扰量相对大小与以下因素有关.
(1) 测力截面所处位置不同,干扰量中占主导的阶数不同.
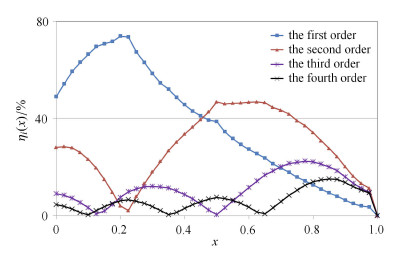
以简谐载荷( $\Delta =0.2$,端部加载)俯仰力矩干扰量为例,各阶俯仰力矩干扰量幅值解析表达如式(25)所示. 图 9中显示了前4阶振动干扰量幅值相对大小. 靠近悬臂梁根部位置,干扰量主要来自1,2阶,第1阶影响大于第2阶;在$x >0.5$时,第2阶的影响超越了第1阶;在靠近自由端位置处,3,4阶以及较高阶影响与1,2阶可比. 实验中,采用不同的模型以及支撑结构对应于天平处在不同位置,气动力干扰量主要来源不同.
| $ \begin{align} & {{A}_{Mi}}(x)=EI{{P}_{0}}\frac{C_{i}^{2}{{W}_{i}}(1)\beta _{i}^{2}}{{{\omega }^{2}}-\omega _{i}^{2}}\{-\cos ({{\beta }_{i}}x)- \\ & \ \ \ \ \ \ \ \ \ \ \ \text{cosh}({{\beta }_{i}}x)+{{r}_{i}}[-\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\} \\ \end{align}$ | (25) |
|
图 9 简谐载荷作用下($\Delta =0.2$)前4阶振型对俯仰力矩干扰量的相对大小 Fig.9 Relative magnitude of interference to pitching moment by the four-order vibration shapes under a harmonic load ($\Delta =0.2$) |
(2) 不同阶振型节点数量及所处位置不同,若载荷作用位置与某阶振型节点接近,则该阶振动未被激发,所带来的干扰 量可忽略.
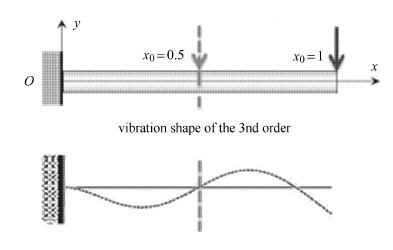
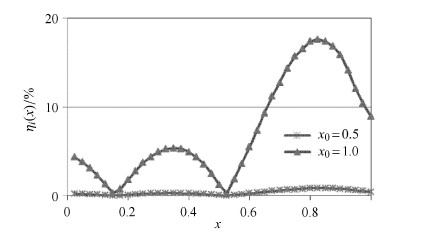
以单个矩形脉冲载荷作用下俯仰力矩干扰量为例,作用在任意位置$x_{0}$位置处的载荷,俯仰力矩干扰量解析表达如式(26). 图 10和图 11分别显示了载荷分别作用在两个不同位置时,第3阶振型对应的俯仰力矩干扰量. 由于$x_{0} =0.5$位置较靠近第3阶振型节点,在整个梁上,第3阶振动引起干扰量几乎处处为零,即该情况下第3阶振动未被激发. 而$x_{0} =1$情况下,第3阶振动对于气动力干扰相对比较明显.
| $\begin{align} & {{A}_{Mi}}\left( x \right)=\frac{\rho A{{P}_{0}}C_{i}^{2}{{W}_{i}}({{x}_{0}})}{\beta _{i}^{2}}\{-\cos ({{\beta }_{i}}x)-\text{cosh}({{\beta }_{i}}x)+\qquad \\ & \ \ \ \ \ \ {{r}_{i}}[-\sin ({{\beta }_{i}}x)-\text{sinh}({{\beta }_{i}}x)]\} \\ \end{align}$ | (26) |
|
图 10 分别在两个不同位置加载及第3阶振型示意图 Fig.10 Schematic of loads acting on two different positions and the third order vibration shape |
|
图 11 载荷在两个不同位置分别作用时第3阶振型对俯仰力矩干扰量的相对大小 Fig.11 Relative magnitude of interference to pitching moment by the third order vibration shape under loads acting on two different positions respectively |
(3) 外激励载荷不同,干扰量主要来源的阶数不同.
表 1给出了不同载荷端部加载情况下俯仰力矩干扰量主要来源,"$\surd $"表示对俯仰力矩干扰量补偿时需考虑该阶振动对俯仰力矩的干扰,箭头("$ \nearrow $")数量表示总体来看干扰量相对大小. 从表 1中得到,不同类型载荷干扰量主要来源不同. 对于单个矩形脉冲载荷 及抛物线载荷,总体来讲,气动力干扰量主要来源于第1阶振动. 即使是同类型的简谐载荷,由于载荷的频率不同,干扰量主要来源不同以及各阶振动相对大小都有所差别.
| 表 1 不同载荷作用下俯仰力矩干扰量的主要来源 Table 1 The main source of pitching moment interferenc under different loads |
(4) 相对于俯仰力矩干扰量分析,法向力干扰量的分析需考虑更高阶的振型.
对比表 1及表 2,以3种简谐载荷为例,总体上来讲,表 1中第3, 4阶振型对俯仰力矩干扰量基本均可以忽略,而对于表 2中法向力干扰量,第3,4阶振型的影响与第1,2阶振型的影响可比. 因此,相对于俯仰力矩干扰量分析,法向力干扰量的分析需考虑更高阶的振型.
| 表 2 不同载荷作用下法向力干扰量主要来源 Table 2 The main source of normal force interference under different loads |
本文应用振动力学理论对测力系统简化模型的自由振动、强迫振动特性进行研究,获得了自由振动各振型 对气动力测量的干扰规律,并在此基础上分析了不同类型冲击载荷引起强迫振动对气动力测量的干扰,以及各振型对气动 力干扰量的比较. 由于俯仰力矩干扰量幅值或法向力干扰量幅值与加速度幅值的"零点位置"不重合,可能会造成误补偿或零补偿,所以传统加速度惯性补偿存在理论上的缺陷. 实验中确定干扰量主要来源需要综合考虑截面位置、载荷作用位置、载荷类型的影响,相对于俯仰力矩干扰量的分析,法向力干扰量的分析需要考虑更高阶振型的影响. 振型节点以及俯仰力矩干扰量幅值和法向力干扰量幅值的零点具有一定特殊性,加速度计布置在振型节点上则无法测量到加速度;若载荷作用在某阶振型节点位置(或附近),该阶振型在对俯仰力矩及法向力的干扰量均较小(或为0);若天平处于某阶振动俯仰力矩干扰量幅值或法向力干扰量幅值零点位置,则该阶振型对俯仰力矩或法向力干扰量为零.
| 1 | 姜宗林, 李进平, 赵伟等. 长试验时间爆轰驱动激波风洞技术研究. 力学学报, 2012, 44(5): 824-831 (Jiang Zonglin, Li Jinping, Zhao Wei, et al. Investigating into techniques for extending the testduring of detonation-driven shock tunnels. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(5): 824-831 (in Chinese)) |
| 2 | Lynn KC, Commo SA, Parker PA. Wind-tunnel balance characterization for hypersonic research applications. Journal of Aircraft,2012, 49(2): 556-565 |
| 3 | 唐志共, 许晓斌, 杨彦广等. 高超声速风洞气动力试验技术进展. 航空学报, 2015, 36(1): 86-97 (Tang Zhigong, Xu Xiaobin, Yang Yanguang, et al. Research progress on hypersonic wind tunnel aerodynamic testing techniques. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 86-97 (in Chinese)) |
| 4 | Robinson MJ, Mee DJ, Tsai CY, et al. Three-component force measurements on a large scramjet in a shock tunnel. Journal of Spacecraft and Rockets, 2004, 41(3): 416-425 |
| 5 | Smith AL, Mee DJ, Daniel WJT, et al. Design, modelling and analysis of six component force balance for hypervelocity wind tunnel testing. Computers & Structures, 2001, 79(11): 1077-1088 |
| 6 | 谢海斌, 谢红卫, 龙志强. 磁悬挂天平校准关系的非线性拟合. 国防科技大学学报,2001, 23(6): 90-94 (Xie Haibin, Xie Hongwei, Long Zhiqiang. Nonlinear fitness of calibration model of magnetic suspension and balance system. Journal of National University of Defense Technology, 2001, 23(6): 90-94 (in Chinese)) |
| 7 | 刘慧敏, 尹力明. 磁悬挂天平俯仰电磁场的二维有限元分析. 计算机仿真, 2005, 22(8): 37-49 (Liu Huimin, Yin Liming. The 2D finite element analysis of msbs lifting electro magnetic field. Computer Simulation, 2005, 22(8): 37-49(in Chinese)) |
| 8 | 罗也凡, 毕志献. 脉冲型风洞用加速度计测力天平. 气动实验与测量控制, 1996, 10(1): 59-64 (Luo Yefan, Bi Zhixian. The accelerometer force balance used in the impulse wind tunnel. Aerodynamic Experiment and Measurement & Control, 1996, 10(1): 59-64 (in Chinese)) |
| 9 | 程忠宇, 陈宏, 张琦. 多加速度计振动分离惯性补偿测力技术. 实验流体力学, 1999, 13(4): 57-61 (Cheng Zhongyu, Chen Hong, Zhang Qi. Inertia compensation technology based on multiaccelerometer vibration separating. Journal of Experiments in Fluid Mechanics, 1999, 13(4): 57-61 (in Chinese)) |
| 10 | Smolinski G. Proof of concept for testing acceleration compensation force balance techniques in short duration flows with a CEV capsule. AIAA Paper, 2007-1010, 2007 |
| 11 | Marineau E, MacLean M, Mundy E, et al. Force measurements in hypervelocity flows with an acceleration compensated strain gage balance. Journal of Spacecraft and Rockets, 2012, 49(3): 474-482 |
| 12 | 贾区耀, 杨益农, 蒋增辉. 风洞自由飞实验结果的精度、准度. 宇航学报, 2009, 30(6): 2082-2085 (Jia Quyao, Yang Yinong, Jiang Zenghui. The precision and accuracy of wind tunnel free-flight experiment result. Journal of Astronautics, 2009, 30(6): 2082-2085 (in Chinese)) |
| 13 | Laurence SJ, Hornung HG. Image-based force and moment measurement in hypersonic facilities. Experiments in Fluids, 2009,46(2): 343-353 |
| 14 | 郭大华, 高冰, 林贞彬. 脉冲风洞中新型自由天平探索. 流体力学实验与测量, 2003, 17(1): 68-72 (Guo Dahua, Gao Bing, Lin Zhenbin. The exploration of a new kind of free-released balance in impulsive wind tunnels. Experiments and Measurement in Fluid Mechnics, 2003, 17(1): 68-72 (in Chinese)) |
| 15 | 刘洪山, 徐翔, 姜华等. 应力波天平在国内激波风洞上的应用. 实验流体力学, 2006, 20(1): 36-39 (Liu Hongshan, Xu Xiang, Jiang Hua, et al. The application of the stress wave force balance in shock tunnel in China. Journal of Experiments in Fluid Mechanics, 2006,20(1): 36-39 (in Chinese)) |
| 16 | 倪振华. 振动力学. 西安:西安交通大学出版社,1989 (Ni Zhenhua. Vibration Mechanics. Xi'an: Xi'an JiaoTong University Press,1989 (in Chinese)) |
 2016, Vol. 48
2016, Vol. 48

