2. 国家计算流体力学实验室, 北京 100191
随着适于不同需求的空天飞行器研制发展,跨越飞行从连续流到稀薄流各流域的飞行器会遇到各种复杂的跨流域气动问题,而不同流域的气体性质差别很大,尤其是近连续滑移过渡流区,在实验技术、数值模拟手段和理论阐述方面都难于获取可靠的气动数据. 为准确模拟跨流域气动问题,需要发展建立统一的理论模型与数值模拟方法[1, 2].
基于速度分布函数的玻尔兹曼方程作为气体动理论的基本方程[3],能描述各流域微观分子输运现象,其零阶和一阶查 普曼-恩斯科(Chapman-Enskog)展开[3]可得到欧拉方程和纳维斯托克斯方程,另一方面,直接模拟蒙特 卡洛方法的解在模拟分子数趋于无穷时收敛于玻尔兹曼方程解[4, 5]. 若能发展某种途径方法求解玻尔兹曼方程,可以建立起一种统一的求解从连续流到自由分子流跨流域空气动力学问题的算法,但 由于其复杂的非线性多维积分-微分属性导致直接精确求解很困难.
近似求解玻尔兹曼方程的方法很多,其中模型方程方法应用较广泛,其松弛项具备玻尔兹曼方程碰撞项的主要特征,常用 的模型方程有巴特纳加-格罗斯-克鲁克模型[6],简称 BGK 模型、 椭球统计巴特纳加-格罗斯-克鲁克模型,简称 ES-BGK [7]、 沙克霍夫(Shakhov)模型[8]等. 在各种模型方程被提出后,国际上即有学者利用计算流体力学技术,从 BGK 等模型方程出 发,将离散坐标法用于速度空间的离散,把模型方程转换为偏微分方程组,应用有限差分格式建立了求解一维、二维模型方程的方 法,并对激波管问题、圆柱绕流、槽道传热等问题进行了模拟分析[9, 10, 11]. 麦尤森斯 [12]发展了一种满足守恒规则和熵耗散原理的离散速度模型,用于 BGK 和 ES-BGK 模型方程模拟较高马赫数流动问题,其可行性已分别在一维、二维及轴 对称稀薄气体流动问题研究方面得到证实[13]. 徐昆等[14]利用上述离散速度坐标法计算原理与 BGK 格式[15]相耦合发展了 统一气体动理学格式(UGKS),使之适于模拟稀薄流到连续流跨流域气体流动问题. 李志辉等[2, 16, 17, 18]利用模型方程方法,将不同流域流态控制参数、宏观流动物理量、气体黏性输运特性、热力学 效应及气体分子相互作用规则、分子模型用统一表达式联系起来,结合离散速度坐标法和改进的高斯型多重积分法,建立了求解 玻尔兹曼模型方程的气体运动论统一算法(GKUA),并已成功用于跨流域各类复杂外形飞行器高超声速气动力/热问题研究[2].
由于速度分布函数$f$是关于速度空间与物理空间的多相多维函数,气体运动论统一算法应用于三维绕流问题模拟时,$f$为一个六维数组,求解时需要占用大量计算机内存,因此提高计算效率就显得很重要. 以往研究经验表明[16, 17, 18],如果采用显式格式,计算时间推进步长受格式稳定性条件限制,特别是在计算连续、近连续流区高超声速绕流问题时效率较低,另一方面,物理空间计算网格设计是否合理、质量是否优质,也会直接影响计算收敛的效率.
因此,为了研究提高气体运动论统一算法计算效率与工程实用性,本文拟采用多块对接网格技术,基于上下 对称高斯-赛德尔(LU-SGS)方法与格心型有限体积法求解玻尔兹曼模型方程,模拟不同圆心距离的并 排圆柱绕流问题. 该问题作为模拟多体干扰流动最简单的研究对象之一,其研究结果能为航天器部件设计及试验提供有用的参考[19], 已有众多学者对其进行了试验与数值模拟研究,如科蓬沃勒等[20]、阿莱姆等[21]对其进行了实验研究, 瑞博夫应用直接模拟蒙特卡洛方法分析了其在高马赫数下稀薄流区的相互干扰特点[22]. 本文将在过渡流区域对并排圆柱的气动特性进行模拟分析,并与直接模拟蒙特卡洛方法计算结果对比分析,以检验本文方 法的准确可靠性.
1 控制方程与数值方法 1.1 控制方程本文研究工作基于无量纲化的沙克霍夫模型方程[8, 16],其表达式可写为
| $ \dfrac{\partial f}{\partial t} + {\pmb V} \cdot \dfrac{\partial f}{\partial {\pmb r} } = \nu (f^N - f) $ | (1) |
| $ f^N = f_M \left[{1 + \dfrac{4}{5}(1 - Pr )\dfrac{{\pmb c} \cdot {\pmb q} }{nT^2}\Big (\dfrac{c^2}{T} - \dfrac{5}{2} \Big )} \right] $ | (2) |
| $ f_M = \dfrac{n}{\left( {\pi T} \right)^{3 / 2}}\exp \left( { - \dfrac{c^2}{T}} \right) ,\ \ {\pmb c} = {\pmb V}-{\pmb u} $ | (3) |
| $ \nu = \dfrac{8nT^{1 - \chi }}{5\sqrt \pi Kn} ,\quad Kn = \dfrac{\lambda _\infty }{L_{\rm ref} } $ | (4) |
当$f$已知时,各宏观参数如数密度$n$、速度${\pmb u}$、温度$T$、热流矢量$ {\pmb q}$等可通过下式对$f$取矩得到[3].
| $ \left( {n,nu,\frac{3}{2}nT + n{u^2},q} \right) = \int {\left( {1,V,{V^2},c{c^2}} \right)f} dV $ | (5) |
对于一维、二维气体流动,通过引入约化速度分布函数$^{[9, 16]}$,对速度分量进行离散降维. 利用气体运动论离散速度坐标法,可将玻尔兹曼模型方程化为在相应离散速度坐标点处关于时间、物理空间的非齐次双曲型守恒偏微分方程组,进而可采用计算流体力学中的计算技术进行求解.
1.2 格心型隐式有限体积方法以二维气体流动为例,经离散速度坐标法降维的玻尔兹曼模型方程一般式可写为
| $ \begin{array}{l} \frac{{\partial {f_{\sigma ,\delta }}}}{{\partial t}} + \frac{{\partial ({V_{x\sigma }}{f_{\sigma ,\delta }})}}{{\partial x}} + \frac{{\partial ({V_{y\delta }}{f_{\sigma ,\delta }})}}{{\partial y}} = {S_\nu }\\ {S_\nu } = \nu \left( {f_{\sigma ,\delta }^N - {f_{\sigma ,\delta }}} \right) \end{array} $ |
采用有限体积法求解上述方程时,首先在控制体积$\varOmega _{IJ} $内积分,有
| $ \dfrac{\partial \bar {f}_{IJ} }{\partial t} = - \dfrac{1}{\varOmega _{IJ} } \oint_{\partial \varOmega } {\pmb F} \cdot {\pmb n}ds + \bar {S}_{vIJ} $ | (6) |
其中,$ {\pmb F} = (V_{x\sigma } f_{\sigma ,\delta } ) {\pmb i} + (V_{y\delta } f_{\sigma ,\delta } ) {\pmb j}$,${\pmb n}$为单元控制体边界沿$I$和$J$增大方向的法向量,符号$\bar {X}_{IJ} $表示 量$X_{IJ} $在控制体积$\varOmega _{IJ} $内的平均值.
定义${\pmb A}_n = A \cdot {\pmb n}$,$A = \partial {\pmb F} / \partial f$,$A = \partial \bar {S}_v / \partial f$, 则基于上下对称高斯-赛德尔(LU-SGS)方法和斯特格-瓦明(Steger-Warming)流通矢 量分裂[23],式(6)可分如下几步进行求解,其中网格界面上采用无波动、无自由参数耗散(NND)格式[23]重构.
第1步:采用显式方法计算出$n$时刻的右端项.
第2步:进行向上扫描
| $ \begin{array}{l} \Delta f_{IJ}^ * = \left( {{\Omega _{IJ}}RHS_{IJ}^n + A_{nI - 1/2,J}^ + \Delta {f_{I - 1,J}}\Delta {s_{I - 1/2,J}} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {A_{nI,J - 1/2}^ + \Delta {f_{I,J - 1}}\Delta {s_{I,J - 1/2}}} \right)/\alpha \\ \alpha = \frac{{{\Omega _{IJ}}}}{{\Delta t}} + A_{nI + 1/2,J}^ + \Delta {s_{I + 1/2,J}} - A_{nI - 1/2,J}^ - \Delta {s_{I - 1/2,J}} + \\ \;\;\;\;\;\;A_{nI,J + 1/2}^ + \Delta {s_{I,J + 1/2}} - A_{nI,J - 1/2}^ - \Delta {s_{I,J - 1/2}} - {\Omega _{IJ}}{A_v} \end{array} $ |
第3步:进行向下扫描
| $ \begin{array}{l} \Delta {f_{IJ}} = \Delta f_{IJ}^ * - (A_{nI + 1/2,J}^ - \Delta f_{IJ}^ * \Delta {s_{I + 1/2,J}} + \\ \;\;\;\;\;\;\;\;\;A_{nI,J + 1/2}^ - \Delta f_{IJ}^ * \Delta {s_{I,J + 1/2}})/\alpha \end{array} $ |
第4步:时间推进:$f_{IJ}^{n + 1} = f_{IJ}^n + \Delta f_{IJ} $.
在求得各控制体内$f_{IJ} ^{n + 1}$后,通过积分可得到控制体内各个宏观流动参数.
1.3 物理空间网格处理方法本文采用的网格拓扑结构为对接型多块结构网格,这样能根据块与块之间的连接信息自动处理任意对接关系,块与块之间通过对接面传递流场参数,把对接面邻近单元按内点处理,能有效地保证流场数值通量守恒,易适应于各种复杂外形飞行器绕流.
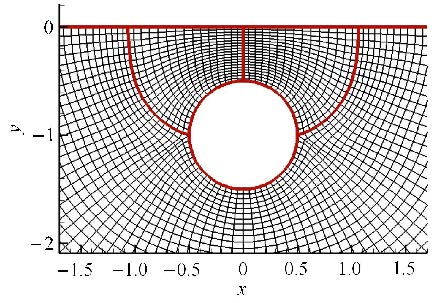
2 近连续过渡流区并排圆柱绕流计算分析作为航天器再入近连续过渡流区多体动力学研究基础,利用上述方法计算分析了两个并排圆柱绕流问题. 图 1绘出了半流场网格布局,定义$H$为两圆柱圆心之间的距离,$D$为圆柱直径.
|
图 1 并排圆柱下半部分绕流场多块对接网格布局 Fig.1 Multiblock patched grid for the flow field |
图 2绘出努森数$Kn_\infty = 0.05$、马赫数$Ma_\infty = 3$在$H$为$2 D$,$4 D$和 $6 D$时本文(图中``GKUA''所示)与直接模拟蒙特卡洛方法所得马赫数对比情况,其中直接模 拟蒙特卡洛方法结果由贝德[24]的``可视化二维直接模拟(DS2V)软件''计算得到,从图中可以看出两者吻合较好. 从图中可以看出,当$H =2 D$时由于两圆柱中间喉部阻塞作用,在$x/D$约为$-2$处形成一个脱体弓形激波,与单圆柱绕流类似;随着$H$增大,喉部阻塞作 用减小,$H =4 D$时在$x/D$约为$-1.5$处形成一道正激波;当$H$增大至$6 D$时,在$x/D$约为$-0.5$处形成一道正激波,此时波后流场结构与前两种情形完全不同,两圆柱前面脱体激波进一步靠 近物面,喉部流场对圆柱的影响进一步减小.

|
图 2 不同间隔并排圆柱流场马赫数等值线云图 Fig.2 Contours of Mach number past two side-by-side cylinders |
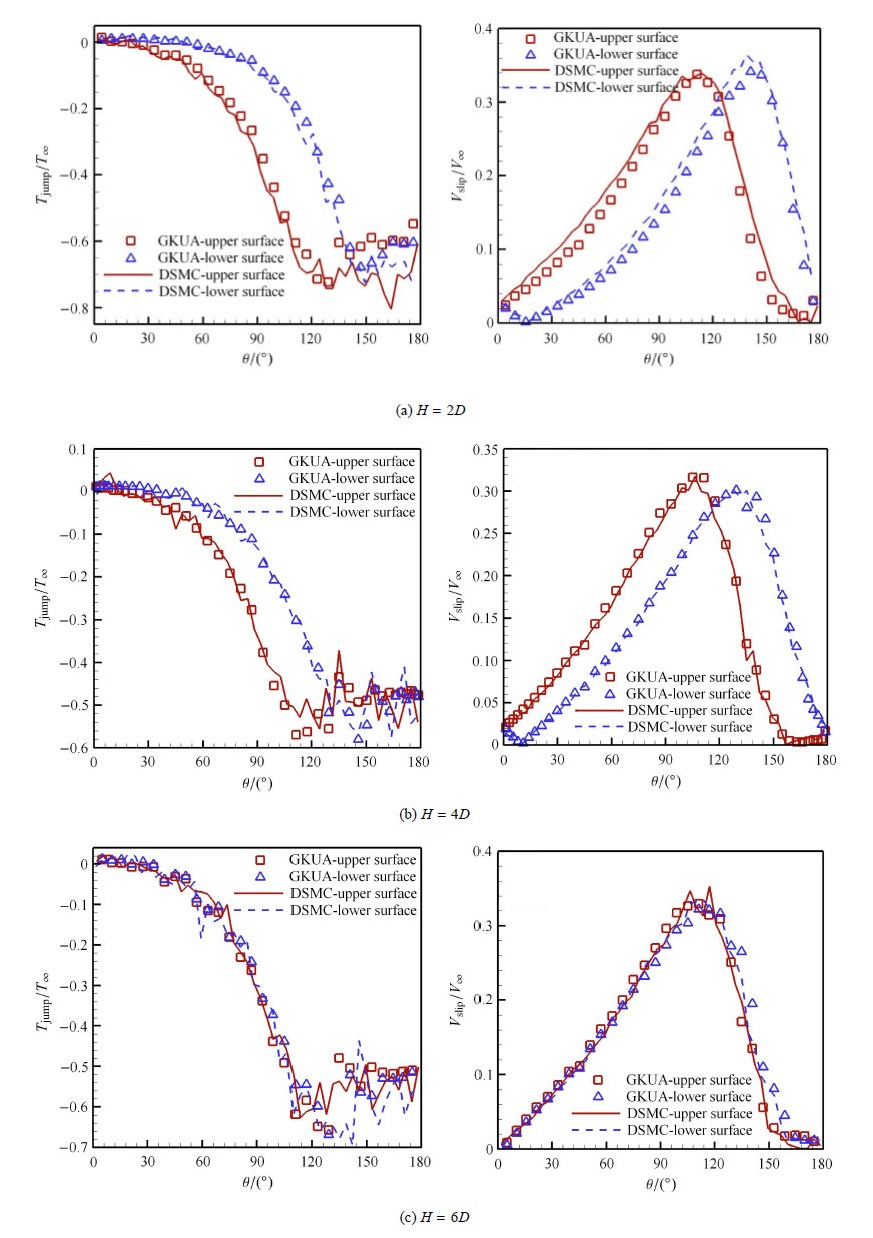
为了定量化比较并排圆柱不同间隔比条件下物面绕流特性与变化规律,图 3绘出不同$H$下上方圆柱上下表面温度跳跃、速度 滑移结果对比情况. 比较表明,本文计算结果与直接模拟蒙特卡洛方法模拟值变化趋势一致,3种情况下均吻合较好,说明本文所采用的方法正确可靠. 同时也看出,温度跳跃在圆柱尾部出现较大的波动,主要是由于尾部流动分离、压力很低、流动速度较小造成的. 同时,$H =2 D$,$4 D$时圆柱上下表面温度跳跃、速度滑移相差较大,说明上下表面绕流非对称性严重,$H$为$2 D$时绕流驻点位置在该圆柱下表面偏离来流方向 $\theta $ 约为20$^{\circ}$处;随着$H$增大,驻点位置前移,且上下表面绕流非对称性减弱;$H=6D$时,驻点位置几乎在圆柱正前 ($\theta =0^{\circ}$) 处,此时流场对单个圆柱的影响迅速减小,将导致单个圆柱所受法向力很小.
|
图 3 沿圆柱物面温度跳跃和速度滑移 Fig.3 Temperature jump and velocity slip along the surfaces |
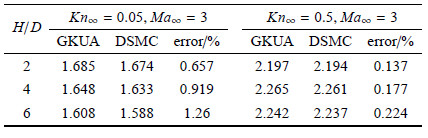
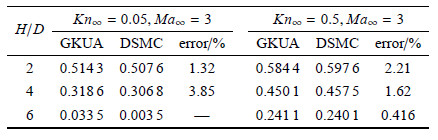
表 1和表 2分别列出了$H$为$2D$,$4D$和$6D$时不同$Kn_\infty $下单边圆柱轴向力系数和法向力系数本文与直接模拟蒙特卡洛方法模拟值的对比. 由表看出,随着$H$的增加,轴向力系数、 法向力系数受圆柱间绕流干扰作用均减小,轴向力系数最大误差为1.26%;由于单边圆柱所受法向力来源于并排圆柱绕流 间干扰效应,法向力系数与并排圆柱间隔呈正相关,表 2反映了这样的变化规律;而$H=6D$、努森数$Kn_\infty = 0.05$、马赫数$Ma_\infty = 3$状态下,本文结果为0.033 51,而直接模拟蒙特卡洛方法模拟值为0.003 498,相差较大,这可能是由于此时圆柱间隔较大, 圆柱间绕流干扰效应较小,直接模拟蒙特卡洛方法在统计流动信息时存在较大统计涨落,淹没了有用信息. 从 表 1和表 2也看出,在并排圆柱间隔与来流马赫数相同条件下,来流努森数($Kn_\infty$)增大时单边圆柱所受轴向力系数、 法向力系数均增大. 上述计算结果变化规律均与理论预测分析相吻合.
| 表 1 并排圆柱绕流不同状态下单边圆柱轴向力系数 Table 1 Axial force coefficients of single cylinder in different states for the flow around the cylinder |
| 表 2 并排圆柱绕流不同状态下单边圆柱法向力系数 Table 2 Normal force coefficients of single cylinder in different states for the flow around the cylinder |
在计算效率方面,相同计算环境下,设显式格式(二阶无波动、无自由参数耗散格式、二阶龙格库塔方法)单步计算时 间为1,计算表明本文隐式方法单步计算时间约为0.63,而收敛到相同精度时隐式方法计算步数远小于显式格式,说明计 算效率得到了大幅提高;与直接模拟蒙特卡洛方法相比,在近连续滑移过渡流区本文方法占优,而在稀薄流区直接模拟蒙 特卡洛方法优势明显. 另一方面,由于速度空间离散后的模型方程在速度空间相互独立、在离散速度点上对分布函数取矩求和时与物理空间无关, 使得气体运动论统一算法非常适合大规模并行计算,且并行效率很高[9],在来流马赫数很高时可通过大规模并行计算 来弥补速度离散点数随马赫数变大而增加导致计算量增大的缺点,扩展了气体运动论统一算法的工程实用性.
3 结 论本文在气体运动论统一算法框架内,采用多块对接网格技术,基于上下对称高斯-赛德尔(LU-SGS)方法与 格心型有限体积法构造了求解玻尔兹曼模型方程的隐式方法,通过模拟二维并排圆柱绕流,并与直接模拟蒙特卡洛方法模拟值 对比,两者吻合较好,证实该方法用于跨流域多体气动力计算的准确可靠性;同时分析表明在一定来流条件下当并排圆柱之间 的距离达到一定程度时可以忽略相互干扰的影响,这将为下一步模拟分析寿命末期航天器离轨陨落解体跨流域气动特性提供一 定的支持和参考.
| 1 | 庄逢甘,崔尔杰,张涵信. 未来空间飞行器的某些发展和空气 动力学的任务. 中国第一届近代空气动力学与气动热力学会议 论文集,2006. 1-12 (Zhuang Fenggan,Cui Erjie,Zhang Hanxin. Some development of future spacecrafts and aerodynamics tasks. In: Proc. of First Aerodynamics and Aerothermodynamics, 2006. 1-12 (in Chinese)) |
| 2 | 李志辉,蒋新宇,吴俊林等. 转动非平衡玻尔兹曼模型方程统 一算法与全流域绕流计算应用. 力学学报, 2014, 46(3): 336-351 (Li Zhihui, Jiang Xinyu, Wu Junlin, et al. Gas-kinetic unified algorithm for Boltzmann model equation in rotational non-equilibrium and its application to the whole range flow regimes. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 336-351 (in Chinese)) |
| 3 | Chapmann S, Cowling TG. The Mathematical Theory of Non- Uniform Gases, 3rd edn. Cambridge: Cambridge University Press,1970 |
| 4 | WagnerW. A convergence proof for Bird's Direct Simulation Monte Carlo method for Boltzmann equation. Journal of Statistic Physics,1992, 66: 1011-1044 |
| 5 | Li ZH, Fang M, Jiang XY, et al. Convergence proof of the DSMC method and the Gas-Kinetic Unified Algorithm for the Boltzmann equation. Sci. China-Phys. Mech. Astron, 2013, 56(2): 404-417 |
| 6 | Bhatnagar PL,Gross EP,Krook M.A model collision processes in gases:I.Small amplitude processes is charged and neutral onecomponent system.Phys Rev,1954,94:511-525 |
| 7 | Holway LH. New statistical models for kinetic theory: methods of construction. Phys Fluids, 1966, 9(9): 1658-1673 |
| 8 | Shakhov EM. Generalization of the krook kinetic relaxation equation. Fluid Dynamics, 1968, 3(5): 95-96 |
| 9 | Shakhov EM.Kinetic model equations and numerical results.In: Oguchi H. ed.Proceedings of 14th International Symposium on Rarefied Gas Dynamics,Tokyo:University of Tokyo Press,1984.137-148 |
| 10 | Yang JY, Huang JC. Rarefied flow computations using nonlinear model Boltzmann equations. J of Comput Phys, 1995, 120: 323-339 |
| 11 | Kudryavtsev AN, Shershnev AA. A numerical method for simulation of microflows by solving directly kinetic equations with WENO schemes. J Sci Comput, 2013, 57: 42-73 |
| 12 | Mieussens L. Discrete-velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries. J of Comput Phys, 2000, 162(2): 429-466 |
| 13 | Ahn JW, Kim C. An axisymmetric computational model of generalized hydrodynamic theory for rarefied multi-species gas flows. J of Comput Phys, 2009, 228: 4088-4117 |
| 14 | Xu K, Huang JC. A unified gas-kinetic scheme for continuum and rarefied flows. J Comput Phys, 2010, 229: 7747-7764 |
| 15 | Xu Kun. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and godunov method. J of Comput Phys, 2001, 171: 289-335 |
| 16 | 李志辉. 从稀薄流到连续流的气体运动论统一数值算法研究. [博 士论文]. 绵阳:中国空气动力研究与发展中心,2001 (Li Zhihui. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum. [PhD Thesis]. Mianyang: China Aerodynamics Research and Development Center, 2001(in Chinese)) |
| 17 | 李志辉, 张涵信. 稀薄流到连续流的气体运动论模型方程算法研究. 力学学报, 2002, 34(2): 145-155 (Li Zhihui, Zhang Hanxin. Study on gas kinetic algorithm for flows from rarefied transition to continuum using Boltzmann model equation. Chinese Journal of Theoretical and Applied Mechanics, 2002, 34(2): 145-155 (in Chinese)) |
| 18 | Li ZH, Zhang HX. Gas-kinetic numerical studies of threedimensional complex flows on spacecraft re-entry. J Comput Phys,2009, 228: 1116-1138 |
| 19 | Riabov VV. Aerodynamics of two side-by-side plates in hypersonic rarefied-gas flows. J of Spacecraft and Rockets, 2002, 39: 910-916 |
| 20 | Koppenwallner G, Legge H. Drag of bodies in rarefied hypersonic flow. In: Moss JN, Scott CD, eds. Progress in Astronautics and Aeronautics, Thermophysical Aspects of Reentry Flows. New York, AIAA, 1994. 44-59 |
| 21 | Alam MM, Zhou Y. Flow around two side-by-side closely spaced circular cylinders. Journal of Fluids and Structures, 2007, 23: 799-805 |
| 22 | Riabov VV. Numerical study of interference between simple-shape bodies in hypersonic flows. Computers and Structures, 2009, 87:651-663 |
| 23 | 张涵信, 沈孟育. 计算流体力学—差分方法的原理和应用. 北 京: 国防工业出版社, 2003 (Zhang Hanxin, Shen Mengyu. Computational Fluid Dynamics—Fundamentals and Applications of Finite Di erence Methods. Beijing: National Defence Industry Press,2003 (in Chinese)) |
| 24 | Bird GA. The DS2V/3V program suite for DSMC calculations. In: Rarefied Gas Dynamics, 24th International Symposium, Melville, NY, 2005.541-546 |
2. National Laboratory for Computational Fluid Dynamics, Beijing 100191, China
 2016, Vol. 48
2016, Vol. 48