水下气泡与液体相互作用规律研究具有重要的理论意义和实际应用价值. 气泡的生成、发展演化过程是涉及气液两相受力、传质、传热等复杂相互作用的动力学过程,蕴含了复杂机理和丰富力学现象. 诸多工程技术领域均涉及液相中气泡的生成和发展. 例如,环境工程、生物工程、冶金以及水利工程. 在污水处理工艺中,将空气中氧强制向液体中转移这种曝气过程,充分体现气泡与液体的相互作用;而冶金工艺中向液态金属中喷吹气体提升冶金质量,也包含了丰富的气泡与液态金属的相互作用机制.
近几十年来,液相中气泡的生成、发展演化过程一直是流体与相关多相流领域研究的热点. 戴维森等[1, 2, 3, 4, 5]对有黏和无黏液体中气泡形成和上升过程进行了深入研究,并根据孔内驱动气体流动状态将气泡形成过程分为恒压和恒流速两种,此后的大量实验研究也大多约定了在恒压[6]或恒流量[7, 8, 9, 10]两种工况下开展.
在气泡形成机制及影响因素方面,大量研究工作针对如孔径[8, 9, 10, 11]、表面张力[10]、孔口表面粗糙 度[8]、液体密度[10, 11, 12]、液体黏性[11, 12]、孔口材料亲水特性[13, 14, 15, 16]、重力场[17, 18]等因素,对气泡形成时间和体积的影响开展了研究. 研究结果表明,当气体流量很低时(即气泡生长发展呈现缓慢的准静态),气泡形成过程受表面张力和浮力的平衡制约. 气泡的体积与孔径、表面张力成比例,与流量几乎无关,气泡形成时间随流量增加减小;当气体流量逐渐增大时,气体注入气泡带来的惯性力成为重要因素. 当惯性力较表面张力占优时,气泡从孔口生长到脱离的时间几乎不受气体流量增加的影响,但气泡脱离孔口时体积随流量增加而增大.
随着研究进展,不同理论模型纷纷被提出来预测气泡形成过程动态变化和脱落时体积. Davidson 等[3, 4]首先提出了单阶段(one-stage)模型,即假设气泡从开始生长到脱离孔口整个过程所受向上浮力和向下的惯性 力始终相等;随后文献[19, 20, 21, 22, 23]在此基础上进一步提出了双阶段(two-stage)模型. 双阶段模型将气泡生长过程分为扩张和颈部拉伸两个阶段. 假设气泡在扩张阶段末才达到上下受力平衡,在颈部拉伸阶段气泡受到的力并不平衡,而是向上的力大于向下的力. 双阶段模型更符合实验观察到的现象,其对气泡脱离体积预测较单阶段模型也更加准确. Longuet-Higgins等[24]根据气泡表面内外压力平衡求解气泡生长过程轮廓变化,并通过与实验中气泡高度变化进行对比验证了理论的正确性. 对气泡生长过程形态动态变化问题,Ogue等[25]和Gerlach等[26] 也通过理论分析的方法对其进行了研究. Gerlach在Longuet-Higgins提出的理论方法的基础上考虑了孔口材料的亲水特性的影响,这也是以往理论研究中很少考虑的. 在亲水材料和疏水材料条件下,理论计算的气泡生长过程轮廓变化与试验完全吻合. Bari等[27]在探究气泡生长过程气泡形状与压力场变化关系的实验中也验证了该模型对气泡脱离体积预测的准确性.
以上提到的理论模型以单周期假设为前提的,未考虑气泡之间的相互影响. 已有的实验研 究[10, 14, 28]表明当气体流量大到一定程度气泡之间相互作用增强,单周期泡流(single or period-1 bubbling)逐渐转变成双周期泡流(period-2 bubbling). 当流量进一步增加,流场中会出现三周期泡流(period-3 bubbling),即会有连续形成的3个气泡在孔口上方发生合并,且流场中总是有规律的重复这一现象. 甚至是四周期(period-4)或混沌泡流(chaotic bubbling). 在多周期泡流中后续气泡在生长过程受前面气泡尾流的影响会提前与孔口分离. 因此,在多周期泡流中两接连形成的气泡体积明显不同. 以单周期假设为前提的模型,预测的气泡体积也均是指该工况下的平均气泡体积,气泡形成频率也是指平均频率,不能正确反映多周期泡流中真实气泡体积. 有学者[28, 29, 30]曾尝试在理论模型中计及气泡之间相互作用,其理论模型依然不能准确预测气泡形成时间和体积. 近年Zhang等[31]提出计及气泡之间非线性作用的理论模型,并通过实验证明,该理论能够很好预测多周期泡流中气泡形成时间和体积. 然而该模型对其他工况的适用性有待验证. 多周期泡流理论发展滞后主要有两个原因. 一方面是问题本身具有高度复杂性,另一方面是缺乏反映多周期泡流气泡形成时间和体积的准确实验数据.
上述研究中,形成气泡的喷管(孔)均为圆孔. 近年来,随着某些特殊应用发展,例如,水下导弹的同心筒破水发射[32, 33]: 利用导弹发动机点火初期高温尾喷流通过包裹导弹的环形通道先期导向水中,在导弹入水前形成气体射(泡)流,进而开辟出后续导弹水下发射的气体通道. 为此,提出了对于环形喷口气体射流及相应泡流发展的研究需求. 目前,国内外对于环形喷口下泡(射)流的研究报道尚不多见,对于环形喷口气体(泡)射流是否与圆形喷口泡(射)流是否有明确差异,气泡生成、发展演化过程是否有其特殊性,尚需进一步研究. 为此,本文设计和建立了一套实验系统,针对环形喷口气泡产生发展演化过程开展了研究,初步探讨了气泡演化的三周期区制以及气泡形态变化等特点.
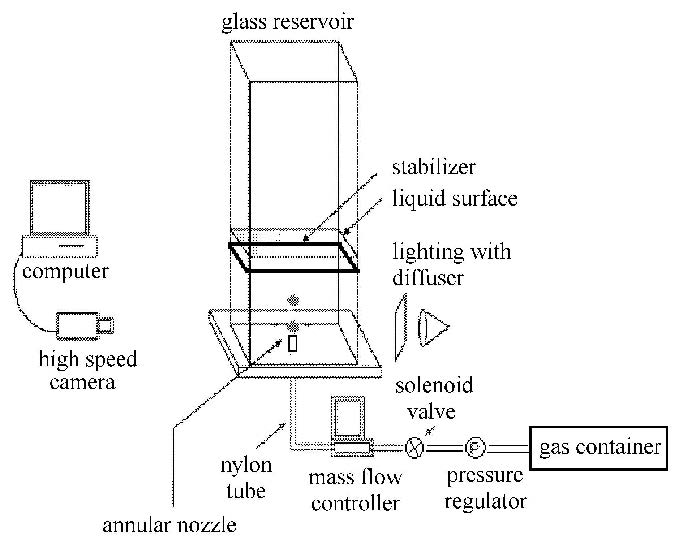
1 实验装置与方法为开展环形喷管水下气泡流态发展过程的研究,设计建立了一套实验系统. 图 1给出了实验系统示意图[10]. 实验系统由储气系统、 流量控制及监测系统、环形喷管、水箱、图像采集系统5部分组成.
|
图 1 实验系统图 Fig.1 Schematic diagram of experimental system |
由于环形喷口泡流的研究尚不多见,为观测和掌握环形喷口泡流生成发展演化的基本过程与特征,在研究初期确定了采用低压气源、 较低驱动气流流速的实验方案. 驱动气体流量控制在 50.8$\sim $237.3 dm$^{3}$/min范围内;根据实验设计,气体由储气罐流出,经压力控制器、单向电磁阀、流量质量控制器到达喷管;管路由 内径6 mm的尼龙管连接,质量流量控制器型号为ALICAT-MC-250SLPM-D,控制精度为0.8%Rdg+0.2%F.S,响应时间为0.1 s.
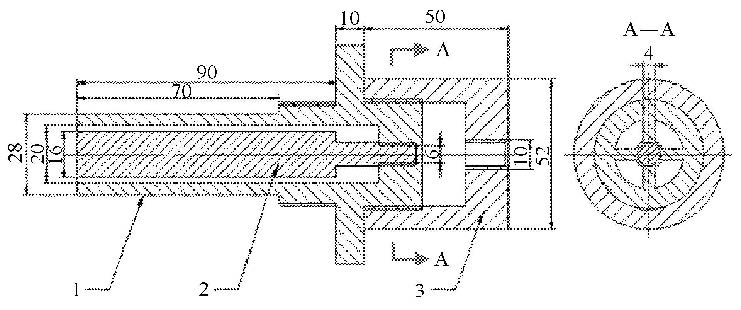
环形喷管是实现环形喷流的关键,图 2给出了自行设计的环形喷管组件的结构示意图. 喷管组件采用铝合金加工形成,主要由套筒、实 心柱和底座等3部分组成,环形喷口尺寸可根据需要变化;目前实验采用的套筒内径$D _{1} =20$ mm,外径$D_{2}=28$ mm,实心柱直径$D_{3}=16$ mm,环形缝隙为$d=2$ mm.
|
图 2 喷管组件结构示意图 1 套筒;2 实心柱;3 底座 Fig.2 Schematic diagram of annular nozzle assembly |
为便于气泡生长演化过程的图像记录,水箱设计为50 cm $\times$50 cm$\times$100 cm的长方体,采用高透明度的亚克力材 料制成. 为防止液面晃动对气泡生长发展产生影响,在液面上方加入破浪板,破浪板浸入水中并与液面保持一致. 在水箱一侧采用高速摄影仪(Fastcam-Ultima APX)记录气泡生长及发展过程;图像采集速度为1 000帧/秒,拍摄持续时间2秒;为保障图像质量,在水箱对侧采用了高频无闪 灯作为补充光源,同时在水箱和光源之间加入均光纸以改善图像效果.
整个实验流程由实验控制系统统一控制执行. 结合实验方案,重点考察了12种不同气体流量下气泡发展过程,同时,初步摸 索了两种水深情况. 表 1给出了本次研究的实验工况,需要注意本文中气体体积流量均是指标准状态下气体体积流量.
| 表 1 实验工况 Table 1 Operating conditions |
实验中获得的高速录像及图片通过编程进行批量处理. 图 3给出了实验图片及灰度处理后边界提取示意图. 在边界提取处理中,将原始 图片转化为灰度图片,并采用基于灰度一阶导数的边缘检测算子 提取气泡边界获得气泡边界的二值化图片. 通过对连续图片气泡边界像素位置进行测量,从而确定气泡形状信息与位移信息.

|
图 3 气泡图片及边界处理示意图 Fig.3 Bubble image and bubble boundary treatment |
众所周知,在驱动气体低压或低流量下能够反 映泡流演化发展的基本特征. 结合表 1的设计实验工况,对12种流量下的泡流发展过程 进行了研究. 实验结果显示,在上述工况下,环形喷管泡流首先 表现出了明显的三周期泡流区制. 如前所述,所谓三周期泡流是指,流场中会出现3个连续生成的气泡并在孔口上方发生聚并,同时,该现象在流场中会稳定、有规律 地重复出现.
图 4选取了两种典型流量($Q=67.8$和 220.4 dm$^{3}$/min),给出了三周期泡流演化发展过程. 为便于后续描述, 这里我们将三周期泡流中发生聚并的3类气泡按出现顺序分别标称为气泡1,气泡2, 气泡3,对应的3个气泡生成发展时间分别称为周期1,周期2,周期3. 这里气泡形成时间定义为一个气泡脱离孔口时与下一个气泡脱离之间的时间间隔,脱离的判定条件是气泡颈部颈缩到最小程度. 图 4(a)中前3个箭头区间(62 ms,32 ms,50 ms)分别表示了实验中发生聚并的3个气泡1,气泡2, 气泡3生成发展时间(即周期1,周期2,周期3),后3个箭头区间(63 ms,31 ms, 52 ms)是下一组发生聚并的气泡形成时间,展示了3类泡产生、聚并现象重复出现的规律性.

|
图 4 三周期泡流演化过程图 Fig.4 Evolution of period-3 bubbling |
从图 4(a)和图 4(b) 中可以发现,气泡1,气泡2,气泡3的形成时间长短具有明显的规律,即:周期1最长,周期3, 周期2次之. 从图片分 析注意到,在气泡2生长过程,由于气泡1尾流的拉拽加速效应,气泡2生成时间明显缩短并迅速与气泡1聚并;在气泡3生长过程中,由于 气泡1、气泡2聚合体离开孔口稍远,其尾流拉拽加速效应减弱,所以气泡3的生成时间增加,但最终气泡3会加速并追赶上第一、二泡聚 合体,形成树型的三泡聚合体. 图 4(b)显示,在流量增大的情况下,仍然出现了与图 4(a)类似的三周期情况,略有不同的是,气泡之间碰撞变形更加剧烈,气泡表面透 明度逐渐降低;与此同时,我们注意到,在流量增大的情况下,气泡1的形成时间增加,气泡2的形成时间是减小的.
实验也尝试了更低流量工况,实验发现,当流量低于50.8 dm$^{3}$/min时气体不能均匀的从环形缝隙喷入水中,而是在环形缝隙非 特定位置间断溢出. 形成的气泡形状、时间等呈现杂乱特点,不再严格意义体现环形喷口特征. 因此,文中未给出该部分数据,重点关注流量在50.8 dm$^{3}$/min及以上时的工况.
2.2 气泡坍塌过程在观察实验流场录像过程中发现,环形喷管生成的气泡在发展过程会出现明显的顶部向下坍塌的现象,坍塌主要发生在第1类型气泡 (气泡1)生长发展过程中. 图 5(a)和图 5(b)分别给出了流量为67.8和101.7 dm$^{3}$/min两工况下气泡1顶部坍塌演化过程.

|
图 5 气泡顶部坍塌演化过程 Fig.5 Evolution of bubble collapse |
图 5中$t_{0}$为气泡1在喷口生成时的初始时刻,从$t_{0} \sim t_{2}$,由于气体的持续注入和前一气泡的拖拽作用,气泡不断向外膨胀胀大,在$t_{2}$时刻上下两气泡发生断裂分离;在分离 的同时,下端气泡顶部出现明显的反向向下运动(如图$t_{2}\sim t_{4}$),并包裹液体形成一道液体射流向下运动,最终撞击喷口中心端面,形成如$t_{5}$所示环状气泡. 图 5(a)和图 5(b)两种工况均明确展示出这一过程.
根据图片观察及气泡受力分析获得的认识,利用图 6给出了这一气泡坍塌过程的分析示意图. 图 6(a)表示上下气泡牵连向上运动过程,在上下气泡分离时刻,下端气泡顶部受力瞬时失衡. 其顶部主要受到指向孔口方向的表面张力$F$. 在张力作用下气泡顶部向下运动,周围伴随液体同时向下运动达到图 6(b)所示的两相界面理论平衡位置;但由于惯性作用,局 部液体继续向下,形成具有一定速度的液体射流(图 6(c)),由于环形喷口(中心为实心)的特殊结构,孔口中心竖直向上方向气体 动量较小,不足以克服惯性液体射流. 液体射流继续向下最终撞击到喷口中心端面,形成环状气泡(图 6(d)).

|
图 6 气泡坍塌过程分析示意图 Fig.6 Digram of bubble collapse process |
结合前述三周期区制中的分析可以发现,坍塌现象主要发生在前气泡尾流拖拽作用较弱的情况下(例如气泡1). 在气泡2和气泡3生长过程 中,由于受前气泡(分别为气泡1、气泡2)尾流拖拽作用,此时气泡顶部所受到向上拖拽力大于向下的表面张力,故而气泡2、气泡3生长过 程很少出现液体射流从气泡顶部刺入的情况.
同时,实验录像显示,当气体流量较低时,气泡表面透明度较好,能够清晰观察到液体射流刺进气泡过程. 当进一步增加气体流量(如大 于169.6 dm$^{3}$/min),泡表面的透明度会逐步降低,呈现类似磨砂玻璃表面的效果(如图 4(b)). 因此,随着流量增大,从动态录像中可以明确感受到坍塌过程,但由于气泡清晰度降低,从静态照片中不再容易清晰判读.
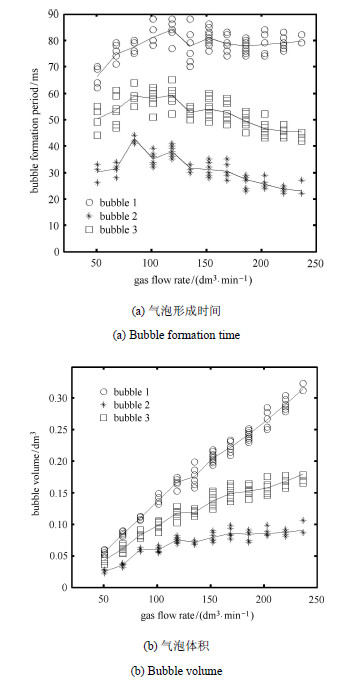
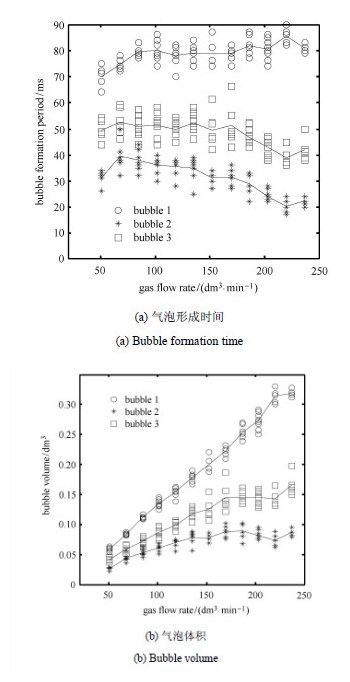
2.3 气泡形成时间和体积随流量的变化气泡形成时间、体积是表征气泡特征的另一类重要观测参数. 气泡形成时间和体积的量化数据对多周期泡流理论模型的建立 发展具有重要的基础作用. 本文实验中研究了不同气体流量(50.8 $\sim $ 237.3 dm$^{3}$/min)下气泡形成时间和体积的变化规律. 气泡形成时间是通过对实验图片逐帧计数获得,对于单一某工况,每工况统计4$\sim $8组三泡聚并过程. 气泡形成时间测量误差为$\pm $1 ms. 本实验是在恒流量工况下进行,因此,气泡体积是通过气泡形成时间乘以气体流量获得. 图 7中离散点是统计获得的气泡形成时间/体积分布,实线是各气泡形成时间/体积均值. 图 7给出了12种不同气体流量条件下,三周期泡流中3类气泡形成时间与体积的比较曲线.
|
图 7 3类气泡形成时间和体积随流量的变化 Fig.7 Bubble formation time and volume with gas flow rate |
图 7(a)给出了气泡形成时间的比较. 从图中可以看出,在同一流量下,三周期泡流中气泡1、气泡3、气泡2的形成时间呈 逐步递减的规律,从统计规律上看,周期1通常是周期2的2$\sim $4倍,周期3是周期2的1.5$\sim $2倍. 同一流量下三周期气泡形成时间的差异在前述三周期区制中已有讨论.
对于不同流量条件,气泡形成时间并未随流量增大呈现单调变化规律,而是有所起伏,且3种气泡形成时间随流量变化规律略 有差异:对于形成时间最长的气泡1,其形成时间(周期1)初始随气体流量增大而逐步变长,但气体流量增大到一定程 度(大于101.7 dm$^{3}$/min)后,气泡1形成时间趋于稳定;而气泡2和气泡3的形成时间(周期2和周期3)则随流量增大呈先增 大后减小的规律.
图 7(b)给出了气泡体积随流量的变化规律. 在同一流量下,气泡1,气泡3,气泡2的体积与其形成时间相呼应,表现为 逐步减小的规律;随着气体流量增大,3类气泡体积均随流量增加而增大,但变化率有所不同:气泡1体积随流量增大基本呈线 性增大,变化率最大,而气泡2和气泡3体积随流量呈减速递增,且气泡2体积随流量变化率最小.
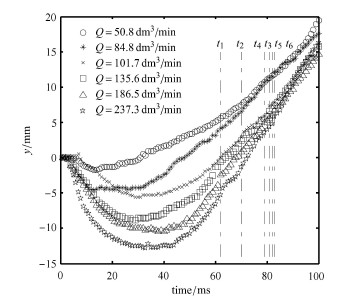
2.4 气泡随流量的位移变化实验中观察到气泡生长过程具有典型的向喷口下方扩张过程. 结合对气泡灰度图的二值化边界提取和底部边界位移测量(如图 3(b)),图 8给出了6种不同流量(50.8$\sim $237.3 dm$^{3}$/min)下,气泡1底部边界在气泡发展过程中纵向位移变化情况.
|
图 8 气泡 1底部纵向位移 Fig.8 The displacement of bubble-1 bottom |
测量时间持续100 ms,从气泡 1开始生长到与孔口脱离以及后续向上运动. 处理过程中我们注意到,在提取气泡底部边界时左右两侧位 置气泡底部位移可能稍有差异,对气泡底部位移取两侧位移均值. 根据灰度分析和边缘检测算法理论,结合原始图片比对,气泡边界提取误差在0.5 mm以内. 测量坐标原点设置在喷口端面中心,纵向位移向上为正. 对应于6种逐步增大的流量条件,$t_1 \sim t_6$ (62 ms, 70 ms,81 ms,79 ms,82 ms,83 ms)分别是不同流量条件下气泡1与孔口脱离时刻.
图 8显示,对应于气泡 1从开始生长到与喷口脱离,气泡 1底部边界具有下沉、回升两个典型运动特征. 在气泡生长初期,由于水的 惯性阻滞作用以及气体的持续注入,使得气泡内部压力较大,气泡沿喷管端面向外扩张. 当气体扩张溢出喷口端面,气泡底部失去喷口端面支撑会出现底部边界下沉扩张现象(此时气泡整体呈周向扩张). 随气泡体积的增加,气泡所受浮力逐渐增大,气泡整体逐渐开始回升. 当气泡底部运动到孔口上方,气泡颈部出现并开始颈缩. 发生聚并的3类气泡生长过程均包括扩张和上浮这两个运动过程,但气泡 2和气泡3扩张幅度较气泡 1小,文中未给出气泡2和气泡3底部位移测量结果.
对比不同流量可知,随流量增加,气泡 1底部下沉速度和下沉最大距离是呈增大趋势的. 同样,回升速度也是随流量增大的. 气泡 1形成时间($t_1 \sim t_6$) 是先增大后保持稳定的.
2.5 水深对气泡形成时间和体积影响无论基于基础理论研究或是应用背景考虑,气泡研究的水深环境都是一个非常重要的影响因素.
限于现有实验条件限制,本研究中仅在目前水箱条件下,设置了35 cm 和 80 cm两种水深条件进行初步摸索. 前述实验结果及图片,如无特殊说明,均是在水深35 cm条件.
图 9给出了80 cm水深条件下气泡形成时间和体积随流量的变化规律,与图 7进行简单的参照对比发现,两种水深下气 泡形成时间、体积的 变化规律基本相同. 这可能与水深变化范围过小有关,但同时也说明,在现有水深变化范围内,气泡形成时间与体积变化规律不会有明显改变. 未来结合应用背景开展研究,通过加大绝对水深、环境压力等方式,将对水深条件影响开展探索.
|
图 9 3类气泡形成时间和体积随流量的变化(80 cm水深) Fig.9 Bubble formation time and volume with gas flow rate (80 cm depth) |
本文通过自行设计建立一套实验系统对环形喷口气泡发展演化过程进行了实验探究. 研究内容包括:环形喷口气泡形成区制,环状气泡形成过程,水深和气体流量对气泡形成时间和体积影响. 基于实验结果分析得出以下结论:
(1) 在目前实验工况条件,泡流发展演化过程呈较明显的三周期区制. 前气泡尾流对后气泡影响是三周期区制形成的重要原因.
(2) 环形喷口气泡在生长过程会出现顶部向下坍塌形成环状气泡的现象,其中气泡表面张力、液体惯性作用、外围流动影响(如尾流拖拽效应强弱)是坍塌形成环形气泡的重要原因;坍塌现象通常发生在气泡 1类型的生长发展过程中.
(3) 气泡形成时间与体积随流量变化而变化. 同一流量下,3类气泡形成时间与体积明显受前后气泡之间相互影响而不同;不同 类型气泡形成时间随流量变化规律不同,但气泡体积均随流量增大而增大.
(4) 在气泡 1生长过程其底部具有下沉、回升两典型运动过程,且其下沉速度、距离以及回升速度受气体流量影响明显.
(5)在目前实验的水深条件(35 cm和80 cm)下,气泡发展变化未表现出明显差异,关于水深对环形喷管气泡发展影响的研究有待后续.
| 1 | Davidson L, Amick EH. Formation of gas bubbles at horizontal orifices. AIChE Journal, 1956, 2(3): 337-342 |
| 2 | Walters JK, Davidson JF. The initial motion of a gas bubble formed in an inviscid liquid. Journal of Fluid Mechanics, 1963, 17(3): 321-336 |
| 3 | Davidson JF, Schueler BOG. Bubble formation at an orifice in a viscous liquid. Transactions of the Institution of Chemical Engineers,1960, 38: 144-154 |
| 4 | Davidson JF, Schueler BOG. Bubble formation at an orifice in an inviscid liquid. Transactions of the Institution of Chemical Engineers,1960, 38: 335-342 |
| 5 | Marmur A, Rubin E. A theoretical model for bubble formation at an orifice submerged in an inviscid liquid. Chemical Engineering Science, 1976, 31(6): 453-463 |
| 6 | Satyanarayan A, Kumar R, Kuloor NR. Studies in bubble formation- II bubble formation under constant pressure conditions. Chemical Engineering Science, 1969, 24(4): 749-761 |
| 7 | Ramakrishnan S, Kumar R, Kuloor NR. Studies in bubble formation-I bubble formation under constant flow conditions. Chemical Engineering Science, 1969, 24(4): 731-747 |
| 8 | Badam VK, Buwa V, Durst F. Experimental investigations of regimes of bubble formation on submerged orifices under constant flow condition. Canadian Journal of Chemical Engineering, 2007,85(3): 257-267 |
| 9 | Terasaka K, Tsuge H. Bubble formation under constant-flow conditions. Chemical Engineering Science, 1993, 48(19): 3417-3422 |
| 10 | Gerlach D, Alleborn N, Buwa V, et al. Numerical simulation of periodic bubble formation at a submerged orifice with constant gas flow rate. Chemical Engineering Science, 2007, 62(7): 2109-2125 |
| 11 | Loubière K, Hébrard G. Bubble formation from a flexible hole submerged in an inviscid liquid. Chemical Engineering Science, 2003,58(1): 135-148 |
| 12 | Duhar G, Colin C. Dynamics of bubble growth and detachment in a viscous shear flow. Physics of Fluids, 2006, 18(7): 3453-3475 |
| 13 | Oguz HN, Prosperetti A. Surface-tension e ects in the contact of liquid surfaces. Journal of Fluid Mechanics, 1989, 203: 149-171 |
| 14 | Buwa VV, Gerlach D, Durst F, et al. Numerical simulations of bubble formation on submerged orifices: Period-1 and period-2 bubbling regimes. Chemical Engineering Science, 2007, 62(24): 7119-7132 |
| 15 | Byakova AV, Gnyloskurenko SV, Nakamura T, et al. Influence of wetting conditions on bubble formation at orifice in an inviscid liquid - mechanism of bubble evolution. Colloids & Surfaces A Physicochemical & Engineering Aspects, 2003, 229(1): 19-32 |
| 16 | Liow JL, Gray NB. A model of bubble growth in wetting and non-wetting liquids. Chemical Engineering Science, 1988, 43(12):3129-3139 |
| 17 | Marco PD, Grassi W, Memoli G, et al. Influence of electric field on single gas-bubble growth and detachment in microgravity. International Journal of Multiphase Flow, 2003, 29(3): 559-578 |
| 18 | Chakraborty I, Ray B, Biswas G, et al. Computational investigation on bubble detachment from submerged orifice in quiescent liquid under normal and reduced gravity. Physics of Fluids, 2009, 21(6):1337-1372 |
| 19 | Kumar R, Kullor NR. The formation of bubbles and drops. Adcance in Chemical Engineering, 1970, 8(1): 255-368 |
| 20 | Wraith AE. Two stage bubble growth at a submerged plate orifice. Chemical Engineering Science, 1971, 26(10): 1659-1671 |
| 21 | Kulkarni AA, Joshi JB. Bubble formation and bubble rise velocity in gas-?liquid systems: A review. Industrial & Engineering Chemistry Research, 2005, 44(16): 5873-5931 |
| 22 | Gaddis ES, Vogelpohl A. Bubble formation in quiescent liquids under constant flow conditions. Chemical Engineering Science, 1986,41(1): 97-105 |
| 23 | Tsuge H, Hibino S. Bubble formation from an orifice submerged in liquids. Chemical Engineering Communications, 1983, 22(1):63-79 |
| 24 | Longuet-Higgins MS, Kerman BR, Lunde K. The release of air bubbles from an underwater nozzle. Journal of Fluid Mechanics, 1991,230: 365-390 |
| 25 | Oguz HN, Prosperetti A. Dynamics of bubble growth and detachment from a needle. Journal of Fluid Mechanics, 1993, 257: 111-145 |
| 26 | Gerlach D, Biswas G, Durst F, et al. Quasi-static bubble formation on submerged orifices. International Journal of Heat & Mass Transfer,2005, 48(2): 425-438 |
| 27 | Bari SD, Robinson AJ. Experimental study of gas injected bubble growth from submerged orifices. Experimental Thermal & Fluidence,2013, 44(1): 124-137 |
| 28 | Chuang SC, Goldschmidt VW. Bubble formation due to a submerged capillary tube in quiescent and coflowing streams. American Society of Mechanical Engineers, 1970, 92(4): 705-711 |
| 29 | Deshpande DA, Deo MD, Hanson FV, et al. A model for the prediction of bubble size at a single orifice in two-phase gas—liquid systems. Chemical Engineering Science, 1992, 47(7): 1669-1676 |
| 30 | Jamialahmadi M, Zehtaban MR, Müller-Steinhagen H, et al. Study of bubble formation under constant flow conditions. Chemical Engineering Research & Design, 2001, 79(5): 523-532 |
| 31 | Zhang L, Shoji M. Aperiodic bubble formation from a submerged orifice. Chemical Engineering Science, 2001, 56(1): 5371-5381 |
| 32 | Weiland CJ, Vlachos PP, Yagla JJ. Concept analysis and laboratory observations on a water piercing missile launcher. Ocean Engineering , 2010, 37(11): 959-965 |
| 33 | Ross CTF. A conceptual design of an underwater missile launcher. Ocean Engineering, 2005, 32(1): 85-99 |
 2016, Vol. 48
2016, Vol. 48
