颗粒离散元的研究域由一系列的刚性颗粒及颗粒间的接触构成,并通过颗粒表述材料的平动及转动过程,通过颗粒间的接触表述材料的变形 及断裂过程. 颗粒离散元作为一种细观尺度下材料损伤断裂行为的数值模拟方法,在材料细观破裂机理及多裂纹扩展机制等方面已得到了广泛的应 用[1].
地质体的渐进破坏过程是地质体内部微裂纹的萌生、发展、交汇及贯通的过程,国内外学者利用颗粒离散元对地质体的渐进破坏过程进 行了大量研究. 谭青等[2]借助颗粒流研究了盾构切削作用下岩石的动态响应机制及破裂规律;石崇等[3]利用颗粒流分析了江坪河水电站陡 岩边坡在地震作用下的失稳机理及潜在破坏模式;张社荣等[4]基于颗粒离散元理论,研究了含2 条预制裂纹的Hwangdeung花岗岩在双轴压缩试验下的裂纹扩展及破坏模式;Ji 等[5]利用颗粒流研究了岩石单轴压缩过程中的声发射现象;Utili等[6]在PFC中引入了一种新的内聚力模型,并将其用于 研究陡崖的风化过程. Oñate等[7]提出了一种适用于描述颗粒离散元弹性-塑性-损 伤-断裂的一体化本 构模型,并通过单轴压缩、三轴压缩及巴西劈裂的数值试验验证了该本构模型的正确性. Huang等[8, 9]利用颗粒离散元探讨了刀具切割岩石、刀具压入岩石的过程中,刀具与岩石的相互作用机理,并给出了引起 岩石发生脆性破坏或韧性破坏的主控因素. 然而,传统颗粒流模型的输入参数为细观参数(如颗粒间的法向及切向接触刚度,颗粒间的细观粘聚力、内摩擦角及抗拉强度等),利用 传统颗粒流研究宏观问题时,需要事先进行大量的标定实验,进而建立宏细观参数间的联系[10, 11, 12, 13].
早期的颗粒离散元主要用于分析散粒体的接触、碰撞及堆积特性,因此一般认为颗粒间的接触为点点接触,采用线性接触模型 或Hertz-Mindlin模型描述颗粒间接触位移与接触力间的对应关系,采用Bonding模型描述颗粒间的粘连情况,采用滑移模型描述颗 粒间的滑动摩擦现象. 为了使颗粒离散元方法能够更为准确地描述材料的连续介质力学特性,国内外学者做了大量的工作. PFC软件[14, 15]中通过平行连接模型(parallel-bond model)实现水泥等材料对颗粒的粘连作用,因而该模型可在一定程度上描述材料的连续介质特性[16, 17, 18]. Griffiths等[19]利用梁单元表征颗粒间的接触关系,通过理论推导建立了梁单元法向、切向刚度与宏观弹性模量与泊松比的对应关系. Chang等[20]给出了一阶应变梯度连续的颗粒体系宏观应力应变关系,从一定程度上建立了宏观弹性参数与颗粒接触刚度、颗粒 尺寸及颗粒排布密度间的关系. Kruyt等[21]通过理论推导,给出了颗粒体系细观参数控制下的宏观弹性模量的上下限,并通过数值模拟证明了理论推导所给 出的上下限的准确性.
为了使颗粒离散元法能够更好地表征地质体的弹性、塑性、损伤及断裂过程,本文基于颗粒间有限接触的假设及拉剪复合应变软化准则,提出了连接键应变软化模型,并利用该模型研究了不同断裂应变下的岩石单轴压缩过程.
1 连接键模型 1.1 连接键的定义在利用离散颗粒体系表征连续介质特性时,每个离散颗粒可视作连续介质中的一个等效质点. 相邻的质点按照连续介质方程相互关联,实现连续介质特性的表达. 连续介质中,相邻两个等效质点间的力学关系主要包括拉压、剪切、弯曲、扭转等4类,本文采用连接键表述上述4类力学关系.
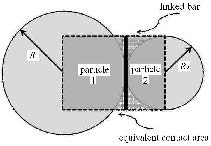
连接键与有限元中的杆件单元类似,具有一定的尺寸及形状,用于传递两个接触颗粒间的力及力矩. 其中,二维接触颗粒间的连接键为一矩形,矩形的一条边长为两个接触颗粒的半径之和,矩形的另一条边长是尺寸较小颗粒所对应的直径;三维接触颗粒间的连接键为一圆柱,圆柱的高为两个接触颗粒的半径之和,圆柱的半径为尺寸较小颗粒所对应的半径,如图 1所示.
|
图 1 连接键模型 Fig.1 Linked bar model |
连接键模型假设颗粒间的接触为面 面接触,颗粒间的等效接触面积为连接键左右两侧颗粒中尺寸较小颗粒的截面积,为
| $ {A_{\rm{c}}} = \left\{ \begin{array}{l} \min (2{R_1},2{R_2})\;\;\;\;(2D)\\ \pi {[\min ({R_1},{R_2})]^2}\;\;(3D)\; \end{array} \right. $ | (1) |
其中,$A_{\rm c}$为连接键的等效接触面积,$R_{1}$,$R_{2}$为两个颗粒的半径. 由于连接键具有自身的特征面积,其接触刚度可根据颗粒的弹性模量、剪切模量获得,为
| $ \left. \begin{array}{l} {K_{\rm{n}}} = \bar E{A_{\rm{c}}}/({R_1} + {R_2})\\ {K_{\rm{s}}} = \bar G{A_{\rm{c}}}/({R_1} + {R_2}) \end{array} \right\} $ | (2) |
其中,$K_{\rm n}$,$K_{\rm s}$为颗粒间的法向及切向刚度,$\bar {E}$,$\bar {G}$为两个接触颗粒的平均弹性模量及剪切模量.
1.2 考虑应变软化效应的接触力及力矩计算连接键模型中力及力矩的计算均基于增量法,且采用显式求解方式.
连接键模型中接触力的计算公式为
| $ \left. {\begin{array}{*{20}{l}} {{F_{\rm{n}}}({t_1}) = {F_{\rm{n}}}({t_0}) - {K_{\rm{n}}}\Delta d{u_{\rm{n}}}}\\ {{F_{\rm{s}}}({t_1}) = {F_{\rm{s}}}({t_0}) - {K_{\rm{s}}}\Delta d{u_{\rm{s}}}} \end{array}} \right\} $ | (3) |
其中,$F_{\rm n}$和$F_{\rm s}$分别为接触面上的法向力(拉伸为负)及切向力,$\Delta d u_{\rm n}$,$\Delta d u_{\rm s}$分别表示两个接触颗粒间的法向及切向位移增量差,$t_{1}$为下一时刻,$t_{0}$为本时刻.
连接键模型中接触力矩的计算公式为
| $ \left. \begin{array}{l} {M_{\rm{n}}}({t_1}) = {M_{\rm{n}}}({t_0}) - {K_{\rm{s}}}J\Delta d{\theta _{\rm{n}}}/{A_{\rm{c}}}\\ {M_{\rm{s}}}({t_1}) = {M_{\rm{s}}}({t_0}) - {K_{\rm{n}}}I\Delta d{\theta _{\rm{s}}}/{A_{\rm{c}}} \end{array} \right\} $ | (4) |
其中,$M_{\rm n}$和$M_{\rm s}$分别为扭矩及弯矩,$\Delta d \theta_{\rm n}$和 $\Delta d \theta_{\rm s}$分别为颗粒间的扭转及弯曲转角增量差,$I$和$J$分别为接触面的惯性矩及极惯性矩,为
| $ \left. \begin{array}{l} J = \pi {[\min (2{R_1},2{R_2})]^4}/32\\ I = J/2 \end{array} \right\} $ | (5) |
为了刻画连接键的连接强度随连接键应变的增加逐渐减弱的特征,本文在连接键上引入了考虑应变软化效应的Mohr-Coulomb准则及最大拉应力准则. 基于上述拉剪复合准则,可对式(3)计算获得的下一时步的试探接触力进行修正.
采用式(6)进行拉伸破坏的判断及法向接触力的修正,为
| $ \left. \begin{array}{l} 如果\;\;\;\;\; - {F_{\rm{n}}}({t_1}) \ge T({t_0}){A_{\rm{c}}}\\ 那么\;\;\;\;{F_{\rm{n}}}({t_1}) = - T({t_0}){A_{\rm{c}}}\\ \;\;\;\;\;\;\;\;\;T({t_1}) = - {T_0}{\varepsilon _{\rm{p}}}/{\varepsilon _{\lim }} + {T_0} \end{array} \right\} $ | (6) |
其中,$T_{0}$,$T(t_{0})$及$T(t_{1})$为初始时刻、本时刻及下一时刻的抗拉强度,$\varepsilon_{\lim}$为 拉伸断裂应变,$\varepsilon_{\rm p}$为本时刻的拉伸塑性应变,为
| $ \varepsilon _{\rm p} = \dfrac{\Delta u_{\rm n} }{R_1 + R_2 } - \dfrac{T(t_0 )}{\mathop{\bar {E}}\limits^{ \ }} $ | (7) |
其中,$\Delta u_{\rm n} $为连接键两侧颗粒的法向位移差.
采用式(8)进行剪切破坏的判断及切向接触力的修正,为
| $ \left. \begin{array}{l} 如果\;\;\;{F_{\rm{s}}}({t_1}) \ge {F_{\rm{n}}}({t_1})\tan \phi + c({t_0}){A_{\rm{c}}}\\ 那么\;\;\;{F_{\rm{s}}}({t_1}) = {F_{\rm{n}}}({t_1})\tan \phi + c({t_0}){A_{\rm{c}}}\\ \;\;\;\;\;\;\;c({t_1}) = - {c_0}{\gamma _{\rm{p}}}/{\gamma _{{\rm{lim}}}} + {c_0} \end{array} \right\} $ | (8) |
其中,$\phi $为内摩擦角,$c_{0}$,$c(t_{0})$及$c(t_{1})$为初始时刻、本时刻及下一时刻的黏聚力,$\gamma_{\lim}$为剪切断裂应变,$\gamma_{\rm p}$为本时刻的剪切塑性应变,为
| $ \gamma _{\rm p} = \dfrac{\Delta u_{\rm s} }{R_1 + R_2 } - \dfrac{c(t_0 ) + F_{\rm n} (t_1 )\tan (\phi) / A_{\rm c} }{\mathop{\bar{G}}\limits^{ \ } } $ | (9) |
其中,$\Delta u_{\rm s} $为连接键两侧颗粒的切向位移差.
由式(6)和式(8)可以看出,连接键的抗拉强度及黏聚力将随着拉伸塑性应变及剪切塑性应变的增加而线性减小,如图 2所示.

|
图 2 抗拉强度及黏聚力的线性软化效应 Fig.2 Linear reduction effect of tensile strength and cohesion |
基于连接键的应变软化模型,可以定义3类损伤因子,分别为拉伸损伤因子$\alpha $,剪切损伤因子$\beta $及联合损伤因子$\chi $,为
| $ \left. \begin{array}{l} \alpha = 1 - T(t)/{T_0}\\ \beta = 1 - c(t)/{c_0}\\ \chi = 1 - (1 - \alpha )(1 - \beta ) \end{array} \right\} $ | (10) |
当满足不等式(11)时,颗粒间的连接键将不再传递力矩(即不进行式(4)的计算)
| $ \left. \begin{array}{l} [\frac{{ - {F_{\rm{n}}}}}{{{A_{\rm{c}}}}} + \frac{{|{M_{\rm{s}}}|}}{I}\min ({R_1},{R_2})] \ge {T_0}\;\;\;\;或\\ [\frac{{\left| {{F_{\rm{s}}}} \right|}}{{{A_{\rm{c}}}}} + \frac{{\left| {{M_{\rm{n}}}} \right|}}{J}\min ({R_1},{R_2})] \ge \frac{{{F_{\rm{n}}}}}{{{A_{\rm{c}}}}}\tan \phi + {c_0} \end{array} \right\} $ | (11) |
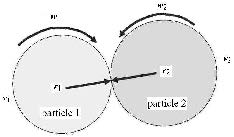
为了更加真实地模拟细观颗粒的运动破坏过程,本文在计算时考虑了颗粒的转动效应,计算示意图如图 3所示.
|
图 3 颗粒的转动计算 Fig.3 Particle-rolling computation |
计算时,首先利用式(12)获得全局增量位移向量$\Delta {\pmb d}$,接着将$\Delta {\pmb d}$转换至接触局部坐标系,利用式(3),式(6)和式(8)获得局部坐标系下的接触力,进而将接触力转化至整体坐标系,并利用式(13)计算施加至颗粒1,2上的转矩.
| $ \Delta {\pmb d} = ({\pmb w}_1 \times {\pmb r}_1 -{\pmb w}_2 \times {\pmb r}_2 )\Delta t + ({\pmb v}_1 - {\pmb v}_2 )\Delta t $ | (12) |
| $ {\pmb M}_1 ={\pmb r}_1 \times {\pmb F}^{(G)} ,\ \ {\pmb M}_2 = - {\pmb r}_2 \times {\pmb F}^{(G)} $ | (13) |
式(12)中,${\pmb w}_1 $及${\pmb w}_2 $分别为颗粒1和2的转动角速度向量;${\pmb r}_1 $和${\pmb r}_2 $分别为颗粒1和2到接触点的相对位置向量(由颗粒质心指向接触点);${\pmb v}_1 $和${\pmb v}_2 $分别为颗粒1和 2质心处的平动速度向量.
式(13)中,${\pmb M}_1 $和${\pmb M}_2 $分别为施加至颗粒1和2上的转矩;${\pmb F}^{(G)}$为全局坐标下的接触力.
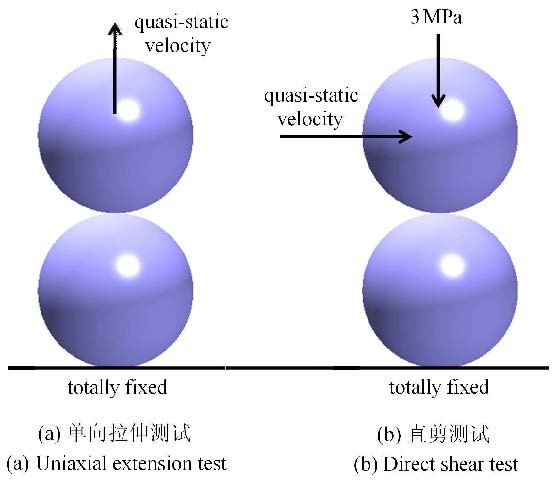
1.3 单一连接键的计算精度验证为了验证连接键模型的计算精度,本节首先探讨单一连接键在单向拉伸及直接剪切下的应力应变关系(图 4). 两个三维颗粒(球)的 半径均为0.5 m,输入的密度为2 500 kg/m$^{3}$,弹性模量为10 GPa,泊松比为0.22,黏聚力及抗拉强度为3 MPa,内 摩擦角30$^\circ$,拉伸断裂应变为0.1%,剪切断裂应变为0.3%. 单向拉伸测试时,下侧颗粒固定,上侧颗粒施加竖直向上的准静态速度载荷;直接剪切测试时,下侧颗粒固定,上侧颗粒在竖直 方向施加3 MPa的压应力,在水平方向施加准静态速度载荷.
|
图 4 单一连接键的精度测试 Fig.4 Precision test of single linked bar |
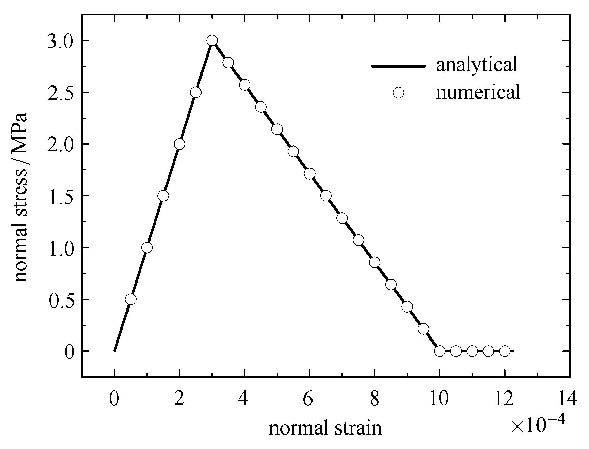
单向拉伸作用下,单一连接键表现出的宏观应力应变关系如图 5所示. 直接剪切作用下单一连接键表现出的宏观剪应力与剪应变 的关系如图 6所示.
|
图 5 拉应力与拉应变的关系 Fig.5 Relationship between normal stress and normal strain |
|
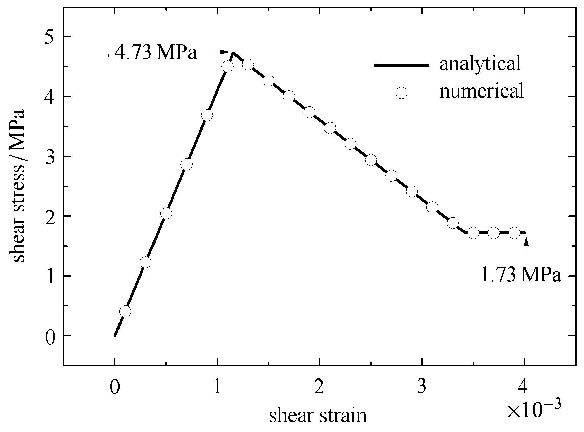
图 6 剪应力与剪应变的关系 Fig.6 Relationship between shear stress and shear strai |
由图 5可得,随着拉伸应变的增加,拉伸应力线性增加;当拉伸应力增大至抗拉强度(3 MPa)后,抗拉强度逐渐丧失,拉伸应 力线性减小;当拉伸塑性应变增大至0.1%时,拉伸应力变为0,连接键发生断裂. 数值解与理论解完全一致,表明了连接键模型在模拟拉伸破坏方面的精度.
由图 6可得,随着剪应变的增加,剪应力线性增加. 根据Mohr-Coulomb准则,抗剪强度可表示为
| $ \tau = c_0 + F_{\rm n} \tan (\phi) / A_{\rm c} $ | (14) |
将材料参数代入式(14)计算可得,该组直剪实验的抗剪强度为4.73 MPa,与图 6给出的峰值应力完全一致;随着错动的加剧,黏聚力逐渐丧失,剪应力线性减小;当剪切塑性应变增大至0.3%时,黏聚力完全丧失,连接键发生剪切断裂;此后,连接键两侧颗粒将发生摩擦滑移,由于法向正应力及摩擦系数的存在,颗粒间存在摩擦应力,为1.73 MPa,这与图 6给出的数值解完全一致. 直剪测试的数值解与理论解完全一致,表明了连接键模型在模拟剪切破坏方面的精度.
1.4 平均配位数对宏观弹性特征的影响由1.3节可知,在研究单一连接键时,直接输入宏观参数即可获得正确的宏观应力应变关系,而不需要做细观参数的标定. 但当系统中存在大量颗粒时,颗粒的配位数将决定系统中连接键的数量,进而影响系统的宏观力学行为. 因此,本节主要探讨配位数对颗粒体系宏观力学行为的影响.
采用颗粒系统与连续介质系统弹性应变能的比值$\lambda $作为因变量,探讨$\lambda $与颗粒平均配位数$\bar {N}$的对应关系. $\lambda $可表示为
| $ \lambda = L_{\rm p} / L_{\rm e} $ | (15) |
其中,$L_{\rm p} $为颗粒系统弹性应变能,$L_{\rm e} $为连续介质系统弹性应变能,为
| $ \left. \begin{array}{l} {L_{\rm{p}}} = \sum\limits_{i = 1}^{{N_p}} {} (F_{\rm{n}}^i\Delta u_{\rm{n}}^i/2 + F_{\rm{s}}^i\Delta u_{\rm{s}}^i/2)\\ {L_{\rm{e}}} = {\rm{ }}\int {{\sigma _{ij}}{\varepsilon _{ij}}} /(2dV) \end{array} \right\} $ | (16) |
其中,$N_{\rm p }$为连接键数量,$F_{\rm n}^i $及$F_{\rm s}^i $为第$i$个连接键的法向及切向力,$\Delta u_{\rm n}^i $及$\Delta u_{\rm s}^i $为第$i$个连接键的法向及切向位移差,$\sigma _{ij} $及$\varepsilon _{ij} $为宏观连续介质的应力及应变张量.
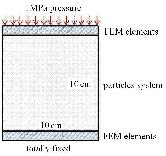
为了分析$\lambda $与$\bar {N}$的对应关系,建立长宽均为10 cm的二维颗粒流模型,并在模型顶部及底部各放置一钢板(采用有限元单元进行离散),且模型的左右两侧为自由边界,如图 7所示.
|
图 7 颗粒系统模型 Fig.7 Model of particles system |
数值计算时,底板固定,在顶板上施加1 MPa的压应力. 颗粒体系的输入弹性模量为30 GPa,泊松比0.3,密度2 500 kg/m$^{3}$.
通过调整图 7颗粒系统中的颗粒数量、颗粒半径、颗粒级配及颗粒间嵌入量等可以实现不同的平均配位数. 按照调整的策略,共包含5种类型,分别为:
工况1:保证颗粒总面积与试样面积一致(0.01 m$^{2}$),改变颗粒半径及颗粒数量(颗粒数量200$\sim $50 000), 共12组算例;
工况2:保证颗粒半径一致(0.728 mm),改变颗粒数量(5 000$\sim $7 000),共6组算例;
工况3:保证颗粒半径及数量一致(半径0.728 mm,数量6 000),改变颗粒排布方式,共6组算例;
工况4:保证颗粒数量一致(6 000),改变颗粒半径(0.67 mm$\sim $0.82 mm),共6组算例;
工况5:设颗粒半径服从均匀分布,保证期望一致(0.7 mm),改变标准差(0$\sim $0.35 mm),共6组算例.
此外,利用91 612个三角形有限元单元进行了相同尺寸及材料参数下的连续介质系统的应变能计算,计算获得的试样 应变能为0.151 N$\cdot$m.
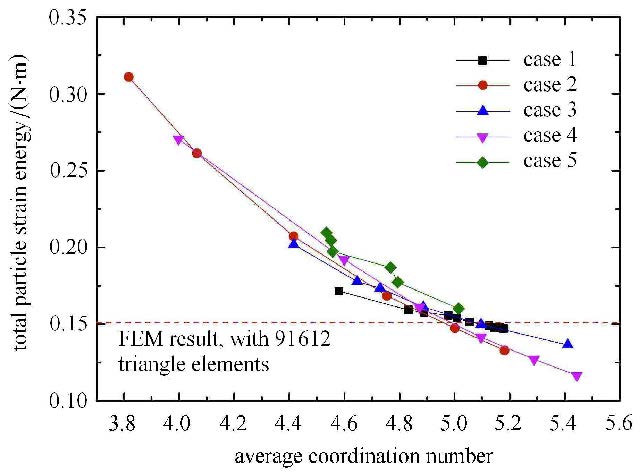
各工况下颗粒体系应变能与平均颗粒配位数的关系如图 8所示. 由图可得,随着平均颗粒配位数的增加,系统应变能逐渐减小,但减小趋势逐渐变缓;当颗粒平均配位数为5时,颗粒系统的应变 能与利用有限元计算获得的应变能基本一致.
|
图 8 颗粒应变能与平均配位数的关系 Fig.8 Relationship between particles' strain energy and average coordination number |
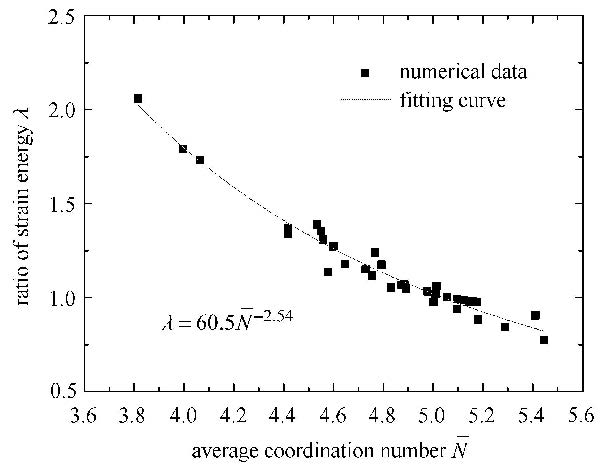
基于式(15),采用衰减型幂函数对细宏观应变能比值与颗粒平均配位数间的关系进行拟合(图 9),拟合相关系数0.967.
|
图 9 细宏观应变能比值与平均配位数的拟合曲线 Fig.9 Fitting curve about ratio of micro and macro strain energy vs average coordination number |
拟合获得的细宏观应变能的比值$\lambda $与颗粒平均配位数$\bar {N}$的对应关系式为
| $ \lambda = 60.5\bar {N}^{ - 2.54} $ | (17) |
由式(17)可知,随着颗粒平均配位数的增加,细宏观应变能的比值$\lambda $逐渐减小. 分析其原因,主要是因为随着颗粒平均配位数的增加,同一颗粒体系的总接触对数在增加;由于接触刚度(连接键刚度)依据式(2)进行计算,并未考虑平均配位数的影响;因此,随着总接触对的增加,系统的总体刚度也将逐渐增加,从而导致相同载荷下系统的应变能呈逐渐减小的趋势.
由式(17)还可以看出,当颗粒平均配位数为5时,细宏观应变能的比值接近于1,表明细、宏观的弹性应变能基本一致;因此,对于基于连接键模型的二维颗粒体系,若保证系统的平均配位数为5,则直接输入宏观弹性参数即可获得宏观弹性特征.
2 岩石单轴压缩过程数值分析 2.1 数值模型及计算工况建立宽5 cm、高10 cm的二维岩石数值模型,并用13 097个颗粒进行离散,其中最小颗粒半径0.228 mm,最大颗粒半径0.422 mm,颗 粒接触数63 252个. 颗粒密度2 500 kg/m$^{3}$,弹性模量30 GPa,泊松比0.22,抗拉强度3 MPa、黏聚力3 MPa,内摩擦角30$^\circ$,局部阻尼0.8. 数值计算时,模型底部进行法向约束,模型顶部施加竖直向下的准静态速度边界(每个迭代步1 nm).
岩石的细观损伤断裂采用本文所述的考虑应变软化效应的Mohr-Coulomb准则及最大拉应力准则实现. 当连接键达到屈服强度时,连接 键的黏聚力及抗拉强度将随着剪切塑性应变及拉伸塑性应变逐渐减小;同时,连接键的拉伸及剪切损伤将逐渐增加;当黏聚力或抗拉强度 衰减至零时,连接键发生断裂,细观裂缝形成.
数值计算时,令拉伸断裂应变与剪切断裂应变一致(即$\kappa = \varepsilon _{\lim } = \gamma _{\lim } $,以下统称断裂应变),取$\kappa $为0,0.1%,0.3%,0.6%,1.2%及2.4%等6个工况,探讨不同断裂应变对岩石宏观应力应变关系及破裂度的影响.
2.2 应力应变关系分析6种工况下岩石试样的本构曲线如图 10所示. 由图可得,不同断裂应变下的岩石单轴压缩过程大致可以分为4个阶段,分别为线性上升段、非线性上升段、非线性下降段及缓变段. 6个工况下线性上升段的长度基本一致,该阶段的最大应力值约为5.9 MPa. 随着断裂应变的增大,非线性上升段呈现出逐渐增加的趋势;断裂应变为0时,非线性上升段仅为线性上升段的20%左右;而当断裂应变为2.4%时,非线性上升段的长度已达线性上升段的2倍以上. 随着断裂应变的增加,非线性下降段的下降速率有所增加,但在断裂应变为0.3%以后,下降速率的变化趋势并不明显. 6个工况下缓变段对应的应力值基本一致,约为0.4$\sim$2 MPa. 由图 10还可以看出,随着断裂应变的增加,本构曲线中的峰值强度及达到峰值强度时的应变也将逐渐增大.

|
图 10 不同断裂应变下的单轴压缩本构曲线 Fig.10 Constitutive curve of uniaxial compression test with different fracture strain |
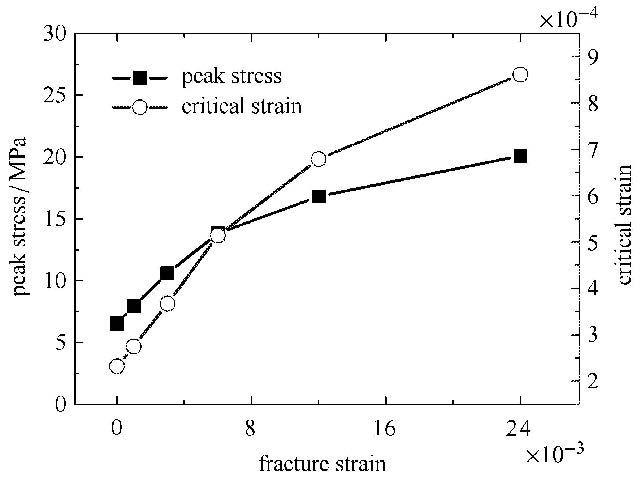
不同工况下,峰值应力及达到峰值应力时的临界应变随着断裂应变的变化规律如图 11所示. 由图可得,随着断裂应变的增加,峰值应力及临界应变均逐渐增加,但增加趋势逐渐变缓;当断裂应变为0时,峰值应力为6.54 MPa,对应的临界应变为232$\times $10$^{-6}$;当断裂应变为2.4%时,峰值应力为20.1 MPa,对应的临界应变为861$\times $10$^{-6}$.
|
图 11 峰值应力及临界应变随断裂应变的变化规律 Fig.11 Relationship between peak stress, critical strain and fracture strain |
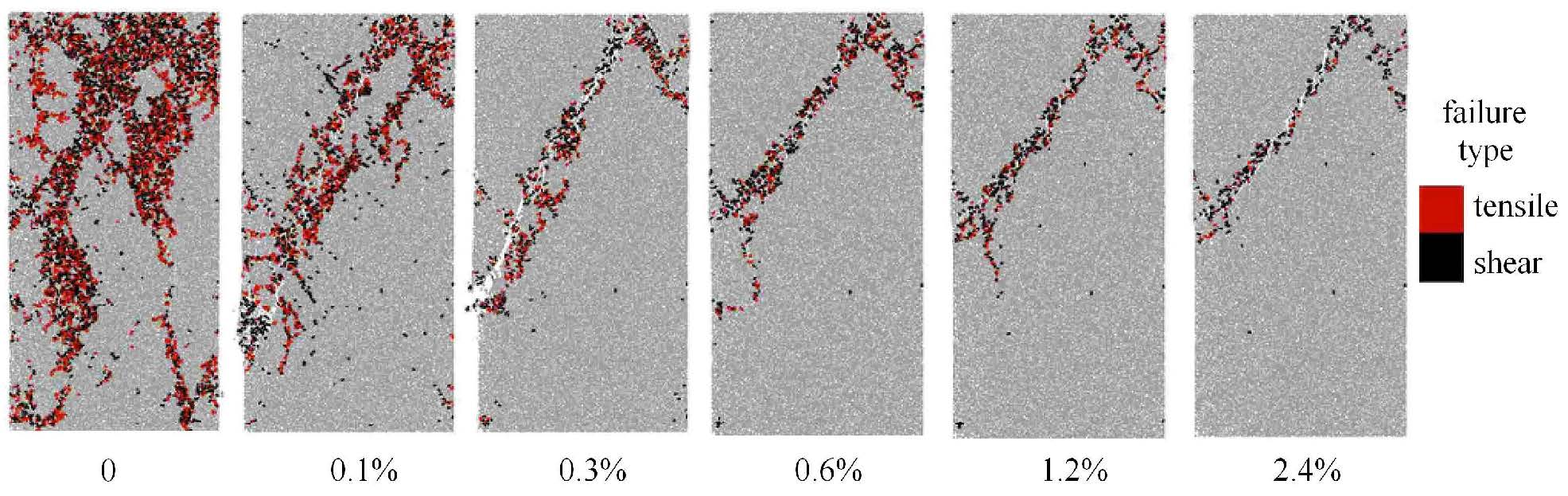
各工况下岩石试样的破坏模式如图 12所示(图中黑色线表示发生剪切破坏的连接键,红色线表示发生拉伸破坏的连接键). 由图 可得,当断裂应变较小时,岩石主要发生拉剪复合型破坏,破坏路径较多,破坏区域较大,且上部以压剪破坏为主,下部以张拉 破坏为主;当断裂应变较大时,岩石主要发生压剪型破坏,破坏位置主要集中在试样中上部,并在模型左右两侧出现两条不对称的剪切带. 从图中还可以看出,当断裂应变大于0.3%时,岩石试样的破坏模式基本不变.
|
图 12 不同断裂应变下的岩石试样破坏模式 Fig.12 Different failure mode of rock sample with different fracture strain |
峰值强度时,各连接键的联合损伤因子如图 13所示. 由图可得,随着断裂应变的增加,岩石试样的损伤从集中损伤逐渐过渡到弥 散型损伤. 当断裂应变为0 时,仅在试样局部位置出现完全损伤,其他位置无损伤;当断裂应变为2.4%时,试样各处均出现了不同程度的损伤破坏,但在中 上部斜向存在损伤较大的区域. 从图 13还可以看出,峰值强度时,岩石试样内部出现了主控断裂带(图中黑色虚线部分);该断裂带将在顶部载荷作用下出现失稳扩展,进而形成贯穿性主控裂缝.

|
图 13 不同断裂应变下岩石试样达到峰值强度时的联合损伤因子云图 Fig.13 Combined damage factor contour of rock sample under peak stress with different fracture strain |
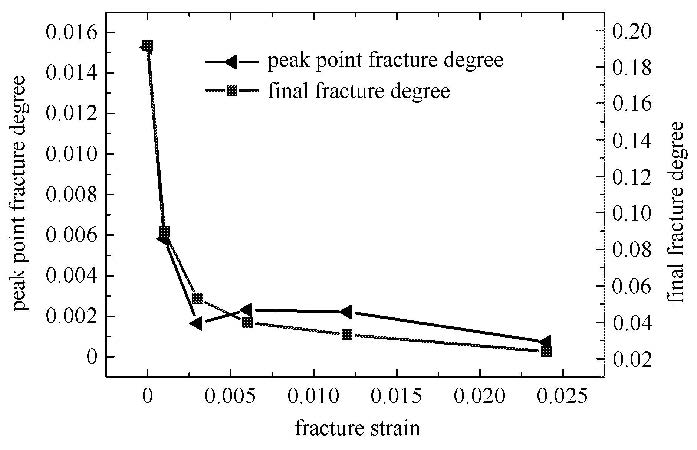
定义破裂度为某一状态下发生断裂的连接键个数与数值模型中总连接键个数的比值,则峰值时的破裂度及终态时的破裂度随着断裂应 变的变化规律如图 14所示. 由图可得,随着断裂应变的增加,峰值时的破裂度及终态时的破裂度均逐渐减小,但减小趋势逐渐变缓. 断裂应变从0 变化至2.4%,峰值时破裂度从1.5%降低至了0.073%,终态时破裂度从19%降低至了2.4%.
|
图 14 峰值破裂度及终态破裂度与断裂应变的关系 Fig.14 Relationship between peak point fracture degree, final fracture degree and fracture strain |
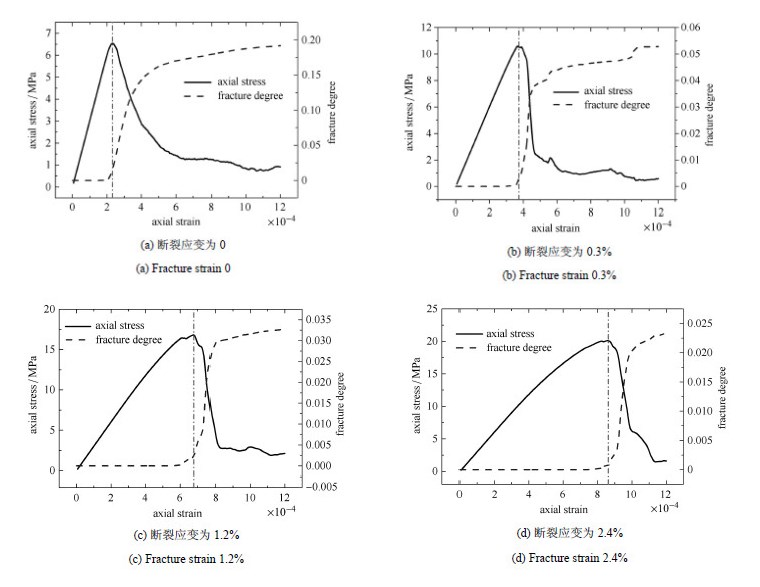
典型断裂应变下轴向应力及破裂度随着轴向应变的变化规律如图 15所示. 由图可得,当轴向应力位于线性上升段时,破裂度为0; 当轴向应力位于非线性上升段时,破裂度缓慢增加;当轴向应力处于峰值点附近时,破裂度突然增加;当轴向应力位于非线性 下降段时,破裂度以较高的速率快速增加;当轴向 应力位于缓变段时,破裂度的增速变缓,并逐渐趋于稳定.
|
图 15 典型断裂应变下轴向应力及破裂度随着轴向应变的变化规律 Fig.15 Relationship between axial stress, fracture degree and axial strain with typical fracture strain |
文章提出了一种连接键应变软化的颗粒接触模型,并通过宏细观应变能等效的方法揭示了平均配位数对颗粒体系宏观弹性特征的影响规律;二维颗粒体系的计算案例表明,当平均配位数为5时,连接键中输入的细观弹性模量及泊松比与颗粒体系宏观响应获得的弹性模量、泊松比基本一致.
利用连接键应变软化模型探讨了岩石单轴压缩过程中应力应变特征及破裂度与断裂应变的对应关系,通过数值计算发现:
(1) 不同断裂应变下的岩石单轴压缩过程大致可以分为4个阶段,分别为线性上升段、非线性上升段、非线性下降段及缓变段. 其中,线性上升段为弹性阶段,非线性上升段为均匀损伤阶段,非线性下降段为宏观主控裂缝的贯通阶段,缓变段为断裂后的试样沿着断口的滑移阶段.
(2) 随着断裂应变的增加,岩石的破裂模式逐渐由拉剪复合型破裂向单一压剪型破裂转化;且随着断裂应变的增加,峰值强度及达到峰值强度时的应变均逐渐增大,但峰值时的破裂度及终态时的破裂度将逐渐减小.
连接键应变软化模型与现有模型的对比分析、粘滞效应对连接键应变软化模型的影响、三维连接键模型中最优配位数的寻找等将是今后的主要研究方向.
| 1 | 徐泳, 孙其诚, 张凌等. 颗粒离散元法研究进展. 力学进展, 2003,33(2): 251-260 (Xu Yong, Sun Qicheng, Zhang Ling, et al. Advances in discrete element methods for particulate materials. Advances in Mechanics, 2003, 33(2): 251-260 (in Chinese)) |
| 2 | 谭青, 徐孜军, 夏毅敏等. 盾构切刀作用下岩石动态响应机制的数 值模拟研究. 岩土工程学报, 2013, 35(2): 235-242 (Tan Qing, Xu Zijun, Xia Yimin, et al. Numerical simulation of dynamic response mechanism of rock by shield machine cutters. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 235-242 (in Chinese)) |
| 3 | 石崇, 王盛年, 刘琳. 地震作用下陡岩崩塌颗粒离散元数值模拟 研究. 岩石力学与工程学报, 2013, 32(S1): 2798-2805 (Shi Chong, Wang Shengnian, Liu Lin. Research of avalanche disaster numerical simulation based on granular discrete element method of high-steep slope under seismic loads. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2798-2805 (in Chinese)) |
| 4 | 张社荣, 孙博, 王超等. 双轴压缩试验下岩石裂纹扩展的离散 元分析. 岩石力学与工程学报, 2013, 32(S2): 3083-3091 (Zhang Sherong, Sun Bo, Wang Chao, et al. Discrete element analysis of crack propagation in rocks under biaxial compression. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3083-3091 (in Chinese)) |
| 5 | Ji SY, Di SC. Discrete element modeling of acoustic emission in rock fracture. Theoretical and Applied Mechanics Letters, 2013,3(2): 021009-021009-5 |
| 6 | Utili S, Nova R. DEM analysis of bonded granular geomaterials. International Journal for Numerical and Analytical Methods in Geomechanics,2008, 32(17): 1997-2031 |
| 7 | Oñate E, Zarate F, Miquel J, et al. A local constitutive model for the discrete element method. Application to geomaterials and concrete. Computational Particle Mechanics, 2015, 2: 139-160 |
| 8 | Huang H, Lecampion B, Detournay E. Discrete element modeling of tool—rock interaction I: Rock cutting. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(13):1913-1929 |
| 9 | Huang H, Detournay E. Discrete element modeling of tool—rock interaction II: rock indentation. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(13): 1930-1947 |
| 10 | Yang BD, Jiao Y, Lei S. A study on the e ects of microparameters on macroproperties for specimens created by bonded particles. Engineering Computations, 2006, 23(6): 607-631 |
| 11 | Yoon J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 871-889 |
| 12 | Coetzee CJ, Els DNJ. Calibration of discrete element parameters and the modelling of silo discharge and bucket filling. Computers and Electronics in Agriculture, 2009, 65(2): 198-212 |
| 13 | Wang Y, Tonon F. Calibration of a discrete element model for intact rock up to its peak strength. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(5): 447-469 |
| 14 | Itasca Consulting Group Inc. PFC3D (Particle Flow Code in 3 Dimensions), Version 4.0, User's Manual. USA: Itasca Consulting Group Inc, 2003 |
| 15 | Jing LR, Stephansson O. Fundamentals of Discrete Element Methods for Rock Engineering: Theory and Applications. Elsevier, Amsterdam,2007 |
| 16 | 吴顺川, 张晓平, 刘洋. 基于颗粒元模拟的含软弱夹层类土质边 坡变形破坏过程分析. 岩土力学, 2008, 29(11): 2899-2904 (Wu Shunchuan, Zhang Xiaoping, Liu Yang. Analysis of failure process of similar soil slope with weak intercalated layer based on particle flow simulation. Rock and Soil Mechanics, 2008, 29(11): 2899-2904 (in Chinese)) |
| 17 | 赵国彦, 戴兵, 马驰. 平行黏结模型中细观参数对宏观特性影 响研究. 岩石力学与工程学报, 2012, 31(7): 1491-1498 (Zhao Guoyan,Dai Bing,Ma Chi. Study of e ects of microparameters on macroproperties for parallel bonded model. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1491-1498 (in Chinese)) |
| 18 | 祁原, 黄俊杰, 陈明祥. 可破碎颗粒体在动力载荷下的耗能特性. 力学学报, 2015, 47(2): 252-259 (Qi Yuan, Huang Junjie, Chen Mingxiang. Energy dissipation characteristics of crushable granules under dynamic excitations. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 252-259 (in Chinese)) |
| 19 | Gri ths DV, Mustoe GGW. Modelling of elastic continua using a grillage of structural elements based on discrete element concepts . International Journal for Numerical Methods in Engineering, 2001,50(7): 1759-1775 |
| 20 | Chang CS, Shi Q, Liao CL. Elastic constants for granular materials modeled as first-order strain-gradient continua. International Journal of Solids and Structures, 2003, 40(21): 5565-5582 |
| 21 | Kruyt NP, Rothenburg L. Micromechanical bounds for the e ective elastic moduli of granular materials. International Journal of Solids and Structures, 2002, 39(2): 311-324 |
 2016, Vol. 48
2016, Vol. 48