2. 西北师范大学物理与电子工程学院, 兰州 730070;
3. 贵州大学理学院, 贵阳 550050
颗粒材料的混合与分聚在工业过程中是非常重要的,例如在医药、食品、化工、陶瓷、冶金、建筑行业等 [1, 2, 3, 4, 5, 6]. 旋转圆筒中颗粒材料在一定的条件下会在轴向或径向 [7, 8, 9, 10, 11, 12] 出现分聚或混合现象. Nityanand 等 [13] 的实验结果表明,不同尺寸的颗粒混合时,随着转速的增加,径向颗粒分聚呈现小颗粒在外围,大颗粒在核心的现象. Kwapinska 等 [14] 通过离散元模拟方法研究了旋转速度、转筒直径、装载量等参数对颗粒径向混合的影响. 赵永志等 [15] 对准二维滚筒内二元颗粒流动进行了数值模拟,发现随着转筒转速等参数的改变,二元颗粒体系会出现分层现象. 当转速较高时,分层效果比较明显;当转速较低时,大颗粒沿着物料表面以较快的速度运动到转筒外围,小颗粒则保持在转筒中心部位. 近几十年来,颗粒体系混合和分聚的研究转向了对非圆形转筒的研究.
随着非圆形转筒的旋转,流层的长度周期性的伸缩变化,以致于颗粒材料展现复杂的混合与分聚现象 [16, 17, 18, 19, 20, 21]. Luding 等 [22] 通过凸与凹圆筒形状结合来控制颗粒分聚,研究了如何把径向颗粒分聚转化为快速的轴向分聚. 但是转速、转筒形状、填充率等因素对于研究颗粒的混合与分聚仍然处于探索中 [23, 24, 25, 26].
本文主要针对不同形状准二维颗粒转筒,研究形状对二元颗粒混合度的影响. 第一部分是实验与分析,通过改变转速和填充率,在3种混合器中分别获得不同的分聚与混合图样,并通过示踪颗粒轨迹进行测量分析,发现圆形混合器中颗粒的分聚现象最明显,正方形混合器中分聚现象最弱. 第二部分是模拟,由模拟得到速度场,发现颗粒分为快速流动的表面颗粒与旋转运动的体颗粒,模拟结果符合实验观察到的现象. 第三部分提出颗粒分聚理论模型,发现在圆形混合器中颗粒分聚现象最明显,正方形混合器中分聚现象最弱. 最后一部分是结论.
1 实验与分析 1.1 实验装置本实验装置由 3 种不同形状的准二维混合器 (圆形、椭圆形、正方形)、步进马达、高速摄像机组成. 混合器的外围由铝合金加工制作,封盖材料为有机玻璃. 圆形混合器的直径 dc = 17 cm,厚度 h = 5.5 mm,椭圆混合器的长轴 a = 17 cm,短轴为 b = 10 cm,厚度 h = 5.5 mm,正方形混合器的边长为l = 12 cm,厚度 h = 5.5 mm. 混合器的正后方装有步进马达,通过步进马达,可以改变混合器的旋转速度. 实验中,我们设置转速 ω 为10 r/min ~ 90 r/min. 混合器的正前方架有分辨率为 640 × 480 像素的高速摄像机 Prosilica(GE680C) 来捕捉颗粒的运动. 高速摄像机与电脑相连接,拍摄时设置每秒钟 60 帧. 颗粒材料选取钢珠( ps = 8.1 g/cm3,ds = 0.5 cm)、透明玻璃珠( pg = 2.6 g/cm3,dg为 0.2 ~ 0.3 cm). 将混合器填充率定义为
| $ Q = \frac{{{V_{\rm{R}}}}}{V} \times 100\% $ | (1) |
式中,VR 为混合器中颗粒的总截面积,V 为混合器的截面积.
我们进行了如下实验:(1)为观察掺杂颗粒的分聚状况,在分别填充 25%,50%,75% 的玻璃珠 (2 ~ 3 mm) 混合器中分别加入 28 颗、98 颗和 54 颗钢珠,改变转速,观察颗粒混合情况. (2) 为观察颗粒的运动轨迹,在分别填充了 25%,50%和75% 玻璃珠 (2 ~ 3 mm) 的混合器中,加入单个 5 mm 钢珠作为示踪颗粒,观察不同转速下钢珠的运动轨迹.
1.2 实验结果圆形混合器、正方形混合器、椭圆形混合器中,在不同转速和填充率下颗粒体系获得的实验结果都是颗粒体系达到稳定之后所得到.
(1) 圆形混合器实验结果
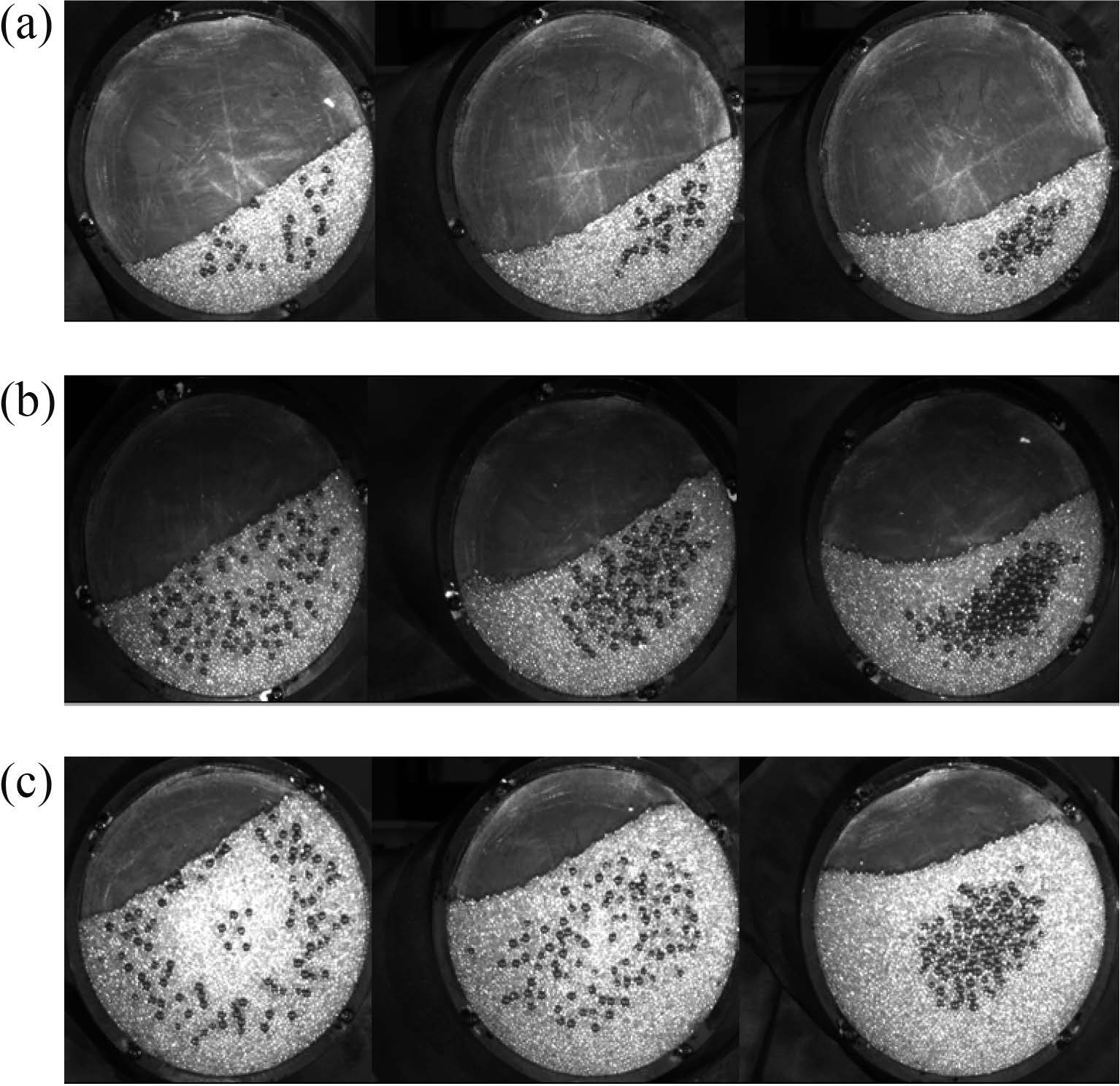
从图 1 不同的填充率下的钢珠分布状况可以看到,颗粒的运动主要分为被转筒带动的旋转运动和在自由表面受重力驱动的快速滑落运动. 随着填充率的增加,受旋转运动作用区域增加;随着转速增加,钢珠的聚集愈明显.
|
图 1 圆形混合器中不同填充率、转速下的实验结果。从左往右转速 ω 是10,60,90 r/min,从上到下填充率是25%,50%,75% Fig.1 Experimental results with different filling conditions and speeds in the circular mixer. From left to right, ω is 10, 60, 90 r/min. From up to down, filling conditions is 25%, 50%, 75% |
(2) 椭圆形混合器实验结果
椭圆形混合器的分聚情况见图 2,由于椭圆边壁的长短轴不对称性影响了颗粒的旋转聚集,钢珠与玻璃珠的分聚不如圆形混合器明显. 不过仍可看出随着转速和填充率的增加,钢珠聚集在中心区域.

|
图 2 椭圆形混合器中不同填充率、转速、颗粒密度下的实验结果。从左往右转速 ω 是10,60,90 r/min,从上到下填充率是25%,50%,75% Fig.2 Experimental results with different filling conditions and speeds in the ellipse mixer. From left to right, ω is 10, 60, 90 r/min. From up to down, filling conditions is 25%, 50%, 75% |
(3) 正方形混合器实验结果
正方形混合器分聚情况如图 3 所示,由于快速运动自由表面区域及旋转运动受容器棱角形状的影响,正方形容器的分聚情形不明显. 这说明几何效应对颗粒的混合影响较大.

|
图 3 正方形混合器中不同填充率、转速下的实验结果。从左往右转速 ω 是10,60,90 r/min,从上到下填充率是25%,50%,75% Fig.3 Experimental results with different filling conditions and speeds in the square mixer. From left to right, ω is 10, 60, 90 r/min. From up to down, filling conditions is 25%, 50%, 75% |
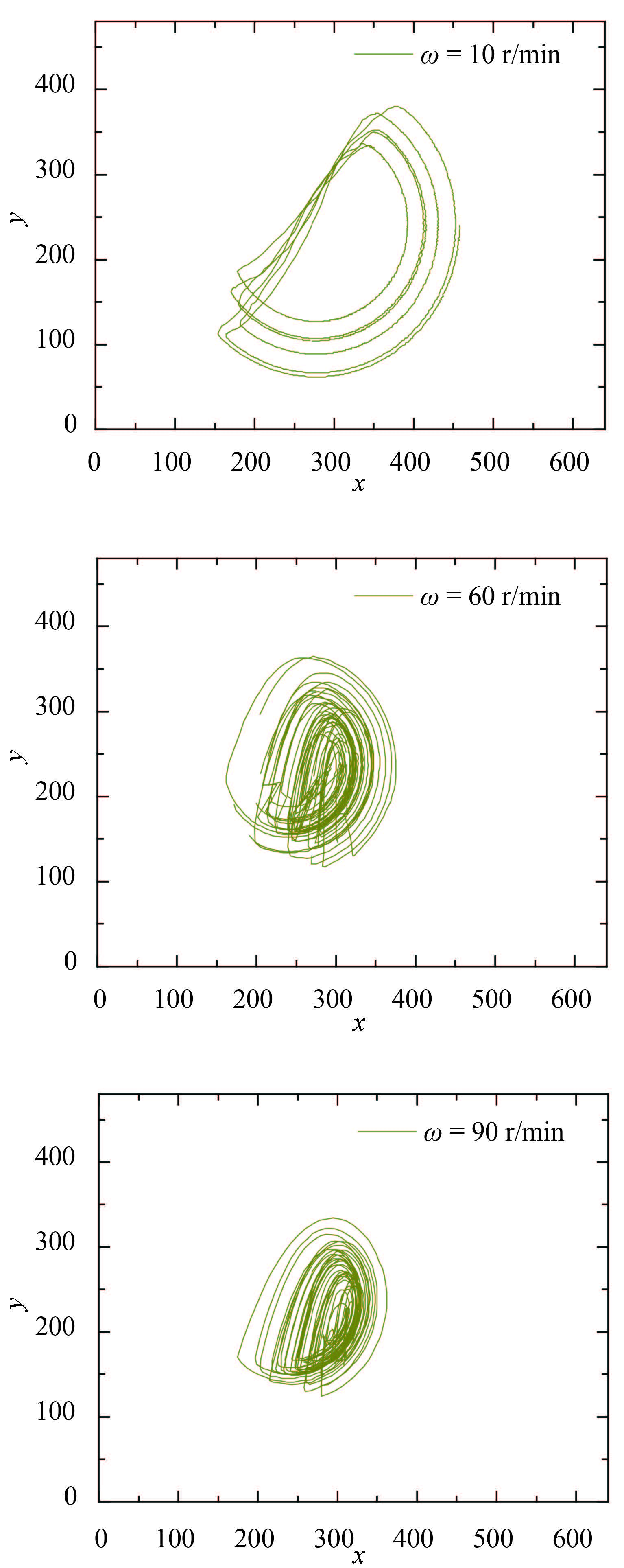
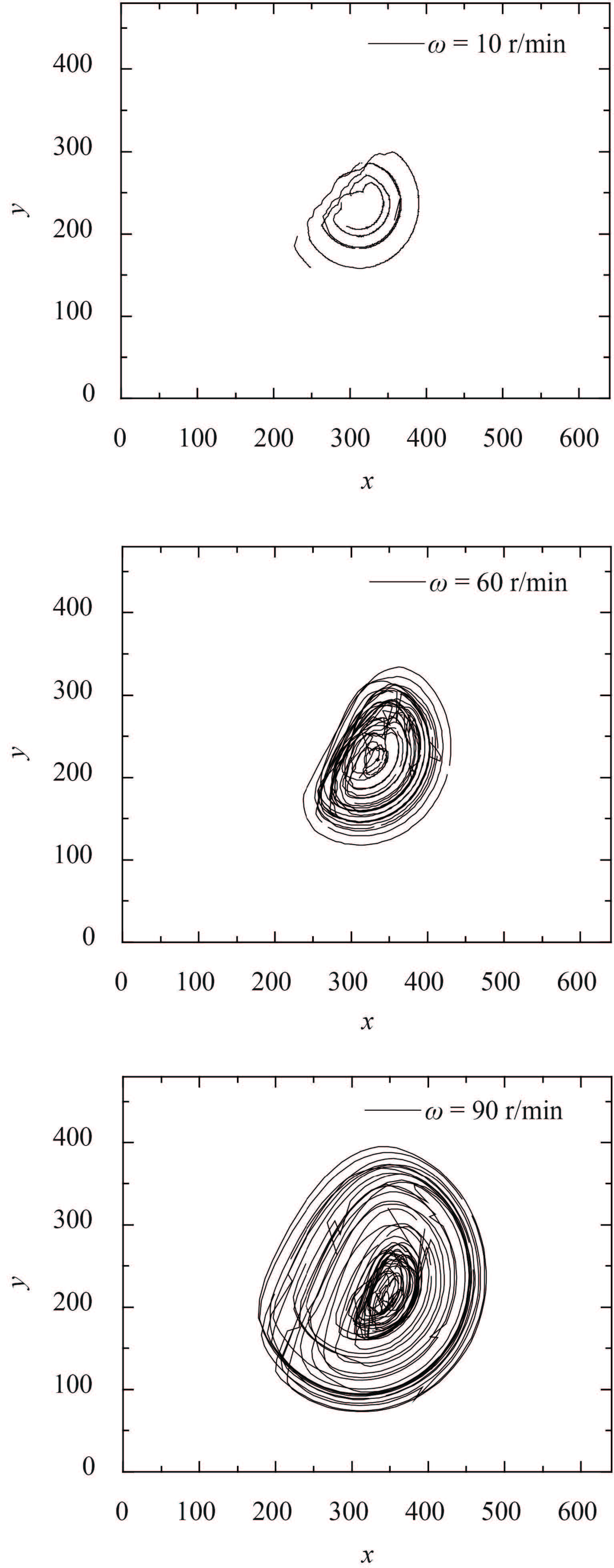
为了观察在不同转速下钢珠的运动轨迹,我们添加并跟踪了一颗 5 mm 钢珠示踪颗粒(钢珠的初始位置随机放置),记录其在填充有 25%,50% 和 75% 玻璃珠 (2 ~ 3 mm )的混合器中的路径. 图 4、图 5 和图 6 分别为不同转速下示踪颗粒在 50% 填充率下 3 种混合器内的运动轨迹. 转速低时,颗粒随转筒原位旋转,到达表面附近缓慢滑落;随着转速的提高,圆形混合器中,颗粒受旋转壁剪切作用,推向中心位置,轨迹呈收缩趋势,见图 4,与图 1(c) 相符;椭圆形混合器中,受椭圆长短轴影响,低速时颗粒旋转轨迹不再是原位旋转,而是在一带状区域内分布;随着转速的提高,颗粒旋转轨迹的分布向中心区域聚拢,见图 5;而正方形混合器由于边界棱角等形状因素影响,颗粒分布较广,没有明显的聚拢出现,见图 6.

|
图 4 圆形混合器中不同转速下示踪颗粒轨迹 Fig.4 Particle radial trajectory at different rotation speeds in the circle mixer |
|
图 5 椭圆形混合器中不同转速下示踪颗粒轨迹 Fig.5 Particle radial trajectory at different rotation speeds in the ellipse mixer |
|
图 6 正方形混合器中不同转速下示踪颗粒轨迹 Fig.6 Particle radial trajectory at different rotation speeds in the square mixer |
我们以颗粒位于混合器各个位置的概率及标准偏差对颗粒的随机分布进行分析,这里概率指颗粒在运动区间内占据某一位置的几率. 颗粒在运动过程中,一定时间内运动范围越大,概率分布越均一,表明颗粒运动的随机性越强,也说明颗粒不会长久地停滞于某一位置. 标准偏差表示颗粒相对于平均位置的离散程度. 标准偏差越大,表明颗粒的随机运动程度越大. 颗粒位置的变化主要分析颗粒在混合器的径向半径 R [27]. 颗粒位置径向分布概率为
| $ {P_{\rm{R}}} = \frac{{{N_{{\rm{Ri}}}}}}{{{N_{\rm{R}}}}} $ | (2) |
式中,PR 为颗粒在径向方向占据某一位置的概率,NRi 为颗粒位于某一径向坐标的次数,NR 为颗粒径向坐标的总取样次数. 标准偏差为
| $ {S_{\rm{R}}} = \sqrt {\frac{{\sum {{{({X_{{\rm{Ri}}}} - \overline X {}_{\rm{R}})}^2}} }}{{{N_{\rm{R}}} - 1}}} $ | (3) |
式中,${\overline X _{\rm{R}}}$ 为颗粒径向坐标的平均值,XRi 为颗粒某一径向坐标.
综观图 4 ~ 图 6 可以发现,示踪颗粒的运动具有规律性与随机性并存特征. 随机性主要体现在颗粒的轨迹是在一定范围内波动的,本文所选的示踪颗粒虽在运动的过程中没能贯穿整个径向区域,但可看出,在不同的混合器中,随着转速的变化,该颗粒出现在径向区域的运动范围也呈现不同特征.
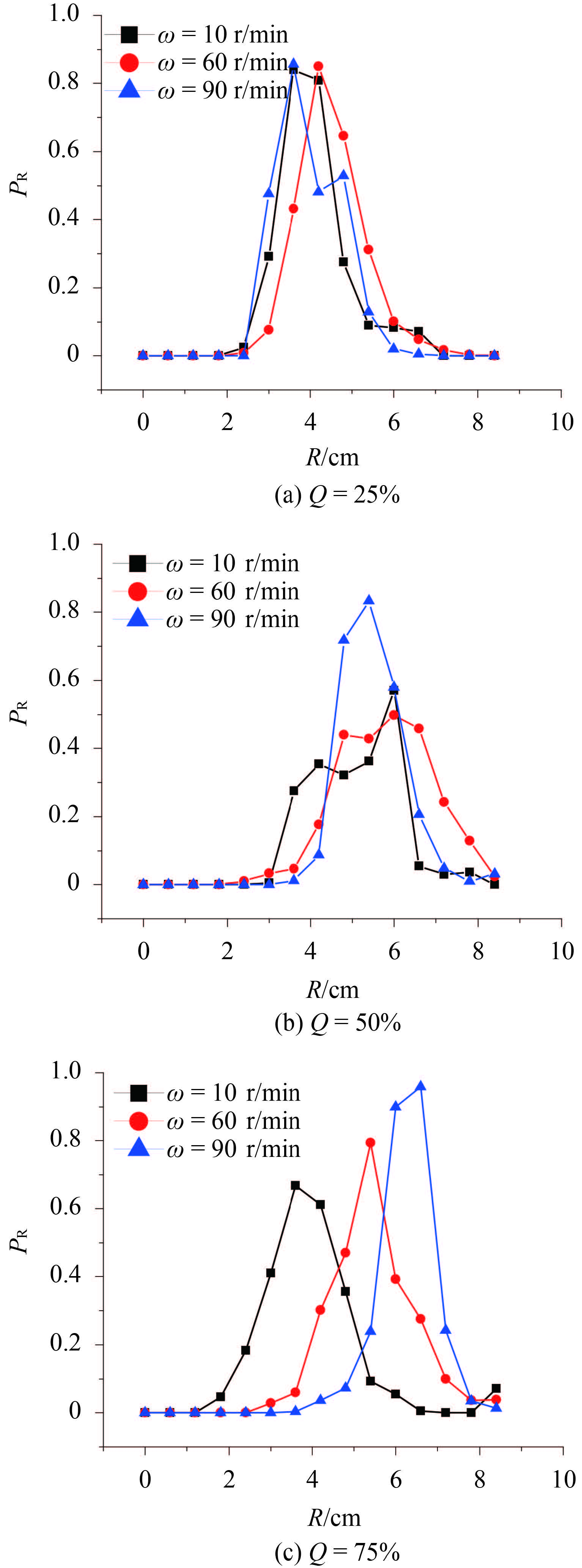
图 7 为圆形混合器中示踪颗粒径向分布概率曲线. 随着填充率的增加,不同转速下径向分布概率发生显著变化. 从图 7 可以看出,转速对径向分布的影响随着填充率的增加变得明显.
|
图 7 圆形混合器中不同转速下颗粒径向分布概率变化曲线 Fig.7 Effect of rotation speed on particle location probability with radical direction in the circle mixer |
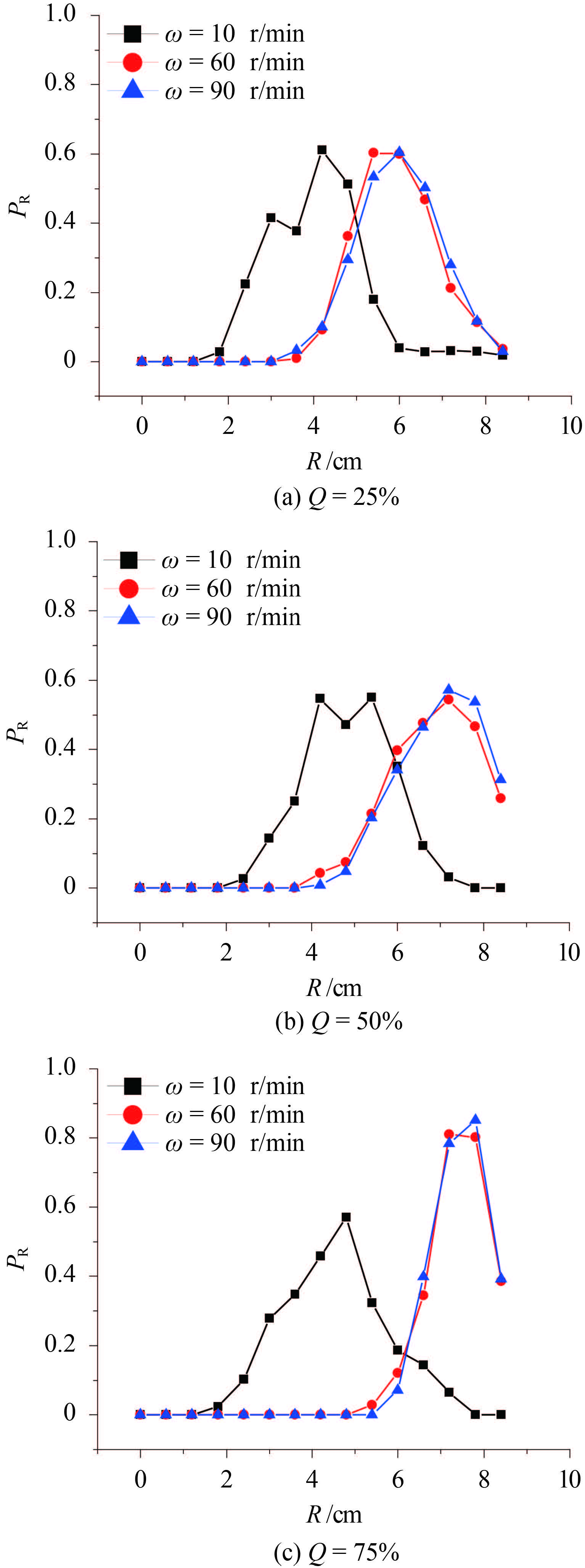
图 8 为椭圆形混合器示踪颗粒径向分布概率曲线. 随着填充率的增加,大转速下示踪颗粒径向分布概率的峰值会略微沿容器半径方向移动. 若给定填充率,随着转速的增加,示踪颗粒径向分布概率的峰值也会沿容器半径方向移动. 当增加到一定的值之后,峰值位置便不再发生变化.
|
图 8 椭圆形混合器中不同转速下颗粒径向分布概率变化曲线 Fig.8 Effect of rotation speed on particle location probability with radical direction in the ellipse mixer |
图 9 为正方形混合器中示踪颗粒径向分布概率曲线的变化. 不论是随着填充率的增加或转速的变化,示踪颗粒在径向分布概率峰值变化都不大,说明由于正方形的几何效应,使得颗粒分散,填充率和转速的影响不明显.

|
图 9 正方形混合器中不同转速下颗粒径向分布概率变化曲线 Fig.9 Effect of rotation speed on particle location probability with radical direction in the square mixer |
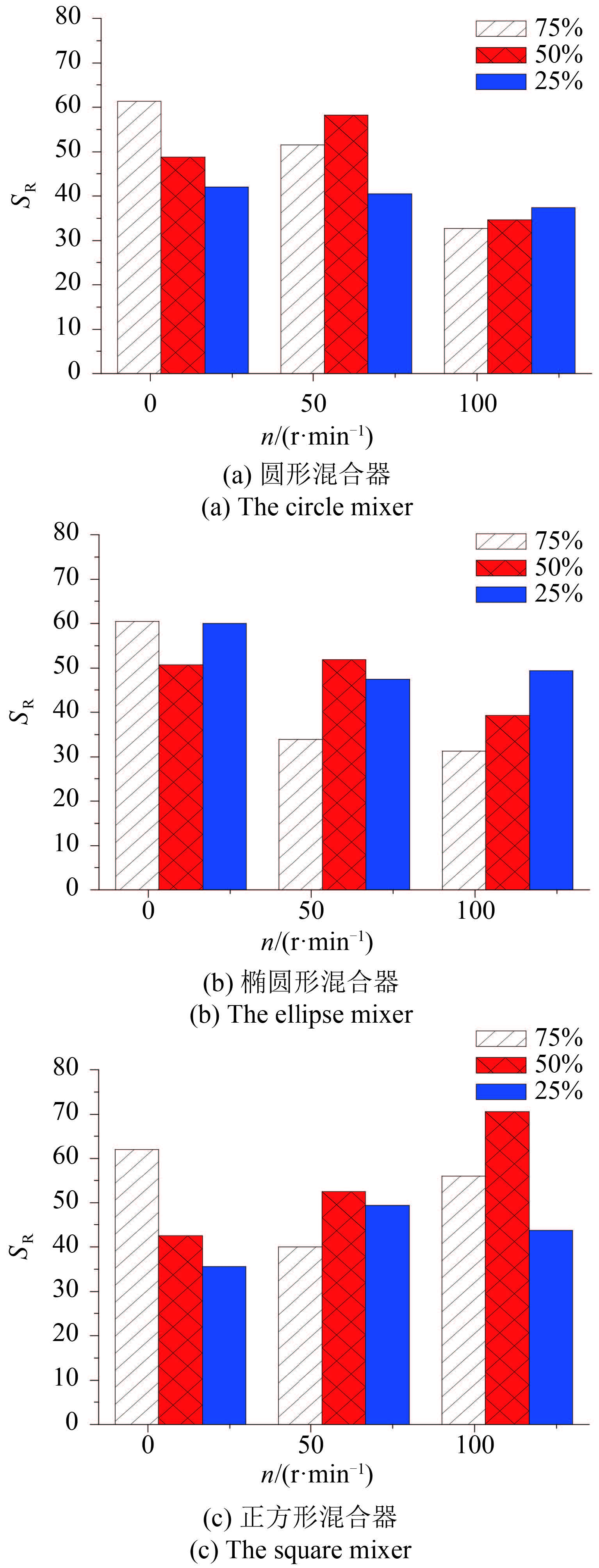
整体来看 (见图 10),在圆形混合器中,随着混合器转速的增大,颗粒在径向分布的涨落有所减少;在正方形混合器中,随着混合器转速的增大,颗粒径向分布的涨落有所增大;在椭圆形混合器中,颗粒径向分布涨落略微减少,但整体随机性比圆形混合器中颗粒随机性要大.
|
图 10 不同转速和填充率下颗粒在径向的位置标准偏差 Fig.10 Effect of rotation speed and filling conditions on standard deviation of particle position changes in radical direction |
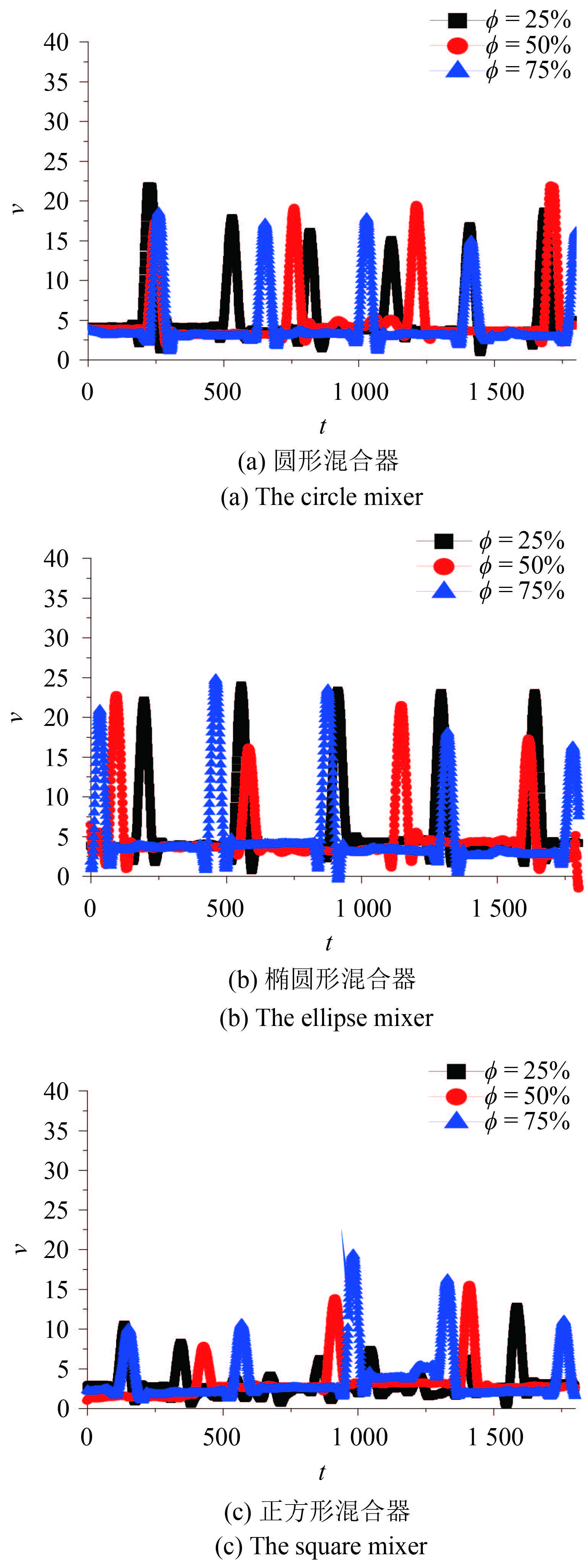
图 11 给出示踪颗粒在 3 种混合器中运动速率变化. 由图可以看到,颗粒先有一段随转筒的低速运动,到达表面后快速滑落,到达底部再被转筒带动直到再次回到表面. 圆形混合器和椭圆混合器中颗粒的流动速率高于正方形混合器中颗粒的流动速率,这说明正方形混合器的拐角限制了颗粒的流动性. 但是从椭圆混合器与正方形混合器中可以看到速率的变化起伏比较大,见图 11(b)(c),这说明随着这两种混合器的旋转,流层不断地发生变化.
|
图 11 不同填充率下示踪颗粒流动速率的变化曲线 Fig.11 Velocity of the particle at different filling conditions |
我们利用 PFC 软件进行模拟,模拟中采用线性接触模型. 当两个颗粒存在接触时,两个接触实体的切向刚度 ks 和法向刚度 kn 通过串联方式相互作用. 线性接触模型中切向刚度 ks 可通过下式计算:${k_{\rm{s}}} = k_{\rm{s}}^{\rm{1}}k_{\rm{s}}^{\rm{2}}/(k_{\rm{s}}^{\rm{1}} + k_{\rm{s}}^{\rm{2}})$ ,法向刚度 kn 可通过下式计算: ${k_{\rm{n}}} = k_{\rm{n}}^{\rm{1}}k_{\rm{n}}^{\rm{2}}/(k_{\rm{n}}^{\rm{1}} + k_{\rm{n}}^{\rm{2}})$. 式中 1 和 2 表示两接触实体 (球或墙面).
图 12 给出模拟的颗粒速度场分布,可以看到颗粒的运动可以分为两个区域,一为处于表面的、分布如半月形的、速度较大的颗粒,这些颗粒在自由表面,受重力驱动,速度较快,速度矢量是比较混乱的,说明剪切混合是比较明显的;另一为受边壁剪切带动的整体旋转运动,两个区域颗粒的交换达成颗粒最后的分聚或混合.
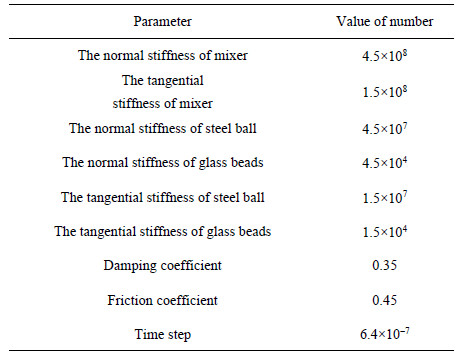
| 表 1 模拟参数 Table 1 Simulation parameters |

|
图 12 在圆形、椭圆形和正方形混合器中颗粒的速度场分布 Fig.12 Velocity fields in the circular, ellipse and square mixers |
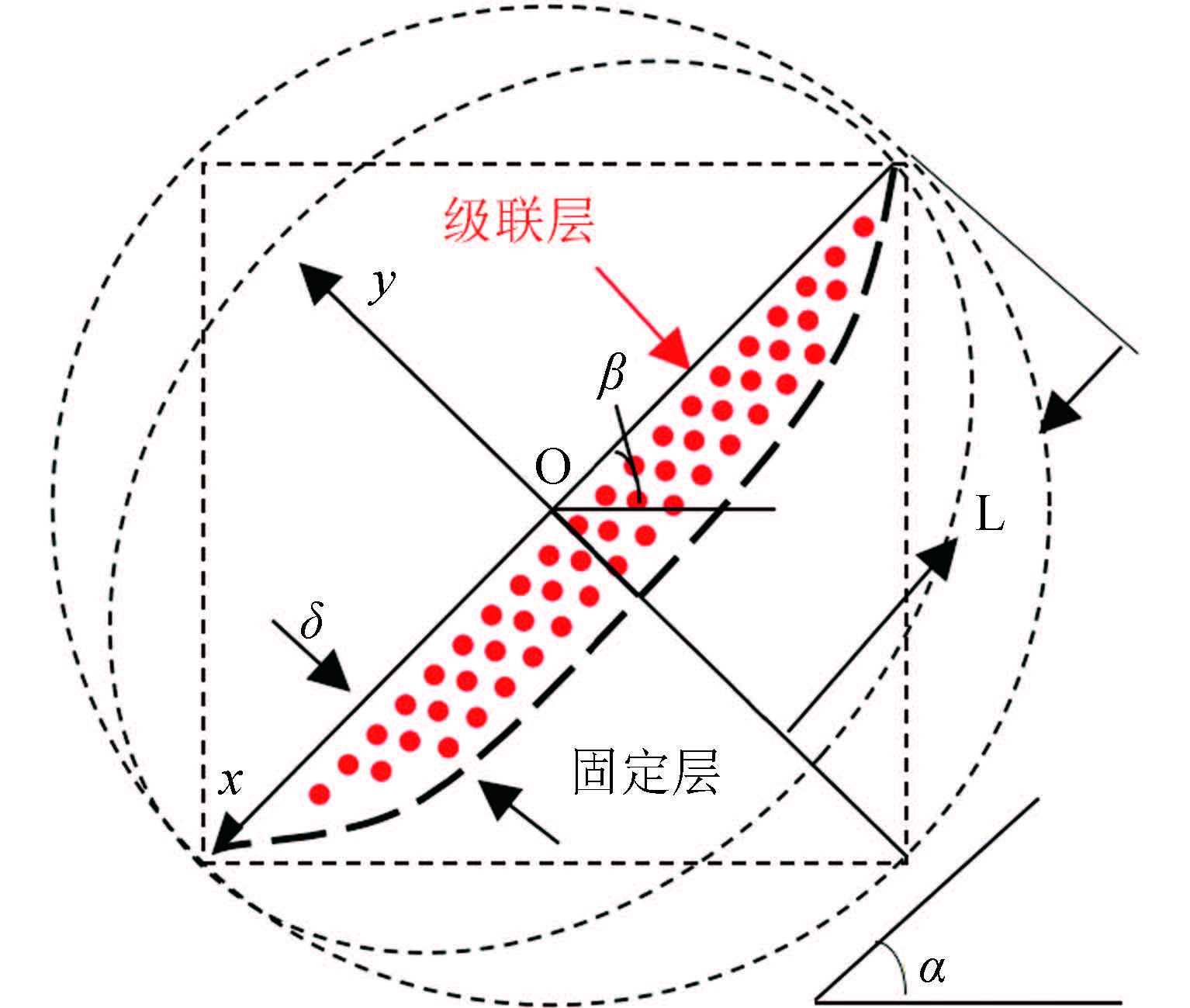
由前面实验和模拟的结果可知在圆形、椭圆形、正方形混合器中颗粒体系的流动主要分两大区域,我们定义为级联层的快速流动区域和以旋转混合器的转速转动的固定层区域. 随着混合器的旋转,级联层与固定层中的颗粒不断处于交换之中,颗粒之间的相互作用主要发生在级联层,如图 13 所示. 因此,我们主要对级联层中的颗粒相互作用进行分析. 假设颗粒流动是稳定的,考虑颗粒的填充度为 50% 时,在级联层中无量纲化的质量守恒方程可写为 [28]
|
图 13 旋转混合器的示意图 Fig.13 The sketch of the rotating mixer |
| $ k\frac{{\partial \phi }}{{\partial \theta }} + \frac{1}{2}\frac{{\partial ({\phi ^2})}}{{\partial \eta }} = - \eta - k\phi f $ | (4) |
上式中 $\eta = x/L(\theta )$ 和 $\phi = \delta (x)/(kL(\theta ))$ 分别是无量纲级联层 x 方向位置与对应层厚的变量,其中 $L(\theta )$ 是流层的长度,$\delta (x)$ 是流层在 x 位置的厚度,$\theta = {\rm{\alpha }} - {\rm{\beta }}$ ,其中 $\alpha $ 为混合器的旋转角,$\beta $ 为颗粒流动的动态相应角,k 是与最大流层厚度与流层长度的比值相关的量,相当于一个扰动因子,$f(\theta ) = {\rm{d}}L/(L{\rm{d}}\theta )$ 是由混合器形状决定的量. 质量守恒方程的扰动解为 [29]
| $ \phi (\eta ,\theta ) = {\phi _0}(\eta ,\theta ) + k{\phi _1}(\eta ,\theta ) + \cdots $ | (5) |
把方程 (5) 代入方程 (4),可以得到流层的厚度
| $ \begin{array}{*{35}{l}} \phi (\eta ,\theta )={{(1-{{\eta }^{2}})}^{1/2}}-kf(\theta )\cdot \\ {} \\ \qquad \quad \ \ \ \left[ \frac{{{\cos }^{-1}}\left| \eta \right|}{2{{(1-{{\eta }^{2}})}^{1/2}}}-\frac{\left| \eta \right|}{2} \right] \\ \end{array} $ | (6) |
对圆形混合器 $\,f(\theta ) = 0$,流层厚度为
| $ \phi (\eta ) = {(1 - {\eta ^2})^{1/2}} $ | (7) |
对于椭圆混合器来说,无量纲化流层的长度随时间的变化关系为 [23]
| $ \begin{array}{*{35}{l}} \left. \begin{array}{*{35}{l}} L=\frac{{\bar{b}}}{{{({{{\bar{b}}}^{2}}{{\cos }^{2}}\theta +{{\sin }^{2}}\theta )}^{1/2}}} \\ {} \\ f(\theta )=\frac{\sin 2\theta }{2({{{\bar{b}}}^{2}}{{\cos }^{2}}\theta +{{\sin }^{2}}\theta )}({{{\bar{b}}}^{2}}-1) \\ \end{array} \right\} \\ \end{array} $ | (8) |
对于正方形混合器 [23]
| $ \left. \begin{array}{*{35}{l}} L=\left\{ \begin{array}{*{35}{l}} \frac{1}{\cos {{\theta }_{\text{m}}}}\ \ ({{\theta }_{\text{m}}}\text{}\pi /4) \\ {} \\ \frac{1}{\sin {{\theta }_{\text{m}}}}\ \ ({{\theta }_{\text{m}}}\ge \pi /4) \\ \end{array} \right. \\ {} \\ f(\theta )=\left\{ \begin{array}{*{35}{l}} \tan \theta \ \ ({{\theta }_{\text{m}}}\text{}\pi /4) \\ {} \\ -\cot \theta \ \ ({{\theta }_{\text{m}}}\ge \pi /4) \\ \end{array} \right. \\ \end{array} \right\} $ | (9) |
上式中无量纲参数 $\overline b = b/a$ ,a 和 b 分别是椭圆的长轴与短轴. 通过以上分析,可以得到圆形、椭圆形和正方形混合器的流层厚度,见图 14. 从图 14(a) 中我们看到随着混合器的旋转,流层的厚度是不变的;而图 14(b) 和 (c) 显示随着混合器的旋转,流层的厚度发生了变化,并且该流层厚度的变化在正方形混合器中更明显.

|
图 14 不同混合器中流层厚度变化关系 Fig.14 The variation of flowing layer thickness in the different mixer |
从图 14(b) 和 (c) 中发现在混合器中流层中心位置厚度变化较为明显,下面我们将对中心流层厚度加以分析. 在 $\eta = 0$,对应最大流层厚度 $\phi$ 为
| $ \phi (0,\theta )=1-kf(\theta )\frac{\pi }{4} $ | (10) |
图 15 表示中层厚度的变化. 对于正方形混合器,当自由面的角度接近正方形的拐角 (θ = 45°) 时,中层厚度出现了明显地偏差,并且是不连续的. 对于椭圆混合器,中心厚度的变化是连续的.

|
图 15 混合器中中层厚度随角度的变化 Fig.15 The scaled mid-layer thickness variation with mixer orientation |
对于含不同组分的颗粒体系的流动,颗粒的扩散主要由两种情况引起:(1) 由颗粒体系不同组分的体积分数梯度引起的密度扩散;(2) 由压力梯度引起的压力扩散. 密度扩散导致颗粒体系混合,但如果存在颗粒尺寸或颗粒密度的差异,压力扩散使得颗粒体系分聚. 考虑由质量 m1 和 m2 的颗粒组分构成的二元系统,则普通扩散流量可写为 [30]
| $ {j^{{f_1}}} = - \frac{{{D_{12}}{m_1}{m_2}{n^2}}}{\rho }\nabla {f_1} $ | (11) |
压力扩散流量可写为 [30]
| $ {j^P} = - \frac{{{D_{1,2}}{\rho _1}{\rho _2}{n^2}}}{{{\rho ^2}T}}({m_1} - {m_2})\nabla P $ | (12) |
式中,${\rho _i} = {n_i}{m_i}$ ($i = 1,2$) 是质量密度,${n_i}$ 是两组分的数密度,$\,{f_1} = {n_1}/n$ 是质量为 ${m_1}$ 的颗粒体系的密度分数,$\rho = {\rho _1} + {\rho _2}$ 是总的质量密度,${D_{12}}$ 是两组分颗粒体系互扩散系数,P 为压强. 在流层中,若颗粒流动时间足够长,则颗粒体系的扩散与分聚使得整个颗粒体系达到平衡,并且在系统中压力梯度为
| $ \frac{{{\rm{d}}P}}{{{\rm{d}}\delta }} = - \rho g\cos \beta $ | (13) |
那么联立式 (11) ~ 式 (13) 可得 $\displaystyle{f_1} = \frac{{{{\rm{e}}^A}}}{{1 + {{\rm{e}}^A}}},$ 其中
| $ {A} = \ln \frac{{{f_0}}}{{1 - {f_0}}} - \\ \frac{{({m_1} - {m_2})g\cos \beta }}{T}(\phi - {\phi _0}) $ | (14) |
随着混合器的旋转,在流层中质量为 m1 的颗粒体系的分聚速度为 [30]
| $ {v_{y1}} = {j^P}/{n_1} = - \frac{{2\beta (1 - \overline \rho ){D_{\rm{coll}}}(1 - {f_1})}}{d} $ | (15) |
在流层中质量为 m2 的颗粒体系的分聚速度为
| $ {v_{y2}} = \frac{{2\zeta (1 - \overline \rho){D_{\rm{coll}}}{f_1}}}{d} $ | (16) |
上式中 ${D_{\rm{coll}}} = f{d^2}{\rm{d}}{u_x}/{\rm{d}}y$ 是扩散系数,$\overline \rho = \rho _2/ {\rho _1} $ ,$\zeta $ 是无量纲分聚速度. 把式 (14) 代入式 (15) 和式 (16) 中,可以分别得到 3 种混合器中质量为 m1 和 m2 的颗粒分聚速度,图 16(a) 和 (b) 分别给出圆形混合器中在边壁附近和在中心部分颗粒 1 和颗粒 2 的分聚速度,图 16(a) 颗粒流入或流出级联层时的分聚速度,图 16(b) 为颗粒在级联层中间位置时的分聚速度;图 16(c) 和 (d) 为椭圆形混合器中在边壁附近和在中心部分颗粒 1 和颗粒 2 的分聚速度,图 16(c) 颗粒流入或流出级联层时的分聚速度,图 16(d) 为颗粒在级联层中间位置时的分聚速度;图 16(e) 和 (f) 为正方形混合器中颗粒的分聚速度,图 16(e) 颗粒流入或流出级联层时的分聚速度,图 16(f) 为颗粒在级联层中间位置时的分聚速度.

|
图 16 在混合器中颗粒分聚速度的变化关系 Fig.16 The change of segregation velocity of the particles in the mixers |
通过计算在 3 种混合器中质量为 m1 和 m2 的颗粒的分聚速度,可得到每个混合器中质量为 m1和 m2 的颗粒速度差
| $ {v_{\rm d}} = {\nu _{y1}} - {\nu _{y2}} $ | (17) |
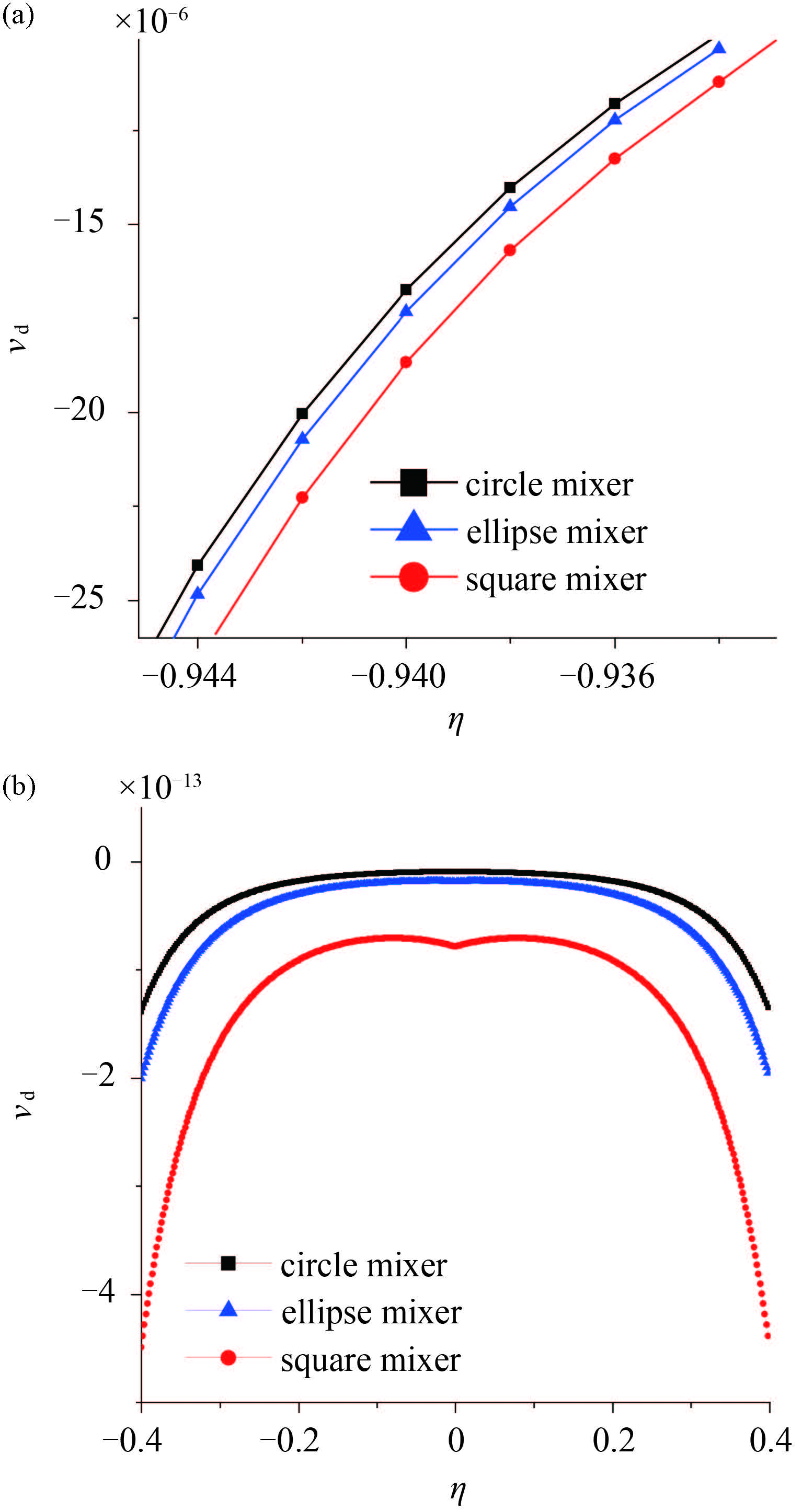
图 17(a) 为 3 种混合器中颗粒流入或流出级联层时的分聚速度差,图 17(b) 为颗粒在级联层中间位置时的分聚速度差. 从图 17(a) 和 17(b) 中可以看到在圆形混合器中颗粒速度差最大,说明颗粒分聚最明显,正方形混合器颗粒速度差最小,说明颗粒混合明显,椭圆形混合器介于二者之间.
|
图 17 在圆形、椭圆形、正方形混合器中 vd 与 η 的变化关系 Fig.17 The relationship between vd and η in the circle, ellipse, square mixer |
本文通过实验观察不同转速与填充率条件下容器形状对颗粒分聚与混合的影响和示踪颗粒的运动轨迹,发现随着转速的增加,圆形混合器中示踪颗粒的轨迹收缩,而正方形混合器中示踪颗粒的轨迹扩张,椭圆形混合器介于二者之间. 另外分析发现在圆形混合器中,随着混合器转速的增大,颗粒在径向的随机性减少;在正方形混合器中,随着混合器转速的增大,颗粒在径向的随机性增大;在模拟中,可以看到颗粒在表面的流动速度较大,尤其在填充率较低时,速度矢量是比较混乱的,说明剪切混合是比较明显的,模拟结果与实验观察相符合.
通过级联层厚度与颗粒分聚速度的理论分析,得到预实验相符的结论:在圆形混合器中颗粒分聚最明显,而正方形混合器中颗粒分聚最弱,椭圆形混合器介于二者之间.
| 1 | Shi Q, Sun G, Hou M, et al. Density-driven segregation in vertically vibrated binary granular mixtures. Phys. Rev.E, 2007, 75: 061302 |
| 2 | Shi QF, Sun G, Hou MY, et al. Segregation in vertically vibrated binary granular mixtures with same size. Chinese Physics Letters,2006, 23(11): 3080 |
| 3 | Shi Q, Yan X, Hou M, et al. Experimental study of segregation patterns in binary granular mixtures under vertical vibration. Chinese Science Bulletin, 2003, 48(7): 627-629 |
| 4 | Liu R, Li YC, Hou MY, et al. Waals-like phase separation instability of a driven granular gas in three dimensions. Phys. Rev. E, 2007,75: 079705 |
| 5 | Liu R, Li YC, Hou MY. Phase separation in a three dimensional granular gas system. Acta Physica Sinica, 2008, 67(8): 4660 |
| 6 | Liu R, Li YC, Hou MY. Oscillatory phenomena of compartmentalized bi-disperse granular gases. Phys. Rev.E, 2009, 79: 052301 |
| 7 | 孙其诚, 厚美瑛, 金峰. 颗粒物质物理与力学. 北京: 科学出版社,2011(Sun Qicheng, Hou Meiying, Jin Feng. Particulate Matter of Physics and Mechanics. Beijing: Science Press, 2011(in Chinese)) |
| 8 | 梁宣文, 李粮生, 侯兆国等. 垂直振动作用下二元混合颗粒分层的 动态循环反转. 物理学报, 2008, 57(4): 2300-2305 (Liang Xuanwen, Li Liangsheng, Hou Zhaoguo, et al. Cycle of segregation patterns in vertically vibrated binary granular mixtures. Acta Phys Sin,2008, 57(4): 2300-2305 (in Chinese)) |
| 9 | 姜泽辉, 陆坤权, 厚美瑛等. 振动颗粒混合物中的三明治式分离. 物理学报, 2003, 52(9): 2244-2248 (Jiang Zehui, Lu Kunquan, Hou Meiying, et al. Sandwich-like segregation in vertically vibrated binary granular mixtures. Acta Phys Sin, 2003, 52(9): 2244-2248 (in Chinese)) |
| 10 | 赵永志, 江茂强, 郑津洋. 巴西果效应分离过程的计算颗粒力学模 拟研究. 物理学报, 2009, 58: 1812 (Zhao Yongzhi, Jiang Maoqiang, Zheng Jinyang. Discrete element simulation of the segregation in Brazil nut problem. Acta Phys Sin, 2009, 58: 1812 (in Chinese)) |
| 11 | 史庆藩, 阎学群, 厚美瑛等. 振动混合颗粒形成的反巴西果分层及 其相图的实验观测. 科学通报, 2003, 48(4): 328-330 |
| 12 | 厚美瑛. 空间环境颗粒物质运动行为的研究. 物理, 2008, 37(10):729-732 (Hou Meiying. Granular behavior inmicrogravity. Physics,2008, 37(10): 729-732 (in Chinese)) |
| 13 | Nityanand N, Manley B, Henein H. An analysis of radial segregation for different sized spherical solids in rotary cylinders. Trans,1986, B17: 247 |
| 14 | Kwapinska M, Saage G, Tsotsas E. Mixing of particles in rotary drums a comparison of discrete element simulations with experimental results and penetration models for thermal processes. Powder Technology, 2006, 161(1): 69-78 |
| 15 | 赵永志, 张宪旗, 刘延雷等. 滚筒内非等粒径二元颗粒体系增混合机理研究. 物理学报, 2009, 58(12): 321-328 (Zhao Yongzhi, Zhang Xianqi, Liu Yanlei, et al. Augmenting the mixing of size-type binary granular systems in a rotating horizontal drum. Acta physica sinica,2009, 58(12): 321-328 (in Chinese)) |
| 16 | Pereira GG, Tran N, Cleary PW. Segregation of combined size and density varying binary granular mixtures in a slowly rotating tumbler. Granular Matter, 2014, 16: 5 |
| 17 | Ingram A, Seville JPK, Parker DJ, et al. Axial and radial dispersion in rolling mode rotating drums. Powder Technology, 2005, 158: 76-91 |
| 18 | McCarthy JJ, Khakhar DV, Ottino JM. Computational studies of granular mixing. Powder Technol, 2000, 109: 72-82 |
| 19 | Ottino JM, Khakhar DV. Mixing and segregation of granular materials. Annu. Rev. Fluid Mech, 2000, 32: 55-91 |
| 20 | Khakhar DV, McCarthy JJ, Shinbrot T, et al. Transverse flowand and mixing of granular materials in rotating cylinders. Phys. Fluids,1997, 9: 31-43 |
| 21 | Lun CKK, Savage SB, Jeffrey DJ, et al. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. J. Fluid Mech, 1984, 140: 223-256 |
| 22 | Gonzalez S, Windows-Yule CRK, Luding S, et al. Shaping Segregation: Convexity vs. Concavity. http://arxivpreprintarxiv,2014:221410.6286 |
| 23 | Ottino JM. The Kinematics of Mixing: Stretching. Chaos, and Transport Cambridge University Press. Cambridge, 1990 |
| 24 | Henein H, Brimacombe JK, Watkinson AP. Experimental studies of transverse bed motion in rotary kilns. Metall. Trans., 1983, 14B:191-205 |
| 25 | Hill KM, Jain NT, Ottino JM. Modes of granular segregation in a noncircular rotating cylinder. Phys. Rev.E, 2001, 64: 011302 |
| 26 | Meier SW, Cisar SE, Lueptow RM, et al. Capturing patterns and symmetries in chaotic granular flow. Phys. Rev.E, 2006, 74: 031310 |
| 27 | 王瑞芳, 李占勇, 窦如彪等. 水平转筒内大豆颗粒随机运动与混合 特性模拟. 农业机械学报, 2013, 44(6): 93-99(Wang Ruifang, Li Zhanyong, Dou Ruibiao, et al. Simulation on random motion and mixing characteristic for soybean in rotary drum. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(6): 93-99 (in Chinese)) |
| 28 | Prasad DVN, Khakhar DV. Granular flow in rotating cylinders with noncircular cross sections. Phys. Rev. E, 2008, 77: 041301 |
| 29 | Khakhar DV, McCarthy JJ, Gilchrist JF, et al. Chaotic mixing of granular materials in two-dimensional tumbling mixers. Chaos,1999, 9: 1 |
| 30 | Ottino JM, Khakhar DV. Mixing and segregation of granular materials. Annu. Rev. Fluid Mech., 2000, 32: 55-91 |
2. College of Physics and Electronics Engineering, Northwest Normal University, Lanzhou 730070, China;
3. College of Science Guizhou University, Guiyang 550025, China
 2016, Vol. 48
2016, Vol. 48