颗粒材料(granular materials)在冲击载荷作用下的动态力学行为是学术界关注的热点问题之一[1, 2, 3, 4, 5]. 颗粒与颗粒间的动力接触作用和颗粒破碎是颗粒材料动态力学行为的两个重要方面. 颗粒间发生点接触或微小面接触,在低应力水平下颗粒即可发生平移与旋转组合的复杂相对运动[2]. 在高应力水平下颗粒材料易发生颗粒破碎现象[3, 4],冲击是产生高应力水平的主要因素之一.
现有的颗粒材料计算模型主要有宏观唯象模型(如各种连续介质力学模型)与细观唯机理模型(如分子动力学模型、多体动力学模型、离散单元模型等)[5]. 连续介质力学模型采用均匀化方法与经验参数描述颗粒尺度细观特性对颗粒体系宏观力学行为的影响,但该方法无法反映颗粒间动力接触作用与颗粒破碎现象[6]. 颗粒离散元法已成为颗粒材料数值模拟最活跃的工具,其用颗粒间的接触作用模型描述颗粒体系的整体性质,因而存在描述颗粒间实际接触作用的接触模型问题 [7],此外,即使是最简单的Hertz法向接触模型也存在切向与法向刚度系数的标定校核过程,增大了计算结果的人为因素.
近场动力学(peridynamics,PD)是一种新兴的非局部、无网格物质点类方法[8, 9, 10],自提出以来就受到国际物理、力学界的广泛关注和高度重视,在多种固体材料和结构的静动力变形与破坏分析中得到成功应用[11, 12, 13].
近年来,近场动力学方法也逐步应用于颗粒材料领域研究. Lammi和Vogler [6]运用基于键作用的近场动力学方法在EMU软件中研究 了石英砂的3种本构模型对冲击波传播的影响;Van Vooren [14]利用近场动力学软件EMU模拟了刚性板冲击石英砂颗粒体系问题,结果 表明,冲击板附近存在严重的颗粒破碎与轻微的颗粒损伤,远离冲击板的颗粒出现破损,并由颗粒密度的改变得到压缩波阵面的传播情况. Peterson [15]运用近场动力学程序Peridigm研究了正弦波形截面板高速冲击石英砂的波传播问题,采用平面应变的简化模型研究了颗粒破碎和颗粒摩擦对波传播的影响. 上述研究均直接运用近场动力学软件,并没有给出颗粒间接触作用在近场动力学模型中的描述方法,也没有给出具体的实施技术. Ren等[16]运用基于状态的近场动力学与光滑粒子流体动力学(SPH)混合建模的方法模拟了由地下爆炸产生冲击波造成的岩土 破碎问题;Lai等[17, 18]发展了适用于干燥和饱和岩土材料的基于非常规状态的近场动力学模型,模拟了冲击载荷作用下岩土体的动力破碎和飞溅现象,并应用于边坡稳定问题. 但上述研究将土体均匀化为连续介质,没有很好的反映岩土材料的力学特性.
本文建立了考虑长程力特性和消除``边界效应''的改进的基于键作用的近场动力学模型,发展了适用于颗粒材料动力破坏分析的近场动力学方法,并应用该方法计算分析了冲击载荷作用下碳化钨陶瓷颗粒体系的动态力学行为.
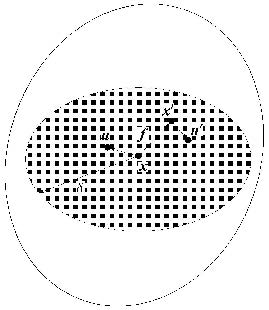
1 基于键作用的近场动力学方法 1.1 基本理论与PMB模型近场动力学基于非连续性和非局部长程作用假定建模,将空间内宏观连续体视为由大量有限体积和有限质量的物质点组成. 如图 1所示,假设空间域$R$内任一物质点$ {\pmb x}$与其近场范围$\delta $内的任意其它物质点${\pmb x}' \in R: \left\| {{\pmb x}' - {\pmb x}} \right\| \leqslant \delta $在某时刻$t$之间存在相互作用力${\pmb f}$,则根据牛顿第二运动定律,得到近场动力学基本运动方程为
|
图 1 近场范围内物质点间相互作用 Fig.1 Schematic of interaction between material points |
| $ \rho \ddot u\left( {x,t} \right) = \int_{{H_x}} {f\left( {u\left( {x',t} \right),u\left( {x,t} \right),x',x} \right)d{V_{x'}} + b\left( {x,t} \right)} $ | (1) |
式中,$\rho $为物质密度;$\ddot{\pmb u} = \dfrac{\partial ^2{\pmb u}({\pmb x},t)}{\partial t^2}$为加速度;${\pmb b}$为体力密度;${\pmb f}$为本构力函数,它包含材料所有本构信息,表示$t$时刻${\pmb x}'$点处单位体积物质点施加于${\pmb x}$点处物质 点的作用力密度;${\rm{d}}{{\rm{V}}_{x'}}$表示物质点${\pmb x}'$处的体积微元;$H = H({\pmb x},\delta ): = \left\{ { {\pmb x}' \in R : \left\{ {\left\| { {\pmb x}' - {\pmb x}} \right\| \leqslant \delta } \right\}} \right\}$为物质点${\pmb x}$的作用范围内物质点${\pmb x}'$的集合,近场范围外物质点与${\pmb x}$之间的作用力${\pmb f}$为0.
在基于键作用的近场动力学理论中,构造物质点间的本构力函数${\pmb f}$是建模的首要问题. Silling 和 Askari[19]提出 了适合各向同性材料的微观弹脆性模型(prototype microelastic brittle,PMB),其本构力函数为
| $ {\pmb f}({\pmb \xi ,\pmb\eta }) = cs\mu \dfrac{{\pmb \xi} + {\pmb\eta} }{\left| { {\pmb \xi }+{\pmb \eta } } \right|} $ | (2) |
式中,${\pmb \eta }$为相对位移${\pmb \eta } = {\pmb u}' - {\pmb u}$,${\pmb \xi }$为相对位置 ${\pmb \xi } = {\pmb x}' - {\pmb x}$;$c$为微观模量,三维问题中$c = \dfrac{12E}{\pi \delta ^4}$,平面应变问题中$c = \dfrac{12E}{\pi \delta ^3(1 + \nu)}$,平面应力问题中$c = \dfrac{6E}{\pi \delta ^3(1 -\nu)}$,一维问题中$c = \dfrac{2E}{A\delta^2}$;$E$为拉压弹性模量,$\nu $为泊松比,$s = \dfrac{\left| {{\pmb \xi } + {\pmb \eta }} \right| - \left| {\pmb \xi } \right|}{\left| {\pmb \xi } \right|}$为物质点对伸长率.
类似断裂力学思想,当$s$超过其临界伸长率$s_0 $,点对间``键''断开,且断开后不再作用,从而模拟材料和结构的开裂破坏过程. 可分别建立三维、二维和一维问题的PMB模型的临界伸长率$s_0 $与能量释放率$G_{\rm F}$的关系[19, 20]. 此外,Gerstle等[20]假设微观键临界伸长率等于单轴拉伸极限应变,通过物体宏观抗拉强度$f_{\rm t}$和弹性模量$E$定义临界伸长率
| $ s_0 = \dfrac{f_{\rm t} }{E} $ | (3) |
引入历史依赖标量函数$\mu $表征物质点对的破坏情况
| $ \mu (\xi ,t) = \left\{ \begin{array}{l} 1,\;\;\;s < {s_0},0 < t' < t\\ 0,\;\;\;\;其他 \end{array} \right. $ | (4) |
进而,Silling 和 Askari [19]定义近场动力学损伤为物质点近场范围内断键数目与键总数之比
| $ \varphi (x,t) = 1 - \frac{{\int_H \mu (x,t,\xi )d{V_{x'}}}}{{\int_H d {V_{x'}}}} $ | (5) |
式中,$0 \leqslant \varphi \leqslant 1$,$\varphi = 0$表示材料未损伤,$\varphi = 1$表示该物质点完全损伤.
1.2 改进的PMB模型的本构力函数Huang等[21, 22]和顾鑫等[13]指出PMB模型中微观模量$c$为常数,无法反映长程力随距离增大而递减的空间分布规律,影响计算精度,提出如下改进的本构力函数
| $ {\pmb f}({\pmb \xi},{\pmb\eta }) = c(0,\delta )g({\pmb \xi },\delta )s\mu \dfrac{{\pmb \xi }+{\pmb \eta }}{\left| {{\pmb \xi} +{\pmb \eta }} \right|} $ | (6) |
式中,$c(0,\delta )$为空间维数相关的材料微观模量;$g({\pmb \xi },\delta )$为反映非局部长程力特性的空间分布函数,其强化了近距离物质点间的相互作用,弱化了远距离物质点的相互作用,本文取$g( {\pmb \xi },\delta )=(1 - ({\left| \xi \right|} /\delta )^2)^2$. 当取$g({\pmb \xi },\delta ) = 1$与$c(0,\delta ) = c$时,改进的PMB模型即退化为原PMB模型.
通过PD应变能密度与连续介质力学应变能密度相等的方法,推导得到材料微观模量$c(0,\delta )$.
对于一般三维问题,以主应变表示的传统连续介质力学弹性应变能密度形式为
| $ V_{\rm el} = \dfrac{1}{2}\left[{\lambda \left( {\varepsilon _1 \mbox{ + }\varepsilon _2 + \varepsilon _3 } \right)^2 + 2G(\varepsilon _1^2 + \varepsilon _2^2 + \varepsilon _3^2 )} \right] $ | (7) |
式中,$\lambda = \dfrac{E\nu }{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)},G = \dfrac{E}{2\left( {1 + \nu } \right)}$为拉密常数.
对于三维问题,当构型在各向均匀拉伸载荷作用下发生纯体积改变时,有各向均匀应变$\varepsilon _1 = \varepsilon _2 = \varepsilon _3 = \varepsilon_0 $;当发生平面内各向均匀变形时,有$\varepsilon _1 = \varepsilon _2 = \varepsilon _0 $,且平面应力问题和平面应变问题的第三主应变分别为$\varepsilon _3 = \dfrac{\nu }{\nu - 1}\left( {\varepsilon _{11} + \varepsilon _{22} } \right)$与$\varepsilon _3 =0$. 则此时传统连续介质力学弹性应变能密度为
| $ {V_{{\rm{el}}}} = \left\{ \begin{array}{l} \frac{{3E}}{{2\left( {1 - 2\nu } \right)}}\varepsilon _0^2,\;\;\;\;\;\;三维\\ \frac{E}{{1 - \nu }}\varepsilon _0^2,\;\;\;\;\;\;\;\;\;\;\;\;\;\;平面应力\\ \frac{E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\varepsilon _0^2,\;\;平面应变 \end{array} \right. $ | (8) |
而同样变形状态对应于近场动力学中,有$s = \varepsilon _0 $,且以三维球坐标形式表示的PD弹性应变能密度为
| $ \begin{array}{l} {V_{{\rm{pd}}}} = \frac{1}{2}\int_H {wd{V_\xi }} = \\ \;\;\;\;\;\;\;\frac{1}{2}\int_0^\delta {\int_0^{2\pi } {\int_0^\pi {\left( {\frac{{c\left( {\xi ,\delta } \right)\varepsilon _0^2\xi }}{2}} \right)} } } {\xi ^2}\sin \varphi d\xi d\theta d\varphi \end{array} $ | (9) |
以平面极坐标形式表示的PD弹性应变能密度为
| $ {V_{{\rm{pd}}}} = \frac{1}{2}\int_H {wd{V_\xi }} = \;\frac{1}{2}\int_0^\delta {\int_0^{2\pi } {\left( {\frac{{c\left( {\xi ,\delta } \right)\varepsilon _0^2\xi }}{2}} \right)\xi d\theta d\xi } } t $ | (10) |
式中,$w({\pmb \eta },{\pmb \xi })$为描述近场范围内两物质点间相互作用强弱的标量函数,其与本构力函数的关系为${\pmb f}({\pmb \eta },{\pmb \xi }) = \dfrac{\partial w({\pmb \eta },{\pmb \xi })}{\partial {\pmb \eta }}$.
对平面问题,取厚度$t = 1$,采用改进PMB模型的本构力函数,求得式(9)与式(10)的具体形式,进而令$V_{\rm el} = V_{\rm pd} $,推导得到
| $ c(0,\delta ) = \left\{ \begin{array}{l} \frac{{36E}}{{\pi {\delta ^4}(1 - 2\nu )}},\;\;\;\;\;三维\\ \frac{{105E}}{{4\pi {\delta ^3}\left( {1 - \nu } \right)}},\;\;\;\;\;平面应力\\ \frac{{105E}}{{4\pi {\delta ^3}\left( {1 + \nu } \right)(1 - 2\nu )}},\;\;\;平面应变 \end{array} \right. $ | (11) |
上述考虑长程力特性的改进PMB模型中,根据应变能密度等效的方法求得微观模量$c(0,\delta )$,在物体内部和边界处均取相同的常数,弱化了边界处的$c(0,\delta )$值,导致计算结果的不准确,即存在所谓的``边界效应''问题. 本文借鉴文献[23]的思想,对边界处$c(0,\delta )$的计算方法进行改进.
在计算边界区域的应变能密度时,仅考虑边界区域近场范围内物质点的贡献,则当发生空间或平面内各向均匀变形 $\varepsilon _0 $ 时,PD应变能密度为
| $ \begin{array}{l} {V_{{\rm{pd}}}}(x) = \frac{1}{2}\int_{{H_\delta }} {w\left( {\eta ,\xi } \right)} = \frac{1}{2}\sum\limits_{j \in {H_i}} {\omega \left( {\eta ,\xi } \right)} {V_j} = \\ \;\;\;\;\frac{1}{4}\sum\limits_{j \in {H_i}} {c\left( {\eta ,\xi } \right)} ){\left[ {1 - {{(\frac{{\left| {{\xi _{ij}}} \right|}}{\delta })}^2}} \right]^2}\varepsilon _0^2\left| {{\xi _{ij}}} \right|{V_j} \end{array} $ | (12) |
式中,$H_i $为$H_\delta $的离散形式,为边界处物质点${\pmb x}_i $近场范围内的物质点${\pmb x}'$的集合.
令$V_{\rm el} = V_{\rm pd} $,即令式(8)与式(12)相等,可推得
| $ {c_i} = \left\{ \begin{array}{l} \frac{{6E}}{{(1 - 2\upsilon )\sum\limits_{_{j \in {H_i}}} {{{\left[ {1 - {{(\frac{{\left| {{\xi _{ij}}} \right|}}{\delta })}^2}} \right]}^2}} \left| {{\xi _{ij}}} \right|{V_j}}},\;\;\;\;\;\;三维\\ ]\frac{{4E}}{{(1 - \upsilon )\sum\limits_{j \in {H_i}} {{{\left[ {1 - {{(\frac{{\left| {{\xi _{ij}}} \right|}}{\delta })}^2}} \right]}^2}\left| {{\xi _{ij}}} \right|} {V_j}}},\;\;\;\;\;\;平面应力\\ \frac{{4E}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)\sum\limits_{j \in {H_i}} {{{\left[ {1 - {{(\frac{{\left| {{\xi _{ij}}} \right|}}{\delta })}^2}} \right]}^2}\left| {{\xi _{ij}}} \right|{V_j}} }},\;\;\;\;\;平面应变 \end{array} \right. $ | (13) |
在改进(或原)PMB解析模型中,${\pmb f}_{ij} = {\pmb f}_{ji} $必然成立,但在采用离散求和方式计算时,$H_i $与$H_j $不一定相同,为保证动量守恒,取
| $ c_{ij} = \dfrac{c_i + c_j }{2} $ | (14) |
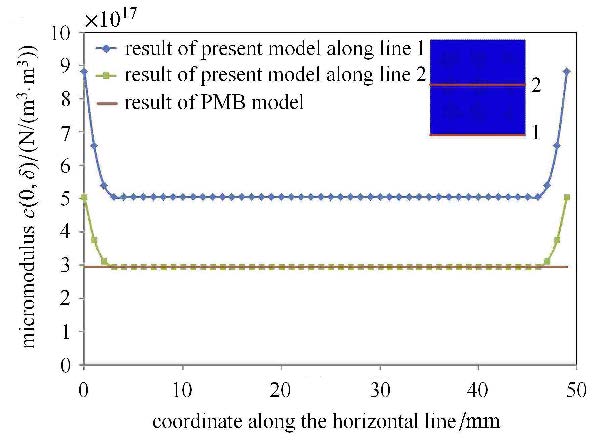
图 2给出了弹性模量$E = 1$ GPa,泊松比$\nu = 1/ 3$,50 mm$\times $ 50 mm 的方形薄板在均匀离散情况下,不同PMB模型计算得到的$c(0,\delta )$值分布情况. 可以看出,本文得到的边界处$c(0,\delta )$值得到强化、不再与内部$c(0,\delta )$值相同,有效解决了``边界效应''问题.
|
图 2 微观模量$c(0,\delta )$值的分布 Fig.2 Distribution of the $c(0,\delta )$ value |
真实物理世界的4种基本作用都具有一定空间尺度,近场动力学认为任何物体间的相互作用都具有非局部特征. Tian和Du[24]指出PD非局部模型是对实际物理过程更合适和更准确的数学表达,而不是局部模型的近似. 近场动力学方法中,单颗粒可视为由许多物质点组成,单颗粒内部物质点间与分属不同颗粒的物质点间均存在非局部长程作用力.
在宏观尺度上,颗粒材料可分为黏性颗粒材料和无黏性颗粒材料,两种材料的PD建模方法不同.
2.1 黏性颗粒材料黏性颗粒材料(如黏土)颗粒间易于形成黏结界面,且多为密相颗粒材料,PD方法分析时可视其为连续体,采用双相材料界面问题在PD中的处理方法. 当物质点分属不同颗粒且物质点间``键''穿越黏结界面时,形成``界面键'',界面键的材料参数可取为颗粒材料参数一定比例的弱化或强化,进而采用PD方法进行计算分析.
2.2 无黏性颗粒材料对砂土、谷物和玻璃珠等无黏性颗粒材料,近场动力学采用短程排斥力描述分属不同颗粒的无损物质点间、单个脱离的物质点间以及单个脱离的物质点与原连续体物质点间的相互作用. 本文类比弹簧挤压模型定义弹性排斥力模型
| $ {\pmb F}_r ({\pmb y}',{\pmb y}) = \min \left\{ {0,c_{ r} \dfrac{\left( {\left\| {{\pmb y}'- {\pmb y}} \right\|} \right)- d}{d}} \right\} \dfrac{{\pmb y }'-{\pmb y }} {\left\| {{\pmb y}'- {\pmb y} } \right\|} $ | (15) |
式中,${\pmb y}',{\pmb y}$为现时构型中物质点的位置矢量;$c_{ r} $为排斥力常数,仅与颗粒材料类型及颗粒特征尺寸有关,可通过与试验对比方法率定;$d$是物质点$ {\pmb x}'$和${\pmb x}$之间的短程排斥力作用的临界距离,采用均匀离散形式时,晶格长度为$\left| {\Delta {\pmb x}} \right|$,可取$d = \left| {\Delta {\pmb x}} \right|$.
为描述颗粒的离散特性,将近场范围局部化,即当分属不同颗粒的物质点间距离小于一个物质点晶格长度时,物质点间发生排斥作用,即
| $ \left| {{\pmb F}_r ({\pmb y}',{\pmb y})} \right| > 0 \ \ {\rm only if } \ \ \left| {{\pmb y}' - {\pmb y}} \right| < d = \left| {\Delta {\pmb x} } \right| $ | (16) |
在颗粒尺度上,该式表明两颗粒发生接触后产生相互作用.
2.3 排斥力常数$c_r $的率定方法采用PD方法分析无黏性颗粒材料时,排斥力模型常数$c_r $的率定至关重要. 本文采用冲击波速响应比对方法,通过以下3个步骤,确定具有特征尺度的给定颗粒材料的排斥力常数$c_r $.
(1)对具有某特征尺度的给定颗粒材料,在选定适合PD计算的物质点尺寸和稳定时间步长后,通过下式计算$c_r $的可能量级范围
| $ {\pmb F}_r ({\pmb y}',{\pmb y}) < 2\rho \dfrac{\left| {\Delta {\pmb x}} \right|}{\Delta t^2} $ | (17) |
该式表示一个时步$\Delta t$时间内仅受排斥力作用时,物质点不产生快速``溃散''现象. 针对弹性排斥力模型,式(15)具体为$c_r > 2\rho \dfrac{\left| {\Delta {\pmb x}} \right|^2}{\Delta t^2\left( {V_{\rm impact} \Delta t -\left| {\Delta {\pmb x} } \right|} \right)}$.
(2)分析模拟中颗粒的运动与破碎形态,缩小$c_r $范围. 合适的排斥力常数范围,应使得颗粒体系存在合理破碎,即使得颗粒体系不发生快速``溃散''现象,不发生破碎后的单一物质点与颗粒的嵌入或渗透,此时排斥力过大或过小.
(3)比较数值计算的冲击波速与物理试验测定的冲击波速数据,准确率定排斥力常数$c_r $.
其中,冲击波速的计算可记录多个时刻和冲击波阵面的物质点位置,线性回归的拟合曲线的斜率为冲击波速. 而波阵面的物质点认定为:在$t\sim t + \Delta t_0 $时间段内,运动速度达到或超过冲击驱动速度一半,且在$t - \Delta t_0 \sim t$时间段内不发生运动的物质点.
3 数值计算方法 3.1 离散格式结点${\pmb x}_i $处的近场动力学运动方程可离散为
| $ \rho \ddot u_i^n = \sum\limits_p f (u_p^n - u_i^n,x_p^n - x_i^n){V_p} + b(x_i^n) $ | (18) |
式中,$n$为时间步号;$\rho _i $表示物质点$i$的质量密度;${\pmb b}$为体力密度矢量;$V_p $为$p$处物质点体积,由空间离散方式决定;$ \ddot {\pmb u}_i^n $为第$n$时步的加速度,通过差分格式迭代求解; ${L_u}(x,t) = {\rm{ }}\sum\limits_p f (u_p^n - u_i^n,x_p^n - x_i^n){V_p} $,它表示第$n$时步时物质点${\pmb x}_i $受其近场范围内所有其他物质点的合作用力,由数值积分方法确定.
如采用中心正交的均匀空间离散,则三维物质点体积为$V_p = \left| {\Delta {\pmb x}} \right|^3$,二维物质点体积为$V_p = \left| {\Delta {\pmb x}} \right|^2$,$\left| {\Delta {\pmb x}} \right|$为物质点(或晶格)长度;时间步进格式采用Verlet-$\!$-Velocity [25]差分格式,则物质点速度和位移
| $ \dot{\pmb u}_i^{n + 1} = \dot{\pmb u}_i^n + \dfrac{\Delta t}{2\rho }({\pmb L}_u + {\pmb b})^n + \dfrac{\Delta t}{2\rho }({\pmb L}_u + {\pmb b})^{n + 1} $ | (19) |
| $ {\pmb u}_i^{n + 1} = {\pmb u}_i^n + \dot{\pmb u}_i^n \Delta t + \dfrac{(\Delta t)^2}{2\rho }({\pmb L}_u + {\pmb b})^n $ | (20) |
近场动力学方法的显式动力实现,需要给定初始坐标${\pmb u}({\pmb x },0)$及初始速度$ \dot{\pmb u }({\pmb x} ,0)$;每一计算时步需记录物质点的加速度、速度、位置等量,通过不断更新位置坐标、计算得到物质点所受的合力,物质点遵循牛顿运动定律,从而实现不断迭代计算.
4 算例与分析Vogler等[26]和Borg等[27, 28]试验测定了刚性板冲击封闭容器中碳化钨陶瓷颗粒的冲击波速响应,碳化钨颗粒具有脆性大、易开裂破碎的特点,为说明PD方法在颗粒材料领域的适用性与可行性,对该试验进行了数值模拟.
4.1 模型建立采用PD平面应变弹性模型,选取 1 mm$\times $2 mm的模拟区域(如图 3);陶瓷颗粒的体积分数约为$55\% $ (空隙率$45\% $),堆积密度约为$\rho _0 = 8.558$ g/cm$^3$,材料参数见表 1.

|
图 3 刚性板冲击陶瓷颗粒试验的二维模型 Fig.3 Two-dimensional simulation model for the impact experiment |
PD方法将单颗粒视为大量物质点组成,方便对任意形状颗粒进行数值分析. 采用数值样本生成技术,可建立具有任意颗粒形状、粒径和空间分布规律的数值样本. 为节省篇幅,本文仅采用单一样本进行多组数值试验. 该模拟区域内共含有1 368个颗粒,采用单一粒径的圆形颗粒,并将其离散为37个方形物质点(选取离散尺寸时,考虑计算量与颗粒特征尺寸两方面的平衡),物质点尺寸为32 / 7 μm,共离散为50 616个物质点. 采用固定2层4 384个物质点的方法模拟固壁边界条件,容器与颗粒间的接触作用通过物质点间的排斥力实施,固壁边界条件会对颗粒材料波速产生轻微影响[26, 27]. 刚性驱动板采用给定速度边界条件实现. 计算时间步长取为$\Delta t = 4e - 10s$,共计算4 μs.
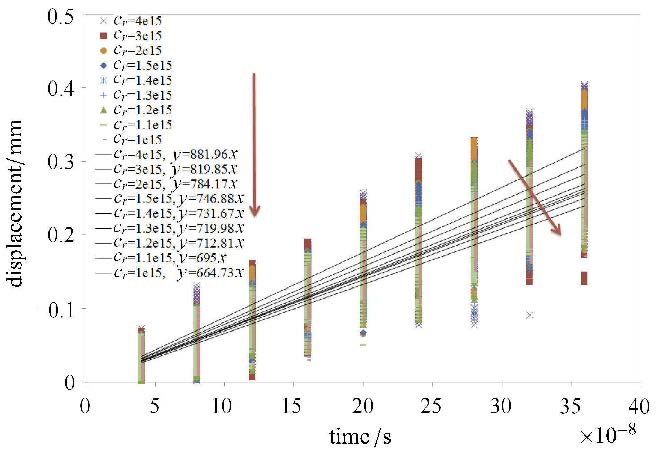
4.2 排斥力常数$c_r $的率定实验采用的碳化钨颗粒可视为一种无黏性颗粒材料,当冲击速度为245 m/s时,利用2.3节所述方法,采用弹性排斥力模型确定排斥力常数. 先采用式(17)确定$c_r > - 8.9\times 10^{17}$,其次分析颗粒体系运动与破碎形态,缩小$c_r $的范围为$\left( { - 5\times 10^{15},- 1\times 10^{14}} \right)$,最后选取多组不同的$c_r $值,采用PD方法计算波速值,并与试验结果比较,则确定该颗粒体系的排斥力常数为$c_r = - 1.1\times 10^{15}$(如图 4).
|
图 4 刚性板以245 m/s速度冲击颗粒体系时,选取不同排斥力试常数计算得到的波速 Fig.4 Wave speed of granular system calculated with distinct repulsive force coefficients under velocity 245 m/s |
利用4.2确定的排斥力常数,模拟颗粒体系在多个冲击速度下的波速响应,并计算冲击动力学中的Hugoniot应力[27],如下式
| $ \sigma _{\rm H} = \rho _0 U_{\rm S} u_{\rm p } $ | (21) |
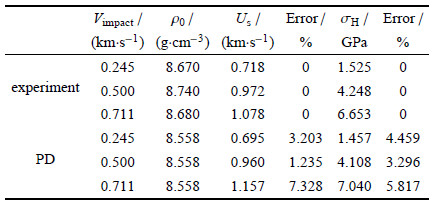
将本文的计算结果与试验结果共同列入表 2.
| 表 2 试验与PD计算结果 Table 2 Results of experiments and PD simulations |
从表 2给出的结果可以看出,PD计算得到的波速与试验测得的波速具有良好的一致性,且颗粒体系的波速是压力相关的,即加载速度越快、压力越大,波速越大. 也表明本文发展的分析方法在预测冲击载荷作用下颗粒材料的冲击波速响应时是可行的.
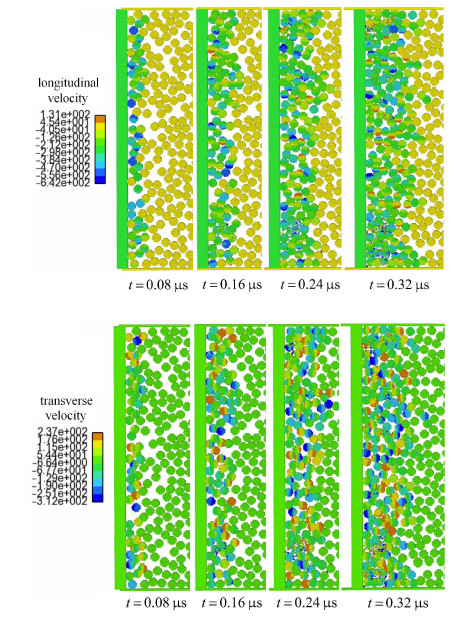
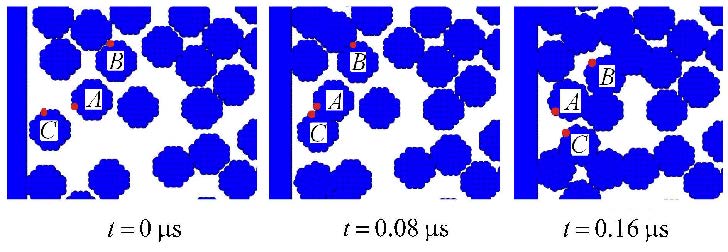
图 5给出了冲击速度245 m/s时,几个不同时刻颗粒体系部分区域纵向和横向速度场分布情况,图 6给出了3个颗粒在不 同时刻的空间形态示意图. 速度图像清晰地显示了颗粒同时发生平移和旋转运动,且冲击前缘颗粒体系被压密,波阵面沿纵向不断向前传播.
|
图 5 不同时刻颗粒体系纵向与横向速度分布(m/s) Fig.5 Longitudinal and transverse velocity fields of granular system at distinct time |
|
图 6 颗粒旋转示意图(以$A, B, C$三个颗粒为例) Fig.6 Schematic of particle rotation (take $A, B, C$ for example) |
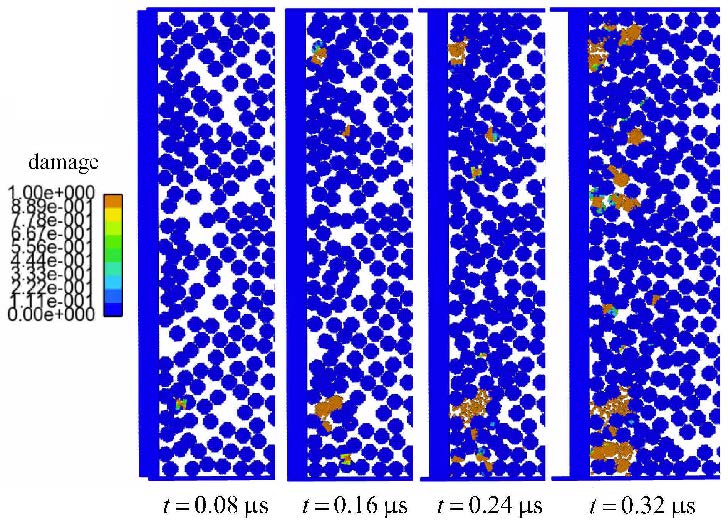
图 7给出了几个不同时刻颗粒体系局部区域的损伤破碎情况. 从图中结果可以看出,冲击板附近同时存在严重的颗粒破 碎与轻微的颗粒损伤,远离冲击板的颗粒出现破损,且颗粒破碎主要是由颗粒间挤压作用、碰撞作用以及相对滑动剪切 作用等3种方式造成的. 上述结果表明,PD方法能够自然描述颗粒的旋转与平移运动、颗粒的变形与破碎现象.
|
图 7 不同时刻颗粒体系的损伤破坏情况 Fig.7 Damage distribution of granular system at distinct time |
(1)在基于键作用的近场动力学理论框架下,本文提出了反映非局部长程力特征和消除``边界效应''的改进PMB模型,发展了适用于颗粒材料动力破坏分析的近场动力学方法,给出了描述颗粒接触作用的物质点层次的排斥力模型,提出了排斥力模型中排斥力常数的确定方法. 并应用该方法计算了冲击载荷作用下碳化钨陶瓷颗粒体系的动态力学行为. 研究结果表明,本文提出的改进PMB模型与发展的颗粒材料PD分析方法可以有效求解和分析颗粒材料的动态力学行为.
(2)本文提出的描述颗粒接触作用的排斥力模型只有一个排斥力常数,并可通过数值试验与已有试验数据的对比确定,降低了人为因素对计算结果的影响. 刚性板冲击碳化钨陶瓷颗粒的计算结果表明,不同冲击速度下,PD计算得到的颗粒体系的波速响应与试验结果高度一致;通过颗粒物质点尺度的相互作用描述单颗粒尺度的接触作用,较好地反映颗粒的摩擦、挤压作用效应;自然展现颗粒发生平移与旋转复杂组合的运动、颗粒变形与破碎现象.
(3)本文基于PD理论和方法初步分析了冲击载荷作用下颗粒材料的冲击波速、颗粒体系的运动、变形与破碎规律. 今后将进一步完善适用颗粒材料的近场动力学模型和计算方法,如完善黏性颗粒材料的分析方法,并考虑颗粒间的黏滞特性建模;可以预见,PD方法在颗粒材料计算力学领域中的研究范围将延伸至颗粒自然堆积过程、剪切带的形成与发展,快速流以及颗粒体系的爆炸冲击等问题.
| 1 | 孙其诚, 王光谦. 颗粒流动力学及其离散模型评述. 力学进展,2008, 38(1): 87-100 (Sun Qicheng, Wang Guangqian. Review on granular flow dynamics and its discrete element method. Advances in Mechanics, 2008, 38(1): 87-100 (in Chinese)) |
| 2 | 孙其诚, 厚美瑛, 金峰等. 颗粒物质物理与力学. 北京:科学出版 社, 2011 (Sun Qicheng, Hou Meiying, Jin Feng, et al. Physics and Mechanics of Granular Materials. Beijing: Science Press, 2011 (in Chinese)) |
| 3 | 王乃东, 姚仰平. 粒状材料颗粒破碎的力学特性描述. 工业建 筑, 2008, 38(8): 17-20 (Wang Naidong, Yao Yangping. Mechanical description for granular material exhibiting particle crushing. Industrial Construction, 2008, 38(8): 17-20 (in Chinese)) |
| 4 | 祁原, 黄俊杰, 陈明祥. 可破碎颗粒体在动力载荷下的耗能特性. 力学学报, 2015, 47(2): 252-259 (Qi Yuan, Huang Junjie, Chen Mingxiang. Energy dissipation characteristics of crushable granules under dynamic excitations. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 252-259 (in Chinese )) |
| 5 | 楚锡华. 颗粒材料的离散颗粒模型与离散—— 连续耦合模型及 数值方法. [博士论文]. 大连:大连理工大学, 2007 (Chu Xihua. The discrete particle and coupled discrete-continuum models and numerical methods for granular materials. [PhD Thesis]. Dalian: Dalian University of Technology, 2007 (in Chinese)) |
| 6 | Lammi CJ, Vogler TJ. Mesoscale simulations of granular materials with Peridynamics. In: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter, 2011 |
| 7 | 徐佩华, 黄润秋, 邓辉. 颗粒离散元法的颗粒碎裂研究进展. 工 程地质学报, 2012, 20(3): 410-418 (Xu Peihua, Huang Runqiu, Deng Hui. Advances in fractures of particles with distinct element method. Journal of Engineering Geology, 2012, 20(3): 410-418 (in Chinese)) |
| 8 | Silling SA. Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids,2000, 48(1): 175-209 |
| 9 | Silling SA, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling. Journal of Elasticity, 2007, 88(2): 151-184 |
| 10 | 黄丹, 章青, 乔丕忠等. 近场动力学方法及其应用. 力学进展,2010, 40(4): 448-459 (Huang Dan, Zhang Qing, Qiao Pizhong, et al. A review on peridynamics method and its application. Advance in Mechanics, 2010, 40(4): 448-459 (in Chinese)) |
| 11 | Kilic B. Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials. [PhD Thesis]. The University of Arizona, 2008 |
| 12 | 胡祎乐, 余音, 汪海. 基于近场动力学理论的层压板损伤分析方 法. 力学学报, 2013, 45(4): 624-628 (Hu Yile, Yu Yin, Wang Hai. Damage analysis method for laminates based on peridynamic theory. Chinses Journal of Theoretical and Applied Mechanics, 2013,45(4): 624-628 (in Chinese)) |
| 13 | 顾鑫, 章青, 黄丹. 基于近场动力学方法的混凝土板侵彻问题研 究. 振动与冲击, 2015(录用待刊) (Gu Xin, Zhang Qing, Huang Dan. A study on penetration problem of concrete slabs with peridynamics. Journal of Vibration and Shock, 2015 (in press) (in Chinese)) |
| 14 | Van Vooren AJ. A multi-scale approach to a greater understanding of the behavior of heterogeneous materials under dynamic loading. [Master Thesis]. Marquette University, 2013 |
| 15 | Peterson AM. Intragranular fracture and frictional e ects on wave propagation through granular media. [Master Thesis]. The University of Texas at San Antonio, 2014 |
| 16 | Ren B, Fan H, Bergel GL, et al. A peridynamics-SPH coupling approach to simulate soil fragmentation induced by shock waves. Computational Mechanics, 2014, 1: 1-16 |
| 17 | Lai X, Liu LS, Liu QW, et al. Slope stability analysis by peridynamic theory. Applied Mechanics and Materials, 2015, 744: 584-588 |
| 18 | Lai X, Ren B, Fan H, et al. Peridynamics simulations of geomaterial fragmentation by impulse loads. International Journal for Numerical and Analytical Methods in Geomechanics, 2015 |
| 19 | Silling SA, Askari E. A meshfree method based on the peridynamic model of solid mechanics. Computers & Structures, 2005, 83(17):1526-1535 |
| 20 | Gerstle WH, Sau N, Sakhavand N. On peridynamic computational simulation of concrete structures. ACI Special Publication, 2009,265 |
| 21 | Huang D, Lu G, Qiao P. An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis. International Journal of Mechanical Sciences, 2015, 94: 111-122 |
| 22 | Huang D, Lu G, Wang C, et al. An extended peridynamic approach for deformation and fracture analysis. Engineering Fracture Mechanics,2015 (in press) |
| 23 | Ganzenmüller GC, Hiermaier S, May M. Improvements to the prototype micro-brittle linear elasticity model of peridynamics. arXiv preprint arXiv: 1312. 5543, 2013 |
| 24 | Tian X, Du Q. Asymptotically compatible schemes and applications to robust discretization of nonlocal models. SIAM Journal on Numerical Analysis, 2014, 52(4): 1641-1665 |
| 25 | Parks ML, Seleson P, Plimpton SJ, et al. Peridynamics with lammps: A user guide v0.3 beta. Sandia Report SAND2011-8523, Sandia National Laboratories, Albuquerque, NM, 2011 |
| 26 | Vogler TJ, Lee MY, Grady DE. Static and dynamic compaction of ceramic powders. International Journal of Solids and Structures,2007, 44(2): 636-658 |
| 27 | Borg JP, Vogler TJ. Mesoscale calculations of the dynamic behavior of a granular ceramic. International Journal of Solids and Structures,2008, 45(6): 1676-1696 |
| 28 | Borg JP, Vogler TJ. Aspects of simulating the dynamic compaction of a granular ceramic. Modelling and Simulation in Materials Science and Engineering, 2009, 17(4): 045003 |
 2016, Vol. 48
2016, Vol. 48