2. 中国科学院水利部成都山地灾害与环境研究所, 成都 610041
颗粒介质的力学行为与密度和加载方式等密切相关,有时类似固体,有时类似流体,人们形象地称之为固态颗粒介 质(granular solids) 和流态颗粒介质(granular fluids). 不同的力学状态之间遵循的力学准则各不相同,且在时间和空间上普遍存在复杂的相互转换过程[1, 2]. 例如,土体边坡失稳、山体滑坡和泥石流的发生,就是颗粒介质由固态转化为流态的复杂流变现象. 发展颗粒介质本构理论,建立起适用于各种不同运动状态的颗粒模型,实现对其力学状态在时间和空间上的统一描述,是颗粒介 质理论研究的前沿科学问题[3, 4, 5],其核心难点是颗粒介质弹性弛豫与失稳的机理、不可恢复应变的细观过程和量化,以 及粘滞应力的确定[6, 7, 8].
热力学以能量传递和转换为主线,是认识物质形式的主要范式, 可以为我们提供统一描述颗粒介质不同流态力学行为的理论框架. 当前,国际主流的颗粒介质热力学理论有岩土内变量热力学[9, 10]和granular solid hydrodynamics理论[11, 12, 13, 14],以及近期发展起来的双颗粒温度理论(two-granular-temperature theory, TGT理论)[15]. TGT理论中,颗粒介质的应力由瞬态弹性应力和动应力组成,且弹性应力可以发生弛豫;应变增量则为弹性应变增量和不可恢复应变 (irreversible strain) 增量之和. 固态颗粒介质的应力主要是弹性应力,在流态颗粒介质中弹性应力和动应力共同起作用,但是应变增量主要是不可恢复应变增量. 确定瞬态弹性应力、动应力和不可恢复应变(irreversible strain)增量是TGT理论的关键. TGT理论提供了描述颗粒不同力学状态及其相互转化的理论框架,但该理论发展时间相对较短,需要开展很多实验和算例来确定参数和验证理论[15].
在颗粒堆积体坍塌过程中,体系依次经历了从静态堆积、失稳流动再到堆积的力学阶段,是典型的颗粒介质固态-液态 相互转换的过程[16, 17],因而通过使用TGT理论对坍塌问题进行分析,可以检验TGT理论的合理性和缺陷. 在本文中,针对前期提出的颗粒介质瞬态弹性能模型,确定了弹性失稳条件(elasticity instability condition),建立了不可恢复应变流动法则,与弹塑性力学中的屈服准则和塑性流动法则进行了对比;发展了针对TGT理论的 物质点方法(material point method,MPM)程序,模拟了180 mm高、100 mm宽、200 mm厚的陶颗粒堆积体坍塌过程,并与物理实验和离散元模拟结果进行对比.
1 弹性稳定性条件结合颗粒介质Jamming 点附近的弹性与密度、颗粒温度和所受荷载相关的特性[18, 19, 20],GSH理论的弹性能模型[11] 和超塑性模型的余能函数[15],文献[8]提出了新的瞬态弹性能模型
| $$ w_{\rm e} = AI_1^{2.5} + CI_1^{0.5} I_2 $$ | (1) |
其中,$A$和$C$是弹性系数,$C = 5q_\phi ^2 A$,其中$q_\phi $由两个弹性系数$A$和$C$确定(见式(3)),与颗粒介质的摩擦系数有关(见式(6)). $I_1 = - \varepsilon _{kk}^{\rm e} $ 和 $I_2 = {\varepsilon _{ij}^{{\rm e},0} \varepsilon _{ij}^{{\rm e},0} }/ 2$ 分别是弹性应变张量$\varepsilon _{ij}^{\rm e} $的第一不变量和偏应变的第二不变量,$\varepsilon _{ij}^{{\rm e},0} \ (= \varepsilon _{ij}^{\rm e}+{I_1 }/ 3)$是零迹张量. 由于颗粒介质只能受压,因此$I_1 \geqslant 0$. 结合声速测试技术,通过微振幅振动激励颗粒力链,由声速可以确定式(1)中的参数.
依据TGT理论,颗粒介质的热力学稳定性之一是弹性稳定,而弹性稳定条件在数学上表述为弹性能关于应变的Hessian矩阵正定. 令$u_{\rm s}= \sqrt {2I_2 } $,有
| $$ \dfrac{\partial ^2w_{\rm e} }{\partial I_1^2 } > 0 ,\ \ \dfrac{\partial ^2w_{\rm e} }{\partial u_{\rm s}^2 } > 0 ,\ \ \dfrac{\partial ^2w_{\rm e} }{\partial I_1^2 }\dfrac{\partial ^2w_{\rm e} }{\partial u_{\rm s}^2 } > \left( {\dfrac{\partial ^2w_{\rm e} }{\partial I_1 \partial u_{\rm s} }} \right)^2 $$ | (2) |
得到颗粒介质的弹性稳定性条件
| $$ \dfrac{I_2}{I^2_1} < \dfrac{5A}C =\dfrac 1{q^2_{\phi}} $$ | (3) |
该式是热力学稳定性对颗粒介质弹性的要求,如果不满足该条件,则弹性失稳,体系发生流变,不需额外引入屈服准则.
从式(1)得到弹性应力$\sigma _{ij}^{\rm e} = {\partial w_{\rm e} }/ {\partial \varepsilon _{ij}^{\rm e} }$,
| $$ \sigma _{ij}^{\rm e} = \Bigg (2.5AI_1^{0.5} + 0.5CI_1^{0.5} \dfrac{I_2 }{I_1^2 }\Bigg) \left( { - \delta _{ij} } \right)I_1 + CI_1^{0.5} \varepsilon _{ij}^{{\rm e},0} $$ | (4) |
由式(3),当$I_1 \to 0$时,$\sigma _{ij}^{\rm e} \to 0$. 弹性等效剪切应力和球应力分别为
| $$ \tau ^{\rm e} = C\sqrt {I_1 } \sqrt {I_2 } ,\quad \sigma _{\rm m}^{\rm e} = - \Bigg( 2.5A\sqrt {I_1 } + 0.5C\sqrt {I_1 } \dfrac{I_2 }{I_1^2 } \Bigg )I_1 $$ | (5) |
得到
| $$ \dfrac{\tau ^{\rm e}}{\sigma _{\rm m}^{\rm e} } = \dfrac{2q_\phi ^2 {\sqrt {I_2 } } / {I_1 }}{1 + q_\phi ^2 {I_2 } /{I_1^2 }} \leqslant q_\phi $$ | (6) |
仅当${\sqrt {I_2 } } / {I_1 } = 1 / {q_\phi }$时,${\tau ^{\rm e}} /{\sigma _{\rm m}^{\rm e} } = q_\phi $,弹性失稳面与Drucker-$\!$-Prager屈服面类似[21, 22]. 如果取Drucker-$\!$-Prager屈服条件恰恰就是${\tau ^{\rm e}} / {\sigma_{\rm m}^{\rm e} } = q_\phi $,当式(3)不成立时,体系发生弹性失稳,此时由于式(6)中${\tau ^{\rm e}} /{\sigma _{\rm m}^{\rm e}}< q_\phi $恒成立,体系依然处于Drucker-$\!$-Prager模型中的弹性区,并未发生屈服,如图 1所示.
|
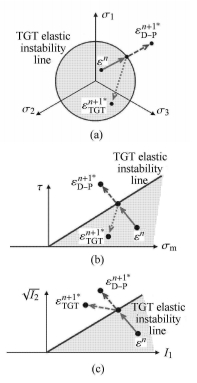
图 1 弹性失稳和 Drucker-Prager 屈服的对比 Fig.1 Comparison between TGT elastic instability and Drucker-Prager failure |
原则上说``屈服''条件是动力学意义上的力学条件,而式(3) 则是弹静力学范畴. 在图 1中,$\varepsilon ^n$为$n$时刻处在弹 性稳定区某一状态,当失稳发生时,$\varepsilon _{\rm D-P}^{n + 1\ast } $和$\varepsilon _{\rm TGT}^{n + 1\ast } $分别为$\varepsilon^n$根据Drucker-$\!$-Prager线弹性屈服和TGT非线性弹性失稳,越过弹性失稳线在($n +1$)时刻的失稳状态. 图 1中可见,在$\pi $平面(a)、$\tau - \sigma _{\rm m} $坐标面(b)中$\varepsilon _{\rm TGT}^{n + 1\ast } $仍然处于应力比${\tau ^{n + 1\ast }}/ {\sigma _{\rm m} ^{n + 1\ast }} < q_\phi $的状态,因而在应力空间中无法用应力比${\tau ^{n + 1\ast }}/ {\sigma _{\rm m}^{n + 1\ast }}$识别TGT模型的弹性失稳,只有$\sqrt {I_2 } - I_1 $平面(c)中通过应变比$\sqrt {I_2 } ^{n + 1\ast } / I_1 ^{n + 1\ast }$才能有效识别其失稳发生.
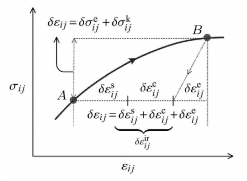
2 不可恢复应变如图 2所示,TGT 理论中颗粒介质应变增量分解为
| $$ \delta \varepsilon _{ij} = \delta \varepsilon _{ij}^{\rm s} + \delta \varepsilon _{ij}^{\rm c} + \delta \varepsilon _{ij}^{\rm e} $$ | (7) |
|
图 2 颗粒介质应变增量及应力的分解 Fig.2 Incremental strains and stresses |
其中,$\varepsilon _{ij}^{\rm s}$是流变应变,主要源自颗粒位置重排. $\varepsilon _{ij}^{\rm c} $是蠕变应变,是弹性应力$\sigma _{ij}^{\rm e} $作用下内部结构调整引起的应变,初步确定为$\partial _t \varepsilon _{ij}^{\rm c} = c_{ijkl} \sigma _{kl}^{\rm e}$,$c_{ijkl} $是弛豫系数,单位为Pa$^{-1}$$\cdot$s$^{-1}$. $\delta \varepsilon _{ij}^{\rm ir} = \delta \left( {\varepsilon _{ij}^{\rm s} + \varepsilon _{ij}^{\rm c} } \right)$是不可恢复应变增量,产生动应力 $\sigma _{ij}^{\rm k} = \eta _{ijkl} \partial _t \varepsilon _{kl}^{\rm ir} $. 更多讨论见文献[7].
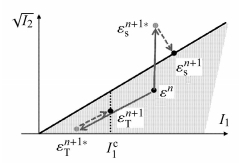
当颗粒体系弹性失稳时,不可恢复应变增量$\delta \varepsilon _{ij}^{\rm ir} $的确定是难点. 参考Drucker-$\!$-Prager模型的塑性流动法则,使用正交的不可恢复应变流动法则(即不可恢复应变增量最小)确定$\delta \varepsilon _{ij}^{\rm ir} $. 具体方法为:在$I_1 > 0$且$ \sqrt {I_2 } > I_1 / q_\phi $的受剪破坏区,当应变状态由弹性区$\varepsilon^n$经试算演化到非弹性区$\varepsilon _{\rm s}^{n + 1\ast } $,则使应变以垂直$I_1 = q_\phi \sqrt {I_2 } $失稳面的方式回到$\varepsilon _{\rm s}^{n + 1} $作为其弹性应变状态,如图 3所示. 另外,考虑到颗粒介质不承受拉力,当$I_1 \leqslant 0$即定义其处于受拉失稳状态. 在颗粒体系顶部和运动前缘,其重力很小,产生的弹性应变也非常小,式(5) 中分母会出现小值,将带来计算误差,因此对于受拉破坏,我们对$I_1 $设计阈值$I_1^{\rm c}$,当试算应变状态$\varepsilon _{\rm T}^{n + 1\ast } $满足$I_1 < I_1^{\rm c} $时即认为其受拉失稳,按应变原方向反向返回到$\varepsilon _{\rm T}^{n + 1} $处(对应$I_1^{n + 1} = I_1^{\rm c} )$作为此时该点的弹性状态. 在MPM程序中,$I_1^{\rm c} $根据计算所使用物质点和网格的大小确定,取单层网格顶层物质点在重力作用下的$I_1 $值的1/10. 在本文中取$I_1^{\rm c} = 1.0\times 10^{ - 7}$.
|
图 3 不可恢复应变流动法则. $\varepsilon _{\rm T}^{n + 1\ast } $和$\varepsilon _{s}^{n + 1\ast } $分别对应试算时发生受拉和受剪破坏时的应变状态,而$\varepsilon _{\rm T}^{n + 1}$和$\varepsilon _{\rm s}^{n + 1} $则对应使用流动法则对$\varepsilon_{\rm T}^{n + 1\ast } $和$\varepsilon _{\rm s}^{n + 1\ast } $修正后的受拉和剪切应变状态 Fig.3 Flow rule for the irreversible strain. $\varepsilon _{\rm T}^{n + 1\ast } $ and $\varepsilon _{\rm s}^{n + 1\ast } $are the attempted strain states that are in the failure area caused by tension and shear, respectively. $\varepsilon _{\rm T}^{n + 1} $ and $\varepsilon _{\rm s}^{n + 1} $ are the final strain states modified from $\varepsilon _{\rm T}^{n + 1\ast } $ and $\varepsilon _{\rm s}^{n + 1\ast } $ according to the flow rule |
为了更好地解决颗粒介质固态-流态转变时间的激波产生和大变形,基于TGT理论的弹性能模型和不可恢复应变正交流动法则,对清华大学张雄教授的开源MPM3D程序进行改进[23]. 控制方程组为
| $$ \left.\!\!\begin{array}{l} {\rm{d}}_t \rho + \rho \partial _i v_i = 0 \\ {\rm{d}}_t \left( {\rho v_i } \right) + \rho v_i \partial _j v_j - \partial _j \sigma _{ji} - \rho b_i = 0 \\ \partial _t \varepsilon _{ij}^{\rm e} = \partial _t \varepsilon _{ij} - \partial _t \varepsilon _{ij}^{\rm ir} \\ \sigma _{ij} = \sigma _{ij}^{\rm e} + \sigma _{ij}^{\rm k} \\ {\rm{d}}_t \left( {\rho T^{\rm g}} \right) = R^{\rm g} \\ R^{\rm g} = \sigma _{ij}^{\rm k} v_{ij} - \varLambda \end{array}\!\!\right\} $$ | (8) |
其中,$\sigma _{ij} $为物质点应力,弹性应力$\sigma _{ij}^{\rm e} $由式(4)确定,动应力$\sigma _{ij}^{\rm k} = \eta \partial _t \varepsilon _{ij}^{\rm ir} $,黏滞系数$\eta $是颗粒温度$T^{\rm g}$的函数,表征颗粒介质内部的耗散作用. $R^{\rm g}$是颗粒体系脉动能量源项,$\varLambda $是脉动能量的耗散率,源自颗粒间的非弹性碰撞和表面摩擦等;颗粒动理学可理论推导稀疏颗粒流中,$\varLambda = \dfrac{24}{\sqrt \pi }(1 - e)G\rho d_{\rm p}^{ - 1} T_{\rm g}^{3 / 2} $,$e$是颗粒恢复系数,$G$反映颗粒浓度的影响,$d_{\rm p}$是颗粒粒径;对于密集体系,Jenkins修正得到$\varLambda = \dfrac{24}{\sqrt \pi }(1 - e)G\rho L^{-1}T_{\rm g}^{3/2}$,$L$是力链长度[24]. 在本文计算中,取$e =0.8$,$L =10 d_{\rm p}$. 变形率张量$\partial _t \varepsilon _{ij} = {\left( {\partial _i v_j +\partial _j v_i } \right)}/2$. $v_{i}$为物质点速度,$b_{i}$为物质点所受体力. 物质点采用如下方程离散
| $$ \rho (x_i ) = \sum_{p = 1}^{n_{\rm p} } {m_{\rm p} \delta (x_i - x_{i{\rm p}} )} $$ | (9) |
式中$n_{\rm p}$为物质点总数,$m_{\rm p}$为单个物质点所代表区域的质量,$x_{i\rm p}$为物质点坐标. 物质点信息和背景网格的节点信息转化通过形函数$N_{I}$完成,以物质点位置$x_{i\rm p}$和结点位置$x_{iI}$的转化为例,$x_{i\rm p}=N_{I}x_{iI}$. 本文采用了八结点正六面体背景网格单元,其形函数为
| $$ N_I = \dfrac{1}{8}\left( {1 + \xi \xi _I } \right)\left( {1 + \eta \eta _I } \right)\left( {1 + \varsigma \varsigma _I } \right) $$ | (10) |
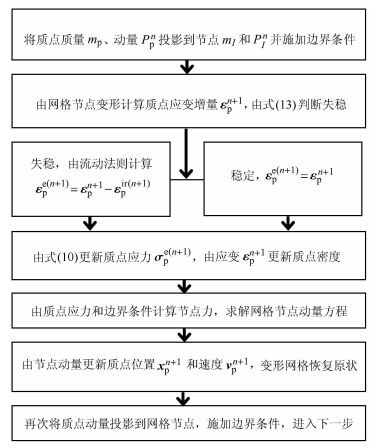
式中的$\xi_{I}$,$\eta_{I}$和 $\zeta_{I}$为结点$I$在单元对应结点处的自然坐标. 通过形函数实现物质点 信息和背景网格结点信息的转换,求解方程. 具体的计算步骤如图 4.
|
图 4 计算流程 Fig.4 Computational procedure |
颗粒介质堆积体坍塌过程是典型的由弹性稳定到失稳流动、由静态到动态的过程. 本文开展了实验测量、DEM和MPM数值模拟.
实验在小型长方体透明有机玻璃箱进行,尺寸为400 mm$\times $200 mm$\times $200 mm (如图 5). 上端开口,底部铺设薄层磨砂纸增加粗糙程度. 距离左侧100 mm处放置玻璃挡板,直立角和扶手保证挡板竖直. 为了便于观察,部分白色陶粒用蓝色钢笔水染为蓝色,将白色和蓝色两种陶粒相间铺设在玻璃挡板左侧,层高20 mm,共9层,在自重下形成密集堆积,其高度$H_{i} =180$ mm,高宽比$a=H_{i}/L_{i} =1.8$. 实验时将玻璃挡板沿$x$方向快速后撤,堆积体逐渐坍塌流动,整个过程用高速摄像机记录.

|
图 5 实验设置示意图 (长度单位:mm) Fig.5 Sketch of the experiment setup (length unit: mm) |
采用游标卡尺测量陶粒粒径,发现粒径$D$在$4.9$ mm$\sim $5.9 mm之间正态分布,颗粒数目约26 000颗. 平均密度值$\rho =2 200$ kg/m$^{3}$,杨氏模量$E =5.5$ GPa. 测量散粒体摩擦角或休止角的方法一般有注入法、排出法和倾斜法等,差别 在3$^\circ$$\sim $5$^\circ$以内. 本文采用注入法,在重力作用下陶粒堆积形成锥角,10次测量角度的结果分布在 18$^\circ$$\sim $22$^\circ$之间,取平均值为21$^\circ$,相应的,摩擦系数 $\mu =0.38$.
在MPM计算时,需确定初始条件和边界条件:使用TGT弹性能(式(1))需要确定两个材料参数,$C$和$q_\phi $. 由于陶瓷颗粒 与玻璃珠的材料性质相近,在本文中采用文献[8]的结果. 由玻璃珠组成的颗粒体系声速测量结果非常完备,通过类似压强与声 速的关系,确定了$C = 1.79$ GPa,$q_\phi \approx 0.452$. $q_\phi $的值也可通过摩擦角 $\varphi $计算得到,其计算公式为[25]
| $$ q_\phi ^2 = \dfrac{ - 3(4\tan ^2\varphi - 3) - 9\sqrt {1 - 4\tan ^2\varphi } }{2(4\tan ^2\varphi + 3)} $$ | (11) |
$\varphi =21^\circ$时对应$q_\phi \approx 0.452$. 考虑到实验结果在$y$方向无变化,进行$x-z$平面二维模拟,使用1 440个物质点和40$\times $40正立方体网格计算,网格边长为10 mm. 在$x=0$处和$x=40$ mm处设置无穿透边界,约束$x$方向动量;在底面$z=0$处设置无滑移边界,约束$x$方向和$z$方向动量.
离散元方法(discrete element method,DEM)是一种成熟的研究颗粒介质力学行为的数值计算方法,近年来转向开源以实现大规模计算和用户的自由拓展(如ESyS-Particle 和Yade等). DEM模拟可作为物理实验和基于TGT理论的MPM计算结果的辅助验证. 使用Yade进行模拟,它是基于Linux系统的DEM开源软件,具有良好的可扩展性,被国际上很多课题组使用[26]. 颗粒间接触力的计算是DEM的核心,采用Hertz-$\!$-Mindlin非线性接触模型[27]. 法向力和切向力的力-位移关系为
| $$ \left.\!\!\begin{array}{l} F_{\rm n} = - k_{\rm n} \delta _{\rm n}^{3 / 2} - \eta _{\rm n} \delta _{\rm n}^{1 / 4} \dot {\delta }_{\rm n} \\ F_{\rm s} = \min \left( { - k_{\rm s} \delta _{\rm n}^{1 / 2} \delta _{\rm s} - \eta _{\rm s} \delta _{\rm n}^{1 / 4} \dot {\delta }_{\rm s},\mu F_{\rm n} } \right) \end{array}\!\!\right\} $$ | (12) |
其中,$k_{\rm n}$和$k_{\rm s} $分别为法向和切向刚度,$\delta _{\rm n} $和$\delta _{\rm s} $为相应变形量,$\dot {\delta }_{\rm n} $和$\dot {\delta }_{\rm s} $为相应的变形率. 颗粒转动方程为
| $$ I_i \dfrac{{\rm{d}}\omega _i }{{\rm{d}} t} = \sum_{j = 1}^n {( {\pmb T}_{\rm s} + {\pmb T}_{\rm r} } ) $$ | (13) |
其中,切向力矩${\pmb T}_{\rm s} = {\pmb R}_{\rm i} \times {\pmb F}_{\rm s} $,滚动摩擦力矩 ${\pmb T}_{\rm r} = - \mu _{\rm r} F_{\rm n} R_{\rm i}\hat{\pmb \omega}$,$I_{\rm i} $为转动惯量,$ \hat{\pmb\omega }$为接触点的单位角速度矢量. DEM计算参数采用与测量得到的陶粒大小和材料参数完全一致,且体系大小相同.
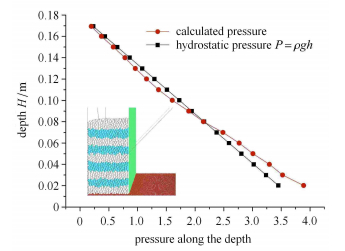
5 结果分析及讨论DEM模拟时,颗粒总数为25 167,在底面铺设一层固定微小颗粒模拟实验中在底面铺的粗糙砂纸,如图 5的插图所示. 颗粒介质坍塌 的快慢和最终堆积形态取决于最初的密度和堆积压力. 如图 6所示,DEM计算得到的压强随着$H$的增加而增大压,并与$\rho gH$的量值做了对比,其中$H$从顶部表面算起的深度,$\rho $为颗粒的体密度. 初始堆积体底部压强较大,挡板撤离时,底部颗粒首先运动,见图 7(a)所示的实验中拍摄的形态照片.
|
图 6 陶颗粒的初始堆积形态和压强分布 Fig.6 The pressure distribution along the height in the initial packing. The inset is the pattern |
图 7(b)和图 7(c)分别为DEM和MPM模拟的坍塌过程速率分布. 由于图 7(a)实验中使用高速相机以每秒25帧的速度拍摄,可以看到颗粒体右上侧部分颗粒由于运动速度较大,发生影像虚化,其影像长度正比于速度大小. 对比图 7(a) $\sim$图 7(c)可以看出,前0.24 s堆积体由准静态变形到动态破坏过程中,数值模拟的形态很好地再现了实验结果,且DEM和MPM的速率分布吻合良好. 在0.04 s,堆积体基本沿对角线(0,0.18)到(0.1,0)斜面发生弹性失稳而启动不可恢复流,速度由该失稳面向自由面$x =0.1$ m处逐渐增大,随后失稳面向原点处演化,失稳面以上部分速度逐渐增大,堆积体崩溃滑出(如0.08 s$\sim $ 0.16 s). 随着颗粒滑出,颗粒体趋于平缓,压强差降低,失稳面以下部分堆积体颗粒受力状态趋于平衡,加速缓慢,而失稳面以上部分则继续以较高速度滑动(0.20 s$\sim $0.24 s). 堆积体进一步坍塌使得压强进一步降低,速度在摩擦作用下开始下降,最终趋于静止(0.40 s,0.52 s).

|
图 7 陶颗粒堆积体坍塌过程中的形态演化实验照片 (a) 和 DEM 和 MPM 模拟得到的沙堆坍塌过程速率场 (b),(c) 和MPM 模拟的失稳区域 (d) 的演化 Fig.7 Photos of the collapsing sand pile (a), simulated speed (b),(c) and instable area (d) distribution during collapse of the sand pile |
图 7实验和DEM结果的对比显示,DEM模拟 再现了坍塌过程中的形态演化;而通过DEM和MPM速率对比,基于TGT弹性模型、弹性失稳准则和正交流动法则的弹塑性模型也 能够很好地再现坍塌演化. 利用该模型计算出的失稳区域分布图 7(d)则进一步清晰地展示了颗粒介质固-流态转换过程. 失稳区根据式(3)确定. 由于$q_\phi \approx 0.452$,当颗粒体系局域${I_2 } /{I_1^2 } < 0.489$ 时该局域相对稳定,而当${I_2 } /{I_1^2 } \to 0.489$ 时认为其趋近不稳定,更易于发生失稳破坏. 图 7(d)显示,在崩塌发生起始阶段,随着颗粒介质右侧约束消失,颗粒体大部分区域达到或接近失稳态,开始由固态转变为流动态, 而仅有坐标轴原点附近的区域因${I_2 } /{I_1^2 } < 0.4 $仍处于绝对的弹性稳定区域,维持颗粒固体行为(0.04 s). 流动前期,稳定区的范围相对变化较小(0.08 s$\sim $0.20 s),后期随着流动速度减弱,颗粒开始沉积,,颗粒物质之间开始发生较大幅度的自我调整,大部分区域开始恢复到弹性稳定 态,颗粒由液态行为向固态转变,而仅有自由表面少量颗粒仍处在失稳状态(0.52 s). 可以看到,基于本文使用的模型,通过弹性稳定与否的判断,能够较好地描述颗粒介质的固-流态转换过程. 颗粒介质由固态向液态的转化意味着弹性能的失稳和弹性应力的消失,相对地,通过颗粒之间的调整使得弹性能重新稳定,弹性应力逐 渐恢复的过程,对应着颗粒介质由液态转变为固态的过程. 注意到该本构模型实际只使用到弹性参数$C$和$q_{\phi}$,其物理概念清晰,采用声速测量技术即可确定. 因此,基于TGT理论为颗粒介质力学行为的描述提供了新思路. 通过颗粒介质坍塌的实验测量与 DEM和MPM数值模拟对比,表明TGT理论确定的弹性失稳条件和相应的不可恢复应变流动法则可以较好地刻画颗粒介质由 弹性稳定到失稳流动、由静态到动态的全过程研究. 其特点是弹性失稳条件是从弹性能模型Hessian 矩阵正定得到的,不必额外引入屈服准则[8, 25].
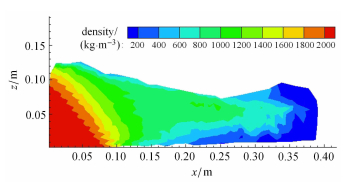
我们也发现了问题:图 7(c)中0.40 s时刻以后,MPM模拟的堆积体前端明显高于DEM模拟(图 7(b))和实验结果(图 7(a)). 图 8显示的MPM计 算最终堆积形态密度分布可以看到在前端的颗粒密度远低于初始原始密度2 200 kg/m$^{3}$,局部甚至低于200 kg/m$^{3}$, 相应颗粒在流动过程中发生了剧烈的塑性膨胀而导致密度陡降. 一方面,从图 7实验结果看到,堆积体末端只有2$\sim $3颗粒粒径厚,此处的颗粒介质行为可能并不满足代表体积元要求的最小尺寸[28],继续使用连续介质模型对该阶段的描述并不恰 当,需要对本构关系做改进;另一方面,根据本文中使用的不可恢复应变流动准则,不可恢复应变导致体应变的改变,在流动后期, 前端颗粒流速极大,更容易产生较大的不可恢复变形,导致体积过分膨胀,影响整体堆积形态,需要对MPM方法做改进.
|
图 8 MPM 模拟得到的最终堆积时的密度分布 Fig.8 Final density profile for MPM simulation result |
可以看出,基于颗粒介质TGT热力学理论中的弹性能模型,及由此导出的弹性应力方程,本文发展了相应的不可恢复应变流动准 则,构建了描述颗粒介质力学行为的本构模型. 该模型能够通过分析弹性能稳定性,得到其失稳条件,且只需确定弹性参数$C$和摩擦角相关的参数$q_{\phi }$即完成对颗粒材料弹性应力和弹性应变的描述. 基于此模型,本文通过对颗粒堆积体坍塌的实验和数值模拟,研究了颗粒介质固-流态转化的问题. 为了克服坍塌过程中出现的大变形带来的数值问题,本文使用了MPM构建该模型的数值模型,并于相应的DEM模拟进行了对比. 数值结果显示,在坍塌前期,颗粒堆积体由静态稳定到逐步失稳破坏发生流动,MPM结果和DEM模拟结果都能很好的再现实验现象, 基于本文模型得到的弹性失稳区演化能够清晰反映颗粒介质的 固-流态转化过程,颗粒介质的固-流态、 流-固态转化分别对应着弹性能的失稳和弹性应力的消失、弹性能重现稳定和弹性应力恢复的过程. 在坍塌后期流动静止段,MPM模拟结果中前端颗粒介质因速率较快导致较大的体积膨胀,使得最终堆积形态和DEM模拟及实验结果有所差异. 这个问题会在后续研究中加以解决.
| 1 | Forterre Y, Pouliquen O. Flows of dense granular media. Annual Review of Fluid Mechanics, 2008, 40(1): 1-24 |
| 2 | Jop P. Rheological properties of dense granular flows. Comptes Rendus Physique, 2015, 16(1): 62-72 |
| 3 | Midi GDR. On dense granular flows. The European Physical Journal E, 2004, 14(4): 341-365 |
| 4 | Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows. Nature, 2006, 441(7094): 727-730 |
| 5 | Delannay R, Louge M, Richard P, et al. Towards a theoretical picture of dense granular flows down inclines. Nature Materials, 2007,6: 99-108 |
| 6 | Kamrin K. Nonlinear elasto-plastic model for dense granular flow. International Journal of Plasticity, 2010, 26(2): 167-188 |
| 7 | Zheng H, Peng Z, Fu L, et al. Expression for the granular elastic energy. Physical Review E, 2012, 85: 051304 |
| 8 | Sun Q, Jin F, Wang G, et al. On granular elasticity. Scientific Reports,2015, 5: 9652 |
| 9 | Collins IF, Houlsby GT. Application of thermomechanical principles to the modelling of geotechnical materials. Proceeding of Royal Society A, 1997, 453: 1975-2001 |
| 10 | Houlsby GT, Puzrin AM. Principles of Hyperplasticity: An Approach to Plasticity Theory Based on Thermodynamic Principles. Springer Science & Business Media, 2007 |
| 11 | Jiang Y, Liu M. Granular elasticity without the Coulomb condition. Physical Review Letters, 2003, 91(14): 144301 |
| 12 | Jiang Y, Liu M. From elasticity to hypoplasticity: dynamics of granular solids. Physical Review Letters, 2007, 99(10): 105501 |
| 13 | Jiang Y, Liu M. Granular solid hydrodynamics. Granular Matter,2009, 11(3): 139-156 |
| 14 | Jiang Y, Liu M. Applying GSH to a wide range of experiments in granular media. The European Physical Journal E, 2015, 38(3): 1-27 |
| 15 | 孙其诚. 颗粒介质的结构与热力学. 物理学报, 2015, 64 (7):076101 (Sun Qicheng. Grnaualr structure and non-equlinrium thermodyanmcis. Acta Physica Sinica, 2015, 64 (7): 076101 (in Chinese)) |
| 16 | Kerswell RR, Lacaze L. Axisymmetric granular collapse: A transient 3D flow test of viscoplasticity. Physical Review Letters, 2009,102(10): 108305 |
| 17 | Lagree P, Staron L, Popinet S. The granular column collapse as a continuum: validity of a two-dimensional Navier-Stokes model with a (I)-rheology. Journal of Fluid Mechanics, 2011, 686: 378-408 |
| 18 | Liu AJ, Nagel SR. Nonlinear dynamics: Jamming is not just cool any more. Nature, 1998, 396(6706): 21-22 |
| 19 | Trappe V, Prasad V, Cipelletti L, et al. Jamming phase diagram for attractive particles. Nature, 2001, 411(6839): 772-775 |
| 20 | Bi D, Zhang J, Chakraborty B, et al. Jamming by shear. Nature,2011, 480(7377): 355-358 |
| 21 | Drucker DC. A more fundamental approach to plastic stress-strain relations. ASME-AMER Soc Mechanical Eng 345 E 47TH ST, New York, NY 10017, 1951 |
| 22 | Drucker DC, Prager W. Soil mechanics and plastic analysis or limit design. Quarterly of Applied Mathematics, 1952, 10: 157-165 |
| 23 | 张雄, 廉艳平, 刘岩等. 物物质点法. 清华大学出版社, 2013 (Zhang Xiong, Lian Yanping, Liu Yan, et al. Material Point Method. Tsinghua University Press, 2013 (in Chinese)) |
| 24 | Jenkins J. Dense shearing flows of inelastic disks. Physics of Fluids,2006, 18(10): 103307 |
| 25 | 孙其诚, 厚美瑛, 金峰. 颗粒介质物理与力学. 北京: 科学出版社,2011 (Sun Qicheng, Hou Meiying, Jin Feng. Physics and Mechanics of Granular Materials. Beijing: Science Press, 2011 (in Chinese)) |
| 26 | Kozicki J, Donze FV. YADE-OPEN DEM: an open-source software using a discrete element method to simulate granular material. Engineering Computations, 2009, (26): 786-805 |
| 27 | Antypov D, Elliott JA. On an analytical solution for the damped Hertzian spring. Europhysics Letters, 2011, 94(5): 50004 |
| 28 | Rycroft CH, Kamrin K, Bazant MZ. Assessing continuum postulates in simulations of granular flow. Journal of the Mechanics and Physics of Solids, 2009, 57(5): 828-839 |
2. Institute of Mountain Hazards and Environment IMHE, Chinese Academy of Sciences, Chengdu 610041, China
 2016, Vol. 48
2016, Vol. 48