2. 西安电子科技大学机电工程学院, 西安 710071
离散颗粒介质受力达到屈服条件后形成颗粒流,该过程在自然界以及工农业生产领域广泛存在, 如滑坡、雪崩、沙丘演化、制药、化工、颗粒介质受冲击后的流变过程以及冲击坑的坍塌等. 然而,颗粒之间的摩擦和非弹性碰撞具有高度的非线性和复杂的耗散机制,并且颗粒尺度、宏观尺度及流体尺度 同时存在[1, 2],使其不能通过统一的理论框架描述[3, 4, 5, 6]. 因此,基于其运动状态通常将颗粒流分为3类[7]:颗粒之间的相互作用以摩擦接触为主,基于土力学理论描述 的变形缓慢的密集准静态颗粒 流[8];颗粒之间主要进行相互碰撞,通过动理论描述的颗粒稀疏的快速气态流[9]; 以及处于这两种运动状态之间的颗粒之间既有碰撞,又有摩擦的密集颗粒 流[2, 10, 11].
在这3种颗粒流动状态之中,密集准静态颗粒流和快速颗粒流的研究相对成熟,而类似于流体的密集颗粒流本构关系在近十几年 才逐渐成为关注的热点. 其中,最主要的一个本构关系是基于局部流变假设,通过对实验结果的无量纲分析得到[11, 12]$\mu = \mu (I)$,该本构关系预测的斜面剪切颗粒流动速度廓线与Bagnold[13]的开创性工作相一致,这里$\mu $是剪切应力$\tau $与法向压力$P$的比值,$I = \dot {\gamma }\sqrt {d^2\rho _{\rm s} / P} $,颗粒粒径为$d$,密度为$\rho _{\rm s} $,剪切应变速率为$\dot {\gamma }$时的惯性数,表示颗粒介质的宏观变形时间$1 / \dot {\gamma }$与颗粒微观运动时间$d / \sqrt {P / \rho _{\rm s} } $的比值. 同时,该模型的三维拓展,可对三维颗粒流的流动特性进行预测[14]. 然而颗粒介质自身的非局部效应使得上述模型对下面两种情形下的颗粒流预测失效:(1)在斜面流动中,较薄(约为几倍粒径厚度)颗 粒介质发生临界流动需要斜面具有更高的倾斜角度[15],而局部模型中颗粒的临界流动与厚度无关,与实际不符. (2)局部模型表明当$\mu $小于静摩擦系数$\mu _{\rm s}$时颗粒静止,现有研究却表明当$\mu < \mu _{\rm s} $时仍然存在缓慢流动,其剪切速率廓线随高度的减小呈指数递减 [11, 16, 17, 18],且在准静态区域内,颗粒流剪切速率与应力无关.
为了克服上述局部模型的局限性,逐渐发展了非局部模型,包括由Ginzberg-$\!$-Landau序参数控制的部分流动理论[19]、塑 形Cosserat模型[20]、动理论描述缓慢颗粒流拓展模型[21, 22]、随机流动模型[23]、局部流变模型的拓 展[24, 25]、基于颗粒流度概念的非局部流变模型[18, 26, 27]及其代表自激发过程的颗粒流变积分方程[28]. 这些模型虽然采用不同的物理假设,但本质上都体现了颗粒尺度上的应力扩散特性. 区别在于代表扩散变量的物理意义、数学形式、所满足的微分方程和积分方程以及影响流动的力学特性各不相同[26]. 由此可见,目前不仅没有统一的模型能够预测所有构型下颗粒介质的流动特性,而且单一斜面颗粒流的流动特性都很难准确度量. 因此,定量预测和描述密集颗粒流的本构关系仍然是一个极大的挑战[26]. 同时,上述所有模型中都将体积分数作为一个奴隶变量,而体积分数的微小变化会影响颗粒介质的临界流动.
因此,本文通过详细考虑应力波动引起的颗粒流变过程中波动幅值概率密度分布的具体形式,并在迭代求解中 考虑剪切速率与体积分数的耦合作用,提出了一种修正的非局部流变模型. 应用该模型对简单斜面剪切流的流动特征进行预测,从定量上给出了与实验结果和数值模拟吻合的颗粒流动的 临界厚度、平均流动速度及剪切速率廓线.
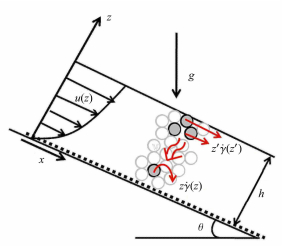
1 修正的非局部流变模型Pouliquen等[28]基于应力波动提出的非局部流变模型的思想为(如图 1所示):在$z'$处两层颗粒之间的剪切运动, 导致$z$面上的剪应力波动$\delta {z}' \to z$,这将有助于$z$层颗粒跳到相邻的空间.
|
图 1 斜面颗粒流中非局部自激发流变模型示意图 Fig.1 Sketch of the non-local self-activated process for flows down inclined planes |
因此,$z$层颗粒的运动由$z'$处的应力波动激发产生. 这样,考虑所有来自$z'$层的应力波动就可得知$z$层的运动情形
| $ \dot {\gamma }(z) = \dfrac{1}{d}\int {\dfrac{\left| {\dot {\gamma }({z}')} \right|}{1 + \dot {\gamma }(z)d / I_0 \sqrt {P(z) / \rho _{\rm p} } }} \cdot \\ \qquad \Bigg \{ \exp \Big [- \dfrac{(\mu _{\rm s} P - \tau )[1 + \beta (z - {z}')^2 / d^2]}{P(z')} \Big] \,-\\ \qquad \exp \Big [ - \dfrac{(\mu _{\rm s} P + \tau )[1 + \beta (z - {z}')^2 / d^2]}{P(z')} \Big] \Bigg \} {\rm{d}} z' $ | (1) |
该积分方程是与颗粒介质所受的法向压力$P(z)$、剪切应力$\tau (z)$以及剪切速率$\dot {\gamma }(z)$有关的非局部流变模型,若给定构型的应力分布,就可预测速度廓线. 模型中引入了3个参数:摩擦系数$\mu_{\rm s} $,特征惯性数$I_0 $,应力波动的空间程度$\beta $.
对于准静态颗粒流,即剪切速率$\lim \dot {\gamma }(z) \to 0$. 方向相同的情形下,$\dot {\gamma }(z)$变为与${z}'$处剪切速率相关的一个线性关系,此关系仅适用于准静态变形[29]. 方程简为$\dot {\gamma }(z) = d^{ - 1}\int {\dot {\gamma }(z')f(\theta ,z,z') {\rm{d}} z'} $,这里
$$ f(\theta ,z,z') = \exp \Bigg\{ - \dfrac{(\mu _2 P - \tau )[1 + \beta (z - {z}')^2 / d^2]}{P({z}')} \Bigg\}\, - \\ \qquad \exp \Bigg \{ - \dfrac{(\mu _2 P + \tau )[1 + \beta (z - {z}')^2 / d^2]}{P({z}')} \Bigg\} $$
因此,$\dot {\gamma }(z)$被认为是$\dot {\gamma }(z')$的线性组合. 离散$\dot {\gamma }(z)$,方程变为$[\dot {\gamma }(z_i )] = [M_{ij}][\dot {\gamma }({z}'_j )]$,其中,$[M_{ij}] = [f(\theta ,z_i ,{z}'_j )]$为系数矩阵. 求解颗粒流动的临界条件就转变为求线性方程组的特征值问题.
考虑沿$x$方向速度为$u(z)$的单向平稳斜面剪切颗粒流. 法向压力$P(z)$以及沿斜面方向的剪切应力$\tau (z)$分别为
$$ P(z) = \rho _{\rm s} \phi g\cos \theta (h - z) \\ \tau (z) = \rho _{\rm s} \phi g\sin \theta (h - z) $$
将应力分布带入$f(\theta ,z,z')$化简后得到
$$ f = \exp \Bigg\{ - \dfrac{(h - z)\{\mu _2 - [1 + \beta (z - {z}')^2 / d^2]\tan \theta \}}{ h - {z}' } \Bigg \} \,-\\ \qquad \exp \Bigg\{ - \dfrac{(h - z)\{\mu _2 + [1 + \beta (z - {z}')^2 / d^2]\tan \theta \}}{ h - {z}' } \Bigg\} $$
进而得到系数矩阵$[M_{ij}]$的具体表达式. 给定颗粒层的厚度$h$,通过求解方程$\det (M) = 0$即可给出能使颗粒流动的 临界角度$\theta _{\rm stop} $. 根据$\theta _{\rm stop} ^{ - 1} = h_{\rm stop} (\theta )$[15, 30]可以得到临界厚度与倾斜角度的关系,这里$h_{\rm stop} (\theta )$为倾斜角度为$\theta $时颗粒流动的临界厚度. 由此可见,在这个特征值问题中,临界角度是一个与颗粒密度、重力和体积分数无关的量. 该模型能很好地反映颗粒流的平均速度$\tilde {u} = \dfrac 1 h\int_0^h u(z){\rm{d}} z$与颗粒层厚度$h$的关系,并能定性预测临界厚度$h_{\rm stop} $与斜面倾斜角度$\theta $的关系以及颗粒流的速度廓线. 但是,由于模型中采用的假设存在缺陷以及将体积分数作为一个奴隶变量,使得斜面剪切流的预测结果与现有的实验模拟 结果定量相差较大. 因此,我们对该非局部流变模型进行修正.
1.1 应力波动幅值的修正非局部流变模型[28]假设:${z}'$处的应力波动幅度$\delta \sigma _0 ({z}')$服从指数分布形式,即在区间${\rm{d}}(\delta \sigma _0 )$内应力$\delta \sigma_0 $的概率分布为
| $$ p{\rm{d}}(\delta \sigma _0 ) = \dfrac{1}{P({z}')}\exp \Big ( - \dfrac{\delta \sigma _0 }{P({z}')} \Big) {\rm{d}} (\delta \sigma _0 ) $$ | (2) |
这里,应力波动幅值$\delta \sigma _0 ({z}')$是具有平均值的随机变量,它与局部颗粒介质的应力量级相当.
目前,密集剪切颗粒流中颗粒之间的接触力没有给定的分布形式. 即使静止密集颗粒介质在各向同性的压力下,其颗粒之 间接触力的相关性以及概率密度都没有统一的定论[31]. 其中,最为简单的接触力概率密度为1995年Liu等[32, 33]提出的$q$模型,概率分布为$p{\rm{d}} (f) = [C^cf^{C - 1}\exp ( - Cf)] / (C - 1)!$,这里$C$为相邻颗粒的个数,$f \equiv F / \bar {F}$是由平均力$\bar {F}$归一化的颗粒之间的接触力. 该模型为一个平均场的近似,忽略了颗粒之间接触的具体情形,对颗粒介质中量级较小的力的概率密度的估计欠佳. 基于此,引出了对数值数据拟合的概率分布表达式
| $$ p {\rm{d}}(f) = a[1 - b\exp ( - \alpha f^c)]\exp ( - \xi f) $$ | (3) |
这里$a$,$b$,$c$,$\alpha $,$\xi $为与颗粒介质特性相关的拟合参 数[31],在许多实验研究中也有类似形式的表达 式[34]. 由此可见,接触力的概率密度分布形式并非简单的指数形式,其前面还有一个系数因子. 研究表明这个系数因子的形式具有不确定性. 在保持概率密度形式(3)不变的前提下,假设应力波动幅值的概率分布函数为
| $$ p {\rm{d}}(\delta \sigma _0 ) = \dfrac{a}{P({z}')}[1 - b\exp ( - \alpha \sigma _0 ^c)] \cdot \\ \qquad \exp \Big ( - \dfrac{\delta \sigma _0 }{P({z}')} \Big) \,{\rm{d}}(\delta \sigma _0 ) $$ | (4) |
这里,$\sigma _0 $是与颗粒介质初始时刻应力分布相关的量. 将关系式(4)代入非局部流变模型的推导过程中,得到剪切速率的积分表达式
| $$ \dot {\gamma }(z) = \dfrac{1}{d}\int {\dfrac{\left| {\dot {\gamma }({z}')} \right|a(1 - b\exp ( - \alpha \sigma _0 ^c))}{1 + \dot {\gamma }(z)d / I_0 \sqrt {P(z) / \rho _{\rm s} } }} \cdot \\ \qquad \Bigg\{ \exp \Big[- \dfrac{(\mu _{\rm s} P - \tau )[1 + \beta (z - {z}')^2 / d^2]}{P({z}')} \Big] -\ \\ \qquad \exp \Big ( - \dfrac{(\mu _{\rm s} P + \tau )[1 + \beta (z - {z}')^2 / d^2]}{P({z}')} \Big ) \Bigg \}\,{\rm{d}}{z}' $$ | (5) |
已知在不同构型下的应力分布,将其代入方程(5),通过离散方程,进行迭代即可得到剪切速率的分布.
在斜面剪切流动中,影响颗粒之间接触力的因素有斜面的倾角$\theta $,颗粒层的厚度$h$,以及颗粒介质的体积分数$\phi $. 模型中$\alpha $与斜面颗粒流的性质有关,假设$\alpha (\theta ,h / d,\phi ) = \tan (\theta )\phi [1 / \ln (h / d)]^{\lg (h / d)}$. $\sigma _0 ^c$与初始床面颗粒介质的应力有关
$$ \sigma _0^c = [(\mu _{\rm s} P(z) - \tau (z)) / \tau ({z}')]^{\exp (d / h)} -\\ \qquad [(\mu _{\rm s} P(z) + \tau (z)) / \tau ({z}')]^{\exp (d / h)} $$
是$z'$处的无量纲应力,由颗粒介质向右运动引起的应力及向左运动引起的应力组成. 将上述各个量代入方程(5)中,得到斜面颗粒流的流变关系
| $$ \dot {\gamma }(z) = \dfrac{1}{d}\int {\dfrac{\left| {\dot {\gamma }({z}')} \right|}{1 + \dot {\gamma }(z)d / I_0 \sqrt {P(z) / \rho _{\rm s} } }} \cdot \\ \qquad \Bigg \{ \exp \Big ( - \dfrac{(\mu _{\rm s} P - \tau )[1 + \beta (z - {z}')^2 / d^2]}{P({z}')} \Big) - \\ \qquad \exp \Big( - \dfrac{(\mu _{\rm s} P + \tau )[1 + \beta (z - {z}')^2 / d^2]}{P({z}')} \Big) \Bigg \} \cdot \\ \qquad \exp ( - \alpha (\theta ,h / d,\phi )\sigma _0 ^c) {\rm{d}} z' $$ | (6) |
至此,我们提出了非局部流变模型中应力概率密度分布的修正. 模型中未引入新的参数,仍是微观摩擦系数$\mu _{\rm s}$, 特征惯性数$I_0 $,应力波动的空间程度$\beta $.
1.2 体积分数与剪切速率的耦合在密集颗粒流的研究中,往往将体积分数$\phi $作为系统的全局特征常数,如局部流变模型[11, 14]和非局部流变 模型[18, 26, 28]在预测颗粒流动特性时将体积分数作为一个奴隶变量. 研究表明密集颗粒介质从固态向流态的相变中,流变特性及其动力学行为对精确体积分数$\phi $变得极为敏感[35]. 体积分数$\phi $的局部微小变化都可能导致局部发生重大的流变过程,且系统的局部体积分数都具有时空变化特性[36] (静止颗粒系统的体积分数不仅是一个时间变量,也是一个空间变量). 因此,对于密集颗粒体系,体积分数的全局变化极为重要(在剪切带问题中[37]),但是单一的全局体积分数完全不能刻 画颗粒系统,局部体积分数$\phi $的变化和波动在颗粒流变中不容忽视.
最近的剪切试验表明均匀应力也能导致局部膨胀或压缩[37]. 因而,在非局部流变模型中引入体积分数的时空变化,有助于深入 了解颗粒介质的流变动力特性. 而目前的实验无法直接精确测量体积分数在空间的分布以及随时间的变化[38],因此,本文忽略体积分数随时间的变化,仅关注 其在空间的分布.
在局部模型中,通过实验和数值模拟的拟合,$\mu (I)$和体积分数$\phi (I)$可以表示为[39]
| $$ \left.\begin{array}{l} \mu (I) = \mu _1 + \dfrac{\mu _{\rm s} - \mu _1 }{I_0 / I + 1} \\ \phi = \phi _{\max } + (\phi _{\min } + \phi _{\max } )I \end{array}\right\} $$ | (7) |
体积分数为惯性数的函数. 本文考虑剪切速率与体积分数的耦合作用,在剪切速率迭代的过程中,体积分数通过
| $$ \phi (z) = \phi _{\max } + I_0 (\phi _{\min } + \phi _{\max } )\dot {\gamma }(z)\sqrt {d^2\rho _{\rm s} / P} $$ | (8) |
进行修正. 这里$\phi (z)$是体积分数随高度的分布. 将修正值反馈于剪切速率的迭代中,如此反复,直到剪切速率与体积分数的值都达到稳定,即可得到当前状态下颗粒流的剪切速率以及体积分数的空间分布. 通过对剪切速率积分可以得到颗粒流的速度分布.
2 斜面颗粒流的预测基于修正后的非局部流变模型,考虑颗粒介质沿粗糙斜面流动这一问题. 在这个构型下,颗粒介质限定在自由表面$z = h$与粗糙底面$z = 0$之间. 在模型中,粗糙表面为第一列颗粒. 已知斜面颗粒介质的应力$P$和$\tau $的分布,离散积分方程(6),将局部流变模型(7)预测的剪切速率与体积分数作为初值,通过迭代得到方程的解. 基于边界不滑移条件(在粗糙底面$z = 0$处,速度$u = 0$),积分剪切速率$\dot {\gamma }(z)$可以得到速度沿高度的分布.
颗粒介质流动的临界条件,即仅在一个有限的参数空间($h$,$\theta $)内积分方程(6)存在解. 给定一个倾斜角度$\theta $,存在 临界厚度$h_{\rm stop} $,在这个临界厚度以下,所有颗粒的速度都为0,积分方程仅有零解. 由于在实验中临界厚度不计粗糙底面这 一层的厚度,因此采用本文中的模型预测临界厚度需要减去一层的厚度才能与实验结果吻合.
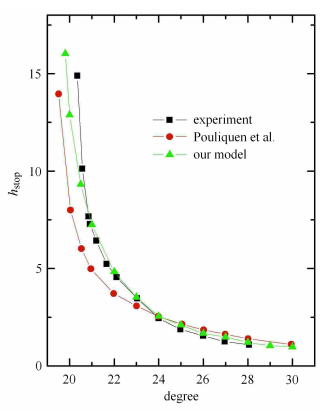
基于修正的非局部流变模型预测的临界厚度与倾斜角度的关系如图 2所示,并与实验结果[30]和非局部流变模型的预测 结果[28]进行比较. 表明临界厚度随倾斜角度增加呈递减趋势,这是由于颗粒层厚度较小时,应力波动的量级远小于颗粒克 服周围颗粒的束缚所需要的应力. 要使发生,必须增加斜面的倾斜角度,从而颗粒层较薄时更难于流动. 与Pouliquen 等的非局部流 变模型相比,本文的修正模型与实验结果在定量上更为吻合,尤其是斜面角度较小时的临界厚度预测值. 一方面是由于更为真实地考虑 了应力波动幅值的分布形式,另一方面在于修正模型中考虑了体积分数对应力分布的影响. 由此可见,本文的修正模型能更好地预测颗粒 介质发生流动的临界条件.
|
图 2 临界厚度 hstop 随斜面倾角 θ 的变化. 方框,圆圈,三角点线分 别为实验结果 [30],非局部流变模型 [28] 和本文提出的 修正模型预测结果 Fig.2 Critical thickness hstop as a function of inclination θ. Box-dotted line,circle-dotted line,and triangle-dotted line are represent data from experiments[30],prediction of the nonlocal rheological model by Pouliquen et al.[28],and prediction of the modified rheological model of this work respectively |
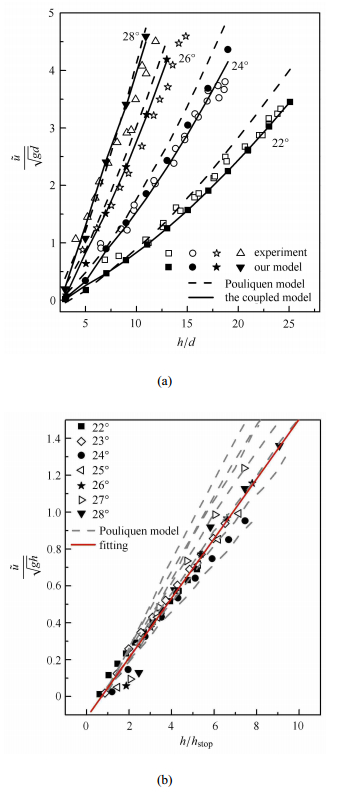
颗粒层厚度达到$h_{\rm stop} $,形成平稳均匀流,积分方程(6)存在迭代解,对所得速度沿高度积分 (即$\tilde {u} = \dfrac 1 h\int_0^h {u(z) {\rm{d}} z} $)得到颗粒流的平均速度. 图 3(a)展示了倾斜角度$\theta $为 $22^ \circ$,$24^ \circ $,$26^ \circ $,$28^ \circ $时颗粒流的平均速度随无量纲颗粒层厚度的变化关系.
|
图 3 不同倾斜角度下 (a) 速度的深度平均随颗粒层厚度的变化关系(b) Froude 数与 h/hstop 的关系 Fig.3 Under different inclinations, (a) the dependence of the average velocity on the dimensionless thickness; (b) the dependence of the Froude number on h/hstop |
图中分别为实验结果,Pouliquen 等模型的预测结果,以及修正应力波动幅值情形下考虑剪切速率与体积分数耦合与否的预测结果. 可见,3种理论预测与实验结果基本一致,平均速度随颗粒层厚度增加而增加,且随倾斜角度的增加这种变化趋势更为显著. 本文基于对应力波动幅值分布的修正,更为充分地体现了颗粒介质流动的非局部效应,使得对平均速度的预测与实验结果更为吻合, 尤其是小倾斜角的情况. 另外,通过考虑体积分数与剪切速率的耦合,表明体积分数对平均速度影响程度约为其平均速度的5%.
实验和数值模拟结果表明无论是薄层亦或是厚层的颗粒流都存在一个简单的尺度关系, Froude数与$h / h_{\rm stop} $具有如下关系
| $$ \dfrac{\tilde {u}}{\sqrt {gh} } = \varsigma \dfrac{h}{h_{\rm stop} } $$ | (9) |
这里Froude数为速度的深度平均$\tilde {u}$与$\sqrt {gh} $的比值,$\varsigma $为实验拟合参数. Pouliquen 等提出的非局部流变模型的思想可以通过调试模型中的参数而达到所有角度下的平均速度与厚度归一化的效果,此种情形下的归一化仅是参数组合的一种偶然情形. 图 3(b) 表明通过对应力分布的修正,使得模型能够更为准确地定量预测临界厚度与角度的关系以及平均速度与颗粒层厚度的关系,从而使得Froude数与$h / h_{\rm stop} $的关系归一化,这是该数学模型内在性质的体现.
上述研究进针对速度的平均值展开,而未考虑速度在颗粒介质内部的分布. 已有的实验和数值研究表明速度随到自由表面距离的增加而减 小,其递减形式呈现出凸、凹和线性这3种形状的速度分布曲线[15, 40]. 本文基于修正的非局部流变模型对不同厚度颗粒流的速度廓线以及剪切速率进行了预测,并与数值模拟结果[15]进行比较.
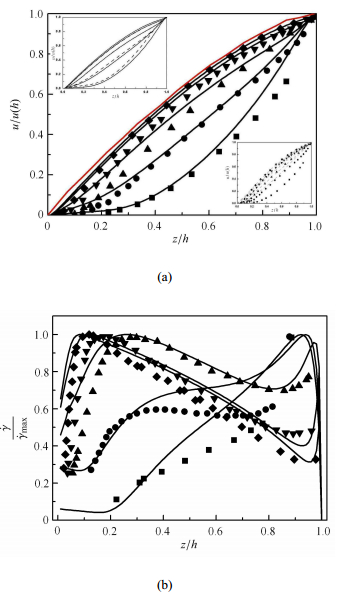
图 4(a)所示为斜面倾斜角度为$24^\circ $,颗粒层厚度从$4d$到$38d$变化的颗粒流速度廓线. 表明,随着颗粒层厚度的变化,速度廓线的形状略有不同. 较厚颗粒流的速度分布服从Bagnold廓线[13],如图中厚度为$38d$,$24d$,$15d$时,随厚度的减小形状略有不同,但整体速度廓线都有上凸的趋势. 而厚度减小到一定值,其速度廓线近似呈线性,如图中颗粒层厚度为$9d$时. 当颗粒层减小至临界流动层附近,其速度廓线与厚层颗粒流的速度廓线定性不同,表现出下凹的趋势. 这种定性的变化特征在应变速率曲线中更为显著,如图 4(b)所示,颗粒层越厚,剪切速率$\dot {\gamma }$由底层向自由表面递减;随着颗粒层厚度的减小,颗粒介质的一部分区域剪切速率$\dot {\gamma }$基本趋于常数,致使速度线性分布;而当颗粒层厚度在临界厚度附近时,剪切速率$\dot {\gamma }$沿自由表面方向有增加的趋势.
|
图 4 (a)斜面倾角为 24°时,颗粒流的速度廓线.点的形状表示不同厚度的数值模拟结果 [15],颗粒层厚度分别为 4d (方框),9d (圆圈), 15d (正三角),24d (倒三角),38d (菱形).黑色实线为修正模型的预测结果,虚线为 Bagnold廓线.左上角插图中实线和虚线为考虑和不考虑体积分数耦合作用的对比;右下角为 Pouliquen等模型与实验结果的比较. (b)剪切速率廓线 Fig.4 (a) Velocity profile along the height at θ = 24°. Filled dots of different shapes represent numerical simulations for Different h from Sibert et al. Filled square,4d; filled circle,9d; filled upper triangle,15d; filled down triangle,24d; filled diamond,38d. The solid lines represent the corresponding predicted results of our modified coupled model for different h. The dashed line is the Bagnold profile. The solid lines and the dotted lines in the top left insert represent results considering and not considering the coupling effect of shear rate and volume fraction. The right down inset is the comparison between the experiments and the predictions of Pouliquen et al. (b) The profile of shear rate along the height |
同时,通过将Pouliquen 等提出的模型预测结果与模拟结果进行比较(图 4(a)右下角),可见本文的理论结果不仅能够预测速度廓线随 厚度定性变化的趋势,而且定量上对薄层颗粒流廓线的预测结果与实验基本吻合. 另外,图 4(a)左上角中的实线和虚线分别表示与体积分数耦合与不耦合的结果,可见体积分数在迭代过程中对速度分布在定量上 有一定的修正,使得预测结果与实际结果更为接近. 因此,在工业生产以及泥石流的预测中,需要更为合理地考虑体积分数对颗粒流动的影响.
3 结 论通过提出应力波动幅值的概率分布的具体形式,并在离散积分的计算中基于剪切速率与体积分数耦合迭代过程考虑体积分数对颗粒 流动的影响,提出了修正非局部流变模型. 将修正模型应用于斜面剪切流临界条件以及运动特性的预测. 结果表明,颗粒流的临界厚度是倾斜角度的减函数,预测结果与实验结果更为接近. 此外,基于修正模型对斜面颗粒流的平均速度随颗粒层厚度的变化关系的预测结果可见,临界厚度以及平均速度的修正,使得Froude数与$h / h_{\rm stop} $的关系归一化,这是修正后数学模型的内在性质的体现. 最后,修正的非局部流变模型预测不同颗粒层厚度下颗粒流的速度和剪切速率廓线,速度廓线随着厚度的增加呈现出凹、线性至凸曲线 的不断过渡,且速度和剪切速率廓线的预测结果与模拟结果吻合较好. 可见修正模型更为合理地考虑了颗粒内部应力波动幅值的概率密度分布,充分体现了颗粒介质的非局部特性,并通过与体积分数的实时 迭代考虑该因素对运动特性的影响.
| 1 | Zheng XJ, Wang DM. Multiscale mechanical behaviors in discrete materials: A review. Acta Mechanica Solida Sinica, 2010, 23(6):579-591 |
| 2 | Pouliquen O, Chevoir F. Dense flows of dry granular material. C. R. Physique, 2002, 3: 163-175 |
| 3 | 季顺迎. 非均匀颗粒材料的类固-液相变行为及本构方程. 力学学 报, 2007, 23(2): 223-237 (Ji Shunying. The quasi-solid-liquid phase transition of non-uniform granular materials and their constitutive equation. Chinese Journal of Theoretical and Applied Mechanics,2007, 23(2): 223-237 (in Chinese)) |
| 4 | Aranson IS, Tsimring LS. Patterns and collective behavior in granular media: Theoretical concepts. Rev Mod Phys, 2006, 78: 641-692 |
| 5 | 蒋亦民, 刘佑. 基于流体动力学理论的颗粒物质本构关系. 科学 通报, 2009, 54(11): 1504-1510 (Jiang Yimin, Liu Mario. A granular constitutive relation derived from hydrodynamics. Chinese Sci Bull, 2009, 54(11): 1504-1510 (in Chinese)) |
| 6 | 季顺迎, 孙其诚, 严颖. 颗粒物质剪切流动的类固-液转化特性及 相变图的建立. 中国科学物理学力学天文学(中文版), 2011,41(9): 1112-1125 (Ji Shunying, Sun Qicheng, Yan Ying. Characteristics in quasi-solid-liquid phase transition of granular shear flow and its phase diagram. Sci. Sin. Phys. Mech. Astron, 2011, 41(9):1112-1125 (in Chinese)) |
| 7 | Jaeger HM, Nagel SR, Behringer RP. Granular solids, liquids, and gases. Rev Mod Phys, 1996, 68: 1259-1273 |
| 8 | Roux JN, Combes G. Quasistatic rheology and the origin of strain. C R Phys, 2002, 3: 131-140 |
| 9 | Goldhirsch I. Rapid granular flows. Annu Rev Fluid Mech, 2003, 35:267-293 |
| 10 | Berzi D. Extended kinetic theory applied to dense, granular, simple shear flows. Acta Mech, 2014, 225: 2191-2198 |
| 11 | Midi GDR. On dense granular flows. Eur Phys J E, 2004, 14: 341-365 |
| 12 | Da Cruz F, Emam S, Prochnow M, et al. Rheophysics of dense granular materials: Discrete simulation of plane shear flows. Phys Rev E, 2005, 72: 021309 |
| 13 | Bagnold RG. Experiments of gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc R Soc Lond A, 1954,255: 49-63 |
| 14 | Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows. Nature, 2006, 441: 727-730 |
| 15 | Silbert LE, Landry JW, Grest GS. Granular flow down a rough inclined plane: Transition between thin and thick piles. Phys Fluids,2003, 15: 1-10 |
| 16 | Mueth DM, Debregeas GF, Karczmar GS, et al. Signatures of granular microstructure in dense shear flows. Nature, 2000, 406: 385-389 |
| 17 | Koval G, Roux JN, Corfdir A, et al. Annular shear of cohesionless granularmaterials: From the inertial to quasistatic regime. Phys Rev E, 2009, 79: 021306 |
| 18 | Kamrin K, Koval G. Nonlocal constitutive relation for steady granular flow. Phys Rev Lett, 2012, 108: 178301 |
| 19 | Aranson IS, Tsimring LS. Continuum theory of partially fluidized granular flows. Phys Rev E, 2002, 65: 061303 |
| 20 | Mohan LS, Rao KK, Nott PR. A frictional cosserat model for the slow shearing of granular materials. J Fluid Mech, 2002, 457: 377-409 |
| 21 | Savage SB. Analysis of slow high-concentration flows of granular materials. J Fluid Mech, 1998, 377: 1-26 |
| 22 | Jenkins JT, Berzi D. Dense inclined flows of inelastic spheres: Tests of an extension of kinetic theory. Granular Matter, 2010, 12: 151-158 |
| 23 | Kamrin K, Bazant MZ. Stochastic flow rule for granular materials. Phys Rev E, 2007, 75: 041301 |
| 24 | Jop P. Rheological properties of dense granular flows. C R Physique,2015, 16: 62-72 |
| 25 | Bouzid M, Trulsson M, Claudin P, et al. Microrheology to probe non-local e ects in dense granular flows. Eur Phy Lett, 2015, 109:24002 |
| 26 | Henann DL, Kamrin K. A predictive, size-dependent continuum model for dense granular flows. Proceedings of the National Academy of Sciences, 2013, 110: 6730 |
| 27 | Kamrin K, Henann DL. Nonlocal modeling of granular flows down Inclines. Soft Matter, 2015, 11: 179-185 |
| 28 | Pouliquen O, Forterre Y. A non-local rheology for dense granular flows. Philos Transact A Math Phys Eng Sci, 2009, 367: 5091-5107 |
| 29 | Pouliquen O, Forterre Y, Le Dizes S. Slow dense granular flows as self-induced process. Adv Complex Syst, 2001, 4: 441-450 |
| 30 | Pouliquen O. Scaling laws in granular ows down rough inclined planes. Phys Fluids, 1999, 11: 542-548 |
| 31 | Müller MK, Luding S, Pöschel T. Force statistics and correlations in dense granular packings. Chemical Physics, 2010, 375: 600-605 |
| 32 | Coppersmith SN, Liu C, Majumdar S, et al. Model for force fluctuations in bead packs. Phys Rev E, 1996, 53 (5): 4673-4685 |
| 33 | Liu C, Nagel SR, Schecter DA, et al. Force fluctuations in bead packs. Science, 1995, 269: 513-515 |
| 34 | Asmus SMF, Pezzotti G. Analysis of microstresses in cement paste by fluorescence piezospectroscopy. Phys Rev E, 2002, 66: 052301 |
| 35 | Haw MD. Volume fraction variations and dilation in colloids and Granular. Phil Trans R Soc A, 2009, 367: 5167-5170 |
| 36 | Haw MD. Void structure and cage fluctuations in simulations of concentrated suspensions. Soft Matter, 2006, 2: 950-956 |
| 37 | Møller PCF, Rodts S, Michels MAJ, et al. Shear banding and yield stress in soft glassy materials. Phys Rev E, 2008, 77: 041507 |
| 38 | Pusey PN, Zaccarelli E, Valeriani C, et al. Hard spheres: crystallization and glass formation. Phil Trans R Soc A, 2009, 367: 4993-5011 |
| 39 | Pouliquen O, Cassar C, Jop P, et al. Flow of dense granular material: Towards simple constitutive laws. J Stat Mech, 2006, (07): P07020 |
| 40 | Silbert LE, Ertas D, Grest GS, et al. Granular flow down inclined plane: Bagnold scaling and rheology. Phys Rev E, 2001, 64: 051302 |
2. School of Electronical and Machanical Engineering, Xidian University, Xi'an 710071, China
 2016, Vol. 48
2016, Vol. 48