饱和与非饱和颗粒材料由众多颗粒与其间充满或部分填充液体的孔隙组成. 它在宏观尺度通常模型化为饱和或非饱和多孔连续体. Terzaghi [1] 提出了饱和多孔介质力学的有效应力定义. 基于有效应力原理,Biot [2, 3, 4, 5] 建立了多孔介质中静力和动力响应流固相耦合作用的控制方程. 考虑孔隙液压所引起之颗粒体积变形对饱和多孔介质固体骨架变形的效应,Zienkiewicz 和Shiomi [6]引入了Biot系数,提出了饱和多孔介质广义有效应力定义. Kytomaa等[7]将饱和颗粒材料在介观尺度模型化为含液离散颗粒集合体,研究了孔隙液压作用引起之单个颗粒压缩变形对饱和多孔介质本构行为的影响.
Bishop [8, 9],Skempton [10],Li等[11],Zienkiewicz 等[12]将有效应力概念推广到含两相或多相不可混孔隙流体的非饱和多孔介质 中. Bishop [8, 9]首先把有效应力概念推广到非饱和多孔介质,用平均孔隙压力表示孔隙多相流体效应. 把有效应力概念简单地推广到非饱和多孔介质的论据不如它在仅有单一孔隙流体存在的饱和多孔介质中那么清楚,对非饱 和多孔介质中各种有效应力定义仍有争论[10, 12, 13]. Gray 和Schrefler [14]在热动力学框架内对非饱和多孔介质有效应力概念作出了一些澄清. Gray 和Miller [15]把热动力约束平均理论引入到多孔介质系统,所提供的一致性框架有助于对Gray和 Schrefler[16]所提出的非饱和多孔介质中的有效应力和总应力张量中的物理量作出解释.
在国内,陈正汉等[17]以热力学和连续介质力学的应力理论为基础,导出了一系列非饱和土应力状态变量; 赵成刚 等[18]基于多相孔隙介质理论提出了非饱和土广义有效应力原理; 邵龙潭等[13]阐明了有效应力、粒间应力和土骨架应力的物理意义及其相互关系;刘艳、赵成刚等[19]综述了非 饱和土力学理论的研究进展. 然而,对于饱和、非饱和多孔介质,还未见基于介观结构特性和介观水力-力学响应状态的有效应力研究的工作发表.
利用介-宏观均匀化过程,人们基于介观水力-力学模型致力于发展定义非饱和多孔介质有效应力与有效压力的方法[20, 21, 22, 23]. 有效压力不再由非饱和多孔连续体理论[9, 24]中所定义的标量表示,而是一个依赖于由固体颗粒、孔隙液体和气体组成的介观结构、反映毛细力各向异性效应的张量.
在介观尺度上,颗粒材料的每个离散颗粒在运动学上除平移自由度还具独立的旋转自由度,在动力学上由一个颗粒到其相邻接触颗粒能传递力偶. 为表征离散颗粒介观结构, 颗粒材料应模型化为在每个材料点定义具有独立旋转自由度的等效多孔Cosserat连续体[25, 26, 27, 28, 29]. 考虑饱和或非饱和颗粒材料,它在介观尺度模型化为含液离散颗粒集合体;而在宏观尺度上模型化为在一个材料点处同时存在固相和饱和液相、或固相与不可混液、气相的饱和或非饱和等效多孔Cosserat连续体元. 尽管如此,孔隙流压对多孔连续体的效应可假定仅对总Cauchy应力的有效Cauchy应力和有效压力的定量剖分有关,而与定义于Cosserat连续体的偶应力无关.
定义于宏观连续体一个材料点的有效压力张量依赖于该材料点由固、液、气三相组成的介观结构. 本文中指定的饱和或非饱和颗粒材料的介观结构由一个参考颗粒与其直接相邻颗粒以及其间的间隙流体组成的两相或三相Voronoi胞元模型描述. 它基于表示干颗粒材料介观结构的单相Voronoi胞元模型[30]. 湿Voronoi胞元模型不仅包含位于湿Voronoi胞元内的参考颗粒与间隙流体, 且包含湿Voronoi胞元外的直接相邻颗粒. 它能用以描述包含局部孔隙比、局部液相和气相饱和度、参考颗粒与其直接相邻颗粒接触拓扑的局部介观结构.
由湿Voronoi胞元模型导出的有效压力张量依赖于胞元内液桥系统的几何特征. 液桥结构的构形随孔隙液体的饱和度增长可从摆动状态演化到索状和毛细状态. 本文将具体考虑离散颗粒系统在低饱和度下以具双联(binary bond)模式的摆动(pendular)构形液桥为特征的介观水力-力学模型[31]. 基于湿颗粒材料的介-宏观均匀化过程与平均场理论定义基于介观水力-力学模型的饱和多孔介质广义有效应力和Biot系数,非饱和多孔介质有效应力、有效压力和Bishop参数.
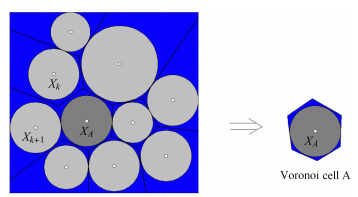
1 饱和多孔介质有效应力和广义有效应力 1.1 饱和多孔介质有效应力图 1表示饱和多孔介质的二维饱和Voronoi胞元模型. 本节用它概念性地描述由一簇浸透孔隙液体的球体组成的三维饱和Voronoi胞元模型.
|
图 1 饱和多孔介质的二维 Voronoi 胞元模型示意图 Fig.1 The two-dimensional Voronoi cell model for saturated granular material |
定义Voronoi胞元边界内颗粒为参考颗粒. 以$ m$ 表示半径为$ r$,体积为 $V_{\rm p}$ 的参考颗粒的直接接触颗粒数,$V$表示定义于参考颗粒处的Voronoi胞元体积. 以$\phi$ 表示Voronoi胞元的孔隙度,Voronoi胞元内的孔隙体积则可表示为 $V_{\rm v}=V-V_{\rm p}=\phi V$. 而$V_{\rm p}$可表示为 $V_{\rm p}=(1-\phi)V$.
基于由饱和离散颗粒集合体到饱和多孔连续体的介-宏观均匀化,定义于Voronoi胞元的饱和多孔连续体的平均Cauchy应 力可表示为
| $$ \bar\sigma_{ji}=\dfrac 1V \int_V \sigma_{ji} {\rm{d}} V=\dfrac 1V \Bigg ( \int_{V_{\rm p}}\sigma_{ji}{\rm{d}} V -\int_{V_{\rm l}} p_{\rm l} \delta_{ji} {\rm{d}} V \Bigg ) $$ | (1) |
式中,$V_{\rm l}$是Voronoi胞元内孔隙液体体积,对饱和多孔介质有$V_{\rm l}=V_{\rm v}$; $\sigma_{ji}$是施加于体积 为$V_{\rm p}$的固体颗粒内任一物质点的Cauchy应力; $p_{\rm l}$是体积为$V_{\rm l}$的孔隙液体中各点孔隙液压,定义压为正. 假定 $V_{\rm l}$中$p_{\rm l}$为常数,式(1)可简化为
| $$ \bar\sigma_{ji}=\dfrac 1V \int_V \sigma_{ji} {\rm{d}} V=\dfrac 1V \Bigg( \int_{V_{\rm p}} \sigma_{ji}{\rm{d}} V - V_{\rm l} p_{\rm l} \delta_{ji} \Bigg ) $$ | (2) |
式(2)第2个等号右端第1项,根据Gauss散度定理和平衡方程可展开为
| $$ \dfrac{1}{V} \int_{V_{\rm p}} \sigma _{ji} {\rm{d}} V = \dfrac{1}{V}\int_{\varGamma _{\rm p} } t_i x_j {\rm{d}}\varGamma = \\ \qquad \dfrac{1}{V}\sum_{c = 1}^m f_i^c x_j^c - \dfrac{1}{V}\int_{\varGamma _{\rm p} } (p_{\rm l} n_i ) \left( {rn_j } \right) {\rm{d}}\varGamma =\\ \qquad \dfrac{r}{V} \sum_{c = 1}^m f_i^c n_j^c - \left( {1 - \phi } \right) p_{\rm l} \delta _{ji} $$ | (3) |
式中 $\varGamma _{\rm p}$是Voronoi胞元内参考颗粒表面,$m$ 是与它直接接触相邻颗粒数, $t_i$是作用于颗粒表面$x_j$处的表面力,$n_j$为该处颗粒表面单位外法线方向. 表面力 $t_i$包含作用于该处的颗粒间接触力$f^c_i$ ($c=1,2,\cdots,m$) 和分布液压$p_{\rm l}$. 式(3)描述了作用于参考颗粒的颗粒间接触力和颗粒表面孔隙液压对于Voronoi胞元总平均 Cauchy应力的贡献. 将式(3)代入式(2)得到
| $$ \bar\sigma_{ji}=\dfrac rV \sum^m_{c=1} f^c_in^c_j-p_{\rm l} \delta_{ji}= \bar \sigma'_{ji}-p_{\rm l}\delta_{ji} $$ | (4) |
式中饱和多孔介质有效Cauchy应力$ \bar\sigma'_{ji}$定义为
| $$ \bar\sigma'_{ji} =\dfrac r V \sum^m_{c=1} f^c_i n^c_j $$ | (5) |
式(4)可改写为用总Cauchy应力$ \bar\sigma_{ji}$ 和孔隙液压$p_{\rm l}$表示的有效Cauchy应力,即
| $$ \bar\sigma'_{ji}=\bar\sigma_{ji}+p_{\rm l}\delta_{ji} $$ | (6) |
它再现了Terzaghi[1]提出的有效应力定义. 式(5)表示,在宏观多孔连续体中定义为控制一个材料点处固体骨架力学行为的 有效应力表征了该处局部离散颗粒系统的介观结构和力链强度. 式(6)表明饱和多孔介质中孔隙液压效应的各向同性.
1.2 饱和多孔介质中广义有效应力利用式(5),略去接触颗粒间的耗散摩擦,由模型化为多孔Cosserat 连续体元的Voronoi胞元导出基于介观力学的本构关系为[30]
| $$ \bar\sigma'_{ji}=D^{\sigma\varepsilon}_{jiqk}\bar\varepsilon_{qk}+D^{\sigma\kappa}_{jiq} \bar\kappa_q $$ | (7) |
式中$\bar\varepsilon_{qk}=\bar u_{k,q}+e_{rkq}\bar\omega_r$,$\bar\varepsilon_{qk},\bar u_{k,q},\bar\omega_r,\bar \kappa_q$ 是由Voronoi胞元模型定义的等效多孔Cosserat连续体元的应变,线位移空间导数,微转角,微曲率. 式(7)中弹性模量张量为[30]
| $$ D_{jiqk}^{\sigma \varepsilon } = \dfrac{r}{V} \sum _{c = 1}^m h\left( {u_{\rm n}^c } \right)k_{\rm s}^c \left( {r + r_{\rm B}^c } \right)t_i^c n_j^c t_k^c n_q^c +\\ \qquad \dfrac{r}{V} \sum _{c = 1}^m h\left( {u_{\rm n}^c } \right)k_{\rm r}^c \left( {r - r_{\rm B}^c } \right)t_i^c n_j^c t_k^c n_q^c +\\ \qquad \dfrac{r}{V} \sum _{c = 1}^m h\left( {u_{\rm n}^c } \right)k_{\rm n}^c \left( {r + r_{\rm B}^c } \right)n_i^c n_j^c n_k^c n_q^c $$ | (8) |
| $$ D_{jiq}^{ \sigma \kappa } = \dfrac{r}{V} \sum _{ c = 1}^{m} h\left( {u_{\rm n}^c } \right)\left( {k_{\rm s}^c - k_{\rm r}^c } \right)r_{\rm B}^c \left( {r + r_{\rm B}^c } \right)t_i^c n_j^c n_q^c $$ | (9) |
式中$ u_{\rm n}^c $是参考颗粒与第$c$个直接相邻颗粒的当前重迭量, $h(u_{\rm n}^c )$是依赖于$ u_{\rm n}^c $的Heaviside单位函数,体现了颗粒接触的丧失和产生及其随 时间的演变. $r^c_{\rm B}$ ($c=1,2,\cdots,m$)表示第$c$个直接相邻颗粒$B$的半径. $k_{\rm s}^c ,k_{\rm r}^c ,k_{\rm n}^c $ 分别是两接触颗粒间相应于切向滑动、滚动摩擦力与法向接触力的刚度系数. $t_i^c$ $ \left( {i = 1,2,3} \right)$, $n_j^c$ $\left( {j = 1,2,3} \right)$代表参考颗粒在接触点$c$处Voronoi胞元边界的单位切向量和法向量.
计及单个颗粒在静水压力$p_{\rm l}$下的可压缩性,其各向同性体积应变$\varepsilon_{\rm v}$ 可表示为
| $$ \varepsilon _{\rm v} = \dfrac{p_{\rm l} }{K_{\rm s} } = \dfrac{3\left( 1 - 2\nu _{\rm s} \right)}{E_{\rm s} }p_{\rm l} = 3bp_{\rm l } $$ | (10) |
式中$K_{\rm s},E_{\rm s},\nu _{\rm s} $是单个颗粒的体积模量、杨氏模量和 泊松比;$b = \left( {1 - 2\nu _{\rm s} } \right) / E_{\rm s} $. 静水压力$ p_{\rm l }$作用下初始半径为$r_0 $的颗粒的当前半径$r$可给出为[7]
| $$ r = r_0 \left( {1 - bp_{\rm l} } \right) = r_0 \eta \leqslant r_0 $$ | (11) |
式中定义
| $$ \eta = \left( {1 - bp_{\rm l} } \right) = 1 - \dfrac{1}{3}\varepsilon _{\rm v} = 1 - \varepsilon _{\rm m} $$ | (12) |
其中
| $$ \varepsilon _{\rm m} = \dfrac{\varepsilon _{\rm v} }{3} = \dfrac{p_{\rm l} }{3K_{\rm s} } = bp_{\rm l} $$ | (13) |
并定义$\varepsilon _{\rm m}$,$\varepsilon _{\rm v} $压为正. 考虑由静水压力引起之颗粒体积应变对基于介观力学的本构关系的影响,由式(7)可给出
| $$ \bar\sigma'_{ji}=(D_{jiqk}^{\sigma \varepsilon } \bar\varepsilon_{qk}+ D_{jiq }^{\sigma \kappa } \bar \kappa_q)_{r_0} +\\ \qquad \dfrac{\partial ( D_{jiqk}^{\sigma \varepsilon } \bar\varepsilon_{qk}+ D_{jiq }^{\sigma \kappa }\bar \kappa_q)_{r_0}} {\partial p_{\rm l}} p_{\rm l} $$ | (14) |
上式右端第2项考虑了作用于等效多孔Cosserat连续体的有效应力随作用于固体颗粒的静水压力的变化; 体现了作用于固体颗粒的静水压力对饱和多孔连续体的模量张量及应变的影响. 其中忽略了参考颗粒及其直接相邻颗粒间孔隙液体压力梯度的影响. 由此可得
| $\begin{array}{l} \frac{{\partial (D_{jiqk}^{\sigma \varepsilon }{{\overline \varepsilon }_{qk}})}}{{\partial {p_{\rm{l}}}}} = \frac{{\partial D_{jiqk}^{\sigma \varepsilon }}}{{\partial {p_{\rm{l}}}}}{\overline \varepsilon _{qk}} + D_{jiqk}^{\sigma \varepsilon }\frac{{\partial {{\overline \varepsilon }_{qk}}}}{{\partial {p_{\rm{l}}}}} = \\ {\gamma _\varepsilon }D_{jiqk}^{\sigma \varepsilon }{\overline \varepsilon _{qk}} + bD_{jiqk}^{\sigma \varepsilon }{\delta _{qk}} \end{array}$ | (15) |
| $\frac{{\partial \left( {D_{jiq}^{\sigma \kappa }{{\bar \kappa }_q}} \right)}}{{\partial {p_{\rm{l}}}}} = \frac{{\partial D_{jiq}^{\sigma \kappa }}}{{\partial {p_{\rm{l}}}}}{\bar \kappa _q} + D_{jiq}^{\sigma \kappa }\frac{{\partial {{\bar \kappa }_q}}}{{\partial {p_{\rm{l}}}}} = {\gamma _\kappa }D_{jiq}^{\sigma \kappa }{\bar \kappa _q}$ | (16) |
其中
| $$ \gamma _\varepsilon = \dfrac{1}{K_{\rm s} } - \dfrac{2b}{\eta } = \dfrac{1}{K_{\rm s} }\left( {1 - \dfrac{2}{3\eta }} \right) ,\ \ \gamma _\kappa = - \dfrac{1}{\eta K_{\rm s} } $$ | (17) |
上式中$ \partial D_{jiqk}^{\sigma \varepsilon } / \partial p_{\rm l} $的计算需要考虑$D_{jiqk}^{\sigma \varepsilon } $随参考颗粒半径$r$、直接相邻颗粒半径$r_{\rm B}^c $及基于Voronoi胞元模型的等效多孔Cosserat连续体的体积变化.
将式(15)和式(16)代回式(14),且略去下标$r_0$可得
| $$ \bar\sigma'_{ji}= D_{jiqk}^{\sigma \varepsilon} \bar\varepsilon_{qk}+ D_{jiq}^{\sigma \kappa} \bar\kappa_q+\\ \qquad \left( \gamma _\varepsilon D_{jiqk}^{\sigma \varepsilon} \bar\varepsilon_{qk}+ b D_{jiqk}^{\sigma \varepsilon} \delta_{qk}+\gamma_k D_{jiq }^{\sigma \kappa} \bar\kappa_q \right ) p_{\rm l} $$ | (18) |
定义$\alpha _{ji } $和$ \beta _{ji} $如下
| $ \alpha _{ji} = \delta _{ji}-\gamma _{\varepsilon } D_{jiqk}^{\sigma \varepsilon } \bar{\varepsilon }_{qk}-b D_{jiqk}^{\sigma \varepsilon } \delta_{qk}=\\ \qquad \delta _{ji} - \dfrac{1}{K_{\rm s} }\left( {1 - \dfrac{2}{3\eta }} \right) D_{jiqk}^{ \sigma \varepsilon } \bar{\varepsilon }_{qk}- \dfrac 1{3K_{\rm s}} D_{jiqk}^{ \sigma \varepsilon }\delta_{qk}$ | (19) |
| $\beta _{ji} = \delta _{ji} - \gamma _{\kappa } D_{jiq}^{\sigma \kappa } \bar \kappa_q=\delta_{ji}+ D_{jiq }^{ \sigma \kappa } \bar\kappa_q \dfrac 1{\eta K_{\rm s}} $ | (20) |
并定义与模型化为等效Cosserat连续体的固体骨架应变度量$\bar{ \varepsilon } _{qk} ,\bar{\kappa }_q$相关联的广义有效应力$ \bar{\sigma }''_{ji}$
| $$ \bar{\sigma }''_{ji}= D_{jiqk}^{\sigma \varepsilon } \bar\varepsilon_{qk} + D_{jiq}^{\sigma \kappa } \bar\kappa_q $$ | (21) |
把式(19)和式(20)代入式(18)得到
| $$ \bar\sigma'_{ji}=\bar\sigma''_{ji}+(2\delta_{ji}-\alpha_{ji}-\beta_{ji})p_{\rm l} $$ | (22) |
由式(6)所定义的有效应力可得广义有效应力 $\bar{\sigma}''_{ji}$与总Cauchy应力$\bar{\sigma }_{ji}$间存在如下联系
| $$ \bar{\sigma}''_{ji}=\bar{\sigma}_{ji} +p_{\rm l}(\alpha_{ji}+\beta_{ji}-\delta_{ji}) $$ | (23) |
由式(9)可得,$\delta _{ji} D_{jiq}^{\sigma \kappa } = D_{iiq}^{\sigma \kappa } = 0$,对式(20)两边同时乘$ \delta _{ji} $可得
| $$ \delta _{ji} \beta _{ji} = \delta _{ji} \delta _{ji} + \delta _{ji} D_{jiq}^{\sigma \kappa } \bar\kappa_q \dfrac 1{\eta K_{\rm s}}=\delta_{ji} \delta_{ji} $$ | (24) |
由此可以假定$ \beta _{ji} = \beta \delta _{ji} $,同时由上式可得
| $$ \beta = 1 ,\quad \beta _{ji} = \delta _{ji} $$ | (25) |
将上式代回式(22)和式(23)可得
| $ \bar {\sigma}'_{ji}=\bar{\sigma}''_{ji}+(\delta_{ji}-\alpha_{ji})p_{\rm l}$ | (26a) |
| $\bar{\sigma}''_{ji}=\bar{\sigma}_{ji}+p_{\rm l}\alpha_{ji} $ | (26b) |
由式(19)和式(26)可得基于介观水力-力学的Biot 系数,$\alpha_{ji}$ 为二阶张量,其对广义有效应力$\bar{\sigma}''_{ji}$的影响为各向异性,且一般地对其剪切分量也有影响. Biot系数$\alpha _{ji} $不仅与介观结构的材料参数,如颗粒半径、固体颗粒的体积模量、颗粒间接触刚度有关,同时与介观结构的模量 张量$D_{jiqk}^{\sigma \varepsilon }$、固体颗粒的体积应变、等效连续体的应力状态有关. 为与由饱和多孔连续体宏观理论导出的标量Biot系数比较,需考虑$\alpha_{ji} $的标量形式.
对式(19)两边同时乘$\delta _{ji} $可得
| $$ \delta _{ji} \alpha _{ji} = \delta _{ji} \delta _{ji} - \delta _{ji} D_{jiqk}^{\sigma \varepsilon } \bar\varepsilon_{qk} \dfrac 1{K_{\rm s}}\Big(1-\dfrac 2{3\eta} \Big) -\\ \qquad \dfrac 1{3K_{\rm s}}\delta_{ji} D_{jiqk}^{\sigma \varepsilon }\delta _{qk} $$ | (27) |
由式(9)可得,$\delta _{ji} D_{jiq}^{\sigma \kappa } = D_{iiq}^{\sigma \kappa } = 0$,同时由式(21)可得
| $$ \delta _{ji} D_{jiqk}^{\sigma \varepsilon } \bar{\varepsilon }_{qk} =\delta_{ji} \bar{\sigma }''_{ji}=3\bar{\sigma }''_{\rm m} $$ | (28) |
上式中$\bar{\sigma }''_{\rm m}$为对应于多孔连续体体积应变的广义有效应力的平均应力. 定义
| $$ K_{\rm T} = \dfrac{1}{9}\delta _{ji} D_{jiqk}^{\sigma \varepsilon } \delta _{qk} $$ | (29) |
由式(27) $\sim$式(29),可以假定
| $$ \alpha _{ji} = \alpha \delta _{ji} $$ | (30) |
将式(28) $\sim$式(30)代回式(27)可以得到基于介观结构与响应的标量形式Biot 系数
| $$ {\alpha } = 1 - \dfrac{\bar{\sigma }''_{\rm m}}{K_{\rm s}} \Big [1- \dfrac 2{3(1-\varepsilon_{\rm m})} \Big ]-\dfrac{K_{\rm T}}{K_{\rm s}} $$ | (31) |
一般地,饱和多孔介质固体骨架承受压缩体积应变,即$\bar{\sigma }''_{\rm m} \leq 0$. 为与宏观饱和多孔连续体理论中由广义Biot公式给出的Biot系数比较,式(31)可改写为
| $$ {\alpha } = 1 - \dfrac{1}{K_{\rm s} }\Big \{ K_{\rm T} - \left| \bar{\sigma }''_{\rm m} \right| \Big [1-\dfrac 2{3(1-\varepsilon_{\rm m})} \Big] \Big \} = 1 - \dfrac{K_{\rm T}^\ast }{K_{\rm s} } $$ | (32) |
一般地$K_{\rm T}^\ast \leqslant K_{\rm T} $. 由式(8)及式(29)可得
| $$ K_{\rm T} = \dfrac{r}{9V} \sum_{c = 1}^m h\left( {u_{\rm n}^c } \right)k_{\rm n}^c \left( {r + r_{\rm B}^c } \right) $$ | (33) |
由式(32)和式(33)可得多孔连续体广义体积模量为
| $$ K_{\rm T}^\ast = \dfrac{r}{9V} \sum_{c = 1}^m h\left( {u_{\rm n}^c } \right)k_{\rm n}^c \left( {r + r_{\rm B}^c } \right) -\\ \qquad \left| \bar{\sigma }''_{\rm m} \right| \Big [1-\dfrac 2{3(1-\varepsilon_{\rm m})} \Big] $$ | (34) |
将式(30)代回式(26b)可得如下基于介观水力-力学的总应力与广义有效应力的关系为
| $$ \bar\sigma ''_{ji}=\bar\sigma_{ji}+\alpha p_{\rm l} \delta_{ji} $$ | (35) |
值得指出,式(32)与在宏观饱和多孔连续体途径中获得的广义有效应力[6, 12]具有相同的形式. 然而,由文献[6, 12]定义的Biot系数$\alpha$是一个常系数
| $$ \alpha = 1 - \dfrac{K_{\rm T} }{K_{\rm s} } $$ | (36) |
而在式(32)中所定义的Biot系数 $\alpha $是一个不仅依赖于材料参数$K_{\rm T},K_{\rm S} $,同时也依赖当前状态变量$\left| \bar{\sigma }''_{\rm m} \right|$和$\varepsilon _{\rm m}$ (即当前时刻的等效连续体的应力状态和颗粒因孔隙液压而产生的体积应变)的变系数.
当单个颗粒的平均体积模量$K_{\rm S} $远大于$K_{\rm T}^\ast $,即$K_{\rm T}^\ast \ll K_{\rm S}$, 因孔隙液体压引起的颗粒体积应变对广义有效应力的影响可略去. 由式(6),式(35),广义有效应力$\bar{\sigma }''_{ji}$退化为经典有效应力$\bar{\sigma }'_{ji}$,即
| $$ \bar{\sigma }''_{ji} \cong \bar{\sigma }'_{ji} =\bar{\sigma }_{ji}+ p_{\rm l} \delta_{ji} $$ | (37) |
Bishop[8],Skempton[10],Bishop和Blight[9],Coussy[24],Zienkiewicz等[12], Gray和Schrefler[16]在多孔连续体理论框架内把由式(6)所表示的饱和多孔介质有效应力概念推广到非饱和情况. 考虑到非饱和多孔介质中孔隙气体(或其他干相孔隙流体(如孔隙油等))的存在,孔隙压力由平均孔隙流体压力定义[8, 10, 11, 12]
| $$ p = \chi p_{\rm l} + \left( {1 - \chi } \right)p_{\rm g} $$ | (38) |
即有效应力定义修改为
| $$ \sigma '_{ji} = \sigma _{ji} + P_{ji} = \left( {\sigma _{ji} + p_{\rm g} \delta _{ji} } \right) - \left( {p_{\rm g} - p_{\rm l}} \right)\chi \delta _{ji} =\\ \qquad \left( {\sigma _{ji} + p_{\rm g} \delta _{ji} } \right) + Q_{ji} $$ | (39) |
式中依赖于饱和度$S_{\rm l} $的加权参数$\chi $称为Bishop参数,$P_{ji} $和$Q_{ji} $分别是非饱和多孔连续体理论中定义为对角线二阶张量的有效压力和基质毛细压力张量,即
| $ P_{ji} = p\delta _{ji} = \left[{\chi p_{\rm l} + \left( {1 - \chi } \right)p_{\rm g} } \right]\delta _{ji}$ | (40) |
| $ Q_{ji} = - \left( {p_{\rm g} - p_{\rm l} } \right)\chi \delta _{ji} $ | (41) |
细观力学研究表明[20],由于液桥分布、液桥力和分支向量分布通常呈各向异性,由非饱和孔隙液体引起的毛细力将导致非饱和多孔介质的诱导各向异性. 非饱和多孔介质总Cauchy应力$\sigma_{ji}$应表示为
| $$ \sigma _{ji} = \sigma'_{ji} - P_{ji} ,\ \ {\pmb \sigma } = {\pmb\sigma }'-{\pmb P} $$ | (42) |
式中控制固体骨架变形的有效应力$\sigma'_{ji} $表征了颗粒间接触力;$P_{ji} $是表示非饱和多孔介质中各向异性毛细效应的二阶张量,它依赖于局部处液桥介观结构、孔隙气体(干相流体)和孔隙液体(湿相流体)压力差和液桥处表面张力.
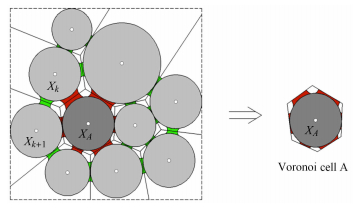
二维非饱和Voronoi胞元模型如图 2所示. 它由Voronoi胞元内的参考颗粒及其位于Voronoi胞元几何边界外的直接相邻颗粒、以及Voronoi胞元内的孔隙流体组成. 在低饱和度下假定颗粒间孔隙液体以``摆动''(pendular)液桥形态存在,如图 2所示.
二维非饱和Voronoi胞元模型描述了模型化为非饱和离散颗粒系统的非饱和颗粒材料介观结构,同时也表示了在 参考颗粒处定义的具有介观结构的等效非饱和多孔Cosserat连续体元. 以$V_{\rm l}^i \left( {i = 1,2,\cdots,m} \right)$表示Voronoi胞元内第$i$个液桥处液体体积,$V_{\rm g}^i \left( {i = 1,2,\cdots,m} \right)$表示Voronoi胞元内围绕参考颗粒两个相邻液桥间的孔隙气体体积. 可表示
| $$ V_{\rm v} = V_{\rm l }+ V_{\rm g } $$ | (43) |
式中
| $$ V_{\rm l }= \sum _{i = 1}^m V_{\rm l}^i ,\ \ V_{\rm g} = \sum_{i = 1}^m V_{\rm g}^i $$ | (44) |
以$p_{\rm l}^i $和$p_{\rm g}^i $分别表示$V_{\rm l}^i $和$V_{\rm g}^i $中平均孔隙液压和气压,则Voronoi胞元内$V_{\rm l} $和$V_{\rm g} $中平均孔隙液压和气压$\bar{p}_{\rm l},\bar p_{\rm g}$可定义为
| $$ \bar p_{\rm l}=\dfrac 1{V_{\rm l}} \sum^m_{i=1} p^i_{\rm l} V^i_{\rm l} ,\ \ \bar p_{\rm g}=\dfrac 1{V_{\rm g}} \sum^m_{i=1} p^i_{\rm g} V^i_{\rm g} $$ | (45) |
Voronoi胞元的总Cauchy应力张量$\bar{\sigma }_{ji}$在均匀化意义下可定义为
| $$ \bar{\sigma }_{ji}=\dfrac 1V \int_V \sigma_{ji} {\rm{d}} V =\dfrac 1V \int_{V_{\rm p}} \sigma_{ji} {\rm{d}} V_{\rm p}+ \\ \qquad \dfrac{1}{V}\left[{ \int_{V_{\rm l} } \left( { - p_{\rm l} } \right)\delta _{ji} {\rm{d}} V_{\rm l} + \int_{V_{\rm g} } \left( { - p_{\rm g} } \right)\delta _{ji} {\rm{d}} V_{\rm g} } \right] $$ | (46) |
利用式(45),式(46)右端第二、第三项可分别表示为
| $ - \dfrac{1}{V} \int_{V_{\rm l} } p_{\rm l} \delta _{ji} {\rm{d}} V_{\rm l} = - \dfrac{1}{V} \sum_{k = 1}^m p_{\rm l}^k V_{\rm l}^k \delta _{ji} = - \phi S_{\rm l} \bar{p}_{\rm l} \delta_{ji} $ | (47) |
| $- \dfrac{1}{V}\int _{V_{\rm g} } p_{\rm g} \delta _{ji} {\rm{d}} V_{\rm g} = - \dfrac{1}{V}\sum _{k = 1}^m p_{\rm g}^k V_{\rm g}^k \delta _{ji} =\\ - \phi S_{\rm g} \bar{p}_{\rm g} \delta_{ji}=-\phi(1-S_{\rm l}) \bar{p}_{\rm g} \delta_{ji}$ | (48) |
式中已定义
| $$ S_{\rm l} = \dfrac{V_{\rm l} }{V_{\rm v} } ,\ \ S_{\rm g} = \dfrac{V_{\rm g} }{V_{\rm v} } ,\ \ S_{\rm l} + S_{\rm g} = 1 $$ | (49) |
应用Gauss定理和平衡条件,略去重力效应,式(46)右端第1项积分可表示为
| $$ \dfrac{1}{V}\int_{V_{\rm p} } \sigma _{ji} {\rm{d}} V_{\rm p} = \dfrac{1}{V}\int_{\varGamma _{\rm p} } t_i x_j {\rm{d}}\varGamma _{\rm p} $$ | (50) |
式中作用于颗粒表面$x_j $处的表面力$t_i \left( {i = 1,2} \right)$包含作用于该处的颗粒间接触力、孔隙液体和气体压力、孔隙液相与气相界面上表面张力,如图 2所示. 式(50)右端积分可展开和计算如下
| $$ \dfrac{1}{V}\int _{\varGamma _{\rm p} } t_i x_j {\rm{d}}\varGamma _{\rm p} = \dfrac{1}{V} \sum _{k = 1}^m f_i^k x_j^k - \\ \qquad \dfrac{1}{V} \sum _{k = 1}^m \int _{\varGamma _{\rm p}^{{\rm l}k} } \left( {p_{\rm l}^k n_i^{{\rm l}k} } \right) \left( {rn_j^{{\rm l}k} } \right){\rm{d}}\varGamma _{\rm p}^{{\rm l}k} -\\ \qquad \dfrac{1}{V} \sum _{k = 1}^m \int _{\varGamma _{\rm p}^{{\rm g}k} } \left( {p_{\rm g}^k n_i^{{\rm g}k} } \right) \left( {rn_j^{{\rm g}k} } \right){\rm{d}}\varGamma _{\rm p}^{{\rm g}k} +\\ \qquad\dfrac{r}{V} \sum _{k = 1}^m \left( {T_i^{k1} n_j^{{\rm l}k1} + T_i^{k2} n_j^{{\rm l}k2} } \right) $$ | (51) |
|
图 2 非饱和多孔介质二维 Voronoi 胞元模型示意图 Fig.2 The two-dimensional Voronoi cell model for unsaturated granular material |
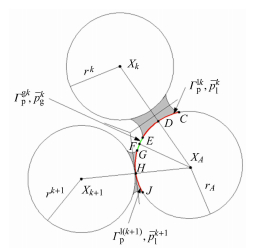
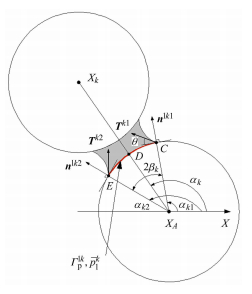
式中$f_i^k $是参考颗粒的第$k$个直接相邻颗粒在接触点$x_j^k $处作用于参考颗粒的颗粒间接触力,$\varGamma _{\rm p}^{{\rm l}k} $是$\varGamma _{\rm p} $上被参考颗粒与第$k$个直接相邻颗粒间液桥湿化的表面部分,$\varGamma _{\rm p}^{{\rm g}k} $是把$\varGamma _{\rm p}$上两个相邻湿化表面部分$\varGamma _{\rm p}^{{\rm l}k} $和$\varGamma _{\rm p}^{{\rm l}\left( {k + 1} \right)} $分隔开的干表面部分,如图 3所示; $n_i^{{\rm l}k}$ 是沿连接参考颗粒和第$k$个直接相邻颗粒形心分支向量的$\varGamma _{\rm p}^{{\rm l}k} $面上外法向单位向量,$n_i^{{\rm g}k} $是$\varGamma _{\rm p}^{{\rm g}k} $中点处外法向单位向量. ${\pmb T }^{k1}$与${\pmb T}^{k2}$是第$k$个液桥半月板液面与颗粒表面$ \varGamma_{\rm p}^{{\rm l}k} $两交汇处作用于颗粒的孔隙液相与气相间表面张力向量;$n_j^{{\rm l}k1} $,$n_j^{{\rm l}k2} $是该两交汇处颗粒表面$ \varGamma_{\rm p}^{{\rm l}k}$的外法向单位向量,如图 4所示.
|
图 3 两个相邻湿化表面部分 Fig.3 Two neighboring wetted boundary segments on the surface of the reference particle |
|
图 4 一个双联液桥处的表面张力 Fig.4 Interfacial tension force vectors at a binary bond liquid bridge |
将式(47)和式(48),式(50)和式(51)代入式(46)得到
| $\bar\sigma_{ji}=\dfrac 1V \sum _{k = 1}^m f^k_i x^k_j -\dfrac r V \sum _{k = 1}^m \int_{\varGamma _{\rm p}^{{\rm l}k} } p^k_{\rm l} n^{{\rm l}k}_i n^{{\rm l}k}_j {\rm{d}} \varGamma^{{\rm l}k}_{\rm p}-\\ \qquad \dfrac{r}{V} \sum _{k = 1}^m \int_{\varGamma _{\rm p}^{{\rm g}k} } p_{\rm g}^k n_i^{{\rm g}k} n_j^{{\rm g}k} {\rm{d}}\varGamma _{\rm p}^{{\rm g}k} - \phi S_{\rm l} \bar{p}_{\rm l} \delta_{ji}-\\ \qquad \phi \left( {1 - S_{\rm l} } \right)\bar{p}_{\rm g}\delta_{ji}+\dfrac rV \sum _{k = 1}^m (T^{k1}_i n^{{\rm l}k1}_j+T^{k2}_i n^{{\rm l}k2}_j) $ | (52) |
定义有效Cauchy 应力
| $$ \bar{\sigma }'_{ji}=\dfrac 1V \sum _{k = 1}^m f^k_i x^k_j $$ | (53) |
它描述了沿接触网络传递的颗粒间接触力. 式(52)表明有效Cauchy应力是总应力$\bar{\sigma }_{ji}$中代表在宏观尺度 控制等效连续体变形和破坏的固体骨架应力的那一部分. 假定$p_{\rm l}^k ,p_{\rm g}^k $分别为沿颗粒表面$\varGamma _{\rm p}^{{\rm l}k} $和$\varGamma _{\rm p}^{{\rm g}k} $均匀分布的孔隙液体和气体压力,以$ \gamma $表示表面张力,将式(53)代入式(52)得到
| $$ \bar\sigma'_{ji}=\bar\sigma_{ji}+\phi \bar p_{\rm g}\delta_{ji}-\phi S_{\rm l} (\bar p_{\rm g}-\bar p_{\rm l})\delta_{ji}+\\ \qquad \dfrac{ 1 - \phi }{\pi } \sum _{k = 1}^m \left( {p_{\rm l}^k F_{ji}^{{\rm l}k} + p_{\rm g}^k F_{ji}^{{\rm g}k} - \dfrac{\gamma }{r}F_{ji}^{\gamma k} } \right) $$ | (54) |
式中,$F_{ji}^{{\rm l}k}$,$F_{ji}^{{\rm g}k}$,$F_{ji}^{{\rm r}k}$分别代表${\pmb F}^{{\rm l}k}$,${\pmb F}^{{\rm g}k}$,${\pmb F}^{{\rm r}k}$的分量,其中$ F_{ji}^{{\rm l}k} = \int_{\alpha _{k1} }^{\alpha _{k2} } n_i^{{\rm l}k} n_j^{{\rm l}k} {\rm{d}}\alpha _k $, $F_{ji}^{{\rm g}k} = \int _{\alpha _{k1}^{\rm g} }^{\alpha _{k2}^{\rm g} } n_i^{{\rm g}k} n_j^{{\rm g}k} {\rm{d}}\alpha _k^{\rm g} $
| ${\pmb F}^{{\rm l}k}= \dfrac{1}{2}\left[\!\!\begin{array}{cc} {2\beta _k + \sin 2\beta _k \cos 2\alpha _k } & {\sin 2\beta _k \sin 2\alpha _k } \\ {\sin 2\beta _k \sin 2\alpha _k } & {2\beta _k - \sin 2\beta _k \cos 2\alpha _k } \end{array}\!\! \right]$ | (55) |
| ${\pmb F}^{{\rm g}k}= \dfrac{1}{2} \left[\!\!\begin{array}{cc} {2\beta _k^{\rm g} + \sin 2\beta _k^{\rm g} \cos 2\alpha _k^{\rm g} } & {\sin 2\beta _k^{\rm g} \sin 2\alpha _k^{\rm g} } \\ {\sin 2\beta _k^{\rm g} \sin 2\alpha _k^{\rm g} } & {2\beta _k^{\rm g} - \sin 2\beta _k^{\rm g} \cos 2\alpha _k^{\rm g}} \end{array}\!\! \right] $ | (56) |
表征了因第$k$个液桥所引起的毛细压力(基质吸力)各向异性.
式(55)中$\alpha _{k1} $,$\alpha _{k2} $如图 4所示; $\alpha _k $是$x$坐标轴和连接参考颗粒与其第$k$个直接相邻颗粒形心的分支向量间的夹角,$\beta _k $是参考颗粒第$k$个液桥的半填充角,它们能由描述第$k$个液桥的介观结构的$\alpha _{k1},\alpha _{k2} $确定
| $$ \alpha _k = \dfrac{\alpha _{k2} + \alpha _{k1} }{2} ,\ \ \beta _k = \dfrac{\alpha _{k2} - \alpha _{k1} }{2} $$ | (57) |
式(56)中$\alpha _k^{\rm g} $和$\beta _k^{\rm g} $如图 5所示,它们能由描述两个相邻液桥介观结构的数据表示,即
| $\left. \begin{array}{l} \alpha _k^{\rm{g}} = \frac{{\alpha _{k2}^{\rm{g}} + \alpha _{k1}^{\rm{g}}}}{2} = \frac{{{\alpha _{\left( {k + 1} \right)1}} + {\alpha _{k2}}}}{2}\\ \beta _k^{\rm{g}} = \frac{{\alpha _{k2}^{\rm{g}} - \alpha _{k1}^{\rm{g}}}}{2} = \frac{{{\alpha _{\left( {k + 1} \right)1}} - {\alpha _{k2}}}}{2} \end{array} \right\}$ | (58) |
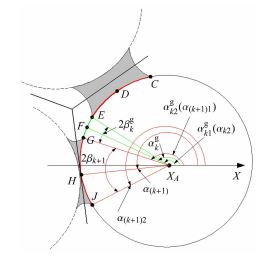
|
图 5 围绕参考颗粒两相邻液桥的取向和构形 Fig.5 Detailed expressions for orientations and configurations of two neighboring liquid bridges around the reference particles |
如图 4所示,式(51)中${\pmb T}^{k1}$和${\pmb T}^{k2}$能表示为
| $$ \left.\!\! {\pmb T}^{k1} = \gamma \left\{\!\!\begin{array}{l} {\cos \left( {\alpha _{k1} + \dfrac{\pi }{2} - \theta } \right)} \\ {\sin \left( {\alpha _{k1} + \dfrac{\pi }{2} - \theta } \right)} \\ \end{array} \!\! \right\} \\ {\pmb T}^{k2} = \gamma \left\{ \!\!\begin{array}{l} {\cos \left( {\alpha _{k2} - \dfrac{\pi }{2} + \theta } \right)} \\ {\sin \left( {\alpha _{k2} - \dfrac{\pi }{2} + \theta } \right)} \end{array} \!\! \right\} \!\!\right\} $$ | (59) |
式中$\theta $表示接触角. 利用式(59),能给出式(54)中张量${\pmb F}^{\gamma k} $
| $$ {\pmb F}^{\gamma k} = \\ \left[\!\!\begin{array}{cc} {\sin \theta + \sin \left( {\theta + 2\beta _k } \right)\cos 2\alpha _k } \!\!\!&\!\!\! {\sin \left( { {\theta } + 2\beta _k } \right)\sin 2\alpha _k } \\ {\sin \left( {\theta + 2\beta _k } \right)\sin 2\alpha _k } \!\!\!&\!\!\! {\sin \theta } - \sin \left( {\theta + 2\beta _k } \right)\cos 2\alpha _k \end{array}\!\! \right] $$ | (60) |
它表示由第$k$个液桥引起的表面张力的各向异性.
注意到式(42),式(54)提供了基于介观水力-力学 的模型有效应力$\bar{\sigma }'_{ji}$与总Cauchy应力$\bar{\sigma }_{ji}$和有效压力张量之间的关系,即可定义有效压力张量如下
| $$ \bar{P}_{ji}=\phi \bar p_{\rm g} \delta_{ji}-\phi S_{\rm l}(\bar p_{\rm g}-\bar p_{\rm l} )\delta_{ji}+\\ \qquad \dfrac{ 1 - \phi }{\pi } \sum _{k = 1}^m \left( {p_{\rm l}^k F_{ji}^{{\rm l}k} + p_{\rm g}^k F_{ji}^{{\rm g}k} - \dfrac{\gamma }{r}F_{ji}^{\gamma k} } \right) $$ | (61) |
对比在非饱和多孔连续体模型中所定义的有效Cauchy应力张量的剖分,基于介观水力-力学模型的有效Cauchy应力张量(54)也能类似地剖分为净应力张量$\bar{\sigma }_{ji}+\bar p_{\rm g} \delta_{ji}$和基质毛细压力张量$\bar{Q}_{ji}$,即
| $$ \bar{\sigma }'_{ji}=\bar{\sigma }_{ji}+\bar P_{ji}=(\bar{\sigma }_{ji}+\bar p_{\rm g} \delta_{ji})+\bar Q_{ji} $$ | (62) |
式中
| $$ \bar{Q}_{ji}=-(1-\phi) \bar p_{\rm g} \delta_{ji}-\phi S_{\rm l} ( \bar p_{\rm g}-\bar p_{\rm l} )\delta_{ji}+\\ \qquad \dfrac{ 1 - \phi }{\pi } \sum_{k = 1}^m \left( {p_{\rm l}^k F_{ji}^{{\rm l}k} + p_{\rm g}^k F_{ji}^{{\rm g}k} - \dfrac{\gamma }{r}F_{ji}^{\gamma k} } \right) $$ | (63) |
上式表明,与多孔连续体模型中定义的各向同性基质毛细压力张量$Q_{ji} = - \chi \left( {p_{\rm g} - p_{\rm l} } \right)\delta _{ji} $不同,基于介观水力-力学模型的基质毛细压力张量为各向异性.
引入表示施加于$\varGamma _{\rm p}^{{\rm l}k} \ \left( {k = 1,2,\cdots,m} \right)$的虚拟孔隙气压分布的系列积分$ - \dfrac{r}{V} \sum _{k = 1}^m \int _{\varGamma _{\rm p}^{{\rm l}k} } p_{\rm g}^k n_i^{{\rm l}k} n_j^{{\rm l}k} {\rm{d}}\varGamma _{\rm p}^{{\rm l}k} $,式(52)改写为
| $\bar{\sigma }_{ji}=\dfrac 1V \sum _{k = 1}^m f^k_i x^k_j +\dfrac r V \sum _{k = 1}^m \int_{\varGamma _{\rm p}^{{\rm l}k} } (p^k_{\rm g}-p^k_{\rm l}) n^{{\rm l}k}_i n^{{\rm l}k}_j {\rm{d}} \varGamma^{{\rm l}k}_{\rm p}-\\ \qquad \dfrac{r}{V}\int_{\varGamma _{\rm p} } p_{\rm g} n_i n_j {\rm{d}}\varGamma _{\rm p} + \dfrac{r}{V}\sum_{k = 1}^m \left( {T_i^{k1} n_j^{{\rm l}k1} + T_i^{k2} n_j^{{\rm l}k2} } \right) -\\ \qquad \phi S_{\rm l} \bar{p}_{\rm l} \delta_{ji}-\phi (1-S_{\rm l})\bar p_{\rm g} \delta_{ji} $ | (64) |
为计算式(64)中积分$\dfrac{r}{V}\int_{\varGamma _{\rm p} } p_{\rm g} n_i n_j {\rm{d}}\varGamma _{\rm p} $和 $\sum_{k = 1}^m \int_{\varGamma _{\rm p}^{{\rm l}k} } p_{\rm g}^k n_i^{{\rm l}k} n_j^{{\rm l}k} {\rm{d}}\varGamma _{\rm p}^{{\rm l}k}$,假定沿颗粒表面$\varGamma _{\rm p} $的孔隙气体压力按下式近似地分布
| $$ p_{\rm g} = \bar{p}_{\rm g}+\dfrac{\partial \bar p_{\rm g}}{\partial \alpha} r=\bar p_{\rm g}+ \Big ( \dfrac{\partial \bar p_{\rm g}}{\partial x} \cos \alpha+\dfrac{\partial \bar p_{\rm g}}{\partial y}\sin \alpha\Big ) r $$ | (65) |
式中,$\dfrac{\partial \bar{p}_{\rm g}}{\partial x}$,$\dfrac{\partial \bar{p}_{\rm g}}{\partial y}$是定义于参考颗粒形心处$\bar{p}_{\rm g}$的梯度,$\alpha $表示${\rm{d}}\varGamma _{\rm p}$的单位外法线向量方向. 利用式(65),式(64)中积分$ - \dfrac{r}{V}\int_{\varGamma _{\rm p} } p_{\rm g} n_i n_j {\rm{d}}\varGamma _{\rm p} $可表示为
| $$ - \dfrac{r}{V}\int_{\varGamma _{\rm p} } p_{\rm g} n_i n_j {\rm{d}}\varGamma _{\rm p} = - \left( {1 - \phi } \right) \bar{p}_{\rm g} \delta_{ji} $$ | (66) |
将式(53),(55),(60)和(66) 代入式(64)得到
| $$ \bar{\sigma }'_{ji}=\bar{\sigma }_{ji}+\bar{p}_{\rm g} \delta_{ji}-\phi S_{\rm l} (\bar p_{\rm g}-\bar p_{\rm l})\delta_{ji}-\\ \qquad \dfrac{ 1 - \phi }{\pi }\sum_{k = 1}^m \left[{\left( {p_{\rm g}^k - p_{\rm l}^k } \right)F_{ji}^{{\rm l}k} + \dfrac{\gamma }{r}F_{ji}^{\gamma k} } \right] $$ | (67) |
基于介观水力-力学模型的有效压力张量和基质毛细压力张量可分别定义为
| $\bar p_{ji}=\bar p_{\rm g} \delta_{ji}-\phi S_{\rm l} (\bar p_{\rm g}-\bar p_{\rm l} ) \delta_{ji}-\sigma_{ji}^{cap}$ | (68) |
| $\bar Q_{ji}=-\phi S_{\rm l} (\bar p_{\rm g}-\bar p_{\rm l} ) \delta_{ji}- \sigma_{ji}^{cap} $ | (69) |
式中定义了组构张量
| $$ \sigma _{ji}^{\rm cap} = \dfrac{ 1 - \phi }{\pi } \sum_{k = 1}^m \left[{\left( {p_{\rm g}^k - p_{\rm l}^k } \right)F_{ji}^{{\rm l}k} + \dfrac{\gamma }{r}F_{ji}^{\gamma k} } \right] $$ | (70) |
式(68) 和 式(69)表明孔隙液体对等效连续体水力-力学行为的影响由气-液相界面两侧气 液相压力差和流-固-气三相交汇处液体表面张力引起的毛细力分布的各向同性与各向异性部分. 织构张量与孔隙液桥分布相关,表征了毛细液压效应的各向异性部分. 其各向异性依赖于非饱和等效多孔连续体Voronoi胞元的介观结构,即围绕Voronoi胞元中参考颗粒的周边颗粒和液桥分布.
为与如式(40)和 式 (41)所示在非饱和多孔连续体理论中唯象地假定的有效压力张量与基质毛细压力张量比较,考虑式(68) 和 式(69)所示$\bar{P}_{ji}$和$\bar{Q}_{ji}$的各向同性情况. 为此,假定在非饱和Voronoi胞元模型中参考颗粒的所有直接相邻颗粒具有相同的几何与物理性质,以及:(1) 围绕参考颗粒的液桥系统的介观结构对称;(2) 非饱和Voronoi胞元内孔隙流体压力均匀地分布,即$p_{\rm g}^k - p_{\rm l}^k = \bar p_{\rm g} - \bar p_{\rm l} $. 由式(68)和 式(69)可得到各向同性情况下基于介观水力-力学模型的有效压力张量与基质毛细压力张量
| $$ \bar p_{ji}=\bar p_{\rm g}\delta_{ji}-\phi S_{\rm l} (\bar p_{\rm g}-\bar p_{\rm l}) \delta_{ji}-\\ \qquad \dfrac{ 1 - \phi }{\pi }m\left[{\left(\bar p_{\rm g}-\bar p_{\rm l} \right) \beta+\dfrac \gamma r \sin \theta } \right] \delta_{ji} $$ | (71) |
| $$ \bar{Q}_{ji}=-\phi S_{\rm l} (\bar p_{\rm g}-\bar p_{\rm l}) \delta_{ji}-\\ \qquad \dfrac{ 1 - \phi }{\pi }m\left[{\left(\bar p_{\rm g}-\bar p_{\rm l} \right) \beta+\dfrac \gamma r \sin \theta } \right] \delta_{ji} $$ | (72) |
由双联模式液桥计算模型[32, 33],式(71)和 式(72)中表面张力可表示为
| $$ \gamma = \rho \left(\bar p_{\rm g}-\bar p_{\rm l} \right) = \dfrac{ r(1-\cos \beta)+d/2}{\cos (\theta+\beta)} (\bar p_{\rm g}-\bar p_{\rm l}) $$ | (73) |
式中$d$是参考颗粒与其一直接相邻颗粒间的间隙(正)或重迭(负),$\rho $是二维液桥的曲率半径. 将式(73)代式(71)得到
| $$ \bar P_{ji}=\bar p \delta_{ji} $$ | (74) |
式中定义了各向同性情况下基于介观-水力-力学模型的有效压力$\bar{p} $及Bishop参数$\bar{\chi } $
| $$ \bar p=\bar \chi \bar p_{\rm l}+(1-\bar \chi) \bar p_{\rm g} $$ | (75) |
| $$ \bar{\chi }=\phi S_{\rm l}+ \dfrac{\left( {1 - \phi } \right)}{\pi }m \cdot $2mm] \qquad \left[{\beta + \sin \theta \dfrac{\left( {1 - \cos \beta } \right) + d / \left( {2r} \right)}{\cos \left( {\theta + \beta } \right)}} \right] $$ | (76) |
值得注意的是,如式(75)所示,在退化的各向同性情况下基于介观水力-力学模型的有效压力与非饱和多孔连续体理论中 唯象地假定的有效压力定义具有相同的形式. 然而,式(75)与式(76)给出的Bishop参数是基于由离散颗粒系统到多孔连续体的介-宏观均匀化过程导出,而非唯象地假定.
若假定接触角$\theta = 0$,表面张力$\gamma $对有效压力张量$\bar{P}_{ji}$的影响将消失. Bishop参数将退化为
| $$ \bar{\chi }=\phi S_{\rm l}+\dfrac{ 1-\phi }{\pi} m \beta $$ | (77) |
如式(76)和式(77)所示,基于介观水力-力学模型所导出的Bishop参数不仅与在非饱和多孔连续体中定义的孔隙度$\phi $和饱和度$S_{\rm l} $有关,且与描述非饱和Voronoi胞元介观结构的参数$m,\beta ,d$等有关;虽然式(77)没有显式地表示与$d$有关,但表征两个直接相邻颗粒间的液桥构形半填充角$\beta $依赖于$d$.
给定颗粒体积,孔隙液体饱和度可由定义于Voronoi胞元的孔隙度、液桥数和单个液桥体积计算
| $$ S_{\rm l} = \dfrac{V_{\rm l} }{V_{\rm v} } = \dfrac{V_{\rm l} \left( {1 - \phi } \right)}{\phi V_{\rm p} } = \dfrac{ 1 - \phi }{\phi \pi r^2}mV_{\rm b / 2} $$ | (78) |
式中表示位于Voronoi胞元内的单个双联液桥体积一半的$V_{\rm b / 2} $可计算如下[33]
| $$ V_{\rm b / 2} = - r^2\dfrac{\left( {1 - \cos \beta + \dfrac{d}{2r}} \right)^2}{\cos^2\left( {\beta + \theta } \right)}\left[{\dfrac{\pi }{2} - \left( {\beta + \theta } \right)} \right] + \\ \qquad r^2\left[{2\left( {1 - \cos \beta + \dfrac{d}{2r}} \right)\sin \beta - \left( {\beta - \dfrac{1}{2}\sin 2\beta } \right)} \right] + \\ \qquad r^2\dfrac{\left( {1 - \cos \beta + \dfrac{d}{2r}} \right)^2}{\cos^2\left( {\beta + \theta } \right)}\dfrac{1}{2}\sin 2\left( {\beta + \theta } \right) $$ | (79) |
式中参考颗粒与其一直接相邻颗粒间的间隙(或重迭)量$d$与Voronoi胞元内颗粒体积、孔隙度、介观结构参数$m$之间关系为
| $$ V = \dfrac{V_{\rm p} }{1 - \phi } = \dfrac{\pi r^2}{1 - \phi } = m\left( {r + \dfrac{d}{2}} \right)^2 {\rm tan}\dfrac{\pi }{m} $$ | (80) |
当颗粒体积和$m$给定,$d$可视为孔隙度的函数,即
| $$ d = 2r\left[{\left( {\dfrac{\pi }{1 - \phi }\dfrac{1}{m {\rm tan}\dfrac{\pi }{m}}} \right)^{1 / 2} - 1} \right] = d\left( \phi \right) $$ | (81) |
将式(79)代入式(78)和利用式(81)可得到
| $ 2\left( {1 - \cos \beta + \dfrac{d}{2r}} \right)\sin \beta - \left( {\beta - \dfrac{1}{2}\sin 2\beta } \right)-\\ \qquad \dfrac{\left( {1 - \cos \beta + \dfrac{d}{2r}} \right)^2}{\cos^2\left( {\beta + \theta } \right)}\left[ {\dfrac{\pi }{2} - \left( {\beta + \theta } \right) - \dfrac{1}{2}\sin 2\left( {\beta + \theta } \right)} \right] =\\ \qquad \dfrac{S_{\rm l} \phi \pi }{\left( {1 - \phi } \right)m} $ | (82) |
式(81)和式(82)表明,当材料参数$r,\theta $和介观结构参数$m$给定时,半填充角$\beta $将是饱和度$S_{\rm l}$和孔隙度$\phi $的函数,因而可令
| $ \psi = \dfrac{m}{\pi }\Bigg (\beta \left( {S_{\rm l} ,\phi ,r,\theta ,m} \right) +\\ \qquad \sin \theta \dfrac{1 - \cos \beta \left( {S_{\rm l} ,\phi ,r,\theta ,m} \right) + d\left( \phi \right) / \left( {2r} \right)}{\cos \left[{\beta \left( {S_{\rm l} ,\phi ,r,\theta ,m} \right) + \theta } \right]} \Bigg ) =\\ \qquad \psi _{ r,\theta ,m} \left( {S_{\rm l} ,\phi } \right) $ | (83) |
并可得到基于介观水力-力学模型的Bishop参数$\bar{\chi }$
| $$ \bar \chi=\phi S_{\rm l}+(1-\phi) \psi_{r,\theta,m}(S_{\rm l},\phi) $$ | (84) |
考虑饱和多孔介质中由孔隙液压引起的固体颗粒压缩体积变形,Zienkiewicz等[6, 12] 引入了饱和多孔介质的广义有效应力概念和相关联的Biot系数. 由饱和多孔介质的多孔连续体理论导出的Biot系数为一仅依赖于 多孔连续体体积模量与单个固体颗粒的材料体积模量之比的常数.
基于介-宏观均匀化过程和Voronoi胞元模型,本文工作表明,Biot系数应是一个变系数,不仅依赖于饱和多孔连 续体和单个固体颗粒的体积模量,同时还与两者的当前状态变量、即与饱和多孔连续体当前平均广义有效应力和静水压力作用下 单个颗粒的当前压缩体积应变有关. 一般情况下,按所建议的基于介观水力-力学模型计算的Biot系数将比按饱和多孔连续体模型所得Biot系数接近于1.
在非饱和多孔连续体理论中定义由不可混孔隙液-气相压力加权平均确定的孔隙液-气相混合体压力 为有效压力. 孔隙流体有效压力在非饱和多孔连续体有效应力上的效应假定为各向同性. 孔隙液-气相压力的权系数由依赖于介质饱和度的称为Bishop参数的标量表示,有效压力张量假定为对角线张量. 但将原有饱和多孔连续体中仅有单一饱和孔隙流体的有效应力概念推广到非饱和多孔连续体的论据不十分清楚. 在多孔连续体理论框架中所建议的各种不同的非饱和多孔介质有效应力定义存在争议.
本文基于介观水力-力学模型所导出的非饱和多孔介质孔隙流体有效压力张量表明,一般地它是表征围绕局部材料点液桥分布、液桥毛细力分布等介观结构和介观结构响应的各向异性张量变量. 有效压力的各向异性特征意味着孔隙液-气混合体不仅对非饱和多孔介质有效应力的静水应力分量、同时也对它的剪切应力分量有影响.
考虑退化的各向同性情况,基于介观水力-力学模型所导出的非饱和多孔介质孔隙流体有效压力张量的标量形式与在非饱和多孔连续体模型中唯象假定的有效压力标量形式相同. 关键区别在于Bishop参数. 本文中给出的Bishop参数是基于由离散颗粒系统到多孔连续体的介-宏观均匀化过程导出,而非唯象地假定. 所导出的Bishop参数不仅与在非饱和多孔连续体中定义的孔隙度$\phi$和饱和度$S_{\rm l}$有关,且与描述非饱和Voronoi胞元介观结构的参数$m,\beta,d$等有关. 而在非饱和多孔连续体理论中引入的Bishop参数为唯象地假定,同时它不能反映非饱和多孔介质介观结构和介观水力-力学响应对Bishop参数的影响.
颗粒材料实际形态较为复杂. 本文旨在从颗粒材料多尺度方法出发,提出基于颗粒材料介观结构和响应的饱和与非饱和多孔连续体的有效应力和广义有效应力表达式, 揭示其介观机理. 为了具体地应用于工程中一些具体的饱和与非饱和颗粒材料的水力-力学行为模拟,考虑颗粒形状的影响是必要的,将是下一步应要开展的工作.
| 1 | Terzaghi K von. The shearing resistance of saturated soils. Proc 1st ICSMFE, 1936, 1: 54-56 |
| 2 | Biot MA. General theory of three-dimensional consolidation. J Appl Phys, 1941, 12: 155-164 |
| 3 | Biot MA. Theory of propagation of elastic waves in a fluid saturated porous solid. J Acoust Soc Am, 1956, 28: 168-191 |
| 4 | Biot MA. Mechanics of deformation and acoustic propagation in porous media. J Appl Phys, 1962, 33: 1482-1498 |
| 5 | Biot MA. Generalized theory of acoustic propagation in porous media. J Acoust Soc of America, 1962, 34: 1254-1264 |
| 6 | Zienkiewicz OC, Shiomi T. Dynamic behavior of saturated porous media:the generalized Boit formulation and its numerical solution. Int J Numer Anal Meth Geomech, 1984, 8: 71-96 |
| 7 | Kytomaa H, Kataja M, Timonen J. On the e ect of pore pressure on the isotropic behavior of saturated porous media. J Appl Phys,1997, 24: 7148-7152 |
| 8 | Bishop AW. The principle of e ective stress. Teknisk Ukeblad, 1959,106(39): 859-863 |
| 9 | Bishop AW, Blight GE. Some aspects of e ective stress in saturated and partly saturated soils. G'eotechnique, 1963, 13(3): 177-197 |
| 10 | Skempton AW. E ective stress in soils, concrete and rock.//Proc. Conf. on Pore Pressure and Suction in Soils, Butterworth, 1960.4-16 |
| 11 | Li XK, Zienkiewicz OC. Multiphase flow in deforming porous media and finite element solutions. Comput. Struct., 1992, 45(2): 211-227 |
| 12 | Zienkiewicz OC, Chan AHC, Pastor M, et al. Computational Geomechanics with Special Reference to Earthquake Engineering. Chichester: Wiley, 1999 |
| 13 | 邵龙潭,郭晓霞. 有效应力新解. 北京: 中国水利水电出版社,2014 (Shao Longtan, Guo Xiaoxia. New Insight on the E ective Stress. Beijing: China Water & Power Press, 2014 (in Chinese)) |
| 14 | Gray WG, Schrefler BA. Thermodynamic approach to e ective stress in partially saturated porous media. Eur J Mech A: Solids,2001, 20(4): 521-538 |
| 15 | Gray WG, Miller TC. Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems. Switzerland: Springer, 2014 |
| 16 | Gray WG, Schrefler BA. Analysis of the solid phase stress tensor in multiphase porous media. Int J Numer Anal Meth Geomech, 2007,31(4): 541-581 |
| 17 | 陈正汉, 秦冰. 非饱和土的应力状态变量研究. 岩土力学, 2012,33(1): 1-11 (Chen Zhenghan, Qin Bing. Onstress state variables of unsaturated soils. Rock and Soil Mechanics, 2012, 33(1): 1-11 (in Chinese)) |
| 18 | 赵成刚, 蔡国庆. 非饱和土广义有效应力原理. 岩土力学, 2009,30(11): 3232-3236 (Zhao Chenggang, Cai Guoqing. Principle of generalized e ective stress for unsaturated soils. Rock and Soil Mechanics,2009, 30(11): 3232-3236 (in Chinese)) |
| 19 | 刘艳, 赵成刚, 蔡国庆等. 非饱和土力学理论的研究进展. 力学与 实践, 2015, 37(4): 457-465 (Liu Yan, Zhao Chenggang, Cai Guoqing, et al. Research progress of unsaturated soil mechanics. Mechanics in Engineering, 2015, 37(4): 457-465 (in chinese)) |
| 20 | Scholtes L, Hicher PY, Nicot F, et al. On the capillary stress tensor in wet granular materials. Int J Numer Anal Meth Geomech, 2009,33: 1289-1313 |
| 21 | Li XS. E ective stress in unsaturated soil: a microstructural analysis. G'eotechnique, 2003, 53: 273-277 |
| 22 | Hicher PY, Chang CS. A microstructural elastoplastic model for unsaturated granular materials. Int J Solids Struct, 2007, 44: 2304-2323 |
| 23 | Hicher PY, Chang CS. Elastic model for partially saturated granular materials. J Eng Mech, 2008, 134(6): 505-513 |
| 24 | Coussy O. Mechanics of Porous Continua. Chichester: Wiley, 1995 |
| 25 | Ehlers W, Ramm E, Diebels S, et al. From particle ensembles to Cosserat continua: homogenization of contact forces towards stresses and couple stresses. Int J Solids Struct, 2003, 40: 6681-6702 |
| 26 | Pasternak E, Muhlhaus HB. Generalised homogenisation procedures for granular materials. J Eng Math, 2005, 52: 199-229 |
| 27 | Chang CS, Kuhn MR. On virtual work and stress in granular media. Int J Solids Struct, 2005, 42: 3773-3793 |
| 28 | Li XK, Liu QP, Zhang JB. A micro-macro homogenization approach for discrete particle assembly-Cosserat continuum modeling of granular materials. Int J Solids Struct, 2010, 47: 291-303 |
| 29 | Alonso-Marroquin F. Static equations of the Cosserat continuum derived from intra-granular stresses. Granul Matter, 2011, 13: 189-196 |
| 30 | Li XK, Du YY, Duan QL. Micromechanically informed constitutive model and anisotropic damage characterization of Cosserat continuum for granular materials. Int J Damage Mech, 2013, 22(5): 643-682 |
| 31 | El Shamy U, Groger T. Micromechanical aspects of the shear strength of wet granular soils. Int J Numer Anal Meth Geomech,2008, 32: 1763-1790 |
| 32 | Souli'e F, Cherblanc F, El Youssoufi MS, et al. Influence of liquid bridges on the mechanical behaviour of polydisperse granular materials. Int J Numer Anal Meth Geomech, 2006, 30: 213-228 |
| 33 | 杜友耀,李锡夔. 二维液桥计算模型及湿颗粒材料离散元模拟. 计算力学学报, 2015, 32: 496-502 (Du Youyao, Li Xikui. 2D computational model of liquid bridge and DEM simulation of wet granular materials. Chinese Journal of Computational Mechanics, 2015,32: 496-502 (in Chinese)) |
 2016, Vol. 48
2016, Vol. 48