随着主动控制技术的发展,飞机设计理念已从被动走向主动,产生了如下跨越式发展:在飞机结构设计中,不再以增加结构重量为代价 来提高结构刚度,进而回避气动弹性问题;而是通过在机翼上布置多个控制面,通过主动控制系统驱动其联合偏转,提高机翼控制气流 的能力,进而主动调节结构气动弹性效应. 人们期望,这样的主动设计理念既可降低飞机结构重量,又能保证飞机结构具有良好的气动弹性性能.
20世纪90年代,美国实施的``主动气动弹性机翼(active aeroelastic wing,AAW)计划''首次验证了上述主动设计理念[1]. 该计划是由美国NASA、波音公司、空军研究实验室等联合发起的一个重大 项目,旨在验证上述先进的飞机设计理念. 该计划以图 1所示的F/A-18A战斗机为原型样机,在理论分析、数值仿真、风洞实验、原型机试飞等多个方面开展了系统 化研究,采用 主动控制技术驱动机翼的控制面,从而改变机翼的形态和表面气流分布,提高机翼控制气流能量的能力[2]. ``AAW计划''的风洞实验和试验机飞行测试结果表明,该技术可在一定程度上提高飞机颤振临界速度、减轻结构重量、减缓机动载荷.
在上述``AAW计划''中,颤振主动抑制(active flutter suppression,AFS)技术因其重要性和复杂性而备受关注. 颤振是飞机气动弹性力学中最重要、但常常难以准确预测的一种动态失稳现象,是结构惯性力、结构弹性力、结构阻尼力与空气动力共同作用下出现的自激振动. 当飞机结构发生颤振时,结构不断地从气流中汲取能量,导致结构振动急剧增加从而发生破坏. 为避免飞机发生颤振,人们早期主要通过增加结构刚度、调整惯性分布等方法来提高飞机发生颤振的临界速度,但这些方法不仅要显著增 加飞机结构重量,而且所能提升的飞行速度范围有限.
随着主动控制技术的发展,人们开始尝试颤振主动抑制技术. 该技术的主要特点是,由布置在机翼表面的传感器获取结构振动信号并反馈 至控制系统,根据控制系统的指令驱动控制面偏转,调节机翼表面的气流分布,从而抑制机翼颤振. 该技术的物理本质是:通过主动控制技术来提高机翼结构的等效刚度和等效阻尼.
气动弹性主动控制技术中另一重要的研究热点是突风载荷减缓(gust load alleviation,GLA)控制. 突风(gust)是一种大气运动现象,表现为风速在空间上和时间上的变化. 突风可认为是3种类型空气流动的叠加:平均风、波动风和紊流[4]. 平均风在小时级别时间尺度上的速度相对恒定,波动风是在几十分钟级别时间尺度上的规则振荡,而大气风的紊流分量则是不规则的,各向异 性的,在几秒钟或几分钟级别时间尺度上准随机变化. 对于长时间处于巡航飞行状态的飞机,难免遭遇严重程度不同的各种突风. 突风导致机翼根部承受很大的动态结构载荷增量,容易使机体产生疲劳破坏. 通常,侧向突风是引起垂尾破坏的重要载荷源,垂直突风则是引起机翼破坏的重要载荷源. 突风干扰还使飞行员难于操纵飞机,降低飞行品质. 此外突风干扰还引起飞行员和成员感到极不舒服,降低乘坐品质.
早期飞机设计中并未考虑突风引起的动态载荷,到20世纪30年代中期起人们才逐渐意识这一问题[5]. 1964年,美国的B-52 轰炸机因低空大气紊流(峰值速度为35 m/s)造成了飞机垂尾折断事故[6]. 该事故促进美、英等国开展了一系列与气动弹性响应控制有关的理论研究和试验工作. 人们发现,飞机结构在突风干扰下会产生附加的气动力和力矩,呈现典型的气动弹性现象,对飞行品质和结构安全产生不利影响. 因此,人们考虑在常规飞行控制系统中引入基于主动控制的GLA功能,即利用主动控制技术来调节结构气动弹性特性,减小突风引起 的结构附加气动力和力矩,从而达到减小机翼弯曲力矩,减轻结构疲劳等多种收益[7].
1 亚音速气动弹性分析与控制 1.1 含操纵面间隙的非线性气动弹性分析近年来,航空科技界日益关注计入非线性因素的气动弹性力学问题,尤其是气动弹性系统的极限环振荡(limit-cycle oscillation,LCO) 问题. 自从美国F-16A战机在带外挂载荷飞行中出现极限环振荡现象后[8],学术界对该问题进行了深入研究[9, 10, 11, 12, 13]. 诱发机翼产生极限环振荡的非线性因素可分为两类,即空气动力非线性和结构非线性. 在空气动力非线性中,最引人关注的是激波运动和流动分离引起的非线性,其次是大攻角飞行引起的非线性. 关于结构非线性问题,学者们则主要研究机翼大变形导致的几何非线性问题[14, 15, 16, 17],包括将大变形机翼简化为二维翼段 时等效非线性弹簧刚度[18, 19, 20]等因素对气动弹性系统的影响.
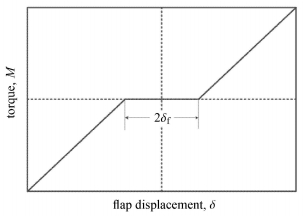
机翼控制面的铰链处普遍具有间隙(free-play). 例如,由于加工装配需求或长时间摩擦,驱动机翼控制面 偏转的作动系统会存在显著间隙. 图 2是由控制面铰链间隙引起的刚度非线性现象,此时控制面铰链力矩呈现分段线性特性:当控制面旋转角度很小(在间隙区间内)时,控 制面的扭转刚度几乎为零;当旋转角度大于间隙角时,扭转刚度回归到正常值.
从飞行力学角度看,机翼控制面主要用于调节飞机的飞行轨迹和飞行品质. 当机翼控制面铰链刚度呈现间隙非线性时,飞机的飞行品质 会受到显著影响. Gold和Karpel[22]研究了控制面铰链刚度的间隙非线性对飞机机动飞行的影响,发现控制面铰链刚度的间隙非线性会引起飞机结构 的极限环振荡. 从气动弹性力学角度看,非线性刚度对结构的气动弹性响应影响也是显而易见的. Conner等[23]以带后缘控制面的二元翼段为对象,采用理论和实验相结合的方式,研究了控制面铰链刚度间隙非线性作用下的结构非 线性气动弹性响应. Tang等[24]建立了含间隙非线性的三自由度气动弹性系统的理论模型,基于该模型分析了结构的极限环振荡现象. Gordon等[25]采用描述函数法研究了含间隙非线性的控制面颤振稳定性.
上述研究主要集中于二维翼段在低速、不可压缩流动下的间隙非线性问题. Dowell等[26]采用跨音速模型降阶方法研究了含间隙非线性 的二元翼段跨音速颤振和极限环. Jones等[27]采用特征系统实现算法(eigensystem realization algorithm, ERA)辨识跨音速来流下的二元翼段系统,并采用对数和双曲正切函数模拟间隙非线性. 其研究结果表明,所提出的方法可快速、精确地识别二元翼段的跨音速颤振边界和极限环.
在含间隙非线性的气动弹性系统颤振主动抑制方面,李道春和向锦武[28]研究了含间隙非线性的二元机翼颤振主动控制问题, 采用基于状态依赖的 Riccati方程设计了非线性颤振控制律. 数值仿真结果表明,所设计的控制律可有效实现对含间隙非线性的二元机翼颤振的抑制.
对于三维气动弹性系统,Shin等[29]的研究结果表明,作动器的间隙非线性对气动弹性系统的非线性行为也具有重要影响. 管 德和宗捷[30]针对操纵系统的结构非线性问题,提出了用于描述函数法的耦合模态和非耦合模态的综合计算模型,并基于该模 型研究了操纵间隙对全动水平尾翼振动的影响. 鉴于三维气动弹性系统的间隙非线性问题计算量巨大,Karpel和Raveh[31]提出采用虚拟质量(fictitious mass, FM)法来简化计算. 该方法通过在发生局部结构变化的有限元节点上添加惯性极大的虚拟质量来模拟局部激励,将局部结构变化这类非线性问题转化到 同一个模态空间内进行分析,为研究高维气动弹性系统的间隙非线性问题提供了一种高效分析方法[32, 33, 34, 35]. Bae等[36]采用虚拟质量法分别在频域和时域内对含控制面间隙的机翼进行了线性和非线性气动弹性分析. 其数值仿真结果表明,在低于颤振边界的较大流速范围内,机翼会出现极限环振荡和混沌运动;随着流速增大,极限环幅值还会发生跳跃.
上述研究主要分析间隙非线性所引起的非线性气动弹性现象,很少涉及间隙非线性对闭环气动伺服弹性系统的影响. Frampton和 Clark[37]以二元翼段为对象,采用理论和实验相结合的方式研究了间隙非线性对闭环气动伺服弹性系统的影响. 其数值仿真和风洞实验结果表明,在不考虑间隙非线性情况下所设计的线性LQG颤振主动抑制控制律,可有效抑制由间隙非线性引起的极限环 振荡. 然而,当三维气动伺服弹性系统中存在间隙非线性时,忽略间隙非线性所设计的AFS系统是否仍然有效?控制器的抑制效果是否会受到影响? 这些都是开放的问题. 此外,当前对AFS技术的研究重点是发展MIMO的低阶、鲁棒数字控制律,当多个控制面同时存在间隙时,对数字控制律的影响还尚待研究. 这类问题的研究难点在于,当多个控制面铰链分别或同时进入间隙区间时,机翼结构刚度会发生多种瞬间变化的组合,导致机翼结构的固有 模态特性也随之发生变化. 因此,基于模态空间的结构动力学响应分析方法已无法适用于含间隙非线性的结构动力学问题.
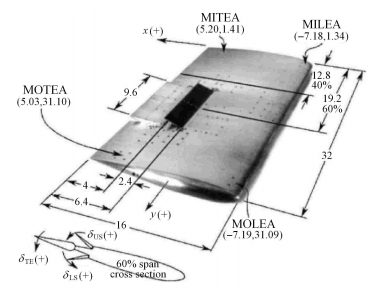
因此,作者提出一种基于虚拟质量单元的非线性气动伺服弹性分析方法[38],将含多个控制面间隙非线性的气动伺服弹 性(aeroservoelasticity, ASE)问题转化为基于模态空间的简单分段线性问题,进而可高效地分析多个间隙非线性对ASE系统的影响. 针对图 3中含前、后缘控制面间隙的机翼有限元模型,在前、后缘控制面的扭转弹簧单元上引入量值很大的虚拟惯性矩,并将对应 的扭转弹簧刚度置零,使机翼等价为固定界面子结构;通过计算固有模态可构造统一的静动态缩聚,大幅降低机翼结构的自由度, 提高非线性动力学计算效率.

|
图 3 控制面间隙非线性建模 Fig.3 Nonlinear modeling of free-play in control surfaces |
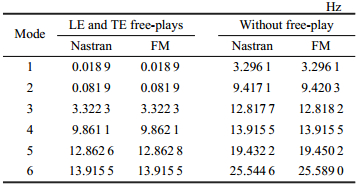
为了验证施加虚拟质量所计算的机翼低阶固有振型${\pmb \varPhi }_{\rm f} $可用于模态缩聚,选取前、后缘控制面在4种不同间隙角组合下的固有频率为考察目标,将基于虚拟质量法的计算结果与直接 MSC/Nastran计算结果作对比. 在基于振型${\pmb \varPhi }_{\rm f} $的模态缩聚下,4种不同间隙角组合的固有振动方程如下
| $\left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb M}_{\rm NM} {\pmb \varPhi }_{\rm f} } \right) \ddot {\pmb\xi }_{\rm f} + \left( { {\pmb \varPhi}_{\rm f}^{\rm T} {\pmb K}_{\rm NM} {\pmb \varPhi }_{\rm f} } \right){\pmb \xi }_{\rm f} = 0 $ | (1) |
| $\left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb M}_{\rm NM} {\pmb \varPhi }_{\rm f} } \right) \ddot {\pmb \xi }_{\rm f} + \left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb K}_{\rm L} {\pmb \varPhi }_{\rm f} } \right) {\pmb \xi }_{\rm f} = 0$ | (2) |
| $\left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb M}_{\rm NM} {\pmb \varPhi }_{\rm f} } \right) \ddot {\pmb \xi }_{\rm f} + \left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb K}_{\rm T} {\pmb \varPhi }_{\rm f} } \right) {\pmb \xi }_{\rm f} = 0 $ | (3) |
| $\left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb M}_{\rm NM } {\pmb \varPhi }_{\rm f} } \right) \ddot{\pmb \xi }_{\rm f} + \left( {{\pmb \varPhi}_{\rm f}^{\rm T} {\pmb K}_{\rm LT } {\pmb \varPhi }_{\rm f} } \right){ \pmb \xi }_{\rm f} = 0 $ | (4) |
其中${\pmb \xi }_{\rm f} $是模态缩聚后的广义坐标,${\pmb M }_{\rm NM } $和${\pmb K}_{\rm NM} $分别是无 间隙时的机翼质量矩阵和刚度矩阵,${\pmb K}_{\rm L} $是仅前缘控制面含间隙的机翼刚度矩阵,${\pmb K}_{\rm T} $是仅后缘控制面含间隙的机翼刚度矩阵,${\pmb K}_{\rm LT} $是前后缘均含间隙的机翼刚度矩阵. 表 1为前后缘均含间隙、无间隙两种情况下机翼固有频率计算结果的对比,表明基于虚拟质量的计算结果与MSC/Nastran计算结果很好吻合.
| 表 1 虚拟质量法与 MCS/Nastran 计算的固有频率对比 Table 1 Comparison between FM method and MSC/Nastran for computed natural frequencies |
基于虚拟质量的间隙非线性建模方法在分析含控制面间隙的气动弹性、气动伺服弹性等问题方面具有较大的应用空间. 例如,对 于含多个控制面间隙 的非线性ASE问题,其运动微分方程可表示为
| $ {\pmb M}\ddot {\pmb X}_{\rm s} + {\pmb D}\dot{\pmb X }_{\rm s} + {\pmb R }\left( {{\pmb X }_{\rm s} } \right) - {\pmb F }_{\rm a} = {\pmb F }_{\rm g} $ | (5) |
式中${\pmb R}\left( {{\pmb X}_{\rm s} } \right)$,${\pmb F}_{\rm a} $,${\pmb F}_{\rm g} $分别为非线性弹性恢复力矢量、非定常气动载荷矢量、外界突风载荷矢量. 对于间隙非线性,其非线性弹性恢复力可表示为
| $$ {\pmb R}\left( {{\pmb X}_{\rm s} } \right) = {\pmb K}{\pmb X}_{\rm s} + {\pmb P}\left\{ {f\left( {\theta _{\rm s} } \right)} \right\} $$ | (6) |
其中${\pmb K}$为无间隙非线性时的结构刚度矩阵,$f\left( {\theta _{\rm s} } \right)$为含间隙非线性的弹性恢复力,${\pmb P}\left( {6\times n,2} \right)$为选择矩阵,其中$n$为机翼模型的有限元结点数. 该矩阵在间隙非线性对应的有限元上取值为1,其他均取0. 式(6)中的 非线性弹性恢复力$f\left( {\theta _{\rm s} } \right)$可由下式计算
| $f\left( {{\theta _{\rm{s}}}} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{\theta _s}} \right| \le {\delta _f}\\ {K_\theta }\left( {{\theta _{\rm{s}}} - {\delta _{\rm{f}}}} \right),\left| {{\theta _s}} \right| > {\delta _f} \end{array} \right.$ | (7) |
根据前缘(leading edge,LE)控制面和后缘(trailing edge,TE)控制面间隙的不同组合以及式(5) $\sim$式(7),含前、后缘间隙的机翼非线性气动弹性系统可用9个分段线性方程来 描述. 为了简明起见,此处仅给出前缘、后缘控制面相对铰链线的扭转变形$\theta_{{\rm s}({\rm LE})} $和$\theta _{{\rm s}({\rm TE})} $分别满足$\theta _{{\rm s}({\rm LE})} < - \delta _{{\rm f}\left( {{\rm LE}} \right)} $和$\theta _{{\rm s}({\rm TE})} \in [- \delta _{{\rm f}\left( {{\rm TE}} \right)}$,$\delta _{{\rm f(TE)}} ]$时的线性子系统方程
| $\begin{array}{l} M{\mathop X\limits^{..} _{\rm{s}}} + D{\mathop X\limits^. _{\rm{s}}} + \left( {K + P\left[{\begin{array}{*{20}{c}} {{K_{{\rm{LE}}}}}&0\\ 0&0 \end{array}} \right]{P^{\rm{T}}}} \right){X_{\rm{s}}} - {F_{\rm{a}}} = \\ \qquad {F_{\rm{g}}} - \left( {P\left[{\begin{array}{*{20}{c}} {{K_{{\rm{LE}}}}}&0\\ 0&0 \end{array}} \right]{P^{\rm{T}}}} \right)\left\{ {{\delta _{{\rm{f}}\left( {{\rm{LE}}} \right)}}} \right\} \end{array}$ | (8) |
借助于施加虚拟质量计算的固有振型${\pmb \varPhi}_{\rm f} $和对应的模态坐标${\pmb \xi }_{\rm f} $,可将式(8)转化为模态空间中的微分方程
| $ {\pmb M}_{{\rm HH}} \ddot{\pmb \xi }_{\rm f} + {\pmb C }_{{\rm HH}} \dot{\pmb \xi }_{\rm f} + {\pmb K }_{{\rm HHT}} {\pmb \xi }_{\rm f} - q_\infty \left[{ {\pmb Q }_{{\rm HH}} {\pmb Q }_{{\rm HC}} } \right]\left\{ \begin{array}{c} {\pmb \xi }_{\rm f} \\ \delta _{{\rm c}\left( {{\rm LE}} \right)} \\ 0 \end{array} \right\} =\\ \qquad - \dfrac{q_\infty }{V_\infty }{\pmb Q }_{{\rm HG}} \left( {ik_{\rm r} } \right)w_{\rm G} \left( {ik_{\rm r} } \right) - {\pmb \varPhi }_{\rm f}^{\rm T} \left[{{\pmb K}_{{\rm NM}} - {\pmb K }_{\rm L} } \right]\left\{ {\delta _{{\rm f}\left( {{\rm LE}} \right)} } \right\}$ | (9) |
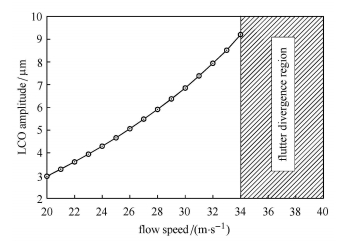
式中${\pmb Q}_{{\rm HH}} $,${\pmb Q}_{{\rm HC}} $和${\pmb Q}_{{\rm HG}} $分别为机翼模态、控制面模态和突风模态对应的广义空气动力矩阵,$\delta _{\rm c\left( {{\rm LE}} \right)} $和$k_{\rm r} $分别为前缘控制面偏转指令和减缩频率. 基于式(9)表示的非线性气动弹性数学模型的 主要特点是:将复杂的含多间隙非线性的气动弹性问题简化为多个分段线性子系统,且每个子系统采用相同的模态坐标来表示,可避免在动响应求解过程中重复求解固有模态及对应的广义空气动力矩阵. 图 4所示为含前、后缘间隙的机翼模型LCO幅值随流速变化情况. 图示结果表明:在来流速度达到线性颤振点之前,机翼的振动幅值随流速增加而增大;当流速增加至颤振临界速度34 m/s时,机翼发生线性颤振.
|
图 4 开环状态下振幅随流速增加变化情况 Fig.4 Open-loop vibratoin amplitudes with an increase of flow speed |
当采用上述建模方法分析非线性ASE问题时,控制面偏转指令$\delta _{{\rm c}\left( {{\rm LE}} \right)} $、实际偏转角度$\delta _{{\rm a}\left( {{\rm LE}} \right)} $和控制面相对铰链线扭转变形$\theta _{{\rm s}\left( {{\rm LE}} \right)} $之间的关系如下
| $$ \delta _{{\rm LE}} \left( t \right) = \delta _{\rm a\left( {{\rm LE}} \right)} \left( t \right) - \delta _{\rm c\left( {{\rm LE}} \right)} \left( t \right) $$ | (10) |
式中$\delta _{{\rm a}\left( {{\rm LE}} \right)} $为前缘控制面实际偏转角度,其计算公式如下
| $$ \left\{ \begin{array}{c} {\delta _{{\rm a}\left( {{\rm LE}} \right)} \left( t \right)} $2mm] {\delta _{{\rm a}\left( {{\rm TE}} \right)} \left( t \right)} \end{array} \right\} = {\pmb P }^{\rm T}{\pmb \varPhi}_{\rm f} {\pmb \xi }_{\rm f} \left( t \right) $$ | (11) |
图 5是流速为36 m/s (高于开环颤振临界速度)时对机翼施加多输入/多输出颤振控制律后的闭环气动伺服弹性响应. 图 示结果表明,虽然MIMO控制律可抑制机翼的颤振,但闭环系统出现了极限环振荡现象.
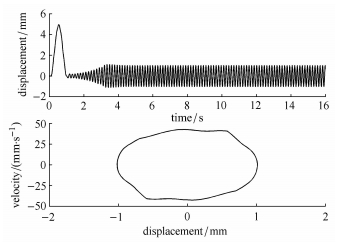
|
图 5 多输入/多输出控制律作用下的闭环 ASE 响应 Fig.5 Closed-loop ASE response under MIMO control |
在颤振主动控制系统中,其控制回路不可避免地存在多种时滞因素. 例如,受控系统响应信号的A/D转换、控制器的运算时间、控制信号的D/A转换、噪声滤波等都会在控制回路中引入时滞[39].
早期的颤振主动抑制研究未涉及反馈时滞对受控气动弹性系统稳定性的影响[40- 43],有关研究集中在近十年中. 例如,Librescu等[44]研究了时滞反馈控制下二维翼段的气动弹性力学行为,讨论了时变外激励作用下的亚临界气动弹性响应问题以及时滞反馈控制下的颤振稳定性问题. Marzocca等[45]研究了时滞因素对线性和非线性控制器作用下的二维气动弹性系统稳定性的影响. 又如,Zhao[46]研究了速度反馈控制中的时滞对二维气动弹性受控系统稳定性的影响. 研究结果表明,单输入时滞会显著降低闭环系统的颤振临界速度. 在此基础之上,Zhao[47]研究了双测量通道中的时滞对气动弹性系统闭环稳定性的影响. 数值仿真结果表明,当采用俯仰角作为反馈信号时,控制回路中的短时滞有助于提高闭环系统的稳定性.
时滞因素对受控气动弹性系统稳定性的影响被揭示之后,人们认识到主动利用时滞效应有望改善闭环系统的稳定性. 例如,Ramesh和Narayanan[48]研究了具有扭转刚度非线性的二维气动弹性系统的混沌现象,设计了时滞状态反馈控制律抑制混沌运动. Yuan等[49]针对二维高超音速翼段设计了Pyragas型的时滞反馈控制器,分析了受控系统的非线性气动弹性行为.
尽管对二维气动弹性系统的时滞问题研究取得不少进展,但对具有工程意义的三维气动弹性系统的时滞问题研究几乎是空白. 无论是研究时滞因素对高维气动弹性系统稳定性影响,还是设计具有反馈时滞的AFS控制系统,均未见有研究进展.
可喜的是,近年来高维线性系统的时滞反馈控制设计取得显著进展. 例如,作者[50]提出一种新的时滞反馈最优控制方法. 该方法将含输入时滞的受控系统离散化,通过一种状态变换将时滞受控系统转化为无时滞离散状态方程,进而运用最优控制理论设计最优时滞反馈控制. 作者将该方法推广到高维状态空间中含反馈时滞的颤振主动控制问题
| $ \dot {\pmb x }(t) = {\pmb A\pmb x }(t) + {\pmb B\pmb u }(t - \tau ) + {\pmb G }w(t) $ | (12) |
| $ {\pmb y }(t)={\pmb C\pmb x }(t)+{\pmb v }(t) $ | (13) |
式中$\tau $为输入时滞. 以小展弦比机翼为例,若选取机翼的前7阶固有模态进行动力学建模,则式(12)和式(13)中的状态变量维数为$ {\pmb x }(t) \in \Re^{24}$. 针对该高维气动弹性系统,可通过引入离散状态变换,将其转化为无时滞的状态方程,进而采用最优控制或鲁棒控制理论设计反馈控制,其主要过程如下:
首先给定系统的采样间隔为$T_{\rm s}$,将反馈回路的时滞表示为
| $$ \tau = \alpha T_{\rm s} - \beta $$ | (14) |
式中$\alpha \in \mathbb{N}^ + $且$0 \leqslant \beta < T_{\rm s} $. 采用零阶保持器进行采样,可将式(12)转化为如下形式的离散化状态方程
| $$ {\pmb x }(k + 1) = {\pmb A }_d {\pmb x }(k) + \left[ {\pmb B }_{d_1 } \ \ {\pmb B }_{d_2 } \right]\left[\begin{array}{c} {\pmb u }(k - \alpha + 1) \\ {\pmb u }(k - \alpha ) \end{array} \right] + {\pmb w }_d (k) $$ | (15) |
式中
| $$ \left. \begin{array}{l} {\pmb A }_d = \exp [{\pmb A }T_{\rm s}] \\ {\pmb B }_{d_1 } = \left( {\int_0^\beta {\exp [{\pmb A }\eta ]d \eta } } \right){\pmb B } \\ {\pmb B }_{d_2 } = \left( {\int_\beta ^{T_{\rm s} } {\exp [{\pmb A }\eta ]d \eta } } \right){\pmb B } \\ {\pmb w }_d (k) = \left( {\int_0^{T_{\rm s} } {\exp \{{\pmb A }[(k + 1)T_{\rm s} - \xi]\}d \xi } } \right){\pmb G }w(k) \end{array} \right \} $$ | (16) |
其次,采用状态变换将含时滞的状态方程(15)转化为无时滞状态方程. 该状态变换方法依据输入时滞量$\tau $的大小,分为如下两种情况讨论:当$0 < \tau \leqslant T_{\rm s} $时,即时滞在设定的采样间隔内,定义如下状态变量
| $$ \bar {\pmb x }(k) = {\pmb A }_d {\pmb x }(k) + {\pmb B }_{d_2 } {\pmb u }(k - 1) $$ | (17) |
可将时滞状态方程(15)转化为如下无时滞状态方程
| $$ \bar{\pmb x }(k + 1) = {\pmb A }_d \bar{\pmb x }(k) + \bar {\pmb B}_d {\pmb u}(k) + {\pmb A}_d {\pmb w}_d (k) $$ | (18) |
式中$\bar{\pmb B}_d = {\pmb A}_d {\pmb B}_{d_1 } + {\pmb B}_{d_2 } $. 当$\tau > T_{\rm s} $时,即时滞大于采样间隔,则定义如下状态变量
| $ \bar{\pmb x}(k) = {\pmb A}_d^\alpha {\pmb x}(k) + \left[{ {\pmb A }_d^0 \bar{\pmb B}_d ,\cdots ,{\pmb A }_d^{\alpha - 2} \bar{\pmb B }_d , {\pmb A }_d^{\alpha - 1} {\pmb B }_{d_2 } } \right] \cdot\\ \qquad \left[\begin{array}{c} {\pmb u }(k - 1) \\ \vdots \\ {\pmb u }(k - \alpha + 1) \\ {\pmb u }(k - \alpha ) \end{array} \right] $ | (19) |
也可将时滞状态方程(15)转化为无时滞状态方程. 此时的状态方程为
| $$ \bar{\pmb x}(k + 1) = {\pmb A}_d \bar{\pmb x}(k) + \bar {\pmb B}_d {\pmb u}(k) + {\pmb A}_d^\alpha {\pmb w}_d (k) $$ | (20) |
上述无时滞转化过程详见文献[51],其主要思想是将受控系统的输入时滞转化到状态方程的系数矩阵中,从而将含时滞的状态方程转化为不含时滞的状态方程.
当获得式(18)或式(20)所描述的无时滞状态方程后,可采用最优控制或鲁棒控制方法设计反馈控制. 需要说明的是,在设计最优控制律时,最优二次型代价函数仍应按照使式(12)中的状态变量和输入变量最小的原则,即
| $J = {\rm{ }}\sum\limits_{k = 0}^{ + \infty } {_{}^{}} \left[ {{x^{\rm{T}}}\left( k \right){Q_1}x\left( k \right) + {u^{\rm{T}}}\left( k \right){Q_2}u\left( k \right)} \right]$ | (21) |
通过给定的${\pmb x }(k)$与$\bar{\pmb x}(k)$之间的关系,将上述代价函数转化为基于等价状态变量$\bar{\pmb x}(k)$的二次 型函数,从而推导时滞最优控制的Riccati方程. 图 6是多输入/多输出时滞最优控制的执行框图.
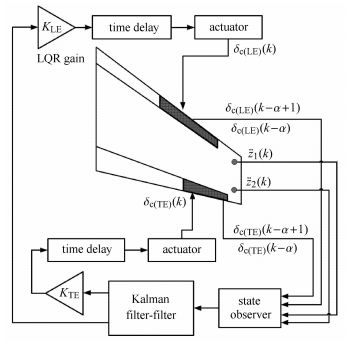
|
图 6 多输入/多输出时滞最优控制框图 Fig.6 Block diagram of the implementation of an MIMO time-delayed optimal controller |
图 7是闭环气动伺服弹性系统的颤振临界速度随时滞变化情况. 对于经典LQG最优控制来说,因其设计过程未计入时滞,因而 其受时滞的影响较大. 随着时滞增加,虽然该LQG最优控制可略微提高闭环系统的颤振临界速度,但当时滞达到15 ms时,闭环系统的稳定性会迅速降低. 与经典LQG最优控制相比,时滞LQG最优控制可显著提升含时滞气动伺服弹性系统保持稳定性的能力. 从图 7对两种不同控制器的比较来看,可以得到如下两点结论:一是若控制回路中存在短时滞,将有助于增加气动伺服弹性系统的 闭环稳定性;二是若控制回路中存在较长的时滞(如本文中给出的15 ms以上的时滞),经典LQG最优控制器将难以维持闭环系统的 稳定性.

|
图 7 不同控制策略所得闭环颤振临界速度对比 Fig.7 Comparision of closed-loop critical flutter speeds with an increase of time delay by different approaches |
在AFS技术的研究中,基于传递函数描述的经典控制理论[42]和基于状态空间描述的最优控制理论[52, 53, 54, 55]已得 到广泛应用. 由于受非定常空气动力计算准确性、结构动力学建模误差、控制回路中滤波器的群时延等不确定因素的影响,对气动伺服弹性系统 几乎难以精确建模,这给AFS控制律设计带来了困难. 为了提高AFS控制律对上述不确定因素的鲁棒性,不少学者开展了鲁棒控制研究. 例如,作者团队[56, 57]研究了二元翼段的鲁棒AFS问题,分别设计了$H_\infty $鲁棒控制律和$\mu $控制器,并进行了风洞实验验证.
对于时变飞行条件或采用时变布局的飞机,在飞机结构气动伺服弹性建模中应设计具有自适应特性的AFS控制律[58]. 近十几年来,针对含结构非线性的二元气动弹性系统,人们已提出多种自适应控制方法. 例如,Ko等[59]针对含扭转刚度非线性的二元翼段,设计了具有全局稳定性的自适应控制方法,抑制气动弹性系统的失稳. Singh和Wang[60]提出SISO的自适应输出反馈控制律,抑制非线性二元翼段的气动弹性失稳. Behal等[61]以含前后缘控制面的非线性二元翼段为研究对象,设计MIMO自适应AFS系统. Wang等[62]针对含未建模非线性以及外界扰动的二元非线性气动弹性系统,采用高增益状态观测器设计MIMO自适应输出反馈控制器,进而抑制结构气动弹性响应和极限环振荡. Zhang和Singh[63]研究了含非结构不确定性的二元气动弹性系统的自适应AFS问题.
相对于二维气动弹性系统的上述研究,对三维气动弹性系统的自适应AFS研究尚很少. 主要原因在于,三维气动伺服弹性系统多为非最小相位系统,现有的直接自适应控制理论应用于非最小相位系统存在理论上的不足. 因此,在针对三维气动弹性系统的自适应控制研究中,多采用间接自适应控制方法. 间接自适应控制律的设计过程分为以下两步:一是采用状态观测或者系统辨识理论在线辨识受控系统的状态方程;二是基于观测或辨识的状态方程,采用线性控制理论(如极点配置法、最优控制)在线计算控制输入. 这类研究的典型代表是20世纪80年代美国学者对F-16战机机翼/外挂系统的颤振主动抑制研究[64, 65, 66]. 20世纪90年代,Andrighettoni和Mantegazza[67]研究了带有前、后缘控制面的三维机翼的MIMO自适应颤振主动抑制问题. 该研究采用ARMAX模型在线辨识受控系统的状态方程,并基于极点配置理论设计离散的状态反馈增益. 虽然数值仿真和风洞实验表明,该方法可有效抑制机翼的颤振,但其抑制效果是否优于传统的鲁棒控制方法尚需进一步验证. 近年来,基于递归神经网络的自适应控制策略已被成功应用于三维气动弹性系统的颤振主动抑制[68, 69]. 然而,由于在控制律运算过程中需要对用于系统辨识的神经网络和用于控制律运算的神经网络分别进行在线辨识,增加了控制系统的复杂性. 若要将这类方法拓展到实际的颤振主动抑制中,需要对神经网络的架构以及辨识算法进行完善.
综上所述,自适应控制方法在颤振主动抑制研究中具有很大的应用空间. 提高自适应AFS控制律的安全性、可靠性和易操作性的关 键在于不确定参数的估计问题. Ioannou等[70]在其自适应控制专著中提出,对于不确定性的参数可通过梯度算法或最小二乘算法进行估计. 为了提高参数估计的准确性以及抗外界干扰的鲁棒性,作者采用一种新的有界增益遗忘(bounded-gain forgetting, BGF)估计器[71]对气动伺服弹性系统的不确定参数进行在线估计,并基于该参数估计方法设计了间接自适应颤振抑制控制律. 以单输入/单输出气动伺服弹性系统为例,其动力学方程可用如下传递函数表示
| $$ \dfrac{y(s)}{u(s)} = \dfrac{b_{n - 1} s^{n - 1} + \cdots + b_1 s + b_0 }{s^n + a_{n - 1} s^{n - 1} + \cdots + a_1 s + a_0 } $$ | (22) |
上述传递函数可简化为如下线性参数化模型
| $$ y = {\pmb \theta }_{\rm p}^{\rm T} {\pmb W} $$ | (23) |
式中${\pmb \theta }_{\rm p}$为待估计参数. 定义如下带有指数遗忘的预测误差代价函数
| $$ J = \int_0^t {\rm e}^{ - \int_s^t \lambda (r){\rm d}r}\left\| { y - \hat {\pmb\theta }_{\rm p}^{\rm T} {\pmb W}(s) } \right\|^2{\rm d}s $$ | (24) |
式中的时变遗忘因子$\lambda (t)$满足如下方程
| $$ \lambda (t) = \lambda _0 \left( {1 - \dfrac{\left\| {\pmb P}\right\|}{k_0 }} \right) $$ | (25) |
其中$\lambda _0 $反映了在参数跟踪速度与参数估计结果的振荡性之间的折中选择;增益边界$k_0 $则反映了参数更新速度与扰动对预测误差的影响. 式(25)表明,时变遗忘因子具有根据矩阵${\pmb P}$范数的大小自动调节遗忘速度的功能. 基于上述时变遗忘因子的定义,可得到增益自适应律
| $$ \dot{\pmb P} = \lambda _0 {\pmb P} - \left( {\lambda _0 / k_0 } \right){\pmb P}\left\| {\pmb P} \right\| - {\pmb P\pmb W \pmb W}^{\rm T}{\pmb P} $$ | (26) |
和参数自适应律
| $$ \dot{\hat{\pmb \theta}}_{\rm p} = - {\pmb P \pmb W}e_1 $$ | (27) |
式中预测误差$e_1 $定义为
| $$ e_1 = \hat {y}_{\rm p} - y_{\rm p} = \left( { \hat{\pmb \theta }_{\rm p}^{\rm T}- {\pmb \theta }_{\rm p}^{\rm T} } \right){\pmb W} $$ | (28) |
BGF估计器具有一定的抗干扰能力. 然而,若受控系统存在未建模动力学和测量噪声,则BGF估计器难以保证参数误差的有界性,因 为参数误差$\hat{\pmb \theta }_{\rm p} - {\pmb \theta }_{\rm p} $取决于外界干扰的幅值和参数变化率. 若受控系统中存在未建模动力学,则其参数变化率有可能会很大,从而难以保证参数误差的有界性. 为保证参数误差的有界性,可采用如下死区技术对参数自适应律(27)进行修正,修正后的参数自适应律为
| $$ \dot{\hat{\pmb \theta}}_{\rm p} = \left\{ \begin{array}{ll} -{\pmb P}\left( t \right){\pmb W}e_{1}^{\rm T} ,& \left| {e_1 } \right| > \varDelta \\ 0 ,& \left| {e_1 } \right| \leqslant \varDelta \end{array} \right. $$ | (29) |
式中$\varDelta $为设定的死区带宽. 当受控系统的参数估计值$\hat {\pmb \theta }_{\rm p} $由式(29)确定后,即可采用经典最优控制方法设计控制器. 图 8给出了自适应颤振主动抑制过程. 采用给定的Hurwitz多项式 对当前时刻的输入$u$和输出$y$进行滤波,增益矩阵${\pmb P}$则由滤波后的信号${\pmb W}$和式(26)求得. 图 9是后颤振点流速为41.5 m/s时的控制效果. 图示结果表明,自适应颤 振控制律能够有 效地抑制气动弹性系统的颤振.

|
图 8 自适应颤振主动抑制框图 [72] Fig.8 Block diagram of the adaptive controller for active flutter suppression[72] |

|
图 9 后颤振点的自适应控制效果 Fig.9 Control effectiveness of the adaptive controller at a post-flutter speed |
跨音速气动弹性分析与控制是飞机气动弹性力学与控制领域内的研究热点和难点. 在跨音速非定常流动中,由激波运动以及流动分 离等引起的空气动力非线性往往会导致结构出现``跨音速凹坑''现象、极限环振荡以及副翼嗡鸣等[73]. 当前,较为精确地模拟上述现象的方法是采用CFD和CSD (computational structure dynamics)耦合方法进行数值模拟[74]. 虽然这类方法能有效描述非线性气动力与弹性结构的相互作用,但由于其计算耗时过大等原因,限制了其在气动弹性和气动 伺服弹性等领域的应用. 本节将介绍跨音速飞行区域的气动弹性分析与控制的最新研究进展.
2.1 跨音速非定常气动力模型降阶鉴于CFD/CSD耦合方法的计算效率过低,近年来航空科技界对基于CFD描述的复杂空气动力系统开展了模型降阶 (reduced-order model,ROM)研究. 所谓模型降阶是指采用较为简单的线性或非线性数学模型来逼近复杂空气动力系统的输入输出映射关系.
例如,Hall等[75]采用本征正交分解(proper orthogonal decomposition, POD)方法对跨音速非定常小扰动流动开展模型降阶研究. 研究结果表明,该方法在预测小扰动跨音速空气动力以及二元翼段的颤振边界方面具有较高精度. Cowan等[76]及Gupta和Bach[77]采用基于自回归滑动平均模型(auto-regressive and moving average, ARMA)的系统辨识方法,对跨音速非定常CFD系统进行线性降阶模型研究. 研究结果表明,ARMA模型能高效、精确地预测具有复杂外形的飞机气动弹性响应. Silva和Bartels[78]采用ERA对基于薄边界层假设的雷诺平均Navier-$\!$-Stokes方程描述的空气动力系统进行线性降阶模型研究, 并成功预测了AGARD 445.6机翼的跨音速颤振边界. 然而,由于该方法在样本采集过程中需要对结构各阶模态的气动力脉冲响应分别进行计算,从而消耗较多 计算时间,而且这样的耗时在处理MIMO空气动力系统辨识时将更为显著. 针对上述问题,Kim等[79, 80]以及Silva[81]分别研究了各阶模态同时激励下的线性模型降阶问题. 由于结构各阶模态的激励信号是相互正交的,因而只需执行一次CFD计算即可获得各阶模态的气动力响应样本,大大降低了样本采集过程中的时间消耗,提高了线性降阶模型的辨识效率. 近年来,Kim[82]提出一种新的线性降阶模型方法,以结构气动弹性响应数据作为训练样本,通过结构状态变量和气动弹性状态变量之间的状态变换获取降阶的空气动力系统状态方程. 该方法已成功用于预测带翼吊发动机短舱的商用运输机颤振边界. Raveh[83]采用滤波后的高斯白噪声作为外激励方式,获取跨音速CFD空气动力系统的输入、输出样本,并采用子空间辨识方法得到线性降阶模型.
相对于线性降阶模型研究而言,非线性降阶模型可望高效、精确地模拟跨音速空气动力系统的非线性行为,是当前研究的热点和难点. 人们已提出和发展了谐波平衡法[84, 85, 86, 87, 88, 89]、基于多层神经网络的非线性降阶方法[90]、基于RBF (radial basis function)神经网络的非线性降阶方法[91]、Kriging代理模型方 法[92],对上述方法优缺点的评述可参阅文献[93].
与上述非线性模型降阶方法相比,基于Volterra级数的非线性降阶方法更早被提出,并且处于不断发展之中. 例如, Silva[94, 95]最早将基于Volterra级数的非线性系统辨识理论应用于非线性空气动力系统的模型降阶研究中,采用空气动力系统的脉冲响应对Volterra核进行直接辨识. Raveh[96]应用Volterra级数方法构造基于阶跃响应的非线性ROM,详细讨论了阶跃激励的幅值和时间步长等因素对非线性ROM辨识精度的影响. Marzocca等[97, 98]将Volterra级数方法应用于亚音速不可压缩流动中的非线性气动弹性响应研究中. 由于其研究主要涉及含结构非线性的二元翼段的气动弹性问题,空气动力计算仍采用亚音速不可压缩流动计算方法,故该研究并不算真正意义上基于Volterra级数的非线性ROM研究. Munteanu等[99]采用Volterra级数方法构造非线性ROM,并用于分析二元翼段和三维复合材料板的气动弹性响应. 但该研究仅是对基于Volterra级数的非线性ROM的初步研究,没有深入分析非线性ROM在预测跨音速颤振边界和非线性气动弹性行为等方面的优势. 为了提高Volterra级数在辨识空气动力系统非线性方面的能力,Balajewicz等[100]将多输入Volterra级数理论应用于多自由度非线性空气动力系统辨识,发现高阶核的引入有助于提高Volterra级数辨识空气动力非线性的能力. 目前,虽然多输入Volterra级数方法已应用于预测二元翼段的跨音速颤振边界和极限环振荡等问题[101],但预测精度尚有待提高. 另外,无论是单输入Volterra级数方法还是多输入Volterra级数方法,其Volterra核的辨识都较为复杂;并且随着级数截断阶次的增加,非线性降阶模型的维数将急剧增大.
对于具有``记忆衰退''特性的非线性系统,除了Volterra级数外,并联Hammerstein模型或者并联Wiener模型同样可用来辨识该类系统. 相对于Volterra级数的辨识方法,基于并联Hammerstein模型或者并联Wiener模型的辨识方法具有结构简单、辨识较为容易等特点[102]. Westwick[103]对该类非线性辨识方法进行了较为深入的研究. 然而,该非线性系统辨识方法还存在一些关键问题亟待解决. 例如,如何保证动态线性部分的稳定性?如何提高非线性辨识能力?以及如何拓展应用到MIMO非线性系统辨识中?
出于对上述问题的思考,作者建立了线性状态方程串联单层神经网络的Wiener模型,并基于MIMO优化方法来递归逼近由CFD计算得 到的非定 常空气动力,从而得到一种新的跨音速、非线性空气动力降阶模型[104]. 该非线性降阶模型如图 10所示,它由多个Wiener模型并联所得. 在每个Wiener模型中,$ {\pmb h}_i ( \cdot )$为动态线性部分,${\pmb F}_i ( \cdot )$为静态非线性函数. ${\pmb u}_{\rm s} (k)$和${\pmb y}_{\rm a} (k)$分别为结构位移 和CFD计算出的空气动力载荷.

|
图 10 非线性模型降阶示意图 Fig.10 Diagram of nonlinear reduced-order modeling |
该非线性降阶模型的辨识过程如下:首先,基于输入、输出样本${\pmb u }_{\rm s} (k)$和${\pmb y }_{\rm a} (k)$,拟合出第一个Wiener模型,即辨识出第一个动态线性单元${\pmb h }_1 ( \cdot )$和静态非线性单元${\pmb F }_1 ({\pmb z }_1 (k))$,并由该Wiener模型计算出气动载荷的预测值${\pmb y }_1 (k)$和气动载荷残值$ \tilde{\pmb y }_1 (k)$;其次,基于结构输入$ {\pmb u }_{\rm s} (k)$和气动载荷残值$ \tilde{\pmb y }_1 (k)$,对第二个动态线性单元${\pmb h }_2 ( \cdot )$和静态非线性单元$ {\pmb F}_2 ({\pmb z}_2 (k))$进行拟合. 重复上述辨识过程,直至气动载荷残值中仅含有噪声成分. 由此可得到非线性降阶模型气动载荷输出表达式
| $$ \tilde{\pmb y }_{\rm a} \left( k \right) = \sum_{i = 1}^{N_{\rm p} } {\pmb y }_i \left( k \right) $$ | (30) |
式中$N_{\rm p} $为并联的Wiener模型个数.
为了精确辨识MIMO空气动力系统,作者还提出一种新的Wiener模型,其结构如图 11所示. 运用MIMO状态空间方程来模拟动态线性部分,其表达式如下
| ${\pmb x }_{\rm a} \left( {k + 1} \right) = {\pmb A }_{\rm a} {\pmb x }_{\rm a} \left( k \right) + {\pmb B }_{\rm a} {\pmb u}_{\rm s} \left( k \right) $ | (31) |
| ${\pmb z }_i \left( k \right) = {\pmb C }_{\rm a} {\pmb x }_{\rm a} \left( k \right) + {\pmb D }_{\rm a} {\pmb u }_{\rm s} \left( k \right) $ | (32) |

|
图 11 Wiener 模型结构图 Fig.11 Structure of a Wiener model |
式中${\pmb x }_{\rm a} \left( k \right) \in \mathbb{R}^n,{\pmb u }_{\rm s} \left( k \right) \in \mathbb{R}^m,{\pmb z }_i \left( k \right) \in \mathbb{R}^l$,$n,m,l$分别为系统的状态、输入和输出的维数. 状态方程系数矩阵$({\pmb A}_{\rm a},{\pmb B}_{\rm a},{\pmb C}_{\rm a},{\pmb D}_{\rm a})$为待辨识的参数. 静态非线性部分采用单层神经网络来描述,表达式如下
| $$ y_{i,l_i } \left( k \right) = \sum_{j = 1_i }^{N_{\rm e} } w_{j,l_i }^{\rm s} \left[{\tanh \left( {{\pmb w }_{j,l_i } {\pmb z }_i \left( k \right) + b_{j,l_i } } \right)} \right] + b_{\left( {N_{\rm e} + 1} \right),l_i } $$ | (33) |
式中$N_{\rm e}$为神经元的个数,${\pmb w }_{j,l_i } ,b_{j,l_i } $为隐层神经元的权值和阀值,$w_{j,l_i }^{\rm s} $和$b_{\left( {N_{\rm e} + 1} \right),l_i } $为输出层神经元的权值和阀值. 对于给定的结构输入${\pmb u }_{\rm s} (k)$和气动载荷残差$ \tilde{\pmb y }_i (k)$,动态线性部分和静态非线性部分的参数可通过Levenberg-$\!$-Marquadt算法优化得到[105].
为验证非线性降阶模型在预测跨音速非定常气动力方面的精度,作者分别以图 12中的Isogai机 翼[106]和图 14中的BACT(benchmark active control technology)机 翼[107]为研究对象,采用非线性模型降阶方法来预测其跨音速非定常气动力. 图 13是马赫数$M_\infty = 0.875$、沉浮和俯仰自由度在有限带宽白噪声激励下,Isogai机翼的升力和力矩系数对比情况. 由图可见,基于非线性降阶模型的计算结果与直接CFD计算结果可很好吻合.
|
图 12 Isogai 二元机翼模型 Fig.12 Isogai two-dimensional wing model |
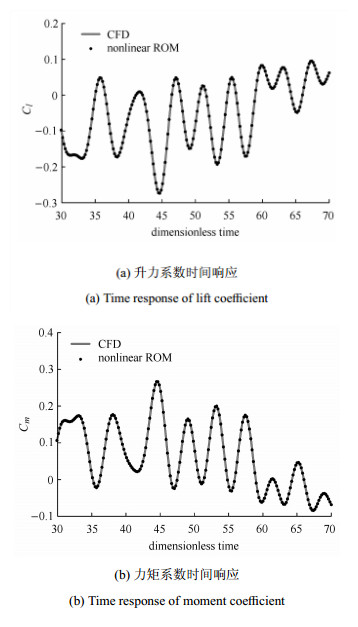
|
图 13 不同方法所得 Isogai 机翼升力和力矩系数对比 Fig.13 Comparison of the lift and moment coefficients of Isogai wing by different approaches |
|
图 14 BACT 机翼模型 Fig.14 BACT wing model |
BACT机翼是NASA兰利研究中心设计用于研究跨音速非定常气动力计算及颤振主动抑制的国际标准模型[108, 109, 110]. 该 模型采用NACA0012翼型作为气动外形,设计了后缘控制面和上、下两个扰流片. 对于这类含控制面偏转的三维复杂流动下非定常气动力模型降阶研究,其难点在于如何提高降阶模型对含激波运动和黏性效应的三 维跨音速空气动力系统的辨识精度和辨识稳定性. 为保证非线性降阶模型中线性状态空间模型的稳定性,作者采用一种基于观测器的子空间辨识方法来辨识线性状态空间模型[111], 其辨识过程如下:
首先,采用含外部输入的向量自回归模型(vector auto-regressive with exogenous inputs, VARX)建立结构运动输入和CFD输出之间的关系
| $$ {\pmb y }_k = \sum_{i = 0}^p {\pmb B }_i {\pmb u }_{k - i} + \sum_{i = 1}^p {\pmb A }_i {\pmb y }_{k - i} $$ | (34) |
式中$p$为过去窗宽度,${\pmb A}_i $和${\pmb B}_i $为待估计的VARX参数. 该VARX参数可表示为如下矩阵形式
| $$ \tilde{\pmb \varXi } \triangleq \left[ {{\pmb B}_p ,} \ \ \cdots \ \ {{\pmb B }_1 ,} \ \ {{\pmb B}_0 ,} \ \ {{\pmb A }_p ,} \ \ { \cdots ,} \ \ {{\pmb A }_2 } ,\ \ {{\pmb A }_1 } \right] $$ | (35) |
式中$\tilde \Xi \in {\mathbb{R}^{l \times }}\left[ {p\left( {l + r} \right) + r} \right]$,$r$和$l$分别为输入和输出的维数. 基于最小二乘法可得到估计值
| $$ \tilde {\pmb \varXi } = {\pmb Y \pmb\varPsi }^ + $$ | (36) |
式中$\left( \cdot \right)^ + $为伪逆算子,矩阵${\pmb Y }$和${\pmb \varPsi }$可由下式计算
| $\left. \begin{array}{l} Y \buildrel \Delta \over = \left[{{y_{p + 1}},{y_{p + 2}},\cdots {y_{N - 1}},{y_N}} \right]\\ \Psi \buildrel \Delta \over = \left[{\begin{array}{*{20}{c}} {{u_1}}&{{u_2}}& \cdots &{{u_{N - p - 1}}}&{{u_{N - p}}}\\ {{u_2}}&{{u_3}}& \cdots &{{u_{N - p}}}&{{u_{N - p + 1}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{u_p}}&{{u_{p + 1}}}& \cdots &{{u_{N - 2}}}&{{u_{N - 1}}}\\ {{u_{p + 1}}}&{{u_{p + 2}}}& \cdots &{{u_{N - 1}}}&{{u_N}}\\ {{y_1}}&{{y_2}}& \cdots &{{y_{N - p - 1}}}&{{y_{N - p}}}\\ {{y_2}}&{{y_3}}& \cdots &{{y_{N - p}}}&{{y_{N - p + 1}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{y_p}}&{{y_{p + 1}}}& \cdots &{{y_{N - 2}}}&{{y_{N - 1}}} \end{array}} \right] \end{array} \right\}$ | (37) |
得到VARX参数后,即可构造Wiener模型的线性状态方程. 为得到状态方程的最优解,可采用子空间辨识的思想来构造状态方程. 此处 仅给出Wiener模型线性状态方程参数 $({\pmb A}_{\rm a},{\pmb B}_{\rm a},{\pmb C}_{\rm a},{\pmb D}_{\rm a})$ 的计算公式
| $\left. \begin{array}{l} \left[{{A_{\rm{a}}}\;\;{B_{\rm{a}}}} \right] = {{\hat x}_{\left( {:,2:N - p} \right)}}{\left[{\begin{array}{*{20}{c}} {{{\hat x}_{\left( {:,1:N - p - 1} \right)}}}\\ {{U_{\left( {:,1:N - p - 1} \right)}}} \end{array}} \right]^ + }\\ \left[{{C_{\rm{a}}}\;\;{D_{\rm{a}}}} \right] = {Y_{\left( {:,1:N - p - 1} \right)}}{\left[{\begin{array}{*{20}{c}} {{{\hat x}_{\left( {:,1:N - p - 1} \right)}}}\\ {{U_{\left( {:,1:N - p - 1} \right)}}} \end{array}} \right]^ + } \end{array} \right\}$ | (38) |
式中$ \hat{\pmb x }$为状态向量的估计,输入矩阵${\pmb U }$的定义与式(37)中${\pmb Y }$的定义类似. 需要说明的是,由式(38)计算出的状态方程的稳定性难以保证. 导致不稳定的原因有两点: 一是基于观测器的子空间辨识算法本身无法保证辨识结果的稳定性,二是考虑边界层分离和黏性效应的CFD系统具有高维、 非线性等特性. 因此,以CFD技术得到的``非线性''数据来进行线性系统辨识,本身就容易导致辨识结果的不稳定性. 为辨识出一个稳定的线性状态方程,需要在每个Wiener模型辨识过程中检验线性部分的稳定性;当线性部分辨识结果不稳定 时,可通过稳定性调节方法来保证其稳定性[112]. 为验证非线性ROM方法在预测含控制面运动的三维跨音速空气动力的辨识精度,以BACT机翼控制面做正弦运动时的气动力响 应作为验证算例. 图 15是控制面受正弦激励时结构前两阶固有模态所对应的广义空气动力时间响应历程. 图示结果表明,非线性ROM的辨识结果与直接CFD结果能很好吻合.

|
图 15 BACT 机翼模型广义空气动力时间响应 Fig.15 Time responses of generalized aerodynamic forces of the BACT wing model |
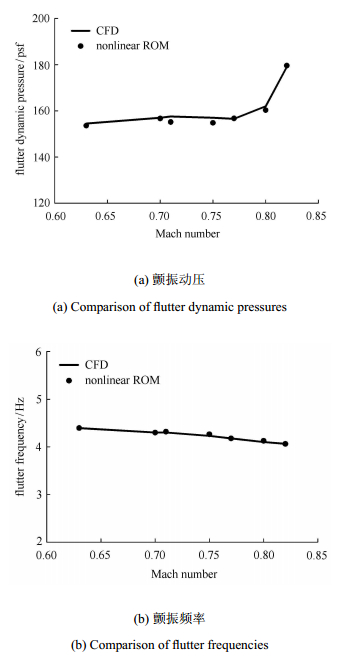
基于CFD/CSD耦合的时间推进方法是预测飞机在跨音速飞行区域中气动弹性稳定性的主流方法. 然而,CFD计算方法的高耗时 性限制了其实际应用. 随着高效、高精度的线性/非线性模型降阶方法的发展,跨音速气动弹性稳定性边界的高效预测已成为可能. 以三维BACT机翼为例,图 16是BACT机翼颤振动压和颤振频率随马赫数变化情况. 结果表明,非线性ROM所预测的颤振边界和CFD计算结果具有很高的吻合度.
|
图 16 不同方法所得 BACT 机翼模型颤振边界对比 Fig.16 Comparison of the flutter boundaries of BACT wing model by different approaches |
非线性ROM方法的另一应用是高效预测空气动力非线性对气动弹性系统的影响,其典型应用是预测极限环振荡. 图 17是非线性ROM方法预测BACT机翼在马赫数为0.77、动压为165 psf时的极限环振荡,并与直接CFD/CSD耦合计算结果进行了对比. 从第二阶模态坐标相图上可见,非线性ROM所预测的LCO幅值与直接CFD方法所预测的幅值吻合的较好,LCO幅值的相对误差约5.7%.

|
图 17 不同方法所得 BACT 机翼模型极限环振荡对比 Fig.17 Comparison of LCO amplitudes of the BACT wing model by different approaches |
虽然跨音速非定常空气动力系统的模型降阶方法研究已有近20年的历史,并在跨音速气动弹性系统的稳定性分析和非线性行为预测方面展示了优越性,但尚存在若干亟待解决的问题. 例如,需要进一步提高非线性降阶方法在空气动力非线性方面的辨识精度,以提高预测跨音速非线性气动弹性行为的精度.
2.3 跨音速气动弹性主动控制与亚音速颤振主动抑制相比,跨音速飞行条件下的颤振主动抑制的研究难度剧增. 在跨音速区域,由于激波运动、黏性效应以及流动分离等因素的存在,跨音速气动伺服弹性系统会呈现明显的非线性特征. 从控制律设计角度来看,这些非线性因素给控制律设计带来众多难以预测的不确定性因素,对控制器的鲁棒性提出更高要求. 因此,在跨音速AFS的研究方面,主要考虑两类问题:一是发展高效、高精度的跨音速气动伺服弹性数学模型,并用于分析系统在开环和闭环状态下的跨音速气动伺服弹性响应;二是设计具有低阶、高鲁棒性能的跨音速AFS控制律.
在高效、高精度的跨音速气动伺服弹性数学建模研究方面,Zhang和Ye[113]以带后缘控制面的二元翼段为对象,采 用ARMA模型建立含控制面运动的跨音速空气动力系统线性降阶模型;并将其与结构动力学方程耦合,建立起线性化的跨音速气 动伺服弹性模型. 该气动伺服弹性模型已被成功用于设计次最优AFS控制律,在数值仿真中展现出很好的颤振抑制效果. 其不足之处是,当马赫数变化时控制律需要重新设计. Stephens等[114]以计入三维气动效应的BACT 机翼为对象,基于ARMA模型的空气动力模型降阶方法建立跨音速气动伺服弹性模型,引入简单PID控制,分析了闭环系统的跨音速气动伺服弹性.
在跨音速AFS控制律设计方面,为了提高控制律对马赫数和激波运动等因素的鲁棒性,Friedmann等[115]以二维跨音速气动弹 性系统为对象,设计了间接自适应AFS控制律,发现该自适应控制律能够有效抑制非线性气动弹性系统的颤振失稳. Mukhopadhyay[116]应用极小化极大方法设计线性的跨音速AFS控制律. 为了提高控制律对飞行参数以及空气动力非线性的鲁棒性,在设计中通过反复调节加权参数来实现设定的鲁棒性能. 基于回差矩阵最小奇异值的鲁棒稳定性分析表明,该线性控制律具有良好的鲁棒性. 与此同时,Mukhopadhyay针对该控制律还开展了跨音速颤振主动抑制风洞实验,验证了该控制器的有效性. Waszak[117]以BACT机翼为对象,分别采用$H_\infty $和$\mu $综合方法设计多变量鲁棒控制律. 数值仿真表明,所设计的控制律在鲁棒性及提高闭环系统稳定性等方面要优于SISO经典反馈控制律. 风洞实验结果表明,该控制律能在较大的马赫数和动压范围内提高闭环系统的稳定性. Scott和Pado[118]基于神经网络模型设计了3种不同的跨音速AFS控制律,并分别进行了风洞实验验证. 第1种控制设计方案是根据来流马赫数和动压的变化,采用神经网络方法在线调节SISO线性控制器参数,并将校正后的 SISO控制器发送给实时控制系统. 风洞实验表明,该控制方案可有效抑制结构颤振响应. 第2种设计方案是基于神经网络模型设计模型预测控制方法. 虽然该方案是真正意义上的自适应控制方案,但并没有取得理想的控制效果,原因是当时的硬件和软件条件无法支撑如此 复杂的非线性控制系统. 第3种设计方案是设计基于神经网络的逆模型控制方法. 风洞实验表明,该控制器能将系统开环颤振动压至少提高20 psf,结构的均方根响应降低40%.
综上所述,与亚音速AFS研究相比,跨音速飞行条件下的AFS研究开展较晚,但研究意义至关重要. 迄今为止,对跨音速气动 伺服弹性建模的研究相对较少,且仍局限于发展线性化的跨音速气动伺服弹性模型,未能考虑激波运动、流动分离等非线性因素对气动伺服弹性系统的影响. 采用CFD/CSD和伺服控制系统相耦合的方法研究非线性气动伺服弹性响应,虽能较为准确地模拟非线性因素对系统的影响,但计算耗时之大难以接受. 在跨音速AFS控制律设计方面,由于受马赫数、飞行动压以及空气动力非线性等因素的影响,跨音速气动伺服弹性系统的动力学特 性会有较大的不确定性和非线性.
为深入研究空气动力非线性对跨音速气动伺服弹性系统动力学特性的影响,作者采用非线性模型降阶方法对跨音速颤振主动抑制问题 开展研究[111]. 对于跨音速气动伺服弹性建模,包含作动器动力学特性在内的气动伺服弹性数学模型可表示为
| $$ \dot {\pmb x}_{\rm s} = {\pmb A }_{\rm s}{\pmb x }_{\rm s} + {\pmb B }_{\rm c} \beta _{\rm c} + q_\infty {\pmb B }_q {\pmb Q }_{\xi \xi } \left( { {\pmb \xi },\beta } \right) $$ | (39) |
式中$\beta _{\rm c} $是控制面偏转指令,广义空气动力矩阵${\pmb Q}_{\xi \xi } \left( {{\pmb \xi },\beta } \right)$是飞机模态坐标向量${\pmb \xi }$以及控制面偏转角度$\beta $的非线性函数, 该非线性函数关系可通过直接CFD方法或者非线性降阶模型方法计算得到. 图 18是控制面激励幅值分别为$\pm 1^\circ$和$\pm 6^\circ$ 时,采用简谐慢扫频方法得到的控制输入与沉浮自由度$h$之间的频率响应曲线. 扫频激励的频率范围为2 Hz$\sim$6 Hz. 图示结果表明,结构的俯仰模态对控制面激励幅值较为敏感,随着控制面幅值增大,空气动力非线性效应开始明显,并起到刚 度硬化作用. 当控制面激励幅值达到$\pm 6^\circ$时,幅频和相频曲线发生了跳跃现象. 出现该现象的原因在于,简谐慢扫频激励只能实现渐近稳定的运动,无法预测到不稳定的解支,从而产生图示的跳跃现象.

|
图 18 不同控制面激励幅值下的跨音速气动伺服弹性系统频率响应对比 Fig.18 Comparison of the frequency responses of transonic ASE system subjected to different excitation amplitudes of control surface |
与亚音速AFS控制律设计相比,跨音速飞行时的颤振主动控制律设计要求更高. 在跨音速区域,激波运动以及流动分离会呈现出较为明显的非线性现象,这要求控制律设计要有足够的稳定性裕度.
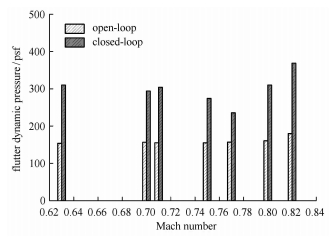
为了在较大马赫数和动压范围内提高飞机的颤振稳定性,作者提出一种基于VARX观测器的间接自适应颤振主动控制器,其设计分为两步:首先,应用基于VARX观测器的递归子空间辨识方法,在线辨识受控系统的状态空间方程;其次,通过在线求解Riccati方程,获得当前时刻的最优控制输入. 控制律设计的关键在于在线辨识闭环系统的状态方程. 为了高效、精确地辨识每个时间步内系统的状态向量和状态矩阵,采用快速矩阵式最小二乘(fast-array RLS)滤波器来在线辨识系统的Markov参数. 图 19是不同马赫数时BACT机翼的开环和闭环颤振临界动压的对比,表明该间接自适应颤振抑制控制律能在较大马赫数和动压范围内改善BACT机翼的跨音速颤振稳定性.
|
图 19 BACT 机翼模型的开环和闭环颤振边界 Fig.19 Open and closed-loop flutter boundaries of BACT wing model |
在气动弹性力学中,突风被分为离散型和连续型两类[119]. 连续突风是一种大气紊流,表现为非确定性的、随机的风速变化;而离散突风表现为确定性的风速变化,具有脉冲型特性.
突风对飞机性能的影响是多重的、负面的,有时是灾难性的. 对于长时间处于巡航状态的客机、运输机、轰炸机,必须在其设计中进行突风响应分析,并研究合理的控制方案以减缓突风载荷.
3.1 系统建模与控制研究突风载荷减缓需基于飞机的全机ASE模型,其中最关键的非定常气动力建模,包括突风气动力和与飞机结构运动有关的气动力.
突风现象非常复杂,为了简化研究需要引入一些假设. 通常,飞机速度远大于突风速度及其变化量,在研究大气紊流对飞机的影响时,可采用Taylor假定将突风速度场``冻结''[120],使突风场速度只依赖于空间坐标而与时间无关. 结合飞行问题时,突风速度场的空间分布可转化为飞机所感受到的突风速度随时间变化. 在突风响应研究中,还常假定突风场变化只依赖于一个空间坐标,即沿着飞机翼展方向的突风速度是不变的[121],如图 20所示. 当然,研究中也可假定展向非均匀的突风速度分布[122],但这方面的研究不多.

|
图 20 飞机穿越一维突风场 Fig.20 Airplane penetrating into one-dimensional gust field |
从20世纪50年代开始,国外学者对大气紊流现象进行了大量理论和实验研究,并提出了Von Karman和Dryden两种功率谱模型. 这两种模型的建立方法有如下差别:Von Karman模型先根据大量测量和统计数据建立大气紊流的频谱函数,再推导出相关函数;Dryden模型则先根据经验建立大气紊流相关函数,然后再推导得到频谱函数描述大气紊流特性. 显然,Von Karman模型能更为真实地反应大气紊流的实际特性,而Dryden模型实质上是对前者的近似. 在高频区,两种频谱函数的斜率不同,Dryden模型存在一定的误差. 但Dryden模型的频谱形式为有理式,在时域中易于实现.
除突风气动力外,研究突风载荷减缓还要考虑飞机结构运动引起的反馈型非定常气动力,其计算非常复杂. 目前,工程上普遍使用的方法是简化气动模型,如采用偶极子网格法,在频域内计算多个缩减频率下的简谐非定常气动力.
突风与控制面偏转联合激励下的飞机系统的开环状态方程可写为
| $$ \dot{\pmb x }_{\rm p} = {\pmb A }_{\rm p} {\pmb x }_{\rm p} + {\pmb B }_{\rm p} {\pmb u }_{\rm p} + {\pmb B }_{\rm pw} \tilde{\pmb w }_{\rm g} $$ | (40) |
式中,状态向量${\pmb x }_{\rm p} $包括与结构运动有关的状态、空气动力状态和作动器状态,${\pmb u }_{\rm p} $包括各控制面的指令偏转角度,$ \tilde{\pmb w }_{\rm g} $由突风速度及其一阶导数组成. 对于连续突风,需要通过突风滤波器将连续突风转化为时域形式. 飞机系统的输出方程为
| $$ {\pmb y }_{\rm p} = {\pmb C }_{\rm p} {\pmb x }_{\rm p} + {\pmb C }_{\rm aw} \tilde {\pmb w}_{\rm g} $$ | (41) |
式中,输出向量${\pmb y }_{\rm p} $可能包括某监控站位处的加速度,或翼根剪力、弯矩和扭矩等信号. 方程(40)和(41)构成了飞机突风减缓研究的数学模型.
飞机突风响应分析是研究GLA控制的基础. 在实践中,可采用频域方法、时域方法、混合法预计飞机对连续突风和离散突风的动力响应[123]. 频域法的关键是与突风相关的广义非定常气动力矩阵的计算与插值;时域法的关键是气动力影响系数矩阵的有理函数拟合. 对于连续紊流风输入,需要根据Von Karman谱或Dryden谱产生大气紊流速度的时域信号. 混合建模方法的优点是不需要对突风项进行有理函数拟合即可求得时域响应[124].
对于理想的GLA控制系统,必须设法消除突风所引起的飞机升力变化. 为此,应使相应的控制面偏转,产生一个大小相等、 方向相反的升力变化来抵消突风影响,这就是GLA的直接力控制方式[125]. 为实现这种控制,飞机上必须具有相应的控制面,例如机翼上可快速调节的襟翼或副翼可作为这种用途的控制面. 这些控制面必须有中立点,以便既能产生正的升力变化,也能产生负的升力变化. 原则上,可使用机翼上的扰流片. 为了减缓飞机上局部位置的阵风法向过载,还可以在指定的位置上安装特殊的控制面[126].
对于工程实用的阵风减缓系统设计,需要采用多目标综合最优的控制方法,即同时考虑刚体飞机的飞行品质、飞机结构动态载 荷指标等多目标要求. 随着现代控制理论的发展,人们提出了多种MIMO控制律设计方法[127, 128, 129],如特征结构配置法、LQG线性二次型高斯最优控制律设计方法等. 其中,特征结构配置方法可直接将若干模态频率和阻尼比配置到飞行品质的要求范围内,但有可能使飞机的其他模态变得不稳定. LQG最优控制方法则极小化所有模态指标,因而具有较好的鲁棒性能. 鲁棒控制已在GLA设计中得到较多应用,如应用于大柔性飞 机[130]、翼身融合体飞机[131, 132]. 基于神经网络[133]和模糊逻辑[134]的人工智能控制律综合方法也被应用到GLA控制研究中,取得了一定的效果.
3.2 突风载荷减缓控制的应用实例最早采用主动控制技术减缓突风载荷的例子是美国洛克希德公司研制的C-5A飞机[135],该机曾因机翼弯曲载荷过大而产 生疲劳问题. 洛克希德公司利用C-5A平台,开发了主动升力分布控制系统(active lift distribution control system, ALDCS),减缓飞机遭遇紊流和法向机动时的机翼弯曲载荷[136]. 该ALDCS与飞机现有的增稳系统集成在一起,共同驱动飞机的副翼和内侧升降舵,可减少机翼根部弯矩达30%以上,但有 不超过5%的扭转增加.
洛克希德公司研制的L-1011-500飞机包括了一个主动控制系统(active control system, ACS),该系统并未显著改变飞机结构,但却实现了GLA. ACS对传感器和驱动的要求与C-5A的ALDCS类似,在翼尖和机身前后布置了垂直加速度计,机身上布置了俯仰速率陀螺仪,水平尾翼和副翼用于实现载荷控制. 研究表明,L-1011-500飞机的GLA控制系统可使飞机尾翼载荷减小20%左右,而ACS对飞机着陆品质的影响可以忽略.
美国波音B-1飞机采用了乘坐品质增强系统来抑制突风扰动引起的结构振动[137]. B-1飞机上的结构模态控制系统利用主动鸭 翼控制面和加速度仪成功抑制了飞行员座舱处振动. 应用主动控制系统后,按增加结构刚度折算,总重量节省约4131.4公斤[138].
波音B-2飞机具有较低的机翼载荷和近中性的俯仰稳定,容易受到大气扰动影响[139]. 波音公司通过对B-2飞机的迎角突风分量、内侧升降舵和位于飞机中心线的专用突风载荷减缓控制面来实现GLA,使飞机发生俯仰运动方式减缓垂直加速度和载荷. 在实践中,通过驱动GLA和内侧升降舵降低了突风激励下的飞机刚体运动,但内侧升降舵激发起飞机的第一阶对称弹性模态;故外侧升降舵需同时反相偏转以抑制该阶模态. 总的来说,B-2飞机的闭环GLA减小了50%的突风载荷增量.
空客公司研制的A320飞机GLA系统采用加速度计产生反馈信号使气动操纵面偏转,在机翼上产生载荷,直接抵消阵风载荷,改善机翼的颤振阻尼和频率响应特性,形成一个闭环控制系统. 该系统采用两外侧扰流板及副翼为气动控制面,可使最大允许起飞重量增加1.3%. 空客公司研制的A330飞机和A340型飞机则配有GLA系统和飞行品质增强系统来提高飞机在大气紊流中飞行的舒适性(comfort in turbulence,CIT). CIT系统的目的是通过控制升降舵和方向舵增加2$\sim $4Hz机身响应的阻尼. 空客公司研制的A380飞机也配有GLA系统[140]. 据报道,波音公司研制的787飞机使用了GLA系统以及飞行品质增强系统,采用静态空气数据传感器来检测横向和垂直大气紊流,使用副翼、扰流板和升降舵抵消大气紊流影响[141].
德国宇航中心(Deutsches Zentrum für Luft- und Raumfahrt,DLR)开展了载荷减缓与乘坐平稳 系统(load alleviation and ride smoothing,LARS)研究,其目的是改善乘坐品质和减轻突风激励下的机翼结构载荷. LARS阵风减缓控制面为襟翼、升降舵和扰流片. 阵风会引起飞机升力的改变,这一升力改变由机翼的直接升力控制(direct lift control,DLC)襟翼来抵消,而DLC襟翼偏转的动量则由升降舵来抵消. LARS提供了3对襟翼,可实现升力的独立控制,达到突风载荷减缓的目的. 由于大多数运输机的第一阶机翼弯曲模态阻尼较小,导致开环突风减缓系统会产生较大的动态载荷振颤. 采用闭环系统可以加大机翼弯曲模态阻尼,减小振颤. 因此,LARS在有效减缓机翼弯矩方面取得了显著效果.
3.3 突风载荷减缓控制新进展近年来,飞机的GLA控制研究在问题建模、气动力计算、突风测量设备、控制器综合方面出现了一些新方法和新趋势.
在飞机气动弹性建模方面,传统的飞行动力学和气动弹性力学仅在各自学科内单独开展研究. 分析飞机的刚体运动行为(如短周期、长周期运动)需要准定常气动力,而分析气动弹性行为则需要非定常气动力. 因此,需要建立包含刚体模态和弹性模态的气动弹性与飞行动力学相统一的模型. Baldelli 和Chen[142]提出的统一建模框架包括:(1)飞机主轴与飞行动力学稳定轴之间的坐标变换;(2)将风洞试验或飞行试验测得的稳定性导数植入到有理函数近似中;(3)在气动弹性公式中,包含了重力分量以及由于前向速度扰动引起的升力和阻力. 目前,该方法已经集成在气动弹性分析软件ZAERO中[143]. 2004年,Meirovitch[144]基于多体动力学领域中的准坐标Lagrange方程,提出了弹性飞机动力学与控制的统一理论,建立了适用于大范围刚体运动和小弹性变形的弹性飞机非线性运动方程. 在应用该方程时,通常利用摄动法将非线性运动方程分解为机动飞机刚体平移和转动的飞行动力学问题,及与弹性变形有关的摄动问题和刚体运动变量的摄动问题,这样处理便于非定常气动力计算和动力学分析.
在非定常气动力计算方面,使用基于CFD的非定常气动力降阶模型获得反馈型非定常气动力模型. 对于基于CFD的突风气动力计算,主要采用场速度法[145] (field velocity method,FVM),也称为网格速度法(grid velocity method,GVM). FVM方法在实施过程中并不真正移动网格,而是通过修正网格速度的方法来实现. FVM方法可有效地单独模拟纯粹的攻角变化和俯仰角速度变化,但FVM方法无法捕捉升力面对突风剖面的影响.
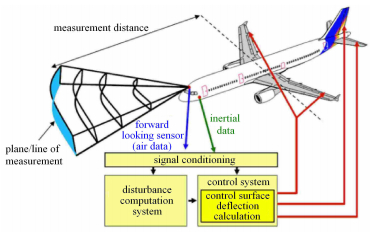
在GLA控制器综合方面,美国在验证GLA控制技术的飞行试验中,采用了各类传感器. 其中,所开发的机载激 光雷达[146] (light detection and ranging,LIDAR)在试飞中被用来检测飞机前方的大气紊流. 由于控制信号时间滞后和控制面偏角速率受限,从飞行控制系统发出指令到副翼偏转到期望角度位置有一个时间滞后, 使控制效果变差. 提前预知前方突风信息是十分有用的,这样可在突风干扰到达飞机之前提供一个超前时间,提前发送控制指令[147]. 因此,基于前馈的GLA控制策略近年来获得了高度重视[148, 149, 150, 151]. 对LIDAR传感器的要求一般是:能提供50$\sim$150 m的前视距离,保证测试的气流是实际影响飞机的气流;传感器具有测量 垂直突风的能力. 国外开发的短脉冲UV多普勒LIDAR满足这些要 求[152],并在空客A340飞机上成功测量了垂直突风速度[153]. 前视突风传感器概念如图 21所示.
|
图 21 基于前视传感器的突风载荷减缓系统 [154] Fig.21 Diagram of the gust load allevivation system with a forward looking sensor[154] |
2002年,欧盟出资8千万欧元,资助空客公司和多个国家的共23个单位开始了AWIATOR (aircraft wing with advanced technology operation)计划,其中德国DLR为空客A340飞机开发一套GLA控制系统. 在GLA技术验证机中,配有机载LIDAR系统,能够为GLA系统提供足够的前视距离. 基于此,DLR提出了一种基于动态前馈控制器的翼根弯矩控制方法. 试飞结果表明,实施GLA控制后,翼根结构载荷减小了30%$\sim$40%,乘坐舒适性改善了5%$\sim$10%[155].在飞机前视突风信息可获得的前提下,使用模型预测控制来实现GLA较为方便. 最近,作者团队[156]采用模型预测控制研究了某民机的GLA控制,发现施加GLA控制后,翼根弯矩均方根值减小了43.3%.
除LIDAR传感器外,GLA控制还可使用alpha传感器. 与LIDAR传感器不同,alpha传感器探测的是传感器安装位置处的当地迎 角$\alpha_{\rm air}(t)$,包括由于突风产生的迎角分量和由于飞机运动产生的迎角分量. GLA控制仅需要突风诱导迎角$\alpha_{\rm w} (t)$,可根据下式计算[157]
| $\begin{array}{l} {\alpha _{\rm{w}}}(t) = \cos (\Phi (t))\left[{\arcsin \left( {\frac{{\dot H(t)}}{{{U_{{\rm{TAS}}}}(t)}}} \right) - \Theta (t)} \right. + \\ \cos (\Phi (t))\left( {{\alpha _{{\rm{air}}}}(t) + \frac{{q(t) \cdot {r_{{\rm{AOA}}}}}}{{{U_{{\rm{TAS}}}}(t)}}} \right) + \\ \left. {\sin (\Phi (t))\left( {\beta - \frac{{r(t) \cdot {r_{{\rm{AOS}}}}}}{{{U_{{\rm{TAS}}}}(t)}}} \right)} \right]n \end{array}$ | (42) |
式中,$\varPhi $为滚转角,$\dot {H}(t)$为飞机垂直速度,$U_{\rm TAS} $为气流速度,$\varTheta $为俯仰角,$q$为俯仰角速率,$r_{\rm AOA} $为飞机重心到alpha传感器之间的距离,$\beta $为侧滑角,$r$为偏航角速率,$r_{\rm AOS} $为飞机重心到侧滑角传感器之间的距离.
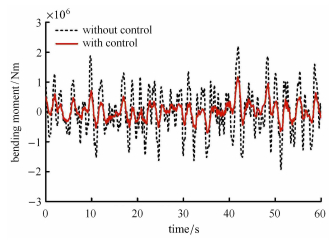
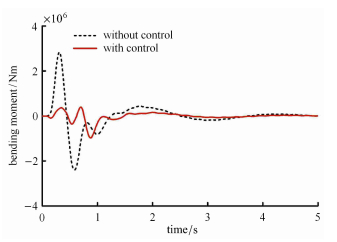
基于图 22中alpha传感器测量的突风扰动信息,作者团队开展了大型运输类飞机的GLA自适应前馈控制研究. 取对称偏转副翼和升 降舵为GLA控制面,飞机飞行速度为244 m/s. 图 23是突风速度均方根$\sigma_{\rm w} = 1.0$ m/s时,开环和闭环状态下翼根弯矩响应的对比. 结果表明,对于连续突风,施加GLA控制后,翼根弯矩的均方根值减小了60.12%. 对于1-cos离散突风,图 24是最大突风速度为5 m/s时开环和闭环翼根弯矩的对比. 该图表明,当施加GLA控制后,翼根弯矩最大值减小了65.81%.
|
图 22 Alpha 传感器和输出信号监控站位 Fig.22 Monitoring positions of alpha sensor and output signals |
|
图 23 Dryden 突风谱下无控与有控翼根弯矩响应对比 Fig.23 Comparison of the bending moments of wing root under Dryden gust with and without control |
|
图 24 1-cos 突风下翼根弯矩响应 Fig.24 Comparison of the bending moments of wing root under 1-cos gust with and without control |
突风载荷减缓是运输类飞机优先采用的三大主动控制技术之一,但其实际应用尚有较大技术风险,必须具有足够的技术储备. 美国在大型飞机研制中使用的GLA控制技术直接得益于20世纪70年代以来积累的成功经验. 在我国航空科技界,尚未见到以验证GLA控制系统为目的飞机试飞.
4 气动弹性控制风洞实验对气动弹性主动控制技术进行风洞实验是将其投入工程应用前必不可少的关键环节. 气动弹性控制律往往是基于较为理想的数学模型来设计的,未涉及一些约束控制器性能的实际因素. 例如,结构建模时无法精确考虑的各种阻尼、空气动力计算的误差等因素都会显著降低控制器的性能. 伺服舵机的功率需求、响应时间滞后等也是约束控制器性能的重要因素. 本节将分别介绍亚音速和跨音速两个方面的气动弹性控制风洞实验研究进展.
4.1 亚音速气动弹性控制风洞实验近20年来,亚音速颤振主动抑制的风洞实验研究取得了较为丰硕的成果. 目前,NASA兰利研究中心在这方面的研究处于世界领先地位. 该研究中心以``AAW计划''为支撑[158],在跨音速动态风洞中开展了颤振主动抑制风洞实验研究. Hoadley和McGraw[159]为主动气动弹性机翼的风洞实验开发了一套多功能数字化控制系统,可同时执行AFS控制和滚转机动载 荷减缓控制. Wieseman等[160]开发了多种在线分析工具,用于支撑主动气动弹性机翼风洞测试. 这些在线分析工具主要用来检验控制律的执行情况、满足控制律设计者的分析需求、提供实时环境下系统的稳定性测量等. Waszak和Srinathkumar[43]采用经典控制理论设计了一套AFS控制律,并进行了风洞实验验证.
自20世纪90年代起,意大利米兰理工大学在亚音速AFS实验研究方面也开展了深入研究. Ghiringhelli等[161]以三维机翼模 型为研究对象,采用极点配置方法设计经典反馈控制律,并进行了风洞实验验证. Andrighettoni和Mantegazza[67]、Bernelli-Zazzera等[68]以图 25中带前后缘控制面的大展弦比机翼(长度 单位为毫米)为对象,分别设计自适应控制律,并进行了风洞实验验证. 近年来,该研究团队又以代号为``X-DIA''的新概念飞机为对象,开展亚音速颤振主动抑制风洞实验研究. 如图 26所示,``X-DIA''飞机是一种具有前掠鸭翼布局的商用运输机. Gaspari等[43]对``X-DIA''飞机的动力学特性、舵机伺服控制、颤振控制系统等方面开展了初步的风洞实验. Mattaboni等[69]采用递归神经网络模型设计全机AFS控制律,并进行了风洞实验研究,证实该控制律可将开环颤振速度提 高15%.

|
图 25 带前、 后缘控制面的大展弦比风洞模型 [67] Fig.25 High aspect ratio wind-tunnel model with leading-edge and trailing edge control surfaces[67] |
我国学者在亚音速AFS风洞实验研究方面也开展了相关工作. 例如,作者团队[56, 57]针对二元翼段的AFS问题,基 于鲁棒控制理论分别设计了$H_\infty $和$\mu $综合控制律,并进行了风洞实验研究. 陈桂彬等以带外挂的三角翼为对象,开展了AFS风洞实验研究. 唐长红和邹丛青[162]以理想极点分布和二次型指标作为双目标进行优化,设计输出反馈控制律,通过风洞实验证实该控制器可将颤振临界速度提高19.5%. 曹奇凯和陈桂彬[163]以最优控制的极点分布为理想极点,采用极点配置方法设计了SISO输出反馈控制器,在采用移相器对闭环系统的相位滞后进行补偿后,在风洞实验中将颤振临界速度提高了14%.
综上所述,亚音速气动弹性控制风洞实验研究取得了可喜的研究进展,但仍存在一些亟待解决的问题,如怎样处理动态测试系统中滤波器引起的群时延、提高作动器伺服跟踪精度、设计具有高稳定性裕度的气动弹性控制律等问题.
对于滤波器引起的群时延问题,作者团队[164]采用理论和实验相结合的方法进行了深入研究,发现群时延较大时会降低闭环系统的稳定性. 从工程应用角度,可通过如下两个途径来解决群时延问题:一是根据受控结构的动力学特性,设计低阶加速度信号滤波器,尽可能降低控制回路中的群时延量;二是努力提高气动弹性控制律的稳定性裕度,进而对控制回路的群时延进行补偿.
提高作动器的伺服跟踪精度是风洞实验成功与否的另一关键所在. 在风载作用下,若舵机伺服跟踪控制效果不好,往往导致控制面偏转指令与实际偏转角度存在一定的幅值和相位的差别,导致气动弹性控制效果欠佳. 在风洞实验过程中,采用带指令成形(command shaping)的增量式PID控制器来跟踪舵机的控制指令是一种较好的方案. 该控制方法的主要优点在于大大降低了控制指令与实际控制面偏转角间的相位差. 增量式PID的控制方程如下
| $$ \Delta V(k) = K_{\rm p} \left( {e(k) - e(k - 1)} \right) + K_{\rm i} e(k) +\\ \qquad K_{\rm d} \left( {e(k) - 2e(k - 1) + e(k - 2)} \right) $$ | (43) |
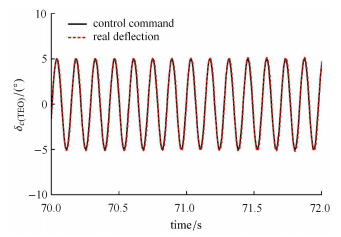
式中$K_{\rm p} $,$K_{\rm i} $和$K_{\rm d} $分别是比例、积分和微分系数,$e\left( k \right)$是当前时刻的角度跟踪误差. 图 27是流速为30 m/s时后缘控制面的偏转指令与实际偏转角度的对比. 由 图可见,带指令成形的PID控制方案在风载作用下能较为精确地跟踪作动器的控制指令.
|
图 27 流速 30 m/s 时作动器伺服跟踪效果 Fig.27 Tracking effectiveness of the actuator at flow speed of 30 m/s |
在气动弹性主动控制律设计中,考虑到气动载荷计算的不精确性、结构动力学建模误差等因素,有必要设计具有 高稳定性裕度的控制律. 本文1.2节中提及的时滞反馈控制方法在提高控制器相位裕度和闭环系统稳定性方面具有独特优势. 作者以图 28所示的小展弦比机翼为对象,开展了时滞最优反馈控制的风洞实验工作.

|
图 28 安装在 NH-2 风洞中的机翼模型 Fig.28 Wing model installed in NH-2 wind tunnel |
时滞最优反馈控制器设计过程可参考文献 [165],在此仅给出其数字化执行框图. 图 29是计入时滞的最优AFS控制器风洞 实验执行框图. 如图所示,计入时滞的最优AFS控制器的反馈信号包括经低通滤波器滤波后的加速度信号、控制指令的前$\alpha $时刻值$\delta _{{\rm c}\rm \left( {TE} \right)} \left( {k - \alpha } \right)$和控制指令的前$\left( {\alpha - 1} \right)$时刻值$\delta _{{\rm c}\left( {TE} \right)} \left( {k - \alpha + 1} \right)$. 图 30是流速为36.5 m/s时,施加时滞最优控制器前后所测量的加速度传感器时间响应历程. 该图表明,施加时滞最优控制器后,机翼模型的颤振得到了有效抑制.
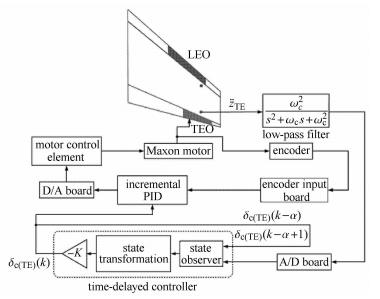
|
图 29 时滞最优控制风洞实验执行框图 Fig.29 Block diagram of the wind-tunnel implementation of time-delayed optimal control |
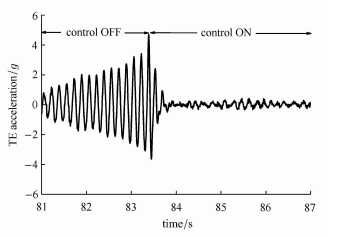
|
图 30 时滞最优控制器风洞实验测试效果 Fig.30 Measured control effectiveness of the time-delayed optimal controller at wind-tunnel tests |
与亚音速颤振主动抑制风洞实验研究相比,跨音速AFS风洞实验研究的起步较晚. 从公开发表的文献看,目前仅有NASA兰利研究中心开展了BACT计划[108, 109, 110]. 如图 31所示,BACT机翼为展弦比为2的平直机翼,在机翼展长的45%位置布置有控制面和上、下扰流片,这是目前世界上用于验证跨音速AFS研究的标准模型. 该模型的风洞实验是在NASA兰利研究中心的跨音速动态风洞中进行的,众多学者对该研究作出了贡献. 例如,Waszak[107]建立了BACT风洞实验模型的数学模型,并通过风洞实验验证了BACT机翼跨音速气动伺服弹性数学建模的准确性. Mukhopadhyay[116]、Waszak[117]、Scott和Pado[118]以及Haley和Soloway[166]分别以BACT机翼为研究对象,通过风洞实验验证了所设计的跨音速AFS控制律.
在跨音速颤振主动抑制风洞实验方面,虽然在BACT机翼上取得了较为理想的结果,但距离工程应用尚存在一定差距. BACT机翼为三维直机翼,气动外形方面考虑了三维跨音速气动力效应,但模型的结构动力学特性主要以沉浮、俯仰两个刚体模态为主,忽略了高阶弹性模态的影响. 对于工程中的三维飞机结构,当结构弹性模态较为密集时,跨音速空气动力非线性对各阶模态的影响十分复杂,显著增加了跨音速颤振主动抑制风洞实验的难度. 近年来,NASA兰利研究中心开展了半展长超声速运输机(semi-span super-sonic transport, S$^{4}$T)气动伺服弹性研究计划[168]. 图 32是S$^{4}$T飞机在NASA跨音速动态风洞中安装情况. 该研究计划重 点关注飞机在高亚音速和跨音速区域的气动弹性主动控制问题. 第一阶段的风洞实验主要测试突风载荷减缓控制与提高乘坐品质两方面. 从风洞实验结果来看,控制律的实际控制效果并不理想,其主要原因是对跨音速空气动力非线性的估计不足.
综上所述,跨音速非定常气动力的非线性特征导致跨音速气动弹性控制风洞实验研究十分困难. 当前,除了需要继续发展低阶、高鲁棒性的气动弹性控制方法外,还需要深入研究非线性空气动力对跨音速气动伺服弹性系统的影响,建立精确的非线性气动伺服弹性数学模型,从而指导跨音速气动弹性控制风洞实验的实施.
5 结 论结构气动弹性分析与控制是飞机设计中的关键动力学与控制问题. 自20世纪80年代起,气动弹性主动控制技术取得了丰硕研究成果,有望为飞机设计带来跨越式发展. 但该技术要真正应用于航空工程,尚有不少具有挑战性的问题. 在今后一个时期,以下几个问题值得关注:
(1)在亚音速气动弹性主动控制方面,为充分发挥主动控制技术在颤振抑制中的作用及扩大颤振抑制范围,应继续开展多输入/多 输出的低阶鲁棒控制器设计研究,并加强风洞实验验证.
(2)在跨音速气动弹性主动控制方面,应重点研究如下几个问题:一是气动力非线性和控制面铰链间隙非线性联合作用下的气动 弹性控制问题;二是提高非线性降阶模型在预测非线性气动弹性/气动伺服弹性行为的精度,特别是考虑初始攻角情况下的非线性 气动弹性/气动伺服弹性问题;三是针对激波运动、气流黏性效应等非线性因素,设计更为有效的鲁棒控制器;四是开展跨音速颤 振主动抑制的风洞实验研究.
(3)在突风载荷减缓控制方面,要充分认识问题的特殊性,包括控制作动方式(如控制面偏转角度和角速率受限)、载荷性质与激 励形式(如气动载荷是具有反馈属性的气动力与具有外激励属性的气动力之叠加)、飞行状态(如高度/动压/马赫数变化)和关键参 数感知方式(如突风速度的感知)等,使得对GLA控制的研究具有针对性. 应重点研究如下几个问题:一是基于CFD的突风和反馈型非定常气动力的降阶建模,为气动伺服弹性建模提供精确的、低维的、好用的非定常气动力模型;二是参变气动伺服弹性系统的建模,以适应飞机飞行参数的变化;三是基于先知突风信息的前馈控制和模型预测控制;四是突风载荷减缓的风洞实验.
| 1 | Pendleton EW, Bessette D, Field PB, et al. Active aeroelastic wing flight research program: Technical program and model analytical development. Journal of Aircraft, 2000, 37(4): 554-561 |
| 2 | 陈桂彬, 邹丛青, 杨超. 气动弹性设计基础. 北京: 北京航空航天大 学出版社, 2004 (Chen Guibin, Zou Congqing, Yang Chao. Fundamentals of Aeroelastic Design. Beijing: Press of Beijing University of Aeronautics and Astronautics, 2004 (in Chinese)) |
| 3 | Pendleton E, Flick P, Paul D, et al. The X-53: A summary of the active aeroelastic wing flight research program. AIAA 2007-1855,2007 |
| 4 | Stull RB. Ahrens CD. Meteorology for Scientists and Engineers. Brooks/Cole, Pacific Grove, California, 2000 |
| 5 | Wright JR. Cooper JE. Introduction to Aircraft Aeroelasticity and Loads. John Wiley and Sons, Ltd., West Sussex, England, 2007 |
| 6 | Burris PM. Bender MA. Aircraft load alleviation and mode stabilization (LAMS) - B-52 system analysis, synthesis, and design. AFFDL-TR-68-161, 1969 |
| 7 | 高金源, 焦宗夏, 张平. 飞机电传操纵系统与主动控制技术, 北京: 北京航空天大学出版社, 2005 (Gao Jinyuan, Jiao Zongxia, Zhang Ping. Aircraft Electrical Control System and Active Control Technology. Beijing: Press of Beijing University of Aeronautics and Astronautics, 2005 (in Chinese)) |
| 8 | Denegri CM. Limit cycle oscillation flight test results of a fighter with external stores. Journal of Aircraft, 2000, 37(5): 761-769 |
| 9 | Chen YM, Liu JK, Meng G. Equivalent damping of aeroelastic system of an airfoil with cubic sti ness. Journal of Fluids and Structures,2011, 27(8): 1447-1454 |
| 10 | Peng C, Han J. Numerical investigation of the e ects of structural geometric and material nonlinearities on limit-cycle oscillation of a cropped delta wing. Journal of Fluids and Structures, 2011, 27(4):611-622 |
| 11 | Thomas JP, Dowell EH, Hall KC. Nonlinear inviscid aerodynamic e ects on transonic divergence, flutter, and limit-cycle oscillations. AIAA Journal, 2002, 40(4): 638-646 |
| 12 | Stanford B, Beran P. Direct flutter and limit cycle computations of highly flexible wings for e cient analysis and optimization. Journal of Fluids and Structures, 2013, 36(1): 111-123 |
| 13 | Munteanu SL, Rajadas J, Nam C, et al. Reduced-order-model approach for aeroelastic analysis involving aerodynamic and structural nonlinearities. AIAA Journal, 2005, 43(3): 560-571 |
| 14 | Patil MJ, Hodges DH. On the importance of aerodynamic and structural geometrical nonlinearities in aeroelastic behavior of highaspect- ratio wings. Journal of Fluids and Structures, 2004, 19(7):905-915 |
| 15 | Tang DM, Dowell EH. E ects of geometric structural nonlinearity on flutter and limit cycle oscillations of high-aspect-ratio wings. Journal of Fluids and Structures, 2004, 19(3): 291-306 |
| 16 | Garcia JA. Numerical investigation of nonlinear aeroelastic e ects on flexible high-aspect-ratio wings. Journal of Aircraft, 2005, 42(4):1025-1036 |
| 17 | Patil MJ, Hodges DH, Cesnik CE. Limit-cycle oscillations in highaspect- ratio wings. Journal of Fluids and Structures, 2001, 15(1):107-132 |
| 18 | Zhao LC, Yang ZC. Chaotic motions of an airfoil with non-linear sti ness in incompressible flow. Journal of Sound and Vibration,1990, 138(2): 245-254 |
| 19 | Yang ZC, Zhao LC. Analysis of limit cycle flutter of an airfoil in incompressible flow. Journal of Sound and Vibration, 1988, 123(1):1-13 |
| 20 | Zhao YH, Hu HY. Aeroelastic analysis of a non-linear airfoil based on unsteady vortex lattice model. Journal of Sound and Vibration,2004, 276(3): 491-510 |
| 21 | Dowell EH, Tang DM. Nonlinear aeroelasticity and unsteady aerodynamics. AIAA Journal, 2002, 40(9): 1697-1707 |
| 22 | Gold P, Karpel M. Reduced-size aeroservoelastic modeling and limit-cycle-oscillation simulations with structurally nonlinear actuators. Journal of Aircraft, 2008, 45(2): 471-477 |
| 23 | Conner MD, Tang DM, Dowell EH, et al. Nonlinear behavior of a typical airfoil section with control surface free-play: A numerical and experimental study. Journal of Fluids and Structures, 1997,11(1): 89-109 |
| 24 | Tang DM, Dowell EH, Virgin LN. Limit cycle behavior of an airfoil with a control surface. Journal of Fluids and Structures, 1998,12(7): 839-858 |
| 25 | Gordon JT, Meyer EE, Minogue RL. Nonlinear stability analysis of control surface flutter with freeplay e ects. Journal of Aircraft,2008, 45(6): 1904-1916 |
| 26 | Dowell EH, Thomas JP, Hall KC. Transonic limit cycle oscillation analysis using reduced order aerodynamic models. Journal of Fluids and Structures, 2004, 19(1): 17-27 |
| 27 | Jones DP, Roberts I, Gaitonde AL. Identification of limit cycles for piecewise nonlinear aeroelastic systems. Journal of Fluids and Structures, 2007, 23(7): 1012-1028 |
| 28 | 李道春, 向锦武. 间隙非线性气动弹性颤振控制. 北京航空航天 大学学报, 2007, 33(6): 640-643 (Li Daochun, Xiang Jinwu. Flutter control of aeroelasticity with freeplay nonlinearity. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(6): 640-643 (in Chinese)) |
| 29 | ShinW, Lee S, Lee I, et al. E ects of actuator nonlinearity on aeroelastic characteristics of a control fin. Journal of Fluids and Structures,2007, 23(7): 1093-1105 |
| 30 | 管德, 宗捷. 结构非线性对颤振特性的影响. 北京航空航天大学学 报, 1994, 20(4): 357-361 (Guan De, Zong Jie. Impact of structural nonlinearities on flutter. Journal of Beijing University of Aeronautics and Astronautics, 1994, 20(4): 357-361 (in Chinese)) |
| 31 | Karpel M, Raveh D. Fictitious mass element in structural dynamics. AIAA Journal, 1996, 34(3): 607-613 |
| 32 | Bae J, Inman DJ, Lee I. E ects of structural nonlinearity on subsonic aeroelastic characteristics of an aircraft wing with control surface. Journal of Fluids and Structures, 2004, 19(6): 747-763 |
| 33 | Kim JY, Kim KS, Lee I, et al. Transonic aeroelastic analysis of allmovable wing with free play and viscous e ects. Journal of Aircraft,2008, 45(5): 1820-1824 |
| 34 | Lee DH, Chen PC. Nonlinear aeroelastic studies on a folding wing configuration with free-play hinge nonlinearity. AIAA 2006-1734,2006 |
| 35 | Lee I, Kim S. Aeroelastic analysis of a flexible control surface with structural nonlinearity. Journal of Aircraft, 1995, 32(4): 868-874 |
| 36 | Bae J, Yang S, Lee I. Linear and nonlinear aeroelastic analysis of fighter-type wing with control surface. Journal of Aircraft, 2002,39(4): 697-708 |
| 37 | Frampton KD, Clark RL. Experiments on control of limit-cycle oscillations in a typical section. Journal of Guidance,Control,and Dynamics, 2000, 23(5): 956-960 |
| 38 | Huang R, Hu HY, Zhao YH. Nonlinear aeroservoelastic analysis of a controlled multiple-actuated-wing model with free-play. Journal of Fluids and Structures, 2013, 42(1): 245-269 |
| 39 | 王在华, 胡海岩. 时滞动力系统的稳定性与分岔: 从理论走向应 用. 力学进展, 2013, 43(1): 3-20 (Wang Zaihua, Hu Haiyan. Stability and bifurcation of delayed dynamic systems: from theory to application. Advances in Mechanics, 2013, 43(1): 3-20 (in Chinese)) |
| 40 | Huang XY. Active control of aerofoil flutter. AIAA Journal, 1987,25(8): 1126-1132 |
| 41 | Luton JA, Mook DT. Numerical simulations of flutter and its suppression by active control. AIAA Journal, 1993, 31(12): 2312-2319 |
| 42 | Waszak MR, Srinathkumar S. Flutter suppression for the active flexible wing: A classical design. Journal of Aircraft, 1995, 32(1): 61-67 |
| 43 | Gaspari AD, Ricci S, Riccobene L, et al. Active aeroelastic control over a multi-surface wing: Modeling and wind-tunnel testing. AIAA Journal, 2009, 47(9): 1995-2010 |
| 44 | Librescu L, Marzocca P, SilvaWA. Aeroelasticity of 2-D lifting surfaces with time-delayed feedback control. Journal of Fluids and Structures, 2005, 20(2): 197-215 |
| 45 | Marzocca P, Librescu L, Silva WA. Time-delay e ects on linear/ nonlinear feedback control of simple aeroelastic systems. Journal of Guidance,Control,and Dynamics, 2005, 28(1): 53-62 |
| 46 | Zhao YH. Stability of a two-dimensional airfoil with time-delayed feedback control. Journal of Fluids and Structures, 2009, 25(1):1-25 |
| 47 | Zhao YH. Stability of a time-delayed aeroelastic system with a control surface. Aerospace Science and Technology, 2011, 15(1): 72-77 |
| 48 | Ramesh M, Narayanan S. Controlling chaotic motions in a twodimensional airfoil using time-delayed feedback. Journal of Sound and Vibration, 2001, 239(5): 1037-1049 |
| 49 | Yuan Y, Yu P, Librescu L, et al. Aeroelasticity of time-delayed feedback control of two-dimensional supersonic lifting surfaces. Journal of Guidance,Control,and Dynamics, 2004, 27(5): 795-803 |
| 50 | Haraguchi M, Hu HY. Using a new discretization approach to design a delayed LQG controller. Journal of Sound and Vibration, 2008,314(3): 558-570 |
| 51 | Huang R, Hu HY, Zhao YH. Designing active flutter suppression for high-dimensional aeroelastic systems involving a control delay. Journal of Fluids and Structures, 2012, 34(1): 33-50 |
| 52 | Mukhopadhyay V. Flutter suppression control law design and testing for the active flexible wing. Journal of Aircraft, 1995, 32(1): 45-51 |
| 53 | Mukhopadhyay V. Digital robust control law synthesis using constrained optimization. Journal of Guidance,Control,and Dynamics,1989, 12(2): 175-181 |
| 54 | Mukhopadhyay V, Newsom JR, Abel I. Reduced-order optimal feedback control law synthesis for flutter suppression. Journal of Guidance, Control,and Dynamics, 1982, 5(4): 389-395 |
| 55 | 杨超, 宋晨, 吴志刚等. 多控制面飞机的全机颤振主动抑制设计. 航空学报, 2010, 31(8): 1501-1508 (Yang Chao, Song Chen, Wu Zhigang, et al. Active flutter suppression of airplane configuration with multiple control surfaces. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1501-1508 (in Chinese)) |
| 56 | 于明礼, 文浩, 胡海岩. 二维翼段颤振的H1 控制. 振动工程学 报, 2006, 19(3): 326-330 (Yu Mingli, Wen Hao, Hu Haiyan. Active flutter suppression of a two-dimensional airfoil using H1 synthesis. Journal of Vibration Engineering, 2006, 19(3): 326-330 (in Chinese)) |
| 57 | 于明礼, 文浩, 胡海岩等. 二维翼段颤振的 控制. 航空学报,2007, 28(2): 340-343 (Yu Mingli, Wen Hao, Hu Haiyan, et al. Active flutter suppression of a two dimensional airfoil section using synthesis. Acta Aeronautica et Astronautica Sinica, 2007, 28(2):340-343 (in Chinese)) |
| 58 | Livne E. Future of airplane aeroelasticity. Journal of Aircraft, 2003,40(6): 1066-1092 |
| 59 | Ko J, Kurdila AJ, Strganac TW. Nonlinear control of a prototypical wing section with torsional nonlinearity. Journal of Guidance, Control, and Dynamics, 1997, 20(6): 1181-1189 |
| 60 | Singh SN,Wang L. Output feedback form and adaptive stabilization of a nonlinear aeroelastic system. Journal of Guidance,Control, and Dynamics, 2002, 25(4): 725-732 |
| 61 | Behal A, Rao VM, Marzocca P, et al. Adaptive control for a nonlinear wing section with multiple flaps. Journal of Guidance, Control,and Dynamics, 2006, 29(3): 744-749 |
| 62 | Wang Z, Behal A, Marzocca P. Model-free control design for multiinput multi-output aeroelastic system subject to external disturbance. Journal of Guidance,Control,and Dynamics, 2011, 34(2):446-458 |
| 63 | Zhang R, Singh SN. Adaptive output feedback control of an aeroelastic system with unstructured uncertainties. Journal of Guidance, Control,and Dynamics, 2001, 24(3): 502-509 |
| 64 | Peloubet Jr RP, Haller RL, Bolding RM. F-16 flutter suppression system investigation feasibility study and wind tunnel tests. Journal of Aircraft, 1982, 19(2): 169-175 |
| 65 | Peloubet RP, Haller RL, Bolding RM. Online adaptive control of unstable aircraft wing flutter. //Proceedings of the 29th Conference on Decision and Control, Honolulu, Hawaii, USA, 1990 |
| 66 | Johnson T, Harvey C, Stein GÌN. Self-tuning regulator design for adaptive control of aircraft wing/store flutter. Automatic Control, IEEE Transactions On, 1982, 27(5): 1014-1023 |
| 67 | Andrighettoni M, Mantegazza P. Multi-input/multi-output adaptive active flutter suppression for a wing model. Journal of Aircraft,1998, 35(3): 462-469 |
| 68 | Bernelli-Zazzera F, Mantegazza P, Mazzoni G, et al. Active flutter suppression using recurrent neural networks. Journal of Guidance, Control, and Dynamics, 2000, 23(6): 1030-1036 |
| 69 | Mattaboni M, Quaranta G, Mantegazza P. Active flutter suppression for a three-surface transport aircraft by recurrent neural networks. Journal of Guidance,Control,and Dynamics, 2009, 32(4): 1295-1307 |
| 70 | Ioannou PA, Sun J. Robust Adaptive Control. Courier Dover Publications,2012 |
| 71 | Slotine JE, Li W. Applied Nonlinear Control. Prentice-Hall Englewood Cli s, NJ: Prentice-Hall, 1991 |
| 72 | Huang R, Hu HY, Zhao YH. Single-input/single-output adaptive flutter suppression of a three-dimensional aeroelastic system. Journal of Guidance,Control,and Dynamics, 2012, 35(2): 659-665 |
| 73 | Bendiksen OO. Role of shock dynamics in transonic flutter. AIAA 1992-2121, 1992 |
| 74 | Liu F, Cai J, Zhu Y, et al. Calculation of wing flutter by a coupled fluid-structure method. Journal of Aircraft, 2001, 38(2): 334-342 |
| 75 | Hall KC, Thomas JP, Dowell EH. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows. AIAA Journal,2000, 38(10): 1853-1862 |
| 76 | Cowan TJ, Arena AS, Gupta KK. Accelerating computational fluid dynamics based aeroelastic predictions using system identification. Journal of Aircraft, 2001, 38(1): 81-87 |
| 77 | Gupta KK, Bach C. Systems identification approach for a computational-fluid-dynamics- based aeroelastic analysis. AIAA Journal, 2007, 45(12): 2820-2827 |
| 78 | Silva WA, Bartels RE. Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3Dv6.0 code. Journal of Fluids and Structures, 2004, 19(6): 729-745 |
| 79 | Kim T. E cient reduced-order system identification for linear systems with multiple inputs. AIAA Journal, 2005, 43(7): 1455-1464 |
| 80 | Kim T, Hong M, Bhatia KG, et al. Aeroelastic model reduction for a ordable computational fluid dynamics-based flutter analysis. AIAA Journal, 2005, 43(12): 2487-2495 |
| 81 | Silva WA. Simultaneous excitation of multiple-input/multipleoutput CFD-based unsteady aerodynamic systems. Journal of Aircraft,2008, 45(4): 1267-1274 |
| 82 | Kim T. System identification for coupled fluid-structure: aerodynamics is aeroelasticity minus structure. AIAA Journal, 2011, 49(3):503-512 |
| 83 | Raveh DE. Identification of computational-fluid-dynamics based unsteady aerodynamic models for aeroelastic analysis. Journal of Aircraft,2004, 41(3): 620-632 |
| 84 | Thomas JP, Dowell EH, Hall KC. A harmonic balance approach for modeling three-dimensional nonlinear unsteady aerodynamics and aeroelasticity.//IMECE-2002-32532, Proceedings of ASME International Mechanical Engineering Conference and Exposition, New Orleans, Louisiana, USA, 2002 |
| 85 | Hall KC, Thomas JP, Clark WS. Computation of unsteady nonlinear flows in cascades using a harmonic balance technique. AIAA Journal,2002, 40(5): 879-886 |
| 86 | Thomas JP, Dowell EH, Hall KC. Modeling viscous transonic limit cycle oscillation behavior using a harmonic balance approach. Journal of Aircraft, 2004, 41(6): 1266-1274 |
| 87 | Thomas JP, Dowell EH, Hall KC, et al. Further investigation of modeling limit cycle oscillation behavior of the F-16 fighter using a harmonic balance approach.AIAA 2005-1917, 2005 |
| 88 | Liu L, Thomas JP, Dowell EH, et al. A comparison of classical and high dimensional harmonic balance approaches for a Du ng oscillator. Journal of Computational Physics, 2006, 215(1): 298-320 |
| 89 | Thomas JP, Custer CH, Dowell EH, et al. Unsteady flow computation using a harmonic balance approach implemented about the OVERFLOW 2 flow solver. AIAA 2009-4270, 2009 |
| 90 | Marques FD, Anderson J. Identification and prediction of unsteady transonic aerodynamic loads by multi-layer functionals. Journal of Fluids and Structures, 2001, 15(1): 83-106 |
| 91 | Zhang WW, Wang B, Ye ZY, et al. E cient method for limit cycle flutter analysis based on nonlinear aerodynamic reduced-order models. AIAA Journal, 2012, 50(5): 1019-1028 |
| 92 | Glaz B, Friedmann PP, Liu L, et al. Reduced-order dynamic stall modeling with swept flow e ects using a surrogate-based recurrence framework. AIAA Journal, 2013, 51(4): 910-921 |
| 93 | 陈刚, 李跃明. 非定常流场降阶模型及其应用研究进展与展望. 力学进展, 2011, 41(6): 686-701 (Chen Gang, Li Yueming. Advances and prospects of the reduced order model for unsteady flow and its application. Advances in Mechanics, 2011, 41(6): 686-701 (in Chinese)) |
| 94 | Silva WA. Application of nonlinear systems theory to transonic unsteady aerodynamic responses. Journal of Aircraft, 1993, 30(5):660-668 |
| 95 | SilvaW. Identification of nonlinear aeroelastic systems based on the Volterra theory: progress and opportunities. Nonlinear Dynamics,2005, 39(1): 25-62 |
| 96 | Raveh DE. Reduced-order models for nonlinear unsteady aerodynamics. AIAA Journal, 2001, 39(8): 1417-1429 |
| 97 | Marzocca P, Librescu L, Silva WA. Aeroelastic response of nonlinear wing sections using a functional series technique. AIAA Journal,2002, 40(5): 813-824 |
| 98 | Marzocca P, Silva WA, Librescu L. Nonlinear open-/closed-loop aeroelastic analysis of airfoils via Volterra series. AIAA Journal,2004, 42(4): 673-686 |
| 99 | Munteanu S, Rajadas J, Nam C, et al. An e cient approach for solving nonlinear aeroelastic phenomenon using reduced-order modeling. AIAA 2004-2037, 2004 |
| 100 | Balajewicz M, Nitzsche F, Feszty D. Application of multi-input Volterra theory to nonlinear multi-degree-of-freedom aerodynamic systems. AIAA Journal, 2010, 48(1): 56-62 |
| 101 | Balajewicz M, Dowell EH. Reduced-order modeling of flutter and limit-cycle oscillations using the sparse Volterra series. Journal of Aircraft, 2012, 49(6): 1803-1812 |
| 102 | Hunter IW, Korenberg MJ. The identification of nonlinear biological systems: Wiener and Hammerstein cascade models. Biol Cybern,1986, 55(2-3): 135-144 |
| 103 | Westwick DT. Methods for the identification of multiple-input nonlinear systems. [PhD Thesis]. McGill University, 1995 |
| 104 | Huang R, Hu HY, Zhao YH. Nonlinear reduced-order modeling for multiple-input/multiple-output aerodynamic systems. AIAA Journal,2014, 52(6): 1219-1231 |
| 105 | More JJ. The Levenberg-Marquardt Algorithm: Implementation and Theory. Springer, 1978: 105-116 |
| 106 | Isogai K. On the transonic-dip mechanism of flutter of a sweptback wing. AIAA Journal, 1979, 17(7): 793-795 |
| 107 | Waszak MR. Modeling the benchmark active control technology wind-tunnel model for application to flutter suppression. AIAA 1996-3437, 1996 |
| 108 | Mukhopadhyay V. Benchmark active control technology: part I. Journal of Guidance, Control, and Dynamics, 2000, 23(5): 913 |
| 109 | Mukhopadhyay V. Benchmark active control technology special section: part II. Journal of Guidance,Control,and Dynamics, 2000,23(6): 1093 |
| 110 | Mukhopadhyay V. Benchmark active control technology special section: part III. Journal of Guidance,Control,and Dynamics, 2001,24(1): 146 |
| 111 | Huang R, Li HK, Hu HY, et al. Open-/closed-loop aeroservoelastic predictions via nonlinear, reduced-order aerodynamic models. AIAA Journal, 2015, 53(7): 1812-1824 |
| 112 | Van Gestel T, Suykens JA, Van Dooren P, et al. Identification of stable models in subspace identification by using regularization. IEEE Transactions on Automatic Control, 2001, 46(9): 1416-1420 |
| 113 | Zhang WW, Ye ZY. Control law design for transonic aeroservoelasticity. Aerospace Science and Technology, 2007, 11(2): 136-145 |
| 114 | Stephens CH, Arena AS, Gupta KK. CFD-based aeroservoelastic predictions with comparisons to benchmark experimental data. AIAA 1999-16615, 1999 |
| 115 | Friedmann PP, Guillot D, Presente E. Adaptive control of aeroelastic instabilities in transonic flow and its scaling. Journal of Guidance, Control,and Dynamics, 1997, 20(6): 1190-1199 |
| 116 | Mukhopadhyay V. Transonic flutter suppression control law design and wind-tunnel test results. Journal of Guidance, Control, and Dynamics,2000, 23(5): 930-937 |
| 117 | Waszak MR. Robust multivariable flutter suppression for benchmark active control technology wind-tunnel model. Journal of Guidance, Control,and Dynamics, 2001, 24(1): 147-153 |
| 118 | Scott RC, Pado LE. Active control of wind-tunnel model aeroelastic response using neural networks. Journal of Guidance Control and Dynamics, 2000, 23(6): 1100-1108 |
| 119 | 赵永辉. 气动弹性力学与控制. 北京: 科学出版社, 2007 (Zhao Yonghui. Aeroelasticity and Control. Beijing: Science Press, 2007 (in Chinese)) |
| 120 | Etkin B. Theory of the flight of airplanes in isotropic turbulencereview and extension. AGARD Rep, 1961, 372 |
| 121 | Karpel M, Moulin B. Aeroservoelastic gust response analysis for the design of transport aircrafts. AIAA 2004-1592, 2004 |
| 122 | Crimaldi JP, Britt RT, Rodden WP. Response of B-2 aircraft to nonuniform spanwise turbulence. Journal of Aircraft, 1993, 30(5):652-659 |
| 123 | 陈磊, 吴志刚, 杨超. 多控制面机翼阵风减缓主动控制与风洞试验 验证. 航空学报, 2009, 30(12): 2250-2256 (Chen Lei, Wu Zhigang, Yang Chao, et al. Active control and wind tunnel test verification of multi-control surfaces wing for gust alleviation. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2250-2256 (in Chinese)) |
| 124 | Karpel M, Moulin B, Chen PC. Dynamic response of aeroservoelastic systems to gust excitation. Journal of Aircraft, 2005, 42(5):1264-1272 |
| 125 | 费玉华. 阵风减缓直接升力控制方案的仿真研究. 飞行力学,2000, 18(1): 69-72 (Fei Yuhua. Direct lift force control plan about gust load alleviation modeling and simulation. Flight Dynamics,2000, 18(1): 69-72 (in Chinese)) |
| 126 | Moulin B, Karpel M. Gust loads alleviation using special control Surfaces. Journal of Aircraft, 2007, 44(1): 17-24 |
| 127 | Gangsaas D, Ly U, Norman DC. Practical gust load alleviation and flutter suppression control laws based on a LQG methodology. AIAA 1981-0021, 1981 |
| 128 | Dillsaver MJ, Cesnik CES, Kolmanovsky IV. Gust load alleviation control for very flexible aircraft. AIAA 2011-6368, 2011 |
| 129 | Matsuzaki Y, Ueda T, Miyazawa Y. Gust load alleviation of a transport-type wing: test and analysis. Journal of Aircraft, 1989,26(4): 322-327 |
| 130 | Cook RG, Palacios R. Robust gust alleviation and stabilization of very flexible aircraft. AIAA Journal, 2013, 51(2): 330-340 |
| 131 | Wildschek A, Stroscher F. Gust load alleviation on a large blended wing body airliner. Proc. of 27th International Congress of the Aeronautic Sciences, 2010. 1-10 |
| 132 | Balas GJ, Moreno C, Seiler PJ. Robust aeroservoelastic control utilizing physics-based aerodynamic sensing. AIAA 2012-4897, 2012 |
| 133 | Gili PA, Ruotolo R. A neural gust alleviation for a non-linear combat aircraft model. AIAA 1997-3761, 1997 |
| 134 | Shao K, Wu ZG, Yang C, et al. Design of an adaptive gust response alleviation control system: simulations and experiments. Journal of Aircraft, 2010, 47(3): 1022-102 |
| 135 | Regan CD, Jutte CV. Survey of applications of active control technology for gust alleviation and new challenges for lighter-weight aircraft. NASA- TM 2012-216008 |
| 136 | Disney TE. The C-5A active load alleviation system. AIAA 1975-991, 1975 |
| 137 | Wykes JH, Mori AS, Borland CJ. B-1 structural mode control system. AIAA 1972-772, 1972 |
| 138 | Honlinger H, Zimmermann H, Sensburg O. Structural aspects of active control technology. Proc. of AGARD Flight Mechanics Panel Symposium, Turin, Italy, 1995 |
| 139 | Britt RT, Volk JA, Dreim DR, et al. Aeroservoelastic characteristics of the B-2 bomber and implications for future large aircraft. Proc. of Structural Aspects of Flexible Aircraft Control Specialists Meeting,2000 |
| 140 | Norris G,Wagner M. Airbus A380: Superjumbo of the 21st Century. Zenith Press, St. Paul, Minnesota, 2005 |
| 141 | Norris G, Wagner M. Boeing 787 Dream Liner. Zenith Press, Minneapolis, Minnesota, 2009 |
| 142 | Baldelli DH, Chen PC. Unified aeroelastic and flight dynamic formulation via rational function approximations. Journal of Aircraft,2006, 43(3): 763-772 |
| 143 | Chen PC, Baldelli DH, Zeng J. Dynamic flight simulation (DFS) tool for nonlinear flight dynamic simulation including aeroelastic e ects. AIAA 2008-6376, 2008 |
| 144 | Meirovitch L, Tuzcu I. Unified theory for the dynamics and control of maneuvering flexible aircraft. AIAA Journal, 2004, 42(4): 714-727 |
| 145 | Raveh DE. Gust response analysis of free elastic aircraft in the transonic flight regime. Journal of Aircraft, 2011, 48(4): 1204-1211 |
| 146 | Bogue RK, Jentink HW. Optical air flow measurements in flight. NASA-TP2004-210735, 2004 |
| 147 | Rabadan GJ, Schmitt NP. Airborne lidar for automatic feedforward control of turbulent in-flight phenomena. Journal of Aircraft, 2010,47(2): 392-403 |
| 148 | Wildschek A, Maier R, Ho mann F. Active wing load alleviation with an adaptive feed-forward control algorithm.//Proc. of AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, August, 2006 |
| 149 | Wildschek A, Maier R, Jategaonkar R. Augmentation of active wing bending control with a supplementary adaptive feed-forward control algorithm.//Proc. of 2nd European Conference for Aerospace Sciences, Brussels, Belgium, EUCASS, 2007 |
| 150 | Zeng J, Moulin B, Callafon R. Adaptive feedforward control for gust load alleviation. Journal of Guidance,Control,and Dynamics,2010, 33(3): 862-872 |
| 151 | Wildschek A, Hanis T, Stroscher F. L-infinity optimal feedforward gust load alleviation design for a large blended wing body airliner. Progress in Flight Dynamics,GNC,and Avionics, 2013, 6: 707-728 |
| 152 | Schmitt N, Rehm W, Ziller T. The AWIATOR airborne LIDAR turbulence sensor. Aerospace Science and Technology, 2007, 11(1):546-552 |
| 153 | Schmitt N, RehmW, Pistner T. Flight test of the AWIATOR airborne LIDAR turbulence sensor.//Proc. of 14th Coherent Laser Radar Conference, Hunstville, AL, June, 2007 |
| 154 | Hahn KU, Schwarz C. Alleviation of atmospheric flow disturbance e ects on aircraft response, The 26th International Congress of the Aeronautical Sciences, Anchorage, Alaska, USA, 2008 |
| 155 | Hecker S, Hahn KU. Advanced gust load alleviation system for large flexible aircraft.//Proc. of First CEAS European Air and Space Conference,2007, CEAS-2007-110, Berlin, Germany |
| 156 | 胡志明, 赵永辉. 基于前视突风探测信息的飞机载荷减缓控制. 航空计算技术, 2015, 45(4): 33-37 (Hu Zhiming, Zhao Yonghui. Load alleviation for an aircraft based on forward looking gust information. Aeronautical Computing Technique, 2015, 45(4): 33-37 (in Chinese)) |
| 157 | Wildschek A, Bartosiewicz A, Mozyrska D. A multi-input multioutput adaptive feed-forward controller for vibration alleviation on a large blended wing body airliner. Journal of Sound and Vibration,2014, 333(17): 3859-3880 |
| 158 | Perry B, Cole SR, Miller GD. Summary of an active flexible wing program. Journal of Aircraft, 1995, 32(1): 10-15 |
| 159 | Hoadley ST, Mcgraw SM. Multiple-function digital controller system for active flexible wing wind-tunnel model. Journal of Aircraft,1995, 32(1): 32-38 |
| 160 | Wieseman CD, Hoadley ST, Mcgraw SM. On-line analysis capabilities developed to support the active flexible wing wind-tunnel tests. Journal of Aircraft, 1995, 32(1): 39-44 |
| 161 | Ghiringhelli GL, Lanz M, Mantegazza P. Active flutter suppression for a wing model. Journal of Aircraft, 1990, 27(4): 334-341 |
| 162 | 唐长红, 邹丛青. 利用双目标优化寻求颤振抑制控制律. 北京航空 航天大学学报, 1990, (2): 56-64 (Tang Changhong, Zou Congqing. Design of active flutter suppression control law using a dual optimization method. Journal of Beijing University of Aeronautics and Astronautics, 1990, (2): 56-64 (in Chinese)) |
| 163 | 曹奇凯, 陈桂彬. 机翼/外挂系统的颤振主动抑制研究. 航空学报,1991, 12(10): 453-458 (Cao Qikai, Chen Guibin. A study of active flutter suppression for a wing/store system. Acta Aeronautica et Astronautica Sinica, 1991, 12(10): 453-458 (in Chinese)) |
| 164 | 于明礼. 基于超声电机作动器的二维翼段颤振主动抑制. [博士 论文]. 南京: 南京航空航天大学,2006 (Yu Mingli. Active flutter suppression of a two-dimensional airfoil using ultrasonic motor. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics,2006 (in Chinese)) |
| 165 | Huang R, Qian WM, Hu HY, et al. Design of active flutter suppression and wind-tunnel tests of a wing model involving a control delay. Journal of Fluids and Structures, 2015, 55(1): 409-427 |
| 166 | Haley P, Soloway D. Generalized predictive control for active flutter suppression. Journal of Guidance,Control,and Dynamics, 2001,24(1): 154-159 |
| 167 | Scott RC, Hoadley ST, Wieseman CD, et al. Benchmark active controls technology model aerodynamic data. Journal of Guidance, Control,and Dynamics, 2000, 23(5): 914-921 |
| 168 | SilvaWA, Perry B, Florance JR, et al. An overview of the semi-span super-sonic transport (S4T) wind-tunnel model program. AIAA 2012-1552, 2012 |
| 169 | Zeng J, Kukreja SL. Flutter prediction for flight/wind-tunnel flutter test under atmospheric turbulence excitation. Journal of Aircraft,2013, 50(6): 1696-1709 |
 2016, Vol. 48
2016, Vol. 48