2. 大连理工大学工业装备结构分析国家重点实验室, 工程力学系, 大连 116024
人体维持平衡主要依靠前庭、视觉及本体感觉3个系统的相互协调来完成,其中前庭系统最为重要.
然而,前庭和半规管结构细微且位置深在,对其结构与功能之间关系及其相关发病机制的研究均受到限制. 目前临床检测和实验研究措施多是通过前庭$\!$-$\!$-$\!$眼动或脊髓反射间接评估前庭$\!$-$\!$-$\!$半规管功能状态,难以满足上述结构$\!$-$\!$-$\!$功能和疾病之间定性、定位甚至定量描述的实践需要,耳器官生物力学特性显著,通过生物数值模拟研究则可以满足现代耳科学研究的需要,已经成为近年来快速发展的一个新兴领域[1].
国内、外关于耳传声与感音功能的研究报道较多[2, 3, 4],其中有限元方法因为可以全面模拟超微结构特征、 复杂几何形态以及生物系统各向异性和非同质性的生物特性, 能够满足研究细微的振动模式、压力分布以及任何位置的力学行为,在耳生物力学研究中优势明显且运用较多[5, 6].
而关于前庭系统平衡功能生物数值模拟研究方面的报道则相对较少. 有学者通过建立或单个,或多个半规管的数学模型,就半规管内淋巴液 的流动规律和壶腹嵴顶的位移特征进行探索. Kassemi 等[7, 8]进一步构建了内耳水平半规管流固耦合有限元模型,Selva等[9]和Wu等[10]通过有限元法分析了头部匀速转动时单个水平半规管中内淋巴液流动与嵴顶运动的相互作用规律. 然而,前庭系统同时包含前庭和3个半规管且相互贯通,外界环境激励引起内淋巴液流动不仅局限于单个半规管或前庭,而是涉及 整个前庭系统. Francesco Boselli等[11]进一步建立了同时包含前庭和3个半规管的三维有限元数值模型,分析了转头运动时椭圆囊中内淋巴液的运动规律.
本研究团队[12]亦曾利用文献数据建立了一例人耳前庭系统生物力学模型,研究了转头时3个半规管内淋巴液的流动特征. 上述报道使得研究人员对前庭系统内复杂的生物力学特征有了进一步的认识.
随着前庭医学的发展和进步,需要建立更加完整的前庭系统生物力学模型来研究前庭$\!$-$\!$-$\!$半规管内的力学行为[13],以更深入地理解 前庭生理以及相关发病机理.
目前CT和MRI获取的内耳图像可满足临床疾病诊断需要,但其图片层厚和图像精度有限,特别是不能够提供内耳膜迷路的结构边界,不 能直接用于内耳生物力学模型的建立. 石蜡连续组织切片层厚为微米级别,可以较好地显示内耳膜性结构,可以为内耳生物力学模型建立提供较为精准的二维解剖数据, Dai等[14]曾就内耳连续组织切片技术进行过相关研究,使得利用组织切片数据建立内耳三维模型具有可行性.
本实验拟通过连续组织切片技术获取一套完整的豚鼠内耳二维结构解剖学数据,最终建立三维有限元模型,通过数值模拟临床冷 热试验对所建模型进行验证,建立可用于前庭$\!$-$\!$-$\!$半规管平衡功能研究的宏观生物力学模型,以为后续研究奠定基础.
1 实验材料健康成年豚鼠1只,体重500 g,雄性,由大连医科大学动物实验中心提供. 耳廓反射灵敏,耳内镜检查未见异常,声导抗、耳声发射、脑干听觉诱发电位检查均无异常.
计算机软件:Photoshop图像处理软件、Mimics和Hypermesh软件、有限元分析软件ANSYS12.0等.
2 实验方法 2.1 制作豚鼠内耳连续组织切片所选健康成年豚鼠1只,用10 %水合氯醛2 ml腹腔注射,麻醉后迅速断头,取出颞骨听泡并予以修剪,保留豚鼠耳蜗及前庭部分,用针尖在蜗尖骨壁钻孔,再挑开蜗窗下缘骨壁,用4 %多聚甲醛进行蜗管内灌流,将内、外淋巴液充分灌流出去,同时固定膜半规管,然后迅速将组织块浸泡于4 %多聚甲醛中固定48小时. 然后,依次经过修剪、脱钙;清洗、脱水;透明、浸蜡;定位、包埋;塑型、切片;H-E染色,其中选择外定位法进行定位,最终制作一套完整的豚鼠内耳组织连续切片,切片厚度6 um.
2.2 摄像并获取二维结构信息采用带微距镜头单反数码相机(CANON EOS 7D MARK II)对豚鼠内耳组织切片进行摄像,相机设定为2 020万像素和最高图像精细度,采用jpg格式保存彩色图像,将图像文件传送至计算机并进一步转换成bmp格式图像,依次进行编号.
2.3 三维重建(1) 运用Adobe Photoshop软件将上述图像转换成黑白色图片,然后进行识别、标记并强调边界,以增强对比度,利于识别内耳膜性结构.
(2) 本试验所获豚鼠内耳组织切片共480张,为减少工作量,本实验每4张连续图片选择1张进行数字化,进而三维重建,即所用图像间隔为18 um. 选择一张质量最好的切片作为定位基准,标记其4个定位点的坐标,将其他图像定位点进行标记,以定位基准图片为标准利用自由变换工具进行旋转、移动等将所有三维重建图片定位点进行拟合.
(3) 将上述图片导入MIMICS10.01软件,识别内耳膜性结构边界并形成边界点坐标.
(4) 运用Hypermesh软件形成豚鼠内耳膜性结构边界的几何面.
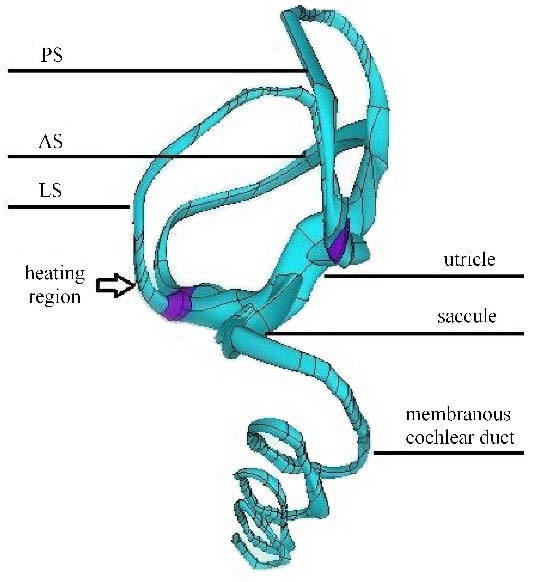
(5) 将所获取的几何面导入到有限元软件ANSYS12.0,进一步生成豚鼠内耳膜性结构的三维几何模型,并进一步完整有限元剖分. 三维模型示意图见图1.
|
图1 豚鼠内耳膜迷路三维模型示意图 Fig.1 The geometrical reconstruction of inner ear membranous labyrinth of guinea pig (PS: posterior semicircular canal,AS: anterior semicircular canal,LS : lateral semicircular canal) |
研究发现冷热试验在外耳道给予44${^\circ}$C的水或气刺激时,水平半规管最靠近颞骨的部位为最终的加温区域,其温度变化幅 度为0.5${^\circ}$C$\sim$1${^\circ}$C [15, 16],因此本实验设定的温度变化区域为外半规管最靠近颞骨的部位, 即半规管壶腹嵴顶管侧.
豚鼠正常体温为37.8${^\circ}$C$\sim$39.5${^\circ}$C,本实验假定豚鼠体温为38${^\circ}$C,即半规管所处环境温 度为38${^\circ}$C,模拟3种温度刺激:水平半规管加温区域升温1${^\circ}$C ($\vartriangle T=+1{^\circ}$C)、降温1${^\circ}$C ($\vartriangle T=-1{^\circ}$C)和升温7${^\circ}$C ($\vartriangle T=+7{^\circ}$C),其中升温7${^\circ}$C是人体所能接受的最高温度刺激,与实际情况有一定差别,但通过与$\vartriangle T=+1{^\circ}$C状况进行对比,能够更为明显地观察到半规管内生物力学响应的变化趋势.
本实验中将外半规管设定为与地面垂直位置如图1所示,在上述加温区域给予温度激励,取外半规管壶腹嵴顶管侧表面中心处的结点 为研究对象,观察该结点在3种温度变化下的位移、速度和压强随时间变化的规律,从而描述在温度场中膜半规管内发生的复杂力学响应.
实验中将内淋巴液描述成微可压缩的牛顿流体,壶腹嵴嵴顶描述成大变形线性弹性材料,内耳膜性结构中内淋巴液与壶腹嵴顶之间是 一种液固耦合行为,此外,除内淋巴液与嵴顶相交的边界之外,膜迷路的物理边界均设置成无滑移边界条件,膜半规管的管壁刚度约 是壶腹嵴嵴顶刚度的1 000倍,因而忽略管壁的变形,膜半规管管壁设置成刚性材料. 本实验中内淋巴液的物理性质选取参考文献[17, 18].
内淋巴液流动的控制方程为
$${{\partial \rho } \over {\partial t}} + \nabla \cdot \left( {\rho u} \right) = 0$$
(1)
$${\rho _{\rm{o}}}{{\partial u} \over {\partial t}} + {\rho _{\rm{o}}}\left( {u - {u_{\rm{m}}}} \right)\nabla \cdot u = - \nabla p + \mu {\nabla ^2}u + \rho g$$
(2)
$$\rho = {\rho _{\rm{o}}}\left[ {1 + {\beta _{\rm{T}}}\left( {T - {T_{\rm{o}}}} \right)} \right]$$
(3)
$${\rho _{\rm{o}}}c{{\partial T} \over {\partial t}} + {\rho _{\rm{o}}}c\left( {u - {u_{\rm{m}}}} \right)\nabla \cdot T = k{\nabla ^2}T$$
(4)
其中,$\rho $,${ u}$,$p$和$T$为变量,分别表示内淋巴液的密度、速度、压强和温度,时间用$t$表示,$\mu $,$\beta _{\rm T}$, $c$和$k$为常数,分别表示内淋巴液的动力黏度、热膨胀系数、热容和热传导率. 下标"o"表示参考状态,下标"m"表示网格的移动,采用任意拉格朗日数值模拟方法.
嵴顶的运动用拉格朗日方程描述如下
$$
\rho ^{\rm s}\dfrac{\partial ^2{ d}}{\partial t^2} = \nabla \cdot { \sigma }_{\rm s}
$$
(5)
其中,$\rho ^{\rm s}$为密度,${ d}$为位移张量,$t$为时间,${ \sigma
}_{\rm s}$为应力张量,后者可表示为
$$
{ \sigma}_{\rm s} = 2\mu { \varepsilon} + \lambda {\rm tr} ({ \varepsilon }) { I}
$$
(6)
${ \varepsilon}$为应变张量,${ I}$表示单位矩阵,
$\mu$ 和$\lambda $为拉梅常数,用杨氏弹性模量$E$和泊松比$\nu$ 表示
$$\mu = {E \over {2(1 + \nu )}}$$
(7)
$$\lambda = {{\nu E} \over {\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}$$
(8)
嵴顶的杨氏模量取为5 Pa,泊松比为0.48[19].
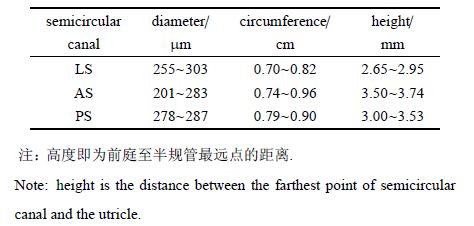
3 结 果 3.1 模型结构特征观察利用石蜡切片技术获得了2套完整的豚鼠内耳组织连续切片资料及其图像,选取1套用于本研究:共获得石蜡 切片480张,片厚6 um;根据二维图像资料进一步建立了内耳前庭$\!$-$\!$-$\!$半规管膜迷路的三维几何模型:3个膜半规管均为呈2/3环形管状结构且互相垂直, 3个半规管的高度、周长、管径等测量数据表1所示,3个半规管基部与椭圆囊相接,其中上半规管内端与后半规管上端合成总脚与前 庭相接,椭圆囊通过椭圆囊球囊管与球囊相通(见图1),反映了豚鼠内耳前庭的空间结构特征.
| 表1 豚鼠膜半规管三维数据测量值 Table 1 Data of the lateral semicircular canal |
首先,观察$\vartriangle T=+1{^\circ}$C时3个半规管的位移响应:其中外半规管、上半规管、后半规管的最大位移响应分别为:1.03 um, 54.1 nm,68.1 nm.
鉴于外半规管位移响应最大,遂决定取外半规 管壶腹嵴顶管侧表面中心处的结点为研究对象,以 观察壶腹嵴顶的生物力学响应,即$\vartriangle T=+1{^\circ}$C,$\vartriangle T=+7{^\circ}$C和$\vartriangle T=-1{^\circ}$C 3种温度刺激时该结点的位移、速度和压强随时间变化特征.
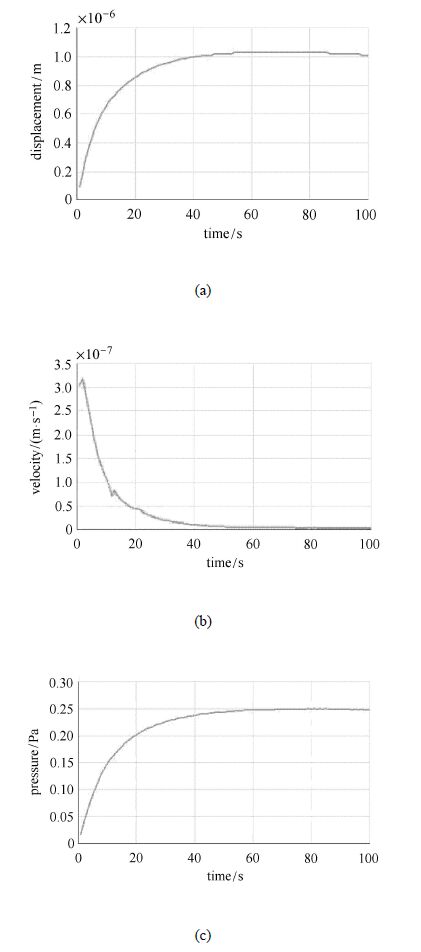
$\vartriangle T=+1{^\circ}$C时,壶腹嵴顶向椭圆囊侧移动,且位移逐渐增大,约60 s达到稳态,此时位移达到1.030 um; 速度逐渐下降,约60 s时速度降为0,达到稳态;压强由0逐渐增大,约60 s时达到稳态,压强最大值为0.250 Pa,如图2所示.
|
图2 $\vartriangle T=+1 {^\circ}$时,(a)嵴顶节点的位移,(b)嵴顶节点的速度,(c)嵴顶表面结点的压强 Fig.2 $\vartriangle T=+1{^\circ}$C,(a) displacement of the cupulaterminllis,(b) velocity of the cupulaterminllis,(c) pressure of the surface of the cupulaterminllis |
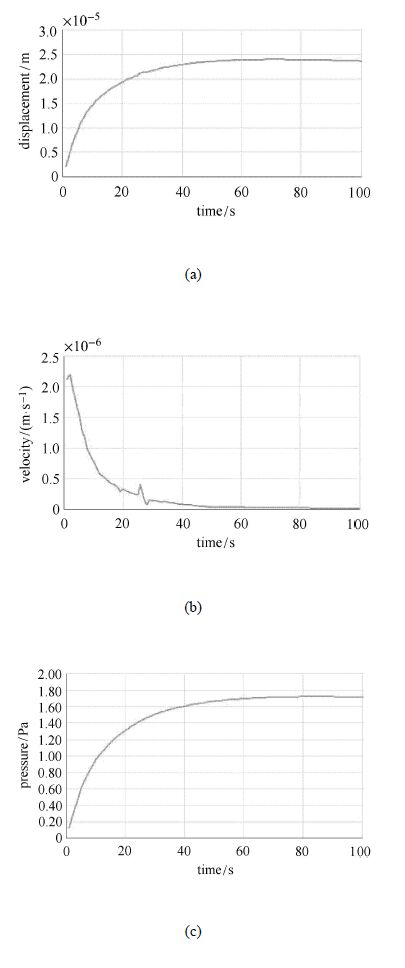
$\vartriangle T=+7{^\circ}$C时, 壶腹嵴顶向椭圆囊侧移动,且位移逐渐增大,约60 s时达到稳态,此时位移为23.98 um;速度逐渐下降, 约60 s时降为0;压强逐渐增大,约60 s时达到稳态,此时压强为1.720 Pa,如图3所示.
|
图3 $\vartriangle T=+7{^\circ}$C时,(a)嵴顶的位移,(b)嵴顶的速度,(c)嵴顶表面结点的压强 Fig.3 $\vartriangle T=+7{^\circ}$,(a) displacement of the cupulaterminllis,(b) velocity of the cupulaterminllis,(c) pressure of the surface of the cupulaterminllis |
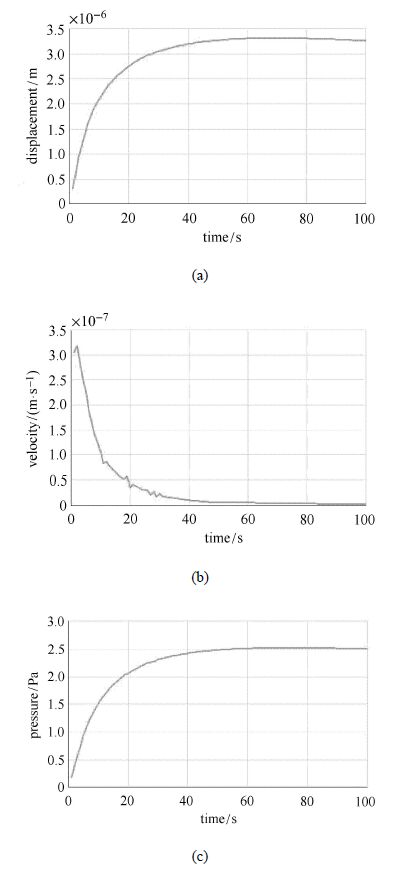
$\vartriangle T=-1{^\circ}$C时,壶腹嵴顶向管侧运动,方向与升高温度时相反,位移逐渐增大,约60 s时达到稳态,此时 位移为3.315um;速度逐渐下降,约60 s时降为0;压强逐渐增大,60 s时达到稳态,值为0.252 Pa, 如图4所示.
|
图4 $\vartriangle T=-1{^\circ}$C时,(a)嵴顶节点的位移,(b)嵴顶节点的速度,(c)嵴顶表面结点的压强 Fig.4 $\vartriangle T=-1{^\circ}$C,(a) displacement of the cupulaterminllis,(b) velocity of the cupulaterminllis,(c) pressure of the surface of the cupulaterminllis |
近年来,CT和MRI均属于无损成像检测技术,但存在对内耳精细结构分辨率低,难以获得小动物模型的理想图像[20]. 不能够满足内耳宏观生物模型的建立需要,因此,本实验选择连续组织切片技术获取内耳结构数据.
三维重建过程的基本步骤为选择相关解剖结构的关键点,然后依次建立成线、面、体等. 本实验组织切片厚度为6 um,共获取480张切片,为了适度减少工作量同时保证所建模型的精准性,本实验每间隔3张切片选择一张进行三维重建,即用于模型建立的切片厚度为24 um.
需要指出的是:(1)所获二维组织切片具有膜性结构局部断裂和移位的现象,实验人员根据毗邻 切片的结构特征和解剖学知识进行相应的图片修复,以确保结构的完整性和精准性;(2)石蜡组织 切片提供的解剖数据为微米级别,可以清楚观察膜迷路内细胞水平的结构特征,能够满足内耳"宏观"生物力学模型的建立要求,而并不能满足耳蜗螺旋器、毛细胞、半规管壶腹嵴顶等"超微结构"生物力学模型的建立要求,后者需要提供纳米级别的解剖学数据,如透射电镜资料等.
4.2 内耳前庭$\!$-$\!$-$\!$半规管生物力学模型的结构特征本实验所建立的前庭结构包括椭圆囊和球囊,半规管包括外、上、后3个半规管,均呈环形,且均与椭圆囊相通,而且上半规管内端、后半规管上端共同组成总脚,与椭圆囊相通,与文献报道一致[21, 22],亦与人体内耳前庭系统结构特征类似.
安淑红等[23]通过制作20例正常国人内耳前庭标本,测量了半规管的管径和高度,其中上半规管管径为1.29$\pm $0.21 mm,高度为5.99$\pm $0.56 mm;水平半规管管径为1.56$\pm $0.23 mm,高度为4.78$\pm $0.49 mm;后半规管管径为1.22$\pm $0.17 mm,高度为6.46$\pm $0.69 mm,与曾令廷等[24], 李书玲等[25]通过MRI测量结果基本一致. 本实验也对豚鼠半规管的周长、管径和高度均进行了测量(见表1),其中半规管高度值为同一数量级,半规管管径则较人体小,最大数值为外半规管0.303 mm, 与Curthoys等[26] 测量结果一致.
Ifediba 等[27]认为半规管的空间结构是其功能基础,上述结构观察发现豚鼠前庭$\!$-$\!$-$\!$半规管尺寸大小与人具有一定差别,但其空间结构特征与人体类似,因此,可以认为在一定程度上豚鼠前庭系统生物数值模拟研究结果可以用于人体平衡功能研究.
4.3 内耳前庭$\!$-$\!$-$\!$半规管生物力学模型的可靠性冷热试验是临床广泛应用的评估半规管功能状态的方法. 而数值模拟的优势在于即可以定性评估前庭$\!$-$\!$-$\!$半规管的功能, 亦可为前庭系统的生理和病理研究提供量化参考依据. 因此,本实验选择数值模拟冷热试验来观察半规管壶腹嵴顶的力学响应,以评估模型的可靠性.
外半规管与外耳道临近,在外耳道内给予温度刺激时,外半规管最先感受到温度变化,本实验观察到$\vartriangle T=+1{^\circ}$C, 外半规管内的位移响应和压强降均较上、后半规管大,临床冷热试验主要记录到水平方向的眼震,提示温度实验对于外半规管刺激最大, 与临床观察到的水平型眼震结果一致[28].
有学者通过实验测量发现在外耳道给予44${^\circ}$C的热水或热气刺激时,水平半规管最靠近颞骨的部位温度升高最为明显,其升 高幅度为0.5${^\circ}$C$\sim$1${^\circ}$C[8, 15, 20, 29],即临床温度实验最终导致的半规管内淋巴液的温度变化幅度 约为1${^\circ}$C,而7${^\circ}$C的变化幅度则不符合实 际情况,本实验和 Kassemi 等[7, 8]给予数值模拟的温度刺激为升高1${^\circ}$C和7${^\circ}$C,其中升高1${^\circ}$C符合实际生理状 况,而升高7${^\circ}$C后半规管内的力学响应变化趋势更为明显,因此更有利观察半规管内生物力学行为特征.
本实验外半规管内壶腹嵴顶管侧结点的力学响应趋势为:(1)在初始时刻加温区(壶腹嵴顶管侧)给定一个温度激励,壶腹嵴顶在温度 升高时向椭圆囊侧运动,温度降低时向管侧运动;(2)所研究结点的位移、速度和压强响应变化特点:在初始时刻运动速度最大,逐 渐趋向稳定,约60 s时刻达到稳定且值最小,此时刻对应位移和压强值最大;其中温度刺激越强烈,半规管壶腹嵴顶的力学响应越大; 温度激励时外半规管壶腹嵴顶力学响应变化也预示着温度升高或降低将会产生相反的眼震.
其中半规管内的力学响应在60 s内即可达到稳定状态,其中外半规管壶腹嵴顶的最大位移响应为1.03 um;Shen 等[29]建 立了人前庭系统有限元模型,数值模拟结果显示温度激励约70 s达到稳态,此时外半规管壶腹嵴顶位移达到最大值为3 um;Harold [30]的数值模拟结果则是外半规管内的力学响应耗时100 s达到稳态,其壶腹嵴顶位移最大值为27.8 um;三者数值模拟 结果基本一致.
总之,利用组织连续切片技术获取豚鼠内耳二维图像数字信息并进行三维重建,所建模型既能够反映解剖结构细节,又能反映其空 间特性;数值模拟温度实验定量描述了前庭系统维持平衡的机理并提供了数据参考.
即本研究所用实验技术及所建立的前庭$\!$-$\!$-$\!$半规管宏观生物力学模型可用于平衡机理和发病机制研究.
| [1] | 姚文娟, 陈懿强, 叶志明 等. 耳听力系统生物力学研究进展. 力学与实践, 2013, 35(6): 1-10 (Yao Wenjuan, Chen Yiqiang, Ye Zhiming, et al. Advance in biomechanics of human ear as hearing system. Mechanics in Engineering, 2013, 35(6): 1-10 (in Chinese)) |
| [2] | Fadaei M, Abouali O, Emdad H, et al. Numerical simulation of wave propagation in a realistic model of the human external ear. Computer Methods in Biomechanics & Biomedical Engineering, 2015, 18: 1797-1810 |
| [3] | 刘迎曦,李生,孙秀珍.人耳传声数值模型. 力学学报,2008, 40(1):107-113 (Liu Yingxi,Li Sheng,Sun Xiuzhen. Numerical modeling of human ear for sound transmission. Chinese Journal of Theoretical & Applied Mechanics, 2008, 40 (1): 107-113 (in Chinese)) |
| [4] | Kwacz M, Marek P, Borkowski P, et al. A three-dimensional finite element model of round window membrane vibration before and after stapedotomy surgery. Biomechanics & Modeling in Mechanobiology, 2013, 12(6): 1243-1261 |
| [5] | Fei Z, Koike T, Jie W, et al. Finite element analysis of the middle ear transfer functions and related pathologies. Medical Engineering & Physics, 2009, 31(8): 907-916 |
| [6] | Song YL, Lee CF. Computer-aided modeling of sound transmission of the human middle ear and its otological applications using finite element analysis. Tzu Chi Medical Journal, 2012, 24(4): 178-180 |
| [7] | Kassemi M, Deserranno D, Oas JG. Fluid-structural interactions in the inner ear. Computers & Structures, 2005, 83(2): 181-189 |
| [8] | Kassemi M, Oas JG, Deserranno D. Fluid-structural dynamics of ground-based and microgravity caloric tests. Journal of Vestibular Research, 2005, 15(2): 93-107 |
| [9] | Selva P, Morlier J, Gourinat Y. Toward a three-dimensional finite-element model of the human inner ear angular accelerometers sensors. International Journal for Computational Vision and Biomechanics, 2010, 3(2): 149-156 |
| [10] | Wu C, Cheng H, Lin Y, et al. Dynamic analysis of fluid-structure interaction of endolymph and cupula in the lateral semicircular canal of inner ear. Journal of Hydrodynamics, Ser. B, 2011, 23(6): 777-783 |
| [11] | Boselli F, Obrist D, Kleiser L. Vortical flow in the utricle and the ampulla: a computational study on the fluid dynamics of the vestibular system. Biomech Model Mechanobiol, 2013, 12(2): 335-348 |
| [12] | 沈双, 孙秀珍, 刘迎曦. 人内耳前庭系统膜迷路流固耦合数值模拟. 力学学报, 2010, 42(3): 415-421 (Shen Shuang,Sun Xiuzhen,Liu Yingxi, et al. Numerical simulation of membranous labyrinth in vestibular system of human inner ear by fluid-structural interaction method. Chinese Journal of Theoretical & Applied Mechanics, 2010, 42(3): 415-421 (in Chinese)) |
| [13] | 张天宇, 吴彩琴, 戴培东. 耳生物力学研究现状与展望 (下). 中国眼耳鼻喉科杂志, 2010, 10(2): 72-74 (Zhang Tianyu, Wu Caiqin, Dai Peidong. Update and prospect of hearing mechanics. Chinese Journal of Ophthalmology and Otorhinolaryngology, 2010, 10(2): 72-74 (in Chinese)) |
| [14] | Dai P, Liu Y, Jiang SC, et al. Stereo morphology of temporal bone and ear. Chinese Medical Journal, 2004, 117(5): 733-737 |
| [15] | O'neill G. The caloric stimulus: temperature generation within the temporal bone. Acta Oto-laryngologica, 1987, 103(3-4): 266-272 |
| [16] | O'neill G. The caloric stimulus: mechanisms of heat transfer. British Journal of Audiology, 1995, 29(2): 87-94 |
| [17] | Steer RW Jr, Li YT, Young LR, et al. Physical properties of labyrinthine fluids and quantification of the phenomenon of caloric stimulation, NASA SP-152 (1968), 409-420 |
| [18] | Kondrachuk AV, Sirenko SP, Boyle R. Effect of difference of cupula and endolymph densities on the dynamics of semicircular canal. Journal of Vestibular Research, 2008, 18(2-3): 69-88 |
| [19] | Damiano ER. Continuum models of rotational and caloric stimulation of the vestibular semicircular canal. [PhD Dissertation]. New York: Rensselaer Polytechnic Institute, Troy, 1993 |
| [20] | 孙程成, 蒋子栋. 小动物内耳影像学研究进展. 中华耳科学杂志, 2014, 12(3): 512-515 (Sun Chengcheng, Jiang Zidong. Advance in iconography of small animals. Chinese Journal of Otology, 2014, 12(3): 512-515 (in Chinese)) |
| [21] | Moreno LE, Rajguru SM, Matic AI, et al. Infrared neural stimulation: beam path in the guinea pig cochlea. Hearing Research, 2011, 282(1-2): 289-302 |
| [22] | Ichijo H. Does the superior semicircular canal receive caloric stimulation? Am J Otolaryngol, 2012, 33(6): 718-722 |
| [23] | 安淑红, 万龙, 徐玉洁. 前庭蜗器的标本制作及相关的解剖学观测. 泰山医学院学报, 2010 (11): 837-840 (An Shuhong, Wan Long, Xu Yujie. Manufacturing of the vestibulocochlear organ Anatomical measurement. Journal of Taishan Medical College, 2010 (11): 837-840 (in Chinese)) |
| [24] | 曾令延, 魏文洲, 李茂进 等. 正常人内耳结构的 MR 测量. 医学影像学杂志, 2006, 16(3): 226-229 (Zeng Lingyan,Wei Wenzhou,Li Maojin,et a1. MRI measurement for inner ear structrues of nomal people. Journal of Medical Imaging, 2006, 16(3): 226-229 (in Chinese)) |
| [25] | 李书玲, 刘怀军. 正常人内耳前庭, 半规管及耳蜗的 MRI 测量. 中华放射学杂志, 2003, 37(1): 55-58 (Li Shuling, Liu Huaijun. MRI measurement for inner ear structures. Chinese Journal of Radiology, 2003, 37(1): 55-58 (in Chinese)) |
| [26] | Curthoys IS, Oman CM. Dimensions of the horizontal semicircular duct, ampulla and utricle in rat and guinea pig. Acta Oto-laryngologica, 1986, 101(1-2): 1-10 |
| [27] | Ifediba MA, Rajguru SM, Hullar TE, et al. The role of 3-canal biomechanics in angular motion transduction by the human vestibular labyrinth. Annals of Biomedical Engineering, 2007, 35(7): 1247-1263 |
| [28] | 张波, 孙敬武. 良性阵发性位置性眩晕患者裸眼及视频眼震图下眼震特征及定位诊断分析. 听力学及言语疾病杂志, 2012, 20(3): 235-237 (Zhang Bo, Sun Jingwu. The observation and diagnosis of 108 patients with benign positional paroxysmal vertigo with naked eyes and VNG. Journal of Audiology and Speech Pathology,2012, 20(3): 235-237 (in Chinese)) |
| [29] | Shen S, Liu Y, Sun X, et al. A biomechanical model of the inner ear: numerical simulation of the caloric test. Scientific World Journal, 2013, 2013(5): 206-232 |
| [30] | Young JH. Analysis of vestibular system responses to thermal gradients induced in the temporal bone. [PhD thesis]. University of Michigan, Ann Arbor |
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanicals, Dalian University of Technology, Dalian 116024, China
 2015, Vol. 47
2015, Vol. 47