2. 中国医学科学院, 阜外心血管病医院心外科, 北京 100037
冠心病是冠状动脉血管发生动脉粥样硬化病变而引起血管狭窄或阻塞的一种心血管疾病,会造成心肌缺血、缺氧或坏死. 心血管 疾病是全球首位死亡原因,每年约有1 730万人死亡,占每年全球死亡人数的30%. 预计到2030年, 每年心血管疾病导致的死亡人数将超过2 360万[1]. 据世界卫生组织统计,在中国约2.3亿人患有心血管疾病,预计到2030年,患病人数将增加50%.
在解剖学上,冠状动脉的狭窄程度与其造成心肌缺血间并无绝对相关性, 中等严重程度的冠状动脉病变也常会引起局部缺血从而导 致冠心病[2]. 血流储备分数(FFR)是临床上判断冠状动脉狭窄是否造成心肌缺血的"金标准"[2, 3, 4, 5], 它弥补了传统的冠状动脉造影技术无法对中度冠状动脉病变做出准确评估的缺点,对病变程度的评估有较高的准确性. 学者们对直径狭窄率(DS,%)、面积狭窄率(AS,%)[6]、最小管腔直径(MLD, mm)、最小管腔面积(MLA,mm2、狭窄长度(LL,mm)[7]、斑块体积(PV, mm3等临床冠状动脉计算机断层造影血管成像(CCTA)测量参数与血流储备分数的关系进行了统计学分析, 发现面积狭窄率(AS)与病变长度(LL)是最强的两个影响因素[8]. 然而临床血流储备分数的分析工作量大而繁复,其有创性更会加重患者的痛苦. 随着计算流体动力学技术的不断发展, 基于传统的计算机断层造影图像建立个性化模型,应用计算流体动力学方法,计算血流储备分数FFRCT 成为了新的研究方向. 有学者对比了患者的FFR临床数据与FFRCT数据,发现二者具有较高的符合度,说明了 FFRCT 的准确性[5]. 另有学者发现随着中度狭窄程度与病变长度的增加,FFRCT 值会逐渐下降到0.80以下,说明中度的病变程度和病变长度也会造成心肌供血不足,与临床结果一致[3]. 还有学者研究表明当病变长度大于10 mm时,血流储备分数与病变长度间表现出较强的相关性, 临床诊断应予以考虑[9].
血流储备分数固然是评判是否缺血的新方法,但冠状动脉粥样硬化病变的发展与血流动力学参数密切相关[10], 对于中 等严重程度的冠状动脉病变依旧是有效的评估方法. 这些血流动力学参数包括: 低和高的壁面剪应力、回流区、速度和压力分布等. 学者们[10, 11, 12, 13]普遍认为低和振荡壁面剪应力是早期冠状动脉粥样硬化斑块形成的主要因素, 而高的壁面剪应力与斑块的破裂更为相关. 一些学者[14, 15]通过研究发现狭窄段下游由于流动分离会产生回流区, 回流区流场复杂不断扰动下游区域,极低的壁面剪应力与内膜增生密切相关. 有学者[16]研究了狭窄程度为30%~60%的冠状动脉病变模型, 发现狭窄程度的增加会增强回流区对下游的扰动,在狭窄段中部形成更高的壁面剪应力. 还有学者[17]发现明显的压力下降发生在狭窄下游,且下降幅度由病变血管的形态决定.
血液在动脉血管中流动时,其压力会使血管产生变形,而血管的变形反过来会影响血液的流动,即流固耦合作用. 有研究[18]发现,刚性壁面与弹性壁面的数值结果相差很大,表现不出局部过高和低的剪应力值,造成结果的不准确. 只有考虑流固耦合作用,才能更好的模拟生理状态下的血液流动.
目前, 对于中等严重程度冠状动脉病变的研究大多集中于血流储备分数的临床统计分析[6, 7, 8, 9]和应用计算流体 动力学的FFRCT分析[2, 3, 4, 5],很少有研究得到其与血流动力学的关系. 本文基于患者的计算机断层造影图像建立三维的个性化模型,考虑壁面弹性, 运用流固耦合方法数值研究中等严重程度的面积狭窄率(AS,50%~75%)和病变长度(LL, 10 mm~20 mm)对壁面剪应力(wss)、回流区长度与剪切速率、狭窄分支血管速度和压力分布 等血流动力学参数的影响.
1 冠状动脉血管三维模型建立选取北京阜外心血管医院冠状动脉搭桥手术患者一例,计算机断层造影图像共360张,层厚0.5 mm. 从中提取左冠状动脉, 建立个性化模型.
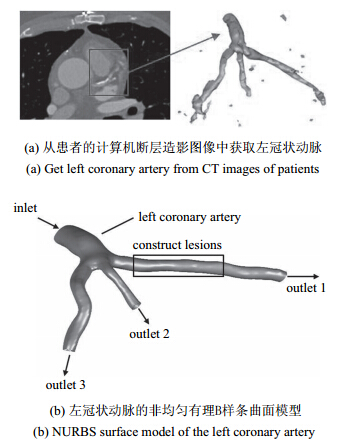
将患者的计算机断层造影图像导入到"Mimics"三维重构软件中,通过鉴别计算机断层造影图像的灰度值设定分割阈值, 手动逐 层擦除无用的组织,从而仅得到目标血管,图 1(a)为在"Mimics"三维重构软件中提取的左冠状动脉模型.方框所示为患者的计算机断层造影图像中的左冠状动脉.
|
图 1 计算模型的建立 Fig.1 Setup of computational models |
为了更加接近真实的情况,将上述薄壁模型沿法向方向向外拉伸0.2 mm. 通过对出入口和管壁表面的优化处理, 生成可以用 于计算的非均匀有理B样条曲面模型,如图 1(b)所示. 以中等严重程度面积狭窄率50%,65%,75%和病变长度10 mm,15 mm, 20 mm构造模型,按照上述方法得到本研究的冠状动脉非均匀有理B样条曲面模型, 图中标示出了计算模型的1个入口和3个出口,方框为建立计算模型时构造病变的位置.
2 计算方法 2.1 材料属性假设血管壁为各向同性的线弹性材料且无渗透. 血管壁密度为1 150 kg/m3,弹性模量为5 MPa,泊松比为0.45[19]. 假设血液为牛顿流体,密度为1 060 kg/m3,动力黏度为0.003 5 Pa·s[20].
2.2 控制方程将血液视为三维、非定常、不可压缩流体,在流固耦合的数值计算中,考虑动网格算法的流体域纳维-斯托克斯方程与动量方程分别为
| \[{\rho _{\text{f}}}\left[ {\frac{{\partial v}}{{\partial t}} + \left( {v - {v_{\text{g}}}} \right) \cdot {\text{ }}\nabla {\text{ }}v} \right] = - \nabla p + \nabla \cdot {\text{ }}T\] | (1) |
| \[\nabla \cdot {\text{ }}v = 0\] | (2) |
计算中不考虑体力,血管壁即固体域运动的控制方程为
| \[\nabla \cdot {\text{ }}{\sigma _{\text{s}}} = {\rho _{\text{s}}} \cdot {a_{\text{s}}}\] | (3) |
流固耦合遵循最基本的守恒原则, 因此在流固耦合面应满足流体与固体应力、位移和流量的守恒
| \[{\sigma _{\text{s}}} \cdot {\text{ }}{n_{\text{s}}} = {\sigma _{\text{f}}} \cdot {n_{\text{f}}}\] | (4) |
| \[{d_{\text{s}}} = {d_{\text{f}}}\] | (5) |
| \[{q_{\text{s}}} = {q_{\text{f}}}\] | (6) |
根据文献[4]和出入口截面所在位置选取出入口的边界条件如图 2所示,一个心动周期为0.8 s,连续计算3个周期,取第2个周期的计算结果进行分析.
由于血管内压力很小,设置流域的压力为0 Pa,不使用标准大气压作为参考压力. 雷诺数Re =ρvd/μ≈ 1 514 < 2 300,其中ρ为血液密度,v为平均入口速度,d 为血管直径,μ 为动力黏度,可知血管内血液流动状态为层流. 这段血管并不是孤立存在的,它的出入口与上游和下游血管相连,出入口设置为支撑约束.
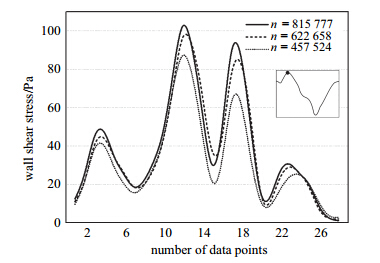
2.4 网格独立性验证本文模型网格分为固体和流体两部分,由于结果主要进行流体分析,在此对流体域的网格进行独立性验证. 以A=75%,LL=20 mm的模型为例,进行3种不同数量的网格划分,如表 1所示. 计算后提取冠脉狭窄分支的壁面剪应力如图 3所示,发现网格数量为633 685时的壁面剪应力值与高网格量较为接近,故采用此网格数量可以满足计算精度要求.
| 表 1 3种不同的网格数量 Table 1 Mesh numbers of three different elements |
|
图 3 t=0.95 s时冠脉狭窄分支的壁面剪应力 Fig.3 Wall shear stress along the branch of coronary artery stenosis at t=0.95 s |
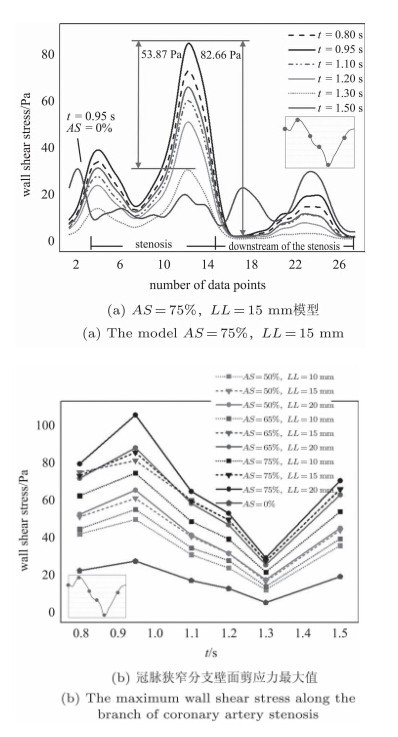
为研究壁面剪应力在流固耦合面上的分布情况,沿有病变血管分支的轴向方向设置数据提取点30个,点间距1.25 mm,如图 4所示. 图 4为面积狭窄率构造的截面简图,其右上角给出了病变长度与节点的位置关系. 图 4下方附有模型三维简图和坐标系,黑色方框意为数据点分布图由此提取. 以AS=75%,LL=15 mm模型为例,分别提取心动周期内6个时间点(0.80 s,0.95 s,1.10 s,1.20 s,1.30 s,1.50 s)的壁面剪应力绘制曲线如图 5(a),数据点3~15为此模型狭窄段,数据点15~28为狭窄段下游. 发现在不同时刻壁面剪应力分布曲线走势大致相同,随着入口流量的增大与减小,壁面剪应力幅值相应改变. 各个时刻的剪应力最大值出现在狭窄段内的同一位置,t=0.95 s时壁面剪应力最大为84.49 Pa,t=1.30 s时壁面剪应力最小为30.62 Pa,数值下降了近2/3. 在t=0.95 s时,对比正常血管分支的壁面剪应力曲线,狭窄会造成剪应力的大幅度增加. 并且在同一时刻,冠脉狭窄分支的最小剪应力值出现在临近狭窄段下游的位置,在t=0.95 s时值为1.83 Pa,与狭窄段剪应力最大值相差最大为82.66 Pa.

|
图 4 模型构造与数据点分布示意图 Fig.4 Schematic diagram of the model geometric parameters and distribution of data points |
图 5(b)为一个心动周期内,6个时刻各个模型狭窄段的壁面剪应力最大值. 可以看出,入口流量的变化影响壁面剪应力分布, 对于正常血管分支,在一个心动周期内,壁面剪应力的最大值变化幅度很小,保持在10~30 Pa区间. 但对于病变模型, AS与LL的变化直接影响心动周期内壁面剪应力变化的幅度. 随着AS与LL的增大,在心动周期内壁面剪应力变化越大. 最大剪应力达到103 Pa,最大降幅达到71.05 Pa. 可见,在短时间内管腔狭窄造成了壁面剪应力的剧烈变化, 进而对血管壁产生严重的损害,与文献[16]结果一致. 有研究[21]表明,当血管壁或内皮细胞被破坏, 胶原蛋白和组织因子暴露于流动的血液,组织因子会产生凝血酶,激活血小板,胶原蛋白会积累活化的血小板,最终造成血栓的形成,进而引起血管的进一步阻塞. 此外, 剪应力剧烈变化引发高的剪应力梯度与局部内膜增厚有着紧密联系. 而狭窄段极高的壁面剪应力, 也可能造成斑块的软化和不稳定,是冠状动脉斑块破裂潜在的危险因素.
|
图 5 一个心动周期的壁面剪应力分布 Fig.5 Distribution of wall shear stress in a cardiac cycle |
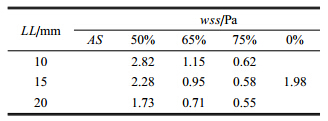
表 2为入口流量最小的时刻(t=1.30 s)狭窄段下游壁面剪应力最小值. 可以发现, 正常血管分支的壁面剪应力最小值为1.98 Pa,只有AS=50%时LL为10 mm和15 mm的模型高过正常水平, 其他模型的壁面剪应力最小值均处于较低水平. 随着AS和LL增大,其他模型的壁面剪应力最小值逐渐降低, 最低达到0.55 Pa. 研究[12]表明,低或振荡的剪切应力能够增强狭窄部位细胞间的黏附分子和组织因子的活性, 可以改变局部的溢流条件造成狭窄上游下游更多组织的损伤,可能扩大病变. 由于狭窄段下游流动停滞, 上游破损的斑块会在此沉积,使下游的官腔狭窄,扩大病变区域,对冠状动脉粥样硬化的进程产生不利影响. 因此不仅是剧烈变化的壁面剪应力,极低的壁面剪应力同样是危险的血流动力学因素,此结论与文献[11, 12]一致.
| 表 2 t=1.30 s狭窄段下游壁面剪应力最小值 Table 2 Minimum shear stress along downstream of the stenosis at t=1.30 s |
冠脉狭窄常导致狭窄段下游形成低速和低剪切速率区,这个区域极易形成回流区. 以AS=65%,LL=15mm模型为例,图 6为其入口流量峰值期(t=0.95 s)时的速度矢量图. 可以看到,在狭窄段流线几乎成平行直线状,但在狭窄段的下游,流线的分布较为复杂,一部分流线继续平缓前行,而另一部分流线却有回流的趋势并最终流向了分支出口,与文献[22]数值模拟的流线趋势相同. 通过观察不同时刻模型的速度矢量图发现,回流区最初形成于靠近狭窄段的下游,随着入口流量的增加,逐渐向下游延伸. 当入口流量减小后,回流区对于下游的扰动并没有停止,与文献[16]结果一致. 这是由于入口边界的条件的时间尺度远小于流场变化的时间尺度.

|
图 6 t=0.95 s回流区速度矢量图 Fig.6 Velocity vector in recirculation zone at t=0.95 s |
图 7为不同AS和LL模型在t=0.95s时与回流区长度和模型最大剪切速率的关系图. 可以看到,AS和LL与回流区长 度及模型最大的剪切速率有很强的关联性. 图中,正常血管分支(AS=0%)无回流区产生;以LL=10 mm的模型为例, 当AS=65%时,回流区长度为10.13 mm,较AS=50%时增加了1倍以上;当AS=75%时, 回流区长度为11.03 mm增长幅度减小,曲线逐渐平缓,呈"S"型. 正常血管分支的最大剪切速率为12 586.9 s-1; 对于LL=15 mm模型,AS=50%时为13 549.6 s-1(增长7.6%); AS=75%时为18 429.5 s-1(增长46.4%)模型最大剪切速率的增长幅度增大,曲线呈抛物线走势, 与文献[14]结果趋势相同. 可见,对于中等严重程度的冠状动脉病变,回流区长度的变化十分显著, 而较大的模型最大剪切速率变化可能存在于更严重的冠状动脉病变中.

|
图 7 t=0.95 s时AS和LL与回流区长度和模型最大剪切速率关系 Fig.7 Relationship among area stenosis,lesion length,recirculation\\ zone length and the maximum shear rate at t=0.95 s |
血液流动受到扰动或是有回流产生,脂质在动脉血管壁面的浓度就会显著增加. 在回流区,这些脂质粒子与血管壁接触的机会和相互作用的时间要比其它区域长得多. 这种由流动引起的脂质浓度的局部性增加是引发动脉粥样硬化局部性和动脉狭窄产生的一个非常重要的原因. 有研究[14]表明,回流区为血栓形成以及血小板激活和聚集提供了有利环境,加快了冠状动脉粥样硬化的进程,中等严重程度冠状动脉狭窄可能发展为完全的血栓闭塞. 同壁面剪应力一样,高的剪切速率会激活血小板和白细胞的活化,促进形成血栓. 可见,回流区是可能导致冠状动脉血栓形成的危险区域,此结论与文献[14]一致.
3.3 面积狭窄率与病变长对冠脉狭窄分支速度和压力分布的影响血液在血管中流动时,由于克服内摩擦力等会引起能量损失,导致流动的前后产生压力差,狭窄段的压力分布是影响冠状动脉粥样硬化进程的另一重要血流动力学参数.
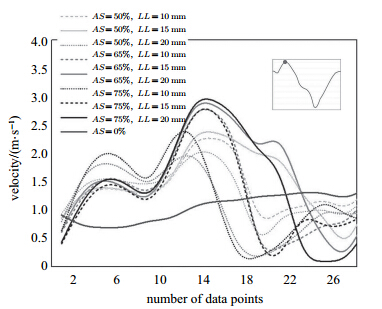
图 8为沿冠脉狭窄分支平行管径方向截面速度曲线. 图 9为入口流量峰值期(t=0.95 s)正常血管分支与不同AS和LL模型狭窄分支压力分布曲线. 从图中看出,正常血管分支的压力分布曲线下降平缓,压力变化范围在8.5~9.5 kPa之间. 对比正常血管分支,官腔狭窄会使狭窄段的压力有明显的降低. 图 9中病变血管的压力分布曲线有两次明显的下降,第一次发生在刚进入狭窄段附近,第二次发生在狭窄段末端. 这2次明显的下降正好是图 8中血流速度急剧增加的位置. 根据伯努利方程,狭窄段不断升高的血流速度导致逐渐下降横向压力作用于狭窄段的斑块表面,这种跨越斑块的压力梯度会不断增大而导致斑块的破裂. 血液中导致冠状动脉粥样硬化的成分会被迫从高压力区运动到低压力区并聚集. 与高的壁面剪应力一样,破裂的斑块会跟随血液流向下游,可能造成下部的阻塞. 随着AS和LL增大,压力下降的幅度逐渐增大,因此黏性(摩擦)损失导致的压降主要取决于狭窄的程度和长度,此结论与文献[3]的数值模拟结果一致.
|
图 8 沿血管分支轴向速度 Fig.8 Axial velocity along the branch of coronary artery stenosis |

|
图 9 t=0.95 s时冠脉狭窄分支的压力分布 Fig.9 Pressure distribution along the branch of coronaryartery stenosis at t=0.95s |
本文通过数值模拟得到的血流动力学参数结果与前人的实验或数值研究结果一致,具体结论如下:
(1) AS与LL会影响病变血管分支的壁面剪应力的变化幅度,AS和LL越大,变化越剧烈. 在短时期内剧烈变化的壁面剪应力易造成血管内壁损伤,易形成血栓造成血管进一步阻塞.
(2) 管腔狭窄会造成下游回流区产生极低的壁面剪应力,AS与LL的增大使下游的壁面剪应力值逐渐向下偏移正常范围. 低的壁面剪应力会改变局部溢流条件,可能扩大病变,造成血管内部更大区域的狭窄.
(3) 回流区易使物质沉积,是造成管腔狭窄的原因之一. AS与LL的增大使狭窄下游回流区长度增加,关系曲线成"S"型. 同时,AS与LL的增大会使模型最大剪切速率增大,关系曲线呈抛物线型.
(4) 管腔狭窄会使速度有明显的增大,从而导致压力分布曲线有明显的下降. 随着AS与LL的增大压力下降幅度增大,可能造成斑块破裂.
综上所述,中等严重程度冠状动脉面积狭窄率和病变长度都是可能导致管腔进一步狭窄的因素,进而造成下部供血不足,临床上应予以重视.
| [1] | Mozaffarian D, Benjamin EJ, Go AS, et al. Heart disease and stroke statistics-2015 update: a report from the american heart association. Circulation, 2015, 131: e29-e322 |
| [2] | Zarins CK, Taylor CA, Min JK. Computed fractional flow reserve (FFTCT) derived from coronary CT angiography. Journal of Cardiovascular Translational Research, 2013, 6(5): 708-714 |
| [3] | Zhang JM, Zhong L, Luo T, et al. Numerical simulation and clinical implications of stenosis in coronary blood flow. In: BioMed Research International, 2014: 1-10 |
| [4] | Taylor CA, Fonte TA, Min JK. Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve. Journal of the American College of Cardiology, 2013, 61(22): 2233-2241 |
| [5] | Koo BK, Erglis A, Doh JH, et al. Diagnosis of ischemia-causing coronary stenoses by noninvasive fractional flow reserve computed from coronary computed tomographic angiograms. Journal of the American College of Cardiology, 2011, 58(19): 1889-1996 |
| [6] | Yong AS, Ng AC, Brieger D, et al. Three-dimensional and two-dimensional quantitative coronary angiography, and their prediction of reduced fractional flow reserve. European Heart Journal, 2011, 32(3): 345-353 |
| [7] | Iguchi T, Hasegawa T, Nishimura S, et al. Impact of lesion length on functional significance in intermediate coronary lesions. Clinical Investigations, 2013, 36(3): 172-177 |
| [8] | Kristensen TS, Engstrømb T, Kelbæk H, et al. Correlation between coronary computed tomographic angiography and fractional flow reserve. International Journal of Cardiology, 2010, 144(2): 200-205 |
| [9] | Alghamdi A, Balgaith M, Alkhaldi A. Influence of the length of coronary artery lesions on fractional flow reserve across intermediate coronary obstruction. European Heart Journal Supplements, 2014, 16(Supplement B): 76-79 |
| [10] | Li ZY, Taviani V, Tang T, et al. The mechanical triggers of plaque rupture: shear stress vs pressure gradient. The British Journal of Radiology, 2009, 82(Spec No 1): S39-S45 |
| [11] | Gijsen F, van der Giessen A, van der Steen A, et al. Shear stress and advanced atherosclerosis in human coronary arteries. Journal of Biomechanics, 2013, 46(2): 240-247 |
| [12] | Yin W, Shanmugavelayudam SK, Rubenstein DA. The effect of physiologically relevant dynamic shear stress on platelet and endothelial cell activation. Thrombosis Research, 2011, 127(3): 235-241 |
| [13] | Dolan JM, Kolega J, Meng H. High wall shear stress and spatial gradients in vascular pathology: A review. Annals of Biomedical Engineering, 2013, 41(7): 1411-1427 |
| [14] | Javadzadegan A, Yong AS, Chang M, et al. Flow recirculation zone length and shear rate are differentially affected by stenosis severity in human coronary arteries. American Journal of Physiology. Heart and Circulatory Physiology, 2013, 73(2): H559-H566 |
| [15] | McGah PM, Leotta DF, Beach KW, et al. A longitudinal study of remodeling in a revised peripheral artery bypass graft using 3D ultrasound imaging and computational hemodynamics. Journal of Biomechanical Engineering, 2011, 133(4)041008: 1-10 |
| [16] | Razavi A, Shirani E, Sadeghi MR. Numerical simulation of blood pulsatile flow in a stenosed carotid artery using different rheological models. Journal of Biomechanics, 2011, 44(11): 2021-2030 |
| [17] | Schrauwen JTC, Wentzel JJ, van der Steen AFW, et al. Geometry-based pressure drop prediction in mildly diseased human coronary arteries. Journal of Biomechanics, 2014, 47(8):1810-1815 |
| [18] | Colciago CM, Deparis S, Quarteroni A. Comparisons between reduced order models and full 3D models for fluid-structure interaction problems in haemodynamics. Journal of Computational and Applied Mathematics, 2014, 265: 120-138 |
| [19] | Wu JH, Liu GY, Huang WH, et al. Transient blood flow in elastic coronary arteries with varying degrees of stenosis and dilatations: CFD modelling and parametric study. Computer Methods in Biomechanics and Biomedical Engineering, 2015, 18(16): 1835-1845 |
| [20] | Chaichana T, Sun Z, Jewkes J. Impact of plaques in the left coronary artery on wall shear stress and pressure gradient in coronary side branches. Computer Methods in Biomechanics and Biomedical Engineering, 2014, 17(2): 108-118 |
| [21] | Furie B, Furie BC. Mechanisms of thrombus formation. The New England Journal of Medicine, 2008, 359(9): 938-949 |
| [22] | 王季尧, 李文平, 王盛章. 冠状动脉中氧输运的数值模拟研究. 生物医学工程学进展, 2012, 33(3): 141-146 (Wang Jiyao, Li Wenping, Wang Shengzhang. A numerical study on oxygen transport in a coronary artery. Shanghai of Biomedical Engineering, 2012, 33(3): 141-146 (in Chinese)) |
2. Department of Cardiac Surgery, FuWai Hospital, Chinese Academy of Medical Sciences, Beijing 100037, China
 2015, Vol. 47
2015, Vol. 47