引 言在离散元方法中,最早采用的是圆盘或球体的规则单元形式,其具有计算简单和易于大规模并行的优点,也能反映颗粒材料的基本力学行为[1, 2, 3]. 当颗粒变形较大时,还需考虑加载和卸载路径影响下的单元塑性变形[4].另外,在球体接触中增加滚动摩擦可提高颗粒系统的稳定性,增强颗粒间的互锁效应[5, 6].然而,随着对离散元方法计算精度要求的提高,为合理描述具有复杂几何形态的颗粒材料,粘接颗粒单元、超二次曲面、多面体单元等不同的非规则单元构造方法不断发展和完善起来[7, 8, 9, 10].其中,多面体单元能更加真实地反映岩石、碎冰等颗粒材料的几何形态,在一定程度上可避免细观计算参数选择的经验性[11, 12, 13, 14, 15].
在多面体单元计算中,为避免角点及棱边接触时的奇异现象,可通过在单元角点和棱边处设置球面和柱面的方法,以增强计算的稳定性[16]. 采用三维扩展圆盘单元可计算碎冰块的碰撞、重叠和堆积问题[17].最近,基于闵可夫斯基和方法发展了扩展多面体单元的粘结$\!$-$\!$-$\!$破坏模型,采用沃洛诺伊切割算法生成具有初始随机裂纹的连续体,并 对其破碎过程进行了离散元计算[18, 19].扩展多面体单元具有相对光滑的角点和棱边,可将块体间的尖锐接触转化为球面或柱面接触,从而简化接触判断[20].然而,目前扩展多面体离散元的接触力都采用线性近似计算模型,接触刚度也通常采用经验值,在很大程度上影响了计算精度.赫兹接触模型是球体单元的主要非线性接触力计算方法,其为扩展多面体单元的接触模型改进提供了很好的研究思路.为此,本文将在此基础上考虑扩展多面体单元在不同接触模式下接触点处的曲率半径进而建立相对合理的非线性接触模型.
近年来,离散元方法在模拟海冰与结构物相互作用的研究中得到了广泛应用[21].采用粘结破碎模型的规则排列颗粒可以模拟平整冰的破碎过程,并通过海冰单轴压缩试验确定粘结强度,进而模拟海冰与海洋结构的相互作用[22];圆盘单元则可模拟碎冰与海洋平台和船舶结构的冰载荷[23, 24];块体离散元对海冰与船体结构的相互作用、冰脊压剪过程可进行有效的数值计算[25, 26].此外,采用粘接块体单元可对平整冰与锥体结构的相互作用进行离散元分析,合理确定冰力的分布规律[27].在碎冰区,海冰具有显著的离散分布特性,冰块呈现出明显的非规则形状.因此,采用扩展多面体单元可对碎冰区的海冰动力过程及其与海洋结构的相互作用进行有效的离散元分析.
为此,本文基于闵可夫斯基和方法将球体单元与多面体单元相叠加构造光滑的扩展多面体单元,并建立不同接触模式下的计算模型. 针对碎冰区冰块的离散分布规律,采用扩展多面体单元对冰块与直立桩柱的相互作用进行离散元分析.
1 基于扩展多面体的离散元方法基于闵可夫斯基和方法可构造非规则的扩展多面体单元,并考虑单元间的不同接触方式,从而发展非线性接触模型的统一表述方式. 在此基础上,借鉴球体单元接触碰撞中的处理方法,对扩展多面体单元的黏滞作用和切向弹性接触力进行简化计算.
1.1 扩展多面体单元的闵可夫斯基和构造方法
若在空间中给出两个任意几何体${ A}$和${ B}$,则闵可夫斯基和可定义为[28, 29]
|
$$
{ A} \oplus { B} = \left\{ {{ x} + {
y} | { x} \in { A} ,{ y} \in { B} } \right\} $$
|
(1) |
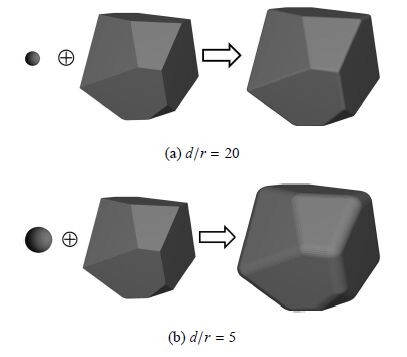
式中,${ x}$和${ y}$分别为${ A}$和${ B}$内的三维坐标点.在非规则颗粒的扩展多面体构造中,将以上两个空间 体分别设定为基本多面体单元和扩展球体单元.当一个任意多面体与球体单元叠加后可形成具有一定光滑度的扩展多面体,如图1所示.这里,$d$为多面体顶点到质心的平均长度,$r$是扩展球体的半径. 通过改变球体半径$r$可调整扩展多面体的尖锐度.
采用闵可夫斯基和方法可将多面体单元的点、线、面转化为球面、圆柱面和平面,其在接触判断和接触力计算中可以有效简化,也避免了多面体单元在角点、棱边接触计算时因接触角度不确定而出现的奇异现象.
若扩展多面体几何特征的集合为$\{{ G }_k \}$ ($k = 1$,2,$\cdots$,$n$),$n$为所有几何特征的总数,则扩展多面体单元$i$和$j$的几何特征集合为$\{{ G }_k^i \}$和$\{{ G }_k^j\}$,由此,两个多面体的接触判断准则为
|
$${\delta _{ij}} = \min ({\rm {dist}}(G_k^i,G_k^j)) - {r_i} - {r_j}\left\{ {\matrix{
\matrix{
< 0{\mkern 1mu} ,{\rm {接触}} \hfill \cr
0{\mkern 1mu} ,{\rm {分离}} \hfill \cr} \hfill \cr
} } \right.$$
|
(2) |
式中,$r_{i}$和$r_{j}$为两个扩展多面体单元的扩展半径.
1.2 扩展多面体单元接触模型的统一表述在扩展多面体单元间的相互作用中,除了弹性变形引起的弹性恢复力,还要考虑到单元之间碰撞产生的能量损耗.由此,单元间接 触力应同时考虑弹性接触力和黏滞力[30]. 对于法向作用力,则可写作
|
$$
F_{\rm n} = K_{\rm n}^\ast \delta _{\rm n}^\kappa + C_{\rm n}^\ast \delta _{\rm n}^{\kappa -1} \dot {\delta
}_{\rm n} $$
|
(3) |
式中,$K_{\rm n}^\ast $为两个接触单元的有效法向接触刚度,其取决于扩展多面体单元的接触模式;$\delta _{\rm n} $和$\dot {\delta }_{\rm n} $分别为单元间的法向重叠量和法向相对速度;$C_{\rm n}^\ast $为有效法向阻尼系数. 对于线性接触模型,有 $\kappa = 1$,而对于非线性接触模型,则 $\kappa =3/2$.
借鉴球体单元的法向黏滞力计算方法[31, 32],扩展多面体单元间的有效法向阻尼系数做相应的简化,得到块体的近似阻尼系数计算公式
|
$$
C_{\rm n} = \zeta _{\rm n} \sqrt {2 MK_{\rm n}^\ast } $$
|
(4) |
式中,$M$为两个接触单元的有效质量; $\zeta_{\rm n}$是无量纲法向阻尼系数,其与材料的黏滞性质密切相关.在线性接触模型中,其是回弹系数的函数;而在非线性接触模型中则由材料的黏滞性质确定[30, 33].
在单元的切向接触力计算中,一般忽略颗粒间的黏滞力[34, 35],则基于明德林(Mindlin)切向接触和摩尔$\!$-$\!$-$\!$库伦摩擦定律,切向接触力可写为
|
$F_{\rm s}^\ast = K_{\rm s}^{\ast } \delta _{\rm n}^{\kappa- 1} \delta _{\rm s}
$
|
(1) |
|
$F_{\rm s} = \min (F_{\rm s}^\ast ,{\rm sign} (F_{\rm s}^\ast )\mu F_{\rm n})
$
|
(6) |
式中,$K_{\rm s}^{\ast } $为有效切向刚度,一般简作$K_{\rm s}^{\ast } = r_{\rm sn} K_{\rm n}^{\ast } $,$r_{\rm sn}$为0.5,0.8或1.0 [1, 30, 32];$\delta_{\rm s}$是单元间的切向位移;$\mu $为单元间的摩擦系数.
在扩展多面体单元的非线性接触计算中,两个接触单元的有效弹性模量$E^\ast
$和接触点处的有效曲率半径$R^\ast $可写作
|
$\dfrac{1}{E^\ast } = \dfrac{1 - v_1^2 }{E_1 } + \dfrac{1 - v_2^2 }{E_2 }
$
|
(7) |
|
$\dfrac{1}{R^\ast } = \dfrac{1}{R_1 } + \dfrac{1}{R_2 } $
|
(8) |
式中,$E_{1}$和$E_{2}$为分别两个接触单元体的弹性模量,$\nu_{1}$和$\nu_{2}$为相应泊松比,$R_{1}$和$R_{2}$为两个多面体在接触点的曲率半径.
2 扩展多面体单元间的接触模型由于扩展多面体单元主要由角点(球体)、棱边(柱体)和平面等元素组成,其有效接触刚度与单元接触模式密切相关.扩展多面 体单元间的接触模式可分为3类,即:球体与球体、柱面、平面接触;柱面与柱面、平面接触;平面与平面接触.下面对不同接触模式下的计算模型进行分析.
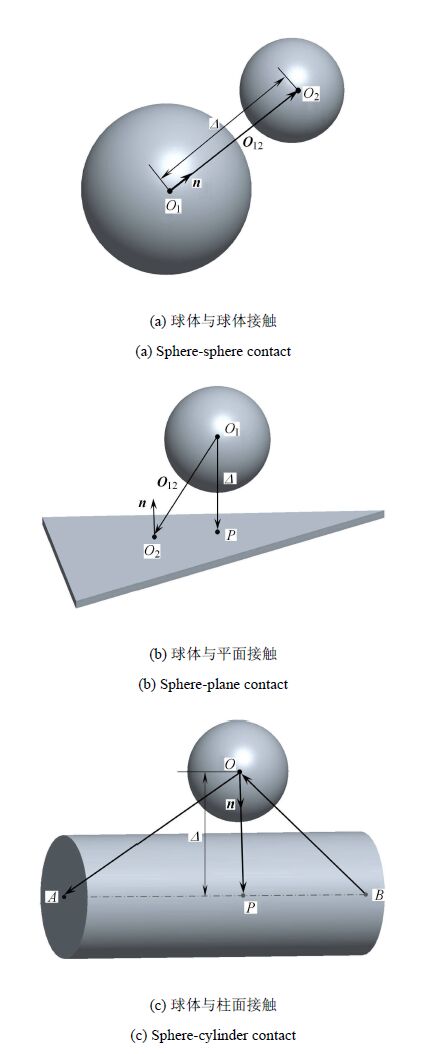
2.1 球体与球体、平面、柱面的接触计算在扩展多面体单元接触模式中,球体与球体、平面的接触计算可基于赫兹接触模型. 对于球体与球体接触,如图2(a)所示,${O}_{1}$与${O}_{2}$是两个球的球心,${ O}_{12}$是球心之间的距离矢量,${ n}$是${O}_{12}$的单位向量. 球体与球体接触通过计算两个球心距离$\varDelta =| {O}_{12}|$,进而计算两个球体的接触变形
|
$$
\delta _{\rm n} = \varDelta - R_1 - R_2 $$
|
(9) |
由此基于赫兹接触理论,球体间的法向弹性接触力为
|
$$
F_{\rm n}^{\rm e} = \dfrac{4}{3}E^\ast \sqrt {R^\ast } \delta _{\rm n}^{\tfrac{3}{2}} $$
|
(10) |
球体与平面的接触判断及计算也具有成熟的计算方法[36],如图2(b)所示. 三角形形心为${ O}_{2}$,$P$为球心 ${
O}_{1}$在三角形所在平面的投影. 球心与平面的距离$\varDelta =| { O}_{12}\cdot { n } |$,${
n}$是平面的单位外法向. 按式(9)计算接触变形$\delta _{\rm n}$,如果同时满足$\delta_{\rm
n} <0$且$P$点在三角形内,则球体与平面接触. 由平面的几何性质,设$R_{1}$是球体半径,令平面的曲率半径$R_{2} \to
\infty $,则有$R^{\ast }=R_{1}$.由此,球体与平面的法向弹性力为
|
$$
F_{\rm n}^{\rm e} = \dfrac{4}{3}E^\ast \sqrt {R_1 } \delta _{\rm n}^{\tfrac{3}{2}} $$
|
(11) |
图2(c)是球面与柱面的接触模式,其中$A$和$B$是柱体轴线的两个端点,$P$是球心$O$到轴线${ A B}$上的投影. 这里
$\varDelta = | { O P}|=| { A O }\cdot { n} |$,${
n}$是球体与柱面的单位接触法向,即向量${ O P}$的单位向量. 由式(9)计算接触变形$\delta_{\rm
n}$,如果同时满足$\delta_{\rm n} <0$且${ A O} \cdot { B O}<0$,那么球体与柱面接触.
赫兹接触假设下球面与柱面接触可通过椭圆积分表进行计算[37]. 基于赫兹接触模型,这里可简作
|
$$
F_{\rm n}^{\rm e} = \dfrac{4}{3}E^\ast (R_{\rm b} R^\ast )^{\tfrac{1}{4}}\delta _{\rm n}^{\tfrac{3}{2}} $$
|
(12) |
式中,$R_{\rm b}$为球体半径.
2.2 柱面与柱面、平面的接触计算
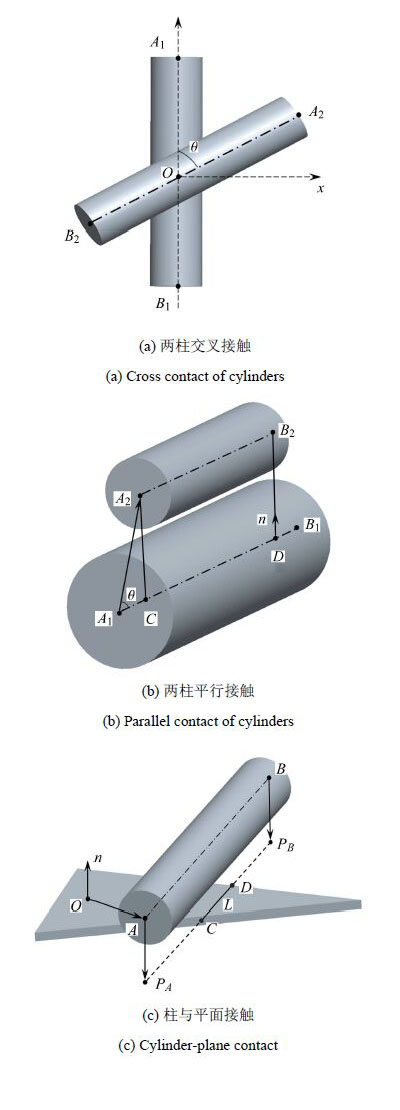
柱面与柱面的接触可以分为两种情况:平行接触和交叉接触. 图3(a)所示为两柱面交叉接触的情况,其接触力可采用赫兹接触模型计算,即
|
$$
F_{\rm n}^{\rm e} = \dfrac{4}{3}E^\ast \sqrt{ \tilde {R}} \delta _{\rm n}^{\tfrac{3}{2}} $$
|
(13) |
式中,$\tilde {R}$是等效高斯曲率半径,$\tilde {R} = \sqrt {{R}'_1 {R}'_2 }
$. ${R}'_1 $和${R}'_2 $为两个接触面的主曲率半径,可按如下方法计算.
设$xOy$平面为两个柱面接触时与接触法向垂直的平面,$O$点为接触点,$\theta $为两个柱面轴线的夹角,且$0 <\theta\leqslant 90^\circ$. 柱面1和柱面2与$xOy$平面的距离$d_1 = x^2 / (2R_1) $和$d_2 = (x\cos \theta - y\sin \theta)^2 / (2R_2) $,则两个柱面之间的距离为
|
$$
d = d_1 + d_2 = ax^2 + 2bxy + cy^2 $$
|
(14) |
这里$a=1/R_{1}+\cos^{2}\theta/R_{2}$,$b =-\sin\theta\cos\theta/(2R_{2})$,$c=\sin^{2}\theta/(2R_{2})$.
该多项式 的二次型矩阵${ M}$为
|
$$M = \left[{\matrix{
a & b \cr
b & c \cr
} } \right](15)$$
|
(15) |
设$T ={\rm tr} ({ M}) = a + c$,$D = \det ({ M}) = ac - b^2$. 那么矩阵${ M}$的本征方程$\det({ M} - \lambda { E} ) = 0$的两个解为
|
$$
\lambda _1 ,\lambda _2 = \dfrac{T\pm \sqrt {T^2 - 4D} }{2} $$
|
(16) |
接触点上对应的两个单元表面的主曲率半径${R}'_1 $和${R}'_2 $则分别是矩阵${
M}$的两个本征值$\lambda _1 $和$\lambda _2 $的倒数[38],即
|
$$
{R}'_1 ,{R}'_2 = \dfrac{2}{T\pm \sqrt {T^2 - 4D} } $$
|
(17) |
对于两个圆柱的平行接触方式,如图3(b)所示,$A_{1}B_{1}$和$A_{2}B_{2}$是两圆柱的中轴线,$\theta$是$A_{1}A_{2}$与$A_{1}B_{1}$的夹角,${CD}$是$A_{2}B_{2}$在$A_{1}B_{1}$上的投影.若两个圆柱平行,即$\cos\langle { A}_{1}{ B}_{1}$,${ A}_{2}{ B}_{2}\rangle=1$,则柱面与平面的距离$\varDelta =|{ C A}_{2} | = |{ A}_{1}{ A}_{2} | \cdot \sin \theta $.按照式(9)计算接触变形$\delta_{\rm n}$,若$\delta_{\rm n}<0$,则判断$A_{2}B_{2}$在$A_{1}B_{1}$所在直线上的投影${CD}$是否与$A_{1}B_{1}$重叠,并在有重叠条件下计算接触长度$L$.
对于平行接触的情况,依据赫兹接触理论人们发展了多个接触模型[39, 40, 41],本文选用如下简化模\linebreak
型[41]
|
$$
F_{\rm n}^{\rm e} = \dfrac{4}{3}LE^\ast \sqrt {R^\ast } \delta _{\rm n}^{\tfrac{3}{2}} $$
|
(18) |
式中,$L$是接触长度.
对于柱面和平面的接触方式,如图3(c)所示,$O$是三角面的形心,$A$和$B$是圆柱轴线的两个端点,$P_{A}$和$P_{B}$
是$A$和$B$在平面上投影,${ C D}$是${ P}_{A}{ P}_{B}$与三角面的重合部分,即接触长度.
若柱面与平面平行,即$\cos\langle { n},{ A B}\rangle =0$,则计算柱面与平面的距离$\varDelta
=|{ A P}_{A} | =| { O A}\cdot { n} |$,按照式(9)计算接触变形$\delta_{\rm n}$.
如果$\delta_{\rm n}<0$,则再判断${ A
B}$在三角面所在平面的投影$P_{A}P_{B}$是否与三角面重叠,有重叠则计算接触长度$L=|{ C D}| $.
类似地,设$R_{1}$是圆柱半径,依据式(18)可令$R_{2} \to \infty $,则有$R^{\ast
}=R_{1}$,由此圆柱和平面的法向弹性力可写作
|
$$
F_{\rm n}^{\rm e} = \dfrac{4}{3}LE^\ast \sqrt {R_1 } \delta _{\rm n}^{\tfrac{3}{2}} $$
|
(19) |
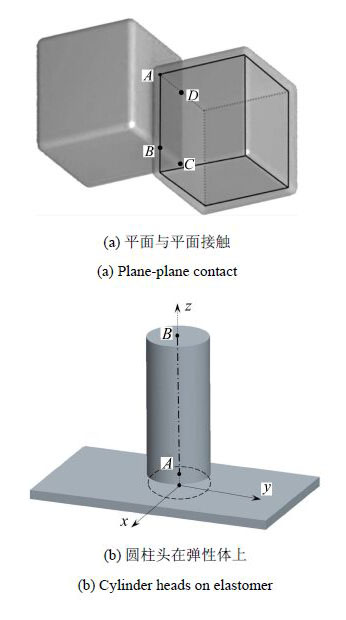
2.3 平面与平面的接触计算
如图4(a)所示,对于扩展多面体单元接触中的平面$\!$-$\!$-$\!$平面接触模型,可考虑表面力作用下弹性半空间体的变形,
如图4(b)所示. 假设刚性圆柱在弹性半空间体上的压力分布为$p(r)$,则接触力为
|
$$
F_{\rm n}^{\rm e} = \int_0^a p(r) \cdot 2π r dr $$
|
(20) |
由赫兹接触模型得到的接触面内的垂直位移是非均匀分布的,由此很难确定接触力与垂直位移的对应关系,且块体在接触时更多考虑的非圆形的接触区域. 因此,这里采用均匀法向位移的解,即假设接触区域内所有点的垂直位移都相等,则有
|
$$
u_z = \dfrac{π p_0 a}{E^\ast } $$
|
(21) |
式中,$a$为接触区域的半径. 由此接触面上的法向应力为
|
$$
p = p_0\Big (1 - \dfrac{r^2}{a^2}\Big)^{ - \tfrac{1}{2}} $$
|
(22) |
这样,作用在该区域上的接触力可写作
|
$$
F_{\rm n}^{\rm e} = 2π p_0 a^2 = 2aE^\ast \cdot u_z $$
|
(23) |
令$\delta_{\rm n}=u_{z}$,则上式可写作适用于非圆截面的形式,即
|
$$
F_{\rm n}^{\rm e} = 2E^\ast \beta \sqrt {\dfrac{A}{π }} \cdot \delta _{\rm n}
$$
|
(24) |
这里$\beta $可根据不同的接触面形状进行取值. 对于扩展多面体单元面与面接触中的多边形接触面,可取$\beta=1.02$[38].
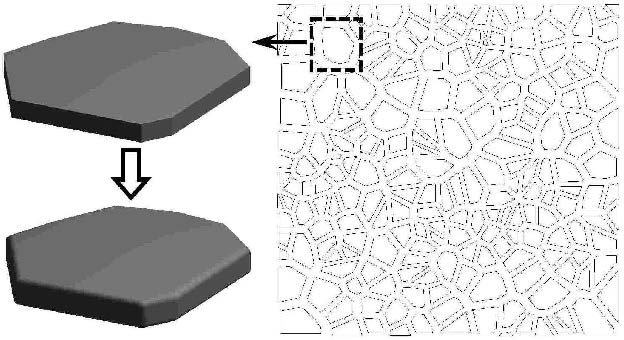
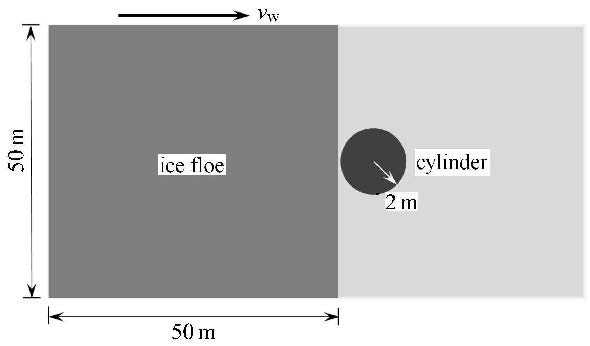
3 碎冰与直立桩柱相互作用的离散元分析在碎冰区,海冰在波浪、海流作用下呈现出明显的离散分布特性,并具有非规则的多边形几何形态,如图5(a)所示. 采用扩展多面体单元可对碎冰块的相互作用及其对冰区海洋结构的碰撞作用进行离散元计算.这里以碎冰区的单桩圆柱结构为例(如图5(b)),对碎冰作用下的冰荷载进行数值计算以验证扩展多面体单元在寒区海洋工程中的适用性.
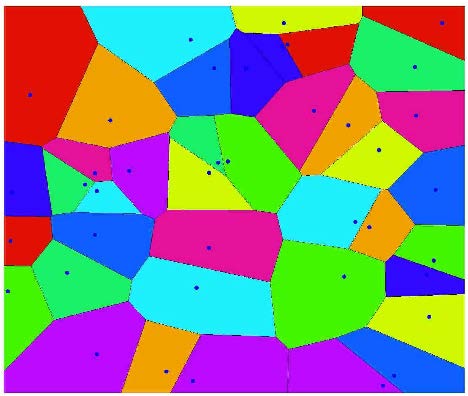
3.1 碎冰生成的沃洛诺伊切割算法为构造具有随机分布和非规则几何形态的碎冰单元,这里采用沃洛诺伊切割算法[42, 43, 44].它首先在计算域内随机生成若干坐标点,并将所有相邻点连成三角形,再作这些三角形各边的垂直平分线,最终每个点被周围的若干个垂直平分线包围,如图6所示.
采用沃洛诺伊切割算法在50 m$\times
$50 m的计算域随机生成200个多边形,并对其设定一定的厚度,采用闵可夫斯基和方法对其
构造生成相应的扩展多面体海冰单元,如图7所示.
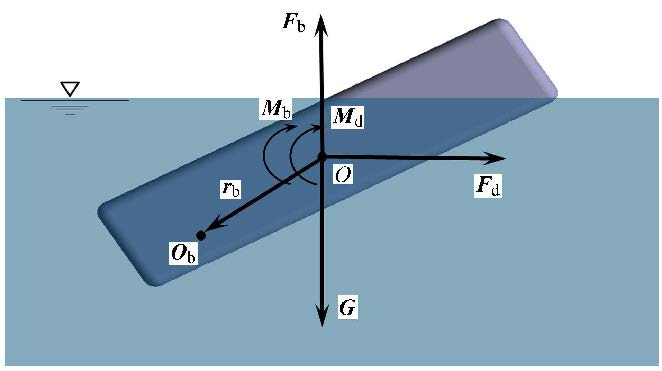
3.2 流体对冰块的作用力碎冰在海流、波浪作用下要受动浮力、拖曳力等动力作用,如图8所示. 这里$O$是冰块的重心,$O_{\rm b}$是冰块的浮心,浮心是指 冰块水面以下部分的形心. ${ r}_{\rm b}$是重心$O$到浮心$O_{\rm b}$的向量.这里主要考虑冰块受的重力${ G}$、浮力${ F}_{\rm b}$、浮力矩${ M}_{\rm b}$,以及水流拖曳力${F}_{\rm d}$和拖曳力矩${ M}_{\rm d}$作用.
浮力矩${ M}_{\rm b}$决定了冰块在水面的摇摆以及最终稳定形态,由浮心和块体形心不平衡引起,可写作
|
$$
{ M }_{\rm b} = { r }_{\rm b} \times { F }_{\rm b} $$
|
(25) |
拖曳力${ F}_{\rm d}$和拖曳力矩${ M}_{\rm d}$写作[23]
|
$$
{ F }_{\rm d} = - \dfrac{1}{2}C_{\rm d}^{\rm F} \rho_{\rm w} A_{\rm sub} ({
v} - { v}_{\rm w} )\left| {{ v} - { v}_{\rm w} } \right| $$
|
(26) |
|
$$
{ M}_{\rm d} = - \dfrac{1}{2}C_{\rm d}^{\rm M} r_{\rm eff}^3 \rho _{\rm w} A_{\rm sub} { \omega } \left| { \omega } \right| $$
|
(27) |
式中,$\rho_{\rm w}$为海水密度;$A_{\rm sub}$为块体与水的接触面积,即块体在水面以下的表面积; $C_{\rm d}^{\rm F} $和$C_{\rm d}^{\rm M}$为拖曳力系数和拖曳力矩系数;${ v}$为冰块速度; ${ v}_{\rm w}$为流速;${\omega }$为块体的转速;$r_{\rm eff}$为块体的有效半径,即所有顶点到质心距离的平均值.
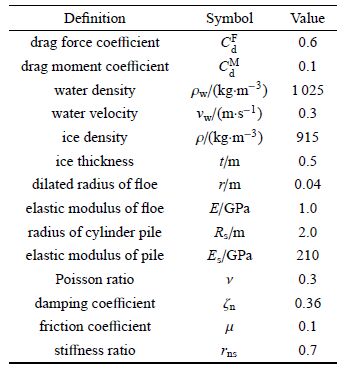
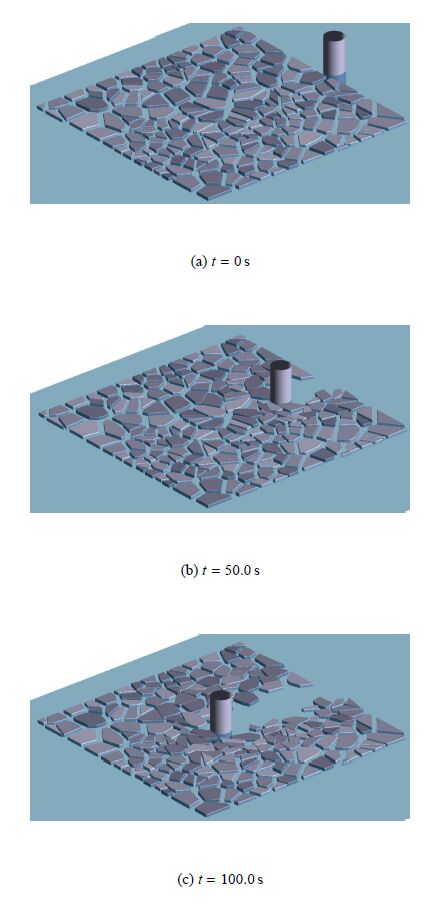
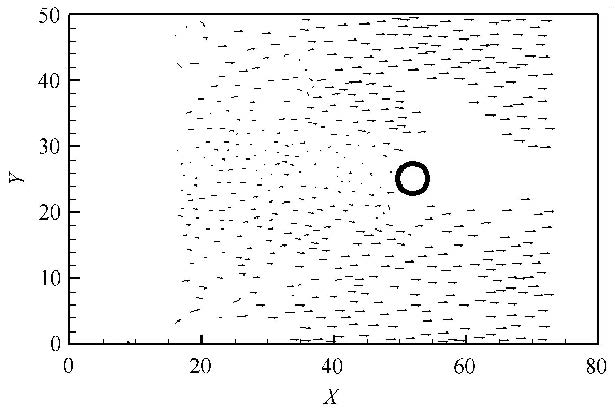
3.3 海冰与直立圆桩的离散元模拟碎冰区及圆桩的分布如图9所示.对碎冰区采用冯洛诺伊切割算法生成200个随机分布的冰块,碎冰的平均尺寸为2.8 m,其初始密 集度约为64%.水流沿$x$方向速度为0.3 m/s. 沿水流方向两侧为周期边界,其他为自由边界.选取典型海冰和海水的物理参数如表1所示,其中海冰密度、弹性模量、泊松比等计算参取采用了渤海海冰的实测值,其他计算参数则参考了相关海冰材料的离散元研究工作?[23, 45, 46, 47].采用以上块体离散元模型对碎冰和圆柱桩腿相互作用的动力过程进行100 s的离散元数值模拟.不同时刻碎冰在水流作用下与圆柱腿相互作用的过程如\图10(a)$\sim $图10(c). 可以发现,冰块在水流的拖曳作用下发生漂移并与圆桩发生碰撞作用.受桩柱的阻挡作用,碎冰区在桩柱后侧有明显的水道.
表1(Table 1)

表1 海冰与直立结构作用的离散元模拟参数Table 1 Major computational parameters of DEM simulation of dynamic ice load on cylinder structure
|
表1 海冰与直立结构作用的离散元模拟参数
Table 1 Major computational parameters of DEM simulation of dynamic ice load on cylinder structure |
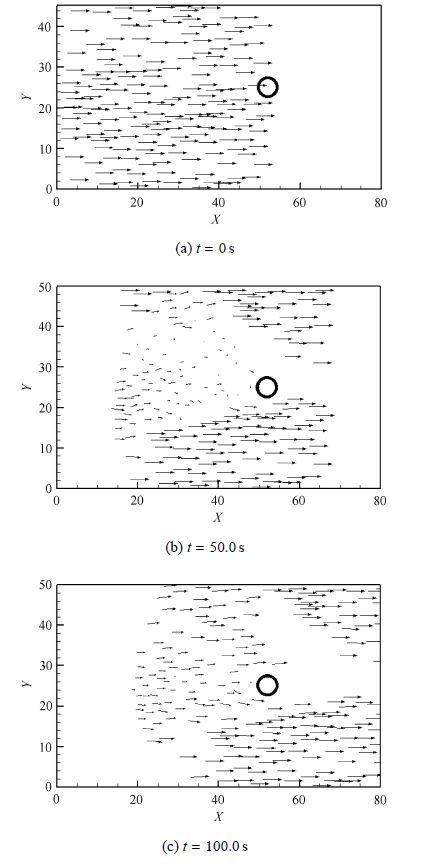
图11所示是海冰在海面上的速度分布图,可以看出初始时刻速度均匀分布,而经过一段时间的相互作用之后在桩柱前速度呈``V''形
分布,说明圆桩的阻挡作用明显,冰块圆桩前由于几何形状和摩擦的作用产生了一定的阻塞.
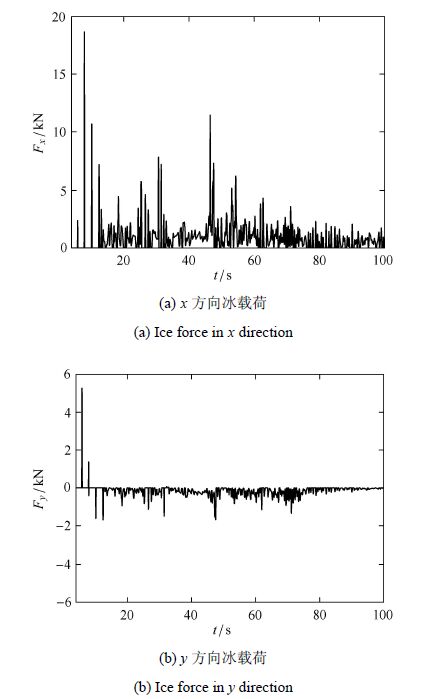
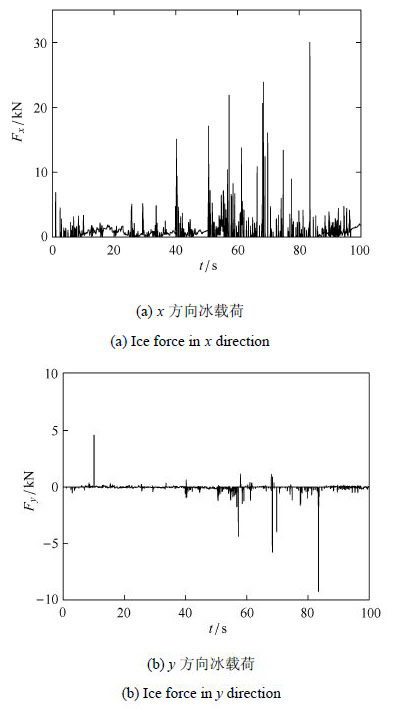
采用扩展多面体单元对桩柱上冰载荷的计算结果如图12所示.
从中可以看出,浮冰受海流拖曳在$x$方向漂流中对桩柱撞击产生的冰荷
载要明显高于其他方向,且在非连续冰块的碰撞下冰载荷具有显著的脉动特性;在$y$方向冰块对圆桩两侧也均有碰撞,其冰载荷出现正
负交替现象.
文献[23]采用圆盘单元对海冰对圆桩的水平冲击载荷进行了离散元分析,并分析了波流、海流、冰块大小等因素的影响.
由于其所选用的冰厚要远小于本文冰厚,其冰载荷幅值也明显低于本文计算结果.
但从计算的冰载荷时程来看,其对圆桩结构的冲击力也具有很强的随机性.
本文计算结果较好地反映了冰块对圆桩结构的碰撞作用,体现出扩展多面体离散元方法在碎冰区海洋结构冰载荷计算的适用性.
但计算参数和模拟结果的合理性还需要进一步参考海冰现场监测结果和室内模型试验进行定量的分析和验证.
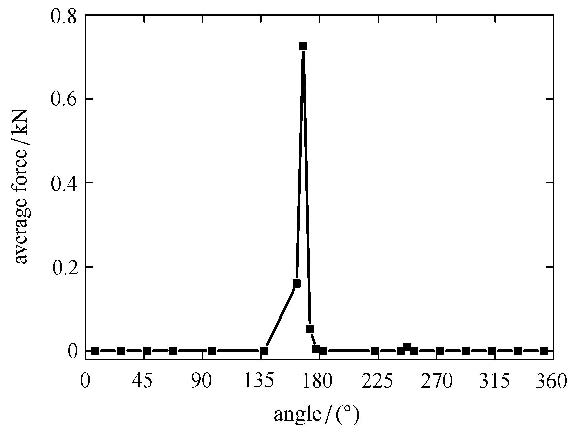
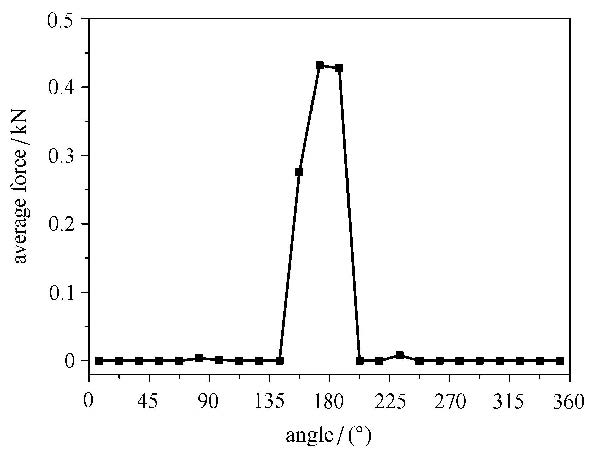
图13是圆桩周向受到冰载荷作用的平均分布情况,圆桩主要受到海冰正面的碰撞作用.
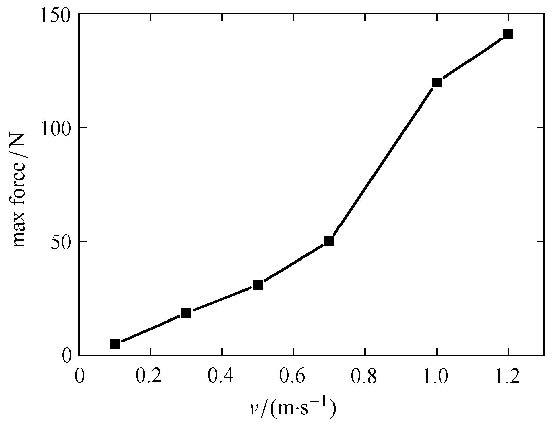
在不同冰速下对海冰与圆桩的冰力进行模拟计算,如图14所示对最大冰力进行统计.从图中可以看出,随着冰速增大,圆桩上 的最大冰力也增加,在冰速超过0.7 m/s后最大冰力会有较大的增幅.
在相同大小的海冰区域范围内,保持海冰密集度为64%并减小单元大小使单元平均尺寸为1.79 m,其他物理参数及边界条件不变,对海冰与圆桩结构作用进行模拟,计算结果如图15所示.从图中可以看出圆桩上的冰力在$x$和$y$方向上的基本规律与单元尺寸2.8 m时类似.但是由于冰块尺寸减小,初始碰撞时碎冰对圆桩的作用力明显变小,且波动较为平稳.在经过了较长时间的作用后,在60$\sim $85 s之间冰力出现了较大的波动,这主要是因为边界对碎冰的约束造成大量冰块在圆桩前阻塞,如图16所示,最终导致较大的冰力波动出现,可以看出阻塞的冰块基本呈``V''形分布. 图17是冰块阻塞时的速度分布,从该图上能更加明显地观察到圆桩对碎冰的阻挡作用.图18是圆桩周向受到冰载荷作用的平均分布情况,圆桩受到海冰正面的碰撞作用明显.
4 结 论本文基于闵可夫斯基和方法将球体与多面体相叠加生成具有光滑角点和棱边的扩展多面体单元.由此,将块体单元间复杂的接触计算转 化为球体、圆柱和平面之间的接触问题.在不同接触类型的接触力计算中,通过采用接触点处接触单元的曲率半径建立了统一的表述关系.
针对碎冰区冰块的几何特性和分布规律,采用沃洛诺伊切割算法生成随机分布的扩展多面体海冰单元,采用扩展多面体单元对碎冰区圆桩结构的冰载荷进行了离散元分析,确定了冰载荷的变化规律,研究了冰速的影响.
针对多桩、浮式等复杂的海洋结构,还需要进一步进行计算模型可靠性的检验,并通过现场实测数据验证计算精度.此外,在对浮冰 的扩展多面体离散元模拟中,尚未考虑冰块在与圆桩结构作用时的破碎现象.这需要在后续工作中建立扩展多面体单元间的粘接$\!$-$\!$-$\!$破碎模型,以更合理地计算海冰与海洋结构的相互作用.
参考文献
| [1] |
Cundall P, Strack O. A discrete numerical model for granular assemblies. Geotechnique, 1979, 29: 47-65 |
| [2] |
徐泳,孙其成,张凌 等. 颗粒离散元法研究进展. 力学进展,2003,33(2): 251-259 (Xu Yong, Sun Qicheng, Zhang Ling, et al. Advances in discrete element methods for particlulate materials. Advances in Mechanics, 2003, 33(2): 251-259 (in Chinese)) |
| [3] |
孙其成,王光谦. 颗粒流动力学及其离散模型评述. 力学进展,2008,38(2): 87-100 (Sun Qicheng, Wang Guangqian. Review on granular flow dynamics and its discrete element method. Advances in Mechanics, 2008,38(2): 87-100 (in Chinese)) |
| [4] |
Zhou Y. A theoretical model of collision between soft-spheres with Hertz elastic loading and nonlinear plastic unloading. Theoretical & Applied Mechanics Letters, 2011, 4: 041006 |
| [5] |
Zhu HP, Yu AB. A theoretical analysis of the force models in discrete element method. Powder Technology, 2006, 161: 122-129 |
| [6] |
Jiang MJ, Yu HS, Harris D. A novel discrete model for granular material incorporating rolling resistance. Computers and Geotechnics, 2005, 32: 340-357 |
| [7] |
Cleary PW. Industrial particle flow modeling using discrete element method. Engineering Computations, 2009, 26(6): 698-743 |
| [8] |
Boon CW, Houlsby GT, Utili S. A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method. Computers and Geotechnics, 2012, 44: 73-82 |
| [9] |
Ferellec JF, McDowell GR. A method to model realistic particle shape and inertia in DEM. Granular Matter, 2010, 12(5): 459-467 |
| [10] |
严颖,季顺迎. 碎石料直剪实验的组合颗粒单元数值模拟. 应用力学学报,2009, 26(1): 1-6 (Yan Ying, Ji Shunying. Numerical simulation of direct shear test for rubbles with clumped particles. Chinese Journal of Applied Mechanics, 2009, 26(1): 1-6 (in Chinese)) |
| [11] |
Hopkins MA, Tuhkuri J. Compression of floating ice fields. Journal of Geophysical Research, 1999, 104(C7): 15815-15825 |
| [12] |
Polojärvi A, Tuhkuri J. On modeling cohesive ridge keel punch through tests with a combined finite-discrete element method. Cold Regions Science and Technology, 2013, 85: 191-205 |
| [13] |
周伟,刘东,马刚 等. 基于随机散粒体模型的堆石体真三轴数值试验研究. 岩土工程学报,2012,34(4): 748-755 (Zhou Wei, Liu Dong, Ma Gang, et al. Numerical simulation of true triaxial tests on mechanical behaviors of rockfill based on stochastic granule model. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 748-755 (in Chinese)) |
| [14] |
王杰,李世海,周东 等. 模拟岩石破裂过程的块体单元离散弹簧模型. 岩土力学,2013,34(8): 2355-2362 (Wang Jie, Li Shihai, Zhou Dong, et al. A block-discrete-spring model to simulate failure process of rock. Rock and Soil Mechanics, 2013, 34(8): 2355-2362 (in Chinese)) |
| [15] |
金峰, 胡卫, 张冲等. 考虑弹塑性本构的三维模态变形体离散元方法断裂模拟. 工程力学, 2011, 28(5): 1-7 (Jin Feng, Hu Wei, Zhang Chong, et al. A fracture simulation using 3-D mode distinct element method (3MDEM) with elastoplastic constitutive model. Engineering Mechanics, 2011, 28(5): 1-7 (in Chinese)) |
| [16] |
Hopkins MA. Discrete element modeling with dilated particles. Engineering Computations, 2004, 21: 422-430 |
| [17] |
Hopkins MA, Shen HH. Simulation of pancake-ice dynamics in a wave field. Annals of Glaciology, 2001, 33: 355-360 |
| [18] |
Galindo-Torres SA, Pedroso DM, Williams DJ, et al. Breaking processes in three-dimensional bonded granular materials with general shapes. Computer Physics Communications, 2012, 183: 266-277 |
| [19] |
Galindo-Torres SA. A coupled discrete element Lattice Boltzmann method for the simulation of fluid-solid interaction with particles of general shapes. Comput Methods Appl. Mech. Engrg, 2013, 265: 107-119 |
| [20] |
Galindo-Torres SA, Pedroso DM. Molecular dynamics simulations of complex-shaped particles using Voronoi-based spheropolyhedra. Physical Review E, 2010, 81: 061303 |
| [21] |
季顺迎, 李春花, 刘煜. 海冰离散元模型的研究回顾及展望. 极地研究, 2012, 24(4):315-329 (Ji Shunying, Li Chunhua, Liu Yu. A review of advances in sea ice discrete element model. Chinese Journal of Polar Research, 2012, 24(4): 315-329 (in Chinese)) |
| [22] |
季顺迎,狄少丞,李正 等. 海冰与直立结构相互作用的离散单元数值模拟. 工程力学,2013,30(1):463-469 (Ji Shunying, Di Shaocheng, Li Zheng, et al. Discrete element modelling of interaction between sea ice and vertical offshore structures. Engineering Mechanics, 2013, 30(1): 463-469 (in Chinese)) |
| [23] |
Sun S, Shen HH. Simulation of pancake ice load on a circular cylinder in a wave and current field. Cold Regions Science and Technology, 2012, 78: 31-39 |
| [24] |
李紫麟,刘煜,孙珊珊 等. 船舶在碎冰区航行的离散元模拟及冰载荷分析. 力学学报,2013, 45(6): 868-877 (Li Zilin, Liu Yu, Sun Shanshan, et al. Analysis of ship maneuvering performances and ice loads on ship hull with discrete element model in broken-ice fields. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 868-877 (in Chinese)) |
| [25] |
Polojärvi A, Tuhkuri J. 3D discrete numerical modelling of ridge keel punch through tests. Cold Region Science and Technology, 2009, 56(1): 18-29 |
| [26] |
Lau M, Lawrence KP, Rothenburg L. Discrete element analysis of ice loads on ships and structures. Ships and Offshore Structures, 2011, 6(3): 211-221 |
| [27] |
Lu W, Lubbad R, Loset S. Simulationg ice-sloping structure interactions with the cohesive element method. Journal of Offshore Mechanics and Arctic Engineering, 2014, 136: 031501 |
| [28] |
Teissandier D, Vincent D. Algorithm to calculate the Minkowski sums of 3-polytopes based on normal fans. Computer-Aided Design, 2011, 43: 1567-1576 |
| [29] |
Li W, McMains S. A sweep and translate algorithm for computing voxelized 3D Minkowski sums on the GPU. Computer-Aided Design, 2014, 46: 90-100 |
| [30] |
Ji S, Shen HH. Effect of contact force models on granular flow dynamics. Journal of Engineering Mechanics, 2006, 132(11): 1252-1259 |
| [31] |
季顺迎, Shen Hayley. 颗粒介质在类固-液相变过程中的时空参数特性. 科学通报, 2006, 51(3): 255-262 (Ji Shunying, Shen Hayley. Characteristics of temporal-spatial parameter in quasi-solid-fluid phase transition of granular material. Chinese Science Bulletin, 2006, 51(3): 255-262 (in Chinese)) |
| [32] |
Ji S, Shen HH. Internal parameters and regime map for soft poly-dispersed granular materials. Journal of Rheology, 2008, 52(1): 87-103 |
| [33] |
Ramírez R, Pöschel T, Brilliantov NV, et al. Coefficient of restitution of colliding viscoelastic spheres. Physical Review E, 1999, 60(4): 4465-4472 |
| [34] |
Shen HH, Sankaran B. Internal length and time scales in a simple shear granular flow. Physical Review E, 2004, 70: 051308 |
| [35] |
Campbell C. Granular shear flows at the elastic limit. J Fluid Mech, 2002, 465: 261-291 |
| [36] |
Kremmer M, Favier JF. A method for representing boundaries in discrete element modelling-part I: Geometry and contact detection. International Journal for Numerical Methods in Engineering, 2001, 51: 1407-1421 |
| [37] |
Puttock MJ, Thwaite EG. Elastic Compression of Spheres and Cylinders at Point and Line Contact. Melbourne: Commonwealth Scientific and Industrial Research Organization, 1969: 6-44 |
| [38] |
Popov VL. Contact Mechanics and Friction: Physical Principles and Applications. Berlin: Springer-Verlag, 2010 |
| [39] |
Hunt KH, Crossley FRE. Coefficient of restitution interpreted as damping in vibroimpact. Journal of Applied Mechanics, 1975, 7: 440-445 |
| [40] |
Pereira CM, Ramalho AL, Ambrósio JA. A critical overview of internal and external cylinder contact force models. Nonlinear Dynamics, 2011, 63: 681-697 |
| [41] |
Lankarani HM, Nikravesh PE. Continuous contact force model for impact analysis in multibody systems. Nonlinear Dynamics, 1994, 5: 193-207 |
| [42] |
Slotterback S, Toiya M, Goff L, et al. Correlation between particle motion and Voronoi-Cell-Shape fluctuations during the compaction of granular matter. Physical Review Letters, 2008, 101: 258001 |
| [43] |
Lee I, Lee K, Torpelund-Bruin C. Voronoi image segmentation and its applications to geoinformatics. Journal of Computers, 2009, 4(11): 1101-1108 |
| [44] |
Mollon G, Zhao J. Fourier-Voronoi-based generation of realistic samples for discrete modelling of granular materials. Granular Matter, 2012, 14: 621-638 |
| [45] |
Ji S, Wang A, Su J, e al. Experimental studies on elastic modulus and flexural strength of sea ice in the Bohai sea. Journal of Cold Regions Engineering, 2011, 25(4): 182-195 |
| [46] |
Ji S, Di S, Liu S. Analysis of ice load on conical structure with discrete element method. Engineering Computations, 2015, 32(4): 1121-1134 |
| [47] |
Polojärvi A, Tuhkuri J. On modeling cohesive ridge keel punch through tests with a combined finite-discrete element method. Cold Regions Science and Technology, 2013, 85: 191-205 |
DILATED POLYHEDRA BASED DISCRETE ELEMENT METHOD AND ITS APPLICATION OF ICE LOAD ON CYLINDRICAL PILE
Liu Lu, Long Xue, Ji Shunying
State Key Laboratory of Structure Analysis of Industrial Equipment, Dalian University of Technology, Dalian 116023, China
Fund: The project was supported by the Special Funding for National Marine Commonwealth Industry of China (201105016, 201205007) and the National Natural Science Foundation of China (41176012, 11372067).
Abstract: With the polyhedron elements with complex geometric shapes, the linear contact force model cannot precisely obtain the contact force and its direction and the contact deformation under various contact patterns. Due that dilated polyhedral element can be generated with superposing one dilating sphere on the surface of one basic polyhedron in the Minkowski sum theory to construct the geometric shape of irregular particle accurately, and then its contact detection between particles can be calculated easily, considering di erent contact patterns between vertices, edges and planes of the dilated polyhedral elements, a unified nonlinear viscoelastic contact force model is developed. In this model, the equivalent radius of curvature is introduced to calculate the elastic contact sti ness in normal direction. Meanwhile, the viscous force and the elastic force in tangential direction are simplified based on the contact force model of spherical element. To simulate the sea ice floes in broken ice region, the sea ice elements are generated randomly with the Voronoi tessellation algorithm. The ice loads on a vertical cylinder pile are simulated with the dilated polyhedral elements considering the buoyancy and drag forces of current. Moreover, the influences of ice velocity and ice floe size on the ice of pile are determined, and the distribution of ice load around the cylindrical pile is obtained. Finally, the limitation of the present dilated polyhedral element and its further modification are discussed.
Key words:
discrete element method(DEM) dilated polyhedral element Minkowski sum Voronoi tessellation algorithm ice load


 2015, Vol. 47
2015, Vol. 47