引 言
泥浆在土中的渗透和沉积对于后期泥膜的形成以及泥浆压力的转化有重要影响. 现有研究成果表明,泥浆颗粒的迁移和沉积特性与浆液浓度[1]、颗粒大小[2, 3]、土体导水系数[4]、孔隙分布和骨架表面粗糙程度[5, 6, 7]等因素有关.目前,针对泥浆渗透的计算理论主要从``对流$\!$-$\!$-$\!$扩散$\!$-$\!$-$\!$吸附(convection-dispersion-retardation)''的角度进行考虑[8, 9],讨论对象为有效粒径在10$\mu $m 以内的胶体或分子等粒子,赫齐格\linebreak等[10]建立了定流速条件下一维问题的颗粒``对流$\!$-$\!$-$\!$扩散''方程,并通过引入沉积系数来表征骨架对迁移颗粒的俘获能力,给出了该沉积系数的经验表达式.赫齐格由试验总结出沉积系数的大小与孔隙内颗粒与骨架的作用力有关,孟旭辉等[11]采用动量交换方法计算了孔隙尺度下多孔介质与流体间的作用力,但没有进一步将流体中的固、液两相分开以计算骨架对颗粒的吸附作用,同时,由于颗粒粒径较小,上述计算方法中介质的变形以及渗流场的非线性变化对颗粒沉积的影响均未被考虑.
岩土工程中,泥浆颗粒的粒径普遍在75$\mu $m以上,赫齐格等[10]指出当颗粒粒径超过30$\mu $m时,计算过程中介质 的变形已经不能忽略.同样,布拉德福认为传统方法计算结果与实测的偏差是因为没有考虑变形对颗粒迁移的影响[12],并近似计算了介质中体积小于颗粒平均体积的孔隙所占的比例[13],最终提出了以叠加形式考虑变形的修正后的经验方程.对于渗流的影响,阿勒姆等[14]设计室内物理阻抗试验研究高岭土悬浮液在砂土中的渗透规律,认为液体的流速对骨架的吸附能力有显著影响且呈非线性.此外,泥浆在土中渗透还会伴随有填充区域的渗透性变化[15, 16]、表层孔隙水压力变化[17]以及土体强度变化[18].白云等[19]提出了泥膜动态形成的过滤模型,刘成等[20]建立了泥膜固含率与有效应力之间的关系,但均未考虑泥浆颗粒在土中的迁移和沉积特性及其对应的针对泥浆渗透过程的计算方法.
基于上述认识,本文的目的在于建立饱和土中综合考虑土体位移场、流体渗流场以及泥浆颗扩散场的描述泥浆渗透过程的多场耦合数理模型.首先,根据颗粒质量守恒定律推导耦合流速的浓度扩散方程,并通过在浓度方程中引入沉积系数来进一步计算沉积颗粒的质量;同时,以沉积量作为耦合项对比奥固结方程中的水量连续方程进行修正,考虑了颗粒沉积对孔隙排水量的影响,最终建立泥浆渗透的``变形$\!$-$\!$-$\!$渗流$\!$-$\!$-$\!$扩散''耦合计算模型.
1 基本方程
在一定的水头(或流速)边界下,毕奥[21]指出固结问题中孔隙水的排出量受到体积应变和静水压力的影响.泥浆在饱和土中的渗透过程也是孔隙中水的排出并逐步在某一深度内形成土粒、泥浆颗粒复合填充层的过程,即该过程中水的排出量还受到沉积在孔隙中的泥浆颗粒的影响. 求解这个问题需要毕奥固结理论和物质迁移理论.毕奥问题中单位体积内的孔隙水排出量与变形、压力的关系可以写成
|
$$cp = \theta - \lambda \varepsilon _{ii}$$
|
(1) |
式中,$\varepsilon _{ii} $为体积应变,$p$为孔隙水压力,$\theta $为孔隙排水量,$c$为储水系数,$\lambda$为有效应力系数.
式(1)的物理意义表示孔隙中的水量变化由孔隙内水的压缩和土的变形两部分影响造成. 实际上式(1)左边的$cp$为孔隙水压力作用下水体积的压缩量,而右边的$\lambda \varepsilon _{ii} $为土体应变产生的孔隙体积增量. 当考虑为悬浮液时,孔隙内水的排出量还受到沉积在孔隙内的颗粒体积的影响. 假设单位体积土体所能俘获的的泥浆颗粒质量为$S_{\rm T}$,根据水量的体积守恒定律,则式(1)应改写为
|
$$cp = \theta - \lambda \varepsilon _{ii} + \dfrac{\beta }{\rho _{\rm s} }S_{\rm T} $$
|
(2) |
式中,$\rho _{\rm s} $为泥浆颗粒密度(2.65 g/cm$^{3}$);$\beta$称为悬浮液颗粒紧致系数[10]的倒数,即沉积颗粒占据的孔隙体积与颗粒本身体积之比,$\beta$与颗粒的形状及排列方式有关,若假设颗粒为均匀圆球且按正立方体排列,则有$\beta $= 6 / $\pi $$;定义浓度为单位体积悬浮液中颗粒的质量,用CT表示该浓度中颗粒可以被土骨架俘获的那部分,简称俘获浓度,这部分颗粒被俘获后就滞留在孔隙中不再迁移;CL表示间隙泥浆浓度,这部分浓度的颗粒可以在孔隙中流动. 于是有
|
$$C_{\rm T} = S_{\rm T} / \varphi ,\ \ \hbox{或} \ \S_{\rm T} = C_{\rm T} \varphi $$
|
(3) |
式中,$\varphi $为孔隙率,$S_{\rm T}$为单位土体体积内沉积下来的颗粒质量.间隙浓度与俘获浓度存在如下关系[10]
|
$$\dfrac{\partial C_{\rm T} }{\partial t} = h \cdot C_{\rm L } $$
|
(4) |
其中$h$为沉积系数,表征土骨架对泥浆颗粒的吸附作用,一般情况下$h<1$且$h$越大,骨架的吸附作用越强,泥浆与地层的匹配程度越好. 赫齐格[10]通过试验得到
|
$$h = h_0 \left[{1 + b\left( {S_{\rm T} + \varphi C_{\rm L} } \right)} \right] $$
|
(5) |
式中,$h_{0}$和$b$与悬浮液颗粒和土颗粒的直径之比、颗粒的比表面积等有关. 对于确定的悬浮液和土体,$h_{0}$和$b$都是常数,需要用试验测定.
将式(3)与式(4)带入式(2)得
|
$$cp = \theta - \lambda {\varepsilon _{ii}} + {{\beta h} \over {{\rho _{\rm {s}}}}}\varphi \int_0^t {{C_{\rm {L}}}{\rm {d}}t} $$
|
(6) |
结合达西定律与连续性方程
|
$$\dot {\theta } + v_{i,i} = 0 $$
|
(8) |
于是式(6)可写成
|
$$C\dot p + \lambda {\dot \varepsilon _{ii}} - {{{\rm {d}}\left( {{{\beta h\varphi } \over {{\rho _{\rm {s}}}}}\int_0^t {{C_{\rm {L}}}{\rm { d}}t} } \right)} \over {{\rm {d}}t}} - {\left( {K{p_{,i}}} \right)_{,i}} = 0$$
|
(9) |
式(9)即为孔隙中考虑颗粒沉积后的水量连续方程.
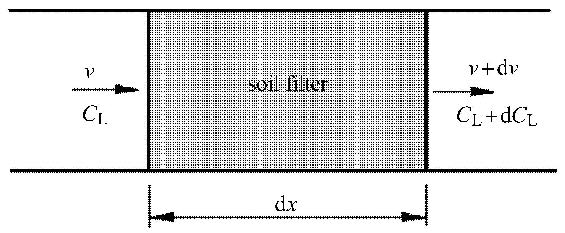
泥浆在土中的迁移特性不仅受到液体渗流的影响,也与自身颗粒的扩散有关. 要使上述问题可解,还需要建立泥浆的浓度扩散方程,考虑如下的一维情形(图1)以建立动态浓度扩散方程.
取断面面积为$A$,长为$\rm {d}x$的土体,孔隙率为$\varphi $,则$\rm {d}t$时间内流入土体的悬浮液颗粒质量为
|
$${\rm {d}}{m_1} = \left( {{v \over \varphi }{C_{\rm {L}}}A\varphi - {{{D_{\rm {L}}}} \over \varphi }{{{\rm {d}}{C_{\rm {L}}}} \over {{\rm {d}}x}}A\varphi } \right){\rm {d}}t = \left( {v{C_{\rm {L}}}A - {D_{\rm {L}}}{{{\rm {d}}{C_{\rm {L}}}} \over {{\rm {d}}x}}A} \right){\rm {d}}t$$
|
(10a) |
流出土块的颗粒质量为
|
$${\rm {d}}{m_2} = [\left( {v + {\rm { d}}v} \right)A\left( {{C_{\rm {L}}} + {\rm { d}}{C_{\rm {L}}}} \right) - {D_{\rm {L}}}{{\left( {{C_{\rm {L}}} + {\rm { d}}{C_{\rm {L}}}} \right)} \over {{\rm {d}}x}}A]{\rm { d}}t$$
|
(10b) |
在式(10a)中,右边括号中第1项为渗流携带进来的颗粒质量(对流项),第2项为土体左侧悬浮液扩散进来的颗粒质量(扩散项),它与浓度梯度的负值成正比,$D_{\rm L}$为扩散系数. 对于式(10b)也可以做类似的分析. 根据$\rm{d}t$时间内悬浮液颗粒质量守恒,即流入土块与流出土块的颗粒质量之差等于土块中颗粒质量的变化
|
$$\rm {d}m = \rm {d}m_1 - \rm {d}m_2 $$
|
(10c) |
其中,$\rm {d}m$包括两部分,沉积颗粒质量的增加和悬浮液中颗粒质量的增加,即
|
$$\rm {d}m = \rm{d}\left( {S_{\rm T} + \varphi C_{\rm L} } \right)A $$
|
(10d) |
合并化简,得动态浓度扩散方程为
|
$${{{\rm {d}}\left( {{S_{\rm {T}}} + \varphi {C_{\rm {L}}}} \right)} \over {{\rm {d}}t}} + {{{\rm {d}}(v{C_{\rm {L}}})} \over {{\rm {d}}x}} - {D_{\rm {L}}}{{{{\rm {d}}^2}{C_{\rm {L}}}} \over {{\rm {d}}{x^2}}} = 0$$
|
(11) |
式(11)为泥浆渗透过程中的考虑流速的动态浓度扩散方程,与传统的扩散方程所不同的是,由于泥浆在土中的渗透伴随压力梯度的变化,其渗流场在深度方向和时间尺度上均不为常数,即式(11)中的流量$v$与浓度$C_{\rm L}$相互耦合关联,求解该问题需要考虑这两个未知变量的解耦方法;另外,由于引入沉积系数后颗粒的沉积量被视为耦合项考虑到该方程中,式(11)中实际包含了间隙浓度与俘获浓度,这与常规的扩散方程也是不同的.当假设土体为各向同性时,式(11)很容易推广到三维的情况,即
|
$${{{\rm {d}}\left( {{S_{\rm {T}}} + \varphi {C_{\rm {L}}}} \right)} \over {{\rm {d}}t}} + {({v_i}{C_{\rm {L}}})_{,i}} - {D_{\rm {L}}}{({C_{\rm {L}}})_{,ii}} = 0$$
|
(12) |
式(9)与式(12)中均包含渗流流速,由固结理论可知,土中渗流场的变化也将导致土体变形的发生,注意到
|
$${\varepsilon _{ij}} = {1 \over 2}\left( {{u_{i,j}} + {u_{j,i}}} \right){\rm { }}$$
|
(13) |
|
$\sigma _{ij,j} = 0 $
|
(14) |
|
$\sigma _{ij} = D_{ijkl} \varepsilon _{kl} - \lambda p\delta _{ij} $
|
(15) |
其中式(13)为几何方程,式(14)为平衡方程,式(15)为物理方程. 联立式(13) $\sim$式(15)可得
|
$${\left[{{1 \over 2}{D_{ijkl}}\left( {{u_{k,l}} + {u_{l,k}}} \right) - {\rm { }}\lambda p{\delta _{ij}}} \right]_{,j}} = 0$$
|
(16) |
到此,式(9),式(12)和式(16)构成变形$\!$-$\!$-$\!$渗流$\!$-$\!$-$\!$扩散耦合的描述泥浆渗透过程及系统物理力学性态变化的基本方程,其中式(9)为考虑颗粒沉积的水量连续方程,式(12)为耦合渗流场的动态浓度扩散方程,式(16)为平衡方程.
另外,泥浆的渗透过程伴随材料孔隙率和渗透特性的变化,颗粒沉积对孔隙率的影响可表示为[10]
|
$$\varphi = \varphi _0 \left( {1 - \beta \dfrac{S_{\rm T} }{\rho _{\rm s} }} \right)$$
|
(17) |
当考虑变形时,式(17)变为
|
$$\varphi = \varphi _0 \left( {1 - \beta \dfrac{S_{\rm T} }{\rho _{\rm s} }} \right) + \lambda \varepsilon_{ii} $$
|
(18) |
式中,$\varphi _0 $表示清洁土体(即土体中还没有悬浮液颗粒的沉积)的初始孔隙率,$\lambda $为有效应力系数.
对于渗透系数$K$,根据康采尼$\!$-$\!$-$\!$卡曼方程(Kozeny-$\!$-Carmen equation)[22],可将土体的渗透性与孔隙大小相关联,马鲁扎斯等[23]得出当悬浮液颗粒直径大于25 μm时,有
|
$$K = {{\varphi _0^3} \over {k\eta \left( {{a_{\rm {c}}}} \right)_0^2}}{\left( {{{1 - \varphi } \over {1 - {\varphi _0}}}} \right)^{ - 4/3}}{\left( {{\varphi \over {{\varphi _0}}}} \right)^3} = {K_0}{\left( {{{1 - \varphi } \over {1 - {\varphi _0}}}} \right)^{ - 4/3}}{\left( {{\varphi \over {{\varphi _0}}}} \right)^3}$$
|
(19) |
式中,$K_{0}$为清洁土体的渗透系数,可用试验方法测定;$\eta$为浆液黏度,就岩土工程中的泥浆护壁问题而言,泥浆的黏度通 常为18$\sim$25 s(雷氏黏度),其波动范围小,且与纯水黏度差别不大,可以保证渗透系数在同一数量级做小幅度变化,因此,假设泥浆黏度对渗透系数的影响可以忽略,由式(19)可知,渗透系数的变化主要来自于孔隙变形以及孔隙被沉积颗粒阻塞而导致的孔隙体积减小.
2 变分原理及有限单元法
2.1 变分原理
由虚功原理,容易将式(16)构造成如下泛函
|
$$\varPhi _1 = {\rm { }}\int_v {\left( {{1 \over 2}{D_{ijkl}}{\varepsilon _{kl}}{\varepsilon _{ij}} - \lambda p{\varepsilon _{ii}}} \right)} {\rm { d}}V - {\rm { }}\int_{{S_\sigma }} {P_i^ * {u_i}{\rm { d}}S} {\rm { }}$$
|
(20) |
其中,$P_{i}^*$为作用在边界上的单位面积上的力,$\varPhi _1 $实际上就是系统势能.
假设孔隙率在每个时间步内为常数,式(9)可化简为
|
$$c\dot p + \lambda \dot \varepsilon_{ii} - \dfrac{\beta h}{\rho _{\rm s} }\varphi C_{\rm L} - \left( {Kp_{,i}} \right)_{,i} = 0 $$
|
(21) |
将上式中对时间的导数用向后两步差分表示,即
|
$$( \dot{ \ } )=a_0( \ )+a_{-1}( \ )_{-1}+a_{-2}( \ )_{-2} $$
|
(22) |
其中
|
$$\left. {\matrix{
{{a_0} = {{2{\Delta _{ - 1}} + {\Delta _{ - 2}}} \over {{\Delta _{ - 1}}\left( {{\Delta _{ - 1}} + {\Delta _{ - 2}}} \right)}}} \hfill \cr
{{a_{ - 1}} = - {{{\Delta _{ - 1}} + {\Delta _{ - 2}}} \over {{\Delta _{ - 1}}{\Delta _{ - 2}}}}} \hfill \cr
{{a_{ - 2}} = {{{\Delta _{ - 1}}} \over {{\Delta _{ - 2}}\left( {{\Delta _{ - 1}} + {\Delta _{ - 2}}} \right)}}} \hfill \cr
} } \right\}$$
|
(23) |
式中,$\varDelta _{ - 1} $与$\varDelta _{ - 2} $表示向后两步的时间增量,下标$-1$与$-2$分别表示$t - \varDelta_{ - 1} $和$t - \varDelta _{ - 1} - \varDelta _{ - 2} $ 时刻物理量的取值. 利用式(22)和式(23),式(21)变为
|
$$c\left( {{a_0}p + {a_{ - 1}}{p_{ - 1}} + {a_{ - 2}}{p_{ - 2}}} \right) + \lambda \left[{{a_0}{\varepsilon _{ii}} + {a_{ - 1}}{{\left( {{\varepsilon _{ii}}} \right)}_{ - 1}} + {a_{ - 2}}{{\left( {{\varepsilon _{ii}}} \right)}_{ - 2}}} \right] - \frac{{\beta h}}{{{\rho _{\text{s}}}}}\varphi {C_{\text{L}}} - {\left( {K{p_{,i}}} \right)_{,i}} = 0$$
|
(24) |
式(24)的弱形式可以写成
|
$$\eqalign{
& \int_V {[c\left( {{a_0}p + {a_{ - 1}}{p_{ - 1}} + {a_{ - 2}}{p_{ - 2}}} \right) + \lambda \left[{{a_0}{\varepsilon _{ii}} + {a_{ - 1}}{{\left( {{\varepsilon _{ii}}} \right)}_{ - 1}} + {a_{ - 2}}{{\left( {{\varepsilon _{ii}}} \right)}_{ - 2}}} \right]} - \cr
& {{\beta h} \over {{\rho _{\rm {s}}}}}\varphi {C_{\rm {L}}} - {\left( {K{p_{,i}}} \right)_{,i}}]\delta p{\rm { d}}V = 0 \cr} $$
|
(25) |
利用分部积分公式和高斯公式进一步整理可得泛函形式
|
$$\eqalign{
& {\Phi _2} = \int_v {\left( {\lambda {\varepsilon _{ii}}p + {c \over 2}{p^2} + {K \over {2{a_0}}}{p_{,i}}{p_{,i}} - {{\beta h\varphi } \over {{a_0}{\rho _{\rm {s}}}}}{C_{\rm {L}}}p} \right){\rm {d}}V} + \cr
& \int_v {{1 \over {{a_0}}}cp\left( {{a_{ - 2}}{p_{ - 2}} + {a_{ - 1}}{p_{ - 1}}} \right){\rm {d}}V} + \cr
& \int_v {{1 \over {{a_0}}}\lambda p\left[{{a_{ - 2}}{{\left( {{\varepsilon _{ii}}} \right)}_{ - 2}} + {a_{ - 1}}{{\left( {{\varepsilon _{ii}}} \right)}_{ - 1}}} \right]{\rm {d}}V} + \int_{Sv} {{1 \over {{a_0}}}v_i^ * {n_i}p{\rm {d}}V} \cr} $$
|
(26) |
式中$v_i^\ast $为边界上的渗流速度.
对式(12),利用式(22),其弱形式如下
|
$$\int_v \{ \varphi [\left( {h + {a_0}} \right){C_{\rm {L}}} + {a_{ - 1}}{\left( {{C_{\rm {L}}}} \right)_{ - 1}} + {a_{ - 2}}{\left( {{C_{\rm {L}}}} \right)_{ - 2}}] + {({v_i}{C_{\rm {L}}})_{,i}} - {D_{\rm {L}}}{({C_{\rm {L}}})_{,ii}}\} \delta {C_{\rm {L}}}{\rm {d}}V = 0$$
|
(27) |
同理可得
|
$$\eqalign{
& \delta {\Phi _3} = \int_v [{C_{\rm {L}}}\delta {C_{\rm {L}}} - {1 \over {\varphi \left( {h + {a_0}} \right)}}{v_i}{C_{\rm {L}}}\delta {\left( {{C_{\rm {L}}}} \right)_{,i}} + \cr
& {{{D_{\rm {L}}}} \over {\varphi \left( {h + {a_0}} \right)}}{\left( {{C_{\rm {L}}}} \right)_{,i}}\delta {\left( {{C_{\rm {L}}}} \right)_{,i}}]{\rm {d}}V + \int_v {{1 \over {h + {a_0}}}} [{a_{ - 1}}{\left( {{C_{\rm {L}}}} \right)_{ - 1}} + {a_{ - 2}}{\left( {{C_{\rm {L}}}} \right)_{ - 2}}]\delta {C_{\rm {L}}}{\rm {d}}V \cr
& + \int_s {{1 \over {h + {a_0}}}} S_i^ * {n_i}\delta {C_{\rm {L}}}{\rm {d}}S(28) \cr} $$
|
(28) |
式中,$S_{i}^{\ast }$为泥浆颗粒流量,$S_{i}^{\ast } = [v_{i}C_{\rm L}-D_{\rm L}(C_{\rm L})_{,i}]/ \varphi $;式中有非线性项$v_i C_{\rm L} \delta \left( {C_{\rm L} } \right)_{,i}$,因此无法直接写出 $\varPhi _3$ 的泛函形式.
到此,泥浆渗透问题的泛函可表示成如下形式
|
$$
\varPhi = \varPhi _1 + \varPhi _2 + \varPhi _3 $$
|
(29) |
在所有满足边界条件的位移场、压力场和浓度场中,式(9),式(12)和式(16)的真实解使式(29)取得极值,即
|
$$
\delta \varPhi = \delta \varPhi _1 + \delta \varPhi _2 + \delta \varPhi _3 = 0
$$
|
(30) |
由$u_i $,$p$和$C_{\rm T}$相互独立,式(30)成立的充要条件为下式成立
|
$$
\delta \varPhi _1 = \delta \varPhi _2 = \delta \varPhi _3 = 0 $$
|
(31) |
也可以写成如下形式
|
$\delta \varPhi _1 + \delta \varPhi _2 = 0 $
|
(32a) |
|
$\delta \varPhi _3 = 0 $
|
(33b) |
由于$\varPhi _1 $和$\varPhi _2$具有泛函的形式,式(32a)对应的有限元方程的系数矩阵是对称的;此外,式(32a)中含有浓度,式(32b)中含有渗流流速与浓度耦合的非线性项$v_iC_{\rm L} \delta \left( {C_{\rm L} } \right)_{,i} $,求解时需要在两式之间进行迭代.
2.2 有限单元法
在计算域上离散后变分泛函可写为
|
$$\eqalign{
& \delta {\Phi _1} = \sum\limits_e \delta {u^{\rm {T}}}\int_{{v_e}} {{B^{\rm {T}}}} DB{\rm {dVu - }} \cr
& \sum\limits_{\rm {e}} \delta {{\rm {u}}^{\rm {T}}}\int_{{{\rm {v}}_{\rm {e}}}} {{{\rm {B}}^{\rm {T}}}} \lambda {\left[{{\rm {1}},{\rm {1}},{\rm {1}},{\rm {0}},{\rm {0}},{\rm {0}}} \right]^{\rm {T}}}{{\rm {N}}_{\rm {p}}}{\rm {dVp - }}\sum\limits_{\rm {e}} \delta {{\rm {u}}^{\rm {T}}}\int_{{{\rm {s}}_{\rm {e}}}} {{{\rm {N}}^{\rm {T}}}} {{\rm {P}}^ * }{\rm {dS}} \cr} $$
|
(33) |
式中,${ u}$和${ p}$为单元节点位移向量和单元节点压力向量,${B}$为单元应变向量与${ u}$的关系矩阵,即
|
$$
{ \varepsilon} = { B}{ u} $$
|
(34) |
${ N}$与${ N}_{p}$分别为单元内的位移和压力插值函数(形函数)矩阵,${ D}$为对应于张量${D}_{ijkl}$的本 构关系矩阵(弹性系数矩阵),$V_{e}$为单元体积,$S_{e}$为单元边界,${ P}^{\ast}$为边界应力向量,符号$\sum\limits_e $表示在所有单元上求和.
|
$$\eqalign{
& \delta {\Phi _2} = \sum\limits_e \delta {p^{\rm {T}}}\int_{{v_e}} {N_p^{\rm {T}}} \lambda \left[{1,1,1,0,0,0} \right]B{\rm {dVu + }} \cr
& \sum\limits_{\rm {e}} \delta {{\rm {p}}^{\rm {T}}}\int_{{{\rm {v}}_{\rm {e}}}} {{\rm {N}}_{\rm {p}}^{\rm {T}}} {\rm {c}}{{\rm {N}}_{\rm {p}}}{\rm {dVp + }}\sum\limits_{\rm {e}} \delta {{\rm {p}}^{\rm {T}}}\int_{{{\rm {v}}_{\rm {e}}}} {{{\rm {1}} \over {{{\rm {a}}_{\rm {0}}}}}} {\rm {B}}_{\rm {p}}^{\rm {T}}{\rm {K}}{{\rm {B}}_{\rm {p}}}{\rm {dVp - }} \cr
& \sum\limits_{\rm {e}} \delta {{\rm {p}}^{\rm {T}}}\int_{{{\rm {v}}_{\rm {e}}}} {{{\beta {\rm {h}}\varphi } \over {{{\rm {a}}_{\rm {0}}}{\rho _{\rm {s}}}}}} {\rm {N}}_{\rm {p}}^{\rm {T}}{{\rm {N}}_{\rm {c}}}{\rm {dV}}{{\rm {C}}_{\rm {L}}}{\rm { + }}\sum\limits_{\rm {e}} \delta {{\rm {p}}^{\rm {T}}}\int_{{{\rm {v}}_{\rm {e}}}} {{{\rm {c}} \over {{{\rm {a}}_{\rm {0}}}}}} {\rm {N}}_{\rm {p}}^{\rm {T}}{{\rm {N}}_{\rm {p}}}{\rm {dV}}\left( {{{\rm {a}}_{{\rm { - 2}}}}{{\rm {p}}_{{\rm { - 2}}}}{\rm { + }}{{\rm {a}}_{{\rm { - 1}}}}{{\rm {p}}_{{\rm { - 1}}}}} \right){\rm { + }} \cr
& \sum\limits_{\rm {e}} \delta {{\rm {p}}^{\rm {T}}}\int_{{{\rm {v}}_{\rm {e}}}} {{\lambda \over {{{\rm {a}}_{\rm {0}}}}}} {\rm {N}}_{\rm {p}}^{\rm {T}}\left[{{\rm {1}},{\rm {1}},{\rm {1}},{\rm {0}},{\rm {0}},{\rm {0}}} \right]{\rm {BdV}} \cdot \left( {{{\rm {a}}_{{\rm { - 2}}}}{{\rm {u}}_{{\rm { - 2}}}}{\rm { + }}{{\rm {a}}_{{\rm { - 1}}}}{{\rm {u}}_{{\rm { - 1}}}}} \right){\rm { + }}\sum\limits_{\rm {e}} \delta {{\rm {p}}^{\rm {T}}}\int_{{{\rm {s}}_{\rm {e}}}} {{{\rm {1}} \over {{{\rm {a}}_{\rm {0}}}}}} {\rm {N}}_{\rm {p}}^{\rm {T}}{\rm {v}}_n^ * {\rm {dS}} \cr} $$
|
(35) |
式中,${ C}_{\rm L}$为单元节点浓度向量,${ B}_{p}$为单元内压力导数向量与${p}$的关系矩阵,即
|
$$
{ p}_{,i} = { B}_p { p} $$
|
(36) |
${ N}_{c}$为单元内的浓度插值函数(形函数)矩阵,${ v}_{n}^{\ast }$为边界上法向渗流速度.
同理,对于$\delta \varPhi _3 $,离散后可得
|
$$\eqalign{
& \delta {\Phi _3} = \sum\limits_e \delta C_{\rm {L}}^{\rm {T}}\int_{{v_e}} {N_c^{\rm {T}}} {N_c}{\rm {dV}}{{\rm {C}}_{\rm {L}}}{\rm { + }}\sum\limits_{\rm {e}} \delta {\rm {C}}_{\rm {L}}^{\rm {T}}\int_{{{\rm {v}}_{\rm {e}}}} {{{\rm {1}} \over {\varphi \left( {{\rm {h + }}{{\rm {a}}_{\rm {0}}}} \right)}}} {\rm {B}}_{\rm {c}}^{\rm {T}}{\rm {v}}{{\rm {N}}_{\rm {c}}}{\rm {dV}}{{\rm {C}}_{\rm {L}}} \cr
& {\rm { + }}\sum\limits_{\rm {e}} \delta {\rm {C}}_{\rm {L}}^{\rm {T}}\int_{{{\rm {v}}_{\rm {e}}}} {{{{{\rm {D}}_{\rm {L}}}} \over {\varphi \left( {{\rm {h + }}{{\rm {a}}_{\rm {0}}}} \right)}}} {\rm {B}}_{\rm {c}}^{\rm {T}}{{\rm {B}}_{\rm {c}}}{\rm {dV}}{{\rm {C}}_{\rm {L}}}{\rm { + }} \cr
& \sum\limits_e \delta C_{\rm {L}}^{\rm {T}}\int_{{v_e}} {{1 \over {h + {a_0}}}} N_c^{\rm {T}}{N_c}{\rm {dV}} \cdot \cr
& [{{\rm {a}}_{{\rm { - 2}}}}{\left( {{{\rm {C}}_{\rm {L}}}} \right)_{{\rm { - 2}}}}{\rm { + }}{{\rm {a}}_{{\rm { - 1}}}}{\left( {{{\rm {C}}_{\rm {L}}}} \right)_{{\rm { - 1}}}}]{\rm { + }}\sum\limits_{\rm {e}} \delta {\rm {C}}_{\rm {L}}^{\rm {T}}\int_{{{\rm {s}}_{\rm {e}}}} {{{\rm {1}} \over {{\rm {h + }}{{\rm {a}}_{\rm {0}}}}}} {\rm {N}}_{\rm {c}}^{\rm {T}}{\rm {S}}_{\rm {n}}^ * {\rm {dS}} \cr} $$
|
(37) |
式中 ${ B}_{c}$为单元内浓度导数向量与${ C}_{\rm L}$的关系矩阵,即
|
$$
\left( {{ C}_{\rm L} } \right)_{,i} = { B}_{ c} { C}_{\rm L}
$$
|
(38) |
${ S}_{n}^{\ast }$为边界上的法向泥浆颗粒流量,${ v}$为单元内的渗流流速向量.
利用式(31),组装得有限元计算格式
|
$$\left[{\matrix{
{{K_u}} & L & {} \cr
{L'} & H & S \cr
{} & {} & C \cr
} } \right] \cdot \left\{ {\matrix{
u \cr
p \cr
{{C_{\rm {L}}}} \cr
} } \right\} = \left\{ {\matrix{
{{F_1}} \cr
{{F_2}} \cr
{{F_3}} \cr
} } \right\}$$
|
(39) |
式中
$${K_u} = \sum\limits_e {\int_{{v_e}} {{B^{\rm{T}}}} } DB{\rm{dV}}$$
$${\rm{H = }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{\rm{N}}_{\rm{p}}^{\rm{T}}} } {\rm{c}}{{\rm{N}}_{\rm{p}}}{\rm{dV + }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{\rm{1}} \over {{{\rm{a}}_{\rm{0}}}}}} } {\rm{B}}_{\rm{p}}^{\rm{T}}{\rm{K}}{{\rm{B}}_{\rm{p}}}{\rm{dV}}$$
$${\rm{C = }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{\rm{N}}_{\rm{c}}^{\rm{T}}} } {{\rm{N}}_{\rm{c}}}{\rm{dV + }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{{{\rm{D}}_{\rm{L}}}} \over {\varphi \left( {{\rm{h + }}{{\rm{a}}_{\rm{0}}}} \right)}}} } {\rm{B}}_{\rm{c}}^{\rm{T}}{{\rm{B}}_{\rm{c}}}{\rm{dV - }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{\rm{1}} \over {\varphi \left( {{\rm{h + }}{{\rm{a}}_{\rm{0}}}} \right)}}} } {\rm{B}}_{\rm{c}}^{\rm{T}}{\rm{v}}{{\rm{N}}_{\rm{c}}}{\rm{dV}}$$
$${\rm{L = - }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{\rm{B}}^{\rm{T}}}} } \lambda {\left[{{\rm{1}},{\rm{1}},{\rm{1}},{\rm{0}},{\rm{0}},{\rm{0}}} \right]^{\rm{T}}}{{\rm{N}}_{\rm{p}}}{\rm{dV}}$$
$${\rm{S = - }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{\beta {\rm{h}}\varphi } \over {{{\rm{a}}_{\rm{0}}}{\rho _{\rm{s}}}}}} } {\rm{N}}_{\rm{p}}^{\rm{T}}{{\rm{N}}_{\rm{c}}}{\rm{dV}}$$
$${{\rm{F}}_{\rm{1}}}{\rm{ = }}\sum\limits_{\rm{e}} {\int_{{{\rm{s}}_{\rm{e}}}} {{{\rm{N}}^{\rm{T}}}} } {{\rm{P}}^ * }{\rm{dS}}$$
$$\eqalign{
& {{\rm{F}}_{\rm{2}}}{\rm{ = - }}\sum\limits_{\rm{e}} {\int_{{{\rm{s}}_{\rm{e}}}} {{{\rm{1}} \over {{{\rm{a}}_{\rm{0}}}}}} } {\rm{N}}_{\rm{p}}^{\rm{T}}{\rm{v}}_{\rm{n}}^ * {\rm{dS - }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{\lambda \over {{{\rm{a}}_{\rm{0}}}}}} } {\rm{N}}_{\rm{p}}^{\rm{T}}\left[{{\rm{1}},{\rm{1}},{\rm{1}},{\rm{0}},{\rm{0}},{\rm{0}}} \right] \cr
& {\rm{BdV}} \cdot \left( {{{\rm{a}}_{{\rm{ - 2}}}}{{\rm{u}}_{{\rm{ - 2}}}}{\rm{ + }}{{\rm{a}}_{{\rm{ - 1}}}}{{\rm{u}}_{{\rm{ - 1}}}}} \right){\rm{ - }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{\rm{c}} \over {{{\rm{a}}_{\rm{0}}}}}} } {\rm{N}}_{\rm{p}}^{\rm{T}}{{\rm{N}}_{\rm{p}}}{\rm{dV}} \cdot \left( {{{\rm{a}}_{{\rm{ - 2}}}}{{\rm{p}}_{{\rm{ - 2}}}}{\rm{ + }}{{\rm{a}}_{{\rm{ - 1}}}}{{\rm{p}}_{{\rm{ - 1}}}}} \right) \cr} $$
$${F_3} = - \sum\limits_e {\int_{{s_e}} {{1 \over {{a_0}}}} } N_c^{\rm{T}}S_n^ * {\rm{dS - }}\sum\limits_{\rm{e}} {\int_{{{\rm{v}}_{\rm{e}}}} {{{\rm{1}} \over {{\rm{h + }}{{\rm{a}}_{\rm{0}}}}}} } {\rm{N}}_{\rm{c}}^{\rm{T}}{{\rm{N}}_{\rm{c}}}{\rm{dV}} \cdot \left[{{{\rm{a}}_{{\rm{ - 2}}}}{{\left( {{{\rm{C}}_{\rm{L}}}} \right)}_{{\rm{ - 2}}}}{\rm{ + }}{{\rm{a}}_{{\rm{ - 1}}}}{{\left( {{{\rm{C}}_{\rm{L}}}} \right)}_{{\rm{ - 1}}}}} \right]$$
写成式(32a)和式(32b)的形式
|
$$\left[{\matrix{
{{K_u}} & L \cr
{L'} & H \cr
} } \right] \cdot \left\{ {\matrix{
u \cr
p \cr
} } \right\} = \left\{ {\matrix{
{{F_1}} \cr
{{F_2} - S \cdot {C_{\rm{L}}}} \cr
} } \right\}$$
|
(40a) |
|
${ C } \cdot { C}_{\rm L} = { F}_3 $
|
(40b) |
由于浓度方程中含有非线性项$v_i { C}_{\rm L} \delta \left( { { C}_{\rm L} } \right)_{,i}$,式(40a)的列向量中含有浓度未知量,式(40b)的系数矩阵中含有压力列向量,即式(40a)和式(40b)的求解需采用迭代法.
最后,方程中的系数$K$,$h$和$\varphi $都随着沉积过程而变化,首先计算每一步的孔隙率$\varphi $,可把 式(4)写成差分格式
|
$$\left. \matrix{
{a_0}{C_{\rm{T}}} + {a_{ - 1}}{({C_{\rm{T}}})_{ - 1}} + {a_{ - 2}}{({C_{\rm{T}}})_{ - 2}}{a_0} = h{C_{\rm{L}}} \hfill \cr
{\rm{或}} \hfill \cr
{C_{\rm{T}}} = {1 \over {{a_0}}}[h{C_{\rm{L}}} - {a_{ - 1}}{({C_{\rm{T}}})_{ - 1}} + {a_{ - 2}}{({C_{\rm{T}}})_{ - 2}}] \hfill \cr} \right\}$$
|
(41) |
这样在解出$C_{\rm L}$后,就可以用上式求得$C_{\rm T}$. 然后联立式(3)和式(13)可求得孔隙率为
|
$$
\varphi = \dfrac{\varphi _0 + \lambda \varepsilon _{ii} }{1 + \dfrac{\beta }{\rho _{\rm s} }C_{\rm T} \varphi _0 } $$
|
(42) |
式中的体积变形$\varepsilon _{ii} $可用位移求得. 求得孔隙率后,可用式(5)和式(19)计算渗透系数$K$和沉积系数$h$.
综上,在一个时间增量步内的计算步骤可叙述如下:
(1) 给出时间增量$\varDelta _t $(即$\varDelta _{ - 1}$),用式(18)计算$a_{0}$,$a_{ - 1}$和$a_{ - 2}$.
(2) 对于第一次迭代,取上一步的$C_{\rm L}$作为试算值,以后各次迭代要用前一个迭代步计算出来的$C_{\rm L}$作为试算值. 用式(41),式(42)求得$C_{\rm T}$和孔隙率$\varphi$,用式(19)求渗透系数$K$. 求式(40a)中的矩阵${ K}_{u}$,${ L}$,${ H}$和向量 ${ F}_{1}$,${ F}_{2}$,${ S}_{1} \cdot { C}_{\rm L}$等并组装,形成方程(40a),并求解得节点位移和压力.
(3) 用节点压力向量计算各单元的渗流速度$v_{i}$,计算式(40b)中的矩阵${ C}_{1}$和向量${ F}_{3}$,形成方程(40b)并求解得节点浓度向量${ C}_{\rm L}$.
(4) 将求得的${ C}_{\rm L}$与试算值比较,若精度(相邻两次迭代下每一节点的相对浓度变化量,本文取0.01)不满足,则保存${ C}_{\rm L}$,转向(2);若精度满足,则保存本步的计算结果. 进入下一时间步(即转向(1)).
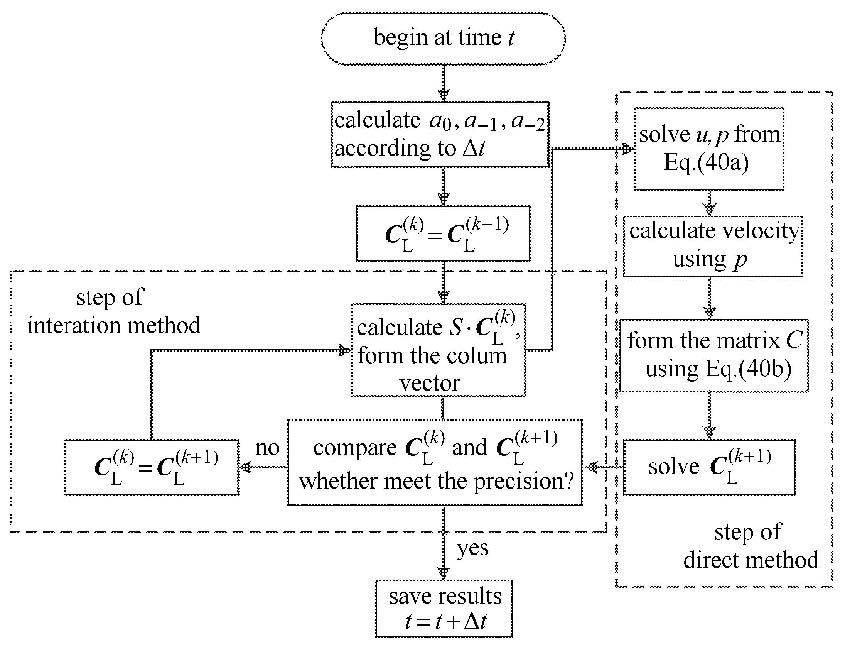
计算流程图如图2所示.
3 模型的初步验证
泥浆在土中的渗透规律多通过室内物理阻抗试验(泥浆成膜性能试验)进行研究[14, 24].上述基本方程及其求解算法的可靠性可以借助对现有试验的模拟与比对进行验证. 首先通过试算的方法确定试验土样的沉积系数,由式(5)可知,$h$的取值需要设计试验进行标定,赫齐格等[10]通过试验得出$b$值很小,可以忽略,为计算方便,假设$h= h_{0}$,本文借助阿勒姆[14]的试验结果对基本方程及其求解方法进行验证,试算沉积系数的具体步骤为:
(1) 通过室内试验测定泥浆在渗透方向上的沉积规律,以质量增量$\Delta m_i $表示;
(2) 根据基本方程,模拟试验条件并建立对应的有限元分析模型,假定沉积系数$h^{i}$,计算得到泥浆沉积质量沿深度方向的分布曲线;
(3) 比较计算曲线与试验所得的质量增量分布,若吻合较好,则取$h =h^{i}$,得到土样的沉积系数;否则转向(2),重新假设$h^{i + 1}$.
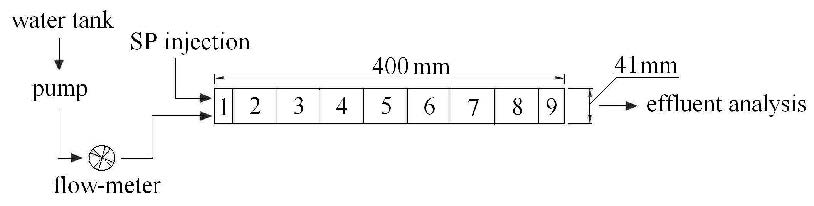
如图3所示,阿勒姆等[14]的室内模型试验采用内径4.1 cm,高40 cm铝制模型箱,模型箱内填充中粗砂作为渗透地层,其渗透系数$K = 7\times 10^{ -4 }$ m/s,孔隙率$\varphi = 0.37$.
试验过程中浆液浓度为1 g/L,入射流速由0.041 cm/s上升至0.209 cm/s(分别为0.041 cm/s,0.083 cm/s,0.125 cm/s,0.167 cm/s和0.209 cm/s).试验结束后将模型箱内砂土分为9部分取出并测量其增重,根据沉积系数的试算步骤,可比对某一流速下的试验所得质量增量的分布与相应边界条件下的基本方程的解来确定试验所用土样的沉积系数,最后在确定沉积系数的情况下计算其他入射体积时的颗粒沉积量分布曲线并与试验结果做比较,两者的吻合程度可以反应计算方法的可靠性.
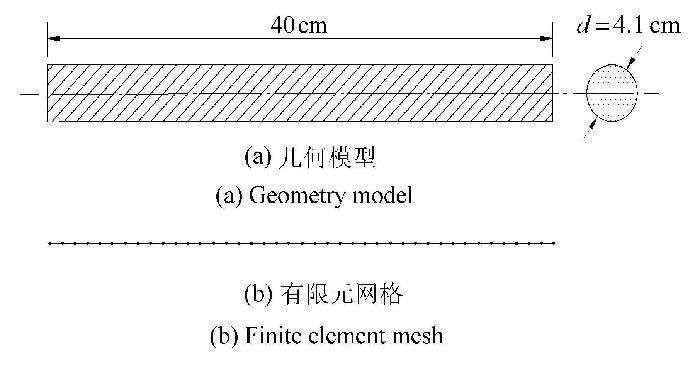
不考虑体力时,阿勒姆的试验方案可简化为一维问题,采用一维等参元进行模拟,单元长度1 cm,共40个单元,每个节点包含3个自由度(位移$u_{x}$、压力$p$和浓度$C_{\rm L}$),时间步长$\rm {d}t = 1$ s,如图4所示.
计算中泥浆的初始浓度为$C_{0} =1$ kg/m$^{3}$,材料的初始渗透系数为$K_{0} = 7 \times 10^{ - 4}$ m/s,初始孔隙率为$\varphi = 0.37$. 其他计算参数为[25, 26]
$$\left\{ \matrix{
{D_{\rm{L}}} = {10^{ - 4}}{{\rm{m}}^2}/{\rm{s}} \hfill \cr
E = 4{\rm{MPa}},\;\nu = 0.3,\;\lambda = 0.8,\;c = 0.01 \hfill \cr
\beta = 6/\pi \hfill \cr} \right.$$
问题的初值及边界条件为
|
$$\left. {\matrix{
\matrix{
{C_{\rm{L}}}\left( {t = 0,x} \right) = 0 \hfill \cr
{C_{\rm{L}}}\left( {t,x = 0} \right) = {C_0} \hfill \cr
{Q_{\rm{c}}}\left( {t,x = 0} \right) = 0 \hfill \cr} \hfill \cr
} } \right\}$$
|
(43) |
|
$$\left. {\matrix{
\matrix{
p\left( {t = 0,x} \right) = 0 \hfill \cr
v\left( {t,x = 0} \right) = {v_0} \hfill \cr
p\left( {t,x = 0.4} \right) = 0 \hfill \cr} \hfill \cr
} } \right\}$$
|
(44) |
|
$$\left. {\matrix{
\matrix{
u\left( {t = 0,x} \right) = 0 \hfill \cr
u\left( {t,x = 0.4} \right) = 0 \hfill \cr} \hfill \cr
} } \right\}$$
|
(45) |
其中,$Q_{\rm c}$为泥浆颗粒流量,$u$为位移. 采用式(40a)和(40b)所示方法对该问题进行求解.
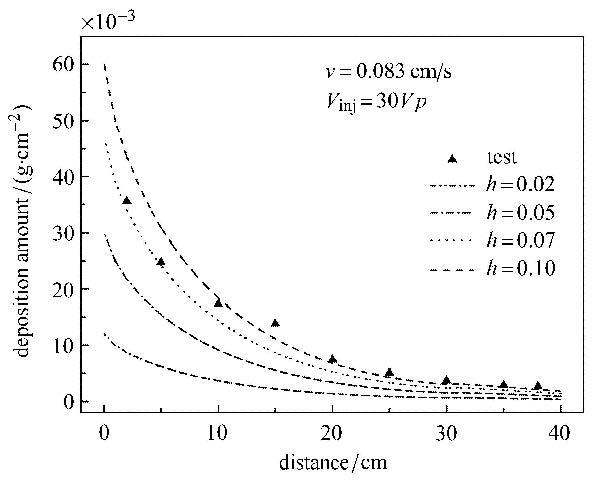
图5为不同试算沉积系数下沉积量沿深度的变化规律,悬浮液的入射速度$v = 0.083$ cm/s,总的射入量$V_{\rm inj} =30Vp$ ($Vp$为孔隙体积).首先根据室内试验中设定的流速计算达到该入射量所需要的时间,然后将该时间作为结束时刻进行模拟,并提取颗粒沉积量计算结果与试验数据进行对比. 由图5可知,颗粒的沉积效应随沉积系数的增大而增加,当$h =0.07$时,计算所得沉积规律与试验结果基本一致,可以认为该条件下中粗砂的沉积系数为0.07.
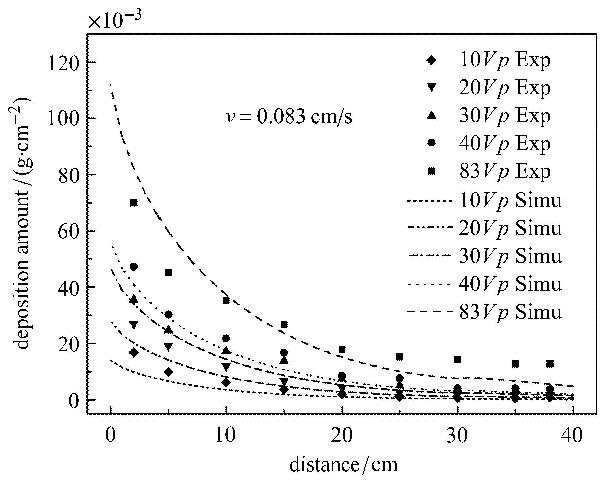
进一步对其他入射体积的计算结果进行比对分析. 图6为$h =0.07$时不同入射体积下沉积量沿深度方向的分布规律及其与试验数据的比较情况.由图6可知,土中颗粒的沉积量随入射体积的增大而增加,且计算所得结果与试验数据均吻合良好,说明该计算方法具有一定的可靠性.对于计算曲线与试验结果的差别,一方面原因是由于有限元模型忽略了重力的作用,计算时被简化为一维问题;另一方面,则是因为没有考虑流速变化对沉积系数的影响.阿勒姆通过试验得出入射流速对沉积效应有显著影响且成非线性,这种影响不仅体现在渗流场、位移场以及扩散场之间的耦合作用关系,同时也表现为流速变化对于颗粒沉积性能,也即沉积系数的影响:前者已在本文建立的耦合计算模型中得到考虑,对于沉积系数的变化,实际上,试算得到的土样沉积系数仅为入射流速为0.083 cm/s时的沉积系数,其它工况(入射流速)下的沉积系数均有不同,沉积系数与渗流场的关系将为进一步研究的方向.
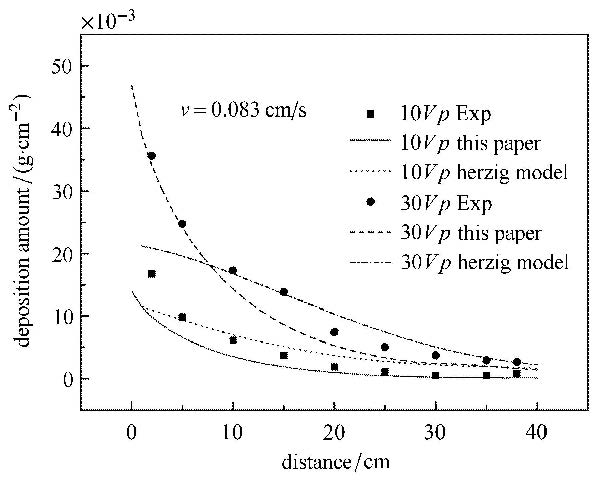
图7为入射流速0.083 cm/s时不同计算方法所得结果的比较. 由图7可知,当入射体积较小时($10 Vp$),本文建立的模型的计算结果与赫齐格的``对流$\!$-$\!$-$\!$扩散''模型均与试验数据吻合较好;然而,随着试验的进行,当注入土体中的悬浮液体积达到$30Vp$时,传统计算方法所得结果开始出现较大偏差,主要表现为浅层土体中的计算沉积量较小,而深层沉积量较大.造成这种偏差的原因是,在靠近悬浮液一侧,传统模型无法考虑渗透力所造成的孔隙压缩、以及颗粒沉积带来的孔隙体积减小,而这两种现象都将加剧颗粒的沉积效应,并通过沉积进一步影响渗流场和位移场的分布;同样,对于中部的土体,由于考虑位移、渗流、沉积的相互作用关系后,实际渗流流速在该区段很小,且前方颗粒已经经过大量沉积,能够到达这部分的悬浮颗粒总量上已经较少,导致总的沉积量明显减小.通过图7的比较可以看出,本文提出的计算方法由于综合考虑了系统在位移场、渗流场以及浓度扩散场中的相互作用关系,计算结果较传统模型更优,与试验数据更为接近.
4 算 例
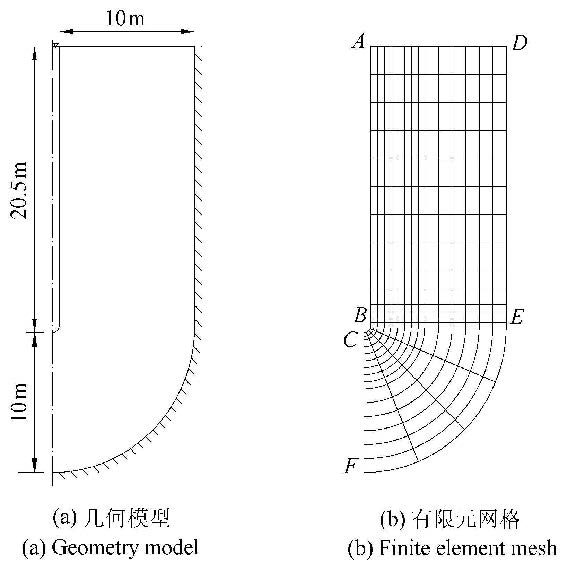
采用本文方法计算泥浆槽壁中的泥浆渗透规律.考虑实际情况的对称性,几何模型如图8(a)所示,其中槽壁深20.5 m,计算范围为垂直槽壁方向以外10 m,假设泥浆液面与地面($AD$段)平齐;对应的有限元网格如图8(b)所示,采用四边形等参单元,将计算区域划分为18$\times$15的有限元网格并对发生渗透的表层土体做适当加密,对应的地层参数同一维试验.$ABC$边界处设置浆液浓度为200 kg/m$^3$(即采用泥浆的比重为1.2),泥浆压力等于重力;$DEF$边界和$CF$边界处颗粒流量$Q_{\rm c }= 0$ 且泥浆压力在$DEF$段为零;位移边界条件按照一般原则设置.
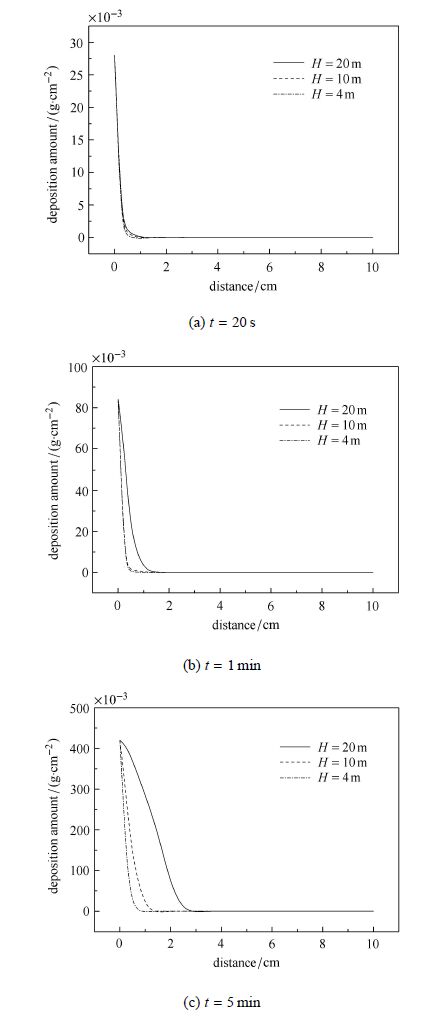
图9为泥浆槽壁内不同深度(4 m,10 m,20 m)处泥浆沿垂直槽壁方向的渗透规律.由图9可知,泥浆颗粒在土层中的填充效果及其影响范围均随深度的增加而增大,实际施工中,常在浅层槽壁发生塌孔现象,说明该区段的颗粒填充效果不佳,这与计算结果是相符合的,成槽时需要严格控制浅层作业范围内的机械垂直度;同一深度下,随着时间的增加,颗粒的沉积量 也在增大. 当$t =5$ min时,深度为20 m处的土层单位体积内的沉积颗粒已经达到0.4 g,分析泥浆的渗透过程可知,泥浆对地层孔隙的填充将导致表层土体迅速被沉积颗粒阻塞而使得泥浆颗粒无法继续进入土层,从而开始在泥浆与土体的接触面形成泥膜,可将该临界状态作为成槽机在某一深度下的下斗挖土时机,为现场施工提供一定的理论支撑.
5 结 语
本文研究了饱和土中泥浆渗透的多场耦合计算方法. 研究工作主要有以下几点:
根据颗粒质量守恒定律推导了耦合流速的浓度扩散方程,并通过在浓度方程中引入沉积系数进一步计算得到了沉积颗粒的质量;同时,为考虑颗粒沉积对孔隙排水的影响,以沉积量作为耦合项对毕奥固结方程中的水量连续方程进行了修正,在此基础上建立了变形$\!$-$\!$-$\!$渗流$\!$-$\!$-$\!$扩散耦合的控制方程及其变分原理,并形成了对应的有限元计算格式;
采用本文的方法模拟现有试验并进行了比对分析,提出了沉积系数的试算方法,对应试验条件下计算所得的预测曲线与试验数据吻合较好;与传统模型的计算结果进行了比较,结果表明,由于考虑了悬浮液渗透过程中位移场、渗流场以及浓度扩散场的相互作用关系,本文所建立的模型能更好反映试验所得结果;将泥浆在槽壁中的渗透简化为二维问题并采用本文方法进行了计算,计算结果与工程认识相符合,泥浆的沉积填充效应随深度的增加而增大,施工时需要严格控制浅层作业段的机械垂直度;成槽机的下斗抓挖时机可以根据地层填充的致密程度进行计算,对现场施工具有一定的指导意义.
参考文献
| [1] |
Moghadasi J, Muller-Steinhagen H, Jamialahmadi M, et al. Theoretical and experimental study of particle movement and deposition in porous media during water injection. J Petrol Sci Eng, 2004, 43:163-181 |
| [2] |
Lee J, Koplik J. Network model for deep bed filtration. Phys Fluids, 2001, 13: 1076-1086 |
| [3] |
Bolster CH, Mills AL, Hornberger GM, et al. Spatial distribution of deposited bacteria following miscible displacement experiments in intact cores. Water Resources Research, 1999, 35(6): 1797-1807 |
| [4] |
Reddi LN, Xiao M, Malay GH, et al. Physical clogging of soil filters under constant flow rate versus constant head. Can Geotech J, 2005, 42: 804-811 |
| [5] |
Tong M, Johnaon WP. Excess colloid retention in porous media as a function of colloid size, fluid velocity, and grain angularity. Environ Sci technol, 2006, 40: 7725-7731 |
| [6] |
Kretzschmar R, Barmettler K, Grolimund D, et al. Experimental determination of colloid deposition rates and collision efficiencies in natural porous media. Water Resources Research, 1997, 33(5): 1129-1137 |
| [7] |
Redman JA, Grant SB, Olson TM, et al. Filtration of recombinant Norwalk virus particles and bacteriophage MS2 in quartz sand: Importance of electrostatic interactions. Environmental Science & Technology, 1997, 31(12): 3378-3383 |
| [8] |
Ghislain De Marsily G. Quantitative Hydrogeology: Groundwater Hydrology for Engineers. Orlando: Academic Press, 1986 |
| [9] |
McDowell-Boyer LM, Hunt JR, Sitar N. Particle transport through porous media. Water Resour Res, 1986, 22: 1901-1921 |
| [10] |
Herzig JP, Leclerc DM, Le Goff P. Flow of suspension through porous media: application to deep bed filtration. Indian Eng Chem, 1970, 62: 8-35 |
| [11] |
孟旭辉,王亮,郭照立. 多孔介质中流固作用力的动量交换计算. 力学学报, 2014, 04: 525-532 (Meng Xuhui, Wang Liang, Guo Zhaoli. Force evaluation using momentum-exchange method in porous media. Chinese Journal of Theoretical and Applied Mechanics, 2014, 04: 525-532 (in Chinese)) |
| [12] |
Bradford SA, Simunek J, Bettahar M, et al. Modeling colloid attachment, straining, and exclusion in saturated porous media. Environmental Science & Technology, 2003, 37(10): 2242-2250 |
| [13] |
Bradford SA, Yates SR, Bettahar M, et al. Physical factors affecting the transport and fate of colloids in saturated porous media. Water Resources Research, 2002, 38(12): 63-1-63-12 |
| [14] |
Alem A, Elkawafi A, Ahfir ND, et al. Filtration of kaolinite particles in a saturated porous medium: hydrodynamic effects. Hydrogeology Journal, 2013, 21: 573-586 |
| [15] |
Watanabe T, Yamazaki H. Giant size slurry shield is a success in Tokyo. Tunnels and Tunnelling, 1981, 13: 13-17 |
| [16] |
韩晓瑞,朱伟,刘泉维等. 泥浆性质对泥水盾构开挖面泥膜形成质量影响. 岩土力学, 2008, S1: 288-292 (Han Xiaorui, Zhu Wei, Liu Quanwei, et al. Influence of slurry property on filter-cake quality on working face of slurry shield. Rock and Soil Mechanics, 2008, S1: 288-292 (in Chinese)) |
| [17] |
闵凡路,朱伟,魏代伟等. 泥水盾构泥膜形成时开挖面地层孔压变化规律研究. 岩土工程学报, 2013, 04: 722-727 (Min Fanlu, Zhu Wei, Wei Daiwei, et al. Change of pore water pressure in soil as filter cakes formed on excavation face in slurry shield. Chinese Journal of Geotechnical Engineering, 2013, 04: 722-727 (in Chinese)) |
| [18] |
胡欣雨,张子新,徐营. 黏性土层中泥水盾构泥浆作用对开挖面土体强度和侧向变形特性影响研究. 岩土工程学报, 2009, 11: 1735-1743 (Hu Xinyu, Zhang Ziyin, Xu Ying. Slurry pressurized effect on strength and deformation characteristics of clay soil at excavationface in slurry shield. Chinese Journal of Geotechnical Engineering, 2009, 11: 1735-1743 (in Chinese)) |
| [19] |
白云,孔祥鹏,廖少明. 泥水盾构泥膜动态形成机制研究. 岩土力学, 2010, S2: 19-24 (Bai Yun, Kong Xiangpeng, Liao Shaoming. Research on dynamic formation mechanism of slurry membrane for slurry shield. Rock and Soil Mechanics, 2010, S2: 19-24 (in Chinese)) |
| [20] |
刘成,孙钧,赵志峰等. 泥水盾构泥膜形成二维理论分析. 岩土力学, 2013, 06: 1593-1597,1628 (Liu Cheng, Sun Jun, Zhao Zhifeng, et al. Two-dimensional theoretical analysis of slurry membrane formation process in slurry shield. Rock and Soil Mechanics, 2013, 06: 1593-1597,1628 (in Chinese)) |
| [21] |
Biot MA. General theory of three-demension consolidation. Journal of Applied Physics, 1941, 12: 155-164 |
| [22] |
Carman PC. Fluid flow through granular beds. Trans Amer Inst Chem Eng, 1937, 15: 150-166 |
| [23] |
Maroudas A, Eisenklam P. Clarification of suspensions: a study of particle deposition in granular media: Part I-Some observations on particle deposition. Chemical Engineering Science, 1965, 20(10): 867-873 |
| [24] |
Ikni T, Benamar A, Kadri M, et al. Particle transport within water-saturated porous media: Effect of pore size on retention kinetics and size selection. Comptes Rendus Geoscience, 2013, 345: 392-400 |
| [25] |
Li YC. Finite element analysis for a finite conductivity fracture in an infinite poroelastic medium. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23: 187-215 |
| [26] |
陈星欣. 饱和多孔介质中颗粒迁移和沉积特性研究. [博士论文]. 北京: 北京交通大学, 2013. 28-29 (Chen Xingxin. Study on the particle transport and deposition in saturated porous media. [PhD Thesis]. Beijing: Beijing Jiaotong University, 2013. 28-29 (in Chinese)) |
A DEFORMATION-INFILTRATION-DISPERSION COUPLING MODEL FOR THE SLURRY INFILTRATION COMPUTATION IN SATURATED SAND
Wu Di
1

, Zhou Shunhua
1, Li Yaochen
2
1. Key Laboratory of Road and Tra c Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China;
2. School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China
Abstract: Soil deformation and water seepage are ignored in the computation of slurry infiltration in traditional method. In this paper, the particle dispersion equation coupled with seepage velocity is derived according to the particle mass conversation, which highlights the dynamic properties of the suspended particles transport and deposition. The continuity equation for the suspension is proposed by modifying the water continuity equation in Biot's consolidation theory considering the e ect of particle deposition in slurry. Based on this, non-linear governing equations for slurry infiltration coupling deformation, infiltration and dispersion are derived and the corresponding variational principles are established. Finite element model based on the principles is established and the equations are solved with both incremental and iterative techniques. Computational results are validated by predicting the data from one-dimensional model test, and better agreement with the experimental data is shown compared to the traditional method which only considered particle convection and dispersion. The slurry infiltration in slurry trench is calculated with the method proposed in this paper. The deposition amount of slurry particles grows with the increasing depth, which indicates that a strict vertical degree control is needed during the shallow slurry trench construction. The excavating schedule can be determined considering the filled extent by the slurry particles according to the computation.
Key words:
slurry infiltration particle dispersion continuity equation multi-field coupling non-linear variational principles
 2015, Vol. 47
2015, Vol. 47
