作为重要的能量转换装置,水力机械广泛应用于国民经济的各个部门.随着现代水力机械的发展,人们对其空化性能和稳定性的要求越来 越高[1, 2, 3].空化是水力机械内部不可避免的一种水动力学现象,空穴的脉动、脱落以及空穴的溃灭过程会诱发结构振动,导致机械效率下降、噪声增大,甚至影响水力机械的安全运行[4, 5, 6]. 研究空化流动中结构的振动特性具有重要的工程意义.
在高速水流中,当水下绕流体表面压力低于当地饱和蒸汽压时,就会发生空化.随着空化数的降低,空穴形态依次可分为初生空化、片 状空化、云状空化和超空化[7, 8, 9].研究表明,空化的发展过程存在显著的非定常特性,同时伴随着复杂的流体作用 力[10, 11, 12].近年来,许多学者对空化的非定常特性进行了研究.Kawanami等[13]应用高速摄像技术研究了云状空化在对流尺度上的脱落机制,认为在空化的非定常发展过程中会出现反向射流,进而造成空泡脱落等不稳定流动特性.张博等[14]测量了空化流动中水翼的升阻力特性,并进行了时频分析,发现在一定的空化数下,空穴脱落导致水翼所受升力呈现高频周期性变化.陈广豪等[15]采用动态压力传感器测量了收缩-扩张流道内的壁面压力,结果表明空化的发生使得压力波动幅度明显增大,当空化数降低到一定程度时,压力变化出现主导频率.
振动是工程中常见的物理现象,在大多数情况下,振动可能会破坏结构的正常功能,降低结构寿命甚至导致其损坏.结构在非定常流体 作用力的影响下,其振动状态与周围的流场形态密切相关[16, 17, 18, 19].王文全等[20]采用加速度传感器和粒子图像测速系统研究了不同雷诺数下弹性薄板的流激振动特性,结果表明薄板的振动对雷诺数非常敏感,在流场和结构的耦合作用下,弹性板表现出非周期、非对称的振动行为.Docoin等[21]测量了水翼表面的压力、边界层速度分布以及水翼的振动速度,指出边界层内的转戾现象会造成水翼的振动.Ausoni等[22]研究了空化对水翼卡门涡街的影响,通过测量涡的脱落频率和水翼的振动特性,发现空化导致涡脱落的频率增大,同时水翼涡致振动的强度增大. 吴钦等[23]基于实验和数值方法研究了绕水翼空化流动的水弹性响应特性.通过对比绕刚/弹性水翼空化流动的流场结构和振动特性发现,空化加剧了弹性水翼的振动,同时水翼的水弹性响应反作用于空化的发展过程及流场旋涡结构的相互作用.
本文采用实验的方法研究了绕水翼空化流动的空穴形态和水翼振动特性.采用高速摄像技术观测了不同空化阶段的空穴形态,采用多普勒激光测振仪测量了水翼的振动速度,研究了不同空化阶段水翼振动速度的变化规律,应用同步测量系统研究了云状空化阶段水翼的空穴形态和振动特性.
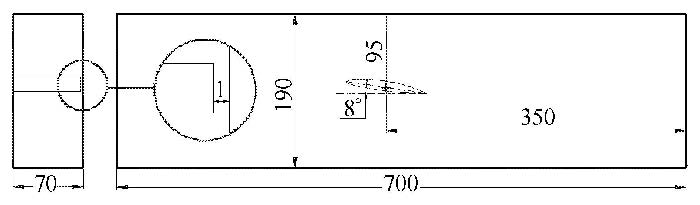
1 实验设备及方法 1.1 实验模型实验在闭式空化水洞中进行,水洞实验段尺寸如图1所示,长700 mm,截面为矩形,宽70 mm,高190 mm,上下表面和外侧装有有机玻璃观察窗,方便观察流场形态. 实验采用NACA66水翼,水翼弦长$c =75$ mm,展长 $b =69$ mm,材质为不锈钢.实验时,水翼一端通过机械锁定装置固定在实验段中,为了准确测量水翼的振动特性,其自由端与实验段侧壁有1 mm左右的间隙,水翼攻角为8°.
|
图1 实验段几何尺寸(单位:mm) Fig.1 Geometries of the test section (unit:mm) |
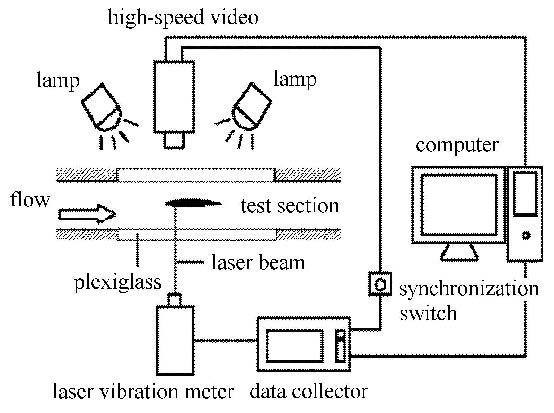
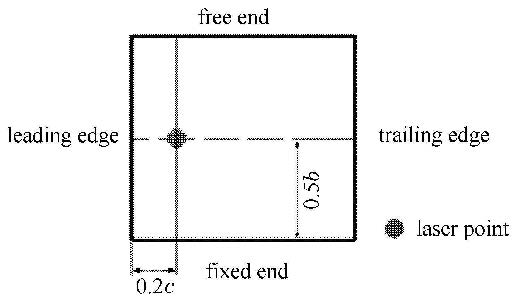
图2给出了实验测量系统的示意图,包括流场形态观测和水翼振动测量两个子系统.实验过程中,透过实验段侧面的有机玻璃窗,采用高速相机实时采集水翼吸力面的空穴形态,高速相机的采集频率为2 500 Hz,能够满足空化流场的研究需要.在振动测量方面,采用单点多普勒激光测振仪实现对水翼振动的非接触式测量.激光测振仪型号为PDV-100,采集频率为20.48 kHz,量程为$\pm 20$ mm/s,测量精度为0.02 μm/s.实验时,测振仪发射的激光束通过实验段下方的有机玻璃照射到水翼压力面上,照射位置如图3,测振仪实时采集水翼的振动速度信号并通过采集卡将数据输出.
|
图2 全流场-振动同步测量系统示意图 Fig.2 Schematic diagram of the synchronous measurement system |
|
图3 激光照射位置示意图 Fig.3 Position of laser point |
为实现空穴形态和水翼振动的同步测量,采用一个同步触发开关同时连接高速相机和激光测振仪,如图2.当开关按下的瞬间会产生电 压信号,在该信号的触发下高速相机和激光测振仪同时启动,开始采集数据,实现同步测量.由于测振仪的采集频率是高速相机的8倍,在进行测量结果的同步分析时以高速相机的采集时刻为基准.
1.3 数据处理方法
实验采用激光测振仪采集水翼振动速度信息后以电压信号形式输出,通过换算关系式可将电压值转换为实际的振动速度值,换算关系为
\[V = A/200\]
(1)
为了分析空穴形态和水翼振动的频率特性,采用小波分析方法对空穴形态和振动数据进行处理,该方法适用于非稳定信号的时频分析[24, 25]. 在软件"Matlab"中使用"Morlet"小波函数进行数据处理和分析,其数学形式为
\[\varphi \left( t \right) = {{\rm{e}}^{{\rm{j}}{w_0}t}}{{\rm{e}}^{ - {\textstyle{1 \over 2}}{t^2}}}\]
(2)
实验中,雷诺数和空化数的定义如下
\[Re = \frac{{{U_\infty }c}}{v}\]
(3)
\[\sigma = \frac{{{P_\infty } - {P_V}}}{{0.5\rho U_\infty ^2}}\]
(4)
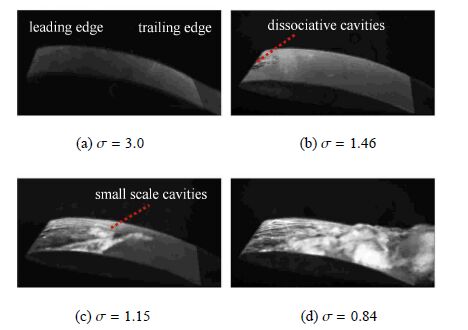
图4给出了$Re=5.5\times 10^{5}$时,不同空化阶段的典型空穴形态. 当$\sigma =3.0$,流场中没有空泡出现. 当$\sigma=1.46$,水翼前缘吸力面开始出现游离状的空穴,其发生和发展过程有较强的随机性,属于初生空化阶段. 当$\sigma=1.15$,水翼吸力面形成了相对稳定的附着型空穴,空穴主体部分呈片状,空穴尾部存在小尺度空泡的脱落和溃灭.当空化数进一步降低至0.84,空化发展至云状空化阶段,空化现象更加剧烈,从图中可以观察到大尺度云状空泡团的脱落现象.值得注意的是,在片状和云状空化阶段,水翼自由端与实验段侧壁之间的间隙会造成带状的间隙空化现象.
|
图4 不同空化数下的流场形态 Fig.4 Flow field with different cavitation numbers |
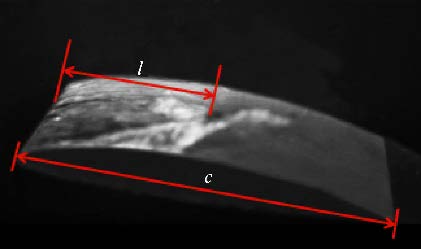
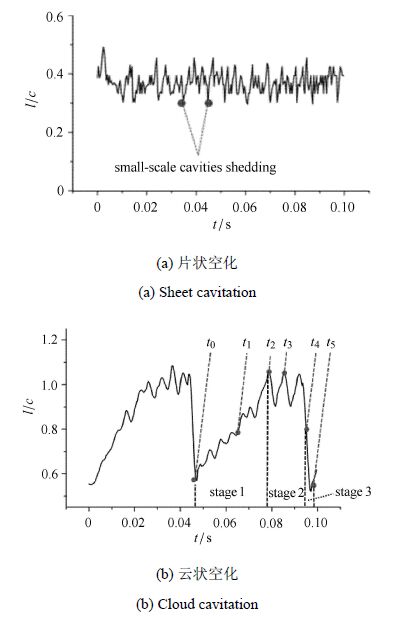
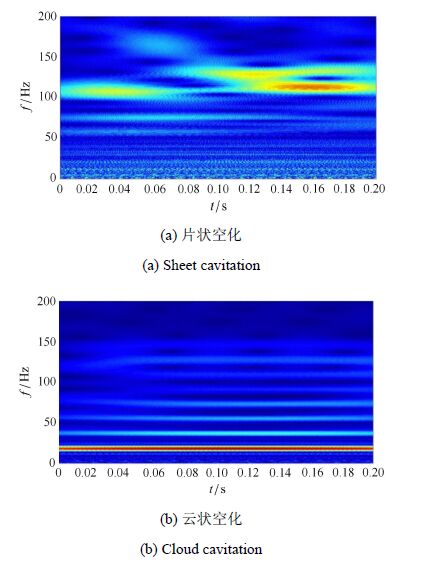
为了进一步研究片状空化和云状空化流动中水翼的空穴发展特性,对两种工况下的空穴长度变化规律进行了分析.图5给出了通过高速摄 像图片测量空穴无量纲长度的方法,其中$l$为测量得到的空穴长度,$c$为测量到的水翼弦长.图6给出了片状空化($\sigma =1.15$)和云状空化($\sigma =0.84$)阶段空穴无量纲长度随时间的变化情况.可以发现在片状空化阶段,附着型空穴的长度在$0.3c\sim 0.5c$之间波动,空穴尾部存在高频的小尺度空泡脱落.其脱落周期在7 ms到10 ms之间.在云状空化阶段,附着型空穴的最大长度可达到1.15$c$,空穴长度的变化呈准周期特性,云状空泡团的脱落周期约为55 ms.图7给出了通过小波分析方法得到的空穴长度变化的时频分布,可以发现片状空穴的长度变化频率分布在100$\sim $140 Hz的频带中,云状空化的长度变化频率集中在18 Hz左右,与空穴长度变化的周期特征相符.
|
图5 空穴长度无量纲长度测量 Fig.5 Dimensionless length of cavity |
|
图6 空穴长度变化规律 Fig.6 Variations of the length of cavity |
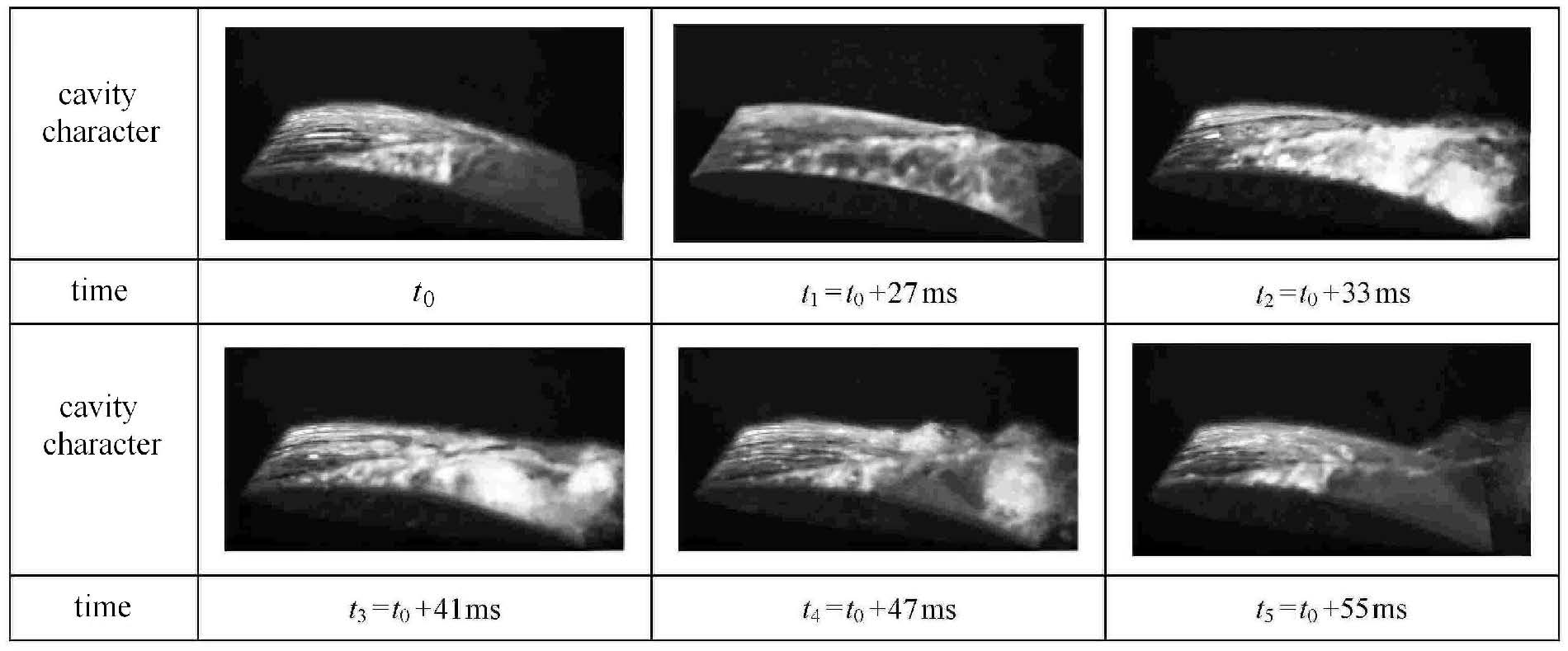
图8给出了云状空化一个周期内不同时刻的空穴形态,其中$t_{0}$ 到$t_{5}$ 6个时刻与图6(b)中的时刻相对应.根据图6中的空穴长度变化特征,空化的发展过程可分为附着型空穴的生长、空穴的脉动以及云状空穴的断裂脱落3个阶段,对应图中的"stage1 $\sim$ stage3".在附着型空穴的生长阶段,上一周期的云状空穴已经脱落溃灭,新的附着型空穴从水翼吸力面前缘开始发展,如$t_{0}$时刻所示. 附着型空穴不断向下游生长,在$t_{2}$时刻发展至最大长度,空穴尾部产生逆时针的空化旋涡.随后在空穴尾部紧贴壁面的区域内诱导了一股指向上游的反向射流,如$t_{3}$ 时刻所示.反向射流向上游方向移动,在空穴前缘附近与主流相遇,附着型空穴被反向射流切断,后部的大尺度云状空泡团脱落,伴随着漩涡运动从水翼表面脱离,如$t_{4}$ 时刻所示. 至$t_{5}$时刻,云状空穴完全脱落并向下游移动,空化又进入新一周期附着型空穴的生长阶段.
|
图7 空穴长度变化的时频图 Fig.7 The spectrograms of cavity length |
|
图8 不同时刻的空穴形态 Fig.8 Cavity characters at different time |
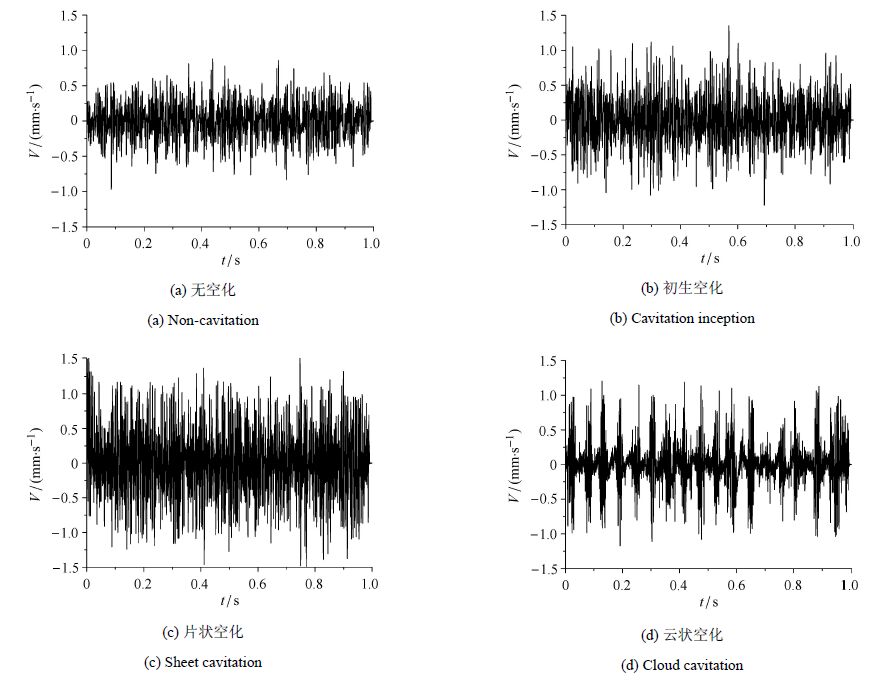
为了研究空化流动中水翼的振动特性,图9给出了上述不同空化数下水翼振动速度的时域分布. 在无空化阶段,水翼的振动速度没有明显规律,振幅处在$-0.5$ mm/s到0.5 mm/s之间.当流场中发生初生空化时,水翼振动速度的振幅有所增加,波动的范围扩展到了$-1$ mm/s到1 mm/s之间.空化发展至片状空化阶段,振动速度曲线的幅值进一步增大,振幅的均方根值由初生空化的0.3 mm/s增加到0.43 mm/s.在云状空化阶段,水翼的振动速度表现为强弱状态交替出现,呈现出周期性的变化规律.
|
图9 水翼振动速度的时域分布 Fig.9 Variation of vibration velocity in the time domain |
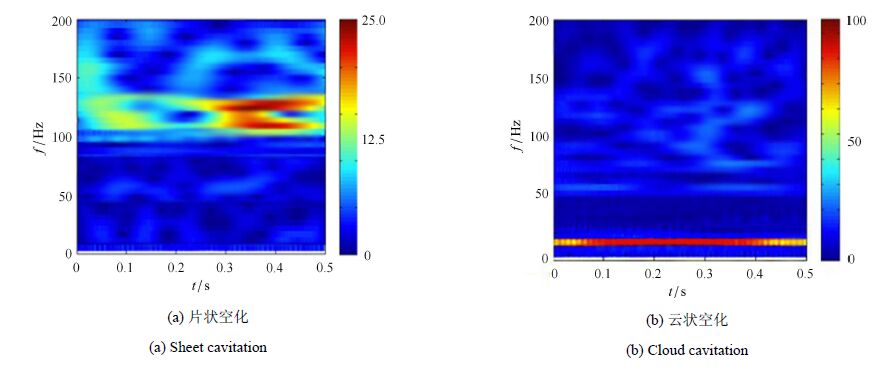
空穴的发生、发展和脱落溃灭会造成水动力的脉动,进而导致水翼的振动.当空化数降低到一定程度时,空化现象造成水动力载荷呈 现周期性变化特征[11, 12].为了研究空化对振动的影响,图10给出了片状空化和云状空化工况下水翼振动速度的时频分布.从图中可以发现,在片状空化阶段,振动的能量集中在100$\sim$140 Hz之间的分散频带上,结合图7(a)可以发现,振动频率的分布特征与该工况下小尺度空穴的脱落频率相符,说明小尺度空穴的脱落会造成一定程度的水动力脉动,水翼在水动力载荷的作用下发生受迫振动,其振动频率与空穴的脱落频率相同.在云状空化阶段,时频图显示此时水翼振动的频率集中在18 Hz左右的频带上,与图7(b)得到的频率相同,表明云状空化阶段的周期性水动力载荷导致水翼振动,其振动频率与大尺度云状空泡团的断裂脱落频率相同.同时该频带对应的能量较高,说明在云状空化阶段,空化发展过程造成的水动力脉动较大,对水翼的振动有较大的影响.
|
图10 水翼振动速度的时频分布 Fig.10 The spectrograms of vibration velocity |
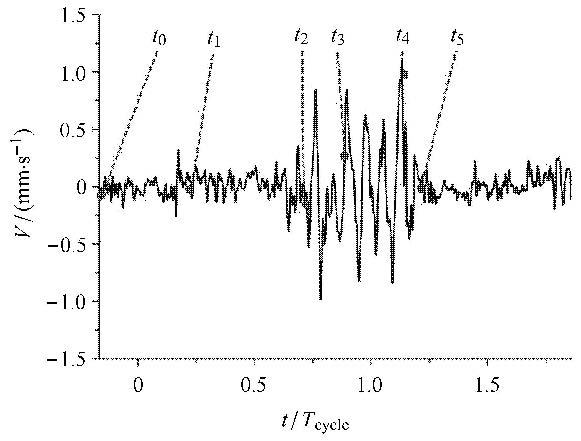
为了分析云状空化阶段水翼强弱交替的振动特性与空穴发展之间的联系,通过同步测量系统采集了云状空化时的空穴形态和振动数据并进行分析. 图11给出了水翼振动速度在1.5个周期内的时域分布,$T_{\rm cycle }$为空化发展周期.结合图6(b)和图8中的对应时刻对水翼振动特性进行了分析.当空化处于附着型空穴的生长阶段时,水翼振动速度较低,以高频的小幅度振动为主,如图8中$ t_{0},t_1,t_2$时刻所示. 空穴生长至最大长度后进入空穴脉动阶段,水翼的振动状态开始发生改变,如$t_{2},t_3,t_{4}$时刻所示,水翼振动速度发生大幅度波动. 观察该阶段的流场结构可以发现空穴尾部处于非常不稳定的状态.Huang等[26]的研究表明,该阶段中,空穴内部流场在反向射流的作用下产生复杂的漩涡结构,造成水翼水动力载荷剧烈变化,这与水翼振动特性的表现相符.附着型空穴被反向射流切断后,空化进入云状空穴的断裂脱落阶段,水翼振动强度减弱,空化进入下一个周期的附着型空穴生长阶段,如$t_{4},t_{5}$ 时刻所示.
|
图11 水翼振动速度曲线的时域分布 Fig.11 Variation of vibration velocity in the time domain |
采用实验方法研究了不同空化数下绕水翼流场的空穴形态和水翼的振动特性,得出以下结论:
(1)随着空化数的降低,流场依次出现无空化、初生空化、片状空化和云状空化的状态. 水翼的振动强度随空化数降低而增强,在云状空化阶段,水翼振动表现出强弱部分交替出现的周期性特征.
(2)在片状空化和云状空化阶段,空穴的脱落对水翼振动有较大影响,空穴脱落诱发水翼振动,其振动频率与空穴脱落频率相同.
(3)云状空化阶段水翼的振动特性与空穴发展过程有密切联系,在附着型空穴生长阶段,水翼振动表现为高频小幅度振动. 在云状空穴的断裂脱落阶段,水翼表现为低频大幅度振动.
| [1] | 韩国明,张信志,刘保国. 大型水轮发电机组振动稳定性与设计准则. 中国机械工程, 2002,13(8):634-636 (Han Guomiong, Zhang Xinzhi, Liu Baoguo. Dynamic analysis and design criteria of vibration stability for large hydro-generator units. China Mechanical Engineering, 2002, 13(8):634-636 (in Chinese)) |
| [2] | 陆燕荪. 中国水电设备制造业的现状与展望. 铸造纵横,2007, 4: 8-10 (Lu Yansun. Present situation and prospect of Chinese hydropower equipment manufacturing industry. Foundry Panorama, 2007, 4: 8-10 (in Chinese)) |
| [3] | Cervone A, Bramanti C, Rapposelli E. Experimental characterization of cavitation instabilities in a two-bladed axial inducer. Journal of Propulsion and Power, 2006, 22: 1389-1395 |
| [4] | 陈喜阳,郭庆,孙建平等. 空化对离心泵低频水力振动影响的数值研究. 华中科技大学学报(自然科学版),2014,46(6):6-11 (Chen Xiyang, Guo Qing, Sun Jianping, et al. Numerical study on effects of cavitations for centrifugal pump low frequency hydraulic vibration. January of Huazhong University of Sci. & Tech.(Natural Science Edition), 2014, 46(6): 6-11 (in Chinese)) |
| [5] | 顾巍,何友声,胡天群. 轴对称体空泡流的噪声特性与空泡界面瞬态特征. 上海交通大学学报,2000,34(8):1026-1030 (Gu Jun, He Yousheng, Hu Tianqun. Noise feature of cavitation flows on axisymmetric bodies and transient characteristics of cavity interface. Journal of Shanghai Jiaotong University, 2000, 34(8): 1026-1030 (in Chinese)) |
| [6] | 李忠,杨敏官,高波等. 空化诱发的轴流泵振动特性实验研究. 工程热物理学报,2013, 33(11):1888-1891 (Li Zhong, Yang Minguan, Gaobo, et al. Experiment study on vibration characteristics induced by cavitation of axial-flow pump. Journal of Engineering Thermophysics, 2013, 33(11): 1888-1891 (in Chinese)) |
| [7] | Wang Guoyu, Senocak I, Shyy W. Dynamics of attached turbulent cavitating flows. Progress in Aerospace Sciences, 2001, 37: 551-581 |
| [8] | Brennen CE. Cavitation and Bubble Dynamics. Oxford Engineering & Sciences Series 44, Oxford: Oxford University Press, 1995 |
| [9] | Franc JP, Avellan F, Belahadji B, et al. La Cavitation: Mecanismes physiques et Aspects industriels. Presses Universitaires de Grenoble, Grenoble (EDP Sciences), France, 1995: 28, 141, 142, 144, 449 (in French) |
| [10] | 赵宇,王国玉,黄彪 等. 非定常空化流动涡旋运动及其流体动力特性. 力学学报,2014, 46(2):191-200 (Zhao Yu, Wang Guoyu, Huang Biao, et al. Study of turbulent vortex and hydraulic dynamics in transient sheet/cloud cavitating flows. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 191-200 (in Chinese)) |
| [11] | 张博,王国玉,黄彪等. 云状空化非定常脱落机理的数值与实验研究. 力学学报, 2009, 41(5): 651-659 (Zhang Bo, Wang Guoyu, Huang Biao, et al. Numerical and experimental studies on unsteady shedding mechanisms of cloud cavitation. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(5): 651-659 (in Chinese)) |
| [12] | Huang B, Wang GY, Zhao Y, et al. Physical and numerical investigation on transient cavitating flows. Science China Technological Science, 2013, 56(9): 2207-2218 |
| [13] | Kawanami Y, Kato H, Yamauchi H, et al. Mechanism and control of cloud cavitation. Journal of Fluids Engineering, 1997, 119(8):788-794 |
| [14] | 张博,王国玉,黄彪等. 绕水翼空化非定常的动力特性.机械工程学报, 2010, 46(6):164-169 (Zhang Bo, Wang Guoyu, Huang Biao, et al. Unsteady dynamics of cavitating flows around a hydrofoil. Joural of Mechanical Engineering, 2010, 46(6): 164-169 (in Chinese)) |
| [15] | Chen GH, Wang GY, Hu CL, et al. Combined experimental and computational investigation of cavitation evolution and excited pressure fluctuation in a convergent-divergent channel. International Journal of Multiphase Flow, 2015, 72: 133-140 |
| [16] | Blevins RD. The effect of sound on vortex shedding from cylinders. Fluid Mech, 1985, 161: 217-237 |
| [17] | Lockey KJ, Keller M, Sick M, et al. Flow-induced vibrations at stay vanes: Experience on site and CFD simulations. Int J Hydropow Dams, 2006, 5: 102-106 |
| [18] | Williamson CHK, Govardhan R. Vortex-induced vibrations. Annu Rev, Fluid Mech, 2004, 36: 413-455 |
| [19] | 及春宁,陈威霖,黄继露等. 串列双圆柱流致振动的数值模拟及其耦合机制. 力学学报, 2014, 46(6): 862-870 (Ji Chunning, Chen Weilin, Huang Jilu, et al. Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanism. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 862-870 (in Chinese)) |
| [20] | 王文全,张立翔,闫妍等. 不同雷诺数下弹性薄板流激振动实验. 北京工业大学学报, 2012, 38(1): 55-59 (Wang Wenquan, Zhang Lixiang, Yan Yan, et al. Fluid-induced vibrations of thin elastic plate for different inflow Reynolds numbers. Journal of Beijing University of Technology, 2012, 38(1): 55-59 (in Chinese)) |
| [21] | Ducoin A, Astolfi J, Gobert M. An experimental study of boundary -layer trasition induced vibrations on a hydrofoil. Journal of Fluids and Structures, 2012, 32: 37-51 |
| [22] | Ausoni P, Farhat M, Escaler X. Cavitation influence on von kármán vortex shedding and induced hydrofoil vibrations. Journal of Fluids Engineering, 2007, 129: 966-973 |
| [23] | Wu Q, Huang B, Wang GY, et al. Experimental and numerical investigation of hydroelastic response of a flexible hydrofoil in cavitating flow. International Journal of Multiphase Flow, 2015, doi: http://dx.doi.org/10.1016/j.ijmultiphaseflow.2015.03.023 |
| [24] | 陈涛,屈梁生,耿中行. 小波分析及其在机械诊断中的应用. 机械工程学报,1997, 3: 76-79 (Chen Tao, Qu Liangsheng, Geng Zhongxing. Application of wavelet analysis in fault diagnosis of machinery. Journal of Mechanical Engineering, 1997, 3: 76-79 (in Chinese)) |
| [25] | 罗光坤, 张令弥. 基于Morlet小波变换的模态参数识别研究. 振动与冲击, 2007, 26(7): 135-138 (Luo Guangkun, Zhang Lingmi. Study on identification modal parameters based on Morlet wavelet transformation. Journal of Vibration and Shock, 2007, 26(7): 135-138 (in Chinese)) |
| [26] | Huang B, Zhao Y, Wang GY. Large eddy simulation of turbulent vortex-cavitation interactions in transient sheet /cloud cavitating flows. Computers & Fluids, 2014, 92: 113-124 |
 2015, Vol. 47
2015, Vol. 47