据统计,碳酸盐岩油藏占世界石油储量的50%以上,全球范围内碳酸盐岩油藏中有30%以上为裂缝-溶洞型油藏.单井产量高的 油井绝大多数分布在缝洞型碳酸盐岩油藏中. 此类油藏的主要储集空间以构造变形产生的构造裂缝与岩溶作用形成的孔、洞、缝为主,其中大型洞穴是最主要的储集空间[1].储集体的显著特点是溶洞发育,同时高角度裂缝发育. 流体按溶洞和断裂面随机分布,油藏由多个大小不同的缝洞组合体组成,油水关系复杂.储层非均质性严重,油藏类型和储层中溶洞裂缝分布特别复杂[2].这类油藏非均质性强,流动机理复杂,储层描述困难,因此缝洞型碳酸盐岩油藏问题的研究成为了世界级难题之一.
碳酸盐岩渗流理论经历了从双重介质理论到三重介质理论和从连续介质理论到离散介质理论的发展.1960年,针对天然裂缝油气藏的 双重介质的概念首次被提出,并由此导出了双重介质的双孔双渗透率渗流模型; 1963年,在前者的基础上,又发展出了均质正交各向异性的双重介质模型[4],这是目前双重介质中应用最为广泛的模型. 受以上双重介质模型的启发,国内外学者针对这种双重连续介质模型进行了大量的研究,分别提出了非稳态窜流的层状[5]和球状[6]双重介质模型,模型考虑基质向裂缝的窜流为非稳态. 1975年,三重介质模型被提出[7]. 该模型在双重介质模型的基础上将基质岩块系统按照孔隙度和渗透率差异性分为两类介质,与裂缝系统组成三重介质. 国内的刘慈群[8]、葛家理[9]等学者在三重介质理论方面做了大量的工作.20世纪80年代,吴玉树和葛家理等针对碳酸盐岩油藏进行了渗流模型的理论分析,讨论了溶洞、裂缝和基质3种介质的渗流模型.1993年,刘曰武等[10]建立了考虑井储和表皮的三重介质试井模型.目前,多重介质模型发展的比较完善,已经扩展到不同井类型[11],不同的流体特征[12]和不同地层特性[13].
多重介质模型在碳酸盐岩油藏试井分析中应用广泛[14].多重介质模型将各个系统在空间上叠加在一起,通过窜流函数将各重介质联系起来.应用于缝洞型碳酸盐岩油藏时,非均质性极强的缝洞型储层被简化为孔隙、溶洞、裂缝在空间上均匀连续分布的连续介质模型.但是在缝洞型碳酸盐岩中,大溶洞的尺度可达米量级,甚至十几米,且溶洞的分布具有随机性,尺度相差大.因此,不宜将缝洞型碳酸盐岩油藏处理为连续介质.在此背景下,等效连续介质模型和离散介质模型开始出现并发展.等效连续介质是在适当的表征体积单元内用各向异性来替代非均质性[15, 16, 17, 18, 19].研究的重点在于确定等效渗透率张量和有效性的判定.离散裂缝模型将裂缝和溶洞简化为裂缝、溶洞网络或者以真实的裂缝溶洞分布描述流体流动[20, 21, 22].研究的重点在于离散介质模型的建立、各介质内的流动模式以及计算方法方面.
等效连续介质模型和离散介质模型目前主要应用于油藏数值模拟,且以二维模型为主,应用于试井的模型还未见报道.本文基于离散裂缝模型,建立了三维离散缝洞数值试井模型.采用混合单元有限元方法求解模型,获得了三维离散缝洞试井模型的试井理论曲线和压力场,分析了井底压力响应特征曲线和压力扩展特征.结合地震和地质资料建立了实际裂缝和溶洞的地质模型,应用离散裂缝模型对实际的压力恢复测试进行了数值试井解释.
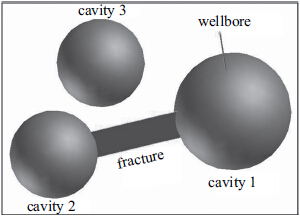
1 物理模型缝洞型油藏中大尺度溶洞是流体的主要储集空间.溶洞为三维体,分布在空间范围内.裂缝作为流通通道,起到沟通溶洞或者井筒的作用.溶洞为不规则的多面体,裂缝为板块,并简化为平面,基质依然采用连续介质体表示.模型示意图如图 1所示.
|
图 1 裂缝溶洞模型示意图 Fig.1 Schematic diagram of fracture-cavity model |
图 1的模型中,储层发育3个大尺度溶洞.为简化描述,将溶洞用球表示,3个溶洞的半径分别为: ${R_1},{R_2},{R_3}$渗透率分别为${K_{v1}},{K_{v2}},{K_{v3}}$ .井钻遇其中一个溶洞,但是未穿过溶洞,钻入溶洞的深度为溶洞半径的1/4.井筒有效井径为${r_{we}} = {r_w}{e^{ - S}},S$为表皮系数.溶洞1和溶洞2由一条裂缝连通,裂缝渗透率为${K_f}$.溶洞1和溶洞2间的距离为$d$.
2 数学模型 2.1 基质流动控制方程| $\frac{{{\partial ^2}{p_{\rm{m}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{p_{\rm{m}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{p_{\rm{m}}}}}{{\partial {z^2}}} = \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial t}}$ | (1) |
其中,${K_m}$为基质水平渗透率,${m^2}; \mu$为流体黏度,$Pa \cdot s;{p_m}$ 为储层压力,$Pa; {\phi_m}$为基质孔隙度; ${C_t}$为综合压缩系数,${Pa^-1}; t$为时间,$s$.
2.2 溶洞流动控制方程假设溶洞区域的流动满足达西定律,可以用一个渗透率和孔隙度不同的区域来表示.不考虑溶洞纵向上渗透率的差异,其流动控制方程为
| $\frac{{{\partial ^2}{p_{\rm{v}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{p_{\rm{v}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{p_{\rm{v}}}}}{{\partial {z^2}}} = \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{{\partial {p_{\rm{v}}}}}{{\partial t}}$ | (2) |
三维空间的裂缝简化为二维平板.裂缝平面所在的局部坐标系用${x}'$和${y}'$表示.裂缝流动控制方程为
| $\frac{{{\partial ^2}{p_{\rm{f}}}}}{{\partial {{x'}^2}}} + \frac{{{\partial ^2}{p_{\rm{f}}}}}{{\partial {{y'}^2}}} = \frac{{\mu {\phi _{\rm{f}}}{C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{{\partial {p_{\rm{f}}}}}{{\partial t}}$ | (3) |
初始条件
| ${p_{\rm{m}}} = {p_{\rm{i}}},\;\;{p_{\rm{f}}} = {p_{\rm{i}}},\;\;{p_{\rm{v}}} = {p_{\rm{i}}}$ | (4) |
内边界条件
| ${\left. {A\frac{K}{\mu }\frac{{\partial {p_{\rm{j}}}}}{{\partial {n_{\rm{i}}}}}} \right|_{{\Gamma _{\rm{i}}}}} = Bq + C\frac{{d{p_{\rm{w}}}}}{{{\rm{d}}t}}$ | (5) |
| ${\left. {{p_{\rm{j}}}} \right|_{{\Gamma _{\rm{i}}}}} = {p_{\rm{w}}}$ | (6) |
油藏边界条件
定压边界
| ${\left. p \right|_{{\Gamma _{\rm{o}}}}} = {p_{\rm{i}}}$ | (7) |
或
封闭边界
| ${\left. {\frac{{\partial p}}{{\partial {n_{\rm{o}}}}}} \right|_{{\Gamma _{\rm{o}}}}} = 0$ | (8) |
溶洞和基质的界面条件
${\left. {{p_{\rm{m}}}} \right|_{{\Gamma _{\rm{v}}}}} = {\left. {{p_{\rm{v}}}} \right|_{{\Gamma _{\rm{v}}}}}$
(9)
其中,${p_i}$为原始地层压力,$Pa;
A$为井筒圆周面的面积,${m^2}; B$为体积系数; $q$为总流量,${m^3}/s; C$为井筒储集系数,${m^3}/Pa; {p_w}$为井底压力,$Pa; M$为溶洞与基质的流度比,$M = {(K/\mu )_v}/{(K/\mu )_m};{\Gamma _i}$为井筒边界; ${n_i}$为井筒边界外法线方向; ${\Gamma _v}$为溶洞边界; ${n_v}$为溶洞边界外法线方向; ${\Gamma _o}$为油藏边界; ${n_o}$为油藏边界外法线方向.
${\left. {{{\left. {\frac{{\partial {p_{\rm{m}}}}}{{\partial {n_{\rm{v}}}}}} \right|}_{{\Gamma _{\rm{v}}}}} = M\frac{{\partial {p_{\rm{v}}}}}{{\partial {n_{\rm{v}}}}}} \right|_{{\Gamma _{\rm{v}}}}}$
(10)
式(1)~ 式(10)构成了三维离散缝洞模型的渗流模型.如果用$FEQ$表示控制方程,那么全区域的模型积分方程可以表示为
| $\begin{array}{*{20}{l}} {\int {\int {\int_\Omega {FEQ} } } \Omega = \int {\int {\int_{{\Omega _{\rm{m}}}} {FEQ} } } {\Omega _{\rm{m}}} + }\\ {\qquad \int {\int {\int_{{\Omega _{\rm{v}}}} {FEQ} } } {\Omega _{\rm{v}}} + \int {\int {\int_{{\Omega _{\rm{f}}}} {FEQ} } } {\Omega _{\rm{f}}}} \end{array}$ | (11) |
| $\begin{array}{*{20}{l}} {\int \int \int_\Omega {FEQ} \Omega = \int \int \int_{{\Omega _{\rm{m}}}} {FEQ} {\Omega _{\rm{m}}} + }\\ {\qquad \int \int \int_{{\Omega _v}} {FEQ} {\Omega _{\rm{v}}} + w \cdot \int \int_{\overline {{\Omega _{\rm{f}}}} } {FEQ} \overline {{\Omega _{\rm{f}}}} } \end{array}$ | (12) |
在离散的单元上使用伽辽金加权余量法[23]推导有限元方程,基质、裂缝和溶洞的插值函数分别为
基质
| ${N_{{\rm{m}}i}} = {a_{{\rm{m}}i}} + {b_{{\rm{m}}i}}x + {c_{{\rm{m}}i}}y + {d_{{\rm{m}}i}}z,\;\;i = 1,2,3,4$ | (13) |
溶洞
| ${N_{{\rm{v}}i}} = {a_{{\rm{v}}i}} + {b_{{\rm{v}}i}}x + {c_{{\rm{v}}i}}y + {d_{{\rm{v}}i}}z,\;\;i = 1,2,3,4$ | (14) |
裂缝
| ${N_{{\rm{f}}i}} = {a_{{\rm{f}}i}} + {b_{{\rm{f}}i}}x' + {c_{{\rm{f}}i}}y',\;\;i = 1,2,3$ | (15) |
(1)基质单元压力
| ${p_{\rm{m}}} = {p_{{\rm{m}}i}}{N_{{\rm{m}}i}} + {p_{{\rm{m}}j}}{N_{{\rm{m}}j}} + {p_{{\rm{m}}k}}{N_{{\rm{m}}k}} + {p_{{\rm{m}}l}}{N_{{\rm{m}}l}}$ | (16) |
(2)溶洞单元压力
| ${p_{\rm{v}}} = {p_{{\rm{v}}i}}{N_{{\rm{v}}i}} + {p_{{\rm{v}}j}}{N_{{\rm{v}}j}} + {p_{{\rm{v}}k}}{N_{{\rm{v}}k}} + {p_{{\rm{v}}l}}{N_{{\rm{v}}l}}$ | (17) |
(3)裂缝单元压力
| ${p_{\rm{f}}} = {p_{{\rm{f}}i}}{N_{{\rm{f}}i}} + {p_{{\rm{f}}j}}{N_{{\rm{f}}j}} + {p_{{\rm{f}}k}}{N_{{\rm{f}}k}}$ | (18) |
在基质和溶洞的四面体单元及裂缝三角形面单元上,可分别得到如下形式的弱积分形式
(1)基质
| $\begin{array}{*{20}{l}} {\int \int \int_{{V_{\rm{m}}}} {\left( {\frac{{\partial {p_{\rm{m}}}}}{{\partial x}}\frac{{\partial \delta {p_{\rm{m}}}}}{{\partial x}} + \frac{{\partial {p_{\rm{m}}}}}{{\partial y}}\frac{{\partial \delta {p_{\rm{m}}}}}{{\partial y}} + \frac{{{K_{{\rm{mz}}}}}}{{{K_{\rm{m}}}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial z}}\frac{{\partial \delta {p_{\rm{m}}}}}{{\partial z}}} \right.} + }\\ {\left. {\qquad \qquad \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial t}}\delta {p_{\rm{m}}}} \right){V_{\rm{m}}} = }\\ {\qquad \qquad \int \int_{{A_{\rm{m}}}} {\delta {p_{\rm{m}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial n}}{A_{\rm{m}}}} } \end{array}$ | (19) |
(2)溶洞
| $\begin{array}{*{20}{l}} {\int \int \int_{{V_{\rm{v}}}} {\left( {\frac{{\partial {p_{\rm{v}}}}}{{\partial x}}\frac{{\partial \delta {p_{\rm{v}}}}}{{\partial x}} + \frac{{\partial {p_{\rm{v}}}}}{{\partial y}}\frac{{\partial \delta {p_{\rm{v}}}}}{{\partial y}} + \frac{{\partial {p_{\rm{v}}}}}{{\partial z}}\frac{{\partial \delta {p_{\rm{v}}}}}{{\partial z}} + } \right.} }\\ {\qquad \left. {\frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{{\partial {p_{\rm{v}}}}}{{\partial t}}\delta {p_{\rm{v}}}} \right){V_{\rm{v}}} = \int \int_{{A_{\rm{v}}}} {\delta {p_{\rm{v}}}\frac{{\partial {p_{\rm{v}}}}}{{\partial n}}{A_{\rm{v}}}} } \end{array}$ | (20) |
(3)裂缝
| $\begin{array}{*{20}{l}} {\int \int_{A'} {\left( {\frac{{\partial {p_{\rm{f}}}}}{{\partial x'}}\frac{{\partial \delta {p_{\rm{f}}}}}{{\partial x'}} + \frac{{\partial {p_{\rm{f}}}}}{{\partial y'}}\frac{{\partial \delta {p_{\rm{f}}}}}{{\partial y'}} + } \right.} }\\ {\qquad \left. {\frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{{\partial {p_{\rm{f}}}}}{{\partial t}}\delta {p_{\rm{f}}}} \right)A' = \int_S {\delta {p_{\rm{f}}}\frac{{\partial {p_{\rm{f}}}}}{{\partial n}}} s} \end{array}$ | (21) |
(1)基质
| $\begin{array}{*{20}{l}} {{V_{\rm{m}}}\left( {b_{{\rm{m}}i}^2 + c_{{\rm{m}}i}^2 + d_{{\rm{m}}i}^2 + \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{1}{{10\Delta t}}} \right)p_{{\rm{m}}i}^{n + 1} + }\\ {\quad {V_{\rm{m}}}\left( {{b_{{\rm{m}}i}}{b_{{\rm{m}}j}} + {c_{{\rm{m}}i}}{c_{{\rm{m}}j}} + {d_{{\rm{m}}i}}{d_{{\rm{m}}j}} + \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{1}{{20\Delta t}}} \right)p_{{\rm{m}}j}^{n + 1} + }\\ {\quad {V_{\rm{m}}}\left( {{b_{{\rm{m}}i}}{b_{{\rm{m}}k}} + {c_{{\rm{m}}i}}{c_{{\rm{m}}k}} + {d_{{\rm{m}}i}}{d_{{\rm{m}}k}} + \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{1}{{20\Delta t}}} \right)p_{{\rm{m}}k}^{n + 1} + }\\ {\quad {V_{\rm{m}}}\left( {{b_{{\rm{m}}i}}{b_{{\rm{m}}l}} + {c_{{\rm{m}}i}}{c_{{\rm{m}}l}} + {d_{{\rm{m}}i}}{d_{{\rm{m}}l}} + \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{1}{{20\Delta t}}} \right)p_{{\rm{m}}l}^{n + 1} - }\\ {\quad \frac{{{A_{\rm{m}}}}}{6}\frac{{\partial p_{{\rm{m}}i}^{n + 1}}}{{\partial n}} - \frac{{{A_{\rm{m}}}}}{{12}}\frac{{\partial p_{{\rm{m}}j,{\rm{m}}k,{\rm{m}}l}^{n + 1}}}{{\partial n}} - \frac{{{A_{\rm{m}}}}}{{12}}\frac{{\partial p_{{\rm{m}}k,{\rm{m}}l,{\rm{m}}j}^{n + 1}}}{{\partial n}} = }\\ {\quad \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{{{V_{\rm{m}}}}}{{10\Delta t}}p_{{\rm{m}}i}^n + \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{{{V_{\rm{m}}}}}{{20\Delta t}}p_{{\rm{m}}j}^n + }\\ {\quad \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{V}{{20\Delta t}}p_{{\rm{m}}k}^n + \frac{{{\phi _{\rm{m}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{m}}}}}\frac{V}{{20\Delta t}}p_{{\rm{m}}l}^n} \end{array}$ | (22) |
(2)溶洞
| $\begin{array}{*{20}{l}} {{V_{\rm{v}}}\left( {b_{{\rm{v}}i}^2 + c_{{\rm{v}}i}^2 + d_{{\rm{v}}i}^2 + \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{1}{{10\Delta t}}} \right)p_{{\rm{v}}i}^{n + 1} + }\\ {\quad {V_{\rm{v}}}\left( {{b_{{\rm{v}}i}}{b_{{\rm{v}}j}} + {c_{{\rm{v}}i}}{c_{{\rm{v}}j}} + {d_{{\rm{v}}i}}{d_{{\rm{v}}j}} + \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{1}{{20\Delta t}}} \right)p_{{\rm{v}}j}^{n + 1} + }\\ {\quad {V_{\rm{v}}}\left( {{b_{{\rm{v}}i}}{b_{{\rm{v}}k}} + {c_{{\rm{v}}i}}{c_{{\rm{v}}k}} + {d_{{\rm{v}}i}}{d_{{\rm{v}}k}} + \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{1}{{20\Delta t}}} \right)p_{{\rm{v}}k}^{n + 1} + }\\ {\quad {V_{\rm{v}}}\left( {{b_{{\rm{v}}i}}{b_{{\rm{v}}l}} + {c_{{\rm{v}}i}}{c_{{\rm{v}}l}} + {d_{{\rm{v}}i}}{d_{{\rm{v}}l}} + \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{1}{{20\Delta t}}} \right)p_{{\rm{v}}l}^{n + 1} - }\\ {\quad \frac{{{A_{\rm{v}}}}}{6}\frac{{\partial p_{{\rm{v}}i}^{n + 1}}}{{\partial n}} - \frac{{{A_{\rm{v}}}}}{{12}}\frac{{\partial p_{{\rm{v}}j,{\rm{v}}k,{\rm{v}}l}^{n + 1}}}{{\partial n}} - \frac{{{A_{\rm{m}}}}}{{12}}\frac{{\partial p_{{\rm{v}}k,{\rm{v}}l,{\rm{v}}j}^{n + 1}}}{{\partial n}} = }\\ {\quad \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{{{V_{\rm{v}}}}}{{10\Delta t}}p_{{\rm{v}}i}^n + \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{{{V_{\rm{v}}}}}{{20\Delta t}}p_{{\rm{v}}j}^n + }\\ {\quad \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{V}{{20\Delta t}}p_{{\rm{v}}k}^n + \frac{{{\phi _{\rm{v}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{v}}}}}\frac{V}{{20\Delta t}}p_{{\rm{v}}l}^n} \end{array}$ | (23) |
(3)裂缝
| $\begin{array}{*{20}{l}} {A\left( {{b_{{\rm{f}}i}}{b_{{\rm{f}}i}} + {c_{{\rm{f}}i}}{c_{{\rm{f}}i}} + \frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{1}{{6\Delta t}}} \right)p_{{\rm{f}}i}^{n + 1} + }\\ {\qquad A\left( {{b_{{\rm{f}}i}}{b_{{\rm{f}}j}} + {c_{{\rm{f}}i}}{c_{{\rm{f}}j}} + \frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{1}{{12\Delta t}}} \right)p_{{\rm{f}}j}^{n + 1} + }\\ {\qquad A\left( {{b_{{\rm{f}}i}}{b_{{\rm{f}}k}} + {c_{{\rm{f}}i}}{c_{{\rm{f}}k}} + \frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{1}{{12\Delta t}}} \right)p_{{\rm{f}}k}^{n + 1} = }\\ {\qquad \frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{1}{{6\Delta t}}p_{{\rm{f}}i}^n + \frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{1}{{12\Delta t}}p_{{\rm{f}}j}^n + }\\ {\qquad \frac{{{\phi _{\rm{f}}}\mu {C_{\rm{t}}}}}{{{K_{\rm{f}}}}}\frac{1}{{12\Delta t}}p_{{\rm{f}}k}^n} \end{array}$ | (24) |
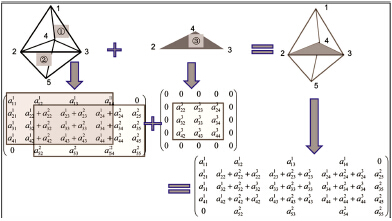
由于各介质的交界面采用的公共结点的方式离散,界面处的压力连续条件已经自动满足.将式(22)~式(24)叠加为整体刚度矩阵,整体刚度矩阵采用稀疏列存储[24](CSC格式).单元刚度矩阵的叠加过程如图 2所示.合成总体刚度矩阵之后采用大型线性方程组的开源求解库PETSc[25]求解有限元方程组,得到各时刻各结点上的压力值.
|
图 2 四面体单元和三角形单元叠加处理过程 Fig.2 Schematic of FEM implementation for matrix and fracture elements |
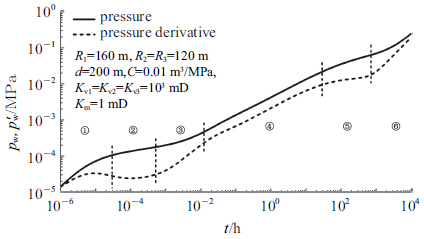
图 3为图 1所示的离散缝洞模型的试井理论曲线.从图 3可以看出,试井曲线大致可以分为6个阶段:
|
图 3 离散缝洞模型试井理论曲线 Fig.3 Log-log type curve of pressure response for discrete-fracture-cavity model |
(1)井筒储存阶段,流体压缩性起主导作用,压力和压力导数呈斜率为1的直线;
(2)溶洞1径向流段,井在溶洞1中,溶洞1中的流体沿径向方向流动到井筒,压力导数为水平直线段;
(3)过渡阶段,随着溶洞1中压力降低,裂缝中的流体和极少量的基质流体开始向溶洞1流动,此时流动偏离径向流,压力和压力导数曲线持续上翘;
(4)裂缝线性流阶段,流体沿裂缝的线性流动,压力和压力导数为1/2斜率的平行线.
(5)系统径向流阶段,远离井筒处,流体流动趋向于径向流动
(6)边界反应阶段,在封闭边界作用下,井底流动压力持续下降,压力和压力导数曲线趋于斜率为1的直线.
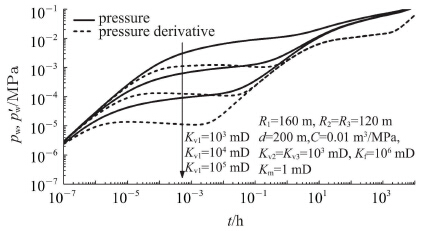
4.2 溶洞1渗透率对试井理论曲线的影响图 4是溶洞1不同渗透率情况下的试井理论曲线.从图 4可以看出,溶洞1的渗透率只影响试井理论曲线的第2阶段,即溶洞1的径向流段.溶洞渗透率越大,压力导数曲线的水平段越低.由于井钻遇溶洞1,可以预见,当溶洞1增大时,第2阶段的压力导数水平线上翘的时间将推后.
|
图 4 溶洞1渗透率对试井理论曲线的影响 Fig.4 Log-log type curve of pressure response with different permeability of cave 1 |
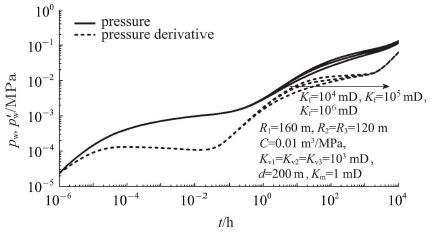
考虑沟通溶洞1和溶洞2的裂缝渗透率的影响,分别取其渗透率为104 mD,105 mD和106 mD,所得的试井理论曲 线如图 5所示.从图 5可以看出,裂缝渗透率主要影响试井理论曲线的第3阶段即过渡段.裂缝渗透率越大,过渡段压力导数曲线越低,且压力和压力导数曲线间的距离越大,主要原因是裂缝渗透率越大,井底压力得到补充越迅速,缓解井底压力下降的能力越强.
|
图 5 裂缝渗透率对模型试井理论曲线的影响 Fig.5 Log-log type curve of pressure response with different permeability of fracture |
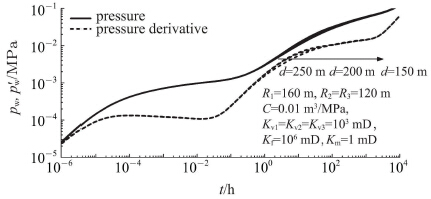
考虑溶洞1和溶洞2间距离的影响.分别取距离为150 m,200 m和250 m,所得的试井理论曲线如图 6所示.从图 6可以看出,溶洞1和溶 洞2的距离主要影响过渡段,但是影响很小,主要原因为溶洞1和溶洞2通过裂缝沟通,而裂缝的渗透率极大,压力沿着裂缝很快就能从溶洞1传播到溶洞2.
|
图 6 溶洞1和溶洞2间距离对试井理论曲线的影响 Fig.6 Log-log type curve of pressure response with different distances between cave 1 and cave 2 |
裂缝作为主要的流通通道对流体流动具有显著的影响,溶洞作为主要的储集空间对流体的储集和渗流也具有明显的影响.通常数值模拟 软件处理大尺度溶洞的方式是通过渗透率和孔隙度模型来实现的,即将代表溶洞的网格块的渗透率和孔隙度设置一个较大的值,而处理小尺度裂缝时采用的是多重介质模型,无法处理大尺度裂缝.本文中笔者通过建立的三维离散缝洞模型来模拟大尺度溶洞和裂缝同时存在的储层中的流动特征.
塔里木油田一口典型缝洞型储层油井A进行了压力恢复测试.在关井进行压力恢复前监测了约16个小时的流压.该井在钻井过程中放空4.26 m,漏失钻井液640.92 ${m^3}$,表明储层内发育大型溶洞.图 7(a)和图 7(b)分别为该井地震反射特征和缝洞单元平面图.从图 7(b)可以看出,该井钻遇一个溶洞,通过裂缝沟通另一个溶洞.井和流体的基础参数为:井筒半径0.074 6 m、储层厚度141 m、基质孔隙度1.29%、原油体积系数1.037、黏度2.19 cp、综合压缩系数1.42×10-3 MPa-1.开井生产1 485 h,平均产量65 ${m^3}/d$.

|
图 7 地震资料解释结果图 Fig.7 Result of seismic data interpretation |
整个数值试井解释流程为:
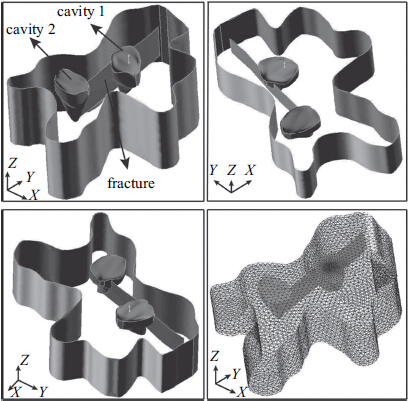
(1)根据地质和地震等静态资料建立油藏模型.理论分析中溶洞采用球代替,但实际中的溶洞形状是不规则的.利用地震资料提取的溶洞信息,笔者建立了如图 8所示的地质模型.溶洞1顶部距储层顶面14.7 m,溶洞1底部距油藏底面36.9 m,溶洞2顶部距油藏顶面12.8 m,溶洞2顶部距油藏底面35.2 m.井筒钻入溶洞1的深度为12.5 m.
|
图 8 A井离散缝洞模型示意图 Fig.8 Geological model of discrete-fracture-cavity |
(2)利用“Gambit”软件对油藏模型进行网格划分.网格结点数为99 931,单元数量为549 287.为更精确描述溶洞和裂缝的流动特征,在井筒周围和溶洞及裂缝区域进行了网格加密.
(3)参数拟合.不断调整油藏参数(溶洞渗透率、裂缝渗透率等)和井筒参数(井筒储存系数、表皮系数等),计算网格结点压力,得到与实 测压力变化一致的油藏参数.这一步主要是进行井底压差的双对数拟合和压力历史的拟合.
双对数拟合图和压力历史拟合图如图 9所示.

|
图 9 试井解释曲线拟合图 Fig.9 The math plot of well test interpretation |
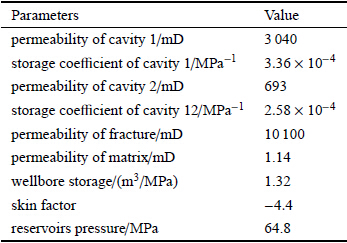
离散缝洞数值试井模型解释得到的储层参数见表 1.从表 1的结果可以看出,裂缝的渗透率最大,达到了10 100 mD;溶洞1的渗透率 也很高为3 040 mD.溶洞1和溶洞2是该井主要的供液的来源,高导流能力裂缝起到沟通溶洞1和溶洞2的作用.
| 表 1 离散缝洞数值试井模型解释结果表 Table 1 The interpretation results of well A with discrete-fracture-cavity model |
图 10是不同时刻过两溶洞的截面的压力场图.从图可以看出,压力首先沿着井所钻遇的溶洞1传播.由于溶洞1渗透率高,压力迅速传遍整个溶洞; 接着压力沿着裂缝迅速扩展到溶洞2.压力的扩展具有明显的方向性和局部扩展特征.在常规的解释方法中,图 9所示的试井测试曲线一般采用径向复合模型解释,而径向复合模型过于简单,忽略了裂缝和溶洞2对流动的重要作用,使用离散缝洞模型可以精细的模拟由于储层非均质性引起的复杂流动特征.

|
图 10 A井不同时刻压力扩展图 Fig.10 Pressure field of Well A |
从图 9(a)所示的试井曲线上看,该井并没有表现出多重介质的渗流特征,而且从现场实测双对数曲线的统计也发现,几乎没有多重介质特征的曲线.这也从侧面反映出缝洞型油藏的渗流无法用多重介质模型来分析.本文建立的离散缝洞数值试井模型可以用于这类复杂油藏的分析,为该类油藏储层的评价提供了有力的技术支撑,对缝洞型碳酸盐岩油藏的合理开发有积极的指导作用.
6 结 论(1)本文建立了三维离散裂缝模型.该模型将空间大尺度的三维裂缝简化为空间的二维平板,大大简化了空间三维裂缝的描述.将溶洞用高渗透率和大孔隙度的不规则多面体代替.溶洞和裂缝在空间分布,溶洞为主要的储集空间,而裂缝则为主要的沟通通道.
(2)建立了离散缝洞模型的有限元求解方法.裂缝区域采用三角形面单元离散,溶洞和基质区域采用三维四面体单元离散,采用混合单元有限元法建立了离散缝洞模型的求解方法.
(3)分析了模型的试井理论曲线和压力场特征.对井底压力响应曲线的6个不同流动阶段进行了详细分析.从压力扩展的过程可以看出,由于裂缝和溶洞的存在,压力的扩展具有明显的方向性.
(4)分析了溶洞1的渗透率、裂缝渗透率和溶洞1与溶洞2距离对试井理论曲线的影响.溶洞1的渗透率对试井理论曲线的影响最大,裂缝的渗透率主要影响试井理论曲线的过渡段,裂缝渗透率越高,过渡段后期曲线下掉幅度越大; 溶洞1和溶洞2间的距离对试井理论曲线的影响较小.
(5)结合实际生产资料及测试资料情况,给出了1口井的实际测试资料的分析结果.通过与实际地震反射资料及生产实际资料的对比,发现本文所建立的模型可以较好地反映裂缝和溶洞的地质动态状况,并与实际生产状况具有较好的一致性.该数值试井模型对缝洞型碳酸盐岩油藏储层的评价提供了有力的技术支撑,对缝洞型碳酸盐岩油藏的合理开发有积极的指导作用.
| [1] | 江怀友,宋新民, 王元基等. 世界海相碳酸盐岩油气勘探开发现状与展望. 海洋石油, 2008, 28(4): 6-13 (Jiang Huaiyou, Song Xinmin, Wang Yuanji, et al. Current situation and forecast of the world's carbonate oil and gas exploration and development. Offshore Oil, 2008, 28(4): 6-13 (in Chinese))( 1) 1) |
| [2] | 焦方正, 窦之林. 塔河碳酸盐岩缝洞型油藏开发研究与实践. 北京: 石油工业出版社, 2008 (Jiao Fangzheng, Dou Zhilin. Research and Practice of Tahe Carbonate Fractured Vuggy Reservoir Development. Beijing: Petroleum Industry Press, 2008 (in Chinese))( 1) 1) |
| [3] | Barenblatt GI, Zheltov IP, Kochina IN. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. Journal of Applied Mathematics and Mechanics, 1960, 24(efeq4): 1286-1303( 1) 1) |
| [4] | Warren JE, Root PJ. The Behavior of Naturally Fractured Reservoirs. SPE 426, 1963( 1) 1) |
| [5] | Kazemi H. Pressure Transient Analysis of Naturally Fractured Reservoirs with Uniform Fracture Distribution. SPE 2156, 1969( 1) 1) |
| [6] | de Swaan OA. Analytic Solutions for Determining Naturally Fractured Reservoir Properties by Well Testing. SPE 5346, 1976( 1) 1) |
| [7] | Clossman PJ. The Acquirer Model for Fissured Reservoir. SPE 4434, 1975( 1) 1) |
| [8] | 刘慈群. 三重介质弹性渗流方程组的精确解. 应用数学和力学, 1981, 2(4): 419-424 (Liu Ciqun. Exact solution for the compressible flow equations through a medium with triple-porosity. Applied Mathematics and Mechanics, 1981, 2(4): 419-424 (in Chinese))( 1) 1) |
| [9] | 吴玉树, 葛家理. 三重介质裂-隙油藏中的渗流问题. 力学学报, 1983, 1(1): 81-85 (Wu Yushu, Ge Jiali. The transient flow in naturally fractured reservoirs with three-porosity systems. Chinese Journal of Theoretical and Applied Mechanics, 1983, 1(1): 81-85 (in Chinese))( 1) 1) |
| [10] | 刘曰武, 刘慈群. 三重介质油气藏数学模型的建立及其渗流机理的研究. 西南石油学院学报, 1993, S1(3): 87-89 (Liu Yuewu, Liu Ciqun. Study on the establishment of triple-porosity medium of reservoir model and percolation mechanism. Journal of Southwest Petroleum Institute, 1993, S1(3): 87-89 (in Chinese))( 1) 1) |
| [11] | 李成勇, 刘启国, 张燃等. 三重介质油藏水平井试井解释模型研究. 西南石油学院学报, 2006, 28(4): 32-35,103 (Li Chengyong, Liu Qiguo, Zhang Ran, et al. The research of well test of horizontal well in triple medium reservoir. Journal of Southwest Petroleum Institute, 2006, 28(4): 32-35,103 (in Chinese))( 1) 1) |
| [12] | 赵玉龙, 张烈辉, 青胜兰. 三重介质油藏非牛顿幂律流体试井模型与典型曲线分析. 水动力学研究与进展A辑, 2010, 25(2): 254-261 (Zhao Yulong, Zhang Liehui, Qing Shenglan. Well test model and typicalcurve analysis of non-newtonian fluid's transient flow in triple media reservoirs. Chinese Journal of Hydrodynamics, 2010, 25(2): 254-261 (in Chinese))( 1) 1) |
| [13] | 同登科, 刘文超, 薛莉莉. 变形三重介质低渗透油藏三渗模型流动特征. 力学季刊, 2010, 31(3): 334-341 (Tong Dengke, Liu Wenchao, Xue Lili. Flow characteristics of triple-permeability model in low permeability reservoir with deformed triple porosity medium. Chinese Quarterly of Mechanics, 2010, 31(3): 334-341 (in Chinese))( 1) 1) |
| [14] | 孙贺东, 施英, 唐海龙等. 三重介质油气藏试井分析研究进展. 油气井测试, 2008, 17(1): 71-74,78 (Sun Hedong, Shi Ying, Tang Hailong, et al. Studied development of well testing analysis for triple medium oil and gas reservoir. Well Testing, 2008, 17(1): 71-74,78 (in Chinese))( 1) 1) |
| [15] | Snow DT. Anisotropie permeability of fractured media. Water Resour Res, 1969, 5(6): 1273-1289( 1) 1) |
| [16] | Neale GH, Nader WK. The Permeability of a Uniformly Vuggy Porous Medium. SPE 3812, 1973( 1) 1) |
| [17] | Kamath J, Lee SH, Jensen CL, et al. Modeling Fluid Flow in Complex Naturally Fractured Reservoirs. SPE-39547-MS, 1998( 1) 1) |
| [18] | Teimoori A. Calculation of the effective permeability and simulation of fluid flow in naturally fractured reservoirs. [PhD Thesis]. Sydney: University of New South Wales, 2005( 1) 1) |
| [19] | 叶祖洋, 姜清辉, 姚池等. 三维裂隙网络非稳定渗流分析的变分不等式方法. 力学学报, 2013, 45(6): 878-887 (Ye Zuyang, Jiang Qinghui, Yao Chi, et al. A variational inequality approach for non-steady seepage flow through three-dimensional fracture network. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 878-887 (in Chinese))( 1) 1) |
| [20] | Jahan Noorishad MM. An upstream finite finite element method for solution of transient transport equation in fractured porous media. Water Resoures, 1982, 3(18): 588-596( 1) 1) |
| [21] | Baca R, Arnett R, Langford D. Modeling fluid flow in fractured-porous rock masses by finite-element techniques. Int J Num Meth Fluids, 1984, 4 : 337-348( 1) 1) |
| [22] | Yao J, Huang ZQ. Discrete Fracture-vug Network Model for Modeling Fluid Flow in Fractured Vuggy Porous Media. SPE 130287,2010( 1) 1) |
| [23] | 张涤明, 蔡崇喜, 章克本等. 计算流体力学. 广州: 中山大学出版社,1991 (Zhang Diming, Cai Congxi, Zhang Keben, et al. Computational Fluid Dynamics. Guangzhou: Sun Yat-Sen University Press, 1991 (in Chinese))( 1) 1) |
| [24] | Bell N. Sparse Matrix Representations & Iterative Solvers, Lesson 1. http://www.bu.edu/pasi/files/2011/01/NathanBell1-10-1000.pdf. 2011-01( 1) 1) |
| [25] | Portable, Extensible Toolkit for Scientific Computation. http://www.mcs.anl.gov/petsc/index.html( 1) 1) |
 2015, Vol. 47
2015, Vol. 47