水平井钻井和水力压裂已成为页岩气藏开发的重要技术,微地震监测表明其压裂往往形成复杂裂缝网络[1]. 裂缝网络的形态决 定了储层改造体积的大小,而储层改造体积直接关系着页岩气藏的产量[2],因此对页岩气藏裂缝网络扩展的研究具有重要意义.
针对裂缝网络的扩展,国内外学者采用不同的方法进行了研究. 王杰等[3]建立了块体单元离散弹簧模型并应用于岩石破裂过程的 数值模拟;Xu等[4]基于等效方法提出了线网模型(wire-mesh);Weng 等[5]提出了非常规裂缝模型(UFM),能够模拟天然裂缝 和人工裂缝之间的相互作用;Meyer等[6]基于离散裂缝网络模型开发了"MShale"软件;Fu等[7]采用水-$地质力学显式耦 合的方式对裂缝性介质的水力压裂进行了研究;Wu和Olson[8]基于修正位移不连续法(DDM)求解了多裂缝同步扩展问题;Olson和 Taleghani [9]采用扩展有限元方法对裂缝扩展问题进行了求解;多簇裂缝同步扩展与单裂缝扩展的不同在于多簇裂缝之间存在应力阴影作用, 该作用影响着裂缝扩展路径和几何形状大小[10].
笔者采用修正DDM方法描述应力与位移不连续量之间的关系,耦合井筒和裂缝内流体流动模型,与已有工作不同在于,基于牛顿迭代法 构造了新的耦合求解算法,该算法具有计算速度快的优点,此外考虑了天然裂缝的影响. 通过与经典模型结果对比验证了本文算法的正确性,最后对多簇压裂和考虑天然裂缝的缝网扩展进行了影响因素分析.
1 数学模型 1.1 岩体变形裂缝扩展过程中,裂缝应力场不仅取决于远场地应力的作用,还有邻近裂缝施加的"应力阴影". Crouch和Starfield[11]给出 了二维不连续位移基本解,Olson[12]在此基础上提出了三维修正系数用以考虑由于有限裂缝高度引起的三维影响. 对于有限单元,位移不连续解为
| $\sigma _{\rm{n}}^i = {\rm{ }}\sum\limits_{j = 1}^N {{G^{ij}}C_{{\rm{ns}}}^{ij}D_{\rm{s}}^j} + {\rm{ }}\sum\limits_{j = 1}^N {{G^{ij}}C_{{\rm{nn}}}^{ij}D_{\rm{n}}^j} $ | (1) |
| $\sigma _{\rm{s}}^i = {\rm{ }}\sum\limits_{j = 1}^N {{G^{ij}}C_{{\rm{ss}}}^{ij}D_{\rm{s}}^j} + {\rm{ }}\sum\limits_{j = 1}^N {{G^{ij}}C_{{\rm{sn}}}^{ij}D_{\rm{n}}^j} $ | (2) |
| $G^{ij} = 1 - \dfrac{d_{ij}^{\,\beta} }{[d_{ij}^2 + (h / \alpha )^2]^{\beta / 2}}$ | (3) |
式中,dij为单元中心之间的距离,m;h为裂缝高度,m; α和β为经验参数.
根据最大周向应力准则,裂缝沿着最大周向应力方向扩展,该方向可由应力强度因子确定
| $\theta = 2\arctan \Bigg (\dfrac{K_{\rm I} \pm \sqrt {K_{\rm I}^2 + 8K_{\rm II}^2 } }{4K_{\rm II} } \Bigg )$ | (4) |
(1) 裂缝中流动
由于裂缝宽度远远小于裂缝长度,忽略裂缝宽度方向的流动,仅考虑压裂液沿裂缝扩展方向上的一维流动. 对于每一裂缝,根据 Reynolds理论和质量守恒得到控制方程
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} \frac{{\partial p}}{{\partial x}} = - \frac{{12\mu q}}{{h{w^3}}}\\ \frac{{\partial q}}{{\partial x}} + h\frac{{\partial w}}{{\partial t}} + {q_l} = 0\\ {q_l} = \frac{{2h{C_l}}}{{\sqrt {t - {\tau _0}(x)} }},t > {\tau _0}(x) \end{array} \end{array}} \right\}$ | (5) |
(2) 井筒中流动
井筒流体流动示意图如图1,由Kirchoff第一定律,井筒注入速率必须满足
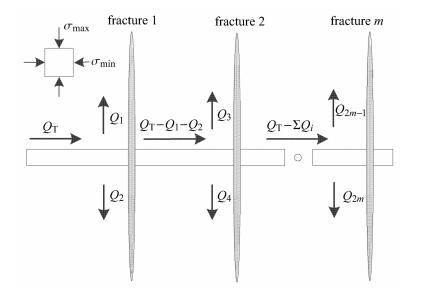
|
图 1 水平井多缝同步扩展示意图 Fig. 1 Schematic diagram of multiple fractures propagation in horizontal well |
| ${Q_{\rm{T}}} = {\rm{ }}\sum\limits_{i = 1}^{2m} {{Q_i}} $ | (6) |
由Kirchoff第二定律,流体压力必须满足
| $p_0 = p_{{\rm w},i} + p_{{\rm pf},i} + p_{{\rm cf},i}$ | (7) |
当水力裂缝逼近天然裂缝时,水力裂缝可能直接贯穿天然裂缝,或者转向天然裂缝进行扩展. 对此,国内外学者从实验和理论推 导等方面进行了较多研究[13]. Renshaw等[14]提出了预测水力裂缝是否贯穿摩擦界面的简单准则,该准则是当摩擦界面另一侧的应力足够重新开裂一条裂缝时, 且摩擦面不发生滑移,则水力裂缝将直接贯穿该摩擦面. Gu等[15]将逼近角推广到任意角度的情况,本文将采用该方法进行判断.
2 数值求解裂缝划分为有限单元,压力和宽度定义在单元中心,单元之间的流量定义在单元边界,由质量守恒可得
| $\begin{array}{l} - \sum\limits_j {q_{ij}^t} {\rm{d}}t = {h_i}{l_i}(w_i^t - w_i^{t - {\rm{d}}t}) + \\ 4{C_{\rm{l}}}{h_i}{l_i}(\sqrt {t - {\tau _o}(i)} - \sqrt {t - {\rm{ d}}t - {\tau _o}(i)} ) \end{array}$ | (8) |
选择流体压力pi (i=1-N)、裂缝分流量Qk (k=1- 2m)、井筒根部压力p0以及时间步长dt为未知量,构建并使用迭代法求解相应的方程组,具体步骤:假设迭代初值, 由流体压力值pi可求得各单元的净压力,利用位移不连续方程可求得对应的垂向和切向位移不连续量,垂向位移不连续量即为宽度, 由方程(8)可得N个方程,由方程(7)可得2m个方程,最后加上全局守恒方程以及方程(6)构成待求量的方程组,未知量个数与方程个数相等. 采用牛顿迭代法求解出上述方程组,当达到收敛条件时即可获得上述未知量的值,将流体压力值代入位移不连续方程便可求得各个单元 垂向和切向位移不连续量.
3 算例分析与讨论 3.1 模型验证为了验证所建模型与算法的正确性,将裂缝条数设为1,比较数值解与经典模型解析解. 模型参数取值:弹性模量E =20 GPa,泊松比v=0.25,注入速度Q0=0.027 m3/s,裂缝高度h=30 m,压裂液黏度 μ=0.1 Pa·s.
考虑滤失效应时,Nordgren[16]推导了高滤失情况下近似解析解,可表示
| $\left. \begin{array}{l} L(t) = \frac{{{q_0}}}{{\pi h{C_{\rm{l}}}}}{t^{1/2}}\\ w(0,t) = 4{[\frac{{2(1 - \nu )\mu q_0^2}}{{{\pi ^3}Gh{C_{\rm{l}}}}}]^{1/4}}{t^{1/8}} \end{array} \right\}$ | (9) |
文献[17]指出,PKN模型的高滤失解也适用于KGD模型,因此本文对比近似解析解(9)与数值解结果. 取滤失系数Cl=5 × 10-5,计算对比结果如图2和图3所示. 由图可知看出裂缝半长数值解随着注入时间增大逐渐靠近解析解,裂缝最大宽度数值解与PKN模型解相差较小,近似解析解适用于高滤失、 长时间的情形,说明了本文模型能够准确地模拟考虑滤失效应的裂缝扩展情形.
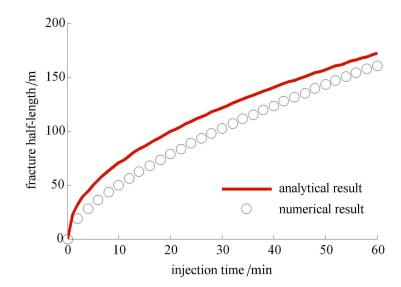
|
图 2 裂缝半长数值解与解析解对比结果 Fig. 2 Contrast of numerical and analytical results for fracture half-length |
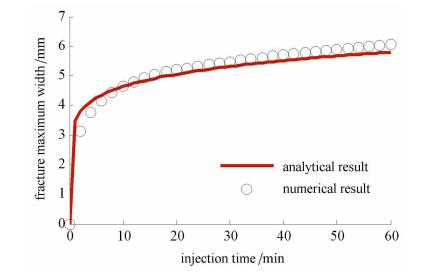
|
图 3 裂缝最大宽度数值解与解析解对比结果 Fig. 3 Contrast of numerical and analytical results for fracture maximum width |
水平井多簇裂缝同步扩展时,裂缝之间存在相互影响,裂缝的扩展方向会发生变化. 模拟计算单元尺寸为0.5 m,模型参数取值与模 型验证算例相同.
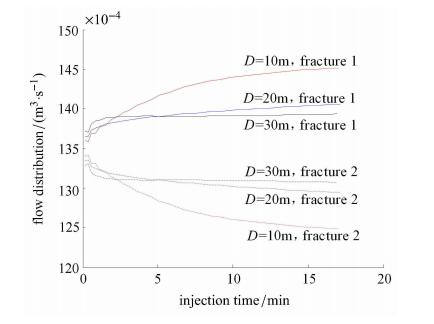
两簇压裂不同裂缝间距时裂缝扩展路径如图4所示,两簇裂缝相背离地扩展,且裂缝间距越小,裂缝扩展方向偏离初始方向的角度 越大;当裂缝间距$D=30$\,m,即等于裂缝高度时,裂缝扩展方向偏离角较小,从而说明了裂缝之间应力阴影作用距离主要集中 在裂缝高度以内. 注入的压裂液流向两簇裂缝,不同裂缝间距时分流量分布如图5所示,当裂缝间距越小,流量分配越不均匀,靠近井筒跟部的裂 缝将获得更多的注入液,从而裂缝宽度也将变得更大.
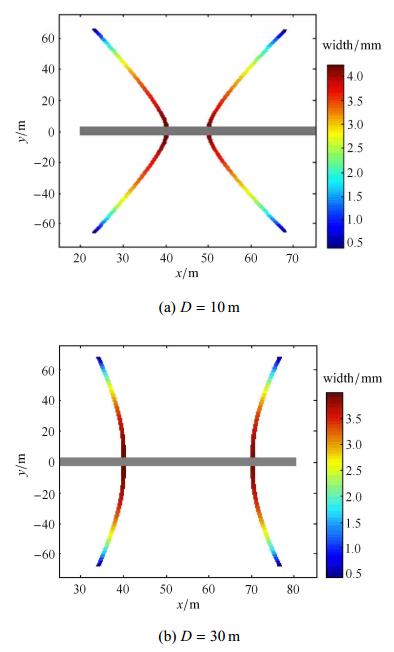
|
图 4 不同裂缝间距时裂缝扩展路径与宽度分布 Fig. 4 Fracture propagation path and width distribution for different fracture spacing |
|
图 5 不同裂缝间距时裂缝分流量变化 Fig. 5 Variation of fracture flow distribution for different fracture spacing |
通过算例分析了逼近角和地应力差对水力裂缝形态的影响,模型参数取值与模型验证算例相同.
(1) 逼近角
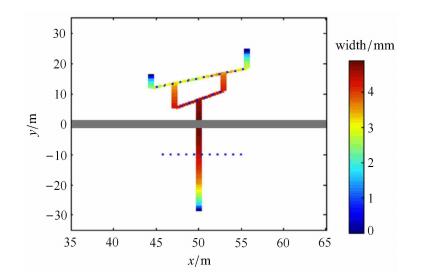
逼近角是水力裂缝贯穿与否的重要因素,不同逼近角情况下水力裂缝扩展路径如图6所示. 图中蓝色虚线代表预制的3条天然裂缝,与y轴方向的夹角分别为45°,60°和90°,最大主地应力方向与y轴方向平行,水力裂缝将沿着y轴方向起裂. 由图可知水力裂缝逼近夹角为45°和60°天然裂缝时裂缝将发生转向扩展,且水力裂缝经过第1条天然裂缝之后分为两个分支裂缝,分支裂缝接触第2条天然裂缝之 后其中两个裂缝端点将会相交形成连通状态,而另外的端点将分出两个分支裂缝;水力裂缝逼近夹角为90°天然裂缝时将发生贯穿扩展,裂缝宽度较之转向扩展段大,说明天然裂缝虽然能使水力裂缝扩展形成复杂网络,但会降低裂缝局部导流能力.
|
图 6 不同逼近角水力裂缝扩展路径 Fig. 6 Hydraulic fracture propagation path for different approaching angles |
(2) 地应力差
地应力差是水力裂缝贯穿与否的另一重要因素,不同地应力差情况下水力裂缝扩展路径如图7所示. 由图可知,水力裂缝能 贯穿夹角为45°天然裂缝,而夹角为75°天然裂缝在高应力差的情况下才能贯穿,因此在两种地应力差情况下裂缝最终形态不相同. 这说明页岩气藏应力各向异性越弱,水力压裂形成的裂缝网络越复杂,反之应力各向异性越强,水力裂缝形态越集中.

|
图 7 不同地应力差水力裂缝扩展路径 Fig. 7 Hydraulic fracture propagation path for different stress differences |
(1)本文建立了岩体变形、裂缝内和井筒流体流动的耦合数学模型,基于牛顿迭代法构造了新的耦合求解算法,算例证明本文方法能 准确地模拟水力裂缝扩展形态;
(2)裂缝间距是多簇裂缝同步扩展形态的重要影响因素,裂缝间距越小,压裂液分配到各条裂缝越不均匀;
(3)逼近角越小或者应力各向异性越弱,水力裂缝越容易发生转向扩展,裂缝网络越复杂;
(4)裂缝之间的应力阴影和天然裂缝作用是造成页岩气藏水力压裂缝网复杂性的重要因素.
| [1] | Fisher MK, Heinze JR, Harris CD, et al. Optimizing horizontal completions in the Barnett shale with microseismic fracture mapping. Journal of Petroleum Technology, 2005, 57(3): 41-42 |
| [2] | Mayerhofer MJ, Lolon E, Warpinski NR, et al. What is stimulated reservoir volume? SPE Production & Operations, 2010, 25(01): 89-98 |
| [3] | 王杰, 李世海, 周东 等. 模拟岩石破裂过程的块体单元离散弹簧模型. 岩土力学, 2013, 34(8): 2355-2362 (Wang Jie, Li Shihai, Zhou Dong, et al. A block-discrete-spring model to simulate failure process of rock. Rock and Soil Mechanics, 2013, 34(8): 2355-2362 (in Chinese)) |
| [4] | Xu W, Ganguly U, Weng X. Wiremesh: a novel shale fracturing simulator. CPS/SPE International Oil & Gas Conference and Exhibition, Society of Petroleum Engineers, 2010 |
| [5] | Weng X, Kresse O, Cohen C, et al. Modeling of hydraulic fracture network propagation in a naturally fractured formation. SPE Production Operations, 2011, 26(4): 368-380 |
| [6] | Meyer B, Bazan L. A discrete fracture network model for hydraulically induced fractures theory, parametric and case studies. SPE Hydraulic Fracturing Technology Conference, Society of Petroleum Engineers, 2011 |
| [7] | Fu P, Johnson SM, Carrigan CR. An explicitly coupled hydro-geomechanical model for simulating hydraulic fracturing in arbitrary discrete fracture networks. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(14): 2278-2300 |
| [8] | Wu K, Olson JE. Simultaneous multifracture treatments: fully coupled fluid flow and fracture mechanics for horizontal wells. SPE Journal, 2014: 1-10 |
| [9] | Olson JE, Dahi-Taleghani A. Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures. SPE Hydraulic Fracturing Technology Conference, Society of Petroleum Engineers, 2009 |
| [10] | Cheng Y. Mechanical interaction of multiple fractures exploring impacts of the selection of the spacing/number of perforation clusters on horizontal shale gas wells. SPE Journal, 2012, 17(4): 992-1001 |
| [11] | Crouch S. Solution of plane elasticity problems by the displacement discontinuity method. I. Infinite body solution. International Journal for Numerical Methods in Engineering, 1976, 10(2): 301-343 |
| [12] | Olson JE. Predicting fracture swarms-the influence of subcritical crack growth and the crack tip process zone on joint spacing in rock. Geological Society, London, Special Publications, 2004, 231(1): 73-88 |
| [13] | Warpinski NR, Teufel LW. Influence of geologic discontinuities on hydraulic fracture propagation. Journal of Petroleum Technology, 1987, 39(2): 209-220 |
| [14] | Renshaw CE, Pollard DD. An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic materials. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1995, 32(3): 237-249 |
| [15] | Gu H, Weng X, Lund J, et al. Hydraulic fracture crossing natural Fracture at non-orthogonal angles, a criterion, its validation and applications. SPE Hydraulic Fracturing Technology Conference and Exhibition, Society of Petroleum Engineers, 2011 |
| [16] | Nordgern RP. Propagation of a vertical hydraulic fracture. Society of Petroleum Engineers Journal, 1972, 12(4): 306-314 |
 2015, Vol. 47
2015, Vol. 47
