由于页岩低孔、低渗的特征,若要获得较高的产能则必须进行大规模的压裂改造. 页岩的可压裂性与压裂最终效果存在密切联系. 国内外对可压裂性认识不一. Chong等[1]将可压裂性视为页岩储层被有效压裂从而获得增产目的的性质,是评价压裂效果的重要指标. Breyer等[2]将页岩的脆性与韧性作为可压裂性的重要评价指标. 蒋廷学等[3]考虑了页岩水平井分段压裂的特殊性,利用压裂液总量与支撑剂总量等分段压力施工参数来建立页岩可压性评价模型. 隋丽丽等[4]根据岩石岩性及其裂隙分形特征,采用裂隙分维数来体现岩石可压裂性. 袁俊亮等[5]采用脆性指数,断裂韧性以及岩石力学参数评价页岩的可压裂性. 侯冰等[6]建立了可压裂性关键评价指标体系,包含地质评价指标、体积压裂评价指标以及工程技术评价指标. 以上参考指标可用于有效构建页岩可压裂性评价模型,指导现场压裂施工. 作为可压裂性评价的重要内容,脆性评价可用于遴选可压裂性高的页岩[7, 8, 9, 10].
关于脆性的定义,国内外学者说法不一. Ramsey等[11]将脆性定义为材料发生脆性破坏时克服其本征内聚力的能力; Morley等[12, 13]认为脆性是指材料在破坏过程中塑性的缺失; Obert 和Duvall[8]采用岩石等材料进行试验,得出材料在加载过程中达到或稍超过其屈服强度的性质称为脆性;地质学学者则认 为脆性是用于描述材料在破坏前所发生塑性形变程度的性质[9]. 李庆辉等[10]通过页岩的实验研究,认为脆性反映了岩石的综合特性,是岩石在破坏过程中产生多裂缝面的能力. 以上从不同学科角度定义了脆性,然而大都是实验现象的体现,并没有从本质出发来定义脆性的概念,缺乏一定的理论依据.
目前有多种材料脆性评价方法[16, 17, 18]. Rickman等[19]提出的弹性参数法是较常用的脆性评价方法. 认为岩石的脆性主要受弹性模量和泊松比等弹性参数的影响,通过对Barnett页岩的经验总结,得出当泊松比越低、弹性模量越高, 岩石的脆性越好的结论,同时设计了一套脆性指数计算方法. 李庆辉\linebreak 等[7]认为岩石的矿物组成特征对脆性指数有一定的贡献,由此在Rickman的基础上,提出采用矿物组成特征、弹性模量 及泊松比三项指标来计算岩石的脆性指数. 然而,基于弹性参数以及矿物组成特征的脆性指数计算方法没有较可靠的理论依据,} 只是简单归一化后取平均值,且弹性参数只能反 映岩石在破坏前弹性阶段了性质,无法揭示体现岩石脆性的破坏全过程. 此外,李庆辉等[4]基于全应力应变曲线,考虑了岩石破坏的全过程,利用曲线峰前和峰后的力学特性来进行脆性评价. 然而,该理论分析计算过程中,仍对峰值应变采用简单的归一化处理,并结合经验公式得到综合脆性指数.
以断裂力学中能量的角度来定量分析岩石的脆性能获得较为可靠的结果. 由于可以把岩石塑性增大的趋势等同于能量耗散机制的作用 在逐渐增加[20],因此可将岩石的脆性评价与其能量耗散机制联系起来. 本文基于岩石破坏的能量耗散机制,重新定义了岩石的脆性以及脆度,并推导岩石在受压和受拉两种加载状态下的脆性指数, 对中国南方龙马溪组页岩进行实验研究与理论计算对比,验证本脆性评价方法的合理性.
1 基于能量耗散的脆性评价在断裂力学的研究中,Griffith[21]以经典力学和能量理论为基础,提出了裂纹扩展的判别依据. Irwin[22]对 Griffith的能量平衡概念作了进一步的推广,通过研究增加的表面能与释放的机械能之间的平衡关系,推导出用于判断理想脆 性裂纹何时扩展的热力学可靠判据. 然而,这些扩展所需的机械能一般都大于裂纹扩展后所增加的表面能.
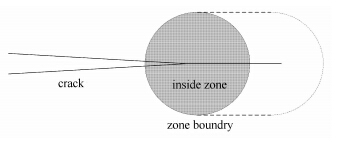
Irwin和Orowan[23]为了把非线性理论与不可逆性的组元搭建到线弹性断裂力学的框架中去,从数学的角度提出了将裂纹系 统划分为两个区域的构想,如图 1所示. 即将裂纹扩展系统的外区仍视为理想线弹性,而内区作为能量吸收过程的主要区域,其中包括了本征键破裂过程. 该理论的常见表达\linebreak 式[20]为
| \[R = 2{\gamma _{\text{B}}} + {R_{\text{P}}}\] | (1) |
当RP时,有R= R0 = 2γB. 此时,岩石属于理想脆性岩石,裂纹扩展所吸收的能量全部用于克服岩石的本征内聚力,即没有能量的耗散过程. 因此岩石在外 界提供的有限能量下,可获得表面能的极大值,从而使得裂纹在数量上和长度上达到最大值.
然而,几乎所有的岩石均有不同程度的塑性. 针对页岩储层岩石,尽管含有石英等脆性矿物,但还含有相当成分的黏土矿物, 这些黏土矿物反映了岩石的塑性,而且所含的石英等脆性矿物也存在一定的塑性. 因此,内区中的能量耗散项RP不能忽略,该项与岩石的本征内聚力项的相对大小反映了岩石的脆度.
通过上述理论分析,对岩石的脆性进行新的定义:岩石的脆性是表征岩石本征内聚力与其裂纹扩展过程中能量耗散项的相对大小, 反映岩石在破坏时不可逆过程的性质,是岩石塑性程度的体现.
当岩石的脆性较高时,能量耗散项与本征内聚力相比,相对较小. 此时,能量几乎转化为裂纹扩展所增加的表面能;当岩石的脆性较低时, 能量耗散项不能忽略,相对克服本征内聚力做功而言,岩石在破坏过程中存在着较大的能量耗散,即本征内聚力与能量耗散项的比值相对较小.
由此,笔者提出脆性指数的新定义:岩石的脆性指数为岩石本征内聚力与其在某种加载方式下破坏时裂纹扩展阻力的比值.
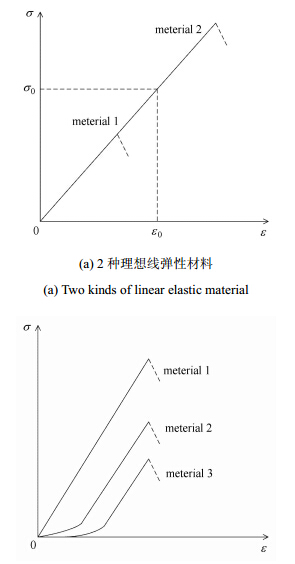
与这种基于能量耗散的脆性评价方法不同,弹性参数法仅考虑岩石破坏前弹性阶段的特征,而岩石的脆性体现在岩石破坏的过程中, 因此只是采用简单的弹性参数来描述岩石的脆性是存在一定问题的. 以下所列举几种材料应力应变关系曲线间的对比可以说明弹性参数法的问题所在. 如图 2(a)所示,材料1和材料2均为理想线弹性材料,具有相同的弹性模量和泊松比,两者采用弹性参数法计算得到的脆度一致. 然而,当加载到某一应力值σ0时,材料1已经发生破坏,而材料2远没有达到破坏的程度,显然这两种材料的脆度是不一样的. 再如图 2(b)所示,图中3种材料的弹性参数大小也十分接近,然而所反映的脆性特征截然不同.
|
图 2 不同材料的应力应变曲线对比图 Fig.2 Stress-strain diagram of different material |
弹性参数法所描述的是岩石破坏前的弹性阶段,在该阶段几乎没有产生塑性变形,只是反映了岩石在这一阶段内的弹性性质, 这与岩石的脆性无关.
综上分析,基于能量耗散的脆性评价反映了岩石破坏时的特征,其比弹性参数法更能有效表征岩石的脆性.
然而,上述理论模型只适用于内区尺寸很小的情况,且没有一套完善的能量耗散机制来确定裂纹的扩展阻力项. 这个模型只适用于 纯现象的描述.
Weertman[24]和Thomson[25]的研究为裂纹尖端屏蔽作用模型的提出打下了基石. 认为对远场外加应力的屏蔽过程即是能量 耗散的过程. 两类特殊的屏蔽构型(桥接界面和前端区)[20]可方便进行非理想韧性材料的断裂力学分析.
本文基于前端区这类屏蔽构型来进行能量耗散项与岩石脆度相结合的理论研究. 如图 3所示,裂纹尖端附加存在一个扩展的前端区,其对尾流区施加了持久的影响. 尾流区的宽度$w$给出了弹塑性边界,在边界外符合弹性变形的本构关系. 不可否认,前端区的形成伴随着岩石内部位错、层错等微观现象的发展,这些缺陷在运动过程中因抵抗晶格摩擦而产生的能量耗散 是不可逆的,这体现在尾流区内残余应变的形成. 对于这些微观现象的研究可以揭示岩石脆性的本质. 目前,有学者[26]采用分子动力学模拟的方法探究裂纹成核与扩展机理. 然而微观研究所涉及的分析过程复杂,实际应用性不强. 因此,本文从宏观断裂力学角度研究裂纹扩展前端区与脆性评价的作用关系,将内部缺陷视为产生能量耗散项的主要因素, 得到理论分析下的脆性评价计算模型,其更实用于页岩的可压裂性评价,指导现场压裂施工.
将前端区所产生的能量耗散项与岩石脆性指数一一对应,当岩石为理想脆性材料时,岩石的脆度达到最高,此时屏蔽对于能量耗散 的贡献为零;当岩石为理想塑性材料时,岩石的脆度达到最低,此时屏蔽区对于能量耗散的贡献最大,即释放的机械能几乎全部转化为 能量的耗散. 因此岩石的脆性指数以能量耗散项的大小体现出来[20]
| \[{R_\mu } = 2w\int_0^{{\varepsilon _\mu }} {{\sigma _\mu }\left( {{\varepsilon _\mu }} \right){\text{d}}{\varepsilon _\mu }} \] | (2) |
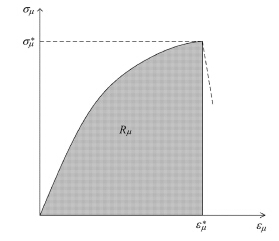
图 4给出了岩石在外加载荷作用下的应力应变函数曲线. 当σμ 达到极限应力值σμ*时,得到εμ 的积分上限为εμ*,代入式(2)中. 此时,处于稳定状态的前端区阻力为
| \[R_\mu ^\infty = 2w\int_0^{\varepsilon _\mu ^ * } {{\sigma _\mu }\left( {{\varepsilon _\mu }} \right){\text{d}}{\varepsilon _\mu }} \] | (3) |
|
图 4 应力-应变函数${\sigma _\mu }\left( {{\varepsilon _\mu }} \right)$ Fig.4 Stress-strain function ${\sigma _\mu }\left( {{\varepsilon _\mu }} \right)$ |
因此处于稳定状态的总稳态阻力为
| \[{R_\infty } = {R_0} + R_\mu ^\infty \] | (4) |
当岩石主要以受压应力作用时,这里仅考虑岩石的II型裂纹剪切破坏,根据裂纹尖端的弹性解,有[20]
| \[r\left( \theta \right) = \left( {1/2\pi } \right){\left[ {{K_{{\text{II}}}}{f_{xy}}\left( \theta \right)/{\tau _{xy}}} \right]^2}\] | (5) |
由远场应力状态可以求得裂纹表面受到的等效剪应力τe
| \[{\tau _{\text{e}}} = \tau _{xy}^\infty - f\sigma _y^\infty \] | (6) |
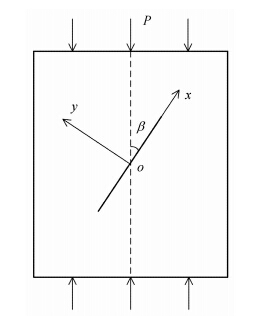
根据图 5的受力情况,当轴向应力P达到极限应力σμ*时,结合上式,可得到极限等效剪应力τe*
| \[\tau _{\text{e}}^ * = \sigma _\mu ^ * \left( {f{{\sin }^2}\beta - \cos \beta \sin \beta } \right)\] | (7) |
将处于平衡状态的条件 ${K_{{\text{II}}}} = {T_\infty }{\text{,}}{\tau _{xy}} = \tau _{\text{e}}^ * {\text{,}}r = w$代入式(5),得到
| \[w = {\Omega _{\text{D}}}{\left( {{T_\infty }/\tau _{\text{e}}^ * } \right)^2}\] | (8) |
若岩石在加载过程中的应力应变关系已由实验测得,则可计算出岩石在破坏前的平均应变能密度大小${\bar U_{\text{D}}}$,以及相应的各个岩石力学参数. 由此可计算总稳态阻力的表达式. 将${T_\infty } = {\left( {E'{R_\infty }} \right)^{1/2}}$结合式(4),式(8),得到近似的总稳态阻力表达式为
| \[{R_\infty } = {R_0}/\left( {1 - 0.04{{\bar U}_{\text{D}}}E'/\tau _{\text{e}}^{ * 2}} \right)\] | (9) |
| \[{R_0}/R_\mu ^\infty = \tau _{\text{e}}^{ * 2}/\left( {0.04{{\bar U}_{\text{D}}}E'} \right) - 1\] | (10) |
| \[{B_{\text{C}}} = {R_0}/R_\mu ^\infty \] | (11) |
利用深水孔隙压力伺服试验系统[7, 27, 28]进行三轴围压实验,可以方便地获取岩样在一定围压条件下,轴向应力与轴向应变的关系曲线以及达到破坏的极限应力,结合岩样在该围压条件下的岩石力学参数,可以根据式(10)和式(11) 直接求解得到 受压脆性指数BC.
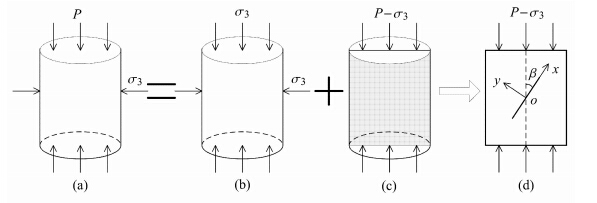
在图 6中,将三轴实验岩样的受力状态(a)分解为(b)和(c)两种情况,(b)种情况中,岩样受均匀应力作用,可以将这种均匀应力 作用仅视为对岩样性质的改变. (c)种情况中,岩样轴向受净压力的作用,围压为0. 为了研究的需要,可以将第一种情况等同为因围压作用而改变性质的岩样在轴向应力为P-σ3的单轴加载实验.
|
图 6 三轴围压实验模型分解示意图 Fig.6 Tri-axial confining loading model decomposition diagram |
假设裂纹在岩样的中间垂直平面内最先发生扩展,研究如图 6(d)所示的平面裂纹扩展,可以将其视为平面应力问题进行求解.
1.2 受拉伸状态脆性评价在巴西实验中,岩样主要以受拉伸的加载方式,这里仅考虑岩石的I型裂纹拉伸破坏,根据裂纹尖端的弹性解,有[20]
| \[r\left( \theta \right) = \left( {1/2\pi } \right){\left[ {{K_{\text{I}}}{f_{yy}}\left( \theta \right)/{\sigma _y}} \right]^2}\] | (12) |
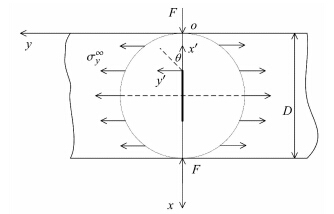
如图 7所示,巴西圆盘在对称载荷F的作用下,可推出圆周上的分布载荷[29, 30],经平面坐标变换,得到圆周上作用着均匀的拉应力σy∞,图中拉应力σy∞方向平行于y轴
| \[\sigma _y^\infty = \frac{{2F}}{{\pi Dl}}\] | (13) |
| \[\sigma _y^ * = \frac{{2{F^ * }}}{{\pi Dl}}\] | (14) |
| \[w = {\text{ }}{\Omega _{\text{D}}}{\left( {{T_\infty }/\sigma _y^ * } \right)^2}\] | (15) |
类似2.1中式(9)和式(10) 的推导过程,可得到受拉伸状态下的本征内聚力与前端区稳态阻力比值的表达式
| \[{R_0}/R_\mu ^\infty = \sigma _y^{ * 2}/\left( {0.014{\mkern 1mu} 4{{\bar U}_{\text{D}}}E'} \right) - 1\] | (16) |
同样定义新的岩石受拉脆性指数BS,使BS与上式比值相等,即
| \[{B_{\text{S}}} = {R_0}/R_\mu ^\infty \] | (17) |
从1.1和1.2的推导结果发现,不同加载方式下的材料脆性是有差异的,以下将通过实验分析两种加载方式下的脆性评价. 同时结合现场数据,对多种脆性评价方法对比分析,来验证基于能量耗散的脆性评价方法的可靠性以及实用性. 再者,围压对岩石的脆性指数存在一定的影响,因此有必要进行不同围压的三轴测试实验,分析两者间存在的关系.
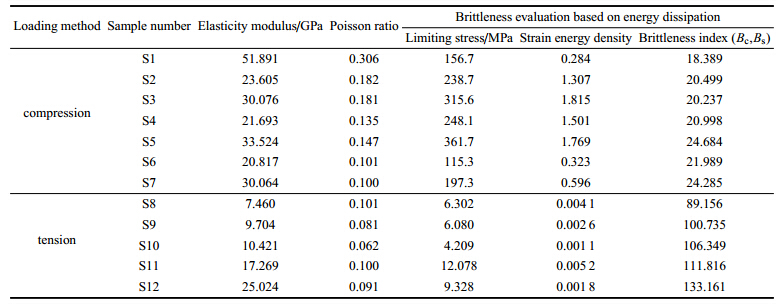
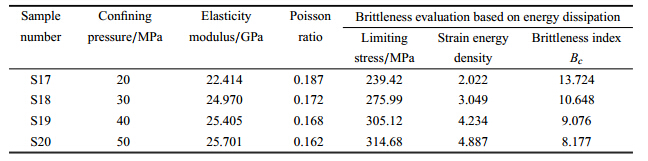
2 实验验证与分析 2.1 不同加载情况下的实例计算采用四川龙马溪页岩天然露头,分别进行受压和受拉两种加载方式的室内实验测试. 首先开展室内三轴围压试验,取7块岩样, 并将尺寸加工成:高50 mm,直径25 mm. 岩样均施加围压为35 MPa. 考虑到在相同层位上岩样具有相近的本征内聚力R0,可以进行相互间的脆性评价. 轴向加载过程中采用恒位移控制加载,并全程记录轴向、径向应变,采用基于能量耗散的泥页岩储层脆性评价 方法,计算受压状态下各岩样的脆性指数. 另一方面采用巴西实验试验机开展室内岩石拉伸破坏实验,另取5块岩样,制成一定厚度的圆 形截面,尺寸为:直径30 mm,厚度10 mm. 加载过程中同样全程记录其应力应变关系,最后计算受拉状态下的各岩样脆性指数. 以上两种加载方式的脆性评价结果如下表 1所示.
| 表 1 两种加载方式下的脆性评价结果表 Table 1 Results of brittleness evaluation under two kinds of different loading |
对比表 1中的极限应力可以明显发现,S1~S7的极限应力远大于S8~S12. 一般而言,岩石的抗拉强度明显低于其抗压强度,即岩石易发生拉伸破坏. 同时,将受拉脆性评价结果与受压脆性评价结果对比发现,受拉状态脆性指数BS显著大于受压状态脆性指数Bc,前者是后者的5倍之多. 说明岩石在拉伸过程中相对与压缩过程更偏向于脆性破坏,即在拉伸破坏过程中,岩石的塑性程度较低,裂纹扩展所耗散的能量较小,外界做功大部分最终转化为裂纹表面所增加的表面能.
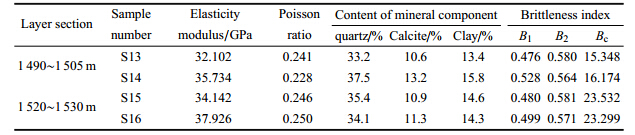
2.2 多种脆性评价方法的对比分析前人研究结果表明[7, 8, 9, 10, 31, 32, 33],岩石脆性越高,则在地层压裂的过程中越易形成较为复杂的裂缝网络, 从而能得到较高的页岩气产能. 对中国南方某页岩气井在埋深为1 480~1 540 m龙马溪组黑色页岩层段[7]进行分析. 该井该层段内进行了3段压裂测试. 压裂测试结果显示,在1 515~1 530 m井段内压力监测显示压力异常,且通过支持剂的注入 量可发现该层段产生的裂缝较多,压裂效果较其他层段更佳.
对该井1 490~1 505\,m和1 520~1 530 m层段取心,制成标准岩样进行室内三轴围压实验,采用弹性参数法、矿物组分法($B_2 = V_{\hbox{石英}} / (V_{\hbox{石英}} + V_{\hbox{方解石}} + V_{\hbox{ 黏土}} )\times 100\% $)以及基于能量耗散的脆性评价法计算这两个深度段的脆性指数分别为B1,B2,Bc,计算结果列入表 2.
| 表 2 3种脆性评价方法计算结果表 Table 2 Results of three different methods for brittleness evaluation |
计算结果显示,采用弹性参数法和矿物组分法计算得到的脆性指数B1,B2在这两个层段内均较为相近,不能反映实际压裂评价 结果. 而基于能量耗散的脆性评价结果显示下部层段岩石的脆性大于上部层段,即下部层段越易发生脆性破坏,压裂过程中能量耗 散少,从而能够形成较大规模的网状裂缝. 这与上述的压裂评价结果相吻合,证明了此种脆性评价方法的可靠性.
上述脆性评价结果分析结合1中的两种脆性评价方法的理论对比分析发现,弹性参数法存在如下几个问题:(1) 只考虑岩石破坏前的弹性参数不能完全反映岩石的脆性特征. 尤其是在受压加载过程中,岩石的塑性程度较高,这种岩石脆性随弹性参数变化的规律将不符合实际情况; (2) 岩石破坏的应力应变曲线上可以得到不同的弹性模量(初始模量、割线模量、切线模量),依据不同弹性模量值可以计算得到多个脆度值,这将对岩石的脆性评价结果产生较大影响;(3) 弹性参数法在计算方法上采用对弹性参数归一化后求平均值,没有一定的理论依据,其结果只能反映在弹性参数影响下的大致趋势. 同时,矿物组分法由于忽略了成岩作用等方面的因素,无法评价即使矿物组成相近,岩石的脆性差异显著的情况. 而基于能量耗散的泥页岩储层脆性评价方法针对岩石的整个破坏过程,其以断裂力学中裂纹扩展的能量耗散机制为理论依据,综合多方面因素,其脆性评价结果更能反映岩石的脆性.
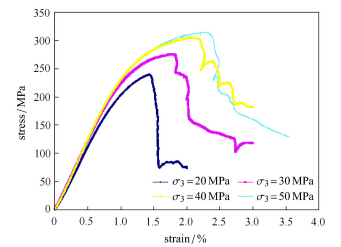
2.3 岩样在不同围压下的测试结果分析仍采用四川龙马溪页岩天然露头,对于同一块页岩露头在相同方向上取心进行三轴围压试验,岩样尺寸为:高50 mm,直径25 mm. 岩样分别施加围压为20 MPa,30 MPa,40 MPa,50 MPa. 测试在不同围压下的应力应变关系. 测试结果(见图 8)表明,岩样在加载过程中弹性模量和泊松比受围压的影响较小, 且由于在同一露头取心,岩样矿物组成相近,因此采用弹性参数法和矿物组分法计算的脆性指数在不同围压下几乎没有区别. 然而岩石在不同围压作用下,其脆性是有差异的,这又一次证明这两种方法存在一定的缺陷.
|
图 8 测试围压对应力应变关系的影响(σ3表示围压) Fig.8 Effect of confining pressure on stress-strain relationship (σ3 is confining pressure) |
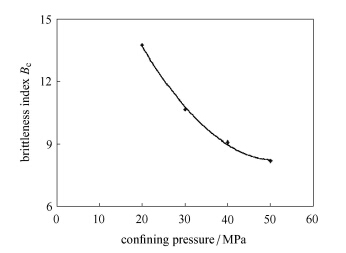
采用基于能量耗散的泥页岩储层脆性评价方法计算不同围压下的岩石脆性指数Bc,并将结果列为表 3. 围压与脆性指 数Bc的关系绘制在图 9中.
| 表 3 不同围压下岩石脆性指数Bc结果表 Table 3 Results of rock brittleness index Bc under different confining pressures |
|
图 9 围压与脆性指数Bc的关系 Fig.9 Relationship between confining pressure and brittleness index Bc |
图 9表明了岩样脆性指数随围压增大而减小的规律,也即在低围压下,岩石易表现为脆性,该结论与Paterson等[34]的研究结 果是一致的. 这是由于围压越大,岩石的塑性越强,因此岩石在破坏过程中,屏蔽区的作用效果越明显,所耗散的能量相对较高,导致脆性指数较低. 实验表明了岩石的脆性是岩石在围压作用下不同塑性程度的体现. 在围压很大的情况下,岩石的脆性指数趋向于零. 这解释了尽管深层岩石的脆性矿物组分含量较高,却因其在地下受高围压作用而不易被压裂.
3 结 论(1) 通过断裂力学裂纹扩展能量耗散机制的研究,对储层岩石的脆性以及脆性指数重新定义. 采用新的脆性指数计算方法定量评价储层岩石的脆性,分别从岩石受拉伸和受压缩两种状态进行推导,其结果反映了岩石的脆性指数受其破坏过程中应力应变关系的影响.
(2) 不同加载方式下的脆性评价实验研究表明,岩石在拉伸加载时的脆性指数远高于压缩加载时的计算结果,即岩石的拉伸破坏更接近于脆性破坏.
(3) 多种脆性评价方法对比,显示了弹性参数法只能大致反映塑性程度较低的岩石受拉破坏过程中的脆性变化规律,矿物组分法不能通过矿物成分的相对大小来反映脆性程度的高低,用这两种方法来进行岩石的脆性评价存在一定的缺陷. 而基于能量耗散的脆性评价方法具有可靠的理论依据,考虑岩石的整个破坏过程,综合了众多影响因素,其评价结果更能反映岩石的脆性.
(4) 储层岩石的脆性指数受围压的影响较为显著,表现为围压越大,岩石的塑性越强,破化时所耗散的能量越大,此时其脆性指数越低.
致 谢 本文在写作过程中得到中国石油大学(北京)石油工程学院研究生李丹丹以及郑小锦的帮助,在此致谢.| [1] | Chong KK, Grieser WV, Passman A. A completions guide book to shale-play development: A review of successful approaches toward shale-play stimulation in the last two decades. In: Proc. of Canadian Unconventional Resources and International Petroleum Conference, Calgary, Alberta, Canada, SPE133874, 2010 |
| [2] | Breyer JA, Alsleben H, Enderlin MB. Predicting fracability in shale reservoirs. AAPG Search and Discovery article, AAPG Hedberg Conference, Austin, Texas, December 5-10, 2010 |
| [3] | 蒋廷学,卞晓冰,苏瑗 等. 页岩可压性指数评价新方法及应用. 石油钻探技术,2014,42(5):16-20 (Jiang Tingxue, Bian Xiaobing, Su Yuan, et al. A new method for evaluating shale fracability index and its application. Petroleum Drilling Techniques, 2014, 42(5): 16-20 (in Chinese)) |
| [4] | 隋丽丽,杨永明,鞠杨 等. 岩石可压裂性分形描述方法初探. 力学与实践,2014,36(6):753-756 (Sui Lili, Yang Yongming, Ju Yang, et al. Fractal description of rock fracture behavior. Mechanics in Engineering, 2014, 36(6): 753-756 (in Chinese)) |
| [5] | 袁俊亮,邓金根,张定宇 等. 页岩气储层可压裂性评价技术. 石油学报,2013,34(3):523-527 (Yuan Junliang, Deng Jingen, Zhang Dingyu, et al. Acta Petrolei Ainica, 2013, 34(3): 523-527 (in Chinese)) |
| [6] | 侯冰,陈勉,王凯 等. 页岩储层可压性评价关键指标体系. 石油化工高等学校学报,2014,27(6):42-49 (Hou Bing, Chen Mian, Wang Kai, et al. The key index system of fracability evaluation in gas shale reservoir. Journal of Petrochemical Universities, 2014, 27(6): 42-49 (in Chinese)) |
| [7] | 李庆辉,陈勉,金衍 等. 页岩气储层岩石力学特性及脆性评价. 石油钻探技术,2012, 40(4):17-22 (Li Qinghui, Chen Mian, Jin Yan, et al. Rock mechanical properties and brittleness evaluation of shale gas reservoir. Petroleum Drilling Techniques, 2012, 40(4): 17-22 (in Chinese)) |
| [8] | 付永强,马发明,曾立新 等. 页岩气藏储层压裂实验评价关键技术. 天然气工业,2011,31(4):51-54+127 (Fu Yongqiang, Ma Faming, Zeng Lixin, et al. Key techniques of experimental evaluation in the fracturing treatment for shale gas reservoirs. Natural Gas Industry, 2011, 31(4): 51-54 (in Chinese)) |
| [9] | 李庆辉,陈勉,Wang FredP 等. 工程因素对页岩气产量的影响-以北美Haynesville页岩气藏为例. 天然气工业,2012,32(4):54-59 (Li Qinghui, Chen Mian,Wang FredP, et al. Influences of engineering factors on shale gas productivity: a case study from the Haynesville shale gas reservoir in North America. Natural Gas Industry, 2012, 32(4): 54-59 (in Chinese)) |
| [10] | 李庆辉,陈勉,金衍 等. 页岩脆性的室内评价方法及改进. 岩石力学与工程学报,2012,31(8):1680-1685 (Li Qinghui, Chen Mian, Jin Yan, et al. Indoor evaluation method for shale brittleness and improvement. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1680-1685 (in Chinese)) |
| [11] | Ramsay JG. Folding and Fracturing of Rocks. London: McGraw-Hill, 1967: 44-47 |
| [12] | Morley A. Strength of Materials. London: Longman Green, 1944: 71-72 |
| [13] | Heteny M. Handbook of Experimental Stress Analysis. New York: John Wiley, 1966: 23-25 |
| [14] | Obert L, Duvall WI. Rock Mechanics and the Design of Structures in Rock. New York: John Wiley, 1967: 78-82 |
| [15] | Jesse VH. Glossary of geology and related sciences. Washington D.C: American Geological Institute, 1960: 99-102 |
| [16] | Honda H, Sanada Y. Hardness of coal. Fuel, 1956, 35(4): 451-461 |
| [17] | Bishop A W. Progressive failure with special reference to the mechanism causing it. Proc Geotech Conf, Oslo, 1967, 2: 142-150 |
| [18] | Hucka V, Das B. Brittleness determination of rocks by different methods. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts Pergamon, 1974, 11(10): 389-392 |
| [19] | Rickman R, Mullen M, Petre E, et al. A practical use of shale petrophysics for stimulation design optimization: all shale plays are not clones of the Barnett Shale. SPE 115258, 2008 |
| [20] | Brain, Lawn. Fracture of Brittle Solids. New York, USA: The University of Cambridge, 1993. 50-59 |
| [21] | Griffith A A. The phenomena of rupture and flow in solids. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 1921: 163-198 |
| [22] | Irwin G R. Fracture in Handbuch Tier Physik, vol. VI, Flügge S (ed.). Göttingen, Heidelberg, Springer-Verlag Berlin, 1958: 557 |
| [23] | Orowan E. Energy Criteria of Fracture. Massachusetts Inst of Tech Cambridge Dept of Mechanical Engineering, 1954 |
| [24] | Weertman J. Fracture mechanics: a unified view for Griffith-Irwin-Orowan cracks. Acta Metallurgica, 1978, 26(11): 1731-1738 |
| [25] | Thomson R. Physics of Fracture. Atomistics of Fracture. US, Springer, 1983: 167-207 |
| [26] | Li D, Wang FC, Yang ZY, et al. How to identify dislocations in molecular dynamics simulations? Science China Physics, Mechanics & Astronomy, 2014, 57(12): 2177-2187 |
| [27] | 金衍,陈勉,周健 等. 岩性突变体对水力裂缝延伸影响的实验研究. 石油学报,2008,29(2):300-303 (Jin Yan, Chen Mian, Zhou Jian, et al. Experimental study on the effects of salutatory barrier on hydraulic fracture propagation of cement blocks. Acta Petrolei Sinica, 2008, 29(2): 300-303 (in Chinese)) |
| [28] | 金衍,陈勉,张旭东. 利用测井资料预测深部地层岩石断裂韧性. 岩石力学与工程学报,2001,20(4):454-456 (Jin Yan, Chen Mian, Zhang Xudong. Determination of fracture toughness for deep well rock with geophysical logging data. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 454-456 (in Chinese)) |
| [29] | 李世愚,和泰名,尹祥础. 岩石断裂力学导论. 合肥: 中国科学技术大学出版社, 2010:187-194 (Li Shiyu, He Taiming, Yin Xiangchu. Introduction of Rock Fracture Mechanics. Hefei: Press of University of Science and Technology of China, 2010: 187-194 (in Chinese)) |
| [30] | 徐芝纶. 弹性力学简明教程. 北京:高等教育出版社,2002:189 (Xu Zhilun. A Concise Course of Elastic Mechanics. Beijing: Higher Education Press, 2002: 189 (in Chinese)) |
| [31] | Hou B, Chen M, Li ZM, et al. Propagation area evaluation of hydraulic fracture networks in shale gas reservoirs. Petroleum Exploration and Development, 2014, 41(6): 833-838 |
| [32] | 金衍,陈勉,张旭东. 天然裂缝地层斜井水力裂缝起裂压力模型研究. 石油学报,2006,27(5):124-126 (Jin Yan, Chen Mian, Zhang Xudong. Hydraulic fracturing initiation pressure models for directional wells in naturally fractured formation. Acta Petrolei Sinica, 2006, 27(5): 124-126 (in Chinese)) |
| [33] | 侯冰,陈勉,程万 等. 页岩气储层变排量压裂的造缝机制. 岩土工程学报,2014,36(11):2149-2152 (Hou Bing, Chen Mian, Cheng Wan, et al. Fracturing mechanism of shale gas reservoir with variable pump rates. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 2149-2152 (in Chinese)) |
| [34] | Paterson M S, Wong T. Experimental Rock Deformation-the Brittle Field. Springer Science & Business Media, 2005 |
 2015, Vol. 47
2015, Vol. 47