水力压裂在工程领域具有十分重要的研究价值. 自上世纪中期以来, 水力压裂技术被石油公司广泛用于石油开采. 水力压裂不仅能增加油井产量, 还能提高油井净现值,实现经济效益. 近期, 水力压裂技术成功应用于页岩气的开采[1]. 尤其在美国, 水力压裂实现了一次页岩气革命.
在页岩气开采中,将压裂液通过高压泵注入井筒,当压力达到地层破裂压力时,将地层压开 (图 1). 此时, 继续保持压力并将压裂支撑剂注入到新形成的裂缝中,以防止裂缝闭合. 此后,页岩气将通过裂缝和井筒释放出来用以收集.
水力压裂技术在其他领域也有应用. 比如在地热工程[3]中,向地层注入低温水,通过天然地层加热, 再抽出高温水给人们供暖. 水力压裂也可能带来不良后果,如地下水的作用可能导致大坝出现裂缝并崩塌[4]. 又如在地球物理中,岩浆在地壳中的流动可能会导致岩体开裂并喷发出来[5],从而造成大规模的自然灾难.
因此,研究水力压裂问题不仅可使人类从中受益,而且还能避免灾难发生. 目前, 水力压裂研究方法包括理论法、数值法和试验法三类. 自20世纪50年代以来, 各国学者纷纷提出不同的理论模型,包括PKN模型[6, 7]、KGD模型[8]、P3D模型[9]和PL3D模型[10]等, 被广泛应用于油藏压裂模拟中. 这些模型通常事先假定扩展路径, 这种假设让模型计算不够准确. 因此,自20世纪80年代以来, 各种更为准确的数值方法纷纷被用来模拟水力压裂问题.
早期模拟水力压裂流行的方法当属位移不连续法 (displacement discontinuity method,DDM),它属于边界元法 (boundary element method,BEM) 的一种[11]. Lecampion和Detournay[12]使用位移不连续法模拟了水力压裂过程. 之后Lecampion[13]又使用扩展有限元法 (extended finite element method,XFEM) 模拟了裂纹尖端在任意给定时刻的发展过程. Dahi-Taleghani[14]使用扩展有限元法研究了有交叉裂缝的压裂过程. Hunsweck等[15]使用有限元法 (finite element method,FEM) 模拟了有流体滞后效应的压裂过程. 近年来的热门数值方法包括: 基于有限元的内聚力模型法 (cohesive zone model) [16, 17]、损伤模型法[18]、裂缝化单元法 (fractured element method) [19, 20],基于边界元的非常规裂缝法 (unconventional fracture method,\linebreak UFM) [21]和基于颗粒的方法[22, 23, 24]等.
以上数值模型可分为两类: 一类是基于连续介质力学的方法,另一类是基于非连续介质力学的方法. 两类方法各具特色: 连续介质方法求解应力场准确,非连续方法求解任意裂纹扩展更有优势. 因此,本文使用有限元和离散元的混合方法 (CDEM) [25, 26, 27, 28]来模拟水力压裂问题. CDEM是连续-非连续单元法 (continuous-discontinuous element method) 的简称,是近期发展起来的一种数值计算方法. 计算时,求解区域被离散为块体单元, 每个块体单元可以是一个有限单元,也可以分为多个有限单元. 根据有限单元刚度矩阵,可写出任意块体的刚度矩阵, 而块体之间不组成总体刚度矩阵. 然后采用动态松弛技术来求解各个块体单元的位移、应变和应力等变量. 此外, 裂缝内渗流场由有限体积法进行求解 (finite volume method,FVM) [29, 30]. 该耦合方法可集成各个数值方法的优势,并提高计算效率.
1 固体计算模型 1.1 应力场计算对于计算域内的每一个块体或单元,应满足应力平衡方程
| \[\rho \mathop u\limits^{..} + \alpha \mathop u\limits^. = \nabla \cdot \sigma + \rho b + f\] | (1) |
应力-应变关系为
| \[\sigma = D:\varepsilon \] | (2) |
几何关系为
| \[\varepsilon = \frac{1}{2}(u\nabla + \nabla u){\text{ }}\] | (3) |
通过变分法,将式(1)化为单元矩阵形式
| \[M{\ddot u^e} + C{\dot u^e} + K{u^{\text{e}}} = {F^{\text{e}}}\] | (4) |
在时间域内,采用显式差分进行迭代求解,迭代格式为
| \[\left. \begin{gathered} {{\dot u}^{n + 1}} = {{\dot u}^n} + {{\ddot u}^n}\Delta t \hfill \\ {u^{n + 1}} = {u^n} + {{\dot u}^{n + 1}}\Delta t \hfill \\ \end{gathered} \right\}\] | (5) |
相邻块体之间依靠接触连接 (图 2),每一个接触由一个法向弹簧和一个切向弹簧组成 (图 3). 采用的破坏准则为最大拉应力准则或摩尔-库伦准则. 相邻块体接触点的相对位移与弹簧力之间满足胡克定律
| \[\Delta {u_{\text{n}}} = \frac{{{F_{\text{n}}}}}{{{K_{\text{n}}}}} = \frac{{({\sigma _{{\text{n}}1}} + {\sigma _{{\text{n2}}}})A}}{{2{K_{\text{n}}}}}\] | (6) |
| \[\Delta {u_{\text{t}}} = \frac{{{F_{\text{t}}}}}{{{K_{\text{t}}}}} = \frac{{({\sigma _{{\text{t}}1}} + {\sigma _{{\text{t}}2}})A}}{{2{K_{\text{t}}}}}\] | (7) |
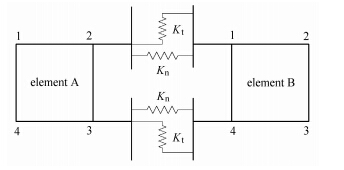
|
图 3 一个二维接触由两个弹簧组成 Fig.3 A 2D contact consists of two springs |
由连续的单元边界面转化为非连续断裂面的计算方法如下所述. 计算单元界面两侧单元应力, 并计算出在单元边界上的法向和切向应力,如果其中一个单元的应力满足下列破坏条件,则单元界面断裂,产生水力裂缝
| \[{\sigma _{\text{n}}}T\] | (8) |
| \[{\sigma _{\text{t}}}c + {\sigma _{\text{n}}}\tan \varphi \] | (9) |
若弹簧满足最大拉应力准则(8),则弹簧发生拉伸破坏,此时弹簧力需要修正为
| \[{F_{\text{n}}} = 0{\text{ }}\] | (10) |
若断裂面上的受力状态,满足摩尔-库伦剪切破坏条件(9),则弹簧力需要修正为
| \[{F_{\text{t}}} = {F_{\text{n}}}\tan \varphi \] | (11) |
弹簧断裂之后,裂缝开度可通过弹簧所连接两端的节点位移差求得
| \[w = {\text{|}}({u_1} - {u_2}) \cdot {n_{12}}|\] | (12) |
裂缝中的渗流满足方程
| \[\frac{1}{{{K_{\text{f}}}}}\frac{{\partial p}}{{\partial t}} - \nabla \cdot \left( {\frac{{{w^2}}}{{12\mu }}\nabla p} \right) = q\] | (13) |
采用中心型有限体积法[29, 30]对式(13)进行数值求解,计算原理如图 4所示.
|
图 4 FVM计算原理图 Fig.4 Principle diagram of the FVM |
根据文献[29, 30]可得相邻两个单元之间的流量与两个单元压力差之间的关系为
| \[{Q_{ij{\text{ }}}} = {\text{ }}{T_{ij}}({p_i} - {p_j})\] | (14) |
| \[{T_{ij}} = \frac{{2{\kappa _i}{\kappa _j}}}{{{\kappa _i}{L_j} + {\kappa _j}{L_i}}}\] | (15) |
| \[{\kappa _i} = \frac{{w_i^3}}{{12\mu }}\] | (16) |
对式(13)在时间域上进行离散,可得
| \[{p_i} = {K_{\text{f}}}(1 - \frac{{{V_i}}}{{{Q_i}}})\] | (17) |
| \[{Q_i} = {Q^{{\text{ext}}}} - \sum\limits_{_j} {{Q_{ij}}} \] | (18) |
水力压裂计算流程如图 5所示,整个计算流程大体可分为3个部分:
(1) FEM计算应力场
包括计算节点加速度、节点速度、节点位移与节点力等.
(2) DEM计算裂缝网络
包括计算弹簧力,调用断裂准则判断是否断裂,更新裂缝网络,计算裂缝开度等.
(3) FVM计算渗流场
包括计算流量、压力等.
以上三场分别通过3个求解器进行求解,彼此之间相互独立. 它们通过数据传递进行联系,实现显式求解过程. 数据交换表明它们之间的耦合关系.

|
图 5 水力压裂计算流程 Fig.5 Flow chart for hydraulic fracturing simulation |
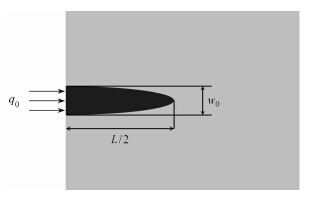
采用KGD模型 (如图 6所示) 进行数值验证,KGD模型假设: (1) 缝高是固定的; (2) 符合平面应变假设; (3) 缝内流体流动符合光滑平板流假设.
|
图 6 KGD模型示意图 Fig.6 Schematic diagram of the KGD model |
由此,Geertsma和de Klerk[8]导出KGD模型中缝长L、井口处缝宽w0随时间t演化关系. 此外,Dahi-Taleghani[14],Valko和Economides[32]及Fu等[33]也给出这两个公式
| \[L(t) = 2 \times 0.539{\left( {\frac{{E'q_0^3}}{\mu }} \right)^{1/6}}{t^{2/3}}\] | (19) |
| \[{w_0}(t) = 2.36{\left( {\frac{{\mu q_0^3}}{{E'}}} \right)^{1/6}}{t^{1/3}}\] | (20) |
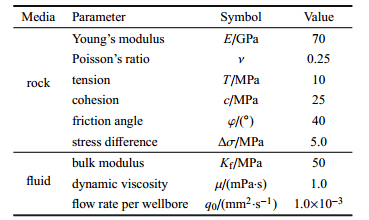
采用100m × 100m的计算区域,如图 7所示,计算网格数分别为细网格7378个,粗网格5620个.假定裂缝从两个不同颜色的交界面产生. 这两个不同颜色的区域具有相同 的计算参数,参数见表 1.

|
图 7 KGD模型计算网格 (a) 细网格 (b) 粗网格 (a) Fine mesh (b) Coarse mesh Fig.7 Mesh for simulation of the KGD model |
| 表 1 KGD模型数值模拟参数 Table 1 Parameters for simulation of the KGD model |
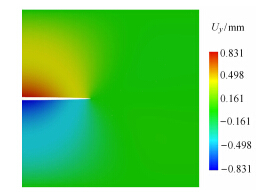
KGD模型中,只有一条拉伸裂缝,不发生剪切破坏,因此计算中c和φ均取一个较大的数. 使用细网格计算得到的裂缝形 状如图 8所示.
|
图 8 t= 50s时y方向位移 Fig.8 y-displacement at t= 50s |
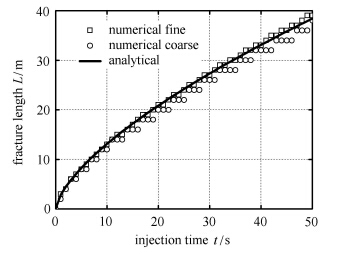
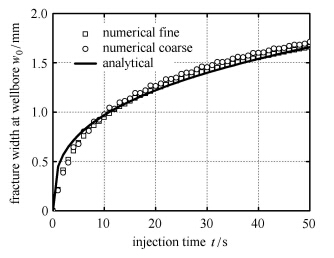
计算数值解与KGD理论解的对比如图 9和图 10所示. 图 9为裂缝长度随时间的变化,图 10为裂缝宽度随时间的变化. 由图 9和图 10可以看出,不管是粗细网格,使用本文提出的混合方法所计算出的数值解与KGD模型的理论解均基本相符, 从而验证本文数值方法的正确性. 但是从两张图中也可以看出,数值解与理论解之间尚存在微小的差异.
|
图 9 半缝长数值解与理论解对比 Fig.9 Comparison between numerical and analytical results in terms of half fracture length |
|
图 10 井口处缝宽数值解与理论解对比 Fig.10 Comparison between numerical and analytical results in terms of fracture width at wellbore |
图 9中采用粗网格(coarse)计算裂缝长度具有跳动性,而不像解析解那样光滑. 图 10中采用粗网格计算裂缝宽度在开始时比理论解小,后期较大. 采用细网格(fine)计算后,图 9和图 10中的数值解与理论解符合更好. 这说明: 数值计算具有网格尺寸效应,越加密的网格,计算结果就会越接近理论解.
值得一提的是,涉及到流固耦合问题的计算是非常耗时的,该算例中细网格数目为7378个,在CPU i7 3770上的计算时间达到10h.
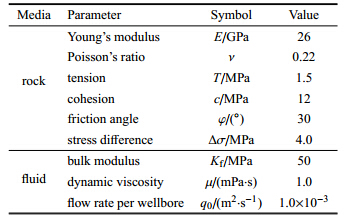
4.2 与数值计算结果对比采用图 11所示计算模型进行数值计算,计算区域为200mm × 200mm,中间压裂孔直径为20mm. 采用Gmsh[34]划分网格,网格数量为3952个. 计算区域受到两向压应力作用,分别为σx= -10.0MPa, σy= -5.0MPa. 该模型中模 拟的是花岗岩的水力压裂过程,其计算参数如表 2所示.
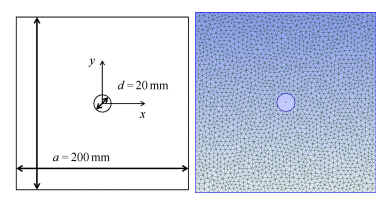
|
图 11 数值计算模型 (a) 几何区域 (b) 计算网格 (a) Area (b) Mesh Fig.11 Numerical simulation model |
| 表 2 花岗岩水力压裂计算参数 Table 2 Simulation parameters of fracturing simulation of granite |
为节省计算时间,假设初始时刻压裂孔内充满流体,且裂隙内具有初始压力p0= 8MPa. 计算得到井口处 (坐标x=-10mm,y=0mm) 压力随时间变化曲线,如图 12所示. 压力曲线呈现先上升,然后波动的趋势,曲线最高点即为岩体的破裂时刻.
从图 12中的原始数据可知,所计算岩体的破裂压力为15.7MPa,相同参数下Shimizu等[22]通过颗粒离散元法模拟结果 (文中Case B3-low) 为17.3MPa. 两者相差-9%,说明模拟结果较准确.
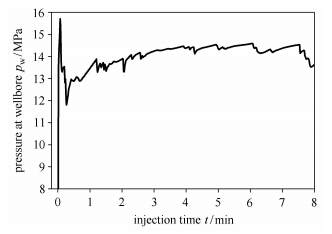
|
图 12 井口处压力时间曲线 Fig.12 Pressure versus time at wellbore |
最终的压裂裂缝形态如图 13所示. 图 13(a)中,井筒在初始时受到水压作用,产生圆环状破裂. 随着流体进一步注入, 裂缝沿着平行于最大压应力的方向向两侧扩展. 裂纹扩展位置和方向, 与Shimizu等[22]给出的颗粒离散元计算结果相近,如图 13(b). 不同之处在于: Shimizu等[22]的结果中井筒附近岩体较完整,而远离井筒的地方出现了若干小的分支裂缝;本文模拟结果中井筒附近产生破裂,而远离井筒的地方裂缝单一.
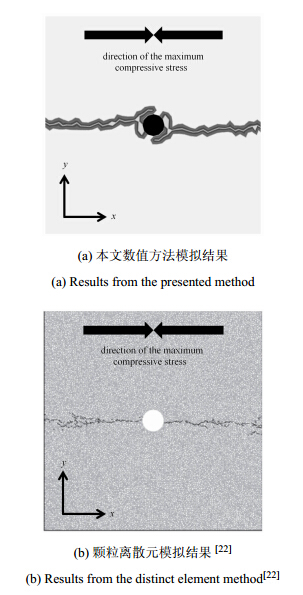
|
图 13 最终压裂裂缝对比 Fig.13 Comparison of ultimate hydraulic fractures |
计算模型采用图 14中含天然裂缝水平井分段压裂模型. 该模型中含有一组天然裂缝,平均缝长为10m, 裂缝与水平方向倾角平均值为6°,裂缝之间的竖向间距平均为15m,相邻水平裂缝间距约为10m. 计算时采用水平井分段同步压裂技术,1,2,3为3个同步压裂射孔位置,射孔间距为20m. 整个模型的尺寸为80m × 120m. 使用Gmsh[34]划分网格,网格尺寸为2m,网格数量为6801个. 计算边界条件为水平地应力σh和竖向地应力 σv约束,以及3个射孔的流量边界q0. 由于计算采用线弹性本构模型,符合叠加原理. 故计算模型取σh =0,σv=Δσ 为两向地应力之差. 其他计算参数如表 3所示.
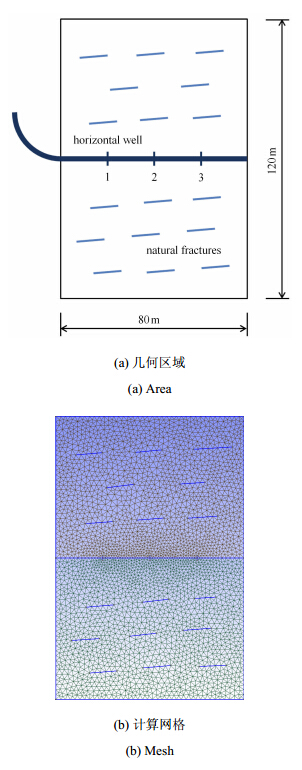
|
图 14 含天然裂缝分段压裂模型 Fig.14 Staged fracturing model with natural fractures |
| 表 3 分段压裂数值模拟参数 Table 3 Parameters for simulation of staged fracturing |
通过数值模拟可以获得各种测井信息,如井口处压力曲线,如图 15所示. 从曲线中可看出井口压力具有很大的波动,这是由于裂缝的动态扩展导致的. 当裂缝内压力不足以导致裂缝扩展时,流体压力上升,当发生断裂时,流体迅速流出, 导致压力下降. 这个压力动态波动过程一定程度可以反映裂缝扩展情况.

|
图 15 3个井口处压力曲线 Fig.15 Pressure at the three wellbores |
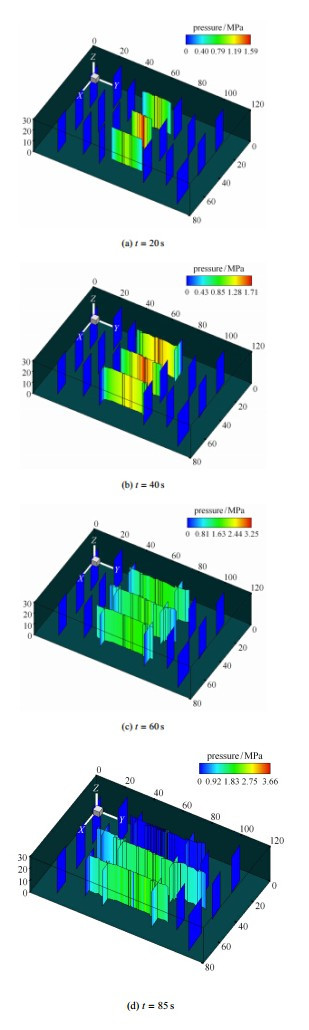
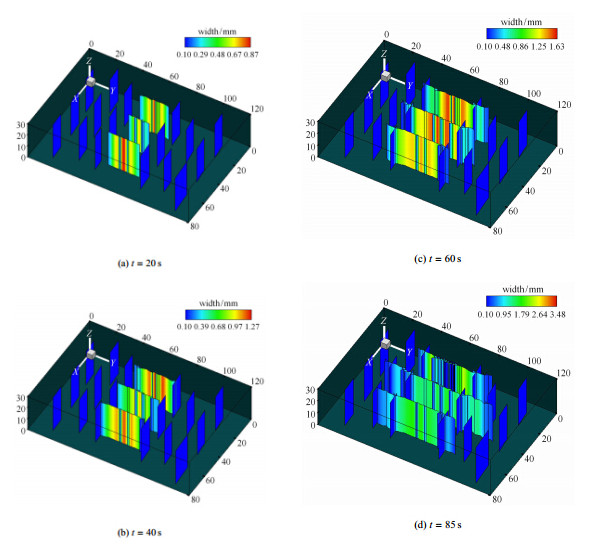
为了更清晰地显示裂缝压力和开度云图,将模型拉伸为准三维模型, 拉伸方向为z方向,拉伸深度为30m. 拉伸后的裂缝压力云图以及裂缝宽度云图分别如图 16和图 17所示.
|
图 16 裂缝内净压力云图 Fig.16 Contour of net pressure in fracture |
|
图 17 裂缝开度云图 Fig.17 Contour of fracture width |
从图 16和图 17中可以看出,3个射孔点1,2,3分别压裂出3条主裂缝,我们分别称之为HF1,HF2和HF3. 3条裂缝扩展并非齐头并进,而是有快有慢.
刚开始时 (图 16(a)和图 17(a),对应于t = 20s之前) HF2的扩展受到周围两条裂缝的影响,扩展速度较慢. 这是由于HF1和HF3扩展后,水压力作用于裂隙面上,使得HF1和HF3之间区域的压应力变大,因此HF2扩展变得相对困难. 然后 (图 16(b)和图 17(b),t=20s之后),HF3率先与天然裂缝贯通, 导致部分流体流量分配给天然裂缝,这时应力场释放,HF2扩展速度变快,形成3条裂缝并驾齐驱的态势. 再到后来 (图 16(c)和图 17(c),t=40s之后) 3条裂缝均与天然裂缝贯穿,应力场进一步改变. 最后 (图 16(d)和图 17(d),t= 85s之前),中间裂缝HF2继续向前发展,但HF1由于计算区域边界效应扩展出分支缝.
通过对比观察图 15~图 17进一步发现,图 15中井口1在60s之后压力出现快速下降趋势. 这是由于裂缝HF1此时与两侧天然裂缝均产生贯通,导致大量流体流走,从而使得井口压力迅速下降. 井口2的压力整体上一直处于上升趋势,这是由于周围两口井的压力导致的. 与上述过程中HF2裂缝在t= 20s后出现缓慢增长有相同的原因. 井口3在75s后压力迅速下降,这是由于裂缝HF3与3条天然裂缝贯穿所导致的.
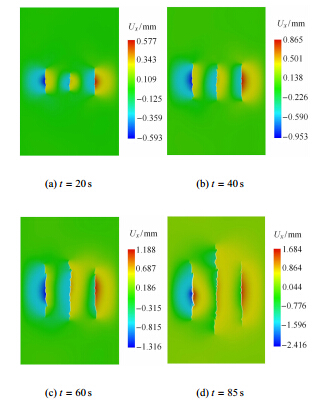
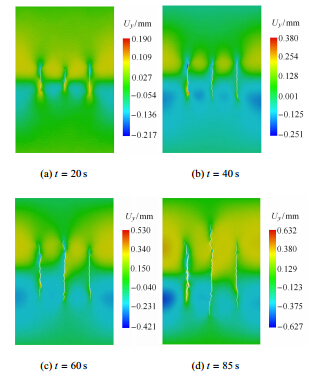
通过观察以上压力曲线、压力云图、开度云图等可以发现裂缝扩展机理,了解整个水力压裂过程的进程. 此外, 还可以通过观察二维云图,来分析水力裂缝的扩展,包括2个方向的位移云图、3个方向的应变云图以及3个方向的应力云图. 图 18所示为不同时刻的x方向位移云图. 通过该图可看出,在两向应力差Δσ 的影响下, 水力裂缝基本沿着垂直于最小压应力的方向扩展. 由于网格的随机性,水力裂缝产生了细小的弯曲. 此外, 由于应力场的变化,也导致裂缝发生一定转向. 图 18(d)中可看出, 裂缝HF1以及裂缝HF3的上下两端均发生明显的向外侧弯曲现象. 这也符合Kresse等[21]在非常规裂缝模型中的模拟结果. 图 19所示为不同时刻的y方向位移云图, 一定程度上反映裂缝两侧剪切位移情况. 从该图可以看出y方向位移比x方向位移小,说明图示裂缝主要以拉伸缝为主.
|
图 18 不同时刻x方向位移云图 Fig.18 Contour of x-displacement at different time |
|
图 19 不同时刻y方向位移云图 Fig.19 Contour of y-displacement at different time |
本文基于连续-非连续单元法 (CDEM) 和中心型有限体积法 (FVM), 提出解决水力压裂流固耦合的二维混合数值计算模型. 该混合模型使用CDEM求解应力场和裂缝扩展过程, 使用FVM求解裂隙渗流场. 应力场、裂缝扩展和渗流场均使用显式迭代求解,并通过彼此之间数据交换实现流固耦合. 此外, 还给出整个水力压裂的计算流程,实现了复杂裂隙网络的水力压裂数值模拟.
通过与KGD水力裂缝扩展理论解对比,裂缝扩展长度与宽度均符合较好, 从而验证本文数值模型正确性. 并通过比较粗、细网格上的数值计算结果, 说明网格尺寸效应. 然后通过与相同参数下Shimizu等的颗粒离散元计算结果进行对比, 破裂压力与裂缝形态整体相符,但存在微小差异,仍可验证本文数值方法的有效性.
初步计算一个含有天然裂缝网络的水平井多段水力压裂案例, 阐述了整个压裂过程中的现象,并研究其压裂机理. 研究表明: 裂缝扩展受整个应力场改变影响很大,会因应力场改变而发生很明显的路径改变, 如图 18中裂缝的转弯; 此外,压裂井口的压力一定程度可以反映裂缝扩展情况. 该案例说明本文数值模型在水力压裂方面具有光明的前景.
本文数值模型的优点是计算准确, 并充分发挥有限元法、离散元法和有限体积法的优势,适用于水力压裂机理研究. 该模型的缺点是计算量大,计算时间较长,有望通过并行化提高计算效率, 从而实现工程级别应用.
| [1] | Gregory KB, Vidic RD, Dzombak DA. Water management challenges associated with the production of shale gas by hydraulic fracturing. Elements, 2011, 7(3): 181-186 |
| [2] | 华油能源集团. 连续油管水力喷砂压裂. http://www.spt.cn/templates/T_XWZX/index.aspx?nodeid=95&page=ContentPage&contetentid=119, 2015-02-11 |
| [3] | Legarth B, Huenges E, Zimmermann G. Hydraulic fracturing in a sedimentary geothermal reservoir: Results and implications. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(7): 1028-1041 |
| [4] | Simoni L, Secchi S. Cohesive fracture mechanics for a multi-phase porous medium. Engineering Computations, 2003, 20(5-6): 675-698 |
| [5] | Rubin AM. Propagation of magma-filled cracks. Annual Review of Earth and Planetary Sciences, 1995, 23: 287-336 |
| [6] | Perkins TK, Kern LR. Widths of hydraulic fractures. Journal of Petroleum Technology, 1961, 13(9): 937-949 |
| [7] | Nordgren RP. Propagation of a vertical hydraulic fracture. SPE Journal, 1972, 12(4): 306-314 |
| [8] | Geertsma J, de Klerk F. Rapid method of predicting width and extent of hydraulically induced fractures. Journal of Petroleum Technology, 1969, 21: 1571-1581 |
| [9] | Settari A, Cleary MP. Development and testing of a pseudo-three-dimensional model of hydraulic fracture geometry. SPE Production Engineering, 1986, 1(6): 449-466 |
| [10] | Siebrits E, Peirce AP. An efficient multi-layer planar 3D fracture growth algorithm using a fixed mesh approach. International Journal for Numerical Methods in Engineering, 2002, 53(3): 691-717 |
| [11] | Crouch SL, Starfield AM. Boundary Element Methods in Solid Mechanics. London: Unwin & Hyman, 1990 |
| [12] | Lecampion B, Detournay E. An implicit algorithm for the propagation of a hydraulic fracture with a fluid lag. Computer Methods in Applied Mechanics and Engineering, 2007, 196: 4863-4880 |
| [13] | Lecampion B. An extended finite element method for hydraulic fracture problems. Communications in Numerical Methods in Engineering, 2009, 25: 121-133 |
| [14] | Dahi-Taleghani A. Analysis of hydraulic fracture propagation in fractured reservoirs: an improved model for the interaction between induced and natural fractures. [PhD Thesis]. University of Texas at Austin, 2009 |
| [15] | Hunsweck MJ, Shen Y, Lew AJ. A finite element approach to the simulation of hydraulic fractures with lag. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(9): 993-1015 |
| [16] | Carrier B, Granet S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Engineering Fracture Mechanics, 2012, 79: 312-328 |
| [17] | Chen Z, Bunger AP, Zhang X, et al. Cohesive zone finite element-based modeling of hydraulic fractures. Acta Mechanica Solida Sinica, 2009, 22(5): 443-452 |
| [18] | Wang SY, Sun L, Au ASK, et al. 2D-numerical analysis of hydraulic fracturing in heterogeneous geo-materials. Construction and Building Materials, 2009, 23(6): 2196-2206 |
| [19] | Wangen M. Finite element modeling of hydraulic fracturing on a reservoir scale in 2D. Journal of Petroleum Science and Engineering, 2011, 77(3): 274-285 |
| [20] | Wangen M. Finite element modeling of hydraulic fracturing in 3D. Computational Geosciences, 2013, 17(4): 647-659 |
| [21] | Kresse O, Weng X, Gu H, et al. Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations. Rock Mechanics and Rock Engineering, 2013, 46(3): 555-568 |
| [22] | Shimizu H, Murata S, Ishida T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(5): 712-727 |
| [23] | Deng S, Li H, Ma G, et al. Simulation of shale-proppant interaction in hydraulic fracturing by the discrete element method. International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 219-228 |
| [24] | Wang T, Zhou W, Chen J, et al. Simulation of hydraulic fracturing using particle flow method and application in a coal mine. International Journal of Coal Geology, 2014, 121: 1-13 |
| [25] | Li SH, Zhao MH, Wang YN, et al. A new numerical method for DEM-block and particle model. International Journal of Rock Mechanics and Mining Sciences, 2004, 41: 414-418 |
| [26] | Li SH, Liu XY, Liu TP, et al. Continuum-based discrete element method and its applications. In: Proceedings of UK-China Summer School/International Symposium on DEM, Beijing, China, 2008, 147-170 |
| [27] | Wang LX, Li SH, Zhang GX, et al. A GPU-based parallel procedure for nonlinear analysis of complex structures using a coupled FEM/DEM approach. Mathematical Problems in Engineering, 2013, Article ID 618980: 1-15 |
| [28] | 王杰, 李世海, 张青波. 基于单元破裂的岩石裂纹扩展模拟方法. 力学学报, 2015, 47(1): 105-118 (Wang Jie, Li Shihai, Zhang Qingbo. Simulation of crack propagation of rock based on splitting elements. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(1): 105-118 (in Chinese)) |
| [29] | Wang LX, Li SH, Ma ZS. A finite volume simulator for single-phase flow in fractured porous media. In: Proceedings of the 6th International Conference on Discrete Element Methods and Related Techniques. Colorado School of Mines, Golden, CO, 2013: 130-135 |
| [30] | 王理想, 李世海, 马照松 等. 一种中心型有限体积孔隙-裂隙渗流求解方法及其OpenMP并行化. 岩石力学与工程学报, 2015, 34(5): 865-875 (Wang Lixiang, Li Shihai, Ma Zhaosong, et al. A cell-centered finite volume method for fluid flow in fractured porous media and its parallelization with OpenMP. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 865-875 (in Chinese)) |
| [31] | 刘洋, 李世海, 刘晓宇. 基于连续介质离散元的双重介质渗流应力耦合模型. 岩石力学与工程学报, 2011, 30(5): 951-959 (Liu Yang, Li Shihai, Liu Xiaoyu. Coupled fluid flow and stress computation model of dual media based on continuum-medium distinct element method.Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 951-959 (in Chinese)) |
| [32] | Valko P, Economides MJ. Hydraulic Fracture Mechanics. New York: Wiley, 1995 |
| [33] | Fu P, Johnson SM, Carrigan CR. An explicitly coupled hydro-geomechanical model for simulating hydraulic fracturing in arbitrary discrete fracture networks. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(14): 2278-2300 |
| [34] | Geuzaine C, Remacle JF. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. International Journal for Numerical Methods in Engineering, 2009, 79(11): 1309-1331 |
 2015, Vol. 47
2015, Vol. 47