2. 中国石油长城钻探工程公司, 北京 100101
页岩储层体积压裂的影响因素很多,外因主要是页岩储层水平主应力的差值,内因主要是页岩储层的脆性系数[1, 2]. 脆性系数是岩石的固有系数,一般无法人为改变,但可以通过采取一定的措施,改变储层水平主应力差值,为缝网结构的产生创造条件.
地层原始应力场特别是初始水平两向主应力差值控制着体积裂缝的形成,当水平最大主应力与水平最小主应力差值较小或相等时,容易形成体积裂缝,反之不易形成体积裂缝[3, 4, 5, 6, 7, 8, 9]. 对于大部分页岩储层,水平两向主应力不相等且相差较大,采用普通分段分簇压裂方法无法产生缝网,因此应探索采取合适的压裂措施,减弱甚至翻转地层水平两向主应力,借助压裂过程中地层的应力释放裂缝形成复杂缝网[10, 11, 12, 13, 14, 15].
国内外很多学者对页岩储层体积压裂的研究作出过贡献,特别是近10年来国内外学者对页岩气体积压裂技术研究的广度和深度都有很大的 提高[16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27].
2010年,Soliman等[16]在Sneddon提出的理论基础上,针对脆性页岩储层,提出了两种产生缝网结构的方法,一种是"Commuter Frac"压裂方法,另一种是"Texas Two-Step"压裂方法.
Roussel和Sharma[17]采用理论分析和数值模拟的方法研究了水平井分段压裂过程中地层应力场的分布和变化情况,给出了裂缝扩展净压力和裂缝条数之间的关系,并给出了压裂过程中裂缝的扩展引起的地层主应力场的方向改变的结果.
雷群等[18]提出了适合低孔隙度、低渗透、不含天然裂缝储层的"缝网压裂"技术. 其核心思想是利用储层两个水平主应力差值与裂缝延伸净压力的关系,实现远井地带(而不仅仅局限于近井筒区域)的"缝网"效果,增加储层基质向人工裂缝供油气能力,提高压裂增产改造效果. 论述了"缝网压裂"技术的适用条件、工艺设计思路及应用方法.
陈作等[19]在总结分析美国页岩气储层的岩性、物性、天然裂缝与力学性质特征的基础上,依据复杂裂缝形成机理,提出了压裂形成复杂缝网、增大改造体积的基本地层条件的观点,归纳了直井和水平井体积压裂改造工艺技术方法等.
翁定为等[20]完善了页岩气藏缝网压裂的概念,指出缝网压裂是在达到预期目标支撑缝长的主裂缝基础上,形成多缝直至形成"缝网"系统. 对不同类型的储层,根据弹性力学理论,给出了缝网形成的力学条件. 指出了缝网压裂的实现方法,即通过控制施工净压力实现缝网压裂. 当人工主裂缝的净压力大于水平主应力差值和岩石抗张强度之和后,可在原始裂缝的基础上形成新裂缝,产生缝网.
上述所有模型都没有模拟压裂过程中地层应力场的变化,也没有给出模拟结果和理论计算的对比分析,在体积压裂的力学条件研究领域仍认识不足,无法满足指导现场施工的要求.
本文拟采用理论分析和数值模拟相结合的方法,模拟压裂过程中地层应力场的变化,研究"Texas Two-Step"压裂方法缝网形成的力学机理. 对于采用"Texas Two-Step"压裂方法无法形成缝网的高应力差储层,拟采用新型的应力"共振"压裂方法,并验证此压裂方法的正确性和适应性.
1 基于应力变化理论的"Texas Two-Step"压裂方法Sneddon在1946年研究了水力裂缝的产生引起的地层应力场的变化,得到了水力裂缝附近地层任意一点裂缝诱导应力的计算公式[28, 29]
| \[\frac{1}{2}(\Delta {\sigma _Y} + \Delta {\sigma _X}) = - {p_{\rm{o}}}[\frac{{r\cos (\theta - 0.5{\theta _1} - 0.5{\theta _2})}}{{\sqrt {{r_1}{r_2}} }} - 1]{\rm{ }}\] | (1) |
| \[\frac{1}{2}(\Delta {\sigma _Y} - \Delta {\sigma _X}) = {p_{\rm{o}}}\frac{{2r\sin \theta }}{L}{(\frac{{{L^2}}}{{4{r_1}{r_2}}})^{3/2}}\sin [3({\theta _1} + {\theta _2})/2]\] | (2) |
式中,$p_{\rm o}$为裂缝内部压力,$\Delta \sigma_X $和$\Delta \sigma_Y$分别为$X$方向和$Y$方向的裂缝诱导应力.
图1为水力裂缝的产生引起的应力场变化示意图,$XY$平面为水平面,$L$为裂缝长度. $\sigma_{\rm h min}$和$\sigma_{\rm h max}$ 分别代表地层初始水平最小主应力和水平最大主应力.

|
图1 水力裂缝的产生引起的应力场变化示意图 Fig.1 The sketch map of stresses changes induced by the creation of hydraulic fracture |
对于$X$轴上任意一点,对式(2)整理可得到
\[\frac{{\Delta {\sigma _X} - \Delta {\sigma _Y}}}{{{p_{\rm{o}}}}} = \frac{{2\left( {2l/L} \right)}}{{{{[1 + {{\left( {2l/L} \right)}^2}]}^{3/2}}}}{\rm{ }}\]
(3)
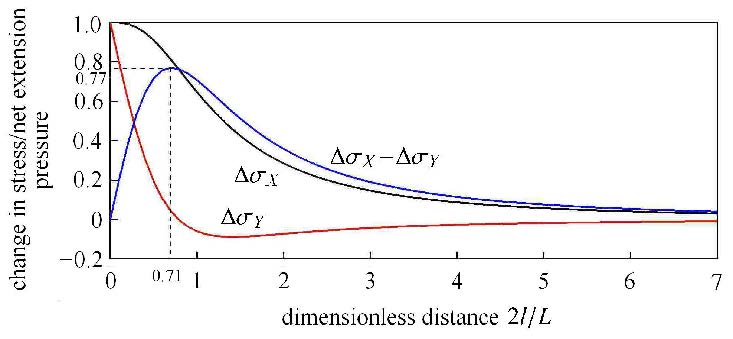
对于$X$轴上任意一点,根据式(1) $\sim$ (3)并进行无量纲处理,可绘制图2,图中$l$为$X$轴上任意一点与裂缝面的距离,即$l = r\sin \theta $,横坐标$2l / L$表示$l$与裂缝半长的无因次距离. 式(3)对无因次距离$2l / L$求一阶导数和二阶导数,可得当$2l / L=0.707$时,$X$方向诱导应力与$Y$方向诱导应力的差值最大,即$\Delta \sigma _{X} - \Delta \sigma _{Y} $达到最大值,如图2中所示.
|
图2 裂缝诱导应力及其差值变化趋势 Fig.2 The curves of fracture induced stresses and their difference |
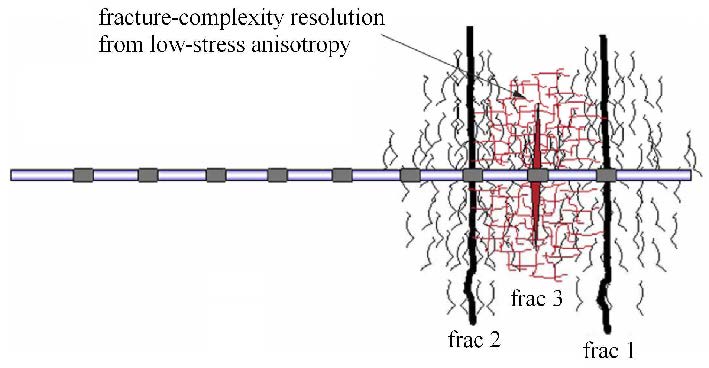
从图2可以看出,在裂缝附近地层$\Delta \sigma _{X} > \Delta \sigma_{Y} $,水力裂缝的形成减弱了裂缝附近地层应力各向异性,基于这一原理,2010年,美国Soliman提出了""压裂方法,即交替压裂方法,如图3所示,压裂顺序为:裂缝1 $\to$ 裂缝2 $\to$ 裂缝3.
|
图3 "Texas Two-Step"压裂方法示意图 (压裂顺序:裂缝1 $\to$裂缝2 $\to$ 裂缝3) Fig.3 The sketch map of the "Texas Two-Step" fracturing method (The fracturing sequence is: Frac 1 $\to$ Frac 2 $\to$ Frac 3) |
"TexasTwo-Step"压裂方法是一种借助人工主裂缝的产生改变裂缝附近地层应力场的理论,应力翻转后的应力场改变应力释放裂 缝的扩展方向,使得不同人工主裂缝产生的应力释放裂缝相互交叉,并进一步连通各条主裂缝,从而形成复杂缝网结构的一种特殊分段压裂方法[30]. 首先在水平井指端压出一条裂缝,对于脆性页岩储层,在形成人工主裂缝的同时,会伴随生成若干应力释放裂缝,这是因为人工主裂缝形成的过程中,裂缝附近地层的应力场变化了,变化了的地层应力场导致了应力释放裂缝的产生. 应力释放裂缝扩展的方向垂直于最小主应力方向,当最小主应力方向发生变化时,应力释放裂缝也随之发生转向.
在形成第1条裂缝后,接着向前压开第2条裂缝,在形成第2条裂缝的同时,同样会伴随产生若干条与主裂缝相互平行的应力释放裂缝.
在压开两条裂缝后,不是继续向前压开裂缝,而是在第1条和第2条裂缝中间部分压开第3条裂缝,由于第1条和第2条裂缝之间 地层的应力场在前两条裂缝形成的过程中改变了,地层应力场的各向异性大大减弱了,在第3条裂缝形成时,第3条裂缝附近的地层应 力场再次改变了,并出现了应力翻转,即原来水平最大主应力方向变成了水平最小主应力方向,原来水平最小主应力方向变成了水平最大主应力方向,第3条裂缝形成的应力释放裂缝的扩展方向是水平的(图中红色小裂缝),就会和前两条主裂缝形成的应力释放裂缝以及人工主裂缝交叉,从而形成相互交叉的缝网结构.
采用同样的压裂顺序压裂水平井的其他井段,全井筒周围地层都可以产生缝网结构,大大提高水平井的气体采收率和经济产能.
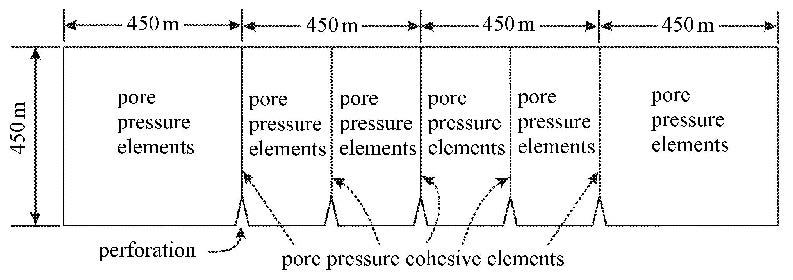
2 "Texas Two-Step"压裂方法数值模拟 2.1 数值模型采用有限元软件建立有限元数值模型,模型示意图如图4所示,模型高度450 m,长度1 800 m,共模拟5条裂缝的起裂和扩展过程, 裂缝间距225 m,最外端2条裂缝距离边界450 m,以消除边界条件的影响.
|
图4 "Texas Two-Step"压裂方法的有限元数值模型示意图 Fig.4 The sketch map of finite element simulation model of the "Texas Two-Step" fracturing method |
采用多孔介质流固耦合单元模拟页岩储层岩石的性质,采用孔隙压力"cohesive"单元模拟水力裂缝的行为. 岩石弹性模量为40 GPa,泊松比为0.17. 页岩气藏渗透率为0.1 mD(页岩基质和微裂缝系统的综合等效渗透率),孔隙度为6%. 初始$X$向有效应力为32 MPa,$Y$向有效应力为37 MPa.孔隙压力"cohesive"单元采用二次应力起裂准则,法向抗张强度为3 MPa,扩展准则采用"Benzeggagh-$\!$-Kenane"形式的损伤模式 (能量BK准则),断裂能为9 000 J/m$^{2}$.
模型中采用"Texas Two-Step"压裂方法进行压裂,从左到右5条裂缝分别记为1,2,3,4,5,压开裂缝的顺序为5,3,4, 1,2. 压裂液黏 度为0.001 Pa$\cdot$s (清水),注入排量为6 m$^{3}$/min (模拟的实际排量为12 m$^{3}$/min,本模型为单翼的一半模型,排量减半),裂缝1, 3和5的注入时间为1 h,裂缝2和4的注入时间是25 min.
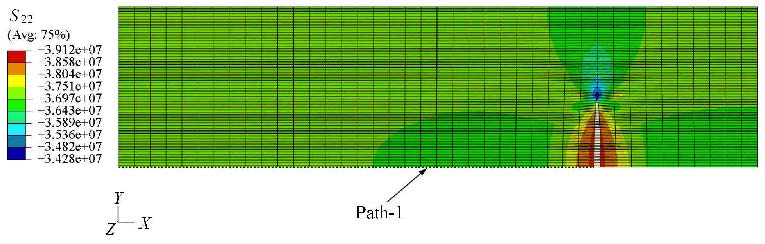
2.2 数值模拟结果图5和图6分别为第1条裂缝形成时$X$方向有效应力($S_{11}$)和$Y$方向有效应力($S_{22}$)分布,图5最大值为34.41 MPa,图6最大值为39.12 MPa,都位于裂缝表面上. 比较图5和6可以看出,$Y$方向的有效应力($S_{22}$)沿$X$方向的应力梯度大于$X$方向的有效应力,且$Y$方向的有效应力沿 图6中的路径"Path-1"出现了先减小后上升的变化情况,而$X$方向的有效应力沿路径"Path-1"是单调减小的,两者变化趋势不相同.

|
图5 第1条裂缝形成时$X$方向有效应力分布 Fig.5 The effective stress distribution in $X$ direction when the first fracture is created |
|
图6 第1条裂缝形成时$Y$方向有效应力分布 Fig.6 The effective stress distribution in $Y$ direction when the first fracture is created |
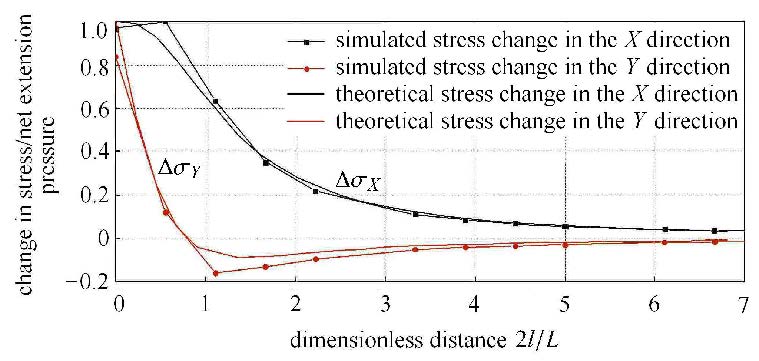
把图5的$X$方向有效应力和图6的$Y$方向有效应力沿着图6的路径"Path-1"进行绘图,并进行无量纲处理,可以得到图7的曲线, 图中纵坐标为地层中的裂缝诱导应力与裂缝扩展净压力的比值,横坐标为路径"Path-1"上任意一点到裂缝表面的距离与裂缝半长的比值.
|
图7 数值模拟结果和公式计算结果对比 Fig.7 The compare between simulation results and formulas |
为了形象的比较数值模拟结果和公式计算结果,理论公式(1)和(2)计算的$ X$方向应力变化和$Y$方向应力变化也一同显示在图中,通过比较可以发现,对于$X$方向和$Y$方向的应力变化情况,数值模拟的 结果和公式计算的结果吻合良好,理论公式和数值模型的正确性都得到了很好的验证.
图8表示最终压裂时刻缝网形成的区域,图中$FV_1$代表$Y$方向与$X$方向主应力的差值,即$\sigma_{Y}-\sigma _{X} $. 由模型 输入参数,我们知道初始时刻地层$Y$方向与$X$方向主应力的差值为5 MPa ($37-32$),$FV_1$为负值表示地层出现了应力翻转,应力释放裂缝的方向发生了翻转,也即形成缝网区域.

|
图8 采用"Texas Two-Step"方法形成的缝网结构区域 Fig.8 The created area of fracture network by adopting the "Texas Two-Step" fracturing method |
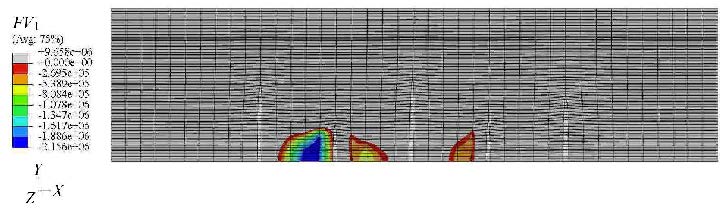
图中强制显示0值为红色云纹,高于0的数值全部采用灰色显示,这样所有小于0的区域就全部采用彩色云纹显示了. 采用同样方法绘制了采用普通分段压裂方法(压裂顺序为5,4,3,2,1)形成的缝网结构区域,如图9所示的彩色区域. 对比图8和图9可以看出,采用``Texas Two-Step''压裂方法形成的缝网区域明显大于普通分段压裂方法,储层改造效果好于普通分段压裂方法.
|
图9 采用普通分段压裂方法形成的缝网结构区域 Fig.9 The created area of fracture network by adopting common staged fracturing method |
由图2可以看到,"Texas Two-Step"压裂方法最大的$\Delta \sigma _{X} - \Delta \sigma _{Y} $发生在距离裂缝面0.707倍裂缝半长处,其值为0.769 8倍的裂缝净压力,但随距离裂缝面的长度增加,衰减较快, 因此"Texas Two-Step"压裂方法只适用于低应力差地层,不适用于高应力差地层. 针对地层初始应力场各向异性差异较大情况,应探索采用其它压裂方法产生缝网结构.
对于地层低水平应力差和高水平应力差的界限,学术界和工程界没有统一的认识,文献[31]对``Texas Two-Step''压裂方法适用的 地层应力差的界限进行了讨论和界定,此文不做详细论述.
从图2可以知道裂缝的产生引起地层最大的$\Delta \sigma _{X} - \Delta \sigma _{Y} $发生在距离裂缝面0.707倍裂缝半长处, 此处的应力变化是最大的,也就是最先发生应力翻转的地点,因此对于初始应力场各向异性较大情况,可以让不同裂缝最大的$\Delta \sigma_{X} - \Delta \sigma_{Y} $发生在同一点,产生应力"共振"现象,则此处可以克服原始应力场较大的应力各向异性,从而产生缝网结构.
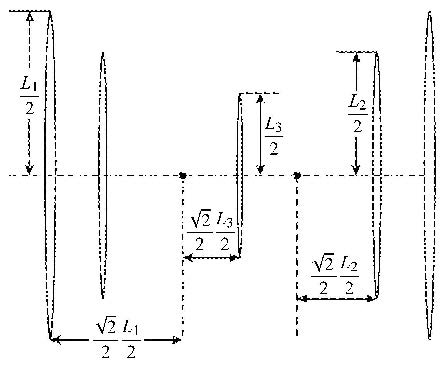
图10为采用三次应力"共振"方式减弱地层应力场的各向异性,从而产生缝网结构的示意图. 对于图中的一点(图中实心圆点处)有3条裂 缝最大的$\Delta \sigma _{X} - \Delta \sigma _{Y} $发生在这里,发生应力"共振"现象,这一点的原始应力场的应力各向异性被大大削弱了,甚至发生应力翻转,从而产生缝网结构. 从左到右,5条裂缝分别记为裂缝1,2,3,4, 5,在施工过程中,只需保证裂缝1先于裂缝2形成,裂缝5先于裂缝4形成,其它压裂顺序组合可根据施工要求灵活调整. 裂缝的间距和裂缝的长度应满足一定的要求. 设最外层裂缝的长度为$L_1 $,次外层裂缝的长度为$L_2 $, 最内层裂缝的长度为$L_3 $,第1条裂缝和第2条裂缝之间的距离为$D_1 $,第2条裂缝和第3条裂缝之间的距离为$D_2 $, 则实现三次应力"共振"压裂方法,裂缝的缝长和裂缝的间距应满足下面的关系
| \[\left. {\begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{\sqrt 2 }}(\frac{{{L_1}}}{2} - \frac{{{L_2}}}{2}) = {D_1}\\ \frac{1}{{\sqrt 2 }}(\frac{{{L_2}}}{2} + \frac{{{L_3}}}{2}) = {D_2}\\ {L_2} > {L_3} \end{array} \end{array}} \right\}\] | (4) |
|
图10 三次应力"共振"压裂方法示意图 Fig.10 The sketch map of the three times stress "resonance" fracturing method |
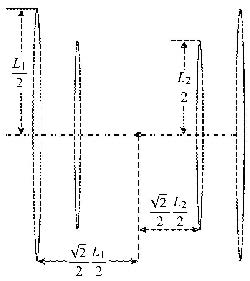
图11为采用四次应力"共振"方式产生缝网结构示意图. 图中有4条裂缝在同一点(图中实心圆点)发生应力"共振",此处最容易 发生应力翻转,从而产生缝网结构. 从左到右4条裂缝分别记为裂缝1,2,3, 4,压裂施工时,只需保证裂缝1先于裂缝2生成,裂缝4先于裂缝3生成,其它压裂顺序可灵活调整. 设最外层裂缝的长度为$L_1 $,最内层裂缝的长度为$L_2 $,第1条裂缝和第2条裂缝之间的距离为$D_1 $, 第2条裂缝和第3条裂缝之间的距离为$D_2 $, 则实现四次应力"共振"压裂方法,裂缝的缝长和裂缝的间距应满足下面的关系
| \[\left. {\begin{array}{*{20}{l}} \begin{array}{l} \frac{1}{{\sqrt 2 }}(\frac{{{L_1}}}{2} - \frac{{{L_2}}}{2}) = {D_1}\\ \frac{1}{{\sqrt 2 }}\frac{{{L_2}}}{2} = \frac{{{D_2}}}{2} \end{array} \end{array}} \right\}\] | (5) |
|
图11 四次应力"共振"压裂方法示意图 Fig.11 The sketch map of the four times stress "resonance" fracturing method |
$X$方向为水平最小主应力方向,大小为25 MPa,$Y$方向为水平最大主应力方向,大小为37 MPa (初始水平主应力差值$FV_1$为 12 MPa),其它储层参数和物性参数与2.1节模型完全相同. 为了满足式(4)的要求,模型的尺寸发生了变化,模型高度为550 m,裂缝间距为150 m,最外面2条裂缝距离边界的距离为300 m.
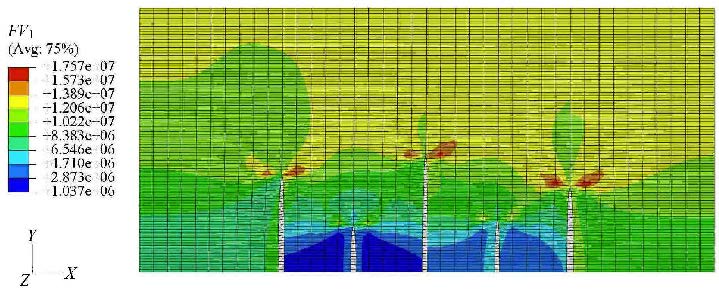
首先采用"Texas Two-Step"压裂方法(压裂顺序为5,3,4,1,2)进行模拟,图12为压裂最终时刻地层两向水平主应力差值分布图, 图中最小值为1.04 MPa,为正值,说明并没有发生应力场的翻转,没有形成缝网. 因此对于初始应力差值较大的情况,采用"Texas Two-Step"压裂方法无法产生缝网结构.
|
图12 地层两向水平主应力差值分布 Fig.12 The distribution of stresses differences between two horizontal principal stresses |
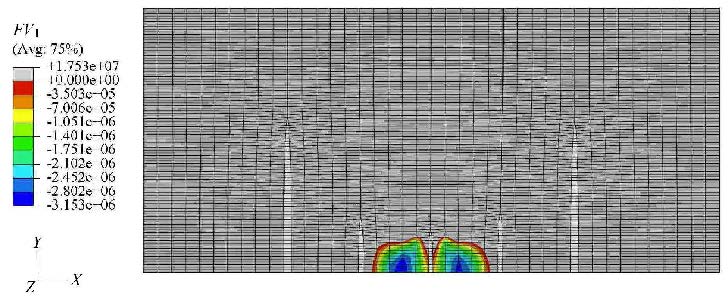
图13为采用三次应力"共振"压裂方法形成的缝网结构区域(彩色区域). 压裂顺序为先压裂最外层2条长裂缝,再压裂中间2条 次长的裂缝,最后压裂中间最短的裂缝. 图中最外层裂缝的半缝长为325 m,次外层裂缝的半缝长为116 m,中间裂缝的半缝长为88 m,基本满足式(4)的要求.
|
图13 采用三次应力"共振"压裂方法形成的缝网结构区域 Fig.13 The created area of fracture network by adopting the triple stress "resonance" fracturing method |
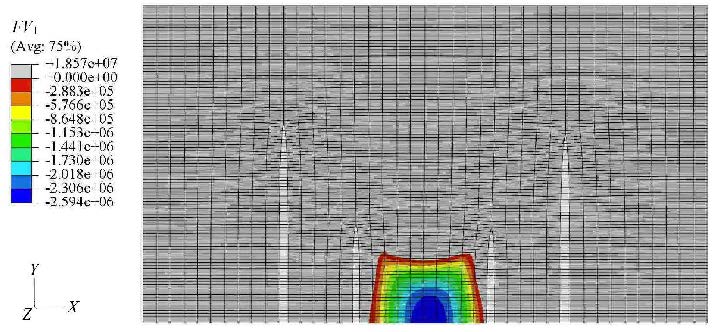
基于同样的原理,图14为采用四次应力"共振"压裂方法形成的缝网结构区域(彩色区域),压裂顺序为先压裂外层2条长裂缝,再压 裂中间2条短裂缝,裂缝长度和裂缝间距应满足式(5)要求.
|
图14 采用四次应力"共振"压裂方法形成的缝网结构区域 Fig.14 The created area of fracture network by adopting the quartic stress "resonance" fracturing method |
本文采用理论分析和数值模拟相结合的方法研究页岩气藏体积压裂缝网形成的力学条件,取得以下结论和认识:
(1)人工主裂缝的产生减弱了裂缝附近地层应力场的各向异性,甚至使裂缝附近地层主应力发生翻转,翻转的应力场致使应 力释放裂缝的延伸方向也发生了转向,转向的应力释放裂缝和先前生成的应力释放裂缝以及人工主裂缝发生交叉连接,从而形成缝网结构.
(2)对于低应力差的页岩储层,采用``Texas Two-Step''压裂方法可以产生缝网. 且采用``Texas Two-Step''压裂方法产生的缝网区域大于采用普通分段压裂方法产生的缝网区域.
(3)人工裂缝诱导应力差值的最大值并不发生在裂缝表面,而是在距离裂缝表面0.707倍的裂缝半长处,利用这一特性,对于初始高应力差页岩储层,提出了三次应力"共振"和四次应力"共振"压裂方法,其原理是使不同裂缝诱导应力差值的最大值发生在同一点,克服初始地层较高的应力差值,产生缝网结构.
(4)对于采用``Texas Two-Step''压裂方法无法产生缝网的高应力差页岩气藏地层,采用三次应力"共振"和四次应力"共振"压裂方法可以产生缝网.
| [1] | Arthur JD, Bohm B, Layne M. Evaluating implications of hydraulic fracturing in shale gas reservoirs. SPE 121038, 2009 |
| [2] | Akbarnejad-Nesheli B, Valko PP, Lee WJ. Relating fracture network characteristics to shale gas reserve estimation. SPE 154841, 2012 |
| [3] | Warpinski NR, Branagm PT. Altered-stress fracturing. SPE 17533, 1989 |
| [4] | Soliman MY, East L, Adams D. Geomechnics aspects of multiple fracturing of horizontal and vertical wells. SPE 86992, 2004 |
| [5] | Cheng Y. Impacts of the number of perforation clusters and cluster spacing on production performance of horizontal shale gas wells. SPE 138843, 2010 |
| [6] | Cheng Y. Boundary element analysis of the stress distribution around multiple fractures: implications for the spacing of perforation clusters of hydraulically fractured horizontal wells. SPE 125769, 2009 |
| [7] | Wikel K. Geomechanics: bridging the gap from geophysics to engineering in unconventional reservoirs. First Break, 2011, 29: 71-81 |
| [8] | Wu R, Kresse O, Weng X, et al. Modeling of interaction of hydraulic fractures in complex fracture networks. SPE 152052, 2012 |
| [9] | Wu K, Olson JE. Investigation of critical in situ and injection factors in multi-frac treatments: guidelines for controlling fracture complexity. SPE 163821, 2013 |
| [10] | Stanojcic M, Rispler K. How to achieve and control branch fracturing for unconventional reservoirs: two novel multistage-stimulation processes. SPE 136566, 2010 |
| [11] | Roussel NP, Sharma MM. Optimizing fracture spacing and sequencing in horizontal well fracturing. SPE 127986, 2010 |
| [12] | Roussel NP, Sharma MM. Quantifying transient effects in altered-stress refracturing of vertical wells. SPE 119522, 2009 |
| [13] | Jo H, Hughes B. Optimizing fracture spacing to induce complex fractures in a hydraulically fractured horizontal wellbore. SPE 154930, 2012 |
| [14] | Barree RD, Gilbert JV, Conway MW. Stress and rock property profiling for unconventional reservoir stimulation. SPE 118703, 2009 |
| [15] | Nagel N, Zhang F, Sanchez-Nagel M, et al. Stress shadow evaluation for completion design in unconventional plays. SPE 167128, 2013 |
| [16] | Soliman MY, Augustine J. Fracturing design aimed at enhancing fracture complexity. SPE 130043, 2010 |
| [17] | Roussel NP, Sharma MM. Strategies to minimize frac spacing and stimulate natural fractures in horizontal completions. SPE 146104, 2011 |
| [18] | 雷群,胥云,蒋廷学 等.用于提高低-特低渗透油气藏改造效果的缝网压裂技术.石油学报,2009,30(2):237-241 (Lei Qun, Xu Yun, Jiang Tingxue, et al."Fracture network" fracturing technique for improving post-fracturing performance of low and ultra-low permeability reservoir. Acta Petrolei Sinica, 2009, 30(2): 237-241 (in Chinese)) |
| [19] | 陈作,薛承瑾,蒋廷学 等.页岩气井体积压裂技术在我国的应用建议.天然气工业,2010,30(10):30-32 (Chen Zuo, Xue Chengjin, Jiang Tingxue, et al. Proposals for the application of fracturing by stimulated reservoir volume (SRV) in shale gas wells in China. Natural Gas Industry, 2010, 30(10): 30-32 (in Chinese)) |
| [20] | 翁定为,雷群,胥云 等.缝网压裂技术及其现场应用.石油学报,2011,32(2):280-284 (Weng Dingwei, Lei Qun, Xu Yun, et al. Network fracturing techniques and its application in the field. Acta Petrolei Sinica, 2011, 32(2): 280-284 (in Chinese)) |
| [21] | Romanson R, East L, Stanojcic M. Novel, multistage stimulation processes can help achieve and control branch fracturing and increase stimulated reservoir volume for unconventional reservoirs. SPE 142959, 2011 |
| [22] | Mayerhofer MJ, Lolon EP, Warpinski NR, et al. What is stimulated reservoir volume (SRV)? SPE 119890, 2008 |
| [23] | Gong B, Qin G, Douglas C, et al. Detailed modeling of the complex fracture network of shale gas reservoirs. SPE 142705, 2011 |
| [24] | Meyer BR, Bazan LW. A discrete fracture network model for hydraulic induced fractures: theory, parametric and case studies. SPE 140514, 2011 |
| [25] | Weng X, Kresse O, Cohen C, et al. Modeling of hydraulic fracture network propagation in a naturally fractured formation. SPE 140253, 2011 |
| [26] | Bunger AP, Zhang X, Jeffrey RG. Parameters effecting the interaction among closely spaced hydraulic fractures. SPE 140426, 2011 |
| [27] | 吴奇,胥云,王晓泉 等.非常规油气藏体积改造技术-内涵、优化设计与实现.石油勘探与开发,2012, 39(3):352-358 (Wu Qi, Xu Yun, Wang Xiaoquan, et al. Volume fracturing technology of unconventional reservoirs: connotation, optimization design and implementation. Petroleum Exploration and Development, 2012, 39(3): 352-358 (in Chinese)) |
| [28] | Sneddon IN. The distribution of stress in the neighbourhood of a crack in an elastic solid. Proc. R. Soc. London, Series A, 1946, 187: 229-260 |
| [29] | Sneddon IN, Elliott HA. The opening of a Griffith crack under internal pressure. Quart Appl Math, 1946, IV, 3: 262-267 |
| [30] | East L, Soliman MY, Augustine J. Methods for enhancing far-field complexity in fracturing operations. SPE 133380, 2010 |
| [31] | 张广明.页岩气藏水平井体积压裂缝网形成的力学条件研究.中国石油勘探开发研究院博士后研究报告,北京,2012 (Zhang Guangming. Research on the mechanical condition of fracture networks for horizontal well volume fracturing in shale reservoirs. Post-doctor Report, Research Institute of Petroleum Exploration & Development, PetroChina, Beijing, 2012 (in Chinese)) |
2. Great Wall Drilling Company, PetroChina, Beijing 100101, China
 2015, Vol. 47
2015, Vol. 47
