2. 加拿大卡尔加里大学化学与石油工程学院, 阿尔伯塔 T2N1N4
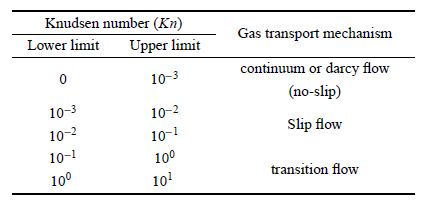
页岩气和致密砂岩气藏储集层在成岩及烃类演化过程中,由于应力和热流体作用,产生孔隙和微裂缝[1, 2]. 微裂缝易在薄 弱面或有机质边缘处形成,呈平板、规则和不规则状[2, 3, 4]. 为了便于描述气体传输机理,常将微裂缝简化为表面光滑的平板状裂 隙[5, 6, 7],其宽度和开度为纳微米级[2, 3]. 微裂缝气体传输机理按克努森数$Kn$(气体平均分子自由程与微裂缝开度比值)判定准则分为连续流动、滑脱流动和过渡流动[5, 6],见表1.
| 表1 气体传输机理分类 Table 1 Different gas transport mechanisms as a function of Knudsen number |
微裂缝形状和尺度影响气体传输特性,尤其微裂缝开度,对页岩气和致密砂岩气藏的生产动态和经济开发起重要作用[2, 8, 9, 10]. Smolouchowski 等学者研究均表明微裂缝形状对气体努森扩散影响很 大[11, 12, 13, 14]. White 研究表明微裂缝形状对气体连续流动影响显著,并提出了修正因子[15]. 总体而言,微裂缝形状对气体传输影响的研究较少.
页岩气和致密砂岩气藏微纳尺度气体传输异常复杂[16, 17, 18, 19],气体传输通常用分子模型、连续性模型和滑脱模型 模拟[6]. 分子模型,也叫分子模拟,主要包括蒙特卡洛直接模拟法[20]、分子动态模拟 法[21]和玻尔兹曼方法[22]. 分子模拟考虑气体分子属性,模拟精度高[23].
然而需要巨大计算资源和时间,无法应用于页岩和致密砂岩微裂缝气体传输模拟[23, 24]. 连续性模型,也称Hagen-Poiseuille 方程,描述气体宏观属性随空间和时间变化,广泛应用于气体传输模拟[25]. 然而,在低压或者小尺度微裂缝条件下,气体分子在壁面滑脱,热动力学平衡假设条件不满足,连续性模型失效[26]. 为此,通过修正非滑脱边界条件推导了滑脱模型[4],其已广泛应用于页岩气传输模拟[5, 27, 28, 29]. 滑脱模型主要包括一阶滑 脱[30]、二阶滑脱[31]与Beskok 和 Karniadakis 模 型[32]. 应用结果表明,一阶滑脱模型低估了气体传输量,且随克努森数增加,偏离程度越大[33];二阶滑脱模型高估了气体传输 量[33];Beskok 和 Karniadakis 模型引入稀有效应系数,虽然提高了计算精度,但壁面处气体流速预测值偏差大[33]. Thomson 和 Owens研究表明,当克努森数很大时,滑脱模型无法退化为努森扩散方程,也就无法描述气体努森扩散[9]. 分子模拟、连续性模型和滑脱模型均有其局限性,因此众多学者试图基于连续性模型、滑脱模型和努森扩散模型,进行不同模型 组合,建立一个能够描述多种传输机理共存的气体传输模型,见表2.
| 表2 不同气体传输模型的对比与评价 Table 2 Comparison and evaluation of different gas transport models |
然而这些模型要么权重系数不合理,要么含有经验系数,要么仅适合于圆形截面气体传输.因此,建立矩形截面微裂缝气体传输新模型,对页岩气和致密砂岩气藏开发具有重要的现实意义. 基于此,本文首先分别阐述并耦合不同气体传输机理,建立微裂缝气体传输模型;紧接着利用分子模拟数据,验证模型可靠性;然后对模型敏感性分析,包括微裂缝形状、尺度和压力对气体传输影响,并讨论滑脱流动和努森扩散在不同开发阶段对气体传输的贡献;最后给出结论.新模型能够描述连续流动,滑脱流动和努森扩散,还能够描述介于滑脱流动和努森扩散之间的过渡流动. 同时还考虑微裂缝形状、尺度和压力对气体传输的影响.
1 模型建立
页岩和致密砂岩微裂缝几何形状复杂,可简化为平板,截面为长方形,则微裂缝截面几何参数表征为
\[\zeta = \frac{w}{h}{\rm{ }}\]
(1)
式中,$\zeta $为微裂缝纵横比,无因次;$w$为微裂缝宽度,m;$ h$为微裂缝开度,m.
微裂缝中的气体克努森数为气体平均分子自由程与微裂缝开度的比值[9],可表达为
\[Kn = \frac{\lambda }{h}{\rm{ }}\]
(2)
式中,$Kn$为克努森数,无因次;$\lambda $为气体平均分子自由程,m. 克努森数是气体传输时稀有效应程度的表征参数,可用来判断气体的传输机理[6].
气体平均分子自由程表达为[45]
\[\lambda = \frac{\mu }{p}\sqrt {\frac{{\pi RT}}{{2M}}} \]
(3)
式中, $\mu$为气体黏度,Pa$\cdot$s;$R$为普适气体常数,J$\cdot$mol$^{-1}$$\cdot$K$^{-1}$;$T$为地层温度,K;$p$ 为地层压力,Pa;$M$ 为气体摩尔质量,kg$\cdot$mol$^{ - 1}$.
1.1 连续流动
当克努森数$Kn<10^{-3}$,气体分子间碰撞占主导地位,气体流动满足连续性条件,为连续流动,可用Hagen-$\!$-Poiseuille方
程表达为[5]
\[{J_{\rm{v}}} = - \frac{\phi }{\tau }\frac{{w{h^3}}}{{12\mu }}\frac{{pM}}{{RT}}\frac{{{\rm{d}}p}}{{{\rm{d}}l}}{\rm{ }}\]
(4)
式(4)考虑了页岩和致密砂岩中微裂缝孔隙度和迂曲度对气体传输的影响,且表明连续流流量反比于气体黏度,正比于气体压力,在低压条件下,气体传输量很小[46].
考虑截面几何形状和尺度的影响,微裂缝中气体连续流动可表达为[47]
\[{J_{\rm{v}}} = - A(\zeta )\frac{\phi }{\tau }\frac{{w{h^3}}}{{12\mu }}\frac{{pM}}{{RT}}\frac{{dp}}{{dl}}{\rm{ }}\]
(5)
其中
\[A(\zeta ) = 1 - \frac{{192}}{{\zeta {\rm{ }}{\pi ^5}}}\sum\limits_{i = 1,3,5, \cdots }^\infty {\frac{{\tanh \left( {I{\rm{ }}\pi \zeta /2} \right)}}{{{i^5}}}} \]
(6)
式中,$ A(\zeta )$为对连续流动影响的微裂缝截面形状因子,无因次,其不受克努森数$K n$变化的影响.
1.2 滑脱流动
当克努森数$10^{-3}<Kn<10^{-1}$,气体分子间碰撞和气体与微裂缝壁面的碰撞均不可忽略,气体分子在壁面发生滑脱,通
过修正滑脱边界条件,则气体滑脱流动可表达为[47]
\[\begin{array}{l}
{J_{{\rm{vs}}}} = - A(\zeta )\frac{\phi }{\tau }\frac{{w{h^3}}}{{12\mu }}\frac{{pM}}{{RT}}\left( {1 + \alpha Kn} \right) \cdot \\
\left( {1 + \frac{{6Kn}}{{1 - bKn}}} \right)\frac{{dp}}{{dl}}
\end{array}\]
(7)
式中,$J_{\rm vs}$为微裂缝气体滑脱流动的质量流量,kg$\cdot$s$^{ - 1}$;$ b$为气体滑脱常数,无因次. 边界为一阶滑脱条件,则$b=0$;边界为二阶滑脱边界条件,则$b=-1$;$\alpha $为稀有效应系数,无因次.
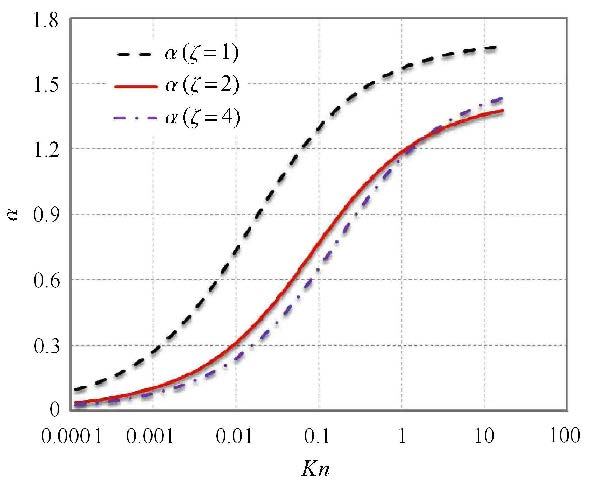
通过分子模拟结果验证表明,在全克努森数范围内,气体滑脱常数$b=-1$更为合理. 稀有效应系数$\alpha $是表征气体黏度随克努森数增大而减小的物理现象,其从连续流动时的“0”逐渐增大到分子流动时的某一常数(特定微裂 缝和气体系统具有相对应的固定常数),且受微裂缝截面形状和气体压力的影响[6]. 确定不同克努森数下对应的稀有效应系数,需要大量准确的实验或分子模拟数据. 根据分子模拟结果,不同纵横比微裂缝气体稀有效应系数和克努森数关系见图1,[47].
|
图1 $\alpha$-$\!$-$Kn$关系曲线[47] Fig.1 The curves for $\alpha$-$\!$-$Kn$ with different aspect ratio in micro fractures of shale and tight gas reservoirs [47] |
当克努森数$Kn \geqslant 1$,气体分子与壁面碰撞占主导地位,为努森扩散,则半径为$h$圆管,气体扩散量可用努森方程表达为[5]
$$
J_{\rm k} = - \dfrac{\phi }{\tau }h^3\left( {\dfrac{M}{2\pi RT}} \right)^{0.5} \dfrac{dp}{dl}
$$
(8)
式中,$J_{\rm k}$为气体努森扩散的质量流量,kg$\cdot$s$^{ - 1}$.
考虑截面形状的影响,则矩形截面微裂缝中的气体努森扩散量可表达为[9]
$$
J_{\rm k} = - B(\zeta )\dfrac{\phi }{\tau }h^3\left( {\dfrac{M}{2 \pi RT}} \right)^{0.5} \dfrac{dp}{dl}
$$
(9)
其中
\[\begin{array}{l}
B(\zeta ) = [{\zeta ^2}\ln \left( {\frac{1}{\zeta } + \sqrt {1 + \frac{1}{{{\zeta ^2}}}} } \right) + \zeta \ln \left( {\zeta + \sqrt {1 + {\zeta ^2}} } \right) - \\
\frac{{{{\left( {{\zeta ^2} + 1} \right)}^{3/2}}}}{3} + \frac{{1 + {\zeta ^3}}}{3}]
\end{array}\]
(10)
式(7)和式(9)对比表明,不同于气体滑脱流动传输量,努森扩散量与气体黏度和气体压力无关.
1.4 模型建立为了合理地考虑页岩和致密砂岩微裂缝中气体不同传输机理对气体传输贡献的影响,基于滑脱流动和努森扩散两种传输机理,分别以气体分子之间碰撞频率和气体分子与壁面碰撞频率占总碰撞频率的比值作为滑脱流动和努森扩散的贡献权重系数,建立微裂缝气体传输模型.
微裂缝中气体分子之间碰撞频率为[9, 47]
$$
f_{\rm m} = \dfrac{v}{\lambda }nhwdl
$$
(11)
微裂缝中气体分子与壁面碰撞频率为[9, 47]
$$
f_{\rm w} = \dfrac{1}{2}nv \left( {h + w} \right)dl
$$
(12)
滑脱流动权重系数为气体分子之间碰撞频率占总碰撞频率的比值
$$
\omega _{\rm vs} = \dfrac{f_{\rm m} }{f_{\rm m} + f_{\rm w} } = \Bigg [1 + \dfrac{Kn\left( {1 +
1/\zeta } \right)}{2} \Bigg]^{-1}
$$
(13)
努森扩散权重系数为气体分子与壁面碰撞频率占总碰撞频率的比值
$$
\omega _{\rm k} = \dfrac{f_{\rm w} }{f_{\rm m} + f_{\rm w} } = \Bigg[1 + \dfrac{2}{Kn\left( {1 +
1/\zeta } \right)} \Bigg]^{-1}
$$
(14)
式中,$\omega_{\rm k}$为气体分子与壁面碰撞频率占总碰撞频率的比值,小数.
结合式(7),式(9),式(13)和式(14),则微裂缝气体传输模型为
$$
J_{\rm t} = \omega _{\rm vs} J_{\rm vs} + \omega _{\rm k} J_{\rm k}
$$
(15)
式中,$ J_{\rm t}$为微裂缝气体传输的质量流量,kg$\cdot$s$^{ - 1}$.
2 模型验证
为了验证模型的可靠性,将计算结果与分子模拟结果进行对比. 为了对比方便,分别以连续流流量和努森扩散量为基础,
将微裂缝中气体传输量无因次化,分别表达为
\[\begin{array}{l}
\frac{{{J_{\rm{t}}}}}{{{J_{\rm{v}}}}} = {\omega _{{\rm{vs}}}}A(\zeta )\left( {1 + \alpha Kn} \right)\left( {1 + \frac{{6Kn}}{{1 - bKn}}} \right) + \\
{\omega _{\rm{k}}}\frac{{12Kn}}{\pi }\frac{{B(\zeta )}}{\zeta }
\end{array}\]
(16)
\[\frac{{{J_{\rm{t}}}}}{{{J_{\rm{k}}}}} = {\omega _{{\rm{vs}}}}\frac{\pi }{{12Kn}}\zeta A(\zeta )\left( {1 + \alpha Kn} \right) \cdot \left( {1 + \frac{{6Kn}}{{1 - bKn}}} \right) + {\omega _{\rm{k}}}B(\zeta ){\rm{ }}\]
(17)
式中,$J_{\rm t}/J_{\rm v}$为以连续流动流量为基础的无因次气体传输量,无因次;$J_{\rm t}/J_{\rm k}$为以努森扩散量为基础的无因次气体传输量,无因次.
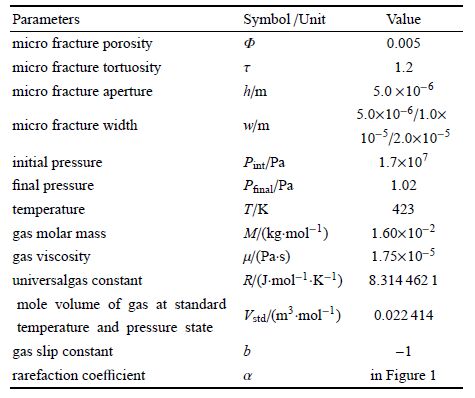
模型计算参数见表3,结果见图2.
| 表3 模型计算参数表 Table 3 Summary of modeling parameters in the calculations |
|
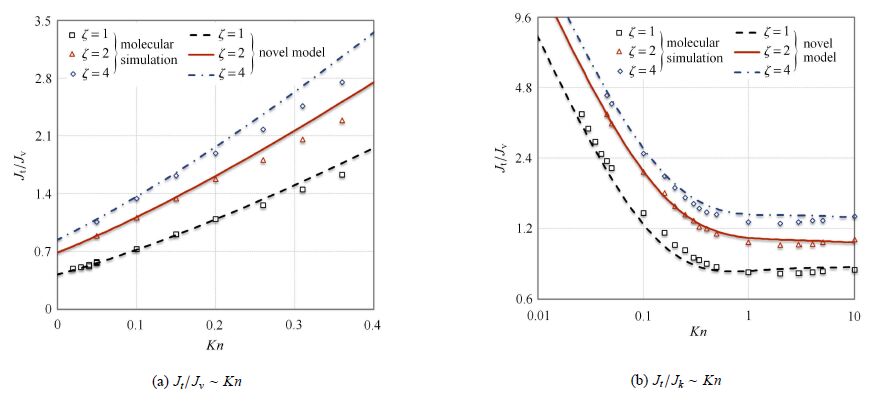
图2
新模型计算和分子模拟的无因次气体传输量对比
Fig.2
Comparison of analytic solutions calculated by new model and molecular simulation data
注:分子模拟数据是Sone 和Hasegawa,[52]基于分子动力学理论,采用漫反射边界条件,使用线性玻尔兹曼方法计算获得了矩形孔中稀薄气体传输的宏观参数,包括气体速度、密度和温度,进而获得了全克努森数范围内的气体传输量. Note that molecular simulation data is calculated by Sone and Hasegawa[52] with using molecular dynamic theory. In detail,using linear Boltzmann method with a boundary of diffusion refection,the gas flux over all the range of Knudsen number is obtained on the basis of macroscopic variable,including gas velocity, density and temperature. |
图2表明:(1)不同截面形状微裂缝,当 $10^{ - 2}<Kn<10$时,模型计算的无因次气体传输量与分子模拟结果具有较好 的一致性,表明新模型能够描述不同截面形状微裂缝中多种传输机理共存的气体传输过程;(2)在全克努森数范围,存在最小传输能力, 即 $Kn=1$时,无因次气体传输最小,这与以往学者通过分子模拟或实验获得的气体传输能力存在最小值的研究结果一致 [22, 48, 49, 50].
这也表明,微裂缝气体传输过程中,随着克努森数增大,气体传输能力先减小后缓慢增大,这也与页岩气中后期开发过程中气体产能降 低缓慢的实际现象相 符[51].
3 结果与讨论
微裂缝中气体传输受截面形状和尺度的影响,且在不同降压开发阶段,滑脱流动和努森扩散对气体传输的贡献是逐渐变化的.
为了方便探讨,将各传输机理对气体传输贡献分别以表观渗透率的形式表达为
\[\begin{array}{l}
{k_{{\rm{vs}} - \omega }} = - {\omega _{{\rm{vs}}}}\frac{{\mu {V_{{\rm{std}}}}}}{{Mwh}}\frac{{{J_{{\rm{vs}}}}}}{{dp/dl}} = \\
{\omega _{{\rm{vs}}}}{V_{{\rm{std}}}}A(\zeta )\frac{\phi }{\tau }\frac{{{h^2}}}{{12}}\frac{p}{{RT}}\left( {1 + \alpha Kn} \right)\left( {1 + \frac{{6Kn}}{{1 - bKn}}} \right)
\end{array}\]
(18)
\[\begin{array}{l}
{k_{k - \omega }} = - {\omega _{\rm{k}}}\frac{{\mu {V_{{\rm{std}}}}}}{{Mwh}}\frac{{{J_{\rm{k}}}}}{{dp/dl}} = \\
{\omega _{\rm{k}}}\mu {V_{{\rm{std}}}}B(\zeta )\frac{\phi }{\tau }\frac{{{h^2}}}{w}{\left( {\frac{1}{{2\pi MRT}}} \right)^{0.5}}
\end{array}\]
(19)
\[{k_{\rm{t}}} = - \frac{{\mu {V_{{\rm{std}}}}}}{{Mwh}}\frac{{{J_{\rm{t}}}}}{{dp/dl}} = {k_{vs - \omega }} + {k_{k - \omega }}{\rm{ }}\]
(20)
|
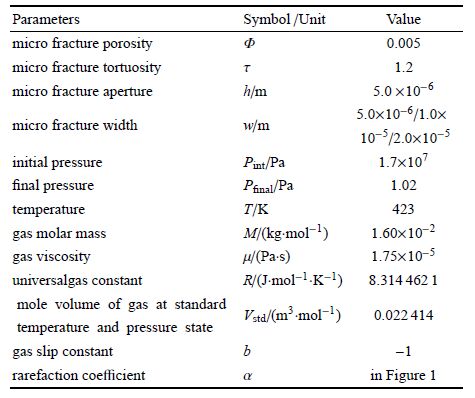
图3 不同微裂缝开度的$k_{\rm vs - \omega}$ 和 $k_{\rm k - \omega} \sim p$关系曲线 Fig.3 The curves for $k_{\rm vs - \omega}$ and $k_{\rm k - \omega} \sim p$ in micro fractures with different aperture and aspect ratio |
在较高压力或者较大微裂缝开度条件下,与气体分子和微裂缝壁面碰撞相比,气体分子之间碰撞占主导地位,气体传输为滑脱流动[41, 47, 53, 54];在较低压力或者较小微裂缝开度条件下,气体分子与微裂缝壁面碰撞占主导地位,为努森扩散[5, 41, 53, 54].
对于滑脱流动,当压力降低,滑脱流动本身传输能力下降,且滑脱流动的权重系数也降低,因此,滑脱流动表观渗透率随压力降低而降低; 同样的,当微裂缝开度减小,滑脱流动本身传输能力下降,且滑脱流动的权重系数也降低,因此,滑脱流动表观渗透率随微裂缝开度减小 而降低[44],见图3.
对于努森扩散,努森扩散本身的传输能力仅与微裂缝尺度,温度和气体摩尔质量有关[55],而与压力无关,这是由于气体在努森扩散流动区域内,平均气体分子自由程受限于微裂缝开度造成的[55, 56, 57, 58, 59, 60, 61].
当压力降低,努森扩散本身传输能力不变,然而努森扩散权重系数却迅速增大,因此,表现为努森扩散表观渗透率增大;同样的,当微裂缝开度减小,努森扩散本身传输能力减小,然而努森扩散权重系数却急剧增大,因此,也表现为努森扩散表观渗透率增大[44],见图3.
图3还表明滑脱流动和努森扩散表观渗透率均随微裂缝纵横比增大而增大;在微裂缝开度$h \geqslant 0.5 u$m,微裂缝气体以滑脱流动为主,努森扩散可忽略不计(图3(a)和图3(b));在微裂缝开度 $h =0.05 u$m,滑脱流动和努森扩散对微裂缝气体传输的贡献相当图3(c);在微裂缝开度$h \leqslant 0.005 u$m,微裂缝气体以努森扩散为主,滑脱流动可忽略不计 图3(d).
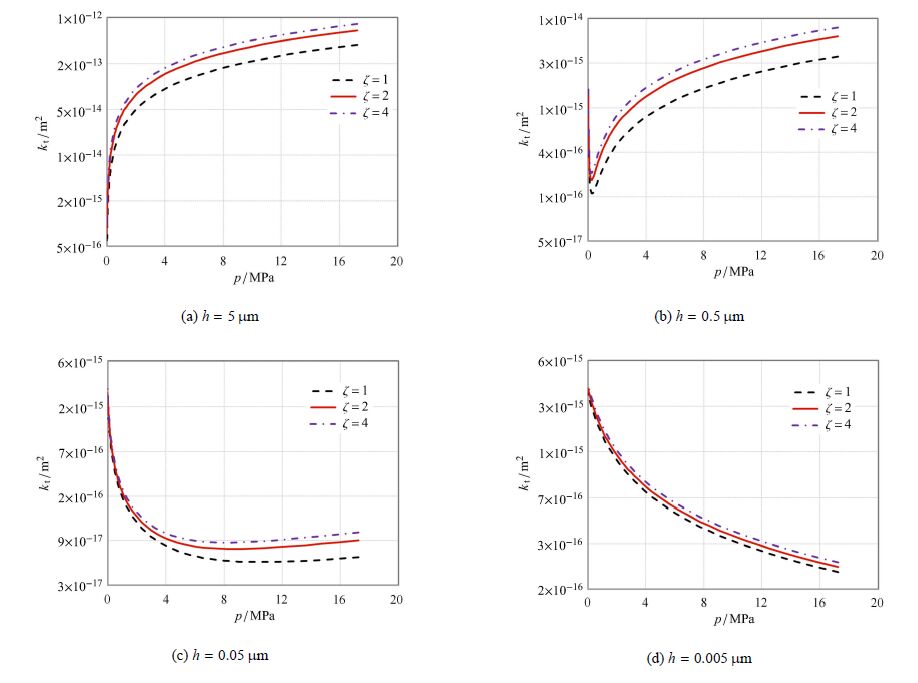
微裂缝气体传输表观渗透率$k_{\rm t}$是由滑脱流动表观渗透率$k_{\rm vs - \omega }$和努森扩散表观渗透率$k_{\rm k- \omega }$组成的,其变化规律受微裂缝开度和压力共同决定的. 图4表明,在微裂缝开 度$h \geqslant 0.5 u$m,气体传输能力随压力降低而减弱,随微裂缝开度减小而减弱,这是由于微裂缝气体一直以滑脱流动为主(图4(a)和图4(b));在微裂缝开度$h =0.05 u$m,气体传输能力随压力降低先减弱后增强,这是由于微裂缝气体先以滑脱流动为主,后逐渐变为努森扩散为主,且气体稀有效应也逐渐增强图4(c);在微裂缝开度$h =0.005 u$m,气体传输能力随压力降低而持续增强,这是由于微裂缝气体一直以努森扩散为主,且气体稀有效应明显图4(d);图4还表明,相同开度且纵横比越大的微裂缝,气体传输能力越强,且在高压力和大开度微裂缝的情况下表现的更明显.
|
图4 不同微裂缝开度的$k_{\rm t}- p$关系曲线 Fig.4 The curves for $k_{\rm t}-p$ in micro fractures with different aperture and aspect ratio |
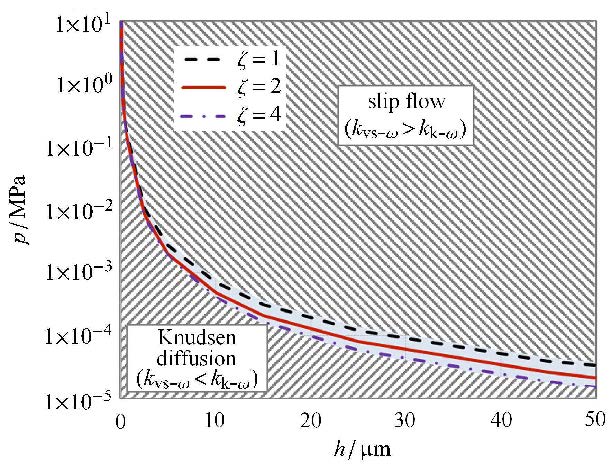
图5 为压力和微裂缝开度的交会图,曲线为滑脱流动和努森扩散表观渗透率等值线. 等值线右上方区域是以滑脱流动为主;等值 线左下方区域是以努森扩散为主. 图5表明:微裂缝开度和压力均大时,主要以滑脱流动为主;微裂缝开度和压力均小时,主要以努森扩散为主;当微裂缝纵横比增大时,表观渗透率等值线向左下方区域移动. 这是因为相同开度下,与纵横比小的微裂缝相比,纵横比大的微裂缝需在更低压力条件下,滑脱流动与努森扩散才表现为同等重要.
|
图5 不同纵横比微裂缝$p$-$h$交会图 Fig.5 Cross plot of $p$-$ h $ in micro fractures with different aspect ratio |
(1)建立了页岩气和致密砂岩气藏微裂缝气体传输模型. 模型可靠性已通过分子模拟数据验证.
该模型能够合理描述微裂缝气体所有传输机理,包括连续流动,滑脱流动和过渡流动.
(2)新模型能够合理刻画不同开发阶段,微裂缝气体各传输机理对传输贡献的逐渐变化过程.
(3)微裂缝形状和尺度影响气体传输. 相同开度且纵横比越大的微裂缝,气体传输能力越强,这种现象在高压和大开度微裂缝的情况下表现的更明显.
本文初步探讨了页岩气和致密砂岩气藏储集层微裂缝气体传输机理、模型和特性,但仅限于理想气体,未考虑真实气体效应[53, 54]、吸附/解吸附和吸附气体表面扩散[62, 63]对气体传输的影响.
| [1] | Chen J, Xiao XM. Evolution of nanoporosity in organic-rich shales during thermal maturation. Fuel, 2014, 129: 173-181 |
| [2] | Rahmanian M, Solano N, Aguilera R. Storage and output flow from shale and tight gas reservoirs. In: Proceeding of SPE Western Regional Meeting, Anaheim, California, May 27-29, 2010. SPE 133611 |
| [3] | Solano NA. Reservoir characterization of the upper Jurassic-lower cretaceous Nikanassin group. [MSc Thesis]. University of Calgary, Calgary, Canada, September, 2010 |
| [4] | Chalmers GR, Bustin RM, Power IM. Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/ transmission electron microscopy image analyses: Examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units. AAPG Bulletin, 2012, 96(6): 1099-1119 |
| [5] | Singh H, Javadpour F, Ettehadtavakkol A, et al. Nonempirical apparent permeability of shale. SPE Reservoir Evaluation & Engineering, 2014, 17(03): 414-424 |
| [6] | Rahmanian M, Aguilera R, Kantzas A. A new unified diffusion-viscous-flow model based on pore-level studies of tight gas formations. SPE Journal, 2013, 18(1): 38-49 |
| [7] | Thomas V, Jorg T. An analytically predictive model for moderately rarefied gas flow. J Fluid Mech, 2012, 698: 406-422 |
| [8] | Ma JS, Sanchez JP, Wu KJ, et al. A pore network model for simulating non-ideal gas flow in micro-and nano-porous materials. Fuel, 2014, 116: 498-508 |
| [9] | Thompson SL, Owens WR. A survey of flow at low pressures. Vacuum, 1975, 25(4): 151-156 |
| [10] | Sun YP, Wu QH, Wei MZ, et al. Experimental study of friction reducer flows in microfracture. Fuel, 2014, 131: 28-35 |
| [11] | Smolouchowski M. Transpiration und diffusion verdunnter gase. Ann Phys, 1910, 33: 1559-1570 |
| [12] | Kennard EH. Kinetic Theory of Gases. New York: McGraw-Hill, 1938 |
| [13] | Eldridge BD, Brown LF. The effect of cross sectional pore shape on knudsen diffusion in porous materials. AIChE J, 1976, 22 (5): 942-944 |
| [14] | Matson SL, Quinn JA. Knudsen diffusion through noncircular pores: textbook errors. AIChE J, 1977, 23(5): 768-770 |
| [15] | White FM. Viscous Fluid Flow. McGraw-Hill International Editions, Mechanical Engineering Series, 1991 |
| [16] | 糜利栋, 姜汉桥, 李俊键等. 页岩储层渗透率数学表征. 石油学报, 2014, 35(5): 928-934 (Mi Lidong, Jiang Hanqiao, Li Junjian, et al. Mathematical characterization of permeability in shale reservoirs. Acta Petrolei Sinica, 2014, 35 (5): 928-934 (in Chinese)) |
| [17] | 李相方, 蒲云超, 孙长宇等. 煤层气与页岩气吸附/解吸的理论再认识. 石油学报, 2014, 35(6): 1113-1129 (Li Xiangfang, Pu Yunchao, Sun Changyu, et al. Recognition of absorption/desorption theory in coalbed methane reservoir and shale gas reservoir. Acta Petrolei Sinica, 2014, 35(6): 1113-1129 (in Chinese)) |
| [18] | 张东晓, 杨婷云. 页岩气开发综述. 石油学报, 2013, 34(4): 792-801 (Zhang Dongxiao, Yang Tingyun. An overview of shale-gas production. Acta Petrolei Sinica, 2013, 34(4): 792-801 (in Chinese)) |
| [19] | 姚同玉, 黄延章, 李继山. 页岩气在超低渗介质中的渗流行为. 力学学报, 2012, 44(6): 990-995 (Yao Tongyu, Huang Yanzhang, Li Jishan. Flow regim for shale gas in extra low permeability porous media. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 990-995 (in Chinese)) |
| [20] | Piekos, ES. DSMC modeling of micromechanical devices. Doctoral dissertation, Massachusetts Institute of Technology, 1995 |
| [21] | Binder K, Horbach J, Kob W, et al. Molecular dynamics simulations. J Phys: Condens Matter, 2004, 16: S429-S453 |
| [22] | Loyalka S, Hamoodi S. Poiseuille flow of a rarefied gas in a cylindrical tube: Solution of linearized Boltzmann equation. Phys Fluids A, 1990, 2 (11): 2061-2065 |
| [23] | Gad-el-hak M. The fluid mechanics of microdevices-The Freeman scholar lecture. Trans ASME: J Fluids Engng, 1999, 121: 5-33 |
| [24] | Coppens MO, Dammers AJ. Effects of heterogeneity on diffusion in nanopores from inorganic materials to protein crystals and ion channels. Fluid Phase Equilib, 2006, 246(1-2): 308-316 |
| [25] | Roy S, Raju R, Chuang HF, et al. Modelling gas flow through microchannels and nanopores. J Appl Phys, 2003, 93: 4870-4879 |
| [26] | Javadpour F, Fisher D, Unsworth M. Nanoscale gas flow in shale gas sediments. J Can Petrol Technol, 2007, 46(10): 55-61 |
| [27] | Javadpour, F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). J Can Petrol Technol, 2009, 48(08): 16-21 |
| [28] | Azom, PN, Javadpour F. Dual-continuum modeling of shale and tight gas reservoirs. In: Proceeding of SPE Annual Technical Conference and Exhibition, San Antonio, Texas, USA, October 8-10, 2012. SPE 159584 |
| [29] | Darabi H, Ettehad A, Javadpour F, et al. Gas flow in ultra-tight shale strata. J Fluid Mech, 2012, 710: 641-658 |
| [30] | Shen S, Chen G, Crone RM, et al. A kinetic-theory based first order slip boundary condition for gas flow. Phys Fluids, 2007, 19(8): 086101 |
| [31] | Maurer J, Tabeling P, Joseph P, et al. Second-order slip laws in microchannels for helium and nitrogen. Phys Fluids, 2003, 15(9): 2613-2621 |
| [32] | Beskok A, Karniadakis GE. A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophy Eng, 1999, 3(1): 43-77 |
| [33] | Sun YH, Chan WK. Analytical modeling of rarefied Poiseuille flow in microchannels. Journal of Vacuum Science & Technology A, 2004, 22(2): 383-394 |
| [34] | Adzumi H. Studies on the flow of gaseous mixtures through capillaries. III. The flow of gaseous mixtures at medium pressures. Bull Chem Soc Jpn, 1937, 12 (6): 292-303 |
| [35] | Brown GP, DiNardo A, Cheng GK, et al. The flow of gases in pipes at low pressures. Journal of Applied Physics, 1946, 17(10): 802-813 |
| [36] | Scott DS, Dullien FAL. Diffusion of ideal gases in capillaries and porous solids. AIChE J, 1962, 8(1): 113-117 |
| [37] | Browne VA, John JEA. Vacuum radial flow from the viscous through the free molecule regime. Vacuum, 1970, 20(12): 525-533 |
| [38] | Ertekin T, King G, Schwerer F. Dynamic gas slippage: a unique dual-mechanism approach to the flow of gas in tight formations. SPE Formation Evaluation, 1986, 1(01): 43-52 |
| [39] | Liu Q, Shen P, Yang P. Pore scale network modeling of gas slippage in tight porous media. In: Proceeding of an AMS-IMS-SIAM Joint Summer Research Conference on Fluid Flow and Transport in Porous Media: Mathematical and Numerical Treatment, South Hadley, Massachusetts, June 17-21, 2001 |
| [40] | 李治平, 李智峰. 页岩气纳米级孔隙渗流动态特征. 天然气工业, 2012, 32(4): 1-4 (Li Zhiping, Li Zhifeng. Dynamic seepage characteristics of shale gas nanoscale pores. Natural Gas Industry, 2012, 32(4): 1-4 (in Chinese)) |
| [41] | Wu KL, Li XF, Wang CC, et al. Apparent permeability for gas flow in shale reservoirs coupling effects of gas diffusion and desorption. In: Proceeding of SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, Colorado, USA, August 25-27, 2014. 1921039 |
| [42] | Wu KL, Li XF, Wang CC, et al. Model for surface diffusion of adsorbed gas in nanopores of shale gas reservoirs. Ind Eng Chem Res, 2015, 54(12): 3225-3236 |
| [43] | Wu KL, Li XF, Guo CH, et al. A unified model for gas transport in nanopores of shale gas reservoirs: coupling pore diffusion and surface diffusion. SPE J, 2015 (in press) |
| [44] | Wu KL, Li XF, Guo CH, et al. Adsorbed gas surface diffusion and bulk gas transport in nanopores of shale reservoirs with real gas effect-adsorption-mechanical coupling. In: Proceedings of SPE Reservoir Simulation Symposium, Houston, Texas, USA, February 23-25, 2015. SPE 173201 |
| [45] | Loeb LB. The Kinetic Theory of Gases, 2nd edn. McGraw-Hill Co. Inc., New York, 1934 |
| [46] | Choi JG, Do DD, Do HD. Surface diffusion of adsorbed molecules in porous media: monolayer, multilayer, and capillary condensation regimes. Ind Eng Chem Res, 2001, 40(19): 4005-4031 |
| [47] | Karniadakis G, Beskok A, Aluru NR. Microflows and Nanoflows: Fundamentals and Simulation. New York: Springer Verlag, 2005 |
| [48] | Cercignani C. Theory and Applications of the Holzmann Equation. Elsevier, New York, 1975 |
| [49] | Williams MMR. Mathematical Methods in Particle Transport Theory. Butterworths, London, 1971 |
| [50] | Kogan MN. Rarefied Gas Dynamics. Plenum, New York, 1969 |
| [51] | 于荣泽, 张晓伟, 卞亚南等.页岩气藏流动机理与产能影响因素分析. 天然气工业, 2012, 32(9): 10-15 (Yu Rongze, Zhang Xiaowei, Bian Yanan, et al.Flow mechanism of shale gas reservoirs and influential factors of their productivity. Natural Gas Industry, 2012, 32(9): 10-15 (in Chinese)) |
| [52] | Sone Y, Hasegawa M. Poiseuille and thermal transpiration flows of a rarefied gas through a rectangular pipe. J Vac Soc of Japan, 1987, 30 (5): 425-428 |
| [53] | Wu KL, Chen ZX, Li XF. Real gas transport through nanopores of varying cross-section type and shape in shale gas reservoirs. Chemical Engineering Journal, 2015, 281: 813-825 |
| [54] | Wu KL, Chen ZX, Wang H, et al. A model for real gas transfer in nanopores of shale gas reservoirs. In: Proceeding of EUROPEC Madrid, Spain, June 1-4, 2015. SPE 174293 |
| [55] | Hinds BJ, Chopra N, Rantell T, et al. Aligned multiwalled carbon nanotube membranes. Science, 2004, 303(5654): 62-65 |
| [56] | Celebi K, Buchheim J, Wyss RM, et al. Ultimate permeation across atomically thin porous graphene. Science, 2014, 344(6181): 289-292 |
| [57] | Nicholson D, Petropoulos JH. Capillary models for porous media. VIII. A study of gaseous flow in the transition from the Knudsen to the Poiseuille flow regimes. Journal of Physics D: Applied Physics, 1978, 11(8): 1179-1187 |
| [58] | Petropoulos JH, Papadokostaki KG. May the Knudsen equation be legitimately, or at least usefully, applied to dilute adsorbable gas flow in mesoporous media. Chemical Engineering Science, 2012, 68(1): 392-400 |
| [59] | Nicholson D, Petropoulos JH. Influence of adsorption forces on the flow of dilute gases through porous media. Journal of Colloid and Interface Science, 1973, 45(3): 459-466 |
| [60] | Pages X, Rouessac V, Cot D, et al. Gas permeation of PECVD membranes inside alumina substrate tubes. Separation and purification technology, 2001, 25(1): 399-406 |
| [61] | Kim HW, Yoon HW, Yoon SM, et al. Selective gas transport through few-layered graphene and graphene oxide membranes. Science, 2013, 342(6154): 91-95 |
| [62] | 吴克柳, 李相方, 陈掌星. 页岩纳米孔吸附气表面扩散机理和数学模型. 中国科学: 技术科学, 2015, 45: 525-540 (Wu Keliu, Li Xiangfang, Chen Zhangxing. The mechanism and mathematical model for the adsorbed gas surface diffusion in nanopores of shale gas reservoirs. Sci Sin Tech, 2015, 45: 525-540 (in Chinese)) |
| [63] | 吴克柳,李相方,陈掌星.页岩气纳米孔气体传输模型. 石油学报, 2015, 36(7): 837-848, 889 (Wu Keliu, Li Xiangfang, Chen Zhangxing. A model for gas transport through nanopores of shale gas reservoirs. Acta Petrolei Sinica, 2015, 36(7): 837-848, 889 (in Chinese)) |
2. Department of Chemical and Petroleum Engineering, University of Calgary, Alberta T2N1N4, Canada
 2015, Vol. 47
2015, Vol. 47