页岩气藏资源丰富,开发潜力巨大,已成为目前研究的热点问题. 页岩气藏渗透率极低[1],往往天然裂缝发育,水平井分段压裂是 开发这类气藏经济有效的方法[2, 3]. 目前国内外学者在页岩气藏压裂水平井数值模拟[4, 5]与试井分析[6, 7, 8]方面做了一系列研究.
Ozkan等[9]基于双重介质模型建立页岩气藏压裂水平井三线性流模型,模型考虑页岩中的黏性流和扩散机制,并同常规砂岩气藏 进行了对比,但忽略了气体在基岩骨架表面的吸附解吸机制. Cheng 等[10]考虑人工裂缝导流能力、吸附解吸、裂缝间距等多种因素建立页岩气藏压裂水平井数值试井模型,但模型仅考虑人工裂 缝周围的次生诱导裂缝,忽略了页岩气藏中广泛分布的天然裂缝;Sung等[11]基于双重介质模型考虑人工裂缝内气体高速非达西流动,基岩骨架吸附解吸等机制建立试井解释模型,但人工裂缝采用是局 部网格加密处理的单孔介质模型,当人工裂缝开度较小时,模型网格剖分量大;Mohammad等[12]将页岩气藏划分为基岩、次生裂缝诱 导、人工裂缝3个区域,针对每一个区域实际情况,考虑应力敏感,吸附解吸,滑脱效应等因素,建立完整的页岩气藏数值模拟模型,研 究上述非线性因素对产能的影响,研究表明裂缝系统的应力敏感与基岩骨架的吸附解吸对气体产能影响较大,在页岩气藏数值模拟中必须予以考虑,非达西流与滑脱效应对产能影响较小可以忽略,模型局限于产能分析,没有研究上述非线性因素对气藏压力响应的影响. Wu等[13]基于MINC模型考虑岩石变形、气体滑脱效应、吸附解吸等机制建立页岩气藏两相渗流数值模拟模型,模型适用性较强, 但是对于人工裂缝的处理局限于局部网格加密,计算效率低,同时压力分析没有考虑压力导数.
张帆[14]基于Langmuir等温吸附方程和Fick扩散定律建立了综合考虑吸附解吸和扩散作用的单重介质页岩气藏多级压裂水平井 的不稳定渗流模型,并进一步考虑基质系统的扩散作用与达西渗流建立双重介质页岩气藏非稳态窜流模型. 樊冬艳[15]针对页岩气藏中吸附气和游离气共存的储集方式,基于双重介质模型建立了考虑吸附解吸的页岩气藏不稳定渗 流数学模型,并定义新的参数来表征基质中吸附解吸气量与游离气弹性释放量的比值,研究表明开采过程中页岩吸附解吸气量所占 比例较大,吸附解吸可以减缓地层中压力波的传播,提高稳产时间. 但是两者的模型都没有考虑裂缝系统应力敏感,非达西流等非线性因素.
针对现有研究不足,本文将采用双重介质(基岩系统与天然裂缝系统)和离散裂缝[16, 17](人工裂缝)混合模型,结合开发实际综合考虑基岩骨架表面气体吸附解吸,天然裂缝系统渗透率的应力敏感,人工裂缝内的非达西流等非线性因素,建立页岩气藏压裂水平井数值试井模型,采用有限元方法进行数值求解. 根据试井特征曲线,分析上述非线性因素对压力响应的影响,为页岩气藏分段压裂水平井开采的压力动态特征描述提供理论指导.
1 页岩气藏压裂水平井试井解释模型根据页岩气藏的特性假定页岩气藏由基岩系统和天然裂缝系统组成,并满足以下基本假设:(1)气藏:盒状封闭; (2)考虑单相气体渗流;(3)人工裂缝内考虑气体非达西渗流;(4)页岩基岩渗透率较低,为纳达西尺度,忽略基岩内的流动; (5)页岩基岩表面吸附有大量的甲烷气体,且吸附规律符合Langmuir等温吸附公式;(6)天然裂缝内气体主要以游离相的形式出现, 是主要的运移通道,遵循达西渗流规律,考虑天然裂缝渗透率的应力敏感性;(7)渗流过程为等温渗流.
1.1 人工裂缝系统数学模型室内和现场研究表明,由于气体黏度低,所以实际气体流速非常高,特别是在压力梯度较大的井筒附近[18]. 惯性力使得气体流动产生高速非达西效 应[19, 20]. 本文考虑与水平井相连的人工裂缝中甲烷气体高速流动产生的非达西效应.
采用考虑二次流动项的Forchheimer方程描述该非达西流动[21],如式(1)所示
$$
-\nabla p_{\rm a} = dfrac{\mu }{k_{\rm a} }v_{\rm a} + \rho Fv_{\rm a}^2
$$
(1)
根据Wattenbarger等的观点,将Forchheimer方程作为达西定律的修正公式[22]表示出来
$$
v_{\rm a} = - dfrac{k_{\rm a} }{\mu }\delta \nabla p_{\rm a}
$$
(2)
式(2)中,$\delta $是与流速有关的非达西流动效应的修正系数,如式(3)所示
$$
\delta = dfrac{1}{1 + dfrac{k_{\rm a} }{\mu }\rho Fv_{\rm a} }
$$
(3)
人工裂缝开度一般为毫米级,流动模拟中,裂缝网格尺寸与基岩网格尺寸相差几个数量级,导致网格剖分数量大增,计算量巨大. 因此本文采用离散裂缝模型将人工裂缝中的流动进行等效降维处理,从而提高计算效率.
如在二维问题中,裂缝简化为线单元,如图1所示.
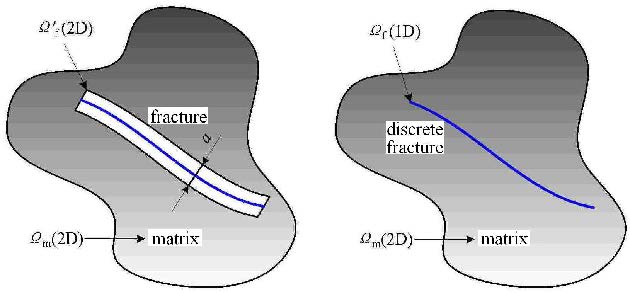
|
图1 离散裂缝模型示意图 Fig.1 The schematic of discrete fracture model |
人工裂缝与天然裂缝交界处的压力处处相等,则人工裂缝的数学模型可表示为
$$\left\{ {\matrix{
{\matrix{
{{\phi _{\rm{a}}}{C_{\rm{a}}}{{\partial {p_{\rm{a}}}} \over {\partial t}} - \nabla \cdot \left( {\delta {{{k_{\rm{a}}}} \over \mu }\nabla {p_{\rm{a}}}} \right) = {q_{\rm{a}}}} \hfill \cr
{{p_{\rm{a}}}\left( {x,y,z;t = 0} \right) = {p_{\rm{i}}}} \hfill \cr
{{p_{\rm{a}}}\left( {x,y,z;t} \right) = {p_{\rm{n}}}\left( {x,y,z;t} \right)\;(x,y,z) \in {\Omega _{\rm{a}}}} \hfill \cr
} } \hfill \cr
} } \right.$$
(4)
其中,$p_{\rm a}$,$p_{\rm n}$,$p_{\rm i}$分别表示人工裂缝内的压力,天然裂缝系统压力,地层的原始压力,Pa;
$\phi_{\rm a}$为人工裂缝内孔隙度;$k_{\rm a}$为人工裂缝内渗透率,m$^{2}$;$C_{\rm
a}$为人工裂缝综合压缩系数,Pa$^{- 1}$;$\mu
$为流体黏度,在本文计算的压力范围内,黏度变化很小,视作常数处理,Pa$\cdot $s;$q_{\rm
a}$为人工裂缝内单位体积源汇处的体积流量值,s$^{ - 1}$;$v_{\rm a}$为人工裂缝内气体流速,m/s;$\varOmega _{\rm
a}$表示人工裂缝边界. $F$,Forchheimer系数,采用Evans和Civan给出的经验公式[23]表示
$$
F = dfrac{4.87\times 10^{c}}{k_{\rm a}^{1.021} }
$$
(5)
系数$c$一般取9,非达西效应越强,$c$取值越大. 在低速流动时,$\delta $为1,Forchheimer方程还原为达西定律.
根据Lee等[24, 25]的研究,把非达西效应考虑成拟表皮,可以很好的解释考虑非达西流的拟压力与拟压力导数曲线特征.
$$
S_{\rm a} = S + Dq_{\rm g}
$$
(6)
其中$D$表示非达西系数
$$
D = dfrac{7.18\times 10^{ - 8}Fk_{\rm a} M_{\rm g} p_{\rm sc} }{hr_{\rm w} T_{\rm sc} \mu }
$$
(7)
其中,$q_{\rm g}$表示气井产量,m$^{3}$/d;$M_{\rm g}$表示气体的摩尔质量,kg$\cdot $mol$^{ - 1}$;$p_{\rm sc}$为标准状态下的压力,取1.013$\times $10$^{5}$ Pa;$h$地层厚度,m;$r_{\rm w}$为井筒半径,m;$T_{\rm sc}$为标准状态下的温度,取293.2 K.
1.2 页岩储层双重介质的单渗模型页岩气藏开发过程中,地层孔隙压力的降低影响储层的孔渗性质. Soeder和Chen等室内试验[26, 27, 28]与理论推导[29]均表明页岩储层渗透率对应力较为敏感,随应力成指数变化趋势. 本文基于渗透率变异模数的指数模型考虑页岩气藏天然裂缝系统渗透率的应力敏感效应. 由于基岩渗透率极低,忽略气体在基岩中的流动,因此不考虑基岩渗透率的应力敏感性.
天然裂缝渗透率随气藏压力的变化关系为
$$
\gamma = dfrac{1}{k_{\rm n} }\dfrac{\partial k_{\rm n} }{\partial \psi _{\rm n} }
$$
(8)
对式(8)积分得
$$
k_{\rm n} = k_{{{\rm n}i}} {\rm e}^{ - \gamma \left( {\psi _{i} - \psi _{\rm n} } \right)}
$$
(9)
页岩储层的渗流方程满足
$$\left. {\matrix{
{\matrix{
{{\partial \over {\partial t}}\left( {{\rho _{\rm{n}}}{\varphi _{\rm{n}}}} \right) + \nabla \cdot \left( { - {{{k_{\rm{n}}}{\rho _{\rm{n}}}} \over \mu }\nabla {p_{\rm{n}}}} \right) = } \hfill \cr
{{{\alpha {k_{\rm{m}}}} \over \mu }\left( {{\rho _{\rm{m}}}{p_{\rm{m}}} - {\rho _{\rm{f}}}{p_{\rm{f}}}} \right)} \hfill \cr
{{\partial \over {\partial t}}\left( {{\rho _{\rm{m}}}{\varphi _{\rm{m}}}} \right) + \left( {1 - {\varphi _{\rm{m}}}} \right){{\partial {Q_{{\rm{ads}}}}} \over {\partial t}} = } \hfill \cr
{ - {{\alpha {k_{\rm{m}}}} \over \mu }\left( {{\rho _{\rm{m}}}{p_{\rm{m}}} - {\rho _{\rm{f}}}{p_{\rm{f}}}} \right)} \hfill \cr
} } \hfill \cr
} } \right\}$$
(10)
其中,$\gamma $表示渗透率变异模数,s/Pa;$\rho_{i}=M_{\rm g}p_{i}\cdot (Z_{i}RT)^{ - 1}$,$i=m,
n$分别代表基岩系统跟天然裂缝系统,kg/m$^{3}$;$Z_{i}$为不同系统压缩因子;$p_{\rm m}$,$p_{\rm
n}$分别表示基岩与裂缝压力,Pa;$R$为理想气体常数,$R=8.314$ J$\cdot $K$^{-1}\cdot
$mol$^{-1}$;$T$为气藏温度,K;$\varphi_{\rm m}$,$\varphi_{\rm
n}$分别表示基岩系统与天然裂缝系统孔隙度;$k_{\rm n}$为天然裂缝系统渗透率,m$^{2}$;$k_{{\rm n}
i}$表示天然裂缝系统本征渗 透率,m$^{2}$;$\mu $为气体黏度,Pa$\cdot $s;$t$为时间,s;$Q_{\rm
ads}$为基岩单位骨架体积的吸附量,满足Langmuir吸附[11, 30]等温公式
$$
Q_{\rm ads } = dfrac{\rho _{\rm s} M_{\rm g} V_{\rm L} }{V_{\rm std } } \cdot dfrac{p_{\rm m} }{p_{\rm m} +
p_{\rm L} }
$$
(11)
化简式(10)可得
\[\left. {\begin{array}{*{20}{l}}
\begin{array}{l}
\mu {\varphi _{\rm{n}}}{C_{\rm{t}}}\frac{{\partial {\psi _{\rm{n}}}}}{{\partial t}} + \nabla \cdot \left( { - {k_{\rm{n}}}\nabla {\psi _{\rm{n}}}} \right) - \\
\gamma {k_{\rm{n}}}{\left( {\nabla {\psi _{\rm{n}}}} \right)^2} = 2\alpha {k_{\rm{m}}}\left( {{\psi _{\rm{m}}} - {\psi _{\rm{n}}}} \right)\\
\mu {\varphi _{\rm{m}}}{C_{\rm{t}}}\frac{{\partial {\psi _{\rm{m}}}}}{{\partial t}} + \\
\left( {1 - {\varphi _{\rm{m}}}} \right)\frac{{{\rho _{\rm{s}}}RT{V_{\rm{L}}}}}{{{V_{{\rm{std}}}}}} \cdot \frac{{\mu Z{p_{\rm{L}}}}}{{{p_{\rm{m}}}{{\left( {{p_{\rm{m}}} + {p_{\rm{L}}}} \right)}^2}}} \cdot \frac{{\partial {\psi _{\rm{m}}}}}{{\partial t}} = \\
- 2\alpha {k_{\rm{m}}}\left( {{\psi _{\rm{m}}} - {\psi _{\rm{n}}}} \right)
\end{array}
\end{array}} \right\}\]
(12)
定义特征参数$\beta $,表示单位时间内由于基质压力降低,基质骨架吸附解吸气量与游离气弹性能释放能量的比值,即
\[\begin{array}{l}
\beta = \frac{{\left( {1 - {\phi _{\rm{m}}}} \right)\partial {Q_{{\rm{ads}}}}/\partial t}}{{\partial \left( {{\rho _{\rm{m}}}{\phi _{\rm{m}}}} \right)/\partial t}} = \\
\left( {1 - {\phi _{\rm{m}}}} \right)\frac{{{\rho _{\rm{s}}}RT{V_{\rm{L}}}}}{{{V_{{\rm{std}}}}{C_{\rm{t}}}{\phi _{\rm{m}}}}} \cdot \frac{{Z{p_{\rm{L}}}}}{{{p_{\rm{m}}}{{\left( {{p_{\rm{m}}} + {p_{\rm{L}}}} \right)}^2}}}
\end{array}\]
(13)
定义无因次参数 \[\begin{array}{l} {\psi _{j{\rm{D}}}} = \frac{{{k_{\rm{n}}}h{T_{{\rm{sc}}}}}}{{qT{p_{{\rm{sc}}}}}}\left( {{\psi _{\rm{o}}} - {\psi _j}} \right)\qquad j = a,m,n\\ \lambda = \alpha {L^2}{k_{\rm{m}}}/{k_{\rm{n}}}{\mkern 1mu} ,\;\;\eta = {\phi _{\rm{m}}}{C_{\rm{g}}} + {\phi _{\rm{n}}}{C_{\rm{g}}}\\ \omega = \frac{{{\phi _{\rm{n}}}{C_{\rm{g}}}}}{\eta }{\mkern 1mu} ,\;\;{t_{\rm{D}}} = \frac{{{k_{\rm{n}}}t}}{{\eta \mu {L^2}}}{x_{\rm{D}}} = \frac{y}{L}{\mkern 1mu} ,\;\;\\ {x_{\rm{D}}} = \frac{y}{L}{\mkern 1mu} ,\;\;{h_{\rm{D}}} = \frac{h}{L} \end{array}\]
对式(4),(12)进行无因次化简得人工裂缝系统
\[\left. \begin{array}{l}
\delta \frac{{{k_{\rm{a}}}}}{{{k_{\rm{n}}}}}\nabla \cdot \nabla \left( {{\psi _{{\rm{aD}}}}} \right) = \\
\frac{{{\phi _{\rm{a}}}{C_{\rm{a}}}}}{{{\varphi _{\rm{m}}}{C_{\rm{m}}} + {\varphi _{\rm{n}}}{C_{\rm{n}}}}}\frac{{\partial {\psi _{{\rm{aD}}}}}}{{\partial {t_{\rm{D}}}}} - 2\pi {h_{\rm{D}}}{q_{{\rm{aD}}}}{\psi _{{\rm{aD}}}}\\
\left( {{x_{\rm{D}}},{y_{\rm{D}}};{t_{\rm{D}}} = 0} \right) = 0{\psi _{{\rm{aD}}}}|\\
\partial {\Omega _{\rm{a}}} = {\psi _{{\rm{nD}}}}n
\end{array} \right\}\]
(14)
基岩和天然裂缝系统
\[\left. \begin{array}{l}
\nabla \cdot \left( {{{\rm{e}}^{ - y\left( {{\psi _i} - {\psi _{\rm{n}}}} \right)}}\nabla {\psi _{{\rm{nD}}}}} \right) = \\
\omega \frac{{\partial {\psi _{{\rm{nD}}}}}}{{\partial {t_{\rm{D}}}}} - \lambda \left( {{\psi _{{\rm{mD}}}} - {\psi _{{\rm{nD}}}}} \right)\\
\left( {1 - \omega } \right)\left( {1 + \beta } \right)\frac{{\partial {\psi _{{\rm{mD}}}}}}{{\partial {t_{\rm{D}}}}} = \\
- \lambda \left( {{\psi _{{\rm{mD}}}} - {\psi _{{\rm{nD}}}}} \right)\\
{\psi _{{\rm{mD}}}}\left( {{x_{\rm{D}}},{y_{\rm{D}}};{t_{\rm{D}}} = 0} \right) = \\
{\psi _{{\rm{nD}}}}\left( {{x_{\rm{D}}},{y_{\rm{D}}};{t_{\rm{D}}} = 0} \right) = 0\\
{\psi _{{\rm{nD}}}}|\partial {\Omega _{\rm{a}}} = {\psi _{{\rm{aD}}}}
\end{array} \right\}\]
(15)
对盒状页岩气藏分段压裂水平井模型进行网格剖分,水平井采用一维线单元,人工裂缝基于离散裂缝模型进行显式降维处理, 采用二维三角面单元进行剖分,基岩和天然裂缝系统采用三维四面体单元进行剖分.
二维人工裂缝面的单元特性矩阵为
$$\eqalign{
& {{{a_{\rm{p}}}{\varphi _{\rm{a}}}{C_{\rm{a}}}} \over {{\varphi _{\rm{m}}}{C_{\rm{m}}} + {\varphi _{\rm{n}}}{C_{\rm{n}}}}}\int\!\!\!\int\limits_{{S_{\rm{f}}}} {N_{{\rm{e}},{\rm{f}}}^{\rm{T}}{N_{{\rm{e}},{\rm{f}}}}} {\rm{d}}{S_{\rm{f}}}{{\partial \psi _{{\rm{aD}}}^{(e)}} \over {\partial {t_{\rm{D}}}}} + \cr
& {{{a_{\rm{p}}}\delta {k_{\rm{a}}}} \over {{k_{\rm{n}}}}}\int\!\!\!\int\limits_{{S_{\rm{f}}}} {\nabla N_{{\rm{e}},{\rm{f}}}^{\rm{T}}\nabla {N_{{\rm{e}},{\rm{f}}}}} {\rm{d}}{S_{\rm{f}}}\psi _{{\rm{aD}}}^{(e)} = \cr
& 2\pi {h_{\rm{D}}}{a_{\rm{p}}}\int\!\!\!\int\limits_{{S_{\rm{f}}}} {{q_{{\rm{aD}}}}N_{{\rm{e}},{\rm{f}}}^{\rm{T}}} d{S_{\rm{f}}} \cr} $$
(16)
储层双重介质区域基岩和裂缝系统的单元特性矩阵为
$$\eqalign{
& \omega \int\limits_{{\Omega _{_{({\rm{e}})}}}} {N_{\rm{e}}^{\rm{T}}{N_{\rm{e}}}{\rm{d}}{\Omega _{\rm{e}}}} {{\partial \psi _{{\rm{nD}}}^{({\rm{e}})}} \over {\partial {t_{\rm{D}}}}}{\mkern 1mu} + \cr
& \int\limits_{{\Omega _{({\rm{e}})}}} {\nabla N_{\rm{e}}^{\rm{T}}\nabla {N_{\rm{e}}}{\rm{d}}{\Omega _e}\psi _{{\rm{nD}}}^{({\rm{e}})} - } \cr
& \lambda \int\limits_{_{{\Omega _{({\rm{e}})}}}} {{N_{\rm{e}}}\left( {\psi _{{\rm{mD}}}^{({\rm{e}})} - \psi _{{\rm{nD}}}^{({\rm{e}})}} \right)N_{\rm{e}}^{\rm{T}}{\rm{d}}{\Omega _{\rm{e}}}} = {\bf{0}} \cr} $$
(17)
$$\eqalign{
& \left( {1 - \omega } \right)\int_{\Omega ({\rm{e}})} {N_{\rm{e}}^{\rm{T}}{N_e}} d{\Omega _{({\rm{e}})}}dfrac\partial \psi _{{\rm{mD}}}^{({\rm{e}})}\partial {t_{\rm{D}}} + \cr
& dfrac{k_{\rm{m}}}{k_{\rm{n}}}\int_{\Omega ({\rm{e}})} {\nabla N_{\rm{e}}^{\rm{T}}\nabla {N_{\rm{e}}}} d{\Omega _{({\rm{e}})}}\psi _{{\rm{mD}}}^{({\rm{e}})} + \cr
& \lambda \int_{\Omega ({\rm{e}})} {{N_{\rm{e}}}\left( {\psi _{{\rm{mD}}}^{({\rm{e}})} - \psi _{nD}^{({\rm{e}})}} \right)} N_{\rm{e}}^{\rm{T}}d{\Omega _{({\rm{e}})}} = 0 \cr} $$
(18)
其中 $$\eqalign{ & \nabla {N_{\rm{e}}} = \left[ {\matrix{ {{{\partial {N_1}} \over {\partial x}}} & {{{\partial {N_2}} \over {\partial x}}} & {{{\partial {N_3}} \over {\partial x}}} & {{{\partial {N_4}} \over {\partial x}}} \cr {{{\partial {N_1}} \over {\partial y}}} & {{{\partial {N_2}} \over {\partial y}}} & {{{\partial {N_3}} \over {\partial y}}} & {{{\partial {N_4}} \over {\partial y}}} \cr {{{\partial {N_1}} \over {\partial z}}} & {{{\partial {N_2}} \over {\partial z}}} & {{{\partial {N_3}} \over {\partial z}}} & {{{\partial {N_4}} \over {\partial z}}} \cr } } \right] \cr & \psi _{\rm{n}}^{({\rm{e}})} = \left( {\matrix{ \matrix{ \psi _{{\rm{n1}}}^{({\rm{e}})} \hfill \cr \psi _{{\rm{n2}}}^{({\rm{e}})} \hfill \cr \psi _{{\rm{n3}}}^{({\rm{e}})} \hfill \cr \psi _{{\rm{n4}}}^{({\rm{e}})} \hfill \cr} \cr } } \right){\mkern 1mu} ,\psi _{\rm{m}}^{({\rm{e}})} = \left( {\matrix{ \matrix{ \psi _{{\rm{m1}}}^{({\rm{e}})} \hfill \cr \psi _{{\rm{m2}}}^{({\rm{e}})} \hfill \cr \psi _{{\rm{m3}}}^{({\rm{e}})} \hfill \cr \psi _{{\rm{m4}}}^{({\rm{e}})} \hfill \cr} \cr } } \right) \cr} $$
2.2 有限元整体特性分析
天然裂缝与人工裂缝组合成裂缝系统,裂缝系统与基岩系统的单元特性矩阵与列阵组合得到油藏的整体矩阵和列阵,如式(19)所示
$$\left. {\matrix{
\matrix{
{A_{\rm{f}}}{{\partial {P_{\rm{n}}}} \over {\partial {t_{\rm{D}}}}} + {B_{\rm{f}}}{P_{\rm{n}}} - C\left( {{P_{\rm{m}}} - {P_{\rm{n}}}} \right) = {Q_{\rm{n}}} \hfill \cr
{A_{\rm{m}}}d{{\partial {P_{\rm{m}}}} \over {\partial {t_{\rm{D}}}}} + {B_{\rm{m}}}{P_{\rm{m}}} + C\left( {{P_{\rm{m}}} - {P_{\rm{n}}}} \right) = 0 \hfill \cr} \hfill \cr
} } \right\}$$
(19)
其中,$N_{\rm p}$为油藏节点总数 $$\eqalign{ & {P_{\rm{m}}} = {[{\psi _{{\rm{mD}},{\rm{1}}}},{\psi _{{\rm{mD}},{\rm{2}}}}, \cdots {\psi _{{\rm{mD}},{N_{\rm{p}}}}}]^{\rm{T}}} \cr & {P_{\rm{n}}} = {[{\psi _{{\rm{nD}},1}},{\psi _{{\rm{nD}},2}}, \cdots {\psi _{{\rm{nD}},{N_{\rm{p}}}}}]^{\rm{T}}} \cr & {A_{\rm{f}}} = \omega \int_{{\Omega _{\rm{e}}}} {N_{\rm{e}}^{\rm{T}}} {N_{\rm{e}}}{\rm{d}}{\Omega _{\rm{e}}} + {{{a_{\rm{p}}}{\phi _{\rm{a}}}{C_{\rm{a}}}} \over {{\phi _{\rm{m}}}{C_{\rm{m}}} + {\phi _{\rm{n}}}{C_{\rm{n}}}}}\int\!\!\!\int\limits_{{S_{\rm{f}}}} {N_{{\rm{e}},{\rm{f}}}^{\rm{T}}{N_{{\rm{e}},{\rm{f}}}}} d{S_{\rm{f}}} \cr & {B_{\rm{f}}} = \int_{{\Omega _{\rm{e}}}} {\nabla N_{\rm{e}}^{\rm{T}}} \nabla {N_{\rm{e}}}d{\Omega _{\rm{e}}} + {{{a_{\rm{p}}}} \over {{k_{\rm{n}}}}}\int\!\!\!\int\limits_{{S_{\rm{f}}}} {\nabla N_{{\rm{e}},{\rm{f}}}^{\rm{T}}\nabla {N_{{\rm{e}},{\rm{f}}}}} d{S_f} \cr} $$ $$\eqalign{ & {A_{\rm{m}}} = \left( {1 - \omega } \right)\int_{{\Omega _{\rm{e}}}} {N_{\rm{e}}^{\rm{T}}} {N_{\rm{e}}}d{\Omega _{\rm{e}}} \cr & {B_{\rm{m}}} = {k_{\rm{m}}}{k_{\rm{n}}}\int_{{\Omega _{\rm{e}}}} {\nabla N_{\rm{e}}^{\rm{T}}} \nabla {N_{\rm{e}}}d{\Omega _{\rm{e}}} \cr & C = \lambda \int_{{\Omega _{\rm{e}}}} {N_{\rm{e}}^{\rm{T}}} {N_{\rm{e}}}d{\Omega _{\rm{e}}} \cr} $$
对方程组采用隐式向后差分格式,利用$k$时刻的基岩压力,求得$k +1$时刻裂缝系统压力值,再反代入基岩的控制方程,
得到$k +1$时刻基岩的压力值. $k +1$时刻裂缝系统压力值为
$$\eqalign{
& \left[ {{{{A_{\rm{f}}}} \over {t_{\rm{D}}^{k + 1} - t_{\rm{D}}^k}} + {B_{\rm{f}}} + C} \right]P_{\rm{n}}^{k + 1} = \cr
& Q_{\rm{n}}^{k + 1} + {{{A_{\rm{f}}}P_{\rm{n}}^k} \over {t_{\rm{D}}^{k + 1} - t_{\rm{D}}^k}} + CP_{\rm{m}}^k \cr} $$
(20)
再计算基岩系统$k +1$时刻的压力值
$$
\left[{\dfrac{{ A}_{\rm m} }{t_{\rm D}^{{k + 1}} - t_{\rm D}^{k} } + { C}} \right]P_{\rm m}^{ k + 1
} = dfrac{{ A}_{\rm m} P_{\rm m}^{k} }{t_{\rm D}^{{k + 1}} - t_{\rm D}^{k} } + { C}P_{\rm n}^{ k +
1 }
$$
(21)
盒状封闭页岩气藏内一口水平井压裂5条垂直裂缝,水平井交于裂缝中心. 页岩气藏和人工裂缝的无因次参数为:压裂裂 缝半长$L_{\rm fD} =0.015$,压裂裂缝开度$a_{\rm p} =10^{-3}$,水平井长度$L_{\rm h}=1$,主裂缝、基岩与天然裂缝的渗透率比值分别为$k_{\rm a}/k_{\rm n}=10^{2}$,$k_{\rm m}/k_{\rm n}=10^{-3}$; 气藏长、宽、厚分别为$x_{ \rm eD}=12$,$y_{ \rm eD}=12$,$h_{\rm D}=0.1$;双重介质区域弹性储容比 $\omega =0.1$,窜流因子 $\lambda =1$;基岩系统孔隙度 $\phi_{\rm m} =0.05$,天然裂缝系统孔隙度 $\phi_{\rm f}=0.005$;气藏的原始压力$p_{\rm i} =10 $ MPa,定产量生产$q =0.1$ m$^{3}$/s,天然裂缝系统渗透率$k_{\rm n} =10^{ - 15}$ m$^{2}$,水平井实际长度$L =1 000$ m.
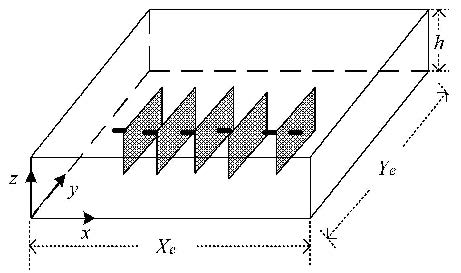
|
图2 页岩气藏压裂水平井示意图 Fig.2 The schematic of fractured horizontal well in shale gas reservoir |
甲烷的摩尔质量$M_{\rm g} =0.016$ kg$\cdot $m$^{ - 3}$,甲烷的摩尔体积$V_{\rm std} =0.022 37 $ m$^{3}\cdot $mol$^{ - 1}$,页岩的密度$\rho_{\rm s}=2 600$ kg$\cdot $m$^{ - 3}$,甲烷气体黏度$\mu =1.2\times 10^{ - 5}$ Pa$\cdot $s,理想气体常数$R=8.314$ J$\cdot $K$^{ - 1}\cdot $mol$^{-1}$,气藏温度$T =323$ K,标准状况下的温度$T_{\rm sc}=273 $ K,Langmuir体积 $V_{\rm L}=5\times 10^{ - 4}$ kg$\cdot $m$^{ - 3}$.
Zerzar等[31]给出未考虑吸附解吸等非线性因素压裂水平井试井压力解,将本文模型进行简化与Zerzar解析解进行对比. 由图3可知本文有限元数值解与Zerzar解析解可以很好地吻合.
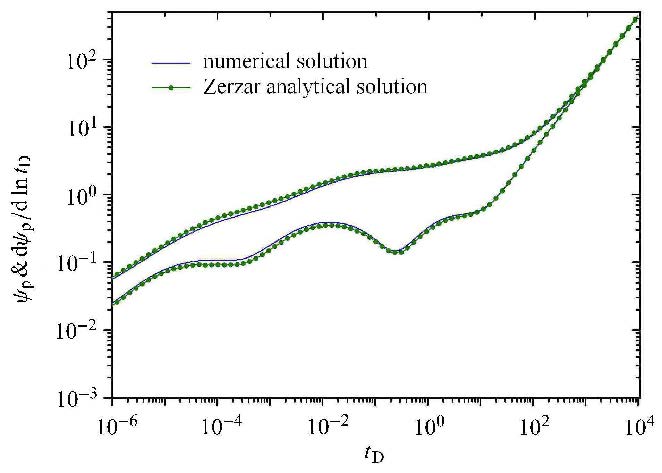
|
图3 有限元数值解与Zerzar解析解对比 Fig.3 Comparison of finite element numerical solution and Zerzar analytical solution |
由图4可知,页岩气藏压裂水平井的流动形 态[32]分为5种:(1)压裂裂缝线性流,流动初期地层中流体线性的流向各条人 工压裂裂缝,在双对数诊断图上表现为无因次拟压力导数曲线为1/2斜率的直线段.
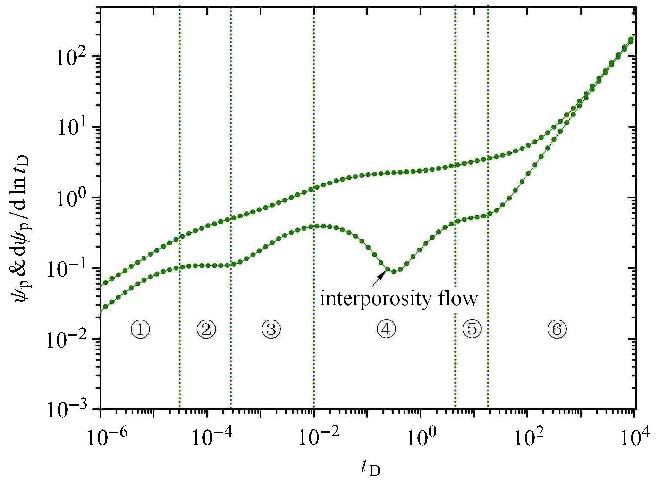
|
图4 页岩气藏压裂水平井压力动态曲线图 Fig.4 Pressure behavior of fracturing horizontal well in shale gas reservoir |
(2)压裂裂缝径向流,在各压裂裂缝周围产生的水平径向流动,只有当人工压裂裂缝较短,且缝距较大时,该流动阶段才会出现,在双对数诊断图上表现为无因次拟压力导数曲线为一水平直线段.

|
图5 裂缝线性流 Fig.5 The schematic of Fracture linear flow |

|
图6 裂缝径向流 Fig.6 The schematic of fracture radial flow |
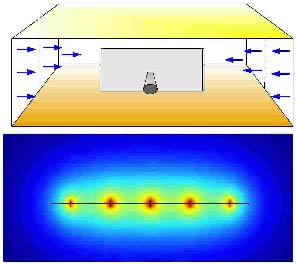
(3)地层线性流,是指在流动中后期,若边界较远,产生的流线相互平行,且垂直于水平井轴线的线性流动.
该流动段的无因次拟压 力导数曲线在双对数图上为1/2斜率的直线段. (4)系统径向流,整个气藏,如果生产时间很长,且压力波未传播到边界,则流体以拟径向流的形式流向水平井及压裂裂缝区域. 该流动段在双对数诊断图上表现为无因次压力导数曲线为0.5值水平直线段.
(5)封闭边界影响,是指压力波传播到封闭外边界以后,地层中出现拟稳态流动,双对数诊断图上表现为无因次拟压力导数曲线上翘 并与无因次拟压力曲线重合.
|
图7 地层线性流 Fig.7 The schematic formation linear flow |

|
图8 系统径向流 Fig.8 The schematic of formation radial flow |
页岩基岩对甲烷的吸附量满足Langmuir吸附等温式,在$p_{\rm L}$不变的情况下,随着$V_{\rm L}$增大,基岩吸附能力增强. 为研究 页岩基岩吸附解吸对压力响应的影响,保持$p_{\rm L}$不变,分别取$V_{\rm L} =0$ (不考虑吸附解吸),5$\times $10$^{ - 4}$ m$^{3}$/kg,15$\times $10$^{ - 4}$ m$^{3}$/kg,25$\times $10$^{ - 4}$ m$^{3}$/kg,将求解结果表示在试井特征曲线上.
由图9可知,吸附解吸对生产早期没有影响;窜流发生后,压降幅度随Langmuir体积的增大而减小,导数曲线上表现为"凹子"加深, 晚期段导数曲线上翘时间推迟.

|
图9 Langmuir吸附体积对试井特征曲线的影响 Fig.9 The effect of Langmuir adsorption volume on well test typical curves |
原因是:生产早期游离气从天然裂缝系统流向人工裂缝,吸附解吸只发生在基岩表面,其对试井特征曲线早期段没有影响;随着天然 裂缝系统压力进一步降低,气体从基岩流向天然裂缝导致基质压力下降,吸附气解吸,延缓了基质中压力降低,压力波传播到边界时间 推迟,Langmuir吸附体积$V_{\rm L}$越大,延缓效应越明显. 吸附解吸并不影响窜流发生的早晚.
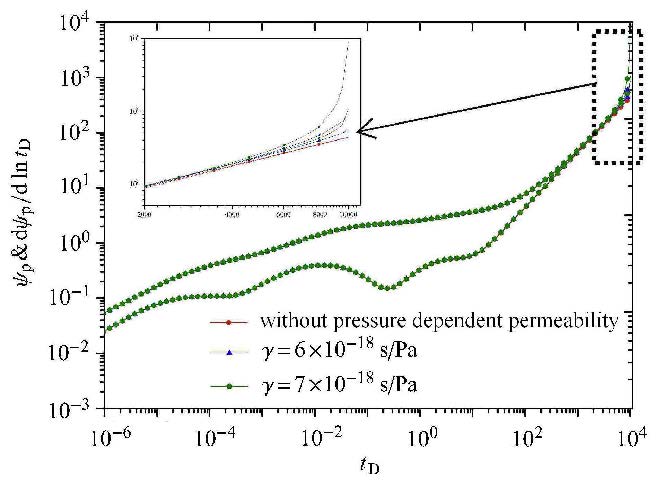
4.2 应力敏感对压力响应的影响页岩气藏储层渗透率具有应力敏感性,为研究天然裂缝系统渗透率的应力敏感性对压力动态的影响,取渗透率变异模数$\gamma=0$ s/Pa (不考虑应力敏感),6$\times $10$^{ - 18}$ s/Pa,7$\times $10$^{ - 18}$ s/Pa,将求解结果表示在试井特征曲线上.
压裂水平井生产时,天然裂缝系统压力降低,导致其孔渗性质发生变化.
由图10可知,天然裂缝系统应力敏感性对试井特征曲线的影 响体现在晚期段,诊断曲线上表现为压力曲线和导数曲线上翘,中早期段几乎没有影响.
|
图10 应力敏感对试井特征曲线的影响 Fig.10 The effect of pressure dependent permeability on well typical curve |
原因是:生产早期地层压降幅度较小,渗透率受应力影响较小;随着时间的增加,压降幅度进一步增大,天然裂缝渗透率降低, 渗流阻力增大,需要更大的生产压差来维持气井稳产. 应力敏感效应越强烈,试井特征曲线上翘的幅度越大.
总体来看,应力敏感效应并不明显,当$t_{\rm D}>10^{3}$之后试井特征曲线才开始出现上翘. 晚期段$t_{\rm D}$从10$^{3}\sim $ 10$^{4}$(约为3$\sim $30年),约中早期段时间跨度9倍,应力敏感对试井特征曲线影响明显.
压裂水平井投产一段时间后(大于3年),应力敏感效应的影响不可忽略.
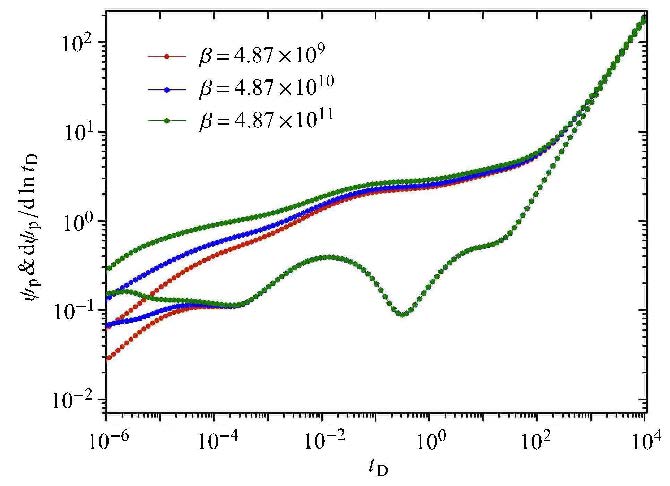
4.3 非达西流对压力响应的影响页岩气藏压裂水平井投产初期,人工裂缝导流能力高,井筒周围气体流速大,流体的惯性作用增强,非达西效应成为主导因素. 分别取$c =9$,10,11,研究人工裂缝内非达西效应强弱对压力响应的影响,将求解结果表示在试井曲线上.
由图12可知,高速非达西效应对试井特征曲线的影响主要发生在早期段,压降幅度随着非达西流效应增强而增大,晚期段影响较小, 达到拟稳态时试井特征曲线基本无差别. 原因是:生产早期,拟表皮随着$F$(非达西流效应)的增大而增大,导致井筒附加压力降增大,在导数曲线上表现为压降幅度变大.井筒附近的高速非达西流效应影响随压力传播范围扩大而减小,导致开发后期,非达西流效应影响变弱.
|
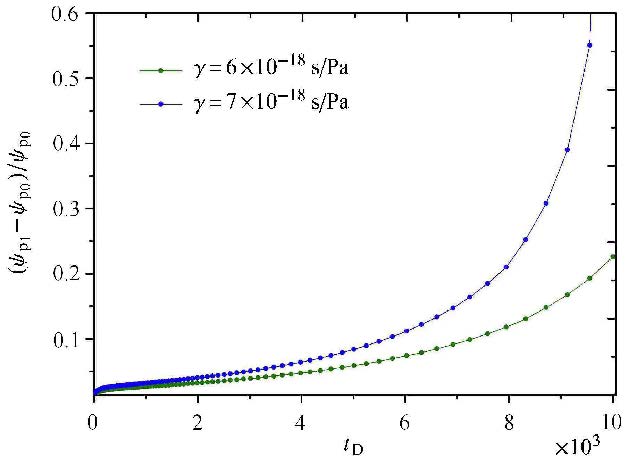
图11 考虑应力敏感与不考虑应力敏感相对压力差 Fig.11 The relative pressure difference of with and without considering pressure dependent permeability |
|
图12 非达西流对试井特征曲线的影响 Fig.12 The effect of non-Darcy flow on well test typical curve |
为验证模型适用性,取美国Barnett页岩气藏一口气井测试实例进行验证.
气藏基础参数为:气藏平均有效厚度27.5 m,平均孔隙度0.052, 井筒半径0.091 m,水平井水平段长度600 m,气体黏度1.32$\times $10$^{ - 5}$ Pa$\cdot $s,气体体积系数1.041,综合压缩系数3.2$\times $10$^{ - 4}$ MPa$^{ - 1}$,实验测得Langmuir体积2.8$\times $10$^{ - 3}$ kg/m$^{3}$,测试前该井产量为25 860 m$^{3}$/d. 应用上述试井解释模型计算该测试井理论压力响应,并利用遗传算法对理论压力响应与实测压力响应进行自动拟合,拟合结果如图13所示. 由图所示的压力恢复双对数拟合结果可得如下试井解释参数:平均渗透率$k =1.163\times 10^{ - 16}$ m$^{2}$, 弹性储能比 $\omega =0.119$,窜流系数 $\lambda =7.63 \times 10^{ - 6}$,裂缝条数$n=3$,裂缝半长$L_{\rm f} =49.3$ m.
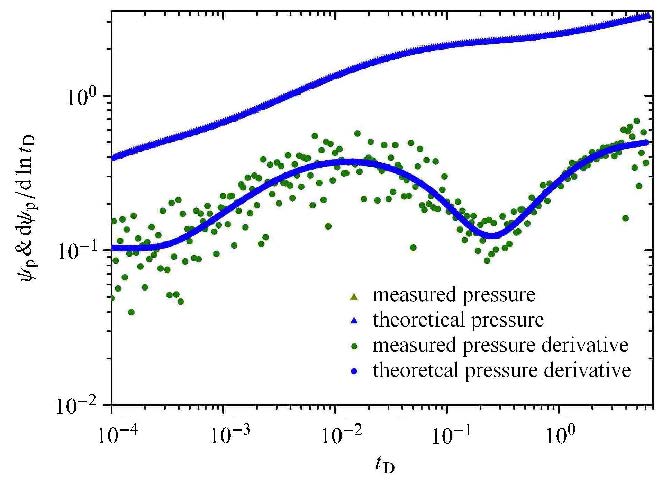
|
图13 测试井理论曲线与实测曲线双对数拟合图 Fig.13 Type Curve matching of theoretical curves and tested curves |
本文基于双重介质和离散裂缝混合模型,建立页岩气藏压裂水平井数值试井模型,模型着重考虑页岩气的吸附解吸,天然微裂缝的应力 敏感性,人工裂缝内的非达西流等非线性因素.
页岩气藏压裂水平井存在压裂裂缝线性流、压裂裂缝径向流、地层线性流、系统径向流及边界影响的拟稳态5种流动形态.
吸附解吸的影响发生窜流之后,Langmuir吸附体积增大,导数曲线上表现为凹槽加深,上翘延迟;天然裂缝系统的应力敏感性主要影响试 井特征曲线的晚期段,在拟压力和拟压力导数曲线上均表现为上翘,应力敏感效应越强,上翘幅度越大;高速非达西流效应对早期段影 响较大,非达西效应越强,拟压力降幅度越大,试井特征曲线上翘. 由试井解释实例可以看出本文提出的页岩气藏压裂水平井数值试井模型具有较好的矿场适用性.
| [1] | 姚同玉,黄延章,李继山. 页岩气在超低渗介质中的渗流行为. 力学学报,2012,44(6):990-995(Yao Tongyu, Huang Yanzhang, Li Jishan. Flow regim for shale gas in extra low permeability porous media. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 990-995(in Chinese)) |
| [2] | Nobakht M, Clarkson CR, Kaviani D. New type curves for analyzing horizontal well with multiple fractures in shale gas reservoirs. In: Proceedings of the SPE Unconventional Resources Conference, Calgary, Alberta, Canada, 15-17 November 2011. Society of Petroleum Engineers, 2011 |
| [3] | Lewis AM, Hughes RG. Production data analysis of shale gas reservoirs. In: Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA, 21-24 September 2008. Society of Petroleum Engineers, 2008 |
| [4] | 姚军,孙海,樊冬艳 等. 页岩气藏运移机制及数值模拟. 中国石油大学学报(自然科学版),2013, 37(1):91-98 (Yao Jun, Sun Hai, Fan Dongyan, et al. Transport mechanisms and numerical simulation of shale gas reservoir. Journal of China University of Petrolem, 2013, 37(1):91-98 (in Chinese)) |
| [5] | Zhang M, Yao J, Sun H, et al. Triple-continuum modeling of shale gas reservoirs considering the effect of kerogen. Journal of Natural Gas Science and Engineering, 2015, 24: 252-263 |
| [6] | Wu YS, Li N, Wang C, et al. A multiple-continuum model for simulation of gas production from shale gas reservoirs. In: Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 16-18 September 2013. Society of Petroleum Engineers, 2013 |
| [7] | Ding D, Wang C, Wu YS. Characterizing hydraulic fractures in shale gas reservoirs using transient pressure tests. In: Proceedings of the SPE Hydraulic Fracturing Technology Conference, Woodlands,Texas, USA, 46 February 2013. Society of Petroleum Engineers, 2013 |
| [8] | Fan DY, Yao J, Sun H, et al. A composite model of hydraulic fractured horizontal well with stimulated reservoir volume in tight oil & gas reservoir. Journal of Natural Gas Science and Engineering, 2015, 24: 115-123 |
| [9] | Ozkan E, Brown ML, Raghavan R, et al. Comparison of fractured-horizontal-well performance in tight sand and shale reservoirs. In: Proceedings of the SPE Western North American Regional Meeting, Anaheim, California, USA, 26-30 January 2009. Society of Petroleum Engineers, 2009 |
| [10] | Cheng YM. Pressure transient characteristics of hydraulically fractured horizontal shale gas wells. In: Proceedings of the SPE Western Regional Meeting, San Jose, California,USA, 24-26 March, 2009. Society of Petroleum Engineers, 2009 |
| [11] | Lee SJ, Kim TH, Lee KS. Type curves for pressure transient analysis of horizontal wells in shale gas reservoirs. In: Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 10-13 March, 2013. Society of Petroleum Engineers, 2013 |
| [12] | Eshkalak MO, Aybar U, Sepehrnoori K. An integrated reservoir model for unconventional resources, coupling pressure dependent phenomena. In: Proceedings of the SPE Eastern Region Meeting, Charleston, WV, USA, 21-23 October, 2014. Society of Petroleum Engineers, 2014 |
| [13] | Wu YS, Li JF, Ding DY, et al. A generalized framework model for simulation of gas production in unconventional gas reservoirs. In: Proceedings of the SPE Reservoir Simulation Symposium, Woodlands, Texas, USA, 18-20 February, 2012. Society of Petroleum Engineers, 2012 |
| [14] | 张帆. 页岩气藏压裂水平井试井分析方法研究. [硕士论文]. 成都:西南石油大学,2014 (Zhang Fan. The research of well test analytical method of fractured horizontal well in shale gas well. [Master Thesis]. Chendu: South West Petroleum University, 2014 (in Chinese)) |
| [15] | 樊冬艳,姚军,孙海 等. 页岩气藏分段压裂水平井不稳定渗流模型. 中国石油大学学报(自然科学版),2014,38(5):116-123 (Fan Dongyan, Yao Jun, Sun Hai, et al. Transient flow model of stage-fractured horizontal wells in shale gas reservoirs. Journal of China University of Petrolem, 2014,38(5):116-123 (in Chinese)) |
| [16] | Kuchuk F, Biryukov D. Pressure-transient behavior of continuously and discretely fractured reservoirs. In: Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, Texas, USA, 8-10 October, 2012. Society of Petroleum Engineers, 2012 |
| [17] | Morton KL, Nogueira PB, Booth R, et al. Integrated interpretation for pressure transient tests in discretely fractured reservoirs. In: Proceedings of the SPE Annual Conference & Exhibition incorporating SPE Europec, Copenhagen, Denmark, 4-7 June 2012. Society of Petroleum Engineers, 2012 |
| [18] | Ramey HJ Jr. Non-Darcy flow and wellbore storage effects in pressure build-up and drawdown of gas wells. SPE Journal, 1058, 1965 |
| [19] | Li D, Engler TW. Literature review on correlations of the non-darcy coefficient. In: Proceedings of the SPE Permian Basin Oil and Gas Recovery Conference, Midland, Texas, USA, 15-16 May 2001. Society of Petroleum Engineers, 2001 |
| [20] | Zhang F, Yang DY. Determination of fracture conductivity in tight formations with non-Darcy flow behavior. In: Proceedings of the SPE Unconventional Resources Conference, Calgary, Alberta, Canada, 30 October-1 November 2012. Society of Petroleum Engineers, 2012 |
| [21] | 张烈辉,朱水桥,王坤等. 高速气体非达西渗流数学模型. 新疆石油地质,2004,25(2):165-167, 176 (Zhang Leihui, Zhu Shuiqiao, Wang Kun, et al. A mathematical model for non-darcy flow at high flow rate. Xing Jiang Petroleum Geology, 2004,25(2):165-167,176 (in Chinese)) |
| [22] | Hagoort J. 气藏工程原理. 周勇等译. 北京:石油工业出版社,1992 (Hagoort J. The Principle of Gas Reservoir. Zhou Yong et al. transl. Beijin:Petroleum Industry Press,1992 (in Chinese)) |
| [23] | Evans RD, Civan F. Characterization of non-Darcy multiphase flow in petroleum bearing formations. Oklahoma University., Norman, OK, USA, 1990 |
| [24] | 庄惠农. 气藏动态描述和试井. 北京:石油工业出版社,2009 (Zhuang Huinong. Gas Reservoir Dynamic Description and Well Testing. Beijing: Petroleum Industry Press, 2009 (in Chinese)) |
| [25] | Lee J. Well Testing. New York: Society of Petroleum Engineers, 1982 |
| [26] | Soeder DJ. Porosity and permeability of eastern Devonian gas shale. SPE Formation Evaluation, 1988, 3(1): 116-124 |
| [27] | Ross DJ, Bustin RM. Characterizing the shale gas resource potential of Devonian-Mississippian strata in the western Canada sedimentary basin: Application of an integrated formation evaluation. AAPG Bulletin, 2008, 92(1): 87-125 |
| [28] | Dong JJ, Hsu JY, Wu WJ, et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(7): 1141-1157 |
| [29] | Chen D, Pan ZJ, Ye ZH. Dependence of gas shale fracture permeability on effective stress and reservoir pressure: Model match and insights. Fuel, 2015, 139: 383-392 |
| [30] | Yu W, Sepehrnoori K, Patzek TW. Evaluation of gas adsorption in marcellus shale. In: Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27-29 October 2014. Society of Petroleum Engineers, 2014 |
| [31] | Zerzar A, Bettam Y. Interpretation of multiple hydraulically fractured horizontal wells in closed systems. In: Proceedings of the SPE International Improved Oil Recovery Conference in Asia Pacific, Kuala Lumpur, Malaysia, 20-21 October 2003. Society of Petroleum Engineers, 2003 |
| [32] | 姚军,刘丕养,吴明录. 裂缝性油气藏压裂水平井试井分析. 中国石油大学学报(自然科学版),2013,37(5):107-113, 119 (Yao Jun, Liu Piyang, Wu Minglu. Well test analysis of fractured horizontal well in fractured reservoir. Journal of China University of Petroleum, 2013,37(5):107-113, 119 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47
