2. 中海油研究总院, 北京 100028;
3. 加拿大卡尔加里大学化学与石油工程学院, 阿尔伯塔 T2N1N4
与常规储层相比,页岩及致密砂岩储层富含纳米级孔隙[1, 2, 3, 4],流体(气与水)在纳米尺度下的传质机理对整个页岩气藏及致密气藏的产能预测、生产动态分析及经济性评估具有重要意义.
近年来,随分子模拟技术及微纳米技术的不断发展,单相气在页岩及致密砂岩纳米孔隙的流动机理被广泛研究,同时大量纳米孔气体传输模型被提出:Jones与Owens[5]通过实验方法确定致密砂岩滑脱效应与绝对渗透率的关系,以修正达西流动方程;Beskok等[6]在考虑稀薄气体流动效应的基础上,结合经验系数修正气体流动方程;Javadpour等[7]将Knudsen扩散和滑脱流动两种传输机理进行线性叠加,得出气体纳米孔隙传输的"表观渗透率"模型;Shi等[8]提出权重系数对扩散和滑脱流动进行非线性叠加,得出不同Knudsen数条件下的渗透率模型;Rahmanian等[9]通过实验手段,确定了扩散与流动的权重系数,叠加得到气体流动模型,但该权重系数存在经验系数;Wu等[10, 11]根据分子碰撞理论重新鉴定了扩散和滑脱流动的权重系数,推导的气体流动模型能够与分子模拟结果较好拟合.总体而言,在纳米孔隙传质过程中,流体分子自由程与流场特征尺度接近,纳米尺度效应不容忽视,连续流动条件下的达西流动方程已不再适用,分子扩散及滑脱效应对气体流动能力影响显著.
然而,目前对于纳米尺度流动的理论及实验的研究,主要侧重于单相流体(单相气体或者单相液体),实际测井数据表明:页岩气藏(尤其无机质孔隙)及致密气藏通常具有一定含水饱和度[12, 13, 14, 15, 16, 17],其值甚至高于常规气藏.对于页岩储层而言,尽管对有机质孔隙是否含水存在一定争议[18],但无机质孔隙通常具有较强的亲水能力,矿物表面一般存在一层紧密排列厚约10$^{-1}$ nm的水膜[19],通过TRA (tight rockanalysis)技术测量的页岩黏土结合水分(CBW)可以达到样品总体积的2.63%$\sim$7.19%[20],无机质孔隙内水分不容忽视.虽然这两类气藏含水饱和度多呈束缚水状态,且通常具有"超低含水饱和度"的现象[14, 15, 16, 17](储层原始含水饱和度小于流动束缚水饱和度),气井在生产过程中产水较少,甚至没有地层水的产出.但不可否认的是,储层条件下的孔隙流体仍然为气水两相,而孔隙水(束缚水)的存在,将在很大程度上制约气相流动,并进一步影响实际气井产能.很遗憾的是,在纳米尺度内开展气水两相流体流动的分子模拟或者室内实验的难度远远大于单相流体(单相气或者水),因此纳米尺度两相作用机理尚未被确定[21];同时目前常用的相渗曲线测定方法,也无法确定束缚水饱和度以下的气相渗透率.总体而言,纳米孔隙气水两相流动的理论研究严重滞后于生产需要,页岩及致密储层含水饱和度对气相流动能力的影响亟需研究.
据此,本文针对于页岩无机质及致密砂岩纳米孔隙,建立了考虑含水饱和度的气相渗透率预测模型,该模型按照3个部分进行论述:(1)基于水膜与水蒸气热力学平衡理论(蒸发、吸附与凝聚)及水膜与气相力学平衡方程(毛管力与分离压),建立纳米孔隙水膜厚度的计算模型,量化水膜厚度与孔径尺度及天然气相对湿度的关系,描述不同孔径内水膜厚度(含水饱和度)分布特征;(2)利用Knudsen数作为单相气体流态划分标准,以分子碰撞频率作为权重系数,考虑天然气组分特征(水蒸气及甲烷)与真实气体效应(偏差因子、压缩系数等),建立储层条件下页岩气纳米孔隙流动的表观渗透率模型,并分析不同孔径(1$\sim$500 nm)对流动的影响;(3)考虑实际储层孔隙分布特征,将单个纳米孔隙的气体流动模型及水膜计算模型拓展至多个纳米孔隙并联情况,并在考虑不同孔隙含水饱和度分布的基础上,最终建立含水饱和度与气相渗透率的关系曲线.本研究将为合理评价及预测储层含水条件下页岩/致密储层气井产能奠定理论基础.
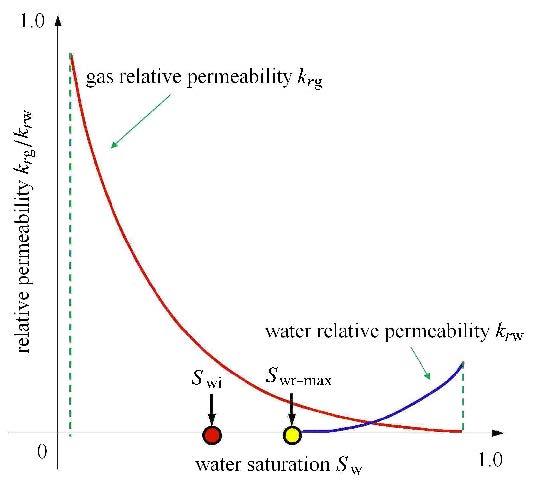
1 纳米孔隙水膜厚度量化分析 1.1 超低含水饱和度气藏含水饱和度的形成存在两种方式[22]: (1) 液相水被气相驱替;(2) 液相水蒸发.对于常规气藏而言,储层原始含水饱和度是在油气充注、运移过程中对液态水的驱替形成的;然而,页岩气藏及致密砂岩气藏通常存在"超低含水饱和度"的现象------原始含水饱和度低于驱替形成的束缚水饱和度.储层原始状态下的含水饱和度为$S_{{\rm w}i}$;储层岩石颗粒表面、角隅及微毛细管孔道中不可流动水与储层总孔隙体积之比为束缚水饱和度 $S_{{\rm w}r}$;如果原始含水饱和度$S_{\rm wi}$小于束缚水含水饱和度最大值$S_{\rm wr -max}$,即为"超低含水饱和度"[14, 15],如图1所示.研究表明,成藏过程中液态水的蒸发以及天然气对水蒸气的携带作 用[16, 17](汽化携液)是造成该现象的主要原因. 国外实验结果表明[23]:饱和水的岩心被气相驱替至束缚水饱和度后($S_{{\rm w}i}$为$23.90% \sim 25.43%$),进一步利用干气继续驱替,含水饱和度进一步降低至12.4%$\sim$14.7%,该过程中束缚水以水蒸气形式被"祛除".
|
图1 超低含水饱和度情况下气水相渗曲线 Fig.1 Gas-water permeability curve under extra low water satuaration |
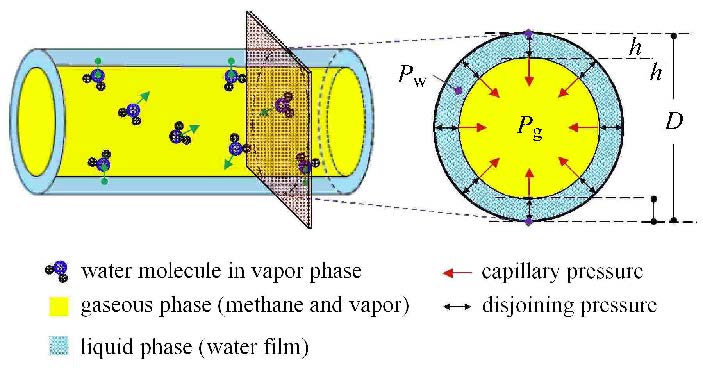
"汽化携液"作用表明,储层液态水与汽态水存在热力学平衡关系:伴随天然气大量生成而水分生成减小,天然气中水分湿度降低,储层液态水膜(或毛管水)蒸发形成水蒸气,孔隙含水饱和度将降低.也即孔隙含水饱和度(液态水)随天然气湿度(汽态水)变化而改变.为量化"超低含水饱和度"条件下储层孔隙水膜厚度及储层含水饱和度分布特征,本文假设:(1) 储层孔隙为均匀圆管;(2)气相流体仅存在甲烷及水蒸气两种组份;(3)页岩无机孔隙及致密砂岩孔隙表面仅吸附水分子,忽略甲烷在无机质孔隙壁面的吸附量[24];(4)水膜为刚性流体,忽略其压缩性;(5) 忽略水膜对甲烷的溶解作用;(6) 忽略储层温度变化;(7)储层气相为连续相,具有统一压力系统及湿度系统.在储层条件下,孔隙水膜厚度及含水饱和度将由水蒸气含量、气相压力、孔隙尺度及温度共同决定,液相水膜与气相(甲烷及水蒸气)的平衡关系如图2所示.
|
图2 圆管孔隙模型水膜受力分析示意图 Fig.2 Schematics of water film force analysis of tube model |
由于圆管孔隙中水膜并非平面,孔隙内气相(甲烷与水蒸气)与单位摩尔的水膜存在化学势差,可以表示为
\[\Delta {\mu ^1} = \int_{{P_{\text{g}}}}^{{P_{\text{w}}}} {{V_{\text{m}}}} dP = {V_{\text{m}}}({P_{\text{w}}} - {P_{\text{g}}})\]
(1)
考虑到页岩无机质具有极强亲水能力,无机质孔隙表面通常吸附水膜,因此忽略甲烷在岩石表面的吸附量(少量甲烷可以吸附在水膜上)[24].从热力学角度分析水蒸气与无机质表面相互作用,单位摩尔水蒸气发生吸附形成单位摩尔液态水的化学势(吸附势)可以用G-M二元气体吸附模型[25]表示为
\[\Delta {\mu ^2} = \int_{{P_v}}^{P_0^ * } {\frac{{RT}}{P}} dP = RT\ln \frac{{P_0^ * }}{{{P_v}}}{\text{ }}\]
(2)
在甲烷与水蒸气混合体系下,水膜饱和蒸汽压$P_{0}^*$可以用Raoult定律[26]描述为
\[{P_0} * = {P_0} \cdot {x_{\text{A}}}\]
(3)
忽略甲烷在水膜中的溶解作用,即$x_{\rm A}=1$,混合体系中水膜的饱和蒸汽压$P_{0}^*$与纯水的饱和蒸汽压$P_{0}$相同
\[P_0^ * = {P_0}\]
(4)
由于化学势$\triangle \mu^{1}$与化学势$\triangle \mu ^{2}$相同,即存在
\[{V_{\text{m}}}({P_{\text{w}}} - {P_{\text{g}}}) = RT\ln \frac{{{P_0}}}{{{P_v}}}\]
(5)
对于纳米级水膜,水分子与固体表面分子的相互作用不可忽略,当固体表面水膜在外力作用下变薄时,水膜两界面相互接近面产生斥力,水膜稳定而厚度不再减小,此斥力称为分离压$\prod (h)$[27]. 如图2所示,在圆管孔隙内,气相压力$P_{\rm g}$、水膜压力$P_{\rm w}$、分离压$\prod (h)$及柱面毛管力$P_{\rm c}$存在一定平衡关系[28]
\[{P_{\text{g}}} - {P_{\text{w}}} = \frac{r}{{r - h}}(\prod (h) + \frac{\gamma }{r})\]
(6)
\[\prod (h) = {\prod _{\text{m}}}(h) + {\prod _{{\text{el}}}}(h) + {\prod _{{\text{st}}}}(h)\]
(7)
由于页岩无机质(黏土)及砂岩(石英)为强水湿矿物,本文将分离压的表达式简化为完全润湿情 况[28]:$\prod (h) = {\prod _{\text{m}}}(h).{\prod _{\text{m}}}(h)$与水膜厚度$h$的关系可以表达为[27]
\[{\prod _{\text{m}}}(h) = \frac{{{A_{\text{H}}}}}{{{h^3}}}\prod \]
(8)
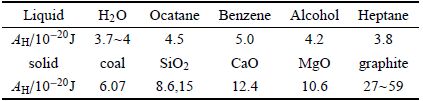
| 表1 一些物质的哈梅克常数 Table 1 Hamaker constant of some material |
两种物质间的哈梅克常数$A_{\rm H}$计算为[31]
\[{A_{\text{H}}} = {(\sqrt {{A_{11}}} - \sqrt {{A_{22}}} )^2}\]
(9)
结合式(5) $\sim $式(9)可以得出水膜厚度$h$与天然气相对湿度$P_{v}/P_{0}$及孔隙半径$r$的关系
\[\frac{r}{{r - h}}(\frac{{{A_{\text{H}}}}}{{{h^3}}} + \frac{\gamma }{r}) = \frac{{RT}}{{{V_{\text{m}}}}}\ln \frac{{{P_v}}}{{{P_0}}}{\text{ }}\]
(10)
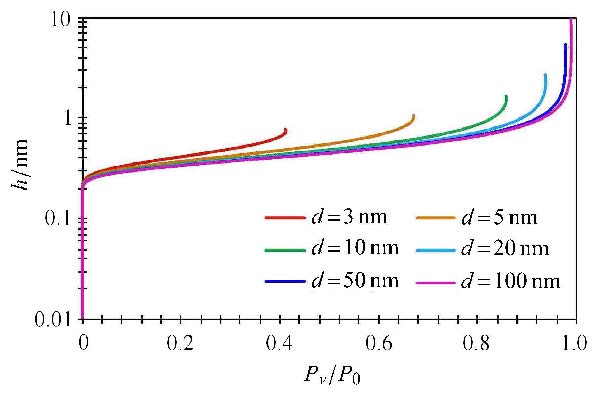
选取参数:$A_{\rm H}=1\times 10^{-20}$J,$\gamma =72\times 10^{ - 3}$ N/m,$T=353$ K(80℃),$V_{\rm m}=18\times 10^{ - 6}$m$^{3}$/mol. 计算不同孔径$d$条件下,水膜厚度$h$随相对湿度$P/P_{0}$变化(图3).可以看出:水膜厚度随$P_{v}/P_{0}$增大而增厚,当$P_{v}/P_{0}$达到一定临界时,水膜厚度迅速增加,孔隙内将充满液态水(毛管水);在天然气相对湿度$P_{v}/P_{0}$相同条件下,不同孔隙尺度内水膜厚度存在差异,孔隙越半径小,水膜越厚.
|
图3 不同孔隙尺度下水膜厚度随相对湿度的变化 Fig.3 Relationship between water film thickness and relative humidity |
在本研究中,页岩储层气相流体假设为甲烷与水蒸气的混合物,同时考虑到页岩实际储层温度(273$\sim$433 K)、压力(1$\sim$80 MPa)系统[8],高温高压条件下气体分子间相互作用力对气体传输的影响不容忽视,需要研究真实气体效应(偏差系数、黏度、平均自由程等)对流动的影响.
对于单相气体在纳米孔隙流动过程中,通常采用Knudsen数作为流动划分的重要依据[32],其中Knudsen数$Kn$可以表示为
\[Kn = \frac{{{\lambda _{\text{g}}}}}{d}\]
(11)
考虑气体偏差因子,真实气体分子平均自由程$\lambda_{\rm g}$可以表示为[33]
\[{\lambda _{\text{g}}} = \frac{{{\mu _{\text{g}}}}}{{{P_{\text{m}}}}}\sqrt {\frac{{\pi ZRT}}{{2M}}} \]
(12)
当$Kn<10^{ - 3}$时,气体分子间的碰撞占主导地位,对于理想气体在孔隙内传质可采用Darcy定律来描述[34]
\[{J_v} = v \cdot {\rho _{\text{g}}} = - \frac{{{k_\infty }}}{{{\mu _{\text{g}}}}} \cdot \frac{{M{P_{\text{m}}}}}{{RT}} \cdot \nabla P\]
(13)
\[{k_\infty } = \frac{{\varphi {d^2}}}{{32\tau }}\]
(14)
对于纳米孔隙,气体流动过程中与孔隙壁面的滑脱效应开始显著,滑脱效应将对气测渗透率产生影响,考虑滑脱效应的渗透率可以用Klinkenberg方程表征为[36]
\[{k_{{\text{slip}}}} = {k_\infty }(1 + \alpha Kn){\text{ }}\]
(15)
考虑气体偏差因子及滑脱效应,真实气体连续流动质量流量可以表示为
\[{J_{{\text{slip}}}} = - \frac{{{k_\infty }}}{{{\mu _{\text{g}}}}} \cdot \frac{M}{{RT}} \cdot \frac{{{P_{\text{m}}}}}{Z} \cdot (1 + \alpha Kn) \cdot \nabla P{\text{ }}\]
(16)
当$Kn>10$时,气体与孔隙壁面的碰撞占主导地位,孔隙内传质可采用Knudsen扩散来描述[34]
\[{J_{{\text{Kn}}}} = - {D_{{\text{Kn}}}}\nabla {\rho _{\text{g}}}\]
(17)
对于理想气体在圆管孔隙Knudsen扩散系数$D_{\rm Kn}$表示为[38]
\[{D_{{\text{Kn}}}} = \frac{d}{3}\sqrt {\frac{{8RT}}{{\pi M}}} \]
(18)
结合式(17)与式(18),理想气体Knudsen扩散质量流量可以表示为
\[{J_{{\text{Kn}}}} = - \frac{d}{3}\sqrt {\frac{{8RT}}{{\pi M}}} \cdot \frac{{{\text{d}}{\rho _{\text{g}}}}}{{dP}} \cdot \nabla P\]
(19)
考虑考虑气体偏差因子$Z$,真实气体Knudsen扩散质量流量可以表示为[11]
\[{J_{{\text{Kn}}}} = - \frac{d}{3}\sqrt {\frac{{8ZRT}}{{\pi M}}} \cdot \frac{M}{{RT}} \cdot \frac{{{P_{\text{m}}}}}{Z}{C_{\text{g}}} \cdot \nabla P\]
(20)
Javadpour[7]提出将"滑脱流"与"努森扩散"叠加表征气体在纳米孔隙的总流量,并进一步用"表观渗透率"表征气体在纳米孔隙的流动能力,Shi等[8]、Rahmanian等[9]、Wu等[10, 11]在其基础上进行修正与改进,其中Wu提出的"权重系数"能够表征分子-分子与分子-壁面的碰撞频率,物理意义较为明确,本研究借鉴其研究成果,以分子之间的碰撞频率和分子与壁面的碰撞频率占碰撞总频率的比值,作为滑脱流动和努森扩散的权重系数($f_{\rm slip}$与$f_{\rm Kn}$)
\[{f_{{\text{slip}}}} = \frac{1}{{1 + Kn}}\]
(21)
\[{f_{{\text{Kn}}}} = \frac{1}{{1 + 1/Kn}}\]
(22)
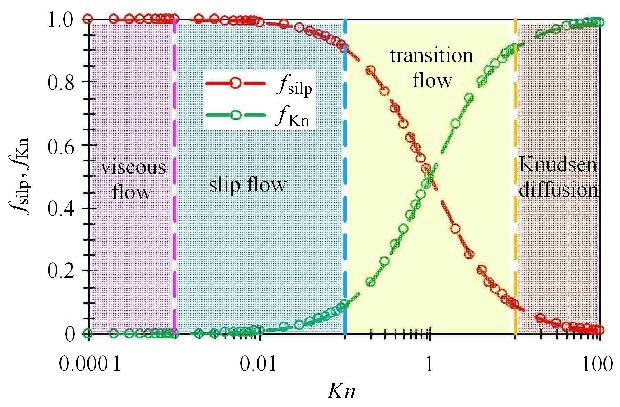
根据式(21)与式(22)计算的不同$Kn$的滑脱流权重系数$f_{\rm slip}$与Knudsen扩散权重系数$f_{\rm Kn}$如图4所示,计算结果 表明:在连续流区域内($Kn<10^{-3}$),$f_{\rm Kn}$几乎为0,Knudsen扩散对几乎不产生影响;在滑脱流区域内(10$^{ - 3}<Kn<10^{-1}$),随着$Kn$增加,Knudsen扩散影响逐渐增大,但$f_{\rm Kn}$值小于0.1,该区域内Knudsen扩散对流动的影响小于10%,气体主要表现为滑脱流动;在过渡流区域内($10^{-1}<Kn<10$),$f_{\rm Kn}$值与$f_{\rm slip}$随$Kn$变化显著,该区域内Knudsen扩散与滑脱流动对流动影响均比较重要;在分子流区域内($Kn>10$),滑脱流权重系数小于0.1,气体主要表现为Knudsen扩散. 综上,该权重系数可以表征全$Kn$范围内的流动状态.
|
图4 不同$Kn$下滑脱流及分子流的权重系数 Fig.4 Weight coefficient under different $Kn$ |
对于真实气体,利用权重系数叠加连续流动及Knudsen扩散,气体在孔隙内的总质量流量可以表示为
\[{J_{\text{T}}} = {f_{{\text{slip}}}}{J_{{\text{slip}}}} + {f_{{\text{Kn}}}}{J_{{\text{Kn}}}}\]
(23)
根据表观渗透率定义[7],总质量流量$J_{\rm T}$与表观渗透率($k_{\rm g})_{\rm a}$的关系可以表示为
\[{J_{\text{T}}} = {v_{\text{T}}} \cdot {\rho _{\text{g}}} = - \frac{{{{({k_{\text{g}}})}_{\text{a}}}}}{{{\mu _{\text{g}}}}} \cdot \frac{{M{P_{\text{m}}}}}{{RT}} \cdot \nabla P\]
(24)
\[\begin{gathered}
{({k_{\text{g}}})_{\text{a}}} = \frac{1}{{1 + {\lambda _{\text{g}}}/d}} \cdot \frac{{{d^2}}}{{32}} \cdot \frac{1}{Z} \cdot (1 + \alpha Kn) + \hfill \\
\frac{1}{{1 + d/{\lambda _{\text{g}}}}} \cdot \frac{{{\mu _{\text{g}}}{C_{\text{g}}}}}{Z} \cdot \frac{d}{3} \cdot \sqrt {\frac{{8ZRT}}{{\pi M}}} \hfill \\
\end{gathered} \]
(25)
对于甲烷-水蒸气混合物,水蒸气含量可以用相对含量与绝对含量两种形式表征.
水蒸气相对含量可以用相对湿度 $\varphi $ 表示
\[\varphi = \frac{{{P_v}}}{{{P_0}}}\]
(26)
水蒸气绝对含量可以用水蒸气在天然气中摩尔量比值$x$表示
\[x = \frac{{{P_v}/{Z_v}}}{{{P_{\text{m}}}/{Z_{\text{m}}}}}\]
(27)
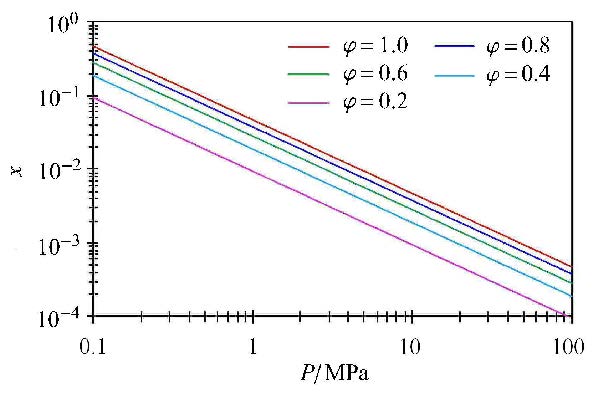
以80℃为例,不同相对湿度及气相压力条件下,水蒸气在天然气中的含量如图5所示,结果表明:在气相压力较高情况下($P>10$ MPa),水蒸气在天然气中的含量极低,一般小于0.5%,可以忽略;随气相压力降低,水蒸气摩尔含量逐渐增加,在$P=1$ MPa时,水蒸气最大含量($\varphi=1.0$)约为4.7%,在$P=0.5$ MPa时,水蒸气最大含量($\varphi =1.0$)约为9.4%.整体而言,在实际储层条件下,天然气中水蒸气摩尔含量小于10%.
|
图5 不同湿度条件下水蒸气在天然气中的含量 Fig.5 Water vapor Content in natural gas under different humidity conditions |
甲烷-水蒸气混合气体的偏差因子$Z$采用混合气体P-R模型[39]进行计算
\[{Z^3} - (1 - {B_{\text{m}}}){Z^2} + ({A_{\text{m}}} - 2{B_{\text{m}}} - 3B_{\text{m}}^2)Z - ({A_{\text{m}}}{B_{\text{m}}} - B_{\text{m}}^2 - B_{\text{m}}^3) = 0\]
(28)
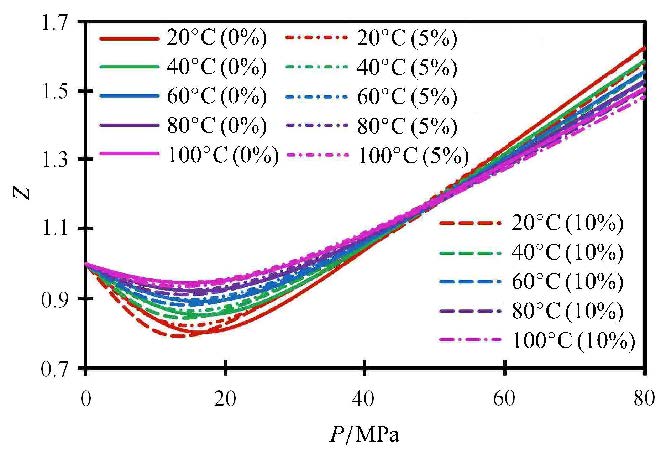
利用该模型计算$P$为$0 \sim 80$ MPa,$T$=20 ℃$\sim $100℃,$x $为0%,5%,10%条件下的气体偏差因子$Z$如图6所示,计算结果表明:温度越低,水蒸气含量对混合气体偏差因子影响越大;但在储层高温条件下(80℃为例),水蒸气含量对$Z$影响较小,小于5%,可以忽略.
|
图6 不同水蒸气含量条件下混合气体偏差因子$Z$ Fig.6 $Z$-factor under different water vapor contents |
甲烷-水蒸气混合气体的压缩系数$C_{\rm g}$采用Tube关系式[39]进行计算
\[{C_{\text{g}}} = \frac{1}{P} - \frac{1}{Z}\frac{{dZ}}{{dP}}\]
(29)
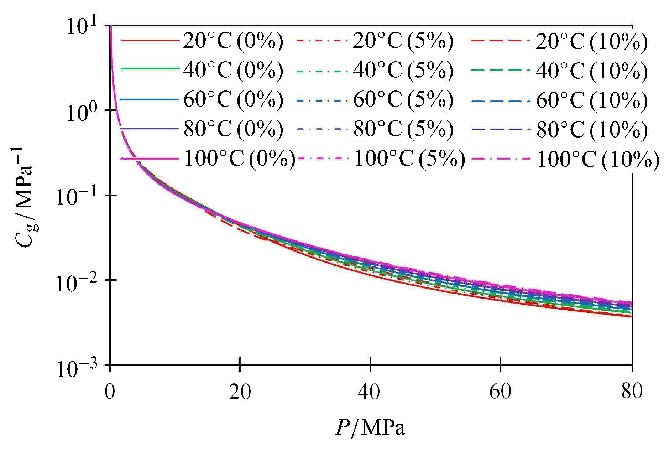
利用该模型计算$P$为$0\sim 80$ MPa,$T$为$20℃ $\sim $ 100℃,$x$为0%,5%,10%条件下的气体压缩系数$C_{\rm g}$如图7所示,计算结果表明:低压状态,水蒸气对混合气体压缩系影响较小;高压状态($P>15$ MPa),水蒸气对混合气体压缩系影响开始显著,但此时水蒸气总体含量极低(小于0.35%),因此,储层条件下水蒸气含量对气体压缩系数$C_{\rm g}$影响较小.
|
图7 不同水蒸气含量条件下混合气体压缩系数$C_{\rm g}$ Fig.7 Compression coefficient of mixed gas under different water vapor contents |
甲烷-水蒸气混合气体的黏度$\mu_{\rm g}$采用Herning模型进行计算[39]
\[{\mu _{\text{g}}} = \frac{{\sum {{\mu _{gi}}} {Y_i}M_i^{0.5}}}{{\sum {{Y_i}} M_i^{0.5}}}\]
(30)
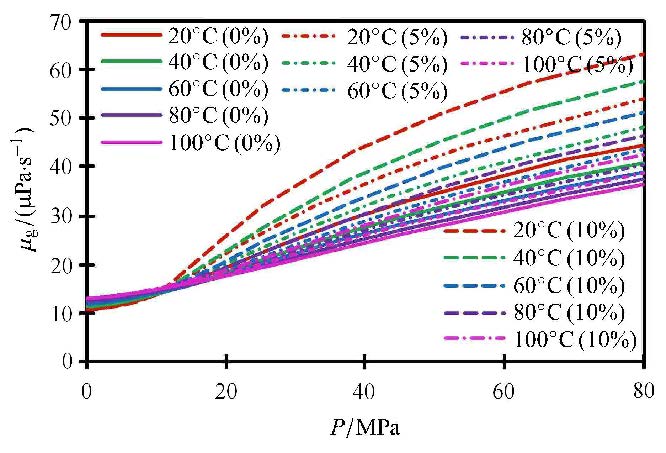
利用该模型计算$P$在$0\sim 80$ MPa,$T$在$20℃ $\sim $ 100℃,$x$在$0$%,5%,10%条件下的 气体黏度$\mu _{\rm g}$如图8所示,计算结果表明:压力越高,水蒸气对混合气体黏度影响越大;尤其当储层压力大于10 MPa,水蒸气含量对黏度的影响不容忽视,但在实际储层中,10 MPa条件下水蒸气含量极低,小于0.5%,因此水蒸气含量对$\mu_{\rm g}$影响较小.
总体而言,水蒸气对天然气高压物性的影响主要表现在高压阶段(大于10 MPa),然而在该压力条件下,水蒸气在气相中的摩尔含量极低(小于0.5%),因此储层条件下,水蒸气对气体高压物性的影响较小;然而值得注意的是,较理想气体而言,储层高温高压对天然气物性的影响不容忽视,为此,本文将进一步研究真实气体效应对表观渗透率计算结果的影响.
|
图8 不同水蒸气含量条件下混合气体黏度 $\mu_{\rm g}$ Fig.8 Mixed gas viscosity under different water vapor content |
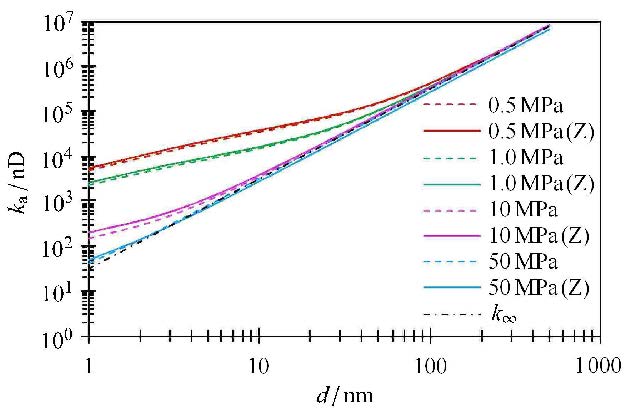
在$T$=80℃条件下,根据 式(25)计算出不同储层平均压力(0.5 MPa,1 MPa,10 MPa,50 MPa)与 孔径1$\sim$500 nm范围内理想气体与真实气体的表观渗透率($k_{\rm g})_{\rm a}$ (图9,虚线为理想气体,实线为真实气体).结果表明,压力及孔隙尺度均对气体表观渗透率产生影响:低压条件下的渗透率远大于高压情况,当压力大于10 MPa,压力对渗透率的影响不明显;同时,气体表观渗透率与孔径呈正相关,孔径越大则渗透率越大.
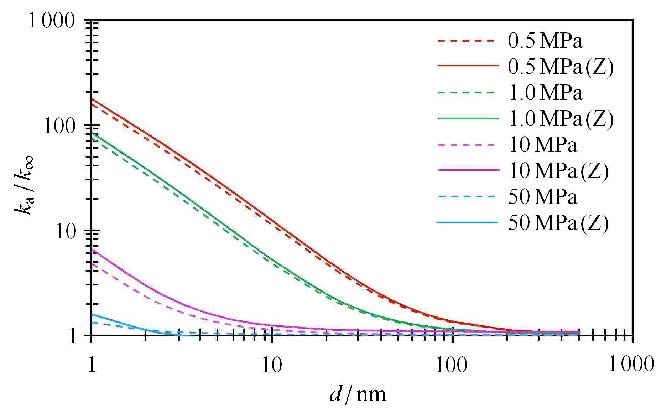
对比不同条件下表观渗透率$(k_{\rm g})_{\rm a}$与绝对渗透率($k_{\infty})$比值(图10,虚线为理想气体,实线为真实气体),结果表明:低压(0.5 MPa)条件下,1$\sim $10 nm孔隙的渗透率$(k_{\rm g})_{\rm a}$大于绝对渗透率($k_{\infty }) 10 \sim 200$倍左右;即使在高压情况下(10 MPa),1$\sim$10 nm孔隙$(k_{\rm g})_{\rm a}$也大于($k_{\infty }) 2 \sim 5$倍,因此在1$\sim$10 nm纳米孔隙内,努森扩散及滑脱引起气体表观渗透率增大的现象不容忽视,随孔隙尺度增大,努森扩散及滑脱效应逐渐减弱.
|
图9 不同孔径及压力条件下的表观渗透率$(k_{\rm g})_{\rm a}$ Fig.9 $(k_{\rm g})_{\rm a}$ curves under different pore diameter and pressure |
|
图10 表观渗透率$(k_{\rm g})_{\rm a}$与绝对渗透率$(k_{\infty })$的比值 Fig.10 Ratio of apparent permeability to absolute permeability |
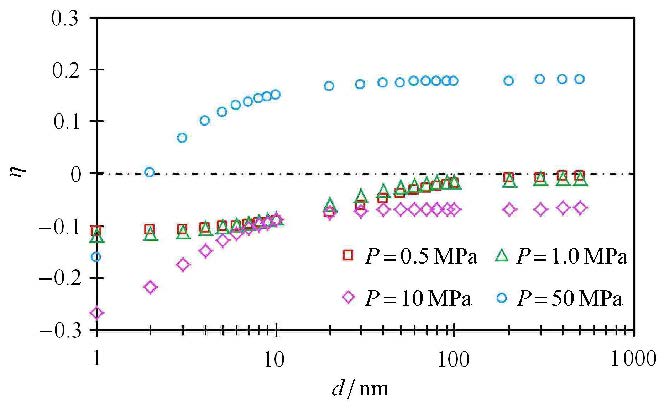
进一步地,本研究了分析不同压力(0.5 MPa,1 MPa,10 MPa,50 MPa)条件下,真实气体高压物性对表观渗透率的影响(图11),其中 $\eta $为真实气体表观渗透率$k(z)$与理想气体表观渗透率$k(i)$的误差系数
\[\eta = \frac{{k(i) - k(z)}}{{k(z)}}\]
(31)
在低压(0.1 MPa与1 MPa)情况下,气体高压物性对计算结果影响不大,误差小于10%;但在高压(10 MPa与50 MPa)情况下,气体高压物性对计算结果影响可达20%$\sim$30%;因此,尽管在实际储层条件下,水蒸气对气体高压物性的影响较小;但对比理想气体而言,真实气体的高压物性对流动能力的影响不容忽视.
|
图11 真实气体与理想气体渗透率误差系数$\eta $ Fig.11 Error coefficient between real gas and ideal gas permeability |
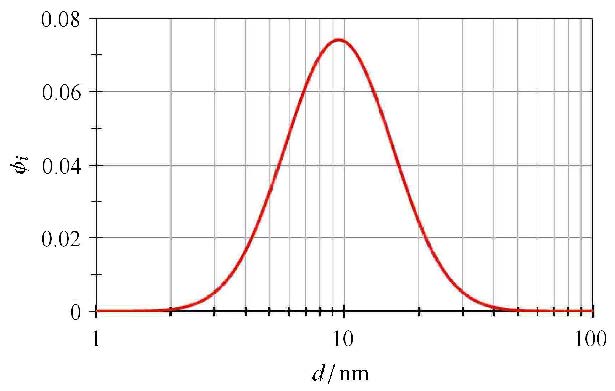
以文献[41]的页岩孔隙分布(图12)为例,研究多孔介质情况下,含水饱和度分布情况及其对流动能力的影响. 孔隙分布满足"对数正态分布"函数[41]
\[{\phi _i}(d) = \frac{1}{{d\sqrt {2\pi } \sigma }}\exp [ - \frac{1}{2}{(\frac{{\ln d - u}}{\sigma })^2}]\]
(32)
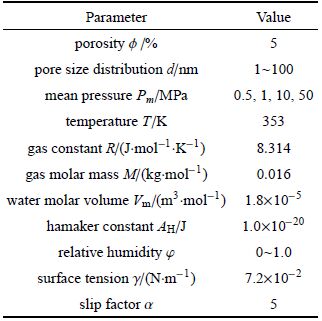
其他基础参数数据如表2所示,与水膜厚度相关的参数(哈梅克常数等)的选取详见第一部分分析;与气体流动相关的参数(滑脱系数、气体高压物性等)的选取详见第2部分分析.
|
图12 孔隙分布特征 Fig.12 Characteristic of pore distribution |
基于第一部分研究,对于单根孔隙而言,根据 式(10)可以确定孔隙内水膜厚度$h_{i}$,相应的含水饱和度 $S_{{\rm w}i}$形式可以表示为
\[{S_{{\text{w}}i}} = 1 - {[1 - \frac{{2{h_i}(d,\varphi )}}{{{d_i}}}]^2}\]
(33)
| 表2 基础数据表 Table 2 Basic parameters for calculation |
对于具有一定孔隙分布特征的岩心,整体含水饱和度$S_{\rm w}$可以表示为
\[{S_{\text{w}}}(\varphi ) = \sum\limits_{i = 1}^{i = n} {{S_{{\text{w}}i}}} \cdot {\phi _i} = \sum\limits_{i = 1}^{i = n} [ 1 - {(1 - \frac{{2{h_i}}}{{{d_i}}})^2}] \cdot {\phi _i}\]
(34)
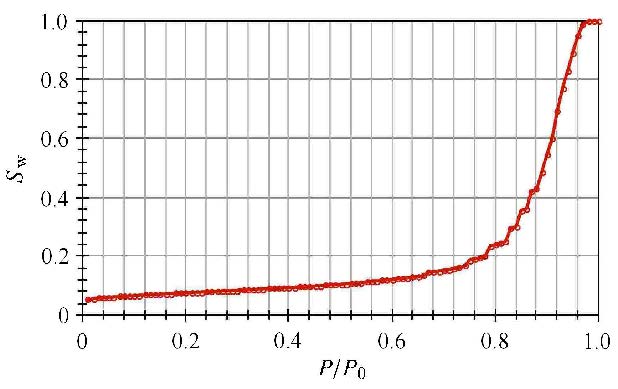
利用式(34)计算得到储层含水饱和度$S_{\rm w}$与相对湿度$\varphi $的关系曲线如图13所示:$S_{\rm w}$随 $\varphi$的增加而增大,在$\varphi =0.8$之前,$S_{\rm w}$缓慢增加,当$\varphi >0.8$,$S_{\rm w}$迅速上升. 由于$S_{\rm w}$为$\varphi $的单调函数,因此可以根据储层含水饱和度$S_{\rm w}$确定储层条件下天然气相对湿度$\varphi$;同时储层条件下各孔隙内天然气湿度相同,可以根据$\varphi $进一步确定不同尺度孔隙的含水饱和度$S_{{\rm w}i}$分布特征.
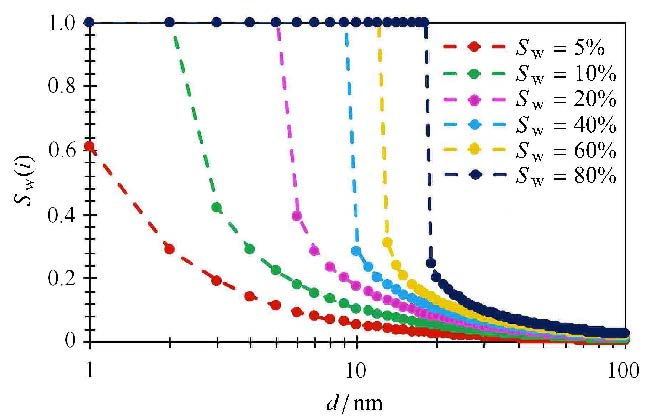
在储层整体含水饱和度$S_{\rm w}$为5%,10%,20%,40%,60%及80%条件下,依据图13得出对应的储层天然气相对湿度 $\varphi $ 分别为:0.01,0.46,0.78,0.87,0.91及0.94. 在不同 $\varphi $ 条件下,根据 式(33)计算得到的不同孔隙含水饱和度分布$S_{{\rm w}i}$,如图14所示. 在低含水饱和度(5%)情况下,所有的孔隙仅仅存在水膜($S_{{\rm w}i}<1$),而未被毛管水填充;随储层含水饱和度$S_{\rm w}$增加,小孔隙逐渐被毛管水充填($S_{{\rm w}i}=1$),而大孔隙表面吸附水膜($S_{{\rm w}i} <1$);在高含水饱和度情况下(40%$\sim $80%),10 nm$\sim$20 nm孔隙将被毛管水充填. 如果在纳米尺度Y-Laplace公式$Pc=4 \cdot \gamma \cos \theta/d$仍然可以适用,那么驱替20 nm孔隙的水,需要克服毛管力14.5 MPa,此类被毛管水填充的微小孔隙在生产过程中可能不起作用.当然,本模型主要针对亲水能力极强的无机质孔隙,对于亲油有的机质孔隙(页岩)而言,有机质孔隙与甲烷分子的作用力大于与水分子的作用力,孔隙内将主要以气相(吸附气与游离气)为主,孔隙被液态水阻塞可能性较低.
|
图13 储层含水饱和度$S_{\rm w}$与相对湿度$\varphi $的关系曲线 Fig.13 Relationship between water satuaration and relative humidity |
|
图14 不同尺度孔隙含水饱和度分布特征$S_{{\rm w}i}$ Fig.14 Water satuaration distribution under different pore diameter |
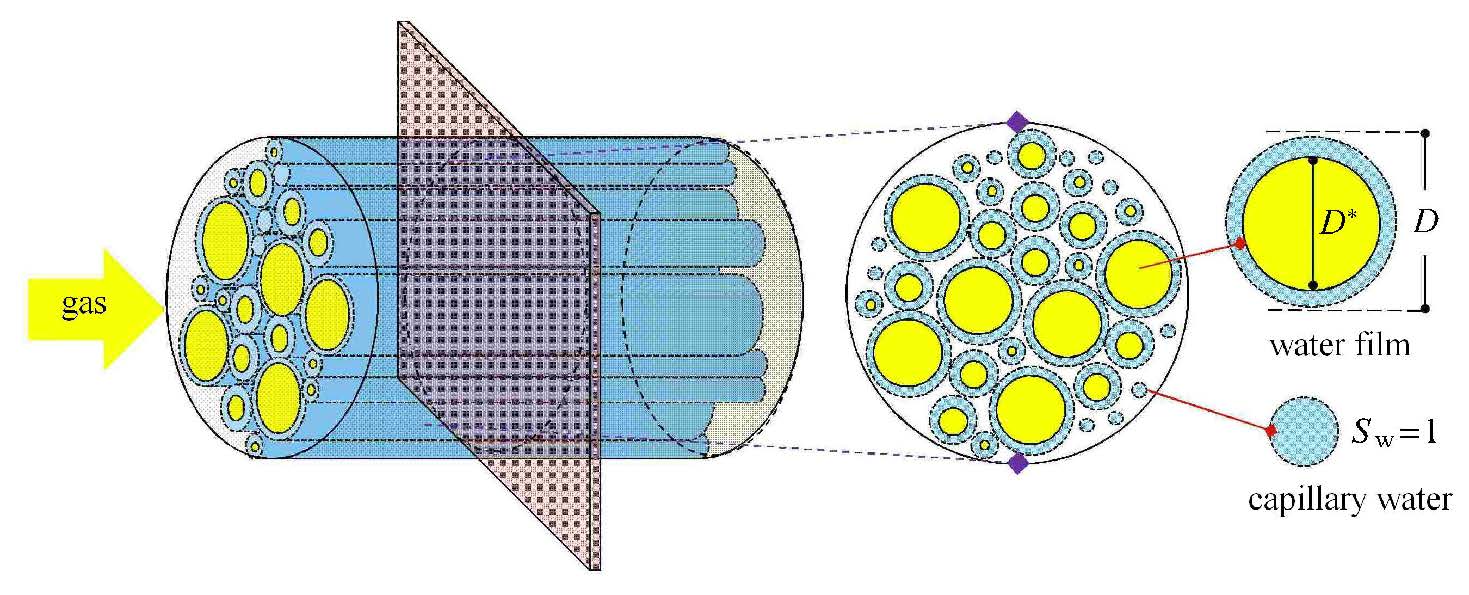
在本模型中,将岩心简化为多根纳米孔隙并联 的情况,孔隙含水分布特征及气相流动特征如图15所示.
|
图15 不同尺度孔隙含水分布特征及气相流动特征 Fig.15 Water satuaration distribution and gas flowing characteristic |
对于孔隙并联的情况,总体渗透率可以表示为
\[{({k_{\text{g}}})_{\text{T}}} = \frac{{\sum\limits_{i = 1}^{i = n} {{{({k_{\text{g}}})}_{{\text{a}}i}} \cdot {A_i}} }}{{{A_{{\text{bulk}}}}}} = \frac{{\sum\limits_{i = 1}^{i = n} {{{({k_{\text{g}}})}_{{\text{a}}i}}} \cdot {A_i}/{A_{\text{T}}}}}{{{A_{{\text{bulk}}}}/{A_{\text{T}}}}}\]
(35)
\[\phi = \frac{{{A_{\text{T}}}}}{{{A_{{\text{bulk}}}}}} = \frac{{{V_{\text{T}}}}}{{{V_{{\text{bulk}}}}}},{\phi _i} = \frac{{{A_i}}}{{{A_{\text{T}}}}} = \frac{{{V_i}}}{{{V_{\text{T}}}}}\]
(36)
结合式(25),(35)及(36),整个岩心气体流动表观渗透率可以表示为
\[\begin{gathered}
{({k_{\text{g}}})_{\text{T}}} = \phi \cdot \sum\limits_{i = 1}^{i = n} {{{({k_{\text{g}}})}_{{\text{a}}i}} \cdot {\phi _i}} = \hfill \\
\phi \cdot \sum\limits_{i = 1}^{i = n} [ \frac{1}{{1 + {\lambda _{\text{g}}}/{d_i}}} \cdot \frac{{d_i^2}}{{32}} \cdot \frac{1}{Z} \cdot (1 + \alpha \frac{{{\lambda _{\text{g}}}}}{{{d_i}}}) + \hfill \\
\frac{1}{{1 + {d_i}/{\lambda _{\text{g}}}}} \cdot \frac{{{\mu _{\text{g}}}{C_{\text{g}}}}}{Z} \cdot \frac{{{d_i}}}{3} \cdot \sqrt {\frac{{8ZRT}}{{\pi M}}} ] \cdot {\phi _i} \hfill \\
\end{gathered} \]
(37)
考虑到含水饱和度分布特征(图15),含水饱和度对气相流动的影响表现为:(1)小孔隙被毛管水堵塞,气体无法流动;(2)大孔隙存在一定厚度水膜,影响孔隙有效流动直径. 定义孔隙有效流动直径为
\[d_i^ * = {d_i} - 2{h_i} = {d_i} \cdot \sqrt {1 - {S_{{\text{w}}i}}} \]
(38)
考虑含水饱和度对有效孔径的影响后,整个岩心气体流动表观渗透率可以表示为
\[\begin{gathered}
({k_{\text{g}}})_{\text{T}}^ * = \phi \cdot \sum\limits_{i = 1}^{i = n} {({k_{\text{g}}})_{{\text{a}}i}^ * } \cdot {\phi _i} = \hfill \\
\phi \cdot \sum\limits_{i = 1}^{i = n} [ \frac{1}{{1 + {\lambda _{\text{g}}}/d_i^ * }} \cdot \frac{{d_i^{ * 2}}}{{32}} \cdot \frac{1}{Z} \cdot (1 + \alpha \frac{{{\lambda _{\text{g}}}}}{{d_i^ * }}) + \hfill \\
\frac{1}{{1 + d_i^ * /{\lambda _{\text{g}}}}} \cdot \frac{{{\mu _{\text{g}}}{C_{\text{g}}}}}{Z} \cdot \frac{{d_i^ * }}{3} \cdot \sqrt {\frac{{8ZRT}}{{\pi M}}} ] \cdot {\phi _i} \hfill \\
\end{gathered} \]
(39)
结合式(37)与(38),气相渗透率即为含水条件下表观渗透率($k_{\rm g})^{\ast }_{\rm T}$与干燥条件下($k_{\rm g})_{\rm T}$的比值
\[{k_{{\text{rg}}}}({S_{\text{w}}}) = \frac{{({k_{\text{g}}})_{\text{T}}^ * }}{{{{({k_{\text{g}}})}_{\text{T}}}}}\]
(40)
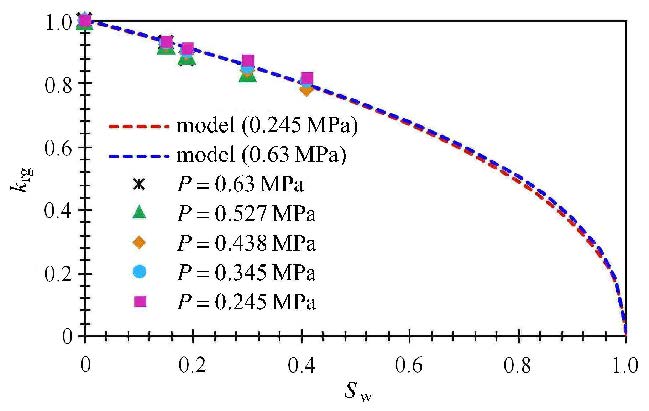
借用Wu 等 [42]在不同束缚水($S_{{\rm w}i}=0%$,15%,19%,30%,42%)及不同平均压力条件下(0.245$\sim $0.63 MPa),并联纳米孔隙气相渗透率测试数据,与本文计算结果进行对比.
Wu Qihua实验纳米孔隙主要成分为石英(强亲水),孔径约为100 nm (粗糙度小于1 nm),驱替过程中,孔隙内束缚水主要以水膜形式存在于孔隙壁表,气体流动通道主要为孔隙中心(图16),与本研究假设情况类似.计算过程中简化为均匀等径孔隙并联情况,取$d =100$ nm,利用 式(39)计算束缚水条件下的气体表观渗透率($k_{\rm g})^{\ast }$,并进一步利用 式(40)计算不同$S_{\rm w}$条件下的相对渗透率$k_{\rm rg}$.
利用式(40),计算$P_{\rm m}$为$0.245$ MPa与0.63 MPa条件下的气相渗透率$k_{\rm rg}$,并与实验结果对比(图17),结果表明:模型计算与实验结果拟合程度 较高,说明本文对束缚水状态下,纳米孔隙流动机理的描述及分析较为合理;因此,可以利用本研究模型进一步分析考虑多孔介质孔隙分布及含水饱和度分布情况下的气体流动能力.
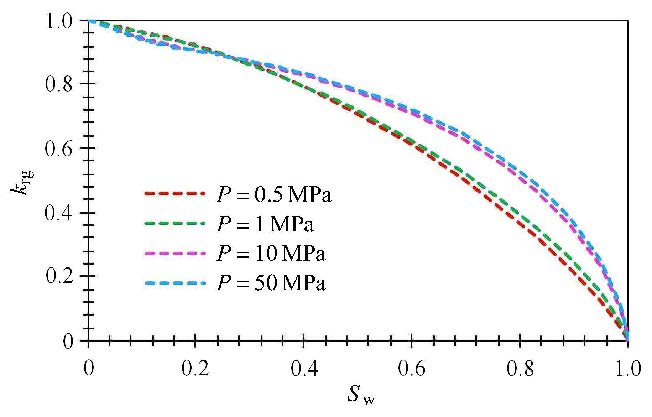
3.5 模型应用以本研究的孔隙分布特征为例(图12),在考虑多孔介质含水饱和度分布特征的基础上(图14),计算不同压力条件下(0.1 MPa,1 MPa,10 MPa,50 MPa)的气相渗透率与含水饱和度关系曲线(图18),结果表明:在储层原始含水饱和度20%的情况下,气相流动能力与干燥情况相比将降低10%;在含水饱和度40%的情况下,气相流动能力将降低20%. 尽管页岩及致密砂岩储层原始含水通常表现为束缚水,但该含水饱和度的存在将明显降低气体流动能力,尤其在高含水饱和度情况下($S_{\rm w}>60%$),该影响更为突出;同时,储层平均压力对气相渗透率也存在影响,高压情况的气相渗透率明显高于低压情况,因此储层平均压力越低,束缚水对气体流动能力的影响越为明显.
|
图18 不同压力条件下的气相渗透率与含水饱和度关系曲线 Fig.18 Relationship of gas relative permability and water satuaration unfer different pressure |
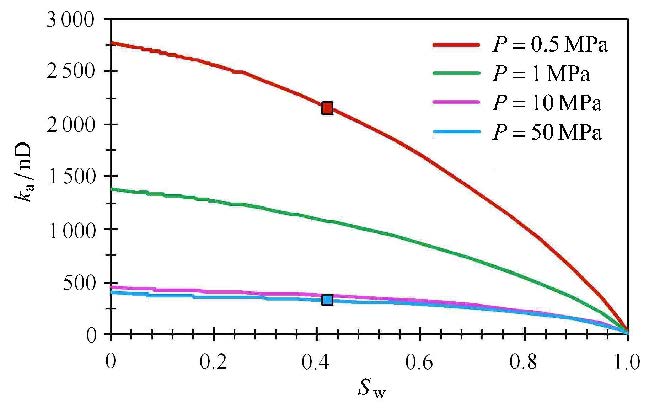
对比不同储层压力条件下气相表观渗透率表明(图19):开发过程随储层压力降低,尤其当压力小于1 MPa时,气体黏度降低,分子自由程增大,"努森扩散"及"滑脱效应"对流动的贡献开始明显,气体流动能力显著增加.以初始含水饱和度$S_{{\rm w}i}=40%$为例,在在储层压力由50 MPa降低至0.5 MPa过程中,气相表观渗透率将由326.15 nD增大至2 158.80 nD,增大约6.6倍,因此,在开发过程中,气体流动能力将得到一定程度改善.
Mahadevan等[22]研究表明:伴随生产过程,气体对水蒸气携带作用可以致使储层水分蒸发,含水饱和度降低,该现象甚至可以缓解致密储层及页岩储层的"水锁现象"等[22].Zuluaga[23]实验结果表明:利用干气驱替处于束缚水饱和度状态的岩心,"汽化携液"作用降低的含水饱和度约10%,因此生产过程中,伴随汽态水产出,"含水饱和度蒸发"现象也将在一定程度上改善气相渗透率.然而,储层水分蒸发对含水饱和度的影响与采气速率、温度、储层压力、渗透率等多因素相关[22],具体量化过程仍需要进一步研究.
|
图19 不同压力条件下的表观渗透率与含水饱和度关系曲线 Fig.19 Relationship of gas apparent permability and water satuaration unfer different pressure |
(1)建立了纳米孔隙水膜厚度计算模型. 模型表明:束缚水膜厚度与孔径及天然气相对湿度有关. 在相同天然气相对湿度条件下,孔径越小,水膜厚度越大;在相同孔径条件下,相对湿度越大,水膜厚度越大.
(2)量化了储层多孔介质含水饱和度分布特征. 结果表明:当储层总含水饱和度一定,不同尺度孔隙含水饱和度存在差异. 在本研究孔隙分布情况下,当含水饱和度达到40%,10 nm以内的孔隙将被毛管水充填;而10 nm以上的孔隙表面仅存在束缚水膜,且孔隙越大水膜越薄.
(3)计算了含水饱和度与气相渗透率的关系曲线. 结果表明:在储层原始含水饱和度20%的情况下,气相流动能力降低10%;在含水饱和度40%的情况下,气相流动能力降低20%. 束缚水对气体流动能力的影响不容忽视.
(4)分析了开发过程中储层渗透率变化特征. 随储层压力降低,"努森扩散"及"滑脱效应"开始显著,将导致气体流动能力增加;同时产气过程伴随"水分蒸发",可以缓解致密储层及页岩储层的"水锁现象",储层渗透率将得到一定程度改善.
| [1] | Mosher K, He J, Liu Y, et al. Molecular simulation of methane adsorption in micro-and mesoporous carbons with applications to coal and gas shale systems. International Journal of Coal Geology, 2013, 109: 36-44 |
| [2] | 陈尚斌, 朱炎铭, 王红岩等. 川南龙马溪组页岩气储层纳米孔隙结构特征及其成藏意义. 煤炭学报, 2012, 37(3): 438-444 (Chen Shangbin, Zhu Yanming, Wang Hongyan, et al. Structure characteristics and accumulation significance of nanopores in Longmaxi shale gas reservoir in the southern Sichuan Basin. Journal of China Coal Society, 2012, 37(3): 438-444 (in Chinese)) |
| [3] | 胡勇, 李熙喆, 万玉金等. 致密砂岩气渗流特征物理模拟. 石油勘探与开发, 2013, 40(5): 580-584 (Hu Yong, Li Xizhe, Wan Yujin, et al. Physical simulation on gas percolation in tight sandstone. Petroleum Exploration and Development, 2013,40(5): 580-584 (in Chinese)) |
| [4] | 朱如凯, 白斌, 崔景伟等. 非常规油气致密储集层微观结构研究进展. 古地理学报, 2013, 15(5): 615-623 (Zhu Rukai, Bai Bin, Cui Jingwei, et al. Research advances of microstructure in unconventional tight oil and gas reservoirs. Journal of Palaeogeography, 2013, 15(5): 615-623 (in Chinese)) |
| [5] | Jones FO, Owens WW. A laboratory study of low-permeability gas sands. Journal of Petroleum Technology, 1980, 32(09): 1631-1640 |
| [6] | Beskok A, Karniadakis GE. Report: a model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophysical Engineering, 1999, 3(1): 43-77 |
| [7] | Javadpour F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). Journal of Canadian Petroleum Technology, 2009, 48(8): 16-21 |
| [8] | Shi JT, Zhang L, Li YS, et al. Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting. In: Society of Petroleum Engineers-SPE Canadian Unconventional Resources Conference, 2013: 1127-1145 |
| [9] | Rahmanian M, Aguilera R, Kantzas A. A new unified diffusion-viscous-flow model based on pore-level studies of tight gas formations. SPE Journal, 2012, 18(1): 38-49 |
| [10] | Wu KL, Li XF, Wang CC, et al. Apparent permeability for gas flow in shale reservoirs coupling effects of gas diffusion and desorption. In: Proc. of Unconventional Resources Technology Conference (URTEC), 2014 |
| [11] | Wu KL, Li XF, Guo CC, et al. Adsorbed gas surface diffusion and bulk gas transport in nanopores of shale reservoirs with real gas effect-adsorption-mechanical coupling. In: Proc. of SPE Reservoir Simulation Symposium, 2015 |
| [12] | Boyer C, Kieschnick J, Suarez-Rivera R, et al. Producing gas from its source. Oilfield Review, 2006, 18(3): 36-49 |
| [13] | Chenevert ME, Sharma MM, Jung CM, et al. The impact of shale preservation on the petrophysical properties of organic-rich shales. In: Proc. of SPE Annual Technical Conference and Exhibition, 2013 |
| [14] | 刘洪林, 王红岩. 中国南方海相页岩超低含水饱和度特征及超压核心区选择指标. 天然气工业, 2013, 33(7): 140-144 (Liu Honglin, Wang Hongyan. Ultra-low water saturation characteristics and the identification of over-pressured play fairways of marine shales in south China. Natural Gas Industry, 2013, 33(7): 140-144 (in Chinese)) |
| [15] | 姚泾利, 王怀厂, 张辉等. 鄂尔多斯盆地东部上古生界致密砂岩超低含水饱和度气藏形成机理义. 天然气工业, 2014, 34(1): 37-43 (Yao Jingli, Wang Huaichang, Zhang Hui, et al. The formation mechanism of Upper Paleozoic tight sand gas reservoirs with ultra-low water saturation in Eastern Ordos Basin. Natural Gas Industry, 2014, 34(1): 37-43 (in Chinese)) |
| [16] | 方朝合, 黄志龙, 王巧智等. 富含气页岩储层超低含水饱和度成因及意义. 天然气地球科学, 2014, 25(3): 471-476 (Fang Chaohe, Huang Zhilong, Wang Qiaozhi, et al. Cause and significance of the ultra-low water saturation in gas-enriched shale reservoir. Natural Gas Geoscience, 2014, 25(3): 471-476 (in Chinese)) |
| [17] | 张浩, 康毅力, 陈一健等. 致密砂岩气藏超低含水饱和度形成地质过程及实验模拟研究. 天然气地球科学, 2005, 16(2): 186-189 (Zhang Hao, Kang Yili, Chen Yijian, et al. The study of geology course and experiment simulation for forming ultra-low water saturation in tight sandstones gas reservoirs. Natural Gas Geoscience, 2005, 16(2): 186-189 (in Chinese)) |
| [18] | Hu YN, Devegowda D, Striolo A, et al. Microscopic dynamics of water and hydrocarbon in shale-kerogen pores of potentially mixed wettability. SPE Journal, 2014, 20(1): 112-124 |
| [19] | 张雪芬,陆现彩,张林晔等. 页岩气的赋存形式研究及其石油地质意义. 地球科学进展, 2010, 25(6): 597-604 (Zhang Xuefen, Lu Xiancai, Zhang Linye, et al. Occurrences of shale gas and their petroleum geological significance. Advances in Earth Science, 2010, 25(6): 597-604 (in Chinese)) |
| [20] | Spears RW, Dudus D, Foulds A, et al. Shale gas core analysis: strategies for normalizing between laboratories and a clear need for standard materials. In: Proc. of SPWLA 52nd Annual Logging Symposium, 2011 |
| [21] | Mattia D, Gogotsi Y. Review: static and dynamic behavior of liquids inside carbon nanotubes. Microfluidics and Nanofluidics, 2008, 5(3): 289-305 |
| [22] | Mahadevan J, Sharma MM, Yortsos YC. Evaporative cleanup of water blocks in gas wells. SPE Journal, 2007, 12(2): 209-216 |
| [23] | Zuluaga E, Muñoz NI, Obando GA. An experimental study to evaluate water vaporisation and formation damage caused by dry gas flow through porous media. In: Proc. of International Symposium on Oilfield Scale, 2001 |
| [24] | Jin Z, Firoozabadi A. Effect of water on methane and carbon dioxide sorption in clay minerals by Monte Carlo simulations. Fluid Phase Equilibria, 2014, 382: 10-20 |
| [25] | Grant RJ, Manes M. Adsorption of binary hydrocarbon gas mixtures on activated carbon. Industrial & Engineering Chemistry Fundamentals, 1966, 5(4): 490-498 |
| [26] | 胡忠鲠. 现代化学基础. 北京: 高等教育出版社, 2000 (Hu Zhonggeng. Basic Modern Chemistry. Beijing: Higher Education Press, 2000 (in Chinese)) |
| [27] | Tharwat T. Encyclopedia of Colloid and Interface Science. Springer, 2013 |
| [28] | Mattia D, Starov V, Semenov S. Thickness, stability and contact angle of liquid films on and inside nanofibres, nanotubes and nanochannels. Journal of Colloid and Interface Science, 2012, 384(1): 149-156 |
| [29] | Deryaguin BV, Churaev NV, Muller VM. Surface Forces. Consultants Bureau. New York, 1987 |
| [30] | 聂百胜, 何学秋, 王恩元等. 煤吸附水的微观机理. 中国矿业大学学报, 2004, 33(4): 379-383 (Nie Baisheng, He Xueqiu, Wang Enyuan, et al. Micro-mechanism of coal adsorbing water. Journal of China University of Mining & Technology, 2004, 33(4): 379-383 (in Chinese)) |
| [31] | 王果庭. 胶体稳定性. 北京: 科学出版社,1990 (Wang Guoting. The Stabilization of Colloid. Beijing: Science Press, 1990 (in Chinese)) |
| [32] | 林建忠. 微纳流动理论及应用. 北京:科学出版社, 2010 (Lin Jianzhong. The Theory and Applications of Micro-flow and Nano-flow. Beijing: Science Press, 2010 (in Chinese)) |
| [33] | Civan F. Effective correlation of apparent gas permeability in tight porous media. Transport in Porous Media, 2010, 82(2): 375-384 |
| [34] | Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena. J Wiley & Sons, New York, 2007 |
| [35] | Rahmanian M, Aguilera R, Kantzas A. A new unified diffusion-viscous-flow model based on pore-level studies of tight gas formations. SPE Journal, 2012, 18(1): 38-49 |
| [36] | Klinkenberg LJ. The permeability of porous media to liquids and gases. In: Drilling and Production Practice, 1941 |
| [37] | Roy S, Raju R, Chuang HF, et al. Modeling gas flow through microchannels and nanopores. Journal of Applied Physics, 2003, 93(8): 4870-4879 |
| [38] | Sakhaee-Pour A, Bryant S. Gas permeability of shale. SPE Reservoir Evaluation & Engineering, 2012, 15(04): 401-409 |
| [39] | 杨胜来, 魏俊之. 油层物理学. 北京: 石油工业出版社, 2004 (Yang Shenglai, Wei Junzhi. Reservoir Physics. Beijing: Petroleum Industry Press, 2011 (in Chinese)) |
| [40] | Takahashi S, Kovscek AR. Wettability estimation of low-permeability, siliceous shale using surface forces. Journal of Petroleum Science and Engineering, 2010, 75(1): 33-43 |
| [41] | Xiong X, Devegowda D, Villazon M, et al. A fully-coupled free and adsorptive phase transport model for shale gas reservoirs including non-darcy flow effects. In: Proc. of SPE Annual Technical Conference and Exhibition, 2012 |
| [42] | Wu QH, Bai BJ, Ma YF, et al. Optic imaging of two-phase-flow behavior in 1d nanoscale channels. SPE Journal, 2014,19(5): 793-802 |
2. CNOOC Research Institute, Beijing 100028, China;
3. University of Calgary, Chemical and Petroleum Engineering, Calgary, Alberta T2N1N4, Canada
 2015, Vol. 47
2015, Vol. 47