2. 中国科学院核能安全技术研究所, 合肥 230031;
3. 中国科学技术大学, 合肥 230026
常规油气藏储层中,岩石的孔喉直径一般超过2 μm,而致密砂岩及页岩中的孔喉直径与其相差1$\sim$3个数量级,页岩气储层孔径一般为5$\sim $200 nm,致密砂岩气储层孔径一般为40$\sim $700 nm [1, 2]. 页岩的微纳孔喉导致页岩在地层条件下的渗透率往往在几十到几百纳达西间[3]. 这时气体分子的平均自由程与孔隙半径的尺度相当,存在滑移、扩散等流动机理,气体流动不再满足连续性假设条件,Navier-Stokes方程已存在偏差. 为此,表示分子平均自由程$\lambda $与流场特征尺度$L$之比的无量纲数克努森数$Kn$常被用来对流动形态进行分类[4]. 当$Kn≤ 10^{ - 3}$时,流动为连续流,满足连续性假设,可以使用无滑移边界条件的Navier-Stokes方程或Darcy定律进行描述;当$10^{ - 3} < Kn < 10^{-1}$时,流动为滑移流,流体分子与壁面分子之间的相互作用不能忽略,但流动依然可以用附加滑移边界条件的Navier-Stokes方程来描述;当$10^{ - 1} < Kn < 10$时,流动为过渡流,流体分子与壁面分子之间的相互作用更加强烈;当$ Kn ≥ 10$时,流动为自由分子流,分子的平均自由程大于孔隙直径,气体分子与孔壁间的碰撞占主导地位.
由于页岩储层中多种流动形态并存,基于连续流的达西定律已不能描述页岩气流动规律,DSMC方法、Boltzmann方法、分子动力学方法等常用来研究微纳尺度的气体流动规律[5, 6, 7, 8, 9]. 基于这些方法,众多学者提出使用滑移边界条件对Navier-Stokes方流动方程进行修正.Maxwell[10]假设流体分子与壁面相互作用时,存在镜面反射和漫反射,并利用$\sigma _v$来描述为漫反射分子的比率,称之为切向动量调节系数 } (tangential momentum accommodation coefficient),推导出一阶滑移速度模型. 通过对Maxwell模型进行扩展,Hsia[11]提出了精度更高的二阶滑移速度模型.二阶滑移速度的一般形式可以表示为${u_{{\text{slip}}}} = {C_1}\lambda {\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}} + {C_2}{\lambda ^2}{\left( {\frac{{{\partial ^2}u}}{{\partial {n^2}}}} \right)_{\text{s}}}$,其中$\lambda$为平均分子自由程, $C_1 $和$C_2 $分别为一阶和二阶滑移系数. Hadjicons- tantinou[12],Aubert等[13],Zhang等[14] 所提出的滑移速度模型都是一般形式的特例. 如果一阶和二阶滑移系数$C_1 $和$C_2$为$Kn$的函数,可以得到更复杂的滑移速度公式,例如,Beskok等[15]模型中的系数是分数形式;Ng[16]模型中的系数是指数形式,另外,Bahukudumbi等[17]和Hwang等[18] 也提出了类似的滑移速公式.早期提出的滑移速度公式主要是为了改进Navier-Stokes方程,使之能准确描述滑移流阶段的速度分布[10, 11].后来部分学者基于流量等效提出的滑移速度模型,使得修正后的Navier-Stokes方程能准确计算不同流态下的流量,从而扩大修正后的Navier-Stokes方程的范围.例如,Ng滑移速度模型下的Navier-Stokes方程能描述$ Kn < 88$时的多种流动形态.
常规的达西定律仅能描述连续流,为使渗流方程能描述滑移流、过渡流、分子流等对流动的影响,渗透率修正是常用使用方法.修正后 的渗透率常称为视渗透率. 早在1941年Klinkenberg [19]就给出了视渗透率公式$K_{\rm a} = K(1 + b_{\rm K } / P)$,其中$K$是固有渗透率(intrinsic permeability),$K_{\rm a} $为视渗透率(apparentpermeability),$b_{\rm K} $为Klinkenberg滑移系数,与气体和多孔介质有关,$P$为压力.随着页岩气的开发,视渗透率的研究日益受到重视.Javadpour等[20, 21]认为页岩气的流动规律不能仅用Darcy定律与Fick定律来描述,并给出了包含扩散、滑移等的视渗透率计算方法.由于页岩存在大量纳米级的孔隙,Darabi等[22]进一步讨论了克努森扩散对流动的影响,认为其对流动的贡献率可达20%.姚同玉等[23]针对纳米孔隙中气体的滑脱效应引入表观渗透率以修正Darcy渗流方程. 考虑到吸附层的非静止性,Zhang等[24]深入研究了表面扩散对流动的影响,发现低压力下的表面扩散对流动有明显的影响.
渗透率的修正不仅有助于准确模拟页岩气在储层中的流动,而且对页岩渗透率测量实验中的数据解释也有很大的影响.在对Pong等(1994)的测试数据进行解释中,Civan发现流动机理对渗透率的解释结果有很大的影响[25, 26]. Li等[27]研究发现,吸附量影响井底压力曲线转角大小,渗透率影响转角位置,并通过短时间的压力数据便有望解释出渗透率与吸附量,从而提供了一种获得渗透率的方法.Clarkson等[28, 29]研究了页岩气流动机理下的生产数据分析方法,Freeman等[30, 31]利用尘气模型研究了页岩气组分变化规律.
本文首先讨论了滑移速度研究进展,然后基于一般形式的二阶滑移速度模型,推导出相应的速度分布公式和渗透率修正公式. 通过对$Kn$分别为0.001,0.01,0.1,0.5和10时的速度分布和渗透率修正系数进行研究,发现不同模型都在滑移流时有效;而基于流量拟合的滑移模型(如Ng模型)不仅在滑移流时适用,而且在过渡流、分子流时都适用. 使用数值模拟程序,研究了不同视渗透率模型对井底压力的影响.
1 修正的二阶渗透率修正模型 1.1 Knudsen数
根据Kinetic气体分子动理论(kinetic theory),气体平均分子自由程$\lambda$可由下式估算[32]
\[\lambda = \frac{\mu }{P}\sqrt {\frac{{\pi {R_{\text{g}}}T}}{{2M}}} \]
(1)
多孔介质孔喉平均半径$R_{\rm h} $,可由下式进行估算[33]
\[{R_{\text{h}}} = 2\sqrt {\frac{{2{\tau _{\text{h}}}K}}{\phi }} \]
(2)
气体在多孔介质流动中的克努森数$Kn$为
\[Kn = \frac{\lambda }{{{R_{\text{h}}}}}\]
(3)
当$ Kn > 10^{-3}$时,壁面处流体的流速不能忽略,流体与壁面间存在相对速度$u_{\rm slip}$,此时流体的流动可用附加滑移速 度边界条件的Navier-Stokes方程进行描述.
在等温条件下的Maxwell[10]滑移速度模型为
\[{u_{{\text{slip}}}} = \frac{{2 - {\sigma _v}}}{{{\sigma _v}}}\lambda {\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}}\]
(4)
由于一阶滑移速度精度有限,Hsia [11]提出了二阶滑移速度模型
\[{u_{{\text{slip}}}} = \frac{{2 - {\sigma _v}}}{{{\sigma _v}}}\lambda {\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}} - \frac{{{\lambda ^2}}}{2}{\left( {\frac{{{\partial ^2}u}}{{\partial {n^2}}}} \right)_{\text{s}}}{\text{ }}\]
(5)
通过对壁面处流体分子镜面反射和漫反射的分析,Beskok等[15]使用泰勒展开方法得到高阶滑移速度模型
\[\begin{gathered}
{u_{{\text{slip}}}} = \frac{{2 - {\sigma _v}}}{{{\sigma _v}}}[\lambda {\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}} + \frac{{{\lambda ^2}}}{2}{\left( {\frac{{{\partial ^2}u}}{{\partial {n^2}}}} \right)_{\text{s}}} + \hfill \\
\frac{{{\lambda ^3}}}{6}{\left( {\frac{{{\partial ^3}u}}{{\partial {n^3}}}} \right)_{\text{s}}} + \cdots ] \hfill \\
\end{gathered} \]
(6)
由于式(6)过于复杂难以求解,因此Beskok通过渐进分析得到下述滑移速度模型[15]
\[{u_{{\text{slip}}}} = \frac{\lambda }{{1 - bKn}}{\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}}\]
(7)
Ng等[16]提出滑移速度模型
\[{u_{{\text{slip}}}} = A\lambda {\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}} - BK{n^C}{\lambda ^2}{\left( {\frac{{{\partial ^2}u}}{{\partial {n^2}}}} \right)_{\text{s}}}\]
(8)
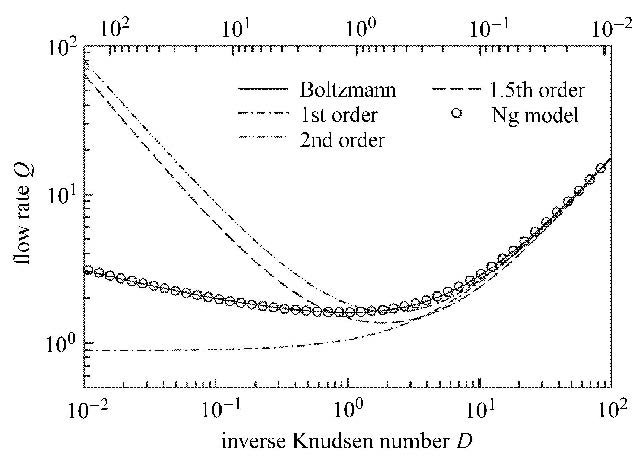
通过对Boltzmann方法计算的流量数据进行数据拟合,得到$A = 1.15$,$B = 0.25$,$C = - 0.65$.其相应的拟合结果如图1所示. 图中横轴为$D = \frac{{\sqrt {{\text{ }}\pi } }}{{2Kn}}$,纵轴为无量纲流量,由此可见Ng的高阶滑移速度模型对$D>0.01$ ($Kn<88$)的情形的 流量都能有效描述.
其他研究[12, 13, 14, 17, 18]也提出了不同的二阶滑移速度边界条件,可统一表示为
\[{u_{{\text{slip}}}} = {C_1}\lambda {\left( {\frac{{\partial u}}{{\partial n}}} \right)_{\text{s}}} + {C_2}{\lambda ^2}{\left( {\frac{{{\partial ^2}u}}{{\partial {n^2}}}} \right)_{\text{s}}}\]
(9)
| 表1 不同模型的$C_1$和$C_2$取值 Table 1 Slip coefficients $C_1$ and $C_2$ of slip velocity models |
柱坐标系下,无限长等截面直圆管中不可压黏性流体的Hagen-Poiseuille流动方程为
\[\mu \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{du}}{{dr}}} \right) = \frac{{dP}}{{dx}}\]
(10)
同时有滑移边界条件和速度有限条件
\[\left. {\begin{array}{*{20}{l}}
\begin{gathered}
{\left. u \right|_{r = R}} = - {C_1}\lambda {\left. {\frac{{\partial u}}{{\partial r}}} \right|_{r = R}} + {C_2}{\lambda ^2}{\left. {\frac{{{\partial ^2}u}}{{\partial {r^2}}}} \right|_{r = R}} \hfill \\
{\left. u \right|_{r = 0}} < \infty \hfill \\
\end{gathered}
\end{array}} \right\}\]
(11)
求解式(10)和(11)可得到圆管内速度分布为
\[u\left( r \right) = \left[ {1 + 2{C_1}Kn - 2{C_2}K{n^2} - {{\left( {\frac{r}{R}} \right)}^2}} \right]{u^{{\text{ref}}}}\]
(12)
\[\begin{gathered}
Q = \int_0^R {2\pi rudr} = \hfill \\
- \frac{{\pi {R^4}}}{{8\mu }}\frac{{dP}}{{dx}}\left( {1 + 4{C_1}Kn - 4{C_2}K{n^2}} \right) \hfill \\
\end{gathered} \]
(13)
由此可得渗透率修正系数
\[Kc = \frac{{Q\left( {Kn} \right)}}{{Q\left( {Kn \to 0} \right)}} = 1 + 4{C_1}Kn - 4{C_2}K{n^2}\]
(14)
相应的气体在多孔介质中达西流动方程可以修正为
\[V = - \frac{{KcK}}{\mu }\nabla p\]
(15)
将表1中Maxwell,Hsia,Beskok和Ng滑移速度模型的滑移系数代入式(12),可以得到各模型的速度分布分别为
\[{u_{{\text{Maxwell}}}}\left( r \right) = \left[ {1 + \frac{{2\left( {2 - {\sigma _v}} \right)}}{{{\sigma _v}}}Kn - {{\left( {\frac{r}{R}} \right)}^2}} \right]{u^{{\text{ref}}}}{\text{ }}\]
(16)
\[{u_{{\text{Hsia}}}}\left( r \right) = \left[ {1 + \frac{{2\left( {2 - {\sigma _v}} \right)}}{{{\sigma _v}}}\left( {Kn + \frac{{K{n^2}}}{2}} \right) - {{\left( {\frac{r}{R}} \right)}^2}} \right]{u^{{\text{ref}}}}\]
(17)
\[\begin{gathered}
{u_{{\text{Beskok}}}}\left( r \right) = \left[ {1 + \alpha \left( {Kn} \right)Kn} \right] \hfill \\
\left[ {1 + \frac{{Kn}}{{1 - bKn}} - {{\left( {\frac{r}{R}} \right)}^2}} \right]{u^{{\text{ref}}}} \hfill \\
\end{gathered} \]
(18)
\[{u_{{\text{Ng}}}}\left( r \right) = \left[ {1 + 2.3Kn + 0.5K{n^{1.35}} - {{\left( {\frac{r}{R}} \right)}^2}} \right]{u^{{\text{ref}}}}\]
(19)
相应的渗透率修正系数分别为
\[K{c_{{\text{Maxwell}}}} = 1 + \frac{{4\left( {2 - {\sigma _v}} \right)}}{{{\sigma _v}}}Kn\]
(20)
\[K{c_{{\text{Hsia}}}} = 1 + \frac{{4\left( {2 - {\sigma _v}} \right)}}{{{\sigma _v}}}\left( {Kn + \frac{{K{n^2}}}{2}} \right)\]
(21)
\[K{c_{{\text{Beskok}}}} = \left[ {1 + \alpha \left( {Kn} \right)Kn} \right]\left( {1 + \frac{{4Kn}}{{1 - bKn}}} \right){\text{ }}\]
(22)
\[K{c_{{\text{Ng}}}} = 1 + 4.6Kn + K{n^{1.35}}\]
(23)
当$Kn$为0.001,0.01,0.1,0.5时,利用式(16) $\sim$式(19),计算可得到Maxwell,Hsia,Beskok和Ng模型下的速度分布,其无量纲结果($u\left( r \right) / u^{\rm ref}$)如图2 所示.
图2(a)表明,$Kn=0.001$时(连续流),速度分布重合,表明在连续流阶段,可以忽略滑移效应.图2(b)表明,当流动处于滑移流阶 段时($Kn=0.01$),4种模型(Maxwell,Hsia,Beskok和Ng模型)计算出的速度分布基本相同,与无滑移边界的结果有一定的差异.这表明在滑移流阶段,4种滑移模型都适用. 图2(c)表明,当流动刚开始进入过渡区时,即自由分子流影响比较小时($Kn=0.1$),4种模型下的速度分布差异开始显现,但由于自由分子流影响很小,因而差别有限.Maxwell和Hsia模型计算的速度分布比较接近,而Beskok模型与Ng模型比较接近,且大于Maxwell和Hsia模型的速度.图2(d)表明当自由分子流影响越来越大时,4种模型的差异也就越来越大. 图2(e)表明,当流动开始进入自由分子流区域时($Kn=10$),在Maxwell和Hsia模型计算的速度分布偏差太大,Beskok模型与Ng模型比较接近,虽然二者速度分布的形态有差异,但在流量计算上却是相当的.这是因为Beskok的滑移模型是建立在Boltzmann和DSMC的速度剖面拟合的基础上,而Ng的滑移速度模型是建立在Boltzmann的流量拟合上的基础上.因而,尽管二者的速度分布有很大差异,但计算显示二者在总流量上却很接近,详见下节的论述.

|
图2 不同$Kn$下的速度场 Fig.2 Velocity profile under different $Kn$ |
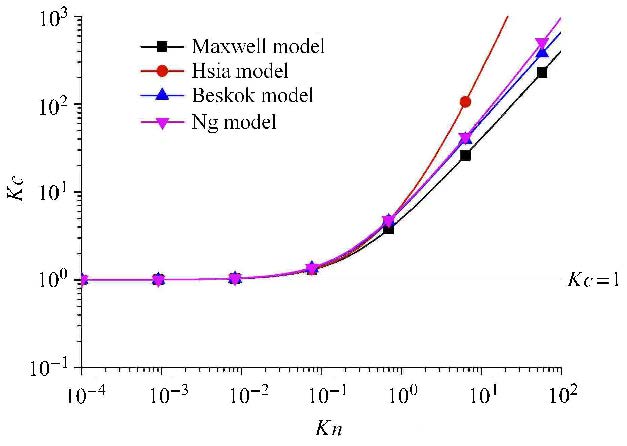
式(13)表明,渗透率的修正是建立在流量修正的基础上的. 因而,渗透率修正系数的差异导致流量计算的差异. 图3给出了$10^{ -4} ≤ Kn ≤ 10^{2}$下的渗透率修正系数. 该图表明,当$Kn ≤0.001$时,4种模型计算出的渗透率等效修正系数$Kc$基本都等于1,说明连续流情形下的滑移效应可以忽略. 但随着$ Kn$的逐渐增大,$Kc$开始逐渐增加,并且不同模型间的差别就越明显.当$Kn>1$时,Hsia模型下的渗透率修正系数增长过快,表明Hsia模型已不适用.Maxwell模型下的渗透率修正系数明显小于Ng模型和Beskok模型下的修正系数.研究已经表明,Maxwell模型、Hsia模型分别仅适用与$Kn ≤ 0.255$和$Kn ≤0.237$的流动区域[34].
虽然Ng模型和Beskok模型都声称适用于自由分子流阶段,但当$Kn>10$时,二者差别开始显现,如$Kn=10$时,其相应的$Kc$分别为69.39和63.63. Ng模型和Beskok模型都是基于微观模拟的结果而建立的滑移边界模型,但在用DSMC和Boltzmann等进行模拟时,所选择的模型参数对计算结果有一定的影响.如DSMC的力场选择、具体模型等,这些可能造成一些差异.另外,Beskok在模型推导时对模型进行了简化,Beskok明确说明了没有考虑分子集聚效应对速度的影响[15],而Niu认为吸附引起的分子集聚效应明显影响着滑移速度[35].
|
图3 4种模型下$Kc$随$Kn$的变化 Fig.3 $Kc$-$Kn$ curve of the four models |
图3也说明,虽然$Kn=0.5$时,Ng模型和Beskok模型的速度分布就有很大差异(图2(d)),但二者的渗透率修正系数却几乎相同.这是由二者滑移速度模型的推导方法差异所造成的.Ng滑移速度模型是建立流量拟合的基础上,而Beskok是建立在速度拟合的基础上的.
2.3 渗透率修正对气井试井曲线的影响本节所用的渗流模型考虑了页岩气多流动机理、吸附机理,相关模型与网格等细节详见文献[27].
主要计算参数为:矩形油藏面积 500 m×500 m,初始地层压力20 MPa,温度50${^\circ}$C,孔隙度0.08,厚度50 m,井位于油藏中心,产量$2.5\times10^4$ m$^{3}$/d,Langmuir体积0.03 m$^3$/d,Langmuir压力7.5 MPa.
计算$R_{\rm h}$分别为1 nm,10 nm,100 nm情形下的$Kn$随压力($0.1 \sim 30$ MPa)的变化关系如图4所示.

|
图4 不同条件下$Kn$随压力的变化 Fig.4 $Kn$ under different pressure |
由图4可以看出,随着压力的降低,$Kn$开始逐渐增加. 在$R_{\rm h} =1$ nm,$P=0.1$ MPa时,$Kn=60.87$,而Ng模型的适用范围 为$Kn<88$,因此据其推导的渗透率修正方法可以对$R_{\rm h}≥ 1$ nm和$P ≥ 0.1$ MPa的情形进行正确计算.
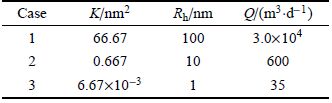
渗透率$K$、孔喉平均半径$R_h$及井产量$Q$等计算参数如表2所示.
| 表2 渗透率$K$、孔喉平均半径$R_{\rm h}$及井产量$Q$ Table 2 Permeability ($K$),average pore throat radius ($R_{\rm h}$) and rate ($Q$) |
针对上述参数,基于文献[27]的方法便可计算表2中3种情形下不同模型的渗透率修正系数$Kc$与压力$P$的关系、井底压力$P_{\rm wf}$ 随生产时间的变化关系.
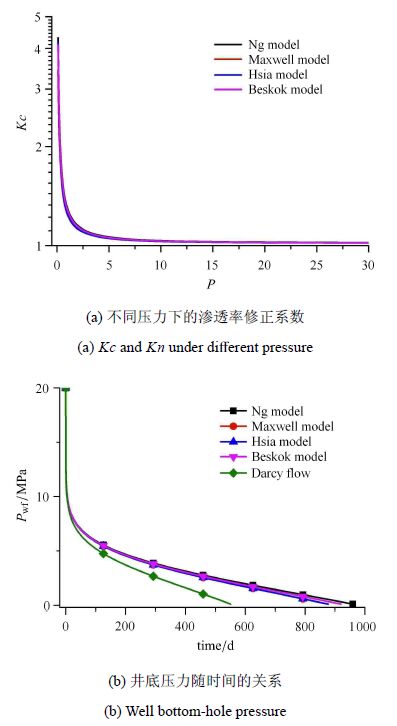
图5为$R_{\rm h}=100$ nm的情形.由图5(a)可以看出,当压力为20 MPa时,$Kn$约为0.005,各种模型计算得到的$Kc$都接近于1 (在1.021$\sim$1.025之间),说明滑移效应对流动的影响非常小.但随着压力的降低,$Kn$开始逐渐增加,相应的渗透率修正系数也开始增加,压力为1 MPa时,$Kn$为0.061,各模型的$Kc$在1.245$\sim$1.305之间. 由图5(b)可以看出滑移速度对井底压力有明显的影响,使井底压力明显升高.但不同滑移模型对井底压力影响小. 这说明,当渗透率较大时,不同滑移模型间的差异小.
|
图5 情形1 ($R_{\rm h}=100$ nm) Fig.5 Case 1 ($R_{\rm h}=100$ nm) |
图6(a)为$R_{\rm h}=10$ nm的情形,由其可以看出,当$R_{\rm h}=10$ nm时,当压力为20 MPa时,$Kn$系数约为0.053,与$K=100$ nm$^{2}$相比增加了9倍,同时各种模型计算得到的$Kc$也都相应增加(在1.212$\sim $1.264之间).这说明滑移效应影响在生产初期就有较为明显的影响.随着压力的降低,$Kn$开始逐渐增加,在压力为1 MPa时,$Kn$约为0.613. 而当$R_{\rm h}=100$ nm时,压力为1 MPa时的$Kn$约为0.061. 因而,$R_{\rm h}=10$ nm时的渗透率修正系数(3.454$\sim$4.339)明显大于$R_{\rm h}=100$ nm时的修正系数.由图6(b)可以看出,相比无滑移情形,各种滑移速度模型计算出的井底压力更大,同时不同滑移模型对井底压力的影响也更大.

|
图6 情形2 ($R_{\rm h}=10$ nm) Fig.6 Case 2 ($R_{\rm h}=10$ nm) |
图7(a)为$R_{\rm h} =1$ nm的情形,由其可以看出,与$R_{\rm h} =10$ nm相比,$Kn$和$Kc$都有明显的增加,例如,压力为20 MPa时的$Kn=0.532$,$Kc$在3.128$\sim $3.873之间.随着压力的降低,增加更为明显,从而滑移流、自由分子流对流动的贡献也就更大. 而且不同模型计算的最大$Kc$也有更大的差别,井底压力为1 MPa时,$Kn$为6.134,不同滑移模型下的$Kc$最多可相差近4倍(25.539$\sim $100.807).根据图7(b),如限定最低井底压力为1 MPa,则根据达西模型计算的稳产时间为11 d,而根据Ng模型和Beskok模型计算的稳产时间分别为694 d和485 d,可见其计算的产能具有明显增加.此外各种滑移速度模型计算出的井底压力明显比不考虑滑移效应的达西模型的井底压力要高,而且Ng模型和Beskok模型的计算结果有了显著差异.根据计算可知,同等条件下,多孔介质的孔喉平均半径越小,滑移效应对流动的影响越大,不同滑移模型间的差异也就更大.

|
图7 情形3 ($R_{\rm h}=1$ nm) Fig.7 Case 3 ($R_{\rm h}=1$ nm) |
基于页岩实际储层温压系统及孔隙分布,计算了$Kn$范围及储层条件下页岩气的流动形态,表明页岩气流动存在滑移流、过渡流与分子自由流.
推导出了一般形式的渗透率修正公式,并基于此一般公式,研究了Maxwell模型、Hsia模型、Beskok模型和Ng模型及其适用范围. 由于Ng模型具有简单、易于实现,其$Kn$的适用范围满足实际页岩储层,因此其可以描述实际储层流动.
对比了Ng模型与其他模型的计算差异. 在滑移流阶段,Ng模型与其他模型的视渗透率基本相同.在分子自由分子流阶段,如$Kn=10$,Ng模型渗透率为达西公式渗透率的69.39倍.在定产量生产条件下,根据Ng模型渗透率计算的稳产时间为达西公式的54倍,即二者产能相差54倍.与其他3个模型相比,Ng模型与Beskok模型的结果最接近,二者产能相差30%.
页岩气中包含多个气体组分,每个组分的$Kn$都有一定的差异.另外,文中的4个模型多是基于吸附量很小的气体所推导出来的,因而 都忽略了吸附的影响.实际的页岩气有较大的吸附量,因而没考虑吸附影响的模型也存在一定的差异.
| [1] | 邹才能, 朱如凯, 吴松涛 等. 常规与非常规油气聚集类型, 特征, 机理及展望-以中国致密油和致密气为例. 石油学报, 2012, 33(2): 173-187 (Zou Caineng, Zhu Rukai, Wu Songtao, et al. Types, characteristics,genesis and prospects of conventional and unconventional hydrocarbon accumulations: taking tight oil and tight gas in China as an instance. Acta Petrolei Sinica, 2012, 33(2): 173-187 (in Chinese)) |
| [2] | Nelson PH. Pore-throat sizes in sandstones, tight sandstones, and shales. AAPG Bulletin, 2009, 93(3): 329-340 |
| [3] | Luffel DL, Hopkins CW, Schettler Jr PD. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, 1993 |
| [4] | Schaaf SA, Chambré PL. Flow of Rarefied Gases. Princenton University Press, 1961 |
| [5] | 蒋建政, 沈青, 樊菁. 不同形状微管道中的气体流动. 力学学报, 2007, 23(2): 145-152 (Jiang Jianzheng, Shen Qing, Fan Jing. Gas flows through micro-pipes with different cross-section shapes. Chinese Journal of Theoretical and Applied Mechanics, 2007, 23(2): 145-152 (in Chinese)) |
| [6] | 田智威, 郑楚光, 王小明. 过渡区气体微尺度流动的格子 Boltzmann 模拟. 力学学报, 2009, 41(6): 828-834 (Tian Zhiwei, Zheng Chuguang, Wang Xiaoming. Lattice Boltzmann simulation of gas micro-flows in transitional regime. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(6): 828-834 (in Chinese)) |
| [7] | Jeong N. Advanced study about the permeability for micro-porous structures using the lattice Boltzmann method. Transport in Porous Media, 2010, 83(2): 271-288 |
| [8] | Park JH, Bahukudumbi P, Beskok A. Rarefaction effects on shear driven oscillatory gas flows: a direct simulation Monte Carlo study in the entire Knudsen regime. Physics of Fluids, 2004, 16(2): 317-330 |
| [9] | Lv J, Cui W, Bai M, et al. Molecular dynamics simulation on flow behavior of nanofluids between flat plates under shear flow condition. Microfluidics and Nanofluidics, 2011, 10(2): 475-480 |
| [10] | Maxwell JC. On stresses in rarified gases arising from inequalities of temperature. Philosophical Transactions of the Royal Society of London, 1879, 170: 231-256 |
| [11] | Hsia YT, Domoto GA. An experimental investigation of molecular rarefaction effects in gas lubricated bearings at ultra-low clearances. Journal of Tribology, 1983, 105(1): 120-129 |
| [12] | Hadjiconstantinou NG. Comment on Cercignani's second-order slip coefficient. Physics of Fluids, 2003, 15(8): 2352-2354 |
| [13] | Aubert C, Colin S. High-order boundary conditions for gaseous flows in rectangular microducts. Microscale Thermophysical Engineering, 2001, 5(1): 41-54 |
| [14] | Zhang H, Zhang Z, Zheng Y, et al. Corrected second-order slip boundary condition for fluid flows in nanochannels. Physical Review E, 2010, 81(6): 66303 |
| [15] | Beskok A, Karniadakis GE. Report: a model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophysical Engineering, 1999, 3(1): 43-77 |
| [16] | Ng EY, Liu N. A multicoefficient slip-corrected Reynolds equation for micro-thin film gas Lubrication. International Journal of Rotating Machinery, 2005, 2005(2): 105-111 |
| [17] | Bahukudumbi P, Beskok A. A phenomenological lubrication model for the entire Knudsen regime. Journal of Micromechanics and Microengineering, 2003, 13(6): 873 |
| [18] | Hwang C, Fung R, Yang R, et al. A new modified Reynolds equation for ultrathin film gas lubrication. Magnetics, IEEE Transactions, 1996, 32(2): 344-347 |
| [19] | Klinkenberg LJ. The permeability of porous media to liquids and gases: Drilling and production practice, 1941. American Petroleum Institute. |
| [20] | Javadpour F, Fisher D, Unsworth M. Nanoscale gas flow in shale gas sediments. Journal of Canadian Petroleum Technology, 2007, 46(10): 55-61 |
| [21] | Javadpour F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). Journal of Canadian Petroleum Technology, 2009, 48(8): 16-21 |
| [22] | Darabi H, Ettehad A, Javadpour F, et al. Gas flow in ultra-tight shale strata. Journal of Fluid Mechanics, 2012, 710: 641-658 |
| [23] | 姚同玉, 黄延章, 李继山. 页岩气在超低渗介质中的渗流行为. 力学学报, 2012, 44(6): 990-995 (Yao Tongyu, Huang Yanzhang, Li Jishan. Flow regim for shale gas in extra low permeability porous media. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 990-995 (in Chinese)) |
| [24] | Zhang L, Li D, Lu D, et al. A new formulation of apparent permeability for gas transport in shale. Journal of Natural Gas Science and Engineering, 2015, 23: 221-226 |
| [25] | Civan F. Effective correlation of apparent gas permeability in tight porous media. Transport in Porous Media, 2010, 82(2): 375-384 |
| [26] | Civan F, Rai CS, Sondergeld CH. Determining shale permeability to gas by simultaneous analysis of various pressure tests. SPE Journal, 2012, 17(3): 717-726 |
| [27] | Li D, Xu C, Wang JY, et al. Effect of Knudsen diffusion and Langmuir adsorption on pressure transient response in tight-and shale-gas reservoirs. Journal of Petroleum Science and Engineering, 2014, 124: 146-154 |
| [28] | Clarkson CR, Qanbari F, Nobakht M, et al. Incorporating geomechanical and dynamic hydraulic-fracture-property changes into rate-transient analysis: example from the haynesville shale. SPE Reservoir Evaluation & Engineering, 2013, 16(3): 303-316 |
| [29] | Clarkson CR, Nobakht M, Kaviani D, et al. Production analysis of tight-gas and shale-gas reservoirs using the dynamic-slippage concept. SPE Journal, 2012, 17(01): 230-242 |
| [30] | Freeman CM, Moridis GJ, Blasingame TA. A numerical study of microscale flow behavior in tight gas and shale gas reservoir systems. Transport in Porous Media, 2011, 90(1): 253-268 |
| [31] | Freeman CM, Moridis GJ, Blasingame TA. Modeling and performance interpretation of flowing gas composition changes in shale gas wells with complex fractures. In: Proc of International Petroleum Technology Conference, 2013 |
| [32] | Loeb LB. The Kinetic Theory of Gases. Courier Corporation, 2004 |
| [33] | Carman PC, Carman PC. Flow of Gases Through Porous Media. Butterworths Scientific Publications London, 1956 |
| [34] | Weng HC. A challenge in Navier-Stokes-based continuum modeling: Maxwell-Burnett slip law. Physics of Fluids, 2008, 20(10): 106101 |
| [35] | Niu C, Hao Y, Li D, et al. Second-order gas-permeability correlation of shale during slip flow. SPE Journal, 2014, 19(05): 786-792 |
2. Institute of Nuclear Energy Safety Technology, Chinese Academy of Science, Hefei 230031, China;
3. University of Science and Technology of China, Hefei 230026, China
 2015, Vol. 47
2015, Vol. 47