1. 中国石油勘探开发研究院廊坊分院, 河北廊坊 065007;
2. 国家能源局页岩气研发实验; 中心, 河北廊坊 065007
2015-03-02 收稿,2015-05-31 录用,2015-06-09 网络版发表
基金项目:国家重大科技专项(2011ZX05018-005)和国家重点基础研究发展计划(973)(2013CB228005)资助项目.
引 言
页岩气是指赋存于以富有机质页岩为主的储集岩系中的非常规天然气[1]. 据预测,世界页岩气资源量为456.24×10$^{12}$m$^{3}$,主要分布于北美、中亚和东亚的中国、中东和北非、拉丁美洲以及欧洲的前苏联等地区,其中,北美的页岩气储量为108.79×10$^{12}$m$^{3}$,占总资源量的23.84%.中国南方海相页岩地层是页岩气主要富集地区,此外,松辽、鄂尔多斯、吐哈、准噶尔等陆相沉积盆地页岩地层也具有页岩气富集的基础和条件[2]. 中国页岩气技术可采资源量估算约为26×10$^{12}$m$^{3}$.页岩气的渗流机理研究是指导页岩气产量预测的重要依据,因此页岩气的渗流机理是页岩气开发的基础.国外学者针对页岩的渗流机理进行了一定量的研究且取得了一些认识,目前普遍认为页岩气流动过程为:首先是裂缝中的气体被采出,裂缝和基质的压力差使得基质表面的吸附气体解吸然后通过裂缝网络流向井筒,该过程气体的流动遵循达西定律[3, 4, 5, 6, 7];基质内部气体在浓度差作用下扩散到表面后通过裂缝流入井筒,扩散过程用Fick定律描述[8, 9, 10, 11, 12, 13, 14].页岩气的基质含有大量的纳米级孔隙,孔隙里面游离气占着一定的比例,气体从基质到裂缝中的流动由Fick定律描述欠妥,除此之外,页岩气流动的物理模拟实验目前相关文献相对较少,本研究针对这些问题,以物理模拟实验为基础研究气体在页岩基质中的流动规律.
1 实验材料及方法
1.1 实验样品和实验方法
页岩样品取自川南地区龙马溪组,取样深度1 408 m.实验设备采用中石油勘探开发研究院廊坊分院自主研发的页岩气解吸-扩散-渗流耦合实验装置,实验流程图见图1.实验步骤如下:(1)所取样品均为现场取芯页岩样品,页岩岩心取上来后用吸水纸擦拭干净并测量长度、直径和重量,然后放入全直径岩心夹持器中. (2)给岩心夹持器加轴压和围压,压力均为40 MPa;(3)打开阀门1和2给岩心夹持器的两端均接入装有甲烷气体的中间容器来饱和岩心,中间容器用ISCO泵稳定气体压力29 MPa,饱和岩心的目的是为了恢复 地层条件下页岩气的存储状态;饱和岩心的时间为240 d,此时给甲烷气瓶提供压力源的ISCO泵液量3 d内不再变化,可以认为页岩岩心已经接近完全饱和状态.(4)岩心饱和完成后关闭阀门1和2并且撤掉高压气瓶,开始解吸-扩散-渗流耦合实验,设定出口压力 为2 MPa,打开阀门2,同时计量岩心夹持器两端的压力、气体流量和时间.(5)实验进行37 d后为了研究不同工作制度下对气体流动规律的影响,撤掉回压阀,出口端的压力变为大气压.
1.2 实验结果
图2为入口压力和出口压力随着时间变化的关系曲线,从图中可以看出开始产气后,页岩基质中压力传播速度很慢,100 d后压力波及到入口边界,压力传播到入口端后,入口端的压力下降非常缓慢.图3为日产气量与时间的变化关系曲线,实验初期气体的产量大并且递减速度非常快,而在实验后期气体的产量小但递减速度非常缓慢,这与页岩气井的实际生产中产量递减规律一致(图4).
2 数学模型及计算
考虑均质的页岩基质,页岩基质中气体的流动包括渗流项以及扩散项,因此其总流动速度$v^{\rm T}$是达西流动速度$v^{\rm D}$和扩散流动速度$v^{\rm K}$之和
|
\[{v^{\text{T}}} = {v^{\text{D}}} + {v^{\text{K}}}\]
|
(1) |
达西流动项可以用达西定理描述
|
\[{v^{\text{D}}} = - \frac{k}{\mu }\nabla p\]
|
(2) |
$k$为基质渗透率,m$^{2}$,$\mu $为气体黏度,Pa$\cdot$s,$p$为气体压力,Pa. 扩散项可以用$Kn$扩散定律描述
|
\[{v^{\text{K}}} = - \frac{D}{{{\rho _{\text{g}}}}}\nabla C\]
|
(3) |
$D$为$Kn$扩散系数,m$^{2}$/s;$C$为气体的质量浓度,kg/m$^{3}$; $\rho_{\rm g}$为气体密度,kg/m$^{3}$.页岩气以吸 附和游离两种状态存在于页岩储层中,以一维情况为例,在页岩气储层中,假设页岩体积单元为$V_{\rm r}$,m$^{3}$,页岩岩石的密度为 $\rho _{\rm r}$,kg/m$^{3}$,页岩储层中气体符合真实气体状态方程,气体摩尔分子量$M_{\rm g}$,mol/kg,则游离气和吸附气在页岩体积单元中的质量浓度分别为
|
\[{C_{{\text{fre}}}} = \frac{{{m_{{\text{fre}}}}}}{{{V_{\text{r}}}}} = \frac{{{\rho _{\text{g}}}{V_{\text{g}}}}}{{{V_{\text{r}}}}} = \frac{{{\rho _{\text{g}}}{V_{\text{r}}}\phi \left( {1 - {S_{\text{W}}}} \right)}}{{{V_{\text{r}}}}} = {\rho _{\text{g}}}\phi \left( {1 - {S_{\text{W}}}} \right)\]
|
(4) |
|
\[{C_{{\text{ads}}}} = \frac{{{m_{{\text{ads}}}}}}{{{V_{\text{r}}}}} = \frac{{{\rho _{\text{r}}}{V_{\text{r}}}{V_{{\text{des}}}}{\rho _{\text{a}}}}}{{{V_{\text{r}}}}} = {\rho _{\text{r}}}{V_{{\text{des}}}}{\rho _{\text{a}}}\]
|
(5) |
|
$$C = C_{\rm fre} + C_{\rm ads} $$
|
(6) |
式中,$C_{\rm fre}$,$C_{\rm ads}$分别为游离气和参与解吸吸附气的质量浓度,kg/m$^{3}$;$m_{\rm fre}$,$m_{\rm ads}$分 别为游离气和吸附气的质量,kg;$V_{\rm r}$,$V_{\rm g}$分别为页岩储层单元体积和气体体积,m$^{3}$; $\rho_{\rm r}$页岩储层单元岩石密度,kg/m$^{3}$; $\rho_{\rm a}$为标况条件下气体密度,kg/m$^{3}$;$V_{\rm des}$页岩参与解吸吸附气量,m$^{3}$/kg;$S_{\rm W}$为含水饱和度,无量纲量; $\phi $ 为页岩孔隙度,无量纲量.
国内外学者普遍认为页岩的等温解吸曲线与等温吸附曲线是可逆的,并且使用Langmuir模型进行解吸曲线的计算;郭为等2012年利用大样量页岩等温吸附解吸实验得出了页岩等温吸附曲线和解吸曲线不重合,且解吸曲线应该用解吸式进行计算的结论,因此页岩解吸附量$V_{\rm des}$的计算按照解吸式模型进行计算[15].
|
\[{V_{{\text{des}}}} = \frac{{{V_{\text{d}}}p}}{{{p_{\text{d}}} + p}} + c\]
|
(7) |
式中,$V_{\rm d}$,$p_{\rm d}$和$c$均为解吸常数,$V_{\rm d}$为页岩解吸过程样最大吸附容量,m$^{3}$/kg;$p_{\rm d}$为吸 附速度、解吸速度与吸附热综合函数,Pa$^{ - 1}$;$c$为匮乏压力下的残余吸附量,m$^{3}$/kg.
气体的密度可以由真实气体的状态方程得到
|
\[{\rho _{\text{g}}} = \frac{{p{M_{\text{g}}}}}{{ZRT}}\]
|
(8) |
将式(2),式(3)代入式(1)可得
|
\[{v^{\text{T}}} = - \left( {\frac{k}{\mu }\nabla p + \frac{D}{{{\rho _{\text{g}}}}}\nabla C} \right)\]
|
(9) |
气体流动的连续性方程为
|
\[\nabla \left( {{\rho _{\text{g}}}{v^{\text{T}}}} \right) = - \frac{{\partial \left[ {{\rho _{\text{g}}}\phi \left( {1 - {S_{\text{W}}}} \right)} \right]}}{{\partial t}} - \frac{{\partial {q_{\text{d}}}}}{{\partial t}} + Q\]
|
(10) |
$q_{\rm d}$表示参与解吸的总吸附气量,$Q$表示源汇项,表示气体的产出或者流入
|
\[{q_{\text{d}}} = \frac{{{\rho _{\text{r}}}{M_{\text{g}}}}}{{{V_{{\text{std}}}}}}\left( {\frac{{{V_{\text{d}}}p}}{{p + {p_{\text{d}}}}} + c} \right)\]
|
(11) |
$V_{\rm std}$为标准状态下气体的摩尔体积,22.4×10$^{ - 3}$m$^{3}$/mol.
|
\[\frac{{\partial {q_{\text{d}}}}}{{\partial t}} = \frac{{\partial {q_{\text{d}}}}}{{\partial p}}\frac{{\partial p}}{{\partial t}}\]
|
(12) |
|
\[\frac{{\partial {q_{\text{d}}}}}{{\partial p}} = \frac{{{\rho _{\text{r}}}{V_{\text{d}}}{M_{\text{g}}}{p_{\text{d}}}}}{{{V_{{\text{std}}}}{{\left( {p + {p_{\text{d}}}} \right)}^2}}}\]
|
(13) |
将式(4) $\sim$式(9),式(11) $\sim$式(13)代入式(10),可得
|
\[\begin{gathered}
\frac{{k{M_{\text{g}}}}}{{RT}}\nabla \left( {\frac{p}{{\mu Z}}\nabla p} \right) + \frac{{D\phi \left( {1 - {S_{\text{W}}}} \right){M_{\text{g}}}}}{{RT}}\nabla \cdot \nabla \left( {\frac{p}{Z}} \right) + \hfill \\
\frac{{D{V_{\text{d}}}{p_{\text{d}}}{\rho _{\text{r}}}{\rho _{\text{a}}}}}{{{{\left( {p + {p_{\text{d}}}} \right)}^2}}}\frac{{\partial p}}{{\partial t}} = \frac{{\phi \left( {1 - {S_{\text{W}}}} \right){M_{\text{g}}}}}{{RT}}\frac{\partial }{{\partial t}}\left( {\frac{p}{Z}} \right) + \hfill \\
\frac{{{\rho _{\text{r}}}{V_{\text{d}}}{p_{\text{d}}}{M_{\text{g}}}}}{{{V_{{\text{std}}}}{{\left( {p + {p_{\text{d}}}} \right)}^2}}}\frac{{\partial p}}{{\partial t}} + Q \hfill \\
\end{gathered} \]
|
(14) |
考虑一维平面流动,方程(14)可以变为
|
\[\begin{gathered}
\frac{{k{M_{\text{g}}}}}{{RT}}\frac{\partial }{{\partial x}}\left( {\frac{p}{{\mu Z}}\frac{{\partial p}}{{\partial x}}} \right) + \frac{{D\phi \left( {1 - {S_{\text{W}}}} \right){M_{\text{g}}}}}{{RT}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left( {\frac{p}{Z}} \right) = \hfill \\
\frac{{\phi \left( {1 - {S_{\text{W}}}} \right){M_{\text{g}}}}}{{RT}}\frac{\partial }{{\partial t}}\left( {\frac{p}{Z}} \right) + \hfill \\
\left[ {\frac{{{\rho _{\text{r}}}{V_{\text{d}}}{p_{\text{d}}}{M_{\text{g}}}}}{{{V_{{\text{std}}}}{{\left( {p + {p_{\text{d}}}} \right)}^2}}} - \frac{{D{V_{\text{d}}}{p_{\text{d}}}{\rho _{\text{r}}}{\rho _{\text{a}}}}}{{{{\left( {p + {p_{\text{d}}}} \right)}^2}}}} \right]\frac{{\partial p}}{{\partial t}} + Q \hfill \\
\end{gathered} \]
|
(15) |
方程(15)只能进行数值计算,利用有限差分法进行差分. 考虑时间向前差分的显式差分,方程左边第1项进行离散
|
\[k\frac{\partial }{{\partial x}}\left[ {\frac{p}{{\mu z}}\frac{{\partial p}}{{\partial x}}} \right] = k\left[ {\left( {\frac{p}{{\mu z}}\frac{{\partial p}}{{\partial x}}} \right)_{i + 1}^n - \left( {\frac{p}{{\mu z}}\frac{{\partial p}}{{\partial x}}} \right)_i^n} \right]/\Delta x\]
|
(16) |
令
|
\[{\lambda _i} = \left( {\frac{p}{{\mu z}}} \right)_i^n = \left[ {\left( {\frac{p}{{\mu z}}} \right)_{i + 2}^n - \left( {\frac{p}{{\mu z}}} \right)_i^n} \right]/2\]
|
(17) |
|
\[\left( {\frac{{\partial p}}{{\partial x}}} \right)_i^n = \frac{{p_{i + 1}^n - p_{i - 1}^n}}{{2\Delta x}}\]
|
(18) |
将方程左边第2项进行离散
|
\[\begin{gathered}
D\phi \left( {1 - {S_{\text{W}}}} \right)\frac{{{\partial ^2}}}{{\partial {x^2}}}\left( {\frac{p}{z}} \right) \hfill \\
= D\phi \left( {1 - {S_{\text{W}}}} \right)\left[ {\left( {\frac{p}{z}} \right)_{i + 2}^n - 2\left( {\frac{p}{z}} \right)_{i + 1}^n + \left( {\frac{p}{z}} \right)_i^n} \right]/\Delta {x^2} \hfill \\
\end{gathered} \]
|
(19) |
方程右边第1项离散
|
\[\begin{gathered}
\frac{{\phi \left( {1 - {S_{\text{W}}}} \right){M_{\text{g}}}}}{{RT}}\frac{\partial }{{\partial t}}\left( {\frac{p}{z}} \right) = \hfill \\
\frac{{\phi \left( {1 - {S_{\text{W}}}} \right){M_{\text{g}}}}}{{RT\Delta t}}\left[ {\left( {\frac{p}{z}} \right)_i^{n + 1} - \left( {\frac{p}{z}} \right)_i^n} \right] \hfill \\
\end{gathered} \]
|
(20) |
方程右边第1项进行离散,令
|
\[A = \frac{{{\rho _{\text{r}}}{\rho _{\text{a}}}D{V_{\text{d}}}{p_{\text{d}}}RT}}{{{M_{\text{g}}}}}\]
|
(21) |
|
\[B = \frac{{{\rho _{\text{r}}}{V_{\text{d}}}{p_{\text{d}}}RT}}{{{V_{{\text{std}}}}}}\]
|
(22) |
|
\[\begin{gathered}
\frac{{B - A}}{{{{\left( {p + {p_{\text{d}}}} \right)}^2}}}\frac{{\partial p}}{{\partial t}} = \hfill \\
\left[ {\frac{{B - A}}{{{{\left( {p_i^{n + 1} + {p_{\text{d}}}} \right)}^2}}}p_i^{n + 1} - \frac{{B - A}}{{{{\left( {p_i^n + {p_{\text{d}}}} \right)}^2}}}p_i^n} \right]/\Delta t \hfill \\
\end{gathered} \]
|
(23) |
将式(16) $\sim$式(23)代入式(15)就能得到时间向前差分的有限差分方程.从图3可看到入口处压力变化非常缓慢,并且在100 d后压力传播到岩心的另一端,因此在计算中假设为定压边界,压力为29 MPa;产气端压力的边界条件和初始条件为:$t$=0 d时,出口压力为29 MPa;$t$ ≤37 d时,产气端压力为2 MPa;$t>37$ d时,出口压力为0.1 MPa;岩心直径为10.5 cm,长度$L$为14.2 cm,将岩心按步长$\Delta x=0.02$ cm进行等分,时间步长为$\Delta t=2$ s,出口处第一个网格的流量就是气体的产量$Q$.
利用"Matlab"软件进行编程计算,可以求得日产气量和压力随着时间的变化关系,表1为编程计算时各个物理量取值,表格中的扩散系数$D $为拟合值,其他各个参数均为平行样品实验测量结果.
表1(Table 1)

表1 数值计算基本参数表Table 1 Parameters of numerical calculation
| Parameter | Value | Parameter | Value |
| $k$ | 2×10$^{ - 25}$m$^{2}$ | $D$ | 2×10$^{ - 12 }$m$^{2}$/s |
| $\phi $ | 0.004 | $S_{\rm W}$ | 0.5 |
| $\rho_{\rm a}$ | 0.668 kg/m$^{3}$ | $\rho_{\rm r}$ | 2.5×10$^{3}$ kg/m$^{3}$ |
| $T$ | 293.15 K | $p_{\rm d}$ | 2.52 MPa |
| $V_{\rm d}$ | 1.2×10$^{ - 3}$m$^{3}$/kg | $c$ | 1×10$^{ - 5}$m$^{3}$/kg |
|
表1 数值计算基本参数表
Table 1 Parameters of numerical calculation |
图5为日产气量随着时间变化的数值计算结果和实验结果对比图,从图中可以看到数值计算结果和实验结果比较吻合;初始阶段,日产气量下降快,到了后期日产气量下降变缓.图6为压力传播随着时间变化的关系图,从图中可以得知,压力的传播过程非常缓慢,100 d时压力传播到入口处,这与实验结果一致,靠近出口端压力下降幅度大,远离出口端压力下降幅度小.
3 影响因素分析
3.1 吸附气体的影响
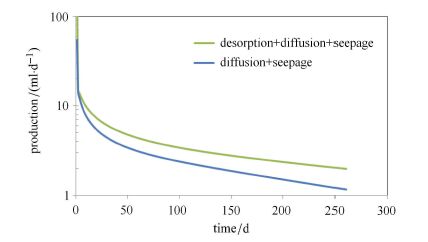
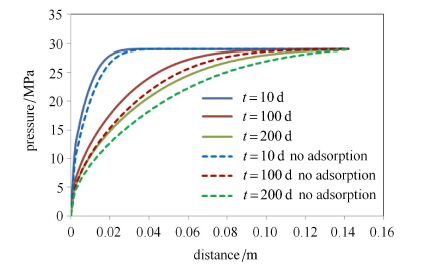
为了对比研究各个影响因素对气体产量的影响,研究对象依然为实验所用的岩心,在计算不同参数对气体产量的影响时,产气端的压力恒定设为0.1 MPa.吸附气体占页岩气很大一部分比例,吸附气体如何影响页岩气的产气量和压力传播的规律对于页岩气藏的有效开发非常重要.图7为有吸附气体和无吸附气体的日产量数值计算结果,从图中可以见到,当无吸附气体时,气体的产量下降非常快;初始阶段有无吸附气体对日产气量影响不大,但是到了后期,有吸附气体的日产量远远大于无吸附气体的日产量,吸附气体在生产后期能够维持日产气量.图8为有吸附气体和无吸附气体时压力的传播过程对比图,从图中可知,无吸附气体时气体的压力传播过程变快,吸附气体的存在可以延缓压力的传播,这是由于吸附气体的解吸能够补充孔隙中气体的压力.
解吸常数$p_{\rm d}$和$V_{\rm d}$也会影响气体的流动规律,图9为不同$V_{\rm d}$条件下,日产气量变化规律,$V_{\rm d}$越大日产气量越大,且产量递减越缓慢. 图10为不同$p_{\rm d}$条件下日产气量变化规律,$p_{\rm d}$越大日产气量越大,$p_{\rm d}$对日产气量的影响程度不及$V_{\rm d}$.
3.2 渗透率和扩散系数的影响
气体在页岩中的流动为渗流和扩散之和,渗透率和扩散系数势必会影响页岩的日产气量. 图11为不同渗透率条件下的日产气量,渗透率越大日产量越高,图12为不同扩散系数条件下的日产气量,扩散系数越大,产气量越高.
3.3 孔隙度的影响
页岩中游离气的含量与孔隙度有关,游离气也会影响气体的流动规律,图13为不同孔隙度条件下的日产气量图,页岩孔隙度越高,游离气含量越多,产气量越大. 因此在页岩气藏开发中,孔隙度是非常重要的一项指标,直接关系到页岩的日产气量.
4 结 论
页岩基质解吸-扩散-渗流耦合实验结果显示气体的初期产量大,下降快,到了后期产量下降缓慢,这种现象与实际生产过程中页岩气井产量一致;压力在页岩中传播缓慢.页岩气的解吸-扩散-渗流耦合数学模型能够描述气体在页岩基质中的流动规律;吸附气体会影响气体的产量和压力传播速度,气体的解吸常数会影响气体的产量,$V_{\rm d}$越大日产气量越大,$p_{\rm d}$越大日产气量越大;页岩基质的渗透率和扩散系数也影响气体的流动规律,渗透率越大日产量越高,扩散系数越大,产气量越高;页岩基质孔隙度影响游离气含量,页岩孔隙度越高,游离气含量越多,产气量越大;在页岩气藏的开发过程中需要考虑气藏的解吸附能力、扩散系数、渗透率和孔隙度等物性参数,得到的数学模型为页岩气的产量预测提供了更准确的计算方法.
参考文献
| [1] |
张东晓, 杨婷云. 页岩气开发综述. 石油学报, 2013, 34(4): 792-801 (Zhang Dongxiao, Yang Tingyun. An overview of shale-gas production . Acta Petrolei Sinica, 2013, 34(4): 792-801 (in Chinese)) |
| [2] |
李玉喜, 张金川.我国非常规油气资源类型和潜力. 国际石油经济,2011, 3: 61-67 (Li Yuxi, Zhang Jinchuan. Unconventional gas & oil resource type and potential of China. International Petroleum Economy, 2011, 3: 61-67 (in Chinese)) |
| [3] |
Carlson NE, Mercer J. Devonian shale gas production: mechanisms and simple models. Journal of Petroleum Technology, 1991, 43(4): 476-482 |
| [4] |
Warren JE, Root PJ. The behavior of naturally fractured reservoirs. Old SPE Journal, 1963, 3(3): 245-255 |
| [5] |
Kuuskpaa VA, Wiicks DE, Thurber JL. Geologic and reservoir mechanisms controlling gas recovery from the Antrim Shale. SPE Annual Technical Conference and Exhibition, 1992 |
| [6] |
Carlso ES. Characterization of devonian shale gas reservoirs using coordinated single well analytical models. SPE Eastern Regional Meeting, 1994 |
| [7] |
Schepers K, Gonzalez R, Koperna G, et al. Reservoir modeling in support of shale gas exploration. Latin American and Caribbean Petroleum Engineering Conference, 2009 |
| [8] |
段永刚, 魏明强, 李建秋 等. 页岩气藏渗流机理及压裂井产能评价. 重庆大学学报, 2011, 34(4): 62-66 (Duan Yonggang, Wei Minqiang, Li Jianqiu, et al. Shale gas seepage mechanism and fractured wells' production evaluation . Journal of ChongQing University, 2011, 34(4): 62-66 (in Chinese)) |
| [9] |
李建秋, 曹建红, 段永刚 等. 页岩气井渗流机理及产能递减分析. 天然气勘探与开发, 2011, 34(2): 34-37 (Li Jianqiu, Cao Jianhong, Duan Yonggang, et al. Seepage mechanism and productivity decline of shale-gas reservoir. Natural Gas Exporation & development, 2011, 34(2): 34-37 (in Chinese)) |
| [10] |
李清泉, 王新海, 尹虎 等. 页岩气藏数值模拟及井底压力动态分析. 东北石油大学学报, 2013, 37(1): 91-96 (Li Qinquan, Wang Xinhai, Yin Hu, et al. Simulation of shale-gas reservoirs and dynamic analysis of bottom hole pressure. Journal of Northeast Petroleum University, 2013, 37(1): 91-96 (in Chinese)) |
| [11] |
任建华, 蔺景德, 张亮 等. 页岩气藏吸附特征及其对产能的影响. 新疆石油地质, 2013, 34(4): 441-444 (Ren Jianhua, Lin Jingde, Zhang Liang, et al. Adsorption characteristics and impact on productivity of shale gas reservoir. Xinjiang Petroleum Geology, 2013, 34(4): 441-444 (in Chinese)) |
| [12] |
李亚洲, 李勇明, 罗攀 等. 页岩气渗流机理与产能研究. 断块油气田, 2013, 20(2): 186-190 (Li Yazhou,Li Yongming,Luo Pan,et al. Study on seepage mechanism and productivity of shale gas. Fault-Block Oil & Gas Field,2013,20(2):186-190 (in Chinese)) |
| [13] |
邓佳, 朱维耀, 刘锦霞 等. 考虑应力敏感性的页岩气产能预测模型. 天然气地球科学, 2013, 24(3): 456-460 (Deng Jia, Zhu Weiyao, Liu Jinxia, et al. Productivity prediction model of shale gas considering stress sensitivity. Natural Gas Geoscience, 2013, 24(3): 456-460 (in Chinese)) |
| [14] |
任飞,王新海,谢玉银 等. 考虑滑脱效应的页岩气井底压力特征. 石油天然气学报, 2013, 35(3):124-126 (Ren Fei, Wang Xinhai, Xie Yuyin, et al. Characteristics of bottom pressure of shale-gas well considering slippage effect. Journal of Oil and Gas Technology, 2013, 35(3): 124-126 (in Chinese)) |
| [15] |
郭为,熊伟,高树生等. 温度对页岩等温吸附/解吸特征影响研究. 石油勘探与开发,2013, 40 (4):481-485 (Guo Wei, Xiong Wei, Gao Shusheng, et al. Impact of temperature on the isothermal adsorption/desorption characteristics of shale gas. Petroleum Exploration and Development, 2013, 40(4):481-485 (in Chinese)) |
GAS DESORPTION-DIFFUSION-SEEPAGE COUPLED EXPERIMENT OF SHALE MATRIX AND MATHEMATIC MODEL
Guo Wei
1

, Hu Zhiming
1, Zuo Luo
1, Gao Shusheng
1, Yu Rongze
1,2, Zeng Bo
1,2
1. Research Institute of Petroleum Exploration & Development-Langfang, Hebei, Langfang 065007, China;
2. National Energy Shale Gas R&D Experiment; Center, Hebei, Langfang 065007, China
Fund: The project was supported by the Major National Science and Technology Projects (2011ZX05018-005) and Key Project of Chinese National Programs for Fundamental Research and Development (973 Program)(2013CB228005).
Abstract: Gas desorption-di usion-seepage coupled experiment was designed and carried out with Longmaxi shale samples collected from South of Sichuan, and both the gas flow characteristics and pressure propagation were then obtained. Shale gas desorption-di usion-seepage coupling mathematical model was derived and numerical solution of the mathematical model using finite difference method was obtained. Numerical simulation results compared with the experimental results show that the model can well describe the gas transport in the shale matrix. And shale matrix permeability, di usion coe cient, desorption constants and other factors can a ect the gas flow through shale matrix as well as pressure propagation, which should be taken into consideration in the development of shale gas reservoir. The presented mathematical model provides a new method to calculate the production capability of shale gas well.
Key words:
shale matrix desorption diffusion seepage experiment mathematical model











 2015, Vol. 47
2015, Vol. 47
