引言

页岩气以其分布范围广、资源量大、稳产周期长等特点，成为当前油气勘探开发的热点. 水平井和大规模水力压裂等技术的进步，为页 岩气藏的商业化开发奠定了工程基础^{[1, 2, 3, 4]}. 页岩中的孔隙主要为纳米和微米级孔隙，因此页岩中的孔隙介质主要为微纳尺度多孔介质. 气体在页岩孔隙中，除了游离气储集方式外，还以吸附气的形式吸附在有机质纳米孔隙表面，与常规油气藏相比有截然不同的储集方式和运移机制^{[5, 6]}. 常规只考虑黏性流动的达西方程无法描述气体在多尺度页岩孔隙中的运移机制^[7].目前页岩气藏数值模拟研究大部分未全面考虑页岩气藏内的黏性流、Knudsen扩散及表面扩散的耦合运移机制^{[8, 9, 10, 11, 12, 13]}，姚军^[14]建立了考虑黏性流、Knudsen扩散的耦合运移模型，但没未考虑表面扩散，且页岩气藏通常发育着微裂缝，但经水力压裂之后会形成宏观大尺度压裂缝，因此裂缝系统具有显著的多尺度特征，单一的连续介质模型或离散裂缝模型均有一定的局限性，如何将两者有机结合是页岩气藏宏观流动模拟的关键，本文全面考虑页岩气藏内的耦合运移机制，采用双重介质模型用来描述基岩与天然微裂缝中的流动，离散裂缝模型模拟压裂后大尺度水力压裂缝中的流动，利用有限元方法进行数值求解，分析不同运移机制、水力裂缝参数和天然裂缝参数对产能的影响，为页岩气藏的高效开发提供理论支持.

1. 页岩气藏运移机制耦合模型

页岩作为典型的微纳尺度多孔介质，气体在页岩中的运移机制主要包括黏性流、Knudsen扩散、表面扩散、分子扩散以及吸附气解吸机制，由此构建气体在页岩基岩和天然裂缝系统中的多重混合运移机制运动方程.

1.1 页岩气藏多重运移机制

根据Javadpour^[14]对页岩基岩孔隙Knudsen数的研究，在页岩基岩孔隙尺寸和压力下，单相气体在基岩孔隙中质量传输主要为黏性流、Knudsen扩散和表面扩散(如图1所示)，若有气体分子吸附在多孔介质表面则还存在吸附气的解吸机制. 由于页岩气藏的主要成分为甲烷气体，故不考虑多相气体间的分子扩散. 采用Knudsen数来判断气体在多孔介质中的运移传输机制，Knudsen 数是气体平均自由程与孔隙直径的比值.

(1)黏性流. 当气体平均运动自由程小于孔隙直径，即Knudsen数远小于1时，气体分子的运动主要受分子间碰撞支配，分子与壁面的碰撞较少，此时在单组分气体之间存在压力梯度所引起的黏性流，黏性流的质量传输可以用达西定律表示为^[16]

$N_{\rm v}=-\dfrac{\rho_{\rm g}k_{\infty}}{\mu_{\rm g}} \nabla p_{\rm g}$

(1)

其中，$N_{\rm v}$为黏性流引起的质量流量(kg/(m$^{2}\cdot $s))，$k_{\infty}$为固有渗透率(m$^{2})$，$p_{\rm g}$为多孔介质孔隙压力(Pa)，$\rho_{\rm g}$为基岩气体的密度(kg/ m$^{3})$，$\mu_{\rm g}$为气体黏度(Pa$\cdot $s).

(2) Knudsen扩散. 当孔隙直径很小时，气体的平均自由程与孔隙直径相近，即Knudsen数约等于1，气体分子与壁面之间的碰撞占主要作用，此时气体之间的质量流量可以用Knudsen扩散表示^[16]为

$N_{\rm k} = - \dfrac{\rho _{\rm g} D_{\rm k} \nabla p_{\rm g} }{p_{\rm g} }$

(2)

其中，$N_{\rm k} $为Knudsen扩散引起的质量流量(kg/(m$^{2}\cdot $s))，$D_{\rm k}$为Knudsen扩散系数(m$^{2}$/s).

(3)表面扩散. 当多孔介质孔隙表面存在吸附气时，多孔介质中存在吸附态气体的表面扩散

$N_{\rm s}=-M_{\rm g}D_{\rm s}\dfrac{C_{\rm s\max}p_{\rm L}}{(p_{\rm g}+p_{\rm L})^2}\nabla p_{\rm g}$

(3)

式中，$N_{\rm s} $为表面扩散引起的质量流量(kg/(m$^{2}\cdot $s))，$M_{\rm g}$为气体的摩尔质量(kg/mol)，$D_{\rm s} $为表面扩散系数(m$^{2}$/s)，$C_{\rm s \max } $为吸附气的最大吸附浓度(mol/m$^{3}$)，$p_{\rm L}$为Langmuir压力(Pa).

(4)页岩气等温吸附方程. 吸附气一般吸附在页岩的基岩表面，吸附量满足Langmuir等温吸附公式^[17]

$q_{\rm ads} = \dfrac{\rho _{\rm s} M_{\rm g} }{V_{\rm std} } \cdot \dfrac{V_{\rm L} p_{\rm g} }{p_{\rm L} + p_{\rm g} }$

(4)

其中，$ q_{\rm ads}$表示页岩单位面积的吸附量( kg/m$^{3})$，$V_{\rm std}$标准状况下的摩尔体积(m$^{3}$/mol)，$q_{\rm std}$表示标准状况下页岩单位质量的吸附体积(m$^{3}$/kg)，$V_{\rm L}$表示Langmuir体积(m$^{3}$/kg)，$\rho_{\rm s }$页岩岩心密度(kg/m$^{3}$).

1.2 页岩气藏运移方程的建立

气体在所有的多孔介质中都存在黏性流和Knudsen扩散，由于多孔介质孔隙尺寸的不同，黏性流和Knudsen扩散在不同多孔介质中所起的作用不同，多孔介质的孔隙尺寸越小，Knudsen扩散的影响越大，反之，多孔介质的孔隙越大，Knudsen扩散的影响越小. 表面扩散只发生在存在吸附气的多孔介质中，同时只有气体是多组分的时候多孔介质中才存在不同气体碰撞产生的分子扩散.

由于裂缝中孔隙尺度较大，气体主要以游离的形式存在，故在页岩天然裂缝中仅考虑气体黏性流和Knudsen扩散，得到页岩气天然裂缝中运动方程为

$N_{\rm t,f} = - \dfrac{\rho _{\rm g} k_{\rm f,a} }{\mu _{\rm f} }\nabla p_{\rm f}$

(5)

式中，$N_{\rm t,f} $为裂缝中的质量流量(kg/(m$^{2}\cdot $s))，$k_{\rm f,a}$为考虑黏性流和Knudsen扩散时多孔介质的视渗透率(m$^{2}$)，$p_{\rm f}$为微裂缝系统的压力值(Pa)，因此微裂缝中的视渗透率可表示为^[17]

$k_{\rm f,a} = k_\infty f(K_{\rm n} ) = k_\infty \left[{1 + \alpha \left( {K_{\rm n} } \right)K_{\rm n} } \right]\left( {1 + \dfrac{4K_{\rm n} }{1 + K_{\rm n}}} \right)$

(6)

式中，$K_{\rm n}$ 为Knudsen数，$\alpha (K_{\rm n} )$为稀薄系数；$k_\infty = \dfrac{b^3}{12a}$，$\phi _{\rm f} = \dfrac{2b}{a}$，$a$表示有效裂缝间距(m)；$b$表示裂缝开度(m).

页岩基岩中既存在吸附气又存在游离气，故应考虑吸附层内表面扩散对气体运移的影响. 假设气体在页岩表面是单分子层吸附，气体在多孔介质中的吸附满足Langmuir等温吸附方程，则可得到考虑黏性流、Knudsen扩散及表面扩散时页岩基岩中的视渗透率为^[19]

$k_{\rm m,a} = k_{\rm a} + M_{\rm g} D_{\rm s} \mu _{\rm g} \dfrac{C_{\rm s\max } p_{\rm L} }{\left( {p_{\rm g} + p_{\rm L} } \right)^2}$

(7)

式中，$k_{\rm m,a} $表示基岩系统中的视渗透率(m$^{2})$；此处，$k_{\rm a} = k_{\rm f,a}$，表示考虑黏性流和Knudsen扩散时多孔介质的视渗透率(m$^{2}$).

2 . 考虑运移机制耦合页岩气藏压裂水平井

由于页岩气藏主要采用水平井结合多段压裂改造进行开采，在此基于离散裂缝模型建立考虑运移机制耦合的页岩气藏压裂水平井数学模型，其中页岩气藏采用双重介质模型，人工裂缝采用离散裂缝模型降维处理，分别得到天然裂缝-基岩双重介质和人工裂缝的数学模型.

2.1 天然裂缝-基岩双重介质数学模型

气体在基岩系统中存在吸附气，吸附气在基岩表面满足Langmuir等温吸附方程，气体在基岩运移包括黏性流、Knudsen扩散和表面扩散机制，在天然裂缝系统主要为黏性流和Knudsen扩散机制，天然裂缝与基岩系统之间满足非稳态窜流方程，气藏外边界封闭，则基岩系统和天然裂缝系统的数学模型为

$\left.\!\!\begin{array}{l} \left[{\gamma \phi _{\rm m} + \dfrac{(1 - \phi _{\rm m} )M_{\rm g} p_{\rm L} V_{\rm L} \rho _{\rm s} }{V_{{\rm std}} (p_{\rm L} + p_{\rm m} )^2}} \right]\dfrac{\partial p_{\rm m} }{\partial t} - \\ \qquad \nabla \cdot \left( {\gamma \dfrac{p_{\rm m} k_{{\rm m,a}} }{\mu _{\rm m} } \nabla p_{\rm m} } \right) =\\ \qquad - \dfrac{\gamma p_{\rm m} \alpha ^\ast k_{{\rm m,a}} }{\mu_{\rm m} }(p_{\rm m} - p_{\rm f} ) \\ \gamma \phi _{\rm f} \dfrac{\partial p_{\rm f} }{\partial t} - \nabla\cdot \left( {\gamma \dfrac{p_{\rm f} k_{\rm f,a} }{\mu _{\rm f} } \nabla p_{\rm f} } \right) = \\ \qquad \dfrac{\gamma p_{\rm m} \alpha ^\ast k_{{\rm m,a}} }{\mu _{\rm m} }(p_{\rm m} - p_{\rm f} ) + q_{\rm f} \delta (M - {M}') \\ p_{\rm m} \Big|_{t = 0} = p_{\rm f} \Big|_{t = 0} = p_{\rm i} \\ \dfrac{\partial p_{\rm m} }{\partial n}\left| {_{\varGamma _1 } } \right. = \dfrac{\partial p_{\rm f} }{\partial n}\left| {_{\varGamma _1 } } \right. = 0 \\ p_{\rm f} (x,y,z;t)\left| {_{\varGamma _3 } } \right. = p_{\rm F} (x,y,z;t)\left| {_{\varGamma _3 } } \right. \end{array}\!\! \right\}$

(8)

其中，$\alpha ^\ast $为形状因子(1/m$^{2}$)，若假定基岩和裂缝为拟稳态窜流时，可得拟稳态窜流时的形状因子$\sigma _{\rm pss}$^[20]

$\sigma _{\rm pss} = 4\Big(\dfrac{1}{a_x ^2} + \dfrac{1}{a_y ^2} + \dfrac{1}{a_z ^2} \Big)$

(9)

$a_{x}$,$a_{y}$和$a_{z}$分别表示$x,y,z$方向的裂缝间距(m). 若假定基岩和裂缝为非稳态窜流，可得非稳态窜流时的形状因 子$\sigma_{\rm TS}$^[21]

$\sigma _{\rm TS} = \sigma _{\rm pss} \dfrac{(p_{\rm i} - p_{\rm f} )^2 - (p_{\rm i} - p_{\rm m} )^2}{2(p_{\rm i} - p_{\rm m} )(p_{\rm m} - p_{\rm f} )}$

(10)

非稳态窜流中，当基岩压力趋近于裂缝压力时，式(10)可以简化为

$\sigma _{\rm TS} = \sigma _{\rm pss} \dfrac{2p_{\rm i} - (p_{\rm f} + p_{\rm m} )}{2(p_{\rm i} - p_{\rm m} )}$

(11)

$\gamma = \dfrac{M}{ZRT}$，$M$为气体摩尔质量(kg/mol)， $Z$为气体压缩因子，$R$为理想气体常数(8.314J/(K$\cdot $mol))，$T$为油藏温度(K)，$\mu _{\rm m},\mu _{\rm f}$为气体分别在基岩和微裂缝压力下的黏度(Pa$\cdot $s)，$\phi_{\rm m},\phi _{\rm f}$分别为基岩和微裂缝系统的孔隙度，$V_{\rm std}$ 为标况下气体摩尔体积(m$^{3}$/mol)，$t$为时间(s)，$\mu _{\rm m}$和$ \mu _{\rm f} $为气体在基岩和微裂缝系统压力下的黏度(Pa$\cdot $s)，$\alpha ^\ast $为形状因子，$p_{\rm F}$为人工裂缝系统压力值(Pa)，$q_{\rm f} $为微裂缝系统流入井筒的流量(cm$^{3}$/s)，$\delta \left( {M - M'}\right)$为$\delta $函数，$M = M'$函数等于1，否则为0.

2.2 人工压裂裂缝系统数学模型

假定气体在人工裂缝处为黏性流，服从Darcy渗流规律，定义气藏的外边界为$\varGamma_1 $，$\varGamma _2 $为生产井的内边界条件，天然裂缝系统与人工裂缝交界的边界定义为$\varGamma _3 $，人工裂缝与天然裂缝系统交界处压力处处相等，则人工裂缝的数学模型可表示为

$\left.\!\!\begin{array}{l} \dfrac{\partial }{\partial t}(\rho _{\rm F} \phi _{\rm F} ) + \nabla \cdot \Big(\dfrac{\rho _{\rm F} k_{\rm F} }{\mu _{\rm F} }\nabla p_{\rm F} \Big) = q_{\rm F} \delta (M - {M}') \\ p_{\rm F} (x,y,z;t = 0) = p_{\rm i} \\ p_{\rm F} \left| {_{\varGamma _2 } } \right. = p_{\rm w} \\ p_{\rm f} (x,y,z;t)\left| {_{\varGamma _3 } } \right. = p_{\rm F} (x,y,z;t)\left| {_{\varGamma _3 } } \right. \end{array}\!\! \right\}$

(12)

式中，$\rho _{\rm F } $为人工裂缝处气体密度(kg/m$^{3}$)，$\phi _{\rm F } $为人工裂缝系统的孔隙度，$k_{\rm F}$表示人工裂缝系统中的视渗透率(m$^{2})$；$\mu _{\rm F } $为人工裂缝系统压力下的黏度(Pa$\cdot $s).

3 . 基于离散裂缝模型分段压裂水平井有限元求解 3.1 模型的有限元求解

对页岩气藏内压裂水平井模型采用有限元数值方法进行求解，其中气藏采用三维四面体单元，基于离散裂缝模型，对人工裂缝系统进行简化降维处理，采用二维三角形单元进行剖分，插值函数采用线性插值，进行单元特性分析，可得到人工裂缝的单元特性矩阵为

$ h_{\rm F} \gamma \phi _{\rm F} \iint\limits_{\varOmega _{\rm e} } {\pmb N}_{\rm e}^{\rm T} {\pmb N }_{\rm e} {\rm d} \varOmega _{\rm e} \dfrac{{\pmb p}_{\rm F,e}^{\rm n + 1} - {\pmb P}_{\rm F,e}^{\rm n } } {t^{n + 1} - t^n} +\\ \qquad h_{\rm F} \iint\limits_{\varOmega _{\rm e} } \nabla {\pmb N}_{\rm e}^{\rm T} \left( {\gamma \dfrac{{\pmb N}_{\rm e} {\pmb p}_{\rm F,e}^{\rm n} k_{\rm F} }{\mu _{\rm f} } } \right)\nabla {\pmb N}_{\rm e} {\rm d} \varOmega _{\rm e }{\pmb p}_{\rm F}^{\rm n + 1} =\\ \qquad h_{\rm F} \iint\limits_{\varOmega _{\rm e} } {\pmb N}_{\rm e}^{\rm T} q_{\rm F}^{\rm n + 1} \delta \left( {M - M'} \right) {\rm d} \varOmega _{\rm e } $

(13)

式中，${\pmb N }_{\rm e} = [N_1 ,N_2 ,N_3]$为单元的形函数，

$\nabla {\pmb N }_{\rm e} = \left[\!\!\begin{array}{l} \dfrac{\partial N_1 }{\partial x} \dfrac{\partial N_2 }{\partial x} \dfrac{\partial N_3 }{\partial x} \\ \dfrac{\partial N_1 }{\partial y} \dfrac{\partial N_2 }{\partial y} \dfrac{\partial N_3 }{\partial y} \end{array}\!\! \right]$

页岩气藏双重介质模型分别整合天然裂缝和基岩系统的单元特性矩阵和列阵，其中假定人工裂缝系统与天然裂缝连通，页岩气藏的流动过程为基岩向天然裂缝供气，天然裂缝流向人工裂缝，最后天然裂缝和人工裂缝同时流向水平井井筒. 根据结点对应关系，将单元特性矩阵里的元素对应到整体序号对应位置，并在没有元素的位置设定为0. 记气藏节点总数为$N_{\rm p} $，则基岩和天然裂缝系统的结点压力值为：${\pmb P}_{\rm m} = \left[{p_{{\rm m},1},p_{{\rm m},2},\cdots,p_{{\rm m},N_{\rm p} } } \right]^{\rm T}$，${\pmb P}_{\rm f} = \left[{p_{\rm f,1} ,p_{\rm f,2} ,\cdots,p_{{\rm f},N_p } } \right]^{\rm T}$，通过有限元推导得到页岩气藏双重介质模型的整体方程组记为

$\left.\!\!\begin{array}{l} \left( {\dfrac{{\pmb A}_{\rm f} }{t^{\rm n + 1} - t^{\rm n}} + {\pmb B }_{\rm f} + {\pmb C}} \right){\pmb P}_{\rm f}^{ \rm n + 1 } = \\ \qquad {\pmb Q }_{\rm f}^{ \rm n + 1 } + \dfrac{{\pmb A }_{\rm f} }{t^{{\rm n} + 1} - t^{\rm n}}{\pmb P}_{\rm f}^{\rm n } + {\pmb C \pmb p}_{\rm m}^{\rm n} \\ \left[{\dfrac{{\pmb A}_{\rm m} }{t^{{\rm n} + 1} - t^{\rm n}} + {\pmb C}} \right]{\pmb p}_{\rm m}^{\rm n + 1} = \dfrac{{\pmb A}_{\rm m} }{t^{{\rm n} + 1} - t^{\rm n}}{\pmb P}_{\rm m}^{\rm n} + {\pmb C \pmb p}_{\rm f}^{\rm n + 1} \end{array}\!\! \right\}$

(14)

式(14)中

${\pmb A}_{\rm f} = \gamma \phi_{\rm f} \iiint\limits_{\varOmega _{\rm e} } {\pmb N}_{\rm e}^{\rm T} {\pmb N}_{\rm e} {\rm d} \varOmega _{\rm e} + h_{\rm F} \gamma \phi _{\rm F} \iint\limits_{\varOmega_{\rm e} } {\pmb N}_{\rm e}^{\rm T} {\pmb N}_{\rm e} {\rm d} \varOmega _{\rm e} $

${\pmb B}_{\rm f} = \iiint\limits_{\varOmega _{e} } \nabla {\pmb N}_{\rm e}^{\rm T}\left( {\gamma \dfrac{{\pmb N}_{\rm e} {\pmb P }_{\rm f}^{\rm n} k_{\rm f,a }}{\mu _{\rm f } } } \right) \nabla {\pmb N}_{\rm e} {\rm d} \varOmega_{\rm e } +$

$\qquad h_{\rm F} \iint\limits_{\varOmega _{\rm e} } \nabla {\pmb N}_{\rm e}^{\rm T} \left({\gamma \dfrac{{\pmb N}_{\rm e} {\pmb P}_{\rm f}^{\rm n} k_{\rm f} }{\mu _{\rm f} }} \right)\nabla {\pmb N}_{\rm e} {\rm d} \varOmega _{\rm e }$

${\pmb C} = \iiint\limits_{\varOmega _{\rm e} } \dfrac{\gamma {\pmb N}_{\rm e} {\pmb p}_{\rm m}^{\rm n} \alpha ^\ast k_{\rm m,a} }{\mu_{\rm m} }{\pmb N}_{\rm e}^{\rm T} {\pmb N}_{\rm e} {\rm d} \varOmega _{\rm e }$

${\pmb Q}_{\rm f}^{ \rm n + 1 } = \iiint\limits_{\varOmega _{\rm m} } {\pmb N}_{\rm e}^{\rm T}q_{\rm f}^{\rm n + 1} \delta \left( {M - M'} \right) {\rm d} \varOmega _{\rm e} +$

$\qquad h_{\rm F} \iint\limits_{\varOmega _{\rm e} } {\pmb N}_{\rm e}^{\rm T} q_{\rm F}^{\rm n + 1} \delta \left( {M - M'} \right) {\rm d} \varOmega _{\rm e} $

${\pmb A}_{\rm m} = \left[{\gamma \phi _{\rm m} + \dfrac{(1 - \phi _{\rm m} )M_{\rm g} p_{\rm L} V_{\rm L} \rho _{\rm s} }{V_{{\rm std}} (p_{\rm L} + {\pmb N}_{\rm e} {\pmb p}_{\rm m}^{\rm n} )^2}}\right]\iiint\limits_{\varOmega _{\rm e} } {\pmb N}_{\rm e}^{\rm T} {\pmb N}_{\rm e} {\rm d} \varOmega _{\rm e }$

${\pmb Q}_{\rm m}^{\rm n + 1} = \iiint\limits_{\varOmega _{\rm m} } {\pmb N}_{\rm e}^{\rm T}q_{\rm m}^{n + 1} \delta \left( {M - M'} \right) {\rm d} \varOmega _{\rm e}$

${\pmb N}_{\rm e} = [N_{1} ,N_{2} ,N_{3} ,N_4]$为单元的形函数

$\nabla {\pmb N}_{\rm e} = \left[\!\!\begin{array}{l} \dfrac{\partial N_1 }{\partial x} \dfrac{\partial N_2 }{\partial x} \dfrac{\partial N_3 }{\partial x}\dfrac{\partial N_4 }{\partial x} \\ \dfrac{\partial N_1 }{\partial y} \dfrac{\partial N_2 }{\partial y} \dfrac{\partial N_3 }{\partial y}\dfrac{\partial N_4 }{\partial y} \\ \dfrac{\partial N_1 }{\partial \mbox{z}} \dfrac{\partial N_2 }{\partial z} \dfrac{\partial N_3 }{\partial z}\dfrac{\partial N_4 }{\partial z} \end{array} \!\! \right]$

时间上采用的是隐式向后差分，利用上一个时间步的基岩压力值，得到该时刻天然裂缝系统的压力值，再利用该时刻的天然裂缝压力值代入基岩系统的整体方程组，得到该时刻基岩系统的压力值，以此类推，得到各个时刻的基岩和天然裂缝系统的压力值.

3.2 模型的正确性验证

为了验证有限元数值算法的正确性，基于盒状封闭气藏双重介质模型，在基岩和微裂缝中仅考虑黏性流的影响，忽略气体其他运移机制，与油气藏数值模拟器Eclipse软件计算结果进行对比，基本参数如表1所示，计算定井底流压为1 MPa时气藏分段压裂水平井产能如图2所示，由图可见，本文采用的有限元数值计算与商业软件Eclipse 计算的压裂水平井产能结果一致，说明本文采用的数值计算方法是正确可行的.

4 . 页岩气藏影响因素分析

对盒状封闭页岩气藏双重介质分段压裂水平井进行数值模拟研究，气藏水平井及裂缝的基本参数见表1，其中页岩气藏中取Langmuir体积和Langmuir压力分别为 2.831 7$\times $10$^{ - 3}$ m$^{3}$/kg，10.4 MPa.

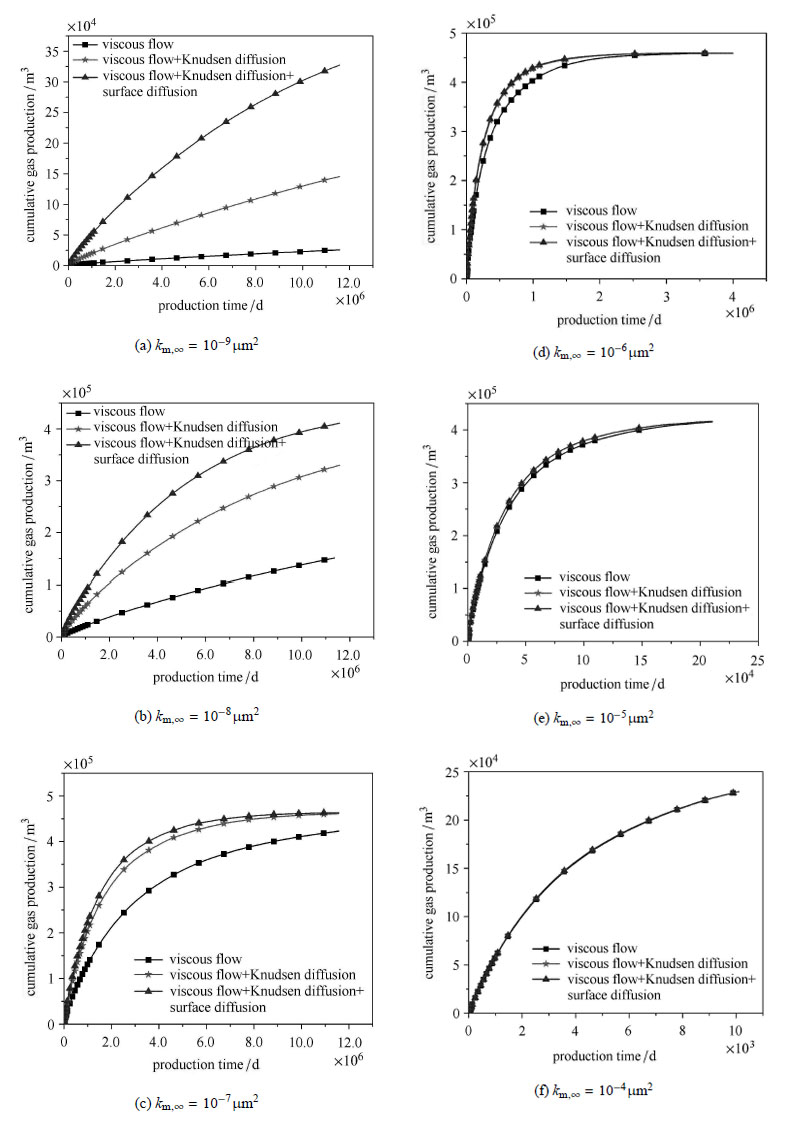
4.1 气体不同运移机制的影响

为了分析不同运移模式对产能的影响，在模型中只考虑页岩基质，忽略微裂缝和人工裂缝，即页岩单孔隙模型水平井，分别对(1)只考虑黏性流(达西方程)；(2)考虑黏性流和Knudsen扩散(DGM模型)；(3)考虑黏性流、Knudsen扩散及表面扩散($k_{\rm m,app}=k_{\rm m,ad} $) 3种情况下的产能进行对比，由于基岩固有渗透率不同时，不同运移模式的差别较大，因此分别取基岩固有渗透率$k_{m,\infty} $为1$\times $10$^{ - 9}\mu $m$^{2}$,1$\times $10$^{ - 8}\mu$m$^{2}$,1$\times $10$^{ - 7}\mu $m$^{2}$,1$\times $10$^{ - 6}\mu$m$^{2}$,1$\times $10$^{ - 5}\mu $m$^{2}$及1$\times $10$^{ - 4}\mu$m$^{2}$ 时页岩气藏的产能，计算结果如图3所示.

图3为不同固有渗透率下各运移机制对累积产量的影响，由图可见表面扩散和Knudsen扩散对单孔隙基岩的产能具有一定的影响，且基岩固有渗透率越小，表面扩散和Knudsen扩散的影响越大，固有渗透率$k_{\rm m,\infty } =10^{ - 9}\mu$m$^{2}$和10$^{ - 8}\mu$m$^{2}$时，表面扩散和Knudsen扩散对基岩的产能影响明显，忽略表面散和Knudsen扩散时预测的产能偏低. $k_{m,\infty} >10^{ - 7}\mu $m$^{2}$时，表面扩散对产能明显减小，且当$k_{m,\infty } >10^{ - 5}\mu$m$^{2}$时，Knudsen扩散对页岩气藏产能的影响也变小，当$k_{m,\infty }\geq 10^{ - 5}\mu$m$^{2}$时，表面扩散和Knudsen扩散的影响非常小，此时可以忽略表面扩散和Knudsen扩散的影响，因此，页岩气藏不同机制的影响大小与固有渗透率的大小有直接的关系.

4.2 人工裂缝参数影响

(1)人工裂缝条数

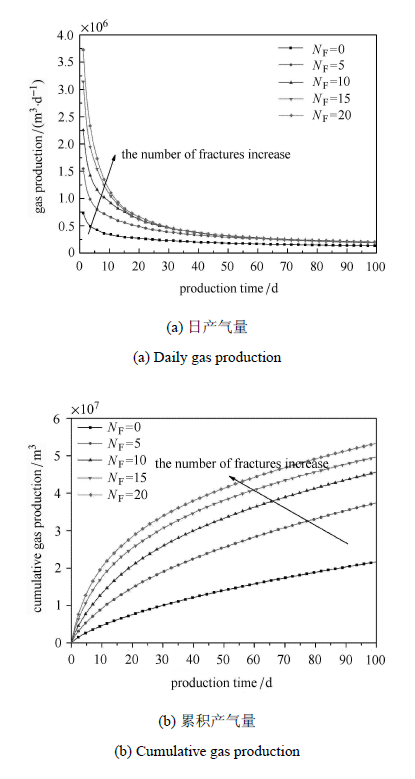
分别取人工裂缝条数为0,5,10,15和20时计算页岩气藏分段压裂水平井产能，分析不同裂缝条数对产能的影响如图4所示.由图可知，人工压裂裂缝条数主要影响水平井生产早期，人工压裂裂缝条数越多，日产气量和累产气量都越大，但随裂缝条数的增加，水平井产能增加的幅度越来越小；且水平井进行压裂和不压裂产量相差较大，所以页岩气藏进行水力压裂后具有较好的生产效果.

(2)人工裂缝开度

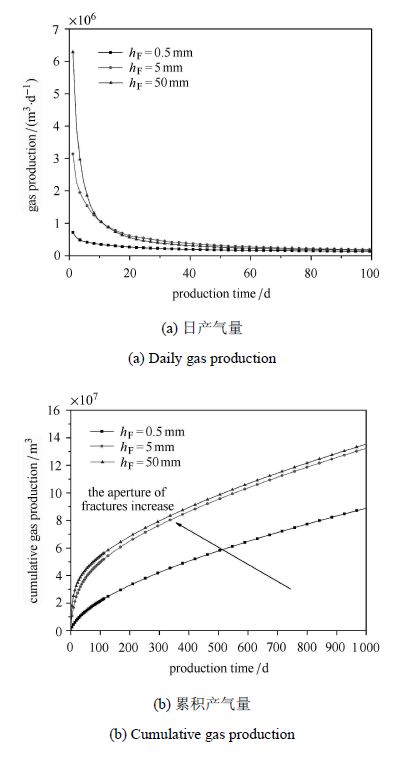
计算人工裂缝开度为0.5 mm,5 mm和50 mm时双重介质页岩气藏压裂水平井的日产量和累积产量随时间的变化，如图5所示. 由图可知，人工裂缝的开度主要影响生产早期，裂缝开度越大，日产气量越高，累积产量越大；且当开度由0.5 mm增加到5 mm时，产量增加幅度明显大于开度由5 mm增加到50 mm，但是随着裂缝开度的增加，产量增加的幅度明显减小，因此通过增加裂缝的开度来提高页岩气藏产量是非常有限的.

(3)人工裂缝半长

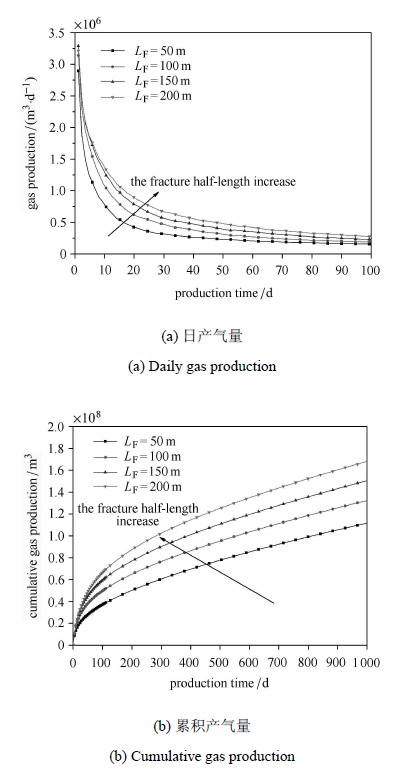
图6表示人工裂缝半长为50 m,100 m,150 m和200 m时双重介质页岩气藏压裂水平井产能的动态变化. 由图可知，与人工裂缝条数和开度一致，裂缝半长也主要影响压裂水平井生产早期，人工压裂裂缝半长越大，页岩气藏的日产气量越大，累积产气量越高；同时随着裂缝半长的线性增长，页岩气藏的累产量几乎等比例增加，因此相对于其它裂缝参数，增加人工裂缝的半长是增加页岩气藏产能的有效方法.

(4)人工裂缝间距

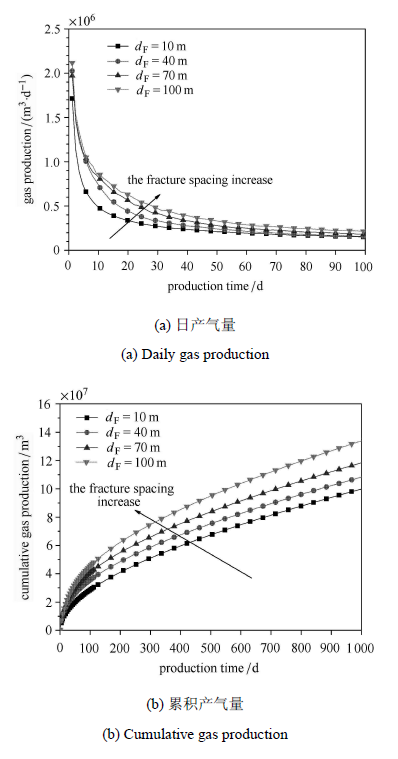
图7表示了人工裂缝数量固定为15条且人工裂缝间距为10 m,40 m,70 m和100 m时双重介质页岩气藏压裂水平井产能的动态变化. 由图可知，当压裂条数固定时，裂缝间距越大，水平井日产气量高，累积产气越大，这是因为压裂条数固定时，裂缝间距越大，说明压裂改造的区域越大，人工裂缝影响的范围越大，因此压裂效果越好.

4.3 天然裂缝参数影响

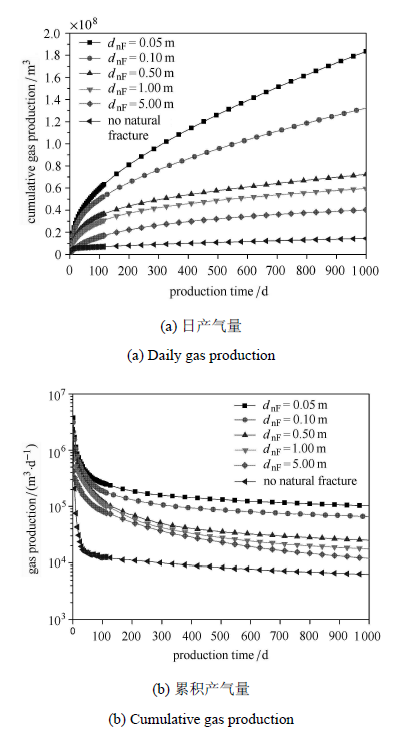
图8表示了天然裂缝间距对双重介质页岩气藏压裂水平井产能的影响，可见天然裂缝的间距对页岩气产能具有非常大 的影响.若天然裂缝发育情况好，天然裂缝间距小，页岩气藏产能较大，说明页岩气藏压裂诱导缝和天然裂缝的发育程度对页岩气藏的产能有较大的影响，水平井进行水力压裂产生人工裂缝，若周围天然裂缝不开启或不发育，则页岩气藏的水平井的产能的提高也是非常有限的，因此页岩气藏要实现高产，除了水力压裂的人工裂缝外，必须要有充足的天然裂缝或人工诱导的微裂缝作为流动通道，仅靠水力压裂的人工裂缝，水平井无法实现高产.

5 . 结论

本文依据页岩气藏自由气和吸附气共存的储集方式，建立了考虑黏性流、Knudsen扩散及表面扩散的耦合运移模型，基于离散裂缝模型建立了分段压裂水平井双重介质模型，并采用有限元方法进行数值求解，分析气体不同运移机制和裂缝参数对产能的影响：

(1)基岩固有渗透率越小，表面扩散的影响越大，固有渗透率小于10$^{ - 8}\mu $m$^{2}$时，表面扩散对基岩的产能影响较大，不能忽略表面扩散的影响，大于等于10$^{ - 6}\mu $m$^{2}$时，表面扩散的影响非常小，此时可以忽略表面扩散的影响.

(2)人工压裂裂缝条数主要影响水平井生产早期，人工压裂裂缝条数越多，日产气量和累产气量都越大，但随裂缝条数的增加，水平井产能增加的幅度越来越小；水平井进行压裂和不压裂产量相差较大，页岩气藏进行水力压裂后具有较好的生产效果.

(3)页岩气藏压裂诱导缝和天然裂缝的发育程度对页岩气藏的产能有很大的影响，水平井光进行水力压裂产生人工裂缝，若周围天然裂缝不开启或不发育，则页岩气藏的水平井的产能也比较低. 页岩气藏要实现高产，除了水力压裂的人工裂缝外，必须要有充足的天然裂缝或人工诱导的微裂缝作为流动通道，仅靠水力压裂的人工裂缝，水平井无法实现高产.