静止圆柱绕流的临界雷诺数$Re_{\rm cr} $约为47[1]:当$Re < Re_{\rm cr} $时流动是对称稳定的;当$Re > Re_{\rm cr} $时,圆柱尾迹开始出现周期性的旋涡脱落,形成著名的卡门涡街. 旋涡脱落引发的周期性流体力诱导圆柱体振动,导致涡致振 动现象. 这种流体诱导结构运动的现象出现在很多工程领域,如航空工程、核工程、海洋工程和风工程等. 当旋涡脱落频率与 结构固有频率接近时,会引发共振现象,导致结构破坏. 因此钝体绕流和涡致振动现象的研究具有重要的工程实际意义,吸引着众 多学者的广泛关注[2, 3, 4]. Bearman[5]和Williamson[6]等对该领域进行了详细的综述和展望.
目前,大部分的涡致振动研究都集中在超临界雷诺数下$Re > Re_{\rm cr} $. 而Cossu[7]和Mittal[8]等的研究表明,在亚临界雷诺数下$Re < Re_{\rm cr} $,圆柱也有可能发生自激振荡,并伴随着周期性的旋涡脱落. Cossu通过全局线性稳定性分析方法(global linear stability analysis, LSA),发现当流体与结构密度比大于1/70时,弹性支撑圆柱绕流的临界雷诺数$Re_{\rm cr} $会降低至静止圆柱绕流临界雷诺数的一半左右. Mittal等通过有限元方法,数值模拟了亚临界雷诺数下弹性支撑圆柱绕流的 涡致振动现象. 他们发现在特定的结构固有频率下,弹性支撑圆柱最低可在$Re\sim 20$时发生涡致振动,而且圆柱体的振动幅值最大可达到圆柱直径的0.45倍.
CFD技术已经广泛应用于流固耦合力学问题的研究. 然而基于CFD技术的流固耦合直接数值模拟的计算花费仍然很大,不适合参 数的分析和系统的设计. 近年来研究者纷纷寻求高效、高精度的非定常气动力模型以适应流固耦合力学的发展.
当前主要有两种模型降阶方法:POD (proper orthogonal decomposition)和系统辨识技术. POD技术的核心是通过样本数据得到一组恰当的正交基函数,使得样本数据在该正交基上的投影 分量依次迅速衰减,从而可以用较少的基展开获得高维数据的近似描述,构造低维动力学模型. 系统辨识方法可以采用基于Volterra级数的积分模型和基于ARX (the autoregressive with exogenous input)的离散差分模型. 在结构小幅运动下,气动力可近似认为是线性的. 基于ARX的降阶模型已成功应用于跨声速颤振分 析[9]和跨声速阵风响应分析[10]等. Cowan等[11]利用系统辨识方法,建立了以结构模态位移作为输入,广义气动力系数作为输出的降阶模型,并耦合结构运动方程成功预测了结构响应. 然而这类系统辨识方法却很少应用于圆柱绕流的非定常气动力建模以及涡致振动分析,这主要是因为研究者认为这种含分离的流动很难采用线化模型进行描述.
本文采用系统辨识方法,尝试建立基于CFD技术的振荡圆柱绕流的气动力降阶模型,在状态空间内耦合结构运动方程和气动力模型,建立了亚临界雷诺数下弹性支撑圆柱绕流的稳定性分析模型. 并基于降阶模型分析了结构参数和来流参数对弹性系统稳定性的影响,并与CFD/CSD直接仿真结果以及文献结果作了对比.
1 非定常气动力计算与建模精确的非定常气动力计算是开展流固耦合研究的基础,本文运用非定常Navier-$\!$-Stokes方程计算气动力,采用非结构网格技术, 运用AUSM+up格式的有限体积法进行空间离散,时间上采用双时间推进方法. 运用RBF插值方法实现非结构网格的运动. 其具体过程详见文献[12].
采用基于ARX模型的系统辨识技术构建非定常气动力ROM,由于本文气动力是在离散空间计算的,因此可以用离散输入输出散差分模型描述多输入多输出系统(MIMO)
| $ y(k) = \sum\limits_{i = 1}^{na} {{A_i}y(k - i)} + \sum\limits_{i = 0}^{nb - 1} {{B_i}u(k - i) + e(k)} $ | (1) |
其中,${ y }$为系统的输出向量,${ u }$为系统的输入向量,${ e}$为0均值的随机噪声. ${ A }_{ i} $和${ B }_{ i} $为待辨识的系数矩阵,$na$和$nb$分别为输出和输入的延迟阶数. 运用最小二乘方法进行参数辨识. 对于本文的气动力模型,圆柱广义位移$ { \xi } = [h,\alpha]$ 为 系统的输入,广义气动力系数${ y}_{ a} = [C_L ,C_m]$ 为 系统的输出.
为了便于进行涡致振动稳定性分析,将式(1)转换为状态空间模型. 定义状态向量$ { x }_{ a} (k)$
| $ { x }_{ a } (k) = [{ y }_{ a } (k - 1), \cdots { y }_{ a } (k - na),\\ \qquad { u }(k - 1),\cdots ,{ u }(k - nb + 1)]^{\rm T} $ | (2) |
则离散空间的气动力状态方程可写为
| $ \left. \begin{array}{l} {x_a}(k + 1) = {{\tilde A}_a}{x_a}(k) + {{\tilde B}_a}u(k)\\ {y_a}(k) = {{\tilde C}_a}{x_a}(k) + {{\tilde D}_a}u(k) \end{array} \right\} $ | (3) |
式中
| $\begin{array}{l} {{\tilde A}_a} = \left[{\begin{array}{*{20}{c}} {{A_1}}&{{A_2}}& \cdots &{{A_{na - 1}}}&{{A_{na}}}&{{B_1}}&{{B_2}}& \cdots &{{B_{nb - 2}}}&{{B_{nb - 1}}}\\ I&0& \cdots &0&0&0&0& \cdots &0&0\\ \vdots &I& \cdots &0&0&0&0& \cdots &0&0\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0& \cdots &I&0&0&0& \cdots &0&0\\ 0&0& \cdots &0&0&0&0& \cdots &0&0\\ 0&0& \cdots &0&0&I&0& \cdots &0&0\\ 0&0& \cdots &0&0&0&I& \cdots &0&0\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0& \cdots &0&0&0&0& \cdots &I&0 \end{array}} \right]\\ {{\tilde B}_a} = {\left[{\begin{array}{*{20}{c}} {{{\tilde B}_0}\;\;0\;\;0\;\; \cdots \;\;0\;\;I\;\;0\;\;0\;\; \cdots \;\;0} \end{array}} \right]^{\rm{T}}}\\ {{\tilde C}_a} = \left[{\begin{array}{*{20}{c}} {{A_1}\;\;{A_2}\;\; \cdots \;\;{A_{na - 1}}\;\;{A_{na}}\;\;{B_1}\;\;{B_2}\;\; \cdots \;\;{B_{nb - 2}}\;\;{B_{nb - 1}}} \end{array}} \right]\\ {D_a} = \left[{{B_0}} \right] \end{array}$ |
为了和结构运动状态方程耦合,运用双线性变换方法(Matlab 里的d2cm命令可实现)将式(3)的离散空间气动力状态方程转化为连续系统状态空间形式
| $ \left.\!\!\begin{array}{l} \dot{ x }_{ a} (t) = { A }_{ a} { x }_{ a } (t) + { B }_{ a } { u} (t) \\ { y }_{ a } (t) = { C }_{ a } { x}(t) + { D }_{ a } { u }(t) \end{array} \!\! \right \} $ | (4) |
圆柱有横向和旋转两个自由度,其示意图如图1所示. 二自由度圆柱刚体运动方程可写为
| $ { M } \cdot \ddot { \xi } + { G } \cdot \dot { \xi } + { K } \cdot { \xi } = { Q} $ | (5) |
其中
| $ { M } = \left[\!\! \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\! \right]\,,\ \ { K }=\left[\!\! \begin{array}{cc} {(2\pi F_n )^2} & 0 \\ 0 & {(2\pi F_n )^2} \end{array}\!\! \right] \\ { G}=\left\{\!\!\begin{array}{cc} {4\pi F_n \zeta } & 0 \\ 0 & {4\pi F_n \zeta } \end{array}\!\!\right\}\,,\ \ { Q }=q\left\{ \!\! \begin{array}{c} {C_L } \\ {8C_m } \end{array} \!\! \right\}\,,\ \ q = \dfrac{2}{\pi M} $ |
|
图 1 两自由度振荡圆柱 Fig. 1 Oscillating cylinder with two degrees of freedom |
$F_n = f_n D / U_\infty $为圆柱的无量纲非耦合固有频率,其中 $f_n $为结构固有频率,$D$为圆柱直径,$U_\infty $为来流速度. $\zeta $为结构阻尼系数,在本文中设定为0. $M = 4m / (\pi \rho D^2)$为质量比,$m$和 $\rho $分别为圆柱的质量和来流的密度,圆柱的位移和速度分别用 $D$和 $U_\infty$ 进行无量纲化. 特别地,定义 $U^ * = 1 / F_n = U_\infty / (f_n D)$为折减速度.
为了便于系统的耦合求解,通常引入结构状态变量${ x }_{ s } = [h,\alpha ,\dot {h},\dot {\alpha }]^{\rm T}$,则结构运动方程可以表示为如下形式的状态方程
| $ \left.\!\!\begin{array}{l} \dot{ x }_{ s } (t) = { A }_{ s } { x}_{s} (t) + q{ B}_{s} { y}_{a} (t) \\ \dot {\xi }(t) = { C}_{s} { x}_{s} (t) + q{ D}_{s} { y}_{a} (t) \end{array} \!\! \right\} $ | (6) |
式中
| $ { A}_{s}= \left[\!\!\begin{array}{cc} {\bf 0} & { I} \\ -{ M}^{- 1}{ K} & -{ M}^{- 1}{ G} \end{array} \!\! \right]\,, \quad { B}_{s} = \left[\!\!\begin{array}{c} {\bf 0} \\ { M}^{ -1} \end{array} \!\! \right] \\ { C}_{s} = \left[\!\!\begin{array}{cc} { I} & {\bf 0} \end{array}\!\!\right]\,, \quad { D}_{s} = {\bf 0} $ |
定义${ x}_{ as} = [{ x}_{s} ,{ x}_{a}]^{\rm T}$,其中${ x}_{s} $为结构状态变量,${ x}_{a} $为气动力状态变量. 耦合气动力状态方程(4)和结构状态方程(6)得到弹性支撑圆柱绕流 稳定性分析的状态方程和输出方程
| $\left. \begin{array}{l} {{\dot x}_{as}}(t) = \left[ {\begin{array}{*{20}{c}} {{A_s} + q{B_s}{D_s}{C_s}}&{amp;q{B_s}{C_a}}\\ {{B_a}{C_s}}&{amp;{A_a}} \end{array}} \right]{x_{as}}(t)\\ \xi (t) = \left[ {\begin{array}{*{20}{c}} {{C_s}}&{amp;{\bf{0}}} \end{array}} \right]{x_{as}}(t) \end{array} \right\}$ | (7) |
这样,弹性支撑圆柱绕流的稳定性分析问题就转化为求解状态方程中矩阵特征值的问题了.
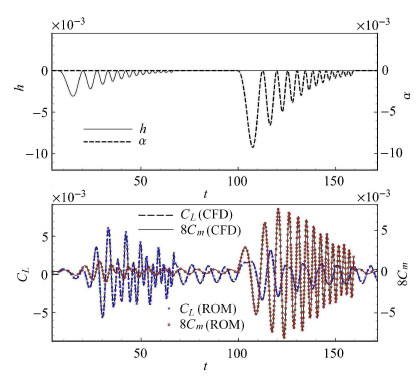
3 算例与分析 3.1 非定常气动力建模训练信号的设计是动力学建模的关键. 信号的频率范围需包含所希望激发的流动模态的频率. 而且训练幅值不能过大,否则 流动的非线性特征比较明显,从而无法用线性方法建立非定常气动力模型. 本文设计了一个幅值衰减,频率不断增加的扫频信号,扫频范围为[0.04,0.20]. 图2给出了$Re =45$时,训练信号作用下,CFD计算结果和辨识模型计算结果的比较. 从图中可以看出,基于最小二乘的辨识方法具有很高的数值精度.
|
图 2 2= 45, 扫频信号输入下CFD 结果和辨识模型解的比较 Fig. 2 Comparison of CFD solutions and the identified model solutions for the chirp input signal at Re = 45 |
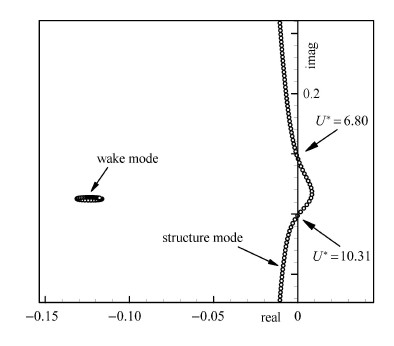
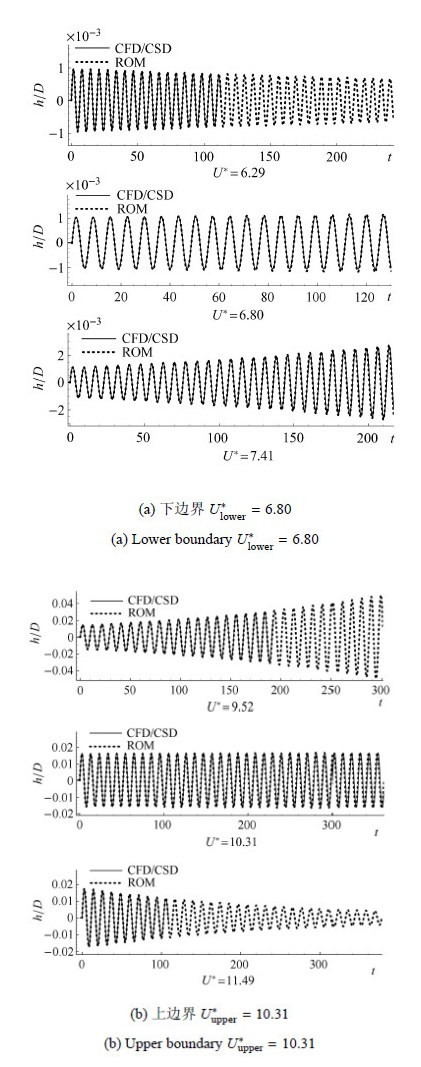
圆柱限定在垂直来流方向运动. 图3给出了$Re = 33$,$M = 50$时弹性系统特征值随结构固有频率$F_n $变化的根轨迹图. 可以看出,系统存在两个最不稳定模态分支:结构模态分支和流动模态分支. 当结构固有频率靠近流动最不稳 定模态的频率时,结构模态分支穿越虚轴,进入右半平面,弹性系统失稳. 从而可知亚临界$Re$下弹性支撑圆柱绕流失稳的根本原因是:结构模态和流动模态耦合作用导致结构模态失稳所致. 图4给出了两个失稳边界附近的时域响应对比. 从图中可以看出,ROM预测结果与直接CFD/CSD仿真结果吻合较好,准确预测了该状态下系统的两个失稳边界:$U_{\rm lower}^\ast = 6.80$,$U_{\rm upper}^\ast = 10.31$.
|
图 3 Re = 33, M = 50 时弹性系统的根轨迹图 Fig. 3 Root loci of the coupled system for Re = 33, M = 50 |
|
图 4 Re = 33, M = 50 临界响应对比 Fig. 4 Comparasions of critical time responses for Re = 33, M = 50 |
图5给出了稳定性边界随质量比变化的趋势. 可以清晰看出质量比对失稳上边界的影响很小;而当质量比逐渐减小时,下边界会 迅速减小. 基于ROM的分析结果与Mittal等 通过数值计算得到的结果吻合良好. 值得注意的是Mittal等 分析的是横向和流向两自由度涡致振动现象. 本文的分析结果从侧面反映了横向自由度的释放对系统的稳定性有着决定性的影响.

|
图 5 稳定性边界随质量比的变化 Fig. 5 Instability boundaries versus the mass ratio |
$Re$对流动和流固耦合系统的动力学特征具有重要的影响. 在这里固定 $M = 50$,研究$Re$的影响. 图6给出了不同$Re$下弹性系统的根轨迹图. 图7给出了稳定性边界随$Re$的变化的稳定性包线. 从图中可以看出在 $Re = 20$时,系统是临界稳定的;当$Re < 20$时,在任何结构固有频率下弹性系统都不会出现失稳,这与Mittal等通过大量数值计算分析的结果一致. 而本文只需要通过几个典型$Re$的信号训练,得到相应$Re$下的降阶气动力模型,然后耦合结构运动方程,得到弹性系统 的降阶模型,通过特征分析便很快能够得到如图7所示的稳定性包线.
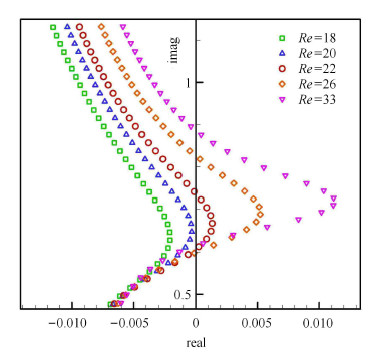
|
图 6 不同Re下弹性系统的根轨迹图 Fig. 6 Root loci of the coupled system for different Re |

|
图 7 稳定性边界随Re的变化 Fig. 7 Instability boundaries varying with Re |
3.2节分析表明,单自由度横向支撑圆柱的失稳临界$Re_{\rm cr} $约为20. 一个很有趣的问题是,弹性支撑圆柱绕流的临界$Re_{\rm cr} $是否能够进一步降低,多自由度释放对弹性系统的稳定性有无影响. 这里同样固定质量比$M =50$, 研究旋转自由度释放对弹性系统稳定性的影响. 图8给出了不同雷诺数下,单自由度旋转支撑圆柱的特征值随$F_n $变化的根轨迹图. 从图中看出各状态下弹性系统都是稳定的,说明单独旋转自由度释放不会影响系统的稳定性,即不会降低 系统的临界雷诺数.
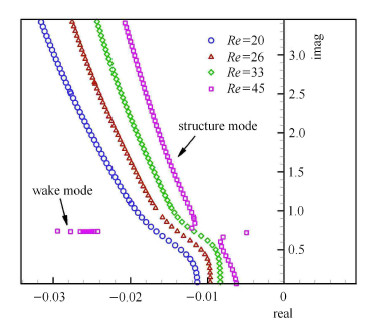
|
图 8 单自由旋转支撑圆柱的根轨迹图 Fig. 8 Root loci of one freedom pitching system |
图9为二自由度弹性系统各$Re$下的根轨迹图,从图中看出二自由度弹性系统的临界$Re$约为18. 图10为$Re = 20$时单自由度 横向支撑圆柱与二自由度支撑圆柱的根轨迹对比. 从图中可以看出,单自由度横向支撑圆柱在$Re = 20$是临界稳定的,而二自由度系统却在$0.088 < F_n < 0.119$区间内发生了失稳,说明旋转自由度的释放进一步降低了系统的稳定性. 图11清晰地给出了单自由度横向支撑圆柱绕流与二自由度弹性支撑圆柱绕流的失稳包线对比.

|
图 9 二自由系统的根轨迹图 Fig. 9 Root loci of two freedom coupled system |

|
图 10 Re = 20 时不同支撑方式根轨迹图对比 Fig. 10 Comparison of root loci for Re = 20 |

|
图 11 稳定性边界对比 Fig. 11 Comparison of instability boundaries |
(1)本文采用系统辨识方法首次建立了绕圆柱流动的非定常气动力模型. 该模型是一个线性动力学模型,能够准确捕获流动的稳定性特征. 这一工作为将来的圆柱绕流主动控制研究奠定了基础.
(2)大部分的涡致振动研究集中在圆柱单自由度横向振动的情形,很少有研究者关注旋转自由度释放对耦合系统的影响. 本文首次研究了旋转自由度释放对系统稳定性特征的影响. 研究表明,相对于单自由度横向支撑方式,旋转自由度的释放能够进一步降低系统的稳定性.
(3) ROM不仅具有很高的计算效率,而且能够深刻揭示弹性支撑圆柱绕流失稳的根本原因:流动模态和结构模态耦合作用导致结构模态失稳所致.
本文结果证明线性模型能够用于解释亚临界$Re$下涡致振动现象的内在机理,这为超临界$Re$下涡致振动锁频现象机理的研究提供了新的思路.
| [1] | Williamson CHK. Vortex dynamics in the cylinder wake. Annual Review of Fluid Mechanics, 1996, 28(1): 477-539 |
| [2] | 陈文曲, 任安禄, 李广望. 串列双圆柱绕流下游圆柱两自由度涡致振动研究. 力学学报, 2004, 36(6): 732-738 (Chen Wenqu, Ren Anlu, Li Guangwang. The numerical study of two-degree of freedom vortex-induced vibrations of the downstream cylinder in tandem arrangement. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(6): 732-738 (in Chinese)) |
| [3] | 宋芳, 林黎明, 凌国灿. 圆柱涡激振动的结构-尾流振子耦合模型研究. 力学学报, 2010, 42(3): 357-365 (Song Fang, Lin Liming, Lin Guocan. The study of vortex-induced vibrations by computation using coupling model of structure and wake oscillator. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 357-365 (in Chinese)) |
| [4] | 王俊高, 付世晓, 许玉旺等. 正弦振荡来流下柔性立管涡激振动发展过程. 力学学报, 2014, 46(2): 173-182 (Wang Jungao, Fu shixiao, Xu yuwang, et al. VIV development process of a flexible cylinder under oscillatory flow. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 173-182 (in Chinese)) |
| [5] | Bearman PW. Circular cylinder wakes and vortex-induced vibrations. Journal of Fluids and Structures, 2011, 27(5): 648-658 |
| [6] | Williamson CHK, Govardhan R. Vortex-induced vibrations. Annual Review of Fluid Mechanics, 2004, 36: 413-455 |
| [7] | Cossu C, Morino L. On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. Journal of Fluids and Structures, 2000, 14(2): 183-196 |
| [8] | Mittal S, Singh S. Vortex-induced vibrations at subcritical Re. Journal of Fluid Mechanics, 2005, 534: 185-194 |
| [9] | 张伟伟, 叶正寅. 基于非定常气动力辨识技术的气动弹性数值模拟. 航空学报, 2006, 27(4): 579-583 (Zhang Weiwei, Ye Zhengyin. Numerical simulation of aeroelasticity basing on identification technology of unsteady aerodynamic loads. Acta Aeronautica et Astronautica Sinica, 2006, 27(4): 579-583 (in Chinese)) |
| [10] | 张伟伟, 叶正寅, 杨青. 基于 ROM 技术的阵风响应分析方法. 力学学报, 2008, 40(5): 593-598 (Zhang Weiwei, Ye Zhengyin, Yang Qing. Gust response analysis using CFD-based reduced order models. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(5): 593-598 (in Chinese)) |
| [11] | Cowan TJ, Arena AS, Gupta KK. Accelerating computational fluid dynamics based aeroelastic predictions using system identification. Journal of Aircraft, 2001, 38(1): 81-87 |
| [12] | 蒋跃文. 基于广义网格的CFD方法及其应用. [博士论文]. 西安:西北工业大学, 2013 (Jiang Yuewen. Numerical solution of Navier-Stokers equations on generalized mesh and its applications. [PhD Thesis]. Xi'an: Northwestern Polytechnical University, 2013 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47