功能梯度材料具有良好的力学性能,它能有效地缓解热应力和残余应力,从而被广泛地应用于航空航天、汽车、能源、建筑和生物医学等领域[1, 2].由于生产过程及工作环境等方面的原因,功能梯度材料不可避免地产生缺陷或裂纹,在动态载荷作用下裂纹的扩展会导致材料破坏失效.因此,研究功能梯度材料动态断裂力学行为对功能梯度材料的安全使用及其结构的设计、优化有着非常重要的意义.
动态断裂力学问题比静态断裂力学问题复杂得多,数值解法是分析这类问题的主要方法.过去几十年,数值方法在分析断裂力学问题中取得了极大成功.主要包括有限差分法[3]、奇异积分方程法[4, 5]、有限元法[6, 7, 8]、边界元法[9, 10, 11, 12, 13, 14]和无网格法[15, 16, 17, 18]等.边界元法是一种半解析的数值方法,它采用解析的基本解且仅在边界上离散,从而降低了求解问题的维数,大大减少了计算量.另外,边界元法只以边界未知量作为基本变量,故而计算精度较高,对应力变化剧烈的问题比较适合.用边界元法求解动态断裂力学问题主要有两种方法:(1)积分变换法;(2)时域基本解法.第1种方法先利用拉普拉斯或傅里叶变换将时域问题转化为频域问题,在求得频域解后,利用积分变换的数值反演得到时域解.该方法涉及大量的复杂运算,且在数值反演时存在数值不稳定性问题.第2种方法利用与时间相关的基本解形成边界积分方程,直接得到时域解.该方法需要推导与时间相关的基本解,对于非均质材料的基本解一般很难获得.
基于开尔文基本解的边界元法仅限于分析均匀或分区域均匀介质中的裂纹问题.近年来,高效伟和张传增等[19]基于开尔文基本解建立了功能梯度材料的边界-域积分方程,并发展了相应的数值方法分析功能梯度材料中的静态断裂力学问题.本文在此基础上基于开尔文基本解,建立功能梯度材料动态断裂力学问题的边界-域积分方程,并使用径向积分法将产生的域积分转化为边界积分,从而形成只含边界积分的纯边界元算法.最后通过数值算例验证本文方法的有效性.
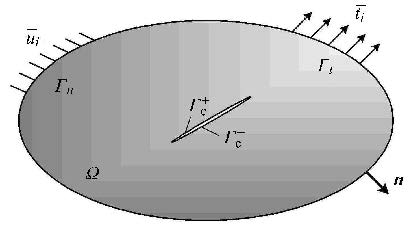
1 功能梯度材料弹性动力学问题的边界-域积分方程考虑如图1所示各向同性、非均质、含裂纹弹性体的线弹性动力学问题,设问题的求解域为$\Omega $,边界为$\Gamma $,则控制方程为
| ${\sigma _{ij,j}} + {f_i} = \rho {\ddot u_i}$ | (1) |
| ${\sigma _{ij}} = {c_{ijkl}}{u_{k,l}}$ | (2) |
|
图 1 含有裂纹的非均质弹性体 Fig.1 A non-homogeneous solid with a crack |
式中,$\rho $为质量密度,${\ddot u_i} = {\partial ^2}{u_i}/\partial {t^2}$为加速度,$u_i $为位移,$u_{k,l} $为位移$u_k $对坐标$x_l $的偏导数,$f_i $为体力,$\sigma _{ij} $为应力张量,$c_{ijkl} $为四阶弹性张量.假设功能梯度材料的弹性模量$E({\pmb x})$为空间坐标的函数,泊松比$v$为常数,则四阶弹性张量$c_{ijkl} $可表示为
| ${c_{ijkl}} = \mu (x)c_{ijkl}^0$ | (3) |
其中,$\mu (x) = E(x)/[2(1 + v)]$为剪切模量,$c_{ijkl}^0$为弹性本构张量.
边界条件为
| ${u_i} = {\bar u_i}{\mkern 1mu} ,\;在边界\Gamma {}_u上$ | (4a) |
| ${t_i} = {\sigma _{ij}}{n_j} = {\bar t_i}{\mkern 1mu} ,在边界{\Gamma _t}上$ | (4b) |
初始条件为
| $u(x,{t_0}) = {u_0}(x){\mkern 1mu} ,\;\;x \in \Omega $ | (4c) |
| $\mathop u\limits^. (x,{t_0}) = {v_0}(x){\mkern 1mu} ,\;\;x \in \Omega $ | (4d) |
式中,${\Gamma _u}$和${\Gamma _t}$分别为本质边界条件和自然边界条件的边界部分.
在不考虑体力情况下,使用权函数$U_{ij} $,由式(1)采用加权残量法,得到平衡方程的弱形式为
| $\int_\Omega {{U_{ij}}({\sigma _{jk,k}} - \rho {{\ddot u}_j})} d\Omega = 0$ | (5) |
将式(2)代入式(5),由分部积分和高斯散度定理得
| $\begin{array}{l} \int_\gamma {{U_{ij}}{\sigma _{jk}}{n_k}d\Gamma } - \int_\gamma {{U_{ij,k}}c_{jkrs}^0{n_s}\mu {u_r}d\Omega } + \\ \int_\Omega {{U_{ij,ks}}c_{jkrs}^0\mu {u_r}d\Omega } + \int_\Omega {{U_{ij,k}}c_{jkrs}^0{\mu _{,s}}{u_r}d\Omega } - \\ \int_\Omega {\rho {U_{ij}}{{\ddot u}_j}d\Omega } = 0 \end{array}$ | (6) |
取权函数$U_{ij} $满足下列方程的基本解
| ${U_{ij,ks}}c_{jkrs}^0 + {\delta _{ir}}\delta (x,{x^p}) = 0$ | (7) |
式中,$\delta (x,{x^p})$为奇点在${x^p}$的狄拉克函数.将式(7)代入式(6),由狄拉克函数的积分性质,可得到
| $\begin{array}{*{20}{l}} {{{\tilde u}_i}({x^p}) = \int_\gamma {{U_{ij}}(x,{x^p}){t_j}(x)d\Gamma } - }\\ {\int_\gamma {{T_{ij}}(x,{x^p}){{\tilde u}_j}(x)d\Gamma } + }\\ {\int_\Omega {{V_{ij}}(x,{x^p}){{\tilde u}_j}(x)d\Omega } - }\\ {\int_\Omega {\frac{\rho }{{\mu (x)}}{U_{ij}}(x,{x^p}){{\tilde u}_j}(x)d\Omega } } \end{array}$ | (8) |
式中$U_{ij} $和$T_{ij} $分别为$\mu = 1$的开尔文位移和面力基本解,其表达式可参考一般的力学边界元专著;由开尔文位移基本解 可得到核函数$V_{ij}$的表达式为
| $\begin{array}{l} {V_{ij}} = {U_{il,k}}c_{lkjs}^0{{\tilde \mu }_{,s}} = \\ \frac{{ - 1}}{{4\pi \alpha (1 - v){r^\alpha }}}\{ {{\tilde \mu }_{,k}}{r_{,k}}\left[{(1 - 2v){\delta _{ij}} + \beta {r_{,i}}{r_{,j}}} \right] + \\ (1 - 2v)({{\tilde \mu }_{,i}}{r_{,j}} - {{\tilde \mu }_{,j}}{r_{,i}})\} \end{array}$ | (9) |
其中,$\tilde {u}_i = \mu u_i $和$\tilde {\mu } = \ln \mu $分别是规则化的位移和剪切模量;$\beta = 2$ (二维问题)或$\beta = 3$ (三维问题),$\alpha = \beta - 1$.方程(8)只适合内部点,对于边界点,令${\pmb x}^p \to \varGamma $,通过求极限 可获得边界积分方程.
2 域积分转化为边界积分积分方程(8)式中含有未知函数的域积分,本文采用径向积分法[20]将其转换成等效的边界积分,从而形成不需要内部网格的纯边界元算法.为此,将式(8)中的未知函数采用增强径向基函数表示为
| $u(x) = \sum\limits_A {\alpha _i^A{\phi ^A}(R)} + a_i^k{x_k} + a_i^0$ | (10) |
式中,$R = \left\| {x - {x^A}} \right\|$为源点${\pmb x}^A$到场点${\pmb x}$之间的 距离,$\phi^A$为径向基函数,$\alpha _i^A $,$\alpha _i^k $和$\alpha _i^0 $为待定系数.
待定系数可由场点${\pmb x}$的支持域内周围节点的值和约束条件通过配点来确定[21, 22].将求得的 系数$\alpha _i^A $,$\alpha _i^k $和$\alpha _i^0 $代入式(8),可得到未知量由结点值表示的形式
| $u(x) = \Phi (x)\left\{ u \right\} = \sum\limits_{i = 1}^n {{\phi _i}{u_i}} $ | (11) |
式中$\varPhi ({\pmb x})$为形函数.将式(11)代入式(8)中的域积分,由径向积分法公式[20],可得到
| $\begin{array}{l} c{{\tilde u}_i}({x^p}) = \int_\gamma {{U_{ij}}(x,{x^p}){t_j}(x)d\Gamma } - \\ \int_\gamma {{T_{ij}}(x,{x^p}){{\tilde u}_j}(x)d\Gamma } + \\ \{ {{\tilde u}_j}\} \int_\gamma {\frac{1}{{{r^\alpha }}}\frac{{\partial r}}{{\partial n}}} F_{ij}^1d\Gamma - \\ \{ {{\tilde u}_j}\} \int_\gamma {\frac{1}{{{r^\alpha }}}\frac{{\partial r}}{{\partial n}}F_{ij}^2d\Gamma } \end{array}$ | (12) |
式中
| $F_{ij}^1 = \int_0^{r({x^p},{x^q})} {{V_{ij}}(x,{x^p})\Phi {r^\alpha }dr} $ | (13a) |
| $F_{ij}^2 = \int_0^{r({x^p},{x^q})} {\frac{\rho }{{\mu (x)}}{U_{ij}}(x,{x^p})\Phi {r^\alpha }dr} $ | (13b) |
式(12)即为关于规则化位移的边界积分方程.
3 数值实施以二维问题为例,将求解问题的边界离散成边界单元,假设离散的边界元模型总共有$N_{ t}$个节点,其中边界节点数为$N_{ b} $,内部节点数为$N_{ i} $.由式(12)经数值积分并施加边界条件后可得到关于所有边界节点和内部节点的常微分方程组
| ${H_b} \cdot {\widetilde u_b} = {G_b} \cdot {t_b} + {V_b} \cdot {\widetilde u_t} - {M_b} \cdot {\mathop {\widetilde u}\limits^{..} _t}$ | (14) |
| $I \cdot {\widetilde u_i} + {H_i} \cdot {\widetilde u_i} = {G_i} \cdot {t_b} + {V_i} \cdot {\widetilde u_t} - {M_i} \cdot {\mathop {\widetilde u}\limits^{..} _t}$ | (15) |
其中,${\widetilde u_b}$和${t_b}$分别为边界节点位移和面力向量,${\widetilde u_i}$为内部节点位移向量,${\widetilde u_t}$为所有节点的位移向量;式(14)和式(15)可合起来写成
| $\begin{array}{l} \left( {\left[{\begin{array}{*{20}{c}} {{H_b}}&{\bf{0}}\\ {{H_i}}&I \end{array}} \right] - \left[{\begin{array}{*{20}{c}} \begin{array}{l} {V_b}\\ {V_i} \end{array} \end{array}} \right]} \right)\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\widetilde u_b}\\ {\widetilde u_i} \end{array} \end{array}} \right\} = \\ \left[{\begin{array}{*{20}{c}} \begin{array}{l} {G_b}\\ {G_i} \end{array} \end{array}} \right]\left\{ {{t_b}} \right\} - \left[{\begin{array}{*{20}{c}} \begin{array}{l} {M_b}\\ {M_i} \end{array} \end{array}} \right]\left\{ {{{\mathop {\widetilde u}\limits^{..} }_t}} \right\} \end{array}$ | (16) |
经过施加边界条件以及简化合并,由上式可得到离散系统的总体常微分方程组
| $M\mathop x\limits^{..} + Kx = F$ | (17) |
式中向量${\pmb x}$为边界节点未知量和内部节点位移.
边界元法离散后形成的系数矩阵为非对称矩阵,由于非对称矩阵在高频谱区产生复数频率,而复数频率容易引起数值不稳定性,因此本文采用稳定性较好的候博特方法[23]求解式(17).在候博特方法有限差分格式中,未知量关于时间的二阶导数可表示为
| ${\mathop x\limits^{..} _{t + \Delta t}} = \frac{{2{x_{t + \Delta t}} - 5{x_t} + 4{x_{t - \Delta t}} - {x_{t - 2\Delta t}}}}{{\Delta {t^2}}}$ | (18) |
其中$\Delta t$为时间步长.采用向后差分法表示未知量关于时间的一阶导数
| ${\mathop x\limits^. _{t + \Delta t}} = \frac{{{x_{t + \Delta t}} - {x_t}}}{{\Delta t}}$ | (19) |
将式(18)和(19)代入式(17),即可得到关于$t + \Delta t$时刻未知量的代数方程组
| $\begin{array}{l} \left( {\frac{2}{{\Delta {t^2}}}M + K} \right){x_{t + \Delta t}} = \\ \frac{5}{{\Delta {t^2}}}{x_t} + \frac{1}{{\Delta {t^2}}}M\left( { - 4{x_{t - \Delta t}} + {x_{t - 2\Delta t}}} \right) + {F_{t + \Delta t}} \end{array}$ | (20) |
由于各向同性、非均质线弹性体裂纹尖端渐近场与各向同性、均质线弹性体裂纹尖端渐近场相\linebreak 同[4],因此由裂纹应力强度因子与裂纹张开位移之间的关系可以得出应力强度因子的表达式
| $\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {K_{\rm{I}}}\\ {K_{{\rm{II}}}}\\ {K_{{\rm{III}}}} \end{array} \end{array}} \right\} = \mathop {\lim }\limits_{r \to 0} \sqrt {\frac{{2\pi }}{r}} \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {H^{({\rm{I}})}}\Delta {u_2}(r)\\ {H^{({\rm{II}})}}\Delta {u_1}(r)\\ {H^{({\rm{III}})}}\Delta {u_3}(r) \end{array} \end{array}} \right\}$ | (21) |
式中,${H^{({\rm{I}})}} = {H^{({\rm{II}})}} = \frac{{2{\mu _{{\rm{tip}}}}}}{{\kappa + 1}},{H^{({\rm{III}})}} = \frac{{{\mu _{{\rm{tip}}}}}}{2}$;
| $\kappa = \left\{ \begin{array}{l} 3 - 4v{\mkern 1mu} ,平面应变\\ \frac{{3 - v}}{{1 + v}},{\mkern 1mu} 平面应力 \end{array} \right.$ | (22) |
其中,$K_{\rm I} $,$K_{{\rm II}} $和$K_{{\rm III}} $分别称为I型、II型和III型裂纹的应力强度因子,$\mu _{\rm tip} $为裂纹尖端剪切模量,$r$为裂纹面上考虑的点到裂纹尖端的距离,$\Delta u_i (r)$为局部坐标系下裂纹张开位移,其表达式为
| $\Delta {u_i}(r) = {u_i}(x \in \Gamma _{\rm{c}}^ + ) - {u_i}(x \in \Gamma _{\rm{c}}^ - )$ | (23) |
为了验证本文方法的有效性,分别对两种不同情况中心裂纹进行分析,并将本文方法的数值解与有限元软件``ABAQUS''计算的结果进行对比.
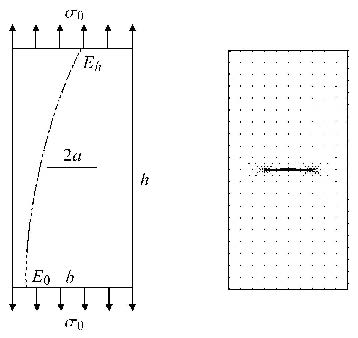
考虑一个处于平面应变状态下,含中心裂纹的功能梯度材料矩形平板,板的上下两边同时作用阶跃函数动载荷 ${\sigma _0} = 0.4{\mkern 1mu} GPa$假设平板为线弹性、各向同性材料,平板的几何尺寸和材料属性为长b = 2cm,高h = 4cm,密度ρ = 5000kg/m3,泊松比$v = 0.3$,裂纹长度$2a = 0.8$cm;平板底部弹性模量$E_0 = 200$GPa,顶部$E_h = 500$GPa,弹性模量沿$y$轴方向成指数函数变化$E({\pmb x}) = E_0 {\rm e}^{\beta y}$,其中$\beta = 25\ln 2.5$.
当中心裂纹为直裂纹时,如图2所示,裂纹与材料梯度变化方向垂直,沿裂纹方向材料属性相同.将平板边界和裂纹上下表面离 散成84个二次单元,域内布置236个内部节点,靠近裂纹尖端的单元网格和节点逐渐变密.
|
图 2 含中心直裂纹的功能梯度材料平板 Fig.2 FGM plate with a vertical central crack |
用本文方法求解式(17)常微分方程组时,时间步长取$\Delta t = 2$ns,解得平板动态响应位移$u$后,由式(21)即可求得动态 应力强度因子$K_{\rm I} (t)$.将计算所得的应力强度因子规则化${\bar K_{\rm{I}}} = {K_{\rm{I}}}/(\sigma \sqrt {\pi a} )$,并与有限元法计算的结果进行比较,其中有限元法离散为4154个单元.由图3可以看出本文方法计算的结果和有限元法计算 的结果吻合得很好.

|
图 3 规则动态应力强度因子 Fig.3 Regular dynamic stress intensity factor |
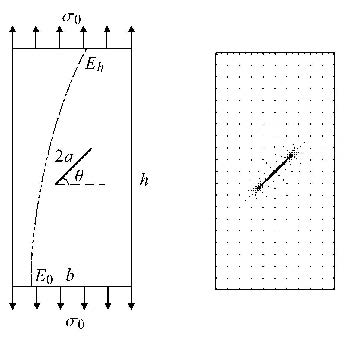
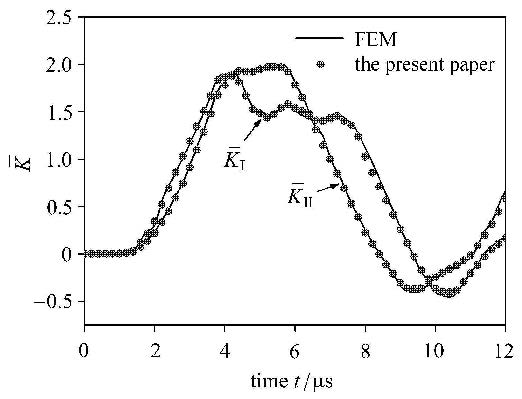
当中心裂纹为斜裂纹时,如图4所示,材料属性沿裂纹长度方向逐渐变化.若裂纹与水平方向成$\theta = 45^ \circ $角,则平板 可以同样离散成84个二次单元,域内布置236个内部节点;而有限元法计算网格为5\,952个单元. 本文方法和有限元法计算的Ⅰ型和Ⅱ型规则化应力强度因子$\bar {K}_{\rm I}$和$\bar {K}_{\rm II}$对比如图5所示,可以看出本文方法计算的结果和有限元法计算的结果吻合得很好.
|
图 4 含中心斜裂纹的功能梯度材料平板 Fig.4 FGM plate with an inclined central crack |
|
图 5 规则化动态应力强度因子 Fig.5 Regular dynamic stress intensity factor |
本文基于各向同性、均质材料、线弹性静力学问题的开尔文基本解,建立了功能梯度材料动态断裂力学问题的边界-域积分方程. 在导出的边界-域积分方程中,由于材料的非均质性和惯性项引起域积分,通过径向积分法将产生的域积分转化为等效的边界积分, 从而得到只需边界离散而无内部网格的边界元算法.采用候博特方法求解关于时间二 阶导数的系统离散的常微分方程组. 最后本文分析了两种不同情况下的裂纹问题,通过与有限元法计算的结果进行对比,证明了本 文方法的有效性.
| [1] | 朱信华, 孟中岩. 梯度功能材料的研究现状与展望. 功能材料, 1998, 29(2): 121-127 (Zhu Xinhua, Meng Zhongyan. Current Research Status and Prospect of Functionally Gradient Materials. Journal of Functional Materials, 1998, 29(2): 121-127 (in Chinese)) |
| [2] | 韩杰才, 徐丽, 王宝林等. 功能梯度材料的研究进展及展望. 固体火箭技术, 2004, 27: 207-215 (Han Jiecai, Xu Li, Wamg Baolin, et al. Progress and prospects of functional gradient materials. Journal of Solid Rocket Technology, 2004, 27: 207-215 (in Chinese)) |
| [3] | Chen YM. Numerical computation of dynamic stress intensity factors by a Lagrangian finite-difference method (the HEMP code). Engineering Fracture Mechanics, 1975, 7(4): 653-660 |
| [4] | Erdogan F. Fracture mechanics of functionally graded materials. Composites Engineering, 1995, 5(7): 753-770 |
| [5] | Li CY, Weng GJ. Dynamic stress intensity factor of a cylindrical interface crack with a functionally graded interlayer. Mechanics of Materials, 2001, 33(6): 325-333 |
| [6] | 李玉龙, 刘元镛. 带裂纹板在冲击载荷作用下动态应力强度因子的数值计算. 航空学报, 1989, 10(5): 227-233 (Li Yulong, Liu Yuanyong. Numerical calculations of dynamic stress intensity factor of center-cracked plate under impact loading. Acta Aeronautica et Astronautic Sinica, 1989, 10(5): 227-233 (in Chinese)) |
| [7] | Anlas G, Santare MH, Lambros J. Numerical calculation of stress intensity factors in functionally graded materials. International Journal of Fracture, 2000, 104(2): 131-143 |
| [8] | Kim JH, Paulino GH. Finite element evaluation of mixed mode stress intensity factors in functionally graded materials. International Journal for Numerical Methods in Engineering, 2002, 53(8): 1903-1935 |
| [9] | 程玉民, 嵇醒, 贺鹏飞. 动态断裂力学的无限相似边界元法. 力学学报, 2004, 36(1): 43-48 (Cheng Yumin, Ji Xing, He Pengfei. Infinite similar boundary element method for dynamic fracture mechanics. Acta Mechanica Sinica, 2004, 36(1): 43-48 (in Chinese)) |
| [10] | 李越川, 杨耀墀. 边界积分方程法在动态断裂力学中的数值计算研究. 应用力学学报, 1990, 7(1): 42-50 (Li Yuechuan, Yang Yaochi. The numerical computation study of boundary integral equation method in dynamic fracture mechanics. Chinese Journal of Applied Mechanics, 1990, 7(1): 42-50 (in Chinese)) |
| [11] | 李春雨, 邹振祝, 段祝平. 功能梯度材料裂纹尖端动态应力场. 力学学报, 2001, 33(2): 270-274 (Li Chunyu, Zou Zhenzhu, Duan Zhuping. Dynamic stress field around the crack tip in a functionally graded material. Acta Mechanica Sinica, 2001, 33(2): 270-274 (in Chinese)) |
| [12] | Zhang Ch, Savaidis A, Savaidis G, et al. Transient dynamic analysis of a cracked functionally graded material by a BIEM. Computational Materials Science, 2002, 26: 167-174 |
| [13] | Zhang Ch, Savaidis A. Time-domain BEM for dynamic crack analysis. Mathematics and Computers in Simulation, 1999, 50: 351-362 |
| [14] | Zhang Ch, Sladek J, Sladek V. Effects of material gradients on transient dynamic mode-III stress intensity factors in a FGM. International Journal of Solids & Structures, 2003, 40(20): 5251-5270 |
| [15] | 李树忱, 程玉民, 李术才. 动态断裂力学的无网格流行方法. 物理学报, 2006, 55(9): 4760-4766 (Li Shuchen, Cheng Yumin, Li Shucai. Meshless manifold method for dynamic fracture mechanics. Acta Physica Sinica, 2006, 55(9): 4760-4766 (in Chinese)) |
| [16] | 龙述尧, 张国虎. 基于MLPG法的动态断裂力学问题. 湖南大学学报 (自然科学版), 2012, 39(11): 41-45 (Long Shuyao, Zhang Guohu. An analysis of the dynamic fracture problem by the meshless Local Petrov- Galerkin method. Journal of Hunan University (Natural Sciences), 2012, 39(11): 41-45 (in Chinese)) |
| [17] | Sladek J, Sladek V, Zhang Ch. An advanced numerical method for computing elastodynamic fracture parameters in functionally graded materials. Computational Materials Science, 2005, 32(3-4): 532-543 |
| [18] | Sladek J, Sladek V, Zhang Ch. Evaluation of the stress intensity factors for cracks in continuously nonhomogeneous solids, part II: Meshless method. Mechanics of Advanced Materials and Structures, 2008, 15(6-7): 444-452 |
| [19] | Gao XW, Zhang Ch, Sladek J, et al. Fracture analysis of functionally graded materials by a BEM. Composites Science and Technology, 2008, 68: 1209-1215 |
| [20] | Gao XW. A boundary element method without internal cells for two-dimensional and three-dimensional elastoplastic problems. ASME Journal of Applied Mechanics, 2002, 69: 154-160 |
| [21] | 高效伟, Zhang Ch. 非均质问题中的无网格边界单元法. 固体力学学报, 2006, 27: 62-69 特刊 (Gao Xiaowei, Zhang Ch. Meshless BEM in nonhomogeneous problems. Acta Mechanic Solida Sinica, 2006, 27: 62-69 (in Chinese)) |
| [22] | Gao XW, Guo L, Zhang Ch. Three-step multi-domain BEM solver for nonhomogeneous material problems. Engineering Analysis with Boundary Elements, 2007, 31: 965-937 |
| [23] | Houbolt JC. A recurrence matrix solution for the dynamic response of elastic aircraft. Journal of Aeronautical Sciences, 1950, 17: 371-376 |
 2015, Vol. 47
2015, Vol. 47
