2. 中国石油天然气股份有限公司塔里木油田分公司勘探开发研究院, 新疆库尔勒841000
对于底水油藏,随着油井的不断生产,底水不断向上锥进. 控制底水的过快过早上升,对于保证油井的长期稳产和提高采收率具有 十分重要的作用. 对于底水问题,目前已经有大量的研究[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]. 其中底水临界产量是控制底水锥进的一个关键参数[24]. Dupuit公式由于形式简单,目前被大量用于计算底水临界产量. 但是根据Dupuit公式(1),临界产量随着打开厚度的降低而增加,当打开厚度为0时,临界产量达到最大值,工程上经常进行的打开 程度优化似乎是没有意义的. 而其他很多研究者获得的临界产量公式[25, 26, 27, 28]中,临界产量与打开程度不是单调的关系. 因此,经过初步分析,该公式存在不合理的地方,需要对Dupuit公式进行详细的研究.
| $ {q_{\rm{c}}} = \frac{{\pi K\Delta \rho g({H^2} - {L^2})}}{{{B_{\rm{o}}}\mu \ln ({r_{\rm{e}}}/{r_{\rm{w}}})}}$ | (1) |
其中,$q_{\rm c}$临界产量,m3/s;$K$为储层渗透率,m2;$\Delta \rho $为油水密度差,kg/m3; $H$为油层厚度,m;L为打开厚度,m;g为重力加速度,m/s2;$\mu $为油的黏度,Pa$\cdot$s;$B_{\rm o}$为油的体积系数;$r_{\rm e} $为供油半径,m;$r_{\rm w}$为井筒半径,m.
1 Dupuit公式的分析 1.1 Dupuit公式存在的问题Dupuit公式作了如下4个假设[24]:(1)流动为稳定状态;(2)储层均质;(3)忽略毛管力;(4)油水密度、黏度等参数为常数. 其实还有个被忽略的假设:临界产量时,水锥顶点正好位于井底. 下面对打开程度很小的生产情况进行近似分析. 当打开程度非常小的时候,比如接近井筒半径($L \approx r_{\rm w}$),可以认为储层井眼周围为半球形流动. 以储层顶部井筒处为坐标原点,向下为$z$轴正方向. 定义流体势为
| $\Phi = p - \rho gz$ | (2) |
其中,$p$为压力,$\rho $为流体密度. 以临界产量生产,油井生产造成的油水界面与井底的势差为
| $\Delta {\rm{ }}{\Phi _{\rm{o}}} = \frac{{{q_{\rm{c}}}\mu {B_{\rm{o}}}}}{{2\pi K}}(\frac{1}{{{r_{\rm{w}}}}} - \frac{1}{H}){\rm{ }}$ | (3) |
油水密度差造成的压差为
| $\Delta p = \Delta \rho g(H - L){\rm{ }}$ | (4) |
油井生产造成的井底流体势差使底水向上运动,油水密度差造成的压差使底水向下运动. 当底水能够保持稳定时,要求
| $\Delta {\Phi _{\rm{o}}} \le \Delta p$ | (5) |
因此可以得到
| $L \le \frac{{2{r_{\rm{w}}}H\ln ({r_{\rm{e}}}/{r_{\rm{w}}})}}{{H - {r_{\rm{w}}}}} - H{\rm{ }}$ | (6) |
容易验证,式(6)常常要求$L<0$. 这是不合理的. 因此,当打开厚度非常小时,按Dupuit公式计算的临界产量进行生产,无法保 持水锥顶点稳定在井底位置.
1.2 临界产量时的水锥高度对于临界产量时对应的水锥高度,一些学者在研究底水锥进问题时有所研究.
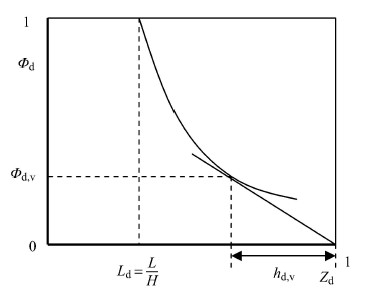
文献[29]在研究底水锥进问题时定义了与前面式(2)略有不同的流体势,具体见文献[29]. 在无量纲的油相势分布 图$\Phi_{\rm d} = \Phi _{\rm d} (z_{\rm d} )$上,从点($z_{\rm d} = 1$,$\Phi _{\rm d} = 0$)开始,作曲线$\Phi _{\rm d} = \Phi _{\rm d} (z_{\rm d} )$的切线,与曲线相切于临界高度$z_{\rm d} = h_{\rm d,v} $处. 计算过程如图1所示. 显然,临界高度不一定到达井底.
另外,文献[30]通过移动球汇法求得了生产造成的压力降落. 生产形成的压力降落使水锥上升,油水密度差使水锥下降,因 此当形成稳定的水锥时,水锥高度对应的由于油水密度差造成的压差与此处的压力降落相等. 文献[30]用图解法求得了这一结果如图2,临界水锥顶点也不在井底.
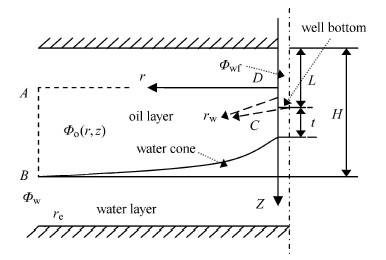
2 新计算方法的推导下面不假设水锥顶点位于井底处,求解底水的临界产量. 除了前述4个假设外,还需作另外的假设. 对于部分打开的底水油藏,文献[28]对文献[25]的假设进行了改进,假设打开部分为径向流,井底以下靠近井筒为半球形流,离井筒较远处为径向流. 其实,井筒附近、井底高度以上一定范围内也接近半球形流. 这个过渡的范围与井径的尺寸应该接近. 建立如下图3所示的坐标系. 坐标原点在井底上方$r_{\rm w}$处,$z$坐标向下为正. 根据前述分析,本文作假设(5):坐标满足$z<0$的储层为径向流,井筒附近坐标满足$z>0$储层为半球形流动.
|
图 3 计算模型示意图 Fig.3 Schematic diagram of computational model |
流体势的定义如式(2). 为了分析方便,以$z=0$所在水平面为位置势0点,设供给边界的水相势为$\Phi_{\rm w}$,当以临界 产量生产时,水相势为常数
| $\Phi _{\rm w} = p_{\rm w} - \rho _{\rm w} gz = {\rm const}$ | (7) |
忽略毛管力,则油水界面两侧的压力相等
| $p_{\rm o} = p_{\rm w} = \Phi _{\rm w} + \rho _{\rm w} gz$ | (8) |
则沿油水界面油相势
| $\Phi _{\rm o} = p_{\rm o} - \rho _{\rm o} gz = \Phi _{\rm w} + \Delta \rho _{\rm w} gz$ | (9) |
油水界面供给边界处
| $\Phi_{\rm o} = \Phi _{\rm w} + \Delta \rho _{\rm w} g(H - L + r_{\rm w} )$ | (10) |
把格林第二定理应用到射孔下部的油相区$ABCD$,对于定义在体积$V$中具有连续一、二阶导数的函数$U$和$W$,有以下式子
| $\mathop {\smallint \smallint \smallint }\limits_V (W\Delta U - U\Delta W){\rm{ d}}V = \mathop \int\!\!\!\int \limits_S (W\frac{{\partial U}}{{\partial n}} - U\frac{{\partial W}}{{\partial n}}){\rm{ d}}S$ | (11) |
其中,$S$为体积$V$的表面,$n$为$S$的外法线方向单位向量. 对于$U$和$W$分别取
| $U = \Phi _{\rm o},\ \ \ W = \ln \dfrac{r}{r_{\rm w} }$ | (12) |
沿$AB,BC,CD$和$DA$ 4条曲线分别计算式(11). 对于$AB$和$BC$段的$\Phi _{\rm o} $,已有式(9)确定了. 对于$CD$段$\Phi _{\rm o} $,利用在井底附近为半球形流动,结合式(9)计算的$C$点的油相势,可 以确定. 经过上述计算可得
| ${q_{\rm{s}}} = \frac{{\pi K\Delta \rho g[{{(H - L + {r_{\rm{w}}})}^2} - {{(t + {r_{\rm{w}}})}^2}]}}{{\mu {B_{\rm{o}}}\ln [{r_{\rm{e}}}/({r_{\rm{w}}} + t)]}}$ | (13) |
利用从井底计算水锥顶点的压力和从边界计算水锥顶点的压力相等可以得到生产压差
| $\Delta \Phi = \Delta \rho g(H - L - t) + \frac{{{q_{\rm{s}}}\mu {B_{\rm{o}}}}}{{2\pi K}}(\frac{1}{{{r_{\rm{w}}}}} - \frac{1}{{t + {r_{\rm{w}}}}})$ | (14) |
对于上部井筒段的流量有
| ${q_{\rm{r}}} = \frac{{2\pi (L - {r_{\rm{w}}})K\Delta \Phi }}{{\mu {B_{\rm{o}}}\ln ({r_{\rm{e}}}/{r_{\rm{w}}})}}$ | (15) |
总流量
| $q = {q_{\rm{r}}} + {q_{\rm{s}}} = \frac{{2\pi K\Delta \rho g(L - {r_{\rm{w}}})(H - L - t)}}{{\mu {B_{\rm{o}}}\ln ({r_{\rm{e}}}/{r_{\rm{w}}})}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\frac{{(L - {r_{\rm{w}}})t}}{{{r_{\rm{w}}}(t + {r_{\rm{w}}})\ln ({r_{\rm{e}}}/{r_{\rm{w}}})}} + 1] \cdot \qquad \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\pi K\Delta \rho g[{{(H - L + {r_{\rm{w}}})}^2} - {{(t + {r_{\rm{w}}})}^2}]}}{{\mu {B_{\rm{o}}}\ln \frac{{{r_{\rm{e}}}}}{{{r_{\rm{w}}} + t}}}}$ | (16) |
当达到临界产量时,关于$t$的方程$q=q(t)$有唯一解,则有$\dfrac{\partial q}{\partial t} = 0$. 经整理得$t$满足如下的方程
| $(2\ln \frac{{{r_{\rm{e}}}}}{{{r_{\rm{w}}} + t}} + 1){(t + {r_{\rm{w}}})^2} = {(H - L + {r_{\rm{w}}})^2}{\rm{ }}$ | (17) |
由式(17)经过迭代可求出$t$,把求出的$t$代入式(16)可以求出临界产量.
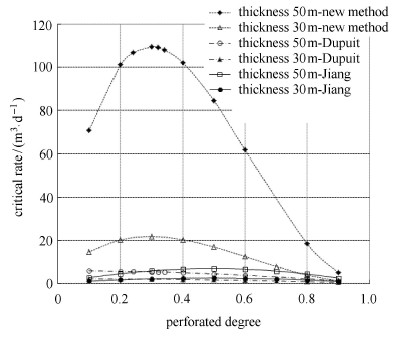
3 新方法的讨论取渗透率10-13m2,井眼半径0.1m,油黏度 3MPa$\cdot$s,油水密度差250kg/m3,供给半径500m,重力加 速度9.8m/s2,油的体积系数1.1. 计算结果如图4. 可以看出,新计算方法计算的临界产量大约在打开程度为0.3时达到最大值. 文献[28]的方法计算的临界产量也大约在打开程度0.5处存在最大值. 现场经验认为打开程度1/3~1/2是最优的,本文计算结果与此接近. 另外可以看出,新方法计算的临界产量比Dupuit公式计算的临界产量大. 原因是Dupuit公式的假设降低了过流面积和假设井底以下流体势是高度的线性函数.
|
图 4 不同打开程度下得临界产量 Fig.4 Critical rates of different perforating level |
以新疆某油田某油井为例进行计算,与几种常用方法的结果进行对比. 该井试井获得的渗透率2.46×10-14m2,井眼半径0.079m,油黏度0.00567Pa$\cdot$s,油水密度差116kg/m3,供给半径535m,重力加速度9.8m/s2,油的体积系数1.1189,油层打开厚度70m,估计油层厚度120m.
该井以40~60m3/d的产量无水生产了1年3个月. 不同方法的计算结果见表1. 如果按照Dupuit公式、文献[26]和文 献[28]公式的计算结果,该井的产量大于临界产量,应该很快见水. 文献[25]公式计算的结果明显偏大,这点也被其他研究者所指出[28]. 本文方法计算的结果比较符合实际.
| 表 1 不同方法计算的临界产量 Table 1 Critical rate computed by differential methods |
通过本文的研究得到以下结论:(1)当处于临界状态时,水锥顶点并不一定位于井底,水锥无法稳定在井底. (2)在不假设水锥位置 的条件下,推导了临界产量公式. 新方法能够计算临界水锥高度和对临界产量进行优化. (3)工程实例计算结果表明,本文方法计算的结果比较符合实际情况.
| [1] | Ahmadi MA, Ebadi M, Hosseini SM. Prediction breakthrough time of water coning in the fractured reservoirs by implementing low parameter support vector machine approach. Fuel, 2014, 117(Part A): 579-589 |
| [2] | Zendehboudi S, Elkamel A, Chatzis I, et al. Estimation of breakthrough time for water coning in fractured systems: Experimental study and connectionist modeling. American Institute of Chemical Engineers, 2014, 60(5):1905-1919 |
| [3] | Amarfio EM, Igbokoyi AO. Breakthrough time correlations for coning in bottom water supported reservoirs. SPE Nigeria Annual International Conference and Exhibition, 5-7 August, 2013, Lagos, Nigeria. SPE 167511-MS |
| [4] | Bahadori A. A mathematical predictive tool for determining the time to water cone breakthrough in horizontal wells. Petroleum Science and Technology, 2013, 31(20): 2047-2055 |
| [5] | Moradi B, Dastkhan Z, Roozbehani B. The design and preparation of a simulator for the water coning phenomenon applying in fractured reservoirs. Petroleum Science and Technology, 2012, 30(15): 1579-1590 |
| [6] | Bahadori A, Nouri A. Prediction of critical oil rate for bottom water coning in anisotropic and homogeneous formations. Journal of Petroleum Science and Engineering, 2012, 82-83:125-129 |
| [7] | 熊小伟, 李云鹏, 张静蕾 等. 一种预测底水油藏水锥动态及见水时间的新方法. 断块油气田, 2014, 21(2):221-223 (Xiong Xiaowei, Li Yunpeng, Zhang Jinglei, et al. A new method to predict water coning performance and water breakthrough time in bottom water oil reservoir. Fault-Block Oil & Gas Field, 2014, 21(2): 221-223 (in Chinese)) |
| [8] | 胡志鹏, 胡望水, 阮洪江 等. 改进的低渗透带隔板底水油藏油井见水时间的预报式. 科学技术与工程, 2014, 14(3): 29-31 (Hu Zhipeng, Hu Wangshui, Ruan Hongjiang, et al. A modified water breakthrough time prediction formula for low-permeability bottom water reservoirs with barrier. Science Technology and Engineering, 2014, 14(3): 29-31 (in Chinese)) |
| [9] | 朱维耀, 黄小荷, 岳明. 底水气藏水平井间水时间研究. 科技导报, 2014, 32(8): 27-31 (Zhu Weiyao, Huang Xiaohe, Yue Ming. prediction of water breakthrough time of horizontal wells in gas reservoirs with bottom water. Science & Technology Review, 2014, 32(8): 27-31 (in Chinese)) |
| [10] | 陈朝晖, 邓勇, 许博 等. 缝洞型底水油藏井底水突破时间预测方法. 石油与天然气地质, 2012, 33(5):791-795. (Chen Zhaohui, Deng Yong, Xu Bo, et al. Bottom water breakthrough prediction in fractured-vuggy reservoirs with bottom water. Oil & Gas Geology, 2012, 33(5): 791-795 (in Chinese)) |
| [11] | Huang SJ, Zeng BQ, Zhao FL, et al. Water breakthrough shape description of horizontal wells in bottom-water reservoir. Mathematical Problems in Engineering, 2014, Article ID 460896 |
| [12] | 章威, 李廷礼, 刘超 等. 底水油藏直井水锥形态的定量描述新方法.天然气与石油, 2014, 32(3): 34-37 (Zhang Wei, Li Tingli, Liu Chao, et al. A new method for quantitative description of water cone shape of vertical well in bottom water reservoir. Natural Gas and Oil, 2014, 32 (3): 34-37 (in Chinese)) |
| [13] | 涂彬, 韩洁, 孙键. 厚层底水油藏油井临界产量计算方法. 石油钻探技术, 2014, 42(4): 107-110 (Tu Bin, Han Jie, Sun Jian. a calculation method of critical production for oil wells in thick reservoirs with bottom water. Petroleum Drilling Techniques, 2014, 42(4): 107-110 (in Chinese)) |
| [14] | Chaperon I. Theoretical study of coning toward horizontal and vertical wells in anisotropic formations. Subcritical and critical rates, SPE 15377, 1986, 521-526 |
| [15] | Giger FM. Analytic 2-D models of water cresting before breakthrough for horizontal wells. SPE Reservoir Engineering , 1989, 4(4): 256-231 |
| [16] | Joshi SD. Horizontal Wells Technology. Tulsa: Penn Well Publishing Company, 1991 |
| [17] | Papatzacos P, Herring TR, Martinsen R, et al. Cone breakthrough time for horizontal wells. SPE Reservoir Engineering, 1991, 6(3): 311-318 |
| [18] | 范子菲,林志芳. 底水驱动油藏水平井临界产量公式及其变化规律研究. 石油勘探与开发,1994,21(1):65-70 (Fan Zifei. A study of critical rate of a horizontal well in a reservoir with bottom-water drive. Petroleum Exploration and Development, 1994, 21(1): 65-70 (in Chinese)) |
| [19] | 吉兰敏, 姜汉桥, 陈民锋 等. 非均质底水油藏临界产量预测. 大庆石油地质与开发, 2009, 28(6): 119-124 (Ji Lanmin, Jiang Hanqiao, Chen Minfeng, et al. Critical production prediction for heterogeneous reservoirs with bottom water. Petroleum Geology and Oilfield Development in Daqing, 2009, 28(6): 119-124 (in Chinese)) |
| [20] | 宋兆杰, 李相方, 李治平 等. 考虑非达西渗流的底水锥进临界产量计算模型. 石油学报, 2012, 33(1): 106-111 (Song Zhaojie, Li Xiangfang, Li Zhiping, et al. A model for calculating critical production rates of water coning with consideration of non-Darcy flow. Acta Petrolei Sinca, 2012, 33(1): 106-111 (in Chinese)) |
| [21] | 李传亮. 修正Dupuit临界产量公式. 石油勘探与开发, 1993, 20(1): 91-95 (Li Chuanliang. A modified Dupuit formula for critical production rate. Petroleum Exploration and Development, 1993, 20(1): 91-95 (in Chinese)) |
| [22] | 卜凌梅, 韩洪宝, 程林松. 底水油藏油井合理射开程度研究.油气地质与采收率, 2004, 11(5): 44-48 (Bu Lingmei, Han Hongbao, Cheng Linsong. Study on rational perforation degree of oil wells in reservoir with bottom water. Petroleum Geology and Recovery Efficiency, 2004, 11(5): 44-45 (in Chinese)) |
| [23] | 吕爱民, 姚军. 裂缝性碳酸盐岩底水油藏合理打开程度与合理井距. 石油勘探与开发, 2008, 35(1): 97-100 (Lü Aimin, Yao Jun. Rational perforating level and well spacing for fractured carbonate reservoirs with bottom water. Petroleum Exploration and Development, 2008, 35(1): 97-100 (in Chinese)) |
| [24] | Hagoort J. Fundamentals of Gas Reservoir Engineering. Amsterdam: Elsevier Science Publishers B.V. 1988 |
| [25] | Guo BY, Lee RLH. A simple approach to optimization of completion interval in oil/water coning systems. SPE Reservoir Engineering, 1993, 8(4): 249-255 |
| [26] | Schols RS. An empirical formula for the critical oil production rate. Erdoel Erdgas, Z, 1972, 88(1): 6-11 |
| [27] | 蒋平, 张贵才, 何小娟 等.底水锥进的动态预测方法. 钻采工艺, 2006, 30(2): 71-73 (Jiang Ping, Zhang Guicai, He Xiaojuan, et al. A dynamic prediction method for bottom water coning. Drilling & Production Technology, 2006, 30(2): 71-73 (in Chinese)) |
| [28] | 蒋平. 底水锥进预测及底水治理决策技术研究. [硕士论文]. 青岛:中国石油大学,2006: 17-18 (Jiang Ping. The study of prediction of water coning and decision-making technique for water shutoff for bottom-water reservoir. [Master Thesis]. Qingdao: China University of Petroleum, 2006: 17-18 (in Chinese)) |
| [29] | Chierici GL,Ciucci GM,Pizzi G. A systematic study of gas and water coning by potentiometric models. Journal of Petroleum Technology, 1964, 16(8): 923-929 |
| [30] | Shirman EI, Wojtanowicz AK. Water cone hysteresis and reversal for well completions using the moving spherical sink method. The 1997 Production and Operation Symposium, Oklahoma city Oklahoma, March, 1997, SPE37467: 611-616 |
2. Research Institute of Exploration and Development, Tarim Oilfield Company, Petro China, Korla, Xinjiang 841000, China
 2015, Vol. 47
2015, Vol. 47