数字图像相关 (digital image correlation,DIC)方法,是20世纪80年代初发展的非接触式光学测量方法[1, 2]. 该方法最初是使用单个摄像机的二维数字图像相关 (two-dimensional DIC,2D-DIC),二维数字图像相关法仅限于测量平面物体表面的面内位移,并且要求摄像机靶面与被测平面物体表面平行. 为了满足对物体表面的三维形貌以及三维变形测量的迫切要求,利用两个摄像机从不同角度对被测物体表面成像的三维数字图像相关 (three-dimensional DIC,3D-DIC)应运而生. 相比于二维数字图像相关法,三维数字图像相关法基于双目视觉原理,需要额外完成摄像机标定和立体匹配这两个关键性步骤. 经过三十多年的发展,数字图像相关法不仅在理论和算法上得到了不断改进和完善[3, 4, 5, 6, 7],并且在非接触位移场和变形场测量中得到了广泛的应用[8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. 数字图像相关法具有实验设备简单、对测量环境要求低、测量范围广和精度高等优势[5, 17],是工程实际应用中非接触二维平面和三维曲表面变形场测量的最佳选择方法.
在很多实际工况下,局域变形场,比如波特文-勒夏特利埃带[16, 18, 19] (Portevin--Le Chatelier,PLC带),试件缺口附近[10, 17]和裂纹尖端[12, 13, 14]等,无法通过应变片测量,因为应变片尺寸内高梯度的应变值会被平均. 此时,采用数字图像相关法虽然能够测量这些高应变梯度的局域变形场,但由于还没有形成数字图像相关法的测量标准,也无法通过与应变片测量这种被公认的测量方法的结果进行对比,数字图像相关法在位移场和应变场测量的可靠性和精度上还存在很多疑问. 比如形函数[20, 21, 22, 23]、模板尺寸[22, 24, 25]、网格步长、插值函数 形式和阶数[26]、应变窗口尺寸等数字图像相关法算法参量的改变,会导致对局域变形场测量结果大不相同. 这些疑问使数字图像相关法的研究者和使用者通常只定性地讨论测量结果[9, 10, 11, 12, 13, 14, 15, 16, 17]. 然而,数字图像相关法测量的可靠性一直是研究者和使用者共同高度关心的问题. 在用数字图像相关法进行具体的局域化变形测量中,我们将面临以下问题: (1)数字图像相关法的算法参量会对位移场和应变场带来什么样的影响; (2)如何判断测量结果是否可靠; (3)如果结果是可靠的,能不能通过设置数字图像相关法的算法参量获得更准确的结果; (4)如果能,应该怎样设置这些参量; (5)反之,能否通过其他方法,比如改进实验条件,来得到精确的结果. 这样的问题急需一一解明,让数字图像相关法的使用者能够判断测量结果的可靠性.
本文用数字图像相关法以合金材料拉伸实验中产生的局域高度非均匀的波特文-勒夏特利埃带为例来讨论上述问题. 波特文-勒夏特利埃带内部的变形属于高阶变形,形式较为复杂,采用一阶和二阶形函数均不能完全描述其变形,研究者可以更好地分析形函数和模板尺寸对局域变形场测量结果的影响; 而波特文-勒夏特利埃带外部属于均匀变形,研究者可以将形函数和模板尺寸在均匀变形区的测量结果作为参考. 本文首先介绍零阶、一阶和二阶形函数,然后通过拉伸实验获得合金材料波特文-勒夏特利埃带实验数据并采用数值模拟方法对散斑图像施加拉伸方向的位移场,最后根据模拟图像的计算结果详细地分析和讨论形函数和模板尺寸对数字图像相关法计算结果的影响,探讨了数字图像相关法在局域化变形测量中存在的一些问题.
1 形函数数字图像相关法是追踪图像模板区域 (子区)中散斑标记点的位移场进行全场非接触测量的光学方法. 在这个过程中,相关函数被用来评价变形前后图像子区的相似程度. 本文使用以归一化的最小平方距离 (zero-mean normalied sum of squared diffrences,ZNSSD)为相关准则的反向组合型高斯-牛顿算法[17] (inverse compositional Gauss-Newton,IC-GN)来优化相关函数. 再根据相关匹配得到的亚像素位移场计算出应变场. 相关函数优化过程中,需要假设图像子区的变形模式,即形函数. 在二维数字图像相关法中,常用的形函数有仅能描述刚体平移的零阶形函数 (zero order)
| $ \left[{\begin{array}{*{20}{c}} {x'}\\ {y'} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1&0&u\\ 0&1&v \end{array}} \right]\;\left[{\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right] $ | (1) |
和增加考虑刚体转动、剪切或伸缩变形的一阶形函数 (first order)
| $ \left[{\begin{array}{*{20}{c}} {x'}\\ {y'} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {1 + {u_x}}&{{u_y}}&u\\ {{v_x}}&{1 + {v_y}}&v \end{array}} \right]\;\left[{\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right] $ | (2) |
此外,还有进一步考虑应变梯度的二阶形函数 (second order)
| $ \left[{\begin{array}{*{20}{c}} {x'}\\ {y'} \end{array}} \right] = \;\left[{\begin{array}{*{20}{c}} {\frac{1}{2}{u_{xx}}}&{{u_{xy}}}&{\frac{1}{2}{u_{yy}}}&{1 + {u_x}}&{{u_y}}&u\\ {\frac{1}{2}{v_{xx}}}&{{v_{xy}}}&{\frac{1}{2}{v_{yy}}}&{{v_x}}&{1 + {v_y}}&v \end{array}} \right]\;\left[{\begin{array}{*{20}{c}} {{x^2}}\\ {xy}\\ {{y^2}}\\ x\\ y\\ 1 \end{array}} \right] $ | (3) |
其中,$\left( {x,y} \right)$和$\left( {{x}',{y}'} \right)$分别表示变形前后以参考子区中心为原点的局部坐标,$u$和$v$分别是参考图像子区中心在$x$,$y$方向的位移,$u_x,u_y,v_x,v_y $ 为相应的位移梯度,$u_{xx},u_{xy},u_{yy},v_{xx},v_{xy} ,v_{yy}$为相应的二阶位移梯度. 从弹性力学有限变形理论角度考虑,一阶形函数仅能描述刚体转动、剪切 ($u_y,v_x $)和伸缩变形 ($u_x,v_y$),而二阶形函数还能描述具有二阶位移梯度的变形; 如梁的弯曲等. 工程测量中往往会遇到更为复杂的变形. 有人认为对于复杂变形情况用二阶形函数能够得到更为准确可靠的测量结果[27].
在一些商业数字图像相关软件中,这三种形函数已作为选项,嵌入到相关计算模块中. 本文使用南京中迅微传感技术公司 (PMLAB)的三维数字图像相关测量软件 (DIC-3D)的形函数选项,开展数字图像相关法测量局域变形散斑场的可靠性研究.
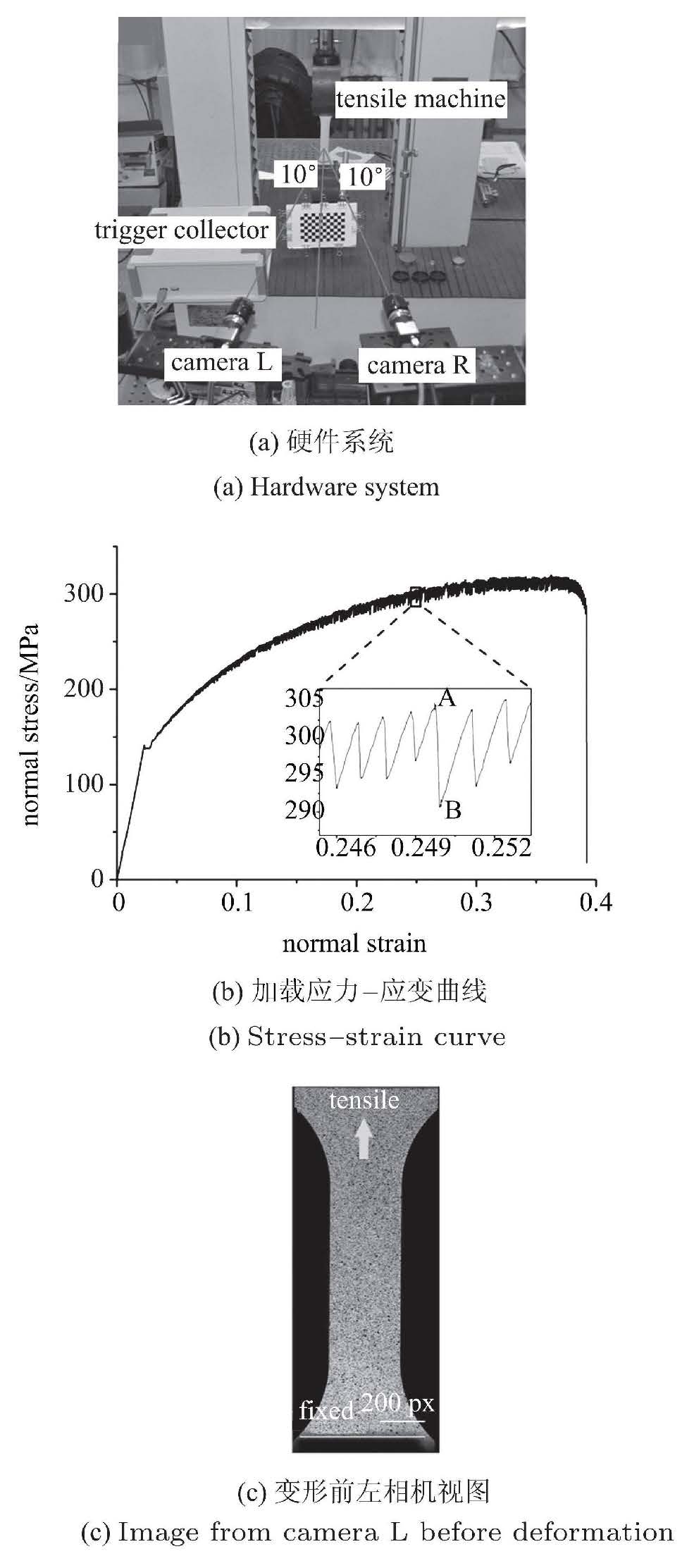
2 拉伸实验 2.1 实验装置为了具体讨论数字图像相关法对局域变形场测量的可靠性问题,下面做一组铝合金材料的拉伸实验. 实验装置如图1(a)所示. 试件为板状试件,试件材料为国标5456铝合金,试件标距长度、宽度与厚度分别为55mm,20mm与1mm. 拉伸机夹头速率3mm/min,载荷采样频率为12.5Hz,加载曲线如图1(b)所示. 由于波特文-勒夏特利埃带产生过程会伴随带内离面凹陷,采用二维数字图像相关法测量会带来高达20%的误差[28, 29]. 为了避免离面位移对应变测量的影响,我们使用双相机进行三维测量,相机采样频率为3Hz,图像分辨率为2048$\times$2048像素. 图1(c)给出了左相机采集得到的参考图像.
|
图 1 拉伸实验装置和数据 Fig.1 Experimental setup and data |
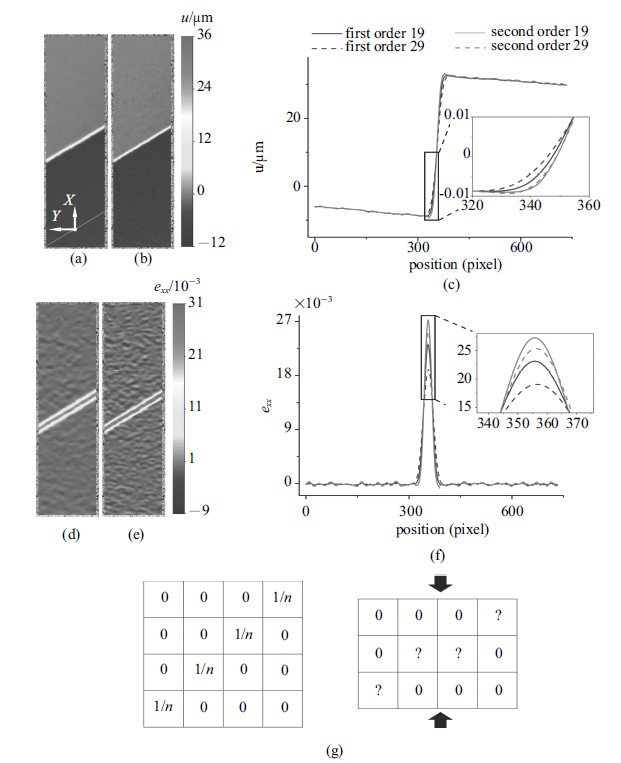
本文主要讨论形函数和模板尺寸对数字图像相关法测量结果的影响,因此在计算和分析时,固定网格步长为1 像素, 应变窗口为17$\times$17个网格点,插值函数为双7次B样条插值. 波特文-勒夏特利埃带内存在剪切变形且变形形式与 拉伸应变类似,一般取拉伸方向的应变进行分析. 图2显示了采用不同形函数和模板尺寸时的计算结果. 该结果为出现加载锯齿跌落前后0.2s间隔 (图1(b)插图中A,B两点)采集到的图像,计算得到的位移场和应变场, 计算区域尺寸为240$\times$900 像素. 图2(a)的底部给出了波特\linebreak 文-勒夏特利埃带的方向 (倾斜线段)和坐标系的定义. 图2(a)和2(b)分别显示了用一阶 (左)和二阶 (右)形函数计算得到的$X$方向位移场. 该位移场存在一倾斜的阶跃 (对应波特文-勒夏特利埃带),且图2(a)中的阶跃宽度略大于图2(b)的阶跃宽度. 为了消去随机噪声的影响,引入一种等效的滤波模板,如图2(g)所示,沿着波特文- 勒夏特利埃带的方向对位移场和应变场滤波. 该等效模板是采用计算软件``矩阵实验室 (MATLAB)''的图像变换函数 (imtransform)拉伸传统模板得到的. 本文用到的等效滤波模板宽为$Y$方向的有效网格点数目,高宽比是波特文- 勒夏特利埃带与$Y$方向夹角的正切值. 沿着$X$方向依次取出与模板尺寸相同的位移场数据, 使之与等效模板作矩阵点乘运算,这样得到 (平滑)位移曲线. 图2(c)显示了一阶和二阶形函数在模板尺寸为19像素 (实线)和29像素 (虚线)时的位移曲线. 波特文-勒夏特利埃带的上部相对于下部有20μm的上移[19]. 图3(c)$\sim$3(f)显示了用不同形函数和模板尺寸时的$X$方向应变场和应变曲线. 波特文- 勒夏特利埃带外部的应变计算受形函数和模板尺寸影响较小,然而,不同的形函数和模板尺寸在波特文- 勒夏特利埃带内部的计算结果相对误差最大可达43% (对应一阶形函数模板29像素的结果$19.1\times10^{-3}$和二阶形函数模板19像素的结果$27.3\times10^{-3}$).
|
图 2 不同形函数和模板尺寸计算得到的位移和应变. 一阶和二阶形函数得到的拉伸方向(a), (b)位移场和(d), (e)应变场. (c)位移曲线. (f)应变曲线. (g)传统平滑模板 (左)和等效平滑模板 (右) Fig.2 Displacement and strain fields and curves with different shape functions and templates. (a), (b) Full field displacement $u$ and (d), (e) strain $e_{xx}$ using first- (left) and second-order (right) shape functions. (c) Smoothed displacement curves and (f) smoothed strain curves. (g) Traditional average template (left) and equivalent template (right) |
上述结果说明,不同的形函数和模板尺寸可能导致大不相同的结果,尤其是在局域变形场测量中. 这就引发了下面的问题: (1)形函数和模板尺寸怎样影响数字图像相关法的计算结果; (2)上述结果是否可靠,如果可靠,哪一个结果精度更高; (3)还有没有更精确的结果. 下文将进一步分析和解释这些问题.
不妨以二阶形函数在模板为19像素时的应变曲线,对该曲线用工程制图软件``Origin''中的高斯 (Gauss)函数
| $ {e_{xx}}(x) = a{e^{ - \frac{{{{(x - b)}^2}}}{{2{c^2}}}}} + d $ | (4) |
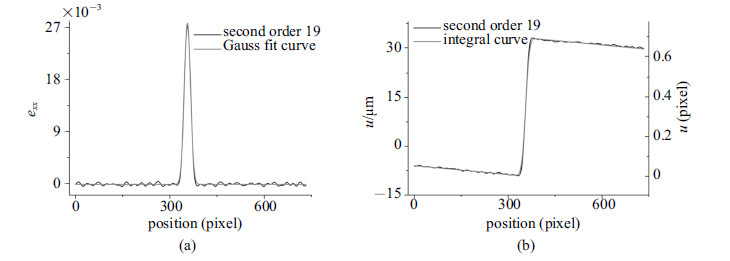
作非线性拟合,如图3(a)所示. 拟合参数为$a = 0.028$,$b = 356$像素,$c = 10$像素,$d = -149\times10^{-6}$. 其中参数$a$为高斯函数的强度,对应波特文-勒夏特利埃带内最大应变值,称之带内最大应变; 参数$b$对应 波特\linebreak 文-勒夏特利埃带最大应变值出现的位置,称之为最大应变位置; 参数$c$为高斯函数的标准差, 它与高斯函数的半高宽$W_{\rm HM}$ (full width at half maximum,本文用它来近似波特文- 勒夏特利埃带的带宽)满足如下关系
|
图 3 测量与拟合结果. (a)应变曲线及其高斯拟合曲线. (b)位移曲线及 (a)中拟合曲线的积分曲线 Fig.3 Experimental setup and data. (a) Smoothed strain curve and its Gaussian fit curve and (b) smoothed displacement curve and the integral curve whose derivative is the fit (a) |
| $ {W_{{\rm{HM}}}} = 2\sqrt {2\ln 2} c $ | (5) |
称之为带宽相关量; 参数$d$对应加载锯齿跌落时波特文-勒夏特利埃带的带外收缩应变量,称之为带外收缩量. 对式 (4)积分可得到位移曲线表达式
| $u(x) = ac\sqrt {\frac{\pi }{2}} [{\rm{erf}}\left( {\frac{{x\; - \;b}}{{\sqrt 2 c}}} \right) + {\rm{erf}}\left( {\frac{b}{{\sqrt 2 c}}} \right)] + dx $ | (6) |
图4(b)给出了实验得到的位移曲线与式(6)对应的位移曲线,它们的形式基本一致,且近似满足线性变换关系.
|
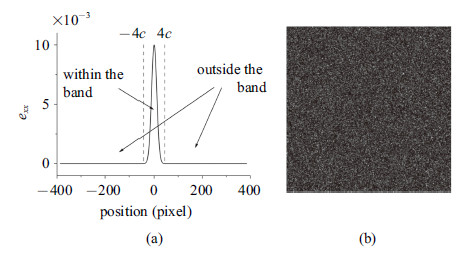
图 4 (a)波特文-勒夏特利埃带带内和带外的划分, (b)模拟生成的参考图像 Fig.4 Area within and outside the band (a) and simulated reference speckle image (b) |
最大应变位置$b$仅与坐标系的选取有关,而带外收缩量$d$描述的是均匀变形,对波特文-勒夏特利埃带内部的非均匀性无影响,因此,忽略最大应变位置$b$和带外收缩量$d$,位移曲线和应变曲线可简化为方程(7)和(8).
| $u\left( x \right) = ac\sqrt {\frac{\pi }{2}} erf\left( {\frac{x}{{\sqrt 2 c}}} \right) $ | (7) |
| $ e(x) = a{{\rm{e}}^{ - \frac{{{x^2}}}{{2{c^2}}}}} $ | (8) |
这样,带内最大应变$a$和带宽相关量$c$完全决定了位移场和应变场. 为了区分波特文-勒夏特利埃带内部非均匀变形和外部均匀变形的误差,这里从应变场出发,以$\pm$4$c$为界线,将波特文-勒夏特利埃带划分成带内和带外两部分,如图4(a)所示. 带外部分应变近似为常数,应变梯度趋于零,为均匀变形区; 带内部分为局域变形区,存在较大的应变和应变梯度.
为了评估全场位移和位移曲线的误差,本文采用两种误差统计方式
| $ {E_{{\rm{FFDE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {{u_{ij}}\; - \;u_{ij}^t} \right)}^2}} } }}{{MN}}} $ | (9) |
和
| $ {E_{{\rm{SDE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^M {{{\left( {\sum\limits_{j = 1}^N {{u_{ij}}} /N\; - \;u_i^t} \right)}^2}} }}{M}} $ | (10) |
分别统计带内和带外的误差. 其中,$u_{ij}$代表$X$方向位移场,$u_{ij}^t$ 代表理论位移场,$u_i^t$代表理论位移曲线,$M$和$N$分别表示$X$和$Y$方向的样本量. 不难看出: $E_{\rm FFDE}$表示全场位移值与理论值之差的方均根,称之为位移总误差; $E_{\rm SDE}$表示$Y$方向位移的均值与理论值之差的方均根,称之为位移平滑误差,平滑误差主要是系统误差.
若不考虑波特文-勒夏特利埃带的倾斜,采用式(7)描述的位移曲线来模拟波特文-勒夏特利埃带$X$方向的位移场[30]. 使80000个强度为600 (灰度量纲),半径为2.5像素的高斯光斑随机分布在1201$\times $1201像素的方形区域内. 在1000$\times$1000像素的方形区域采样得到模拟散斑图像. 散斑分布区中心、图像采样区中心与世界坐标系中心均重合. 图4(b)显示了参考阶段的散斑图像. 对散斑颗粒施加不同的变形,生成两组变形图像: (1)带宽相关量$c$固定为11像素时,带内最大应变$a$分别取0.0025,0.005,0.01,0.02,0.04和0.08; (2)带内最大应变$a$固定为0.01时,带宽相关量$c$分别取4,8,16,32,64和128像素. 对这两组变形图像的计算和分析将在下一节详细讨论.
4 讨 论 4.1 变形固定时通过3.2节中对波特文-勒夏特利埃带的简化和模拟,模拟散斑图像由带内最大应变$a$和带宽相关量$c$决定. 本小节讨论带内最大应变$a$和带宽相关量$c$固定时 ($a= 0.01$,$c = 11$像素),即变形量固定时,形函数和模板尺寸对数字图像相关法计算结果的影响,带内最大应变$a$和带宽相关量$c$变化时的情况将分别在4.2和4.3节中讨论. 图5显示了用零阶、一阶和二阶形函数在模板尺寸分别为9像素、19像素、29像素和39像素时的计算结果. 图5(a)$\sim$5(c)分别显示了模板尺寸为29像素时,采用零阶 (上)、一阶 (中)和二阶 (下)形函数计算得到的X方向位移场. 图5(d)描述了对应的理论位移曲线和用一阶和二阶形函数在模板尺寸为19像素(实线)、29像素(虚线)和39像素(点线)时得到的位移误差曲线. 位移误差曲线是用平滑位移曲线与理论位移曲线相减得到的. 在波特文-勒夏特利埃带外部,一阶和二阶形函数的位移误差基本相同,但一阶形函数在波特文-勒夏特利埃带内部的误差明显大于二阶形函数的带内误差. 图5(d)的插图表明当形函数与变形不匹配时,较大的模板会导致较大的误差. 图5(e)$\sim$5(h)显示了对应的应变场和应变曲线,采用二阶形函数的应变计算结果优于一阶形函数的结果.

|
图 5 不同形函数和模板尺寸得到的拉伸方向的(a)$\sim$(d)位移和(e)$\sim$(h)应变 Fig.5 Displacement (a)$\sim$(d) and strain (e)$\sim$(h) fields and (error) curves using different shape functions and templates |
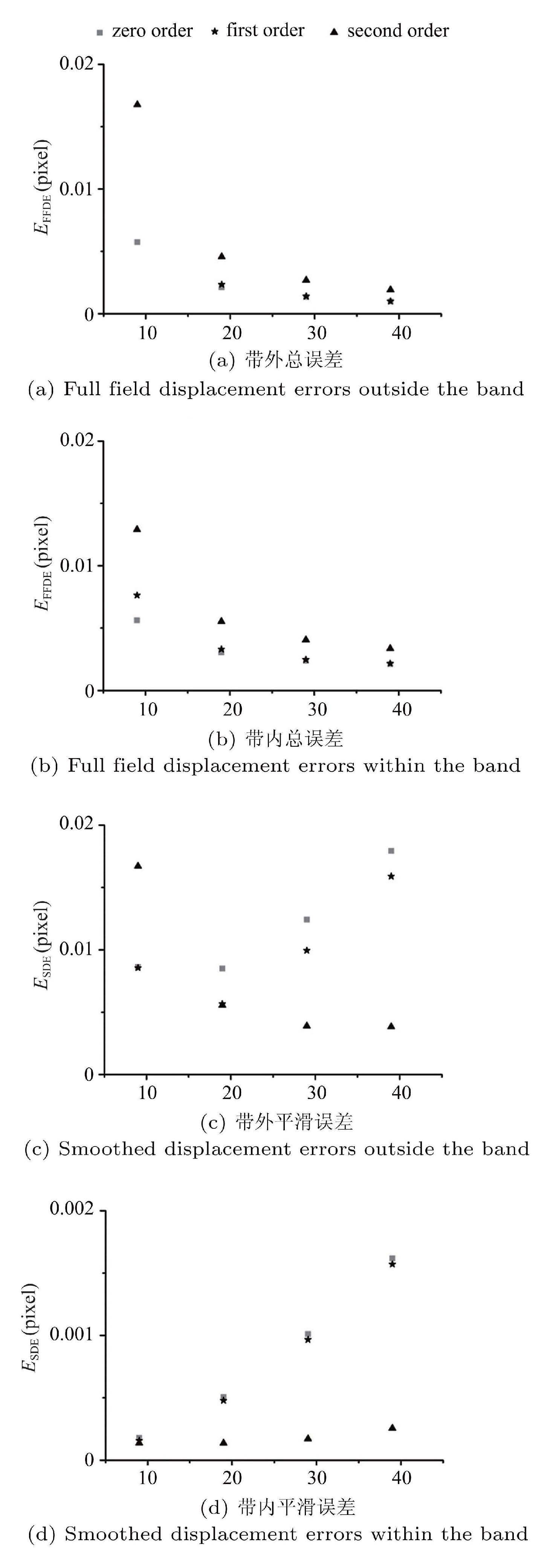
根据式(9)和式(10),分别统计不同形函数不同模板尺寸时的带内和带外的位移总误差 ($E_{\rm FFDE}$)和位移平滑误差 ($E_{\rm SDE}$),如图6所示. 图6(a)和6(c)分别显示了不同形函数带外位移总误差和平滑误差随模板的变化. 3种形函数的带外位移总误差和带外位移平滑误差均随着模板的增大减小. 这是因为带外部分是均匀变形区,3种形函数都能完全描述这一变形,此时,较大的模板导致较稳定的结果. 3种形函数的带外位移总误差 ($\sim$0.01像素)和带外位移平滑误差 ($\sim$0.001像素)在同一量级,且带外位移总误差比带外位移平滑误差大一个量级,这说明带外部分的位移总误差主要为随机误差.
|
图 6 带外和带内的位移总误差和位移平滑误差 Fig.6 Displacement errors within and outside the band |
图6(b)和6(d)分别显示了3种形函数的带内位移总误差和带内位移平滑误差. 如图6(d)所示,零阶和一阶形函数的带内位移平滑误差均随模板的增大而增大,但二阶形函数的带内位移平滑误差却基本不变 (略微呈先减小后增大趋势). 此外,二阶形函数的带内位移平滑误差随模板增大先缓慢减小后增大,其随模板的变化远没有零阶和一阶形函数变化剧烈. 这是因为二阶形函数考虑了应变梯度,能够更好的匹配带内的变形. 假设带内和带外的随机误差相当,而带外部分的总误差主要是随机误差,那么带内部分的随机误差可以用带外部分的总误差来近似. 这样,图6(b)显示的带内位移总误差可以看成是图6(a)中的带外位移总误差与图6(d)中的带内位移平滑误差之和. 如图6(b)所示,零阶和一阶形函数的带内位移总误差均随模板的增大先减小后增大,而二阶形函数的带内位移总误差却只有减小的趋势. 此外,当模板较大时,二阶形函数的带内位移总误差明显小于零阶和一阶形函数的带内位移总误差.
一般地,模板越大,随机误差越小,但在形函数与变形不匹配时,模板越大,欠匹配越严重,系统误差也越大. 由于各阶形函数都不能完全描述带内的变形,所以当模板大于某个临界值 (临界模板)时,带内位移总误差肯定会与模板尺寸正相关. 这里零阶和一阶形函数的临界模板均在19像素左右. 尽管二阶形函数的带内位移总误差还没有出现随模板增大而增大的趋势,但肯定存在一个大于39像素的临界模板. 到目前为止,我们得到了形函数和模板影响计算结果的第一个机制,即二阶形函数有较大的临界模板且在高应变梯度时能够得到更好的计算结果.
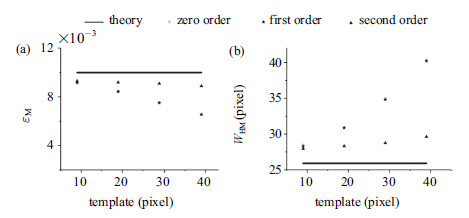
对各阶形函数在不同模板下的应变曲线作非线性拟合 (3.1节式(4)),得到带内最大应变 (maximum strain value within the band,$\varepsilon_{\rm M}$)和带宽 ($W_{\rm HM}$),将其与理论值比较,如图7所示. 图7(a)显 示了随着模板的增大,各阶形函数得到的带内最大应变逐渐减小,与理论值的差距逐渐增大. 图7(b)显示了随着模板的增大, 各阶形函数得到的带宽逐渐增大,与理论值的差距也逐渐增大. 二阶形函数得到的带内最大应变和带宽均比零阶和一阶形函数的结果更接近理论值,其受模板尺寸影响也较小. 换而言之, 二阶形函数在带内部分能够得到更好的应变结果.
|
图 7 带内最大应变(a)和带宽(b)受形函数和模板尺寸的影响 Fig.7 Maximum strain value within the band (a) and full width (b) at half maximum of different shape functions and templates |
综上所述,形函数与模板对位移和应变计算的影响是密切相关的. 此外,其对均匀应变区和非均匀应变区的影响也大不相同. 但对于给定的变形, 找到最优的形函数和模板是能够实现的. 下面针对不同的应变梯度变形场(带内最大应变$a$和带宽相关量$c$共同决定)进一步揭示 形函数与模板对数字图像相关法计算的影响.
4.2 仅带内最大应变$a$改变4.1节针对固定的变形讨论了形函数和模板对计算结果的影响,本小节取出3.2节中生成的第一组散斑图像 (带内最大应变$a$改变)来讨论不同应变梯度下,形函数和模板对计算结果的影响.
首先考虑模板固定为29像素时,带内最大应变$a$的影响. 图8(a)$\sim$8(c)给出了带内最大应变$a = 0.01$时,零阶 (左)、一阶 (中)和二阶 (右)形函数的全场位移误差. 理论位移曲线和零阶、一阶和二阶形函数的位移误差曲线如图8(d)所示. 图8(e)$\sim$8(h)分别显示了带内最大应变$a=0.02$时对应的结果. 上下对比,带内最大应变$a$从0.01变成0.02时,带外位移误差基本不变,带内位移误差增加了一倍.

|
图 8 不同带内最大应变时的位移误差. (a)$\sim$(c) $a = 0.01$. (e)$\sim$(g) $a =0.02$时3种形函数的位移误差分布.(d) $a=0.01$. (h) $a = 0.02$时的理论位移曲线和位移误差曲线 Fig.8 Displacement errors of different maximum strain, within the band. (a)$\sim$(c) $a = 0.01$ and (e)$\sim$(g) $a = 0.02$, full field displacement errors calculated using 3 shape functions. (d) $a = 0.01$ and (h) $a = 0.02$, theoretical displacement curve and smoothed\\ displacement error curves using 3 shape functions |
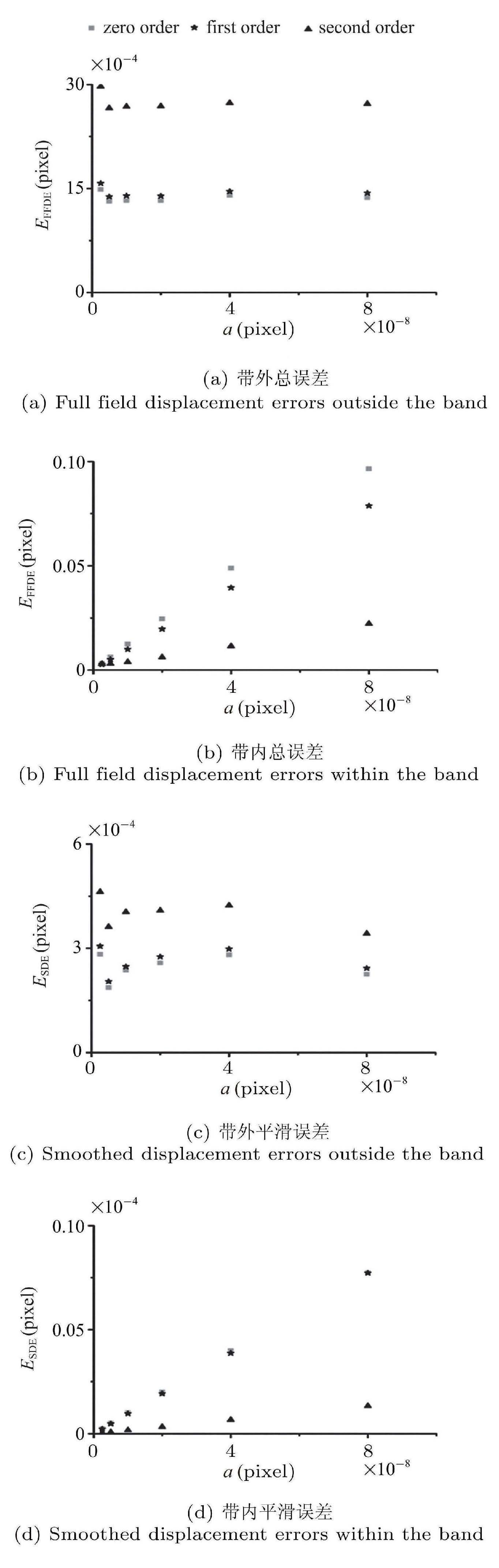
图9显示了带内最大应变$a$变化时,带内和带外的位移总误差和平滑误差. 图9(a)和图9(c)中的带外位移总误差和带外位移平滑误差几 乎不随$a$改变,说明带内最大应变对带外位移误差没有影响. 二阶形函数的带外位移总误差和带外位移平滑误差均比零阶和一阶形函数相应误差稍大一些,但其在同一量级. 各阶形函数的带内位移总误差和带内位移平滑误差均与$a$成正比,如图9(b)和图9(d)所示. 概括起来,即带内最大应变对带外位移误差无影响,与带内位移误差成正比.
|
图 9 不同带内最大应变时, 带内和带外的位移总误差和平滑误差 Fig.9 Displacement statistical errors of different maximum strain within the band |
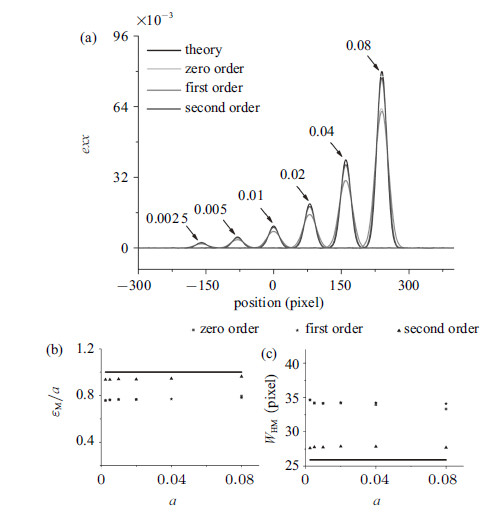
下面考虑各阶形函数在带内最大应变$a$变化时得到的应变曲线,如图10(a)所示. 其中,$a$ 从0.0025到0.08变化时的应变曲线分别向右移动了$-160$,$-80$,0,80,160和240像素 (负号表示向左移动). 可以看到,带外的应变基本相同,而带内的应变呈指数增加. 各阶形函数得到的应变与理论值的绝 对差距越来越大,但其相对误差基本不变. 另外,二阶形函数的应变结果始终最接近理论值. 图10(b)显示了带内最大应变的计算值($\varepsilon_{\rm M}$)与理论值$a$的比值 ($\varepsilon_{\rm M}/a$)基本不随$a$变化. 图10(c)显示了带宽在$a$改变时也保持不变. 这些结果都说明带内最大应变与带内应变误差成正比且不影响带宽.
|
图 10 不同带内最大应变时的应变曲线及其拟合参数 Fig.10 Strain curves and the fitting parameters of different maximum strains within the band |
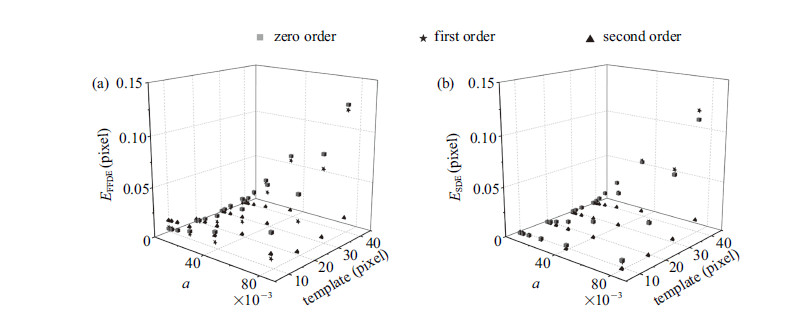
上述结果均是在模板固定为29像素时得到的,下面考虑模板变化时的情形. 图11显示了带内最大应变$a$和模板尺寸同时变 化时,各阶形函数的带内位移总误差和带内位移平滑误差. 图11(b)说明了二阶形函数的带内平滑误差较小,尤其是带内最大应变和模板均较大时. 图11(a)表明当模板较小时,随机误差影响较大,二阶形函数的带内总误差最大,但在带内最大应变和模板较大时,二阶形函数的带内位移总误差远小于一阶形函数的带内位移总误差. 此外,各阶形函数的临界模板均随着带内最大应变的增大而减小.
|
图 11 不同带内最大应变和模板尺寸时, 3种形函数得到的带内位移误差. (a)带内位移总误差. (b)带内位移平滑误差 Fig.11 Displacement errors of different maximum strains within the band and templates. (a) Full field displacement errors within the band. (b) Smoothed displacement errors within the band |
综上所述,在带宽相关量$c$ 固定为11像素,带内最大应变$a$变化时,二阶形函数尽管在波特文-勒夏特利埃带带外部分 的误差较大,但其在带内部分的位移和应变计算结果均优于零阶和一阶形函数. 在下一小节中,将讨论带宽相关量$c$变化 (带宽也相应改变)时的情况.
4.3 仅带宽相关量$c$改变上一小节讨论了带内最大应变$a$改变的情形,本小节取出3.2节中生成的第二组散斑图像 (带宽相关量$c$改变),具体讨论带宽改变时形函数和模板对计算结果的影响.
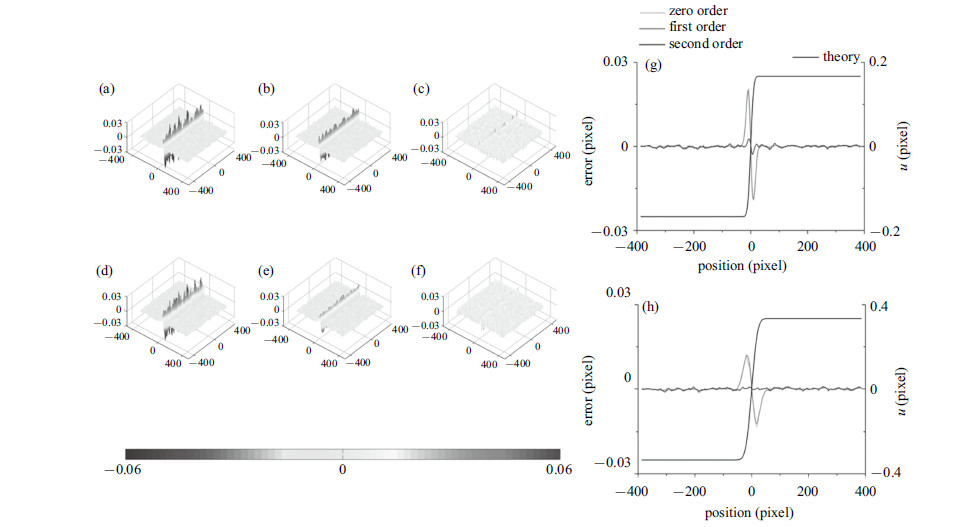
和前面一样,首先考虑模板固定为29像素时,各阶形函数得到的结果. 图12(a)$\sim$12(c)给出了带宽相关量$c = 8$像素时,零阶 (左)、一阶 (中)和二阶 (右)形函数的全场位移误差. 理论位移曲线和零阶、一阶和二阶函数的位移误差曲线如图12(d)所示. 图12(e)$\sim$12(h)显示了带宽相关量$c= 16$ 像素时对应的结果. 上下对比,$c = 16$像素时较$c = 8$像素时的带外误差基本不变,带内误差明显增大.
|
图 12 不同带宽时的位移误差. (a)$\sim$(c) $c= 8$像素. (e)$\sim$(g) $c = 16$像素时3种形 函数的位移误差分布. (d) $c = 8$.(h) $c = 16$像素时的理论位移曲线和位移误差曲线 Fig.12 Displacement errors of different band widths. (a)$\sim$(c) $c = 8$ pixel and (e)$\sim$(g) $c = 16$ pixel, full field displacement errors calculated using 3 shape functions. (d) $c = 8$ pixel and (h) $c = 16$ pixel, theoretical displacement curve and smoothed displacement error curves using 3 shape functions |
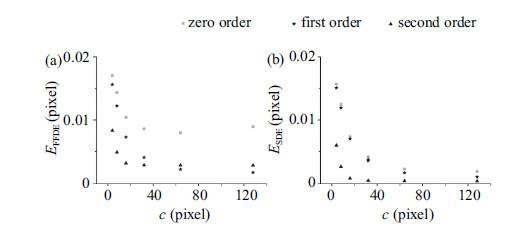
图13显示了带宽相关量$c$变化时,带内位移总误差和带内位移平滑误差. 图13(a)中的带内位移总误差和图13(b)中的带内位移平滑误差均随$c$的增大而先快速减小后缓慢减少,这是由于带宽相关量$c$增大时应变场的非均匀性迅速降低. 与4.2节中提到的带内位移误差与带内最大应变$a$成正比不同,带内位移误差与带宽相关量$c$并不是简单的线性关系. 这是因为4.2节中,带宽和模板均未改变,而本节中模板仍然固定,但带宽却是变化的. 如图13(b)所示,当模板较小时,二阶形函数的带内位移平滑误差小于零阶和一阶形函数的带内位移平滑误差; 但当模板较大 ($\geqslant 64$像素)时,各阶形函数的带内位移平滑误差基本相同. 在图13(a) 中,模板较小时二阶形函数带内位移总误差较小,但在模板大于64像素时,二阶形函数的带内位移总误差反而大于一阶形函数的带内位移总误差. 其原因是模板较大时,应变梯度较低,一阶和二阶形函数均能较好地描述带内变形,但二阶形函数的随机误差更大.
|
图 13 不同带宽时带内位移误差 Fig.13 Displacement statistical errors of different band widths |
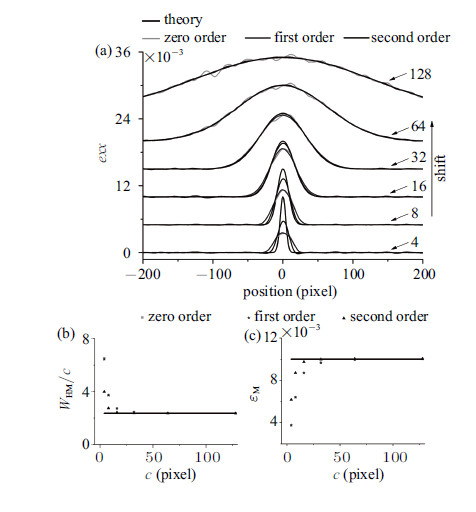
再来考虑各阶形函数在带宽相关量$c$变化时的应变曲线,如图14(a)所示. 其中,$c$从4到128像素变化时的应变曲线分别向上移动了0,0.005,0.010,0.015,0.020和0.025. 可以看到,在波特文-勒夏特利埃带外部,各阶形函数的应变曲线基本重合,且其在带宽相关量$c$的增大基本保持不变. 在带内,零阶和一阶应变曲线基本重合 (零阶形函数在$c$较大时波动很大),二阶形函数的应变曲线最接近理论值. 图14(b)和14(c)分别显示了各阶形函数带宽 ($W_{\rm HM}$)与带宽相关量$c$的比值 ($W_{\rm HM}/c$)和带内最大应变的计算值 ($\varepsilon_{\rm M}$)随$c$的变化情况. 可以看到,在带宽相关量$c$较小时,各阶形函数的误差均较大,但随着$c$的增大,各阶形函数计算结果与理论值的差距均减小.
|
图 14 不同带宽时的应变曲线及其拟合参数 Fig.14 Strain curves and the fitting parameters of different band widths |
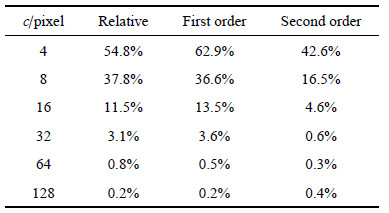
表1给出了用不同方法计算得到的带内最大应变的误差. 第二列中的相对误差表示一阶和二阶形函数计算的带内最大应变的绝对差值与一阶形函数得到的带内最大应变的比值. 第三列和最后一列分别是一阶和二阶形函数与理论值的相对误差. 如果认为与理论值的相对误差小于5%的结果是可靠的,那么,当一阶和二阶形函数的相对误差小于10%时,二阶形函数的计算结果是可靠的. 这里,我们建议使用这个判据来衡量数字图像相关法测量结果的可靠性. 对于两者误差大于10%的情况,将第五节中具体讨论. 对于两者误差更小的情况,比如表1中$c$较大时的结果. 可以看到,当一阶和二阶形函数结果的相对误差约为3.1% ($c= 32$像素)时,二阶形函数的误差仅为0.6%,而一阶形函数的误差也只有3.6%,此时,一阶形函数的阶数结果也是可靠的. 当一阶和二阶形函数的相对误差可以忽略不计时 ($c\geqslant64$ 像素),一阶和二阶形函数的计算结果均是可靠的.
| 表 1 带内最大应变的误差 Table 1 Errors of the maximum strain within the band |
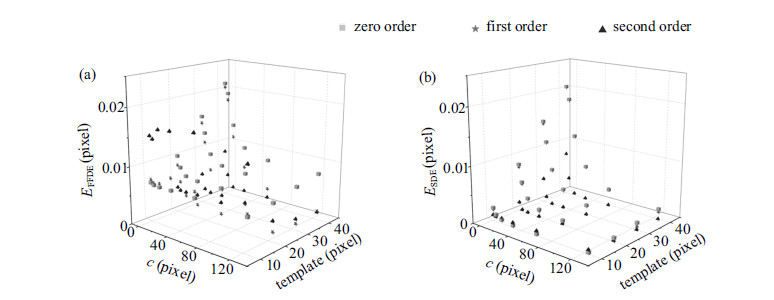
下面加入模板尺寸的影响,考虑带宽相关量$c$变化时,形函数和模板尺寸共同影响下的带内位移总误差和带内位移平滑误差,如图15所示. 先看图15(b),二阶形函数的带内位移平滑误差在大部分情况 (除带宽较大且模板较小时)均是最小的. 图15(a)显示了在模板较大时,二阶形函数的带内位移总误差均最小. 需要说明的是,在模板较小时,二阶形函数的随机误差很大,导致其总误差也较大. 此外,带宽增大时,各阶形函数的临界模板均增大.
|
图 15 不同带宽相关量和模板尺寸时的带内位移误差. (a)带内位移总误差. (b)带内位移平滑误差 Fig.15 Displacement errors of different band widths and templates. (a) Full field displacement errors within the band.(b) Smoothed displacement errors within the band |
在本小节中,我们发现二阶形函数在变形场应变梯度较大 ($c$较小)时的计算结果最好,但对低应变梯度变形场($c$较大)的计算结果稍微逊于一阶形函数的结果. 这是由于在应变梯度较大时,子区内二阶及二阶以上的变形不能被忽略,一阶形函数仅能够描述一阶变形,而二阶形函数能够描述更复杂的变形. 在应变梯度较低时,子区内二阶和二阶以上的变形可以忽略,一阶形函数足以很好的描述其变形,二阶形函数虽然也能描述其变形,但其引入的参量更多,在适用于更高阶变形的同时,对一阶变形的测量时的不确定性增加. 要使二阶形函数在均匀区域测量的误差和一阶形函数的结果一致,需要采用更大的模板以减小这种不确定性.
本节通过3个小节具体讨论不同情形时形函数和模板对数字图像相关法计算结果的影响. 由于这些讨论更多的是针对带有不同应变梯度的散斑场,与具体的变形形式关系不大. 推而广之,对于试件缺口附近和裂纹尖端等局部变形场同样适用. 到目前为止,我们找到了一些形函数和模板尺寸影响数字图像相关法计算结果的深层机制,并且给出了一个判断计算结果是否可靠的依据. 针对得到不可靠的计算结果的情形,我们将在下一节提出一种改进实验来获得可靠的结果.
5 其他实验影响在3.2节中,得到的一组波特文-勒夏特利埃带的实验数据显示,在模板为19像素和29像素时一阶和二阶形函数得到的带内最大应变的相对误差分别是18%和33%. 根据4.3节中提出的判据,这个大于10%的误差意味着即使采用二阶形函数也不能得到可靠的结果 (相对误差小于5%). 尽管如此,在4.2和4.3节中,我们也发现较小的带内最大应变和较大的带宽都可以得到较小的误差. 它们可以通过提高图像采样频率和增大图像空间分辨率来实现. 一组只通过增加试件厚度 (从1mm到3mm)来增大带宽 (试件厚度增加,波特文-勒夏特利埃带的带宽增加[19])的实验被用来验证这种方法. 图16显示了用一阶和二阶形函数在模板为19像素 (实线)和29像素 (虚线)时的位移曲线 (左)和应变曲线(右). 相比于图2中的位移和应变曲线,图16中,一阶和二阶形函数得到的位移和应变之间的差距均明显减小. 一阶和二阶形函数在模板为19像素和29像素时,得到的带内最大应变的相对误差分别从18%和33%降到6%和7%. 这个小于10%的误差说明了上述方法的可行性,此时二阶形函数的结果是可靠的,其与真实值的差距在5%以内.

|
图 16 验证实验得到的 (a)位移曲线和 (b)应变曲线 Fig.16 Smoothed displacement curves (a) and strain curves (b) |
本文以合金材料拉伸实验中出现的高应变梯度的波特文-勒夏特利埃带为例,详细地讨论了形函数和模板对局域变形场的位移和应 变计算的影响. 实验和数值模拟均证明了:
(1)在均匀变形区,一阶和二阶形函数的计算结果相当 (但对于二阶的形函数需要更大的模板才能获得与一阶形函数相当的随机 误差[27]);
(2)在局域变形场,模板尺寸相同时二阶形函数较一阶形函数有明显的优势 (二阶形函数欠匹配带来的系统误差较小,而随机误差相较 于系统误差是高阶小量).
对于数字图像相关法在局域化变形测量中存在的问题,本文也一一给出了解答:
(1)数值模拟揭示了在局域变形测量中,形函数和模板尺寸等计算参量对数字图像相关法计算结果的影响:
(a)二阶形函数有较大的临界模板并且在模板较大时,能获得比一阶形函数更好的结果;
(b)带内最大应变与位移误差和应变误差均成正比,且对波特文-勒夏特利埃带的带宽无影响;
(c)二阶形函数在波特文-勒夏特利埃带带宽较小时能得到更好的结果,但在带宽很大时的结果反而更差.
(2)为了判断数字图像相关法测量结果的可靠性,提出了当一阶和二阶形函数相对误差小于10%时,二阶形函数阶数结果是 可靠的判据. 该判据是通过特定的局域变形场(波特文-勒夏特利埃带)分析得到的,且受模板尺寸制约. 其他局域变形场(比如试件缺口附近和裂纹尖端),也属于高阶变形,但变形形式与波特文-勒夏特利埃带不同,分析的结果随之改变,在考虑二阶以上变形影响较小时,上述判据同样适用. 我们下一步研究工作将针对``像素应变梯度'' (即每像素的应变梯度)进行讨论,以期得到定量的、普适的判据.
(3)实验和数值模拟的计算结果表明,可以通过设置数字图像相关法的算法参量来获得更为准确的结果;
(4)在局域变形测量中,建议采用二阶形函数和较大 (降低随机误差)的模板尺寸; 如果要采用一阶形函数,需要采用较小(降低系统误差)的模板尺寸;
(5)对于测量结果不满足该判据的情况 (即一阶和二阶形函数计算结果的带内最大应变相对误差大于10%),给出了通过提高采样频率和空间分辨率来获取可靠结果的方法.
这样,数字图像相关法局域化变形测量中的问题均被解答,为数字图像相关法的使用者在局域变形场测量中评估计算结果提供了一些参考方法.
| [1] | Peters WH, Ranson WF. Digital imaging techniques in experimental stress analysis. Optics Engineering, 1981, 21: 427-431 |
| [2] | Schreier H, Orteu JJ, Sutton MA. Image correlation for shape, motion and deformation measurements: Basic concepts, theory and applications. New York: Springer, 2009 |
| [3] | 李喜德, 谭玉山. 数字散斑强度相关计量的特性研究. 光学学报, 1992, 12 (12): 1135-1139 (Li Xide, Tan Yushan. Investigation of the specifics of digital speckle intensity correlation metering. Acta Optica Sinica, 1992, 12(12): 1135-1139 (in Chinese)) |
| [4] | 潘兵, 谢惠民, 续伯钦等. 数字图像相关中的亚像素位移定位算法发展. 力学进展, 2005, 35 (3): 345-352 (Pan Bing, Xie Huimin, Xu Boqin, et al. Development of sub-pixel displacements registration algirithms in digital image correlation. Advances in Mechanics, 2005, 35(3): 345-352 (in Chinese)) |
| [5] | Zhang ZF, Kang YL, Wang HW, et al. A novel coarse-fine search scheme for digital image correlation method. Measurement, 2006, 39(8): 710-718 |
| [6] | 杨勇, 王琰蕾, 李明等. 高精度数字图像相关测量系统及其技术研究. 光学学报, 2006, 26 (2): 197-201 (Yang Yong, Wang Yanlei, Li Ming, et al. Research of high-accuray digital image correlation measurement system. Acta Optica Sinica, 2006, 26(2): 197-201 (in Chinese)) |
| [7] | 潘兵, 谢惠明, 戴福隆. 数字图像相关中亚像素位移测量算法的研究. 力学学报, 2007, 39 (2): 245-252 (Pan Bing, Xie Huimin, Dai Fulong. An investigation of sub-pixel displacements registeration algorithms in digital image correlation. Journal of Theoretical and Applied Mechanics, 2007, 39(2): 245-252 (in Chinese)) |
| [8] | Li XD, Deng B, Shi HJ. Displacement measurements in micro-region with generalized digital speckle correlation method. Proc. SPIE, 2002, 4537: 366-369 |
| [9] | 王怀文, 亢一澜, 谢和平. 数字散斑相关方法与应用研究进展. 力学进展, 2005, 35 (2): 195-203 (Wang Huaiwen, Kang Yilan, Xie Heping. Advance in digital speckle correlation and its application. Advances in Mechanics, 2005, 35(2): 195-203 (in Chinese)) |
| [10] | 潘兵, 谢惠民, 续伯钦等. 应用数字图像相关方法测量含缺陷试样的全场变形. 实验力学, 2007, 22 (3-4): 379-384 (Pan Bing, Xie Huimin, Xu Boqin, et al. Full-field deformation measurement of specimen with discontinuity using digital image correlation. Journal of Experimental Mechanics, 2007, 22(3-4): 379-384 (in Chinese)) |
| [11] | 曾祥福, 刘程林, 马少鹏. 高速三维数字图像相关系统及其动载三维变形测量. 北京理工大学学报, 2012, 32 (4): 364-369 (Zeng Xiangfu, Liu Chenglin, Ma Shaopeng. Measurement of dynamic three-dimensional deformation of structures using high-speed 3-D digital image correlation system. Transactions of Beijing Institute if Technology, 2012, 32(4): 364-369 (in Chinese)) |
| [12] | Kang YL, Zhang ZF, Wang HW, et al. Experimental investigations of the effect of thickness on fracture toughness of metallic foils. Materials Science and Engineering A, 2005, 394(1-2): 312-319 |
| [13] | 陈琳, 卢荣胜. 数字图像相关法测量含缺陷试样全场变形量. 激光杂志, 2014, 35 (11): 16-19 (Chen Lin, Lu Rongsheng. Digital image correlation method for full-field deformation measurement of specimen with discontinuity. Laser Journal, 2014, 35(11): 16-19 (in Chinese)) |
| [14] | 朱珍德, 张勇, 李术才等. 用数字图像相关技术进行红砂岩细观裂纹损伤特效研究. 岩石力学与工程学报, 2015, 24 (7): 1123-1128 (Zhu Zhende, Zhang Yong, Li Shucai, et al. Studies on microcosmic crack damage properties of a red sandstone with digital image technique. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1123-1128 (in Chinese)) |
| [15] | 刘聪, 陈振宁, 何小元. 3D-DIC在土木结构力学性能试验研究中的应用. 东南大学学报 (自然科学版), 2014, 44 (2): 339-344 (Liu Cong, Chen Zhenning, He Xiaoyuan. Application of 3D-DIC in experimental study on mechanical properties of civil structures. Journal of Southeast University (Nature Science Edition), 2014, 44(2): 339-344 (in Chinese)) |
| [16] | 蔡玉龙, 符师桦, 王玉辉等. 基于三维数字图像相关法的5456铝镁合金锯齿形屈服研究. 金属学报, 2014, 50 (12): 1491-1497 (Cai Yulong, Fu Shihua, Wang Yuhui, et al. Serrated yielding of 5456 aluminium magne sium alloy based on three dimensional digital image correlation. Acta Metallurgica Sinica, 2014, 50(12): 1491-1497 (in Chinese)) |
| [17] | Gao Y, Cheng T, Su Y, et al. High-efficiency and high-accuracy digital image correlation for three-dimensional measurement. Optics Lasers in Engineering, 2015, 65: 73-80 |
| [18] | Zhang QC, Toyooka S, Meng ZB, et al. Investigation of slipband propagation in aluminum alloy with dynamic speckle interferometry. SPIE, 1999, 3585: 389-398 |
| [19] | Zhang QC, Jiang ZY, Jiang HF, et al. On the propagation and pulsation of Portevin-Le Chatelier deformation bands: An experimental study with digital speckle pattern metrology. International Journal of Plasticity, 2000, 40(2): 393-400 |
| [20] | Schreier HW, Sutton MA. System errors in digital image correlation due to undermatched subset shape functions. Experimental Mechanics, 2002, 42(3): 303-310 |
| [21] | 王学滨, 杜亚志, 潘一山. 考虑一阶和二阶位移梯度的数字图像相关方法在剪切带测量中的比较. 工程力学, 2013, 30 (7): 282-297 (Wang Xuebin, Du Yazhi, Pan Yishan. A comparsion of DIC methods considering the first- and second-order displacement gradients in shear band measurements. Engineering Mechanics, 2013, 30(7): 282-297 (in Chinese)) |
| [22] | Bornert M, Brémand F, Doumalin P, et al. Assessment of digital image correlation measurement errors: Methodology and results. Exp Mech , 2009, 49(3): 353-370 |
| [23] | Yu LP, Pan B. The errors in digital image correlation due to overmatched shape functions. Meas Sci Technol , 2015, 26: 045202 |
| [24] | Gates M, Gonzalez J, Lambros J. Subset refinement for digital volume correlation: Numerical and experimental applications. Exp Mech , 2015, 55(1): 245-259 |
| [25] | Pan B, Xie HM, Wang ZY, et al. Study on subset size selection in digital image correlation for speckle patterns. Optics Express, 2008, 16(10): 7037-7048 |
| [26] | Lu L, Wang Z, Vo M, et al. Accuracy enhancement of digital image correlation with B-spline interpolation. Opt. Lett., 2011, 36: 3070-3072 |
| [27] | Lu H, Cary PD. Deformation measuement by digital image correlation: implemention of a second-order displacement gradient. Experimental Mechanics, 2000, 40(4): 393-400 |
| [28] | Sutton MA, Yan JH, Tiwari V, et al. The effect of out-of-plane motion on 2D and 3D digital image correlation measurements. Optics Lasers in Engineering, 2008, 46 (10): 746-757 |
| [29] | Cheng T, Xu XH, Cai YL, et al. Investigation of Portevin-Le Chatelier effect in 5456 Al-based alloy using digital image correlation. Optics Lasers in Engineering, 2015, 65: 89-92 |
| [30] | Zhou P, Goodson KE. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation (DISC). Optics Engineering, 2001, 40(8): 1613-1620 |
 2015, Vol. 47
2015, Vol. 47