引 言
柔性体的变形场离散问题是柔性多体系统动力学中的热点和难点,如何正确合理的描述柔性体的变形场是柔性多体系统动力学的研究 核心之一. 目前运用较广的主要有假设模态法、有限元法等几类[1, 2]. 假设模态法[3, 4, 5]源于结构力学中梁的振动振型函数,其突出优点是积分过程简单方便,且能用较少的模态获得较好的逼 近结果,计算效率高. 但当柔性体形状不规则或结构复杂时,其振动振型如何描述本身就是难题. 有限元法[6, 7]将具有无限自由度的连续弹性体离散为有限自由度的单元集合体,是目前发展成熟,应用广泛并被高度 认可的变形场离散方法. 由于它在处理复杂几何形体的各类线性和非线性问题时所表现出的通用性和灵活性,许多涉及固体及结构的实际工程问题都使用商业 有限元进行求解分析. 但由于使用单元或网格,使其存在许多固有缺陷[8]. 有限元法的局限性主要有:前处理繁琐,需要花费大量时间划分网格;网格畸变将导致精度降低或计算失败;不易构造出高阶连续的场 函数,所得应力在各单元边界上通常不连续;另外,复杂三维结构的网格生成和重分也是相当困难和费时的[9]. 国内外已有学者开始寻找新的变形场离散方法并应用于柔性旋转悬臂梁的动力学研究中,如绝对节点坐标法[10, 11, 12]、B样 条插值[13, 14]及贝塞尔(Bezier)插值方法[15].
近年来,无网格法(meshfree method)被提出并用于解决复杂的工程和科学问题. 无网格法在建立整个问题域的系统代数方程时,只需节点信息,无需划分网格. 在 构造形函数的过程中,采用更多的节点插值,通常具有高阶连续性,从而提高了计算精度. 上述诸多优势使无网格法迅速成为计算方法研究的热点. 现有的无网格法有多种,如无网格点插值法(point interpolation method,PIM)[16, 17, 18]、无网格径向基插值法(radial point interpolation method,RPIM)[19]、无单元迦辽金法(element-free Galerkin method,EFG)[20, 21]、无网格局部彼得罗夫-伽辽金法(meshless local Petrov-Galerkin method,MLPG)[22, 23]、再生核粒子法(reproducing kernel particle method,RKPM)[24, 25]等. 光滑节点插值法(node-based smoothed point interpolation method,NS-PIM)最近被提出并成功应用于一维和二维弹性力学的静力学及频率分析中[26, 27, 28],获得了与解析解吻合很好的结果. 目前,将无网格法应用于柔性多体系统动力学的研究中鲜有报道[29, 30].
基于欧拉-伯努利理论梁的控制方程为4阶微分方程,早期求解该方程通常将位移及其1阶导数作为独立变量,形函数 为3次多项式形式. 本文采用光滑节点插值法,独立变量只有位移,形函数采用简单的线性插值即可求解上述4阶微分方程问题. 选用容易求解析解的悬臂梁,对其两种受力情况进行静力学分析,并首次将其应用到柔性多体系统动力学中,进行旋转柔性梁的频率分析. 在静力学分析中,将仿真结果与解析解对比表明该方法虽用简单的线性插值形函数描述梁的位移场,但精度却很高. 进一步研究表明,采用模态高于9阶的假设模态法会使刚度阵条件数变差,导致结果发散. 在频率分析中,与有限元法、假设模态法和解析解对比,可知该方法能提供固有频率的下界值,而有限元法和假设模态法能提供固有 频率的上界值,说明该方法结合有限元法可以从频率的上下界最大程度的逼近真实解. 光滑节点插值法形函数结构简单、独立变量少且能提供固有频率下界值,因此,具有较高的推广价值.
1 静力学分析
1.1 欧拉-伯努利梁的弱式方程
欧拉-伯努利梁的强式方程可表示为如下4阶微分方程
|
$ EId\frac{{{d^4}v}}{{d{x^4}}} = {b_y}{\rm{ }} $
|
(1)
|
式中,$EI$为抗弯刚度,$v$为挠度函数,$b_{y}$为体力. 根据不同的问题,其边界条件可表示为如下形式
|
$ v({x_0}) = {v_\Gamma }在边界{\Gamma _v}上 $
|
(2)
|
|
$ - \frac{{dv({x_0})}}{{dx}} = {\theta _\Gamma }{\mkern 1mu} ,\;\;在边界{\Gamma _\theta }上 $
|
(3)
|
|
$ M({x_0}) = - EI\frac{{{d^2}v}}{{{\rm{d}}{x^2}}} = {M_\Gamma }_M{\mkern 1mu} ,\;\;在边界{\Gamma _M}上 $
|
(4)
|
|
$ Q({x_0}) = - EI\frac{{{d^3}v}}{{{\rm{d}}{x^3}}} = {Q_\Gamma }{\mkern 1mu} ,\;\;在边界{\Gamma _Q}上 $
|
(5)
|
式(2)和式(3)表示本质边界条件,式(4)和式(5)表示自然边界条件. $M(x_{0})$和$Q(x_{0})$分别代表弯矩和剪力. 在整个问题域$\varOmega
$中,式(1)的标准迦辽金弱式可表示为
|
$ \begin{array}{l}
\int_\Omega {EI} \frac{{{d^2}(\delta v)}}{{d{x^2}}}\frac{{{d^2}v}}{{d{x^2}}}dx = \\
\int_\Omega {\delta v{b_y}} dx + {Q_\Gamma }\delta v{|_{{\Gamma _Q}}} - {M_\Gamma }\frac{{(\delta v)}}{{dx}}{|_{{\Gamma _M}}}
\end{array} $
|
(6)
|
挠度函数$v$由强式方程(1)要求的至少4阶连续降为弱式要求的至少2阶连续.
1.2 迦辽金方程的弱-弱形式
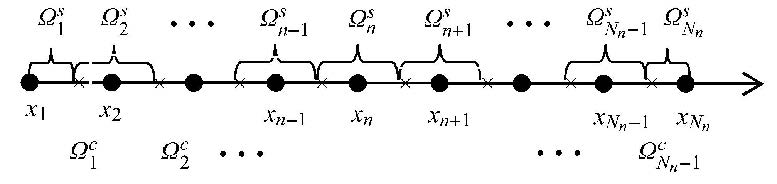
迦辽金方程的弱-弱(weakened weak form,W2)形式是指将式(6)中要求的至少2阶连续函数降为1阶连续函数. 如图1所示,将梁离散为$N_{n}$个节点,每两个相邻节点形成一个背景网格$\varOmega_n^c $. 对于每一个节点,需要形成一个用于积分运算的光滑域$\varOmega _n^s $,该光滑域由相邻两个背景网格的中点构成,可以形成$N_{s}$个光滑域,因此有$N_{n}=N_{s}$. 边界上的光滑域受2个节点影响,内部光滑域受3个节点影响,如节点1、2影响$\varOmega _1^s $,节点$n -1$,$n$和$n +1$影响$\varOmega _n^s $.
利用梯度光滑技术[31],在每一个光滑域中,挠度的2阶导数可以表示为
|
$ \frac{{\overline {{d^2}v} }}{{d{x^2}}} = \frac{1}{{l_i^s}}\int_{\Gamma _i^S} {} \left( {n(x)\frac{{dv}}{{dx}}} \right)dx $
|
(7)
|
式中,$l_i^s $是光滑域$\varOmega _i^s $的长度,$\varGamma _i^s $是光滑域$\varOmega
_i^s $的边界,$n(x)$为光滑域$\varOmega _i^s
$边界上的单位外法线,对于梁而言,其值为1或$-1$. 将式(7)代入式(6)中,可得迦辽金方程的弱-弱形式
|
$ \begin{array}{l}
\sum\limits_{i = 1}^{{N_n}} {\frac{1}{{l_i^s}}} \left[{\int_{\Gamma _i^s} {\left( {n(x)\frac{{d\delta v}}{{dx}}} \right)} dx} \right]\left[{EI\int_{\Gamma _i^s} {\left( {n(x)\frac{{d\delta v}}{{dx}}} \right)} } \right] = \\
\;\;\;\;\;\;\;\;\;\;\;\int_\Omega \delta v{b_y}dx + {\left. {{Q_\Gamma }\delta v} \right|_{{\Gamma _Q}}} - {M_\Gamma }{\left. {\frac{{d\delta v}}{{dx}}} \right|_{{\Gamma _M}}}
\end{array} $
|
(8)
|
1.3 光滑节点插值法公式
对于欧拉-伯努利梁,有限元通常在每个节点采用2个独立变量,即节点挠度和其1阶导数,而光滑节点插值法只将节点挠度作为独立变量,因此在每个背景网格中,挠度函数只需线性插值函数即可. 其挠度函数可表示为
|
$ v(x) = \left\{ {{\phi _n}(x)\;\;{\phi _{n + 1}}(x)} \right\}\left\{ {\begin{array}{*{20}{c}}
{{v_n}}\\
{{v_{n + 1}}}
\end{array}} \right\}{\mkern 1mu} ,\;\;x \in \Omega _n^c $
|
(9)
|
其中,$v_{n}$和 $v_{n + 1}$分别为节点$n$和$n$+1的挠度,$\phi _n
(x)$为形函数,可表示为如下简单形式
|
$ \left. {\begin{array}{*{20}{c}}
{{\phi _n}(x) = 1 - (x - {x_n})/l_n^c}\\
{{\phi _{n + 1}}(x) = (x - {x_n})/l_n^cn}
\end{array},x \in \Omega _n^c} \right\} $
|
(10)
|
式中,$l_n^c $为$\varOmega _n^c $的长度. 将式(9)代入式(7)中,对于内部各节点可得
|
$ \begin{array}{l}
\frac{1}{{l_i^s}}\int_{\Gamma _i^s} {\left( {n(x)\frac{{dv}}{{dx}}} \right)dx} = \frac{1}{{l_i^s}}\underbrace {{{\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
- {\phi _{(n - 1),x}}({x_{n - 1/2}})\\
\left( {{\phi _{n,x}}({x_{n + 1/2}}) - {\phi _{n,x}}({x_{n - 1/2}})} \right)\\
{\phi _{(n + 1),x}}({x_{n + 1/2}})
\end{array}
\end{array}} \right\}}^{\rm{T}}}}_{{B_n}}\underbrace {\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{v_{n - 1}}\\
{v_n}\\
{v_{n + 1}}
\end{array}
\end{array}} \right\}}_{{d_n}} = \\
\;\;\;\;\;\;\;\;\;\;\;\;{B_n}{d_n}{\mkern 1mu} ,\;\;\;\;\;n = 2,3 \cdots ,{N_n} - 1
\end{array} $
|
(11)
|
其中,$x_{n - 1 / 2} = x_n - l_n^c / 2$,$x_{n + 1 / 2} = x_n + l_n^c / 2$,$\phi _{n,x}
$表示$\phi _n $对$x$求1阶导数.
对于左端边界光滑域($n =1$),式(7)可表示为
|
$ \frac{1}{{l_1^s}}\int_{\Gamma _l^s} {\left( {n(x)\frac{{dv}}{{dx}}} \right)dx} = \frac{1}{{l_1^s}}\underbrace {{{\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
\left( {{\phi _{1,x}}({x_{1 + 1/2}}) - {\phi _{1,x}}({x_1})} \right)\\
\left( {{\phi _{2,x}}({x_{1 + 1/2}}) - {\phi _{2,x}}({x_1})} \right)
\end{array}
\end{array}} \right\}}^{\rm{T}}}}_{{B_1}}\underbrace {\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{v_1}\\
{v_2}
\end{array}
\end{array}} \right\}}_{{d_1}} = {B_1}{d_1} $
|
(12)
|
同理,对于右端边界光滑域($n=N_{n}$),式(7)可表示为
|
$ \begin{array}{l}
\frac{1}{{l_{{N_n}}^s}}\int_{\Gamma _{Nn}^s} {\left( {n(x)\frac{{dv}}{{dx}}} \right)dx} = \\
\frac{1}{{l_{{N_n}}^s}}\underbrace {{{\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{\phi _{({N_n} - 1),x}}({x_{{N_n}}}) - {\phi _{({N_n} - 1),x}}({x_{{N_n} - 1/2}})\\
{\phi _{{N_n},x}}({x_{{N_n}}}) - {\phi _{{N_n},x}}({x_{{N_n} - 1/2}})
\end{array}
\end{array}} \right\}}^{\rm{T}}}}_{{B_{{N_n}}}}\underbrace {\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{v_{{N_n} - 1}}\\
{v_{{N_n}}}
\end{array}
\end{array}} \right\}}_{{d_{{N_n}}}} = \\
\;\;\;\;\;\;\;\;\;\;\;{B_{{N_n}}}{d_{{N_n}}}
\end{array} $
|
(13)
|
将式(11)$\sim $式(13)代入式(8)中,可得欧拉-伯努利梁的平衡方程为
式中,$U = {\left\{ {{v_1}\;\;{v_2}\;\; \cdots \;\;{v_{Nn}}} \right\}^{\rm{T}}}$为节点挠度向量,${ F}$为节点力向量,表示为
|
$ \begin{array}{l}
F = {\int_\Omega \Phi ^{\rm{T}}}(x){b_y}dx{ + ^{\rm{T}}}(x){Q_\Gamma }d\Gamma - \\
\;\;\;\;\;\;\int_{{\Gamma _M}} \Phi _{,x}^{\rm{T}}(x){M_\Gamma }d\Gamma
\end{array} $
|
(15)
|
其中,${\varPhi }(x)$为形函数向量. ${ K}$为刚度阵,由同有限元类似的过程组合而成,表示为
|
$ K = \sum\limits_{n = 1}^{{N_n}} {{K_n}} $
|
(16)
|
式中${ K}_n $为光滑域$\varOmega _n^s $中计算得到的刚度阵,表达式为
|
$ {K_n} = EI{({B_n})^{\rm{T}}}{B_n}{l_n} $
|
(17)
|
1.4 数值算例
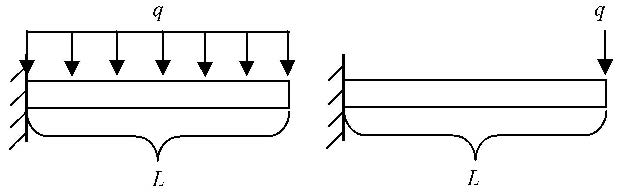
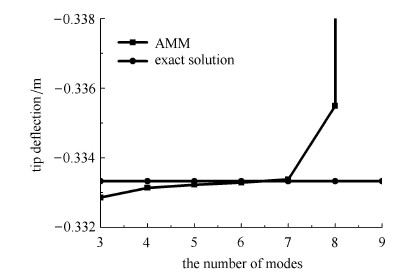
图2为悬臂梁的两种受力情况,分别受分布力与集中力作用. 为对比简便,将梁抗弯刚度、长度及作用力均取为1. 图3表示在这两 种受力情况下,分别使用有限元法、假设模态法、光滑节点插值法及解析解计算的梁中各点挠度. 其中假设模态法取横向3阶模态,有限元法取10个单元,光滑节点插值法取21个节点. 如图所示,3种离散方法所得结果与解析解基本一致,说明光滑节点插值法即使使用线性插值,也可以保证很高的精度. 在假设模态法的使用中,通常认为模态阶数取的越多,结果越精确. 但本文研究发现,对于悬臂梁,当所取模态阶数大于9阶时,结果趋于发散. 如图4所示. 主要因为模态阶数过多导致刚度阵${ K}$的条件数变差,所以分析悬臂梁时取3$\sim $6阶模态即可. 图5表示自由端受集中力作用时三种离散方法所得应变能与解析解结果的对比,从图5(a)中可看出,随着自由度数的增加,结 果逐渐趋于精确解. 其中,有限元精度最高,与解析解一致,因为解析解表达式为3阶多项式,被包含在有限元的形函数中. 在自由度低于20时,光滑节点插值法精度较低,因为其形函数采用简单的线性插值,当自由度大于20时,结果趋于精确解. 同时发现光滑节点插值法的一个重要特性:从应变能的上界趋近精确值,说明光滑节点插值法具有偏柔性的特点. 从图5(b)中可以看出,假设模态法并没有出现模态阶数取的越多精度越高的情况,且从应变能的下界趋近精确值,说明假设 模态法具有偏刚性的特点.
2 频率分析
2.1 悬臂梁的自由振动
欧拉-伯努利梁的自由振动控制方程为4阶微分方程,表达式为
|
$ EI\frac{{{d^4}v}}{{d{x^4}}} + \rho S\frac{{{d^2}v}}{{d{x^2}}} = 0 $
|
(18)
|
式中,$\rho $为密度,$S$为横截面积. 式(18)的迦辽金弱式为
|
$ \int_\Omega {EI} \frac{{{d^2}(\delta v)}}{{d{x^2}}}\frac{{{d^2}v}}{{d{x^2}}}dx + {\rm{ }}\int_\Omega \rho S\delta v\frac{{{d^2}v}}{{d{t^2}}}dx = 0 $
|
(19)
|
将式(7)代入式(19)中,可得梁自由振动的迦辽金弱-弱式方程
|
$ \begin{array}{l}
\sum\limits_{i = 1}^{{N_n}} {\frac{1}{{l_i^s}}} \left[{\int_{\Gamma _i^s} {\left( {n(x)\frac{{d\delta v}}{{dx}}} \right)dx} } \right]\left[{EI\int_{\Gamma _i^s} {\left( {n(x)\frac{{dv}}{{dx}}} \right)dx} } \right] + \\
\;\;\;\;\;\;\;\int_\Omega \rho S\delta v\frac{{{d^2}v}}{{d{t^2}}}dx = 0
\end{array} $
|
(20)
|
将式(11)$\sim $式(13)代入式(20)中,可得如下矩阵形式的自由振动方程
|
$ KU + M\ddot U = {\bf{0}} $
|
(21)
|
式中刚度阵${ K}$与上一节的计算过程相同,质量阵${ M}$可近似为如下对角阵
|
$ M = {\rm{diag}}\left( {{m_1}\;\;{m_2}\;\; \cdots \;\;{m_{{N_n}}}} \right) $
|
(22)
|
其中$m_{n}$为节点$n$在其光滑域内的集中质量,表达式为
|
$ {m_n} = \rho Sl_n^s $
|
(23)
|
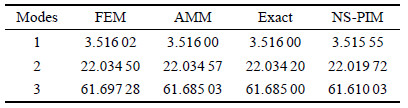
表1为悬臂梁自由振动时前3阶固有频率. 为比较的公平性,有限元法和光滑节点插值法使用相同的自由度数,即有限元将梁离散 为40个单元,光滑节点插值法将梁离散为81个节点,假设模态法取3阶模态. 从表1中可以看出,有限元法与假设模态法所得结果总是比精确解大,提供固有频率的上界值,而光滑节点插值法所得结果总 是比精确解小,提供固有频率的下界值,这也是光滑节点插值法的重要特性. 对于精度而言,假设模态法最高,因为其形函数本身就是梁的振动振型函数,若假设模态不能正确描述梁的振动振型,则其精 度并不能得到保证. 光滑节点插值法形函数虽使用简单的线性插值,但精度仍然很高,与精确解相比误差很小.
表 1(Table 1)
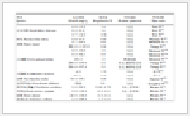
表 1 悬臂梁自由振动在3种离散方法中的固有频率比较Table 1 Natural frequency of cantilever beam with three discrete methods
|
表 1 悬臂梁自由振动在3种离散方法中的固有频率比较
Table 1 Natural frequency of cantilever beam with three discrete methods |
2.2 柔性旋转悬臂梁的横向弯曲固有频率分析
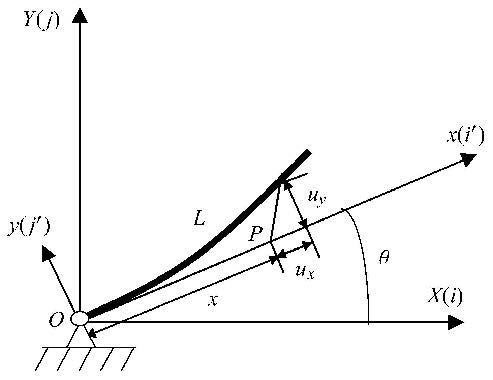
图6为水平面内运动的柔性旋转悬臂梁系统,以转动中心$O$为原点建立惯性坐标系$O_{ij}$,在柔性梁上建立浮动坐 标系$O_{i'j'}$. 柔性梁的长度、密度、横截面积、抗弯刚度分别为$L$,$\rho $,$S$和 $EI$,$\theta $为大范围运动转角.
如图6所示,柔性梁上任意点$P$变形后的矢径在惯性坐标系$O_{ij}$中可表示为
|
$ r = \Theta ({\rho _0} + u) $
|
(24)
|
式中
|
$ \left. {\begin{array}{*{20}{c}}
{{\rho _0} = {{\left\{ {x,0} \right\}}^{\rm{T}}}}\\
{u = {{\left\{ {{u_x},{u_y}} \right\}}^{\rm{T}}}}\\
{\Theta = \left\{ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{ - \sin \theta }\\
{\sin \theta }
\end{array}}&\begin{array}{l}
\cos \theta \\
\cos \theta
\end{array}&\begin{array}{l}
\\
\end{array}
\end{array}} \right\}}
\end{array}} \right\} $
|
(25)
|
其中,${\varTheta }$为浮动坐标系相对于惯性坐标系的方向余弦矩阵. 变形矢量${ u}$在浮动基下的坐标为
|
$ u = \left\{ {\begin{array}{*{20}{l}}
{{u_x}}\\
{{u_y}}
\end{array}} \right\} = \left\{ {\begin{array}{*{20}{l}}
{{w_1} + {w_{\rm{c}}}}\\
{{w_2}}
\end{array}} \right\} $
|
(26)
|
式中,$w_1 $为柔性梁轴向拉伸量,$w_2 $为柔性梁横向弯曲挠度,$w_{\rm c}$为柔性梁横向弯曲引起的纵向缩短量,即变形位移的二次耦合项,表达式为
|
$ {w_{\rm{c}}} = - \frac{1}{2}\int_0^x {{{\left( {\frac{{\partial {w_2}}}{{\partial \zeta }}} \right)}^2}} d\zeta $
|
(27)
|
系统动能为
|
$T = \frac{1}{2}\int_V \rho {\dot r^{\rm{T}}}\dot rdV $
|
(28)
|
系统变形势能表示为
|
$ \begin{array}{l}
U = \frac{1}{2}\int_0^L E S{\left( {\frac{{\partial {w_1}}}{{\partial x}}} \right)^2}dx + \\
\;\;\;\;\frac{1}{2}\int_0^L E I{\left( {\frac{{{\partial ^2}{w_2}}}{{\partial {x^2}}}} \right)^2}dx
\end{array} $
|
(29)
|
梁轴向和横向变形位移函数可表示为
|
$ \left. {\begin{array}{*{20}{c}}
{{w_1} = \left\{ {{\phi _i}(x)\;\;{\phi _{i + 1}}(x)} \right\}\left\{ {\begin{array}{*{20}{c}}
{{u_{xi}}}\\
{{u_{x(i + 1)}}}
\end{array}} \right\} = }\\
{\Theta (x){A^i}(t)}\\
{{w_2} = \left\{ {{\phi _i}(x)\;\;{\phi _{i + 1}}(x)} \right\}\left\{ {\begin{array}{*{20}{c}}
{{u_{yi}}}\\
{{u_{y(i + 1)}}}
\end{array}} \right\} = }\\
{\begin{array}{*{20}{l}}
{{\Theta ^i}(x){B^i}(t)}
\end{array}{\mkern 1mu} }
\end{array},\;x \in \Omega _i^c} \right\} $
|
(30)
|
式中,形函数的表达式见式(10),${ A}^{i}(t)$ 和 ${ B}^{i}(t)$分别表示节点$i$和$i+1$轴向和横向变形随时间变化的列矢量. 取总体轴向和横向变形位移列阵为
|
$ \left. {\begin{array}{*{20}{c}}
{A = {{\left\{ {{u_{x1}}\;\;{u_{x2}}\;\; \cdots \;\;{u_{x{N_n}}}} \right\}}^{\rm{T}}}}\\
{B = {{\left\{ {{u_{y1}}\;\;{u_{y2}}\;\; \cdots \;\;{u_{y{N_n}}}} \right\}}^{\rm{T}}}}
\end{array}} \right\} $
|
(31)
|
则有
|
$ {A^i} = {R^i}A{\mkern 1mu} ,\;\;\;\;{B^i} = {R^i}B $
|
(32)
|
其中,${ R}^{i}$为转化矩阵,可表示为节点编号: $1,2,\cdots,i,i+1,\cdots,N_{n}$
|
$ {R^i}\left. { = \left\{ \begin{array}{l}
0\;\;\;\;\;0\;\;\;\; \cdots \;\;\;1\;\;\;\;0\;\;\;\; \cdots \;\;\;{\rm{0}}\\
{\rm{0}}\;\;\;\;\;{\rm{0}}\;\;\;\; \cdots \;\;\;{\rm{1}}\;\;\;\;{\rm{0}}\;\;\;\; \cdots \;\;\;0
\end{array} \right.} \right\} $
|
(33)
|
将式(32)代入式(30)中,可得
|
$ \left. {\begin{array}{*{20}{c}}
{{w_1} = \Phi (x)A(t)}\\
{{w_2} = \Phi (x)B(t)}
\end{array},\;\;\;x \in \Omega _i^c} \right\} $
|
(34)
|
其中,${\varPhi} (x) ={\varPhi}^i(x){ R}^i$.
将式(34)代入式(26)中,可得梁上任意点的变形位移为
|
$ u = \left\{ {\begin{array}{*{20}{l}}
{{u_x}}\\
{{u_y}}
\end{array}} \right\} = \left\{ {\begin{array}{*{20}{l}}
\begin{array}{l}
\Phi (x)A(t) - \frac{1}{2}{B^{\rm{T}}}(t)H(x)B(t)\\
\Phi (x)B(t)
\end{array}
\end{array}} \right\} $
|
(35)
|
式中,${ H} (x)$为耦合形函数,表达式如下
|
$H(x) = {R^{i{\rm{T}}}}{\int_0^x \Phi ^{i'{\rm{T}}}}(\zeta ){\Phi ^{i'}}(\zeta )d\zeta {R^i} $
|
(36)
|
其中,${\varPhi}^{i'} (\zeta )$表示${\varPhi}^i(\zeta )$对$\zeta $求一阶导数.
将式(35)代入系统的动能和变形势能表达式中,取广义坐标$q = {\left\{ {\theta ,{A^{\rm{T}}},{B^{\rm{T}}}} \right\}^{\rm{T}}}$,运用第二类拉格朗日方程
|
$ \frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial \mathop q\limits^. }}} \right) - \frac{{\partial T}}{{\partial q}} = - \frac{{\partial U}}{{\partial q}} + {F_q} $
|
(37)
|
式中,${ F}_q = \left\{ { {\tau},{\bf 0},{\bf 0}} \right\}^{\rm T}$为广义力列阵,$\tau $为刚体上合外力关于转动中心$O$的主矩. 经过复杂的推导可得系统的动力学方程为
|
$ \left. {\left\{ \begin{array}{l}
{M_{11}}\;\;\;\;{M_{12}}\;\;\;\;\;{M_{13}}\;\;\\
{M_{21}}\;\;\;\;{M_{22}}\;\;\;\;\;0\\
M31\;\;\;\;0\;\;\;\;\;\;\;\;{M_{33}}\;
\end{array} \right.} \right\}\left\{ \begin{array}{l}
{\ddot \theta }\\
\mathop A\limits^{..} \\
\mathop B\limits^{..}
\end{array} \right\} = \left\{ \begin{array}{l}
{Q_\theta }\\
{Q_A}\\
{Q_B}
\end{array} \right\} $
|
(38)
|
式中
|
$ \begin{array}{l}
{M_{11}} = \frac{1}{3}\rho S{L^3} + 2SA + {A^{\rm{T}}}MA + \\
\;\;\;\;\;\;\;\;\;{B^{\rm{T}}}MB\underline { - {B^{\rm{T}}}DB}
\end{array} $
|
(39)
|
|
$ {M_{21}} = M_{12}^{\rm{T}} = - MB $
|
(40)
|
|
$ {M_{31}} = M_{13}^{\rm{T}} = - {S^{\rm{T}}} + {M^{\rm{T}}}A $
|
(41)
|
|
$ {M_{22}} = {M_{33}} = M $
|
(42)
|
|
$ {Q_\theta } = \tau - 2\dot \theta [S\mathop A\limits^. + {A^{\rm{T}}}M\mathop A\limits^. + {B^{\rm{T}}}M\mathop B\limits^. \underline { - {B^{\rm{T}}}D\mathop B\limits^. }]{\rm{ }} $
|
(43)
|
|
$ {Q_A} = {\dot \theta ^2}{S^{\rm{T}}} + 2\dot \theta M\mathop B\limits^. + ({\dot \theta ^2}M - {K_1})A $
|
(44)
|
|
$ {Q_B} = {\dot \theta ^2}(M\underline { - D} )B - 2\dot \theta M\mathop A\limits^. - {K_2}B $
|
(45)
|
|
$ {K_1} = ES{\int_0^L \Phi ^\prime }^{\rm{T}}{\Phi ^\prime }dx $
|
(46)
|
|
$ {K_2} = ES{\int_0^L \Phi ^{\prime \prime }}^{\rm{T}}{\Phi ^{\prime \prime }}dx $
|
(47)
|
以上各式中${ S}$,${ M}$,${ D}$,${ K}_1 $和${ K}_2 $为常系数矩阵,带下划线的项是附加耦合项,由考虑横向变形引起的纵向缩短而产生.
为了分析柔性旋转悬臂梁的横向弯曲振动,假定大范围转动为匀速,即$\ddot {\theta } = 0$,并忽略梁的纵向振动效应. 则其横向弯曲振动方程可表示为
|
$ {M_{33}}\ddot B + [{\dot \theta ^2}(D - {M_{33}}) + {K_2}]B = {\bf{0}} $
|
(48)
|
式中,${ M}_{ 33 } $是动力柔化项,${ D}$是由于考虑了横向弯曲引起的纵向缩短量$w_c $产生的,称为动力刚化阵,整体上${ D}-{ M}_{33} $产生动力刚化效应,而${ K}_2 $则是结构动力学中的静刚度阵.
对式(48)进行无量纲化处理,引入下列无量纲变量
|
$ \varsigma = t/T{\mkern 1mu} ,\;\xi = x{\rm{ / }}L{\mkern 1mu} ,{\rm{ }}{\kappa _2} = B/L{\mkern 1mu} ,\;\gamma = T\dot \theta $
|
(49)
|
其中,$T = (\rho SL^4/EI )^{1/2}$.
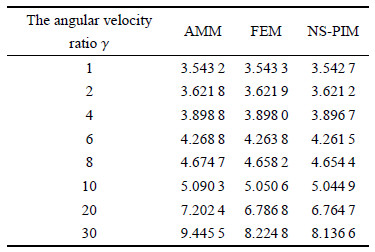
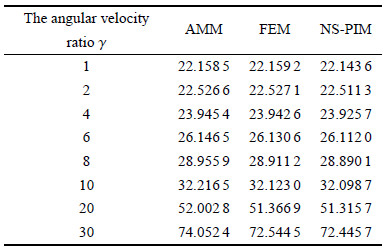
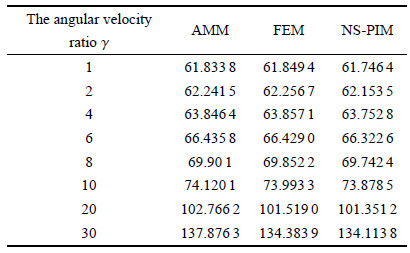
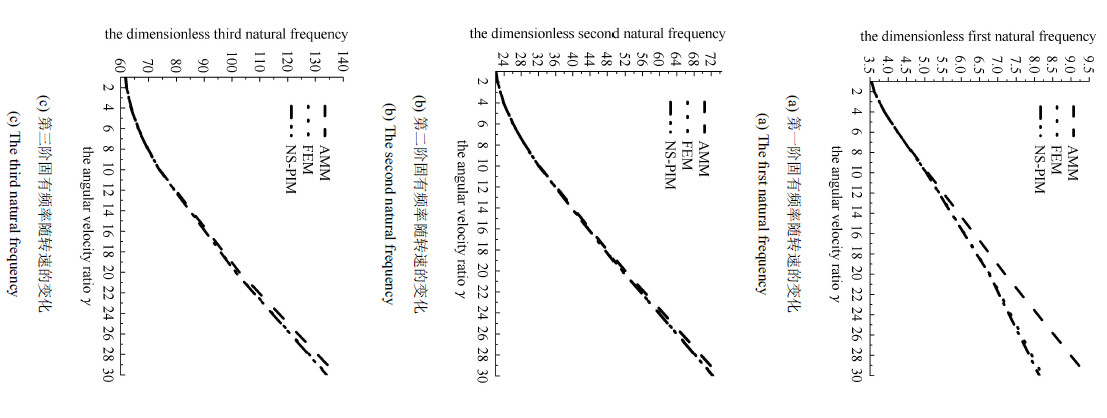
表2 $\sim $表4为柔性梁匀速旋转时,3种离散方法所得的横向弯曲无量纲前三阶固有频率. 假设模态法取3阶模态、有限元法离散 为10个单元、光滑节点插值法取81个节点. 从表中可以看出,3种离散方法的前三阶固有频率都随着转动速度的增大而增大,但假设模态法的精度逐渐变低且增大趋势最快,因此并 不适用于高速转动情形;而光滑节点插值法与有限元法的结果在不同转速下基本一致,说明该方法的正确性及比假设模态法更广 的适用性. 同时发现,光滑节点插值法的结果总是比有限元法的小,说明该方法提供固有频率的下界值,而有限元法提供固有频率的上界值. 图7为3种离散方法前三阶固有频率在不同转速下的对比图,从图中可更明显地看出随着转速的增大,假设模态法与有限元法和 光滑节点插 值法的误差越来越大. 对于没有解析解的柔性旋转悬臂梁系统,可通过有限元法提供的上界值和光滑节点插值法提供的下界值,取中间值来最大 程度地逼近真实 解,使数值结果精度更高.
表 2(Table 2)

表 2 柔性梁在不同转速下3种离散方法横向弯曲无量纲第一阶固有频率比较Table 2 The dimensionless first natural frequency with different rotation speed of three discrete methods
|
表 2 柔性梁在不同转速下3种离散方法横向弯曲无量纲第一阶固有频率比较
Table 2 The dimensionless first natural frequency with different rotation speed of three discrete methods |
表 3(Table 3)

表 3 柔性梁在不同转速下3种离散方法横向弯曲无量纲第二阶固有频率比较Table 3 The dimensionless second natural frequency with different rotation speed of three discrete methods
|
表 3 柔性梁在不同转速下3种离散方法横向弯曲无量纲第二阶固有频率比较
Table 3 The dimensionless second natural frequency with different rotation speed of three discrete methods |
表 4(Table 4)

表 4 柔性梁在不同转速下3种离散方法横向弯曲无量纲第三阶固有频率比较Table 4 The dimensionless third natural frequency with different rotation speed of three discrete methods
|
表 4 柔性梁在不同转速下3种离散方法横向弯曲无量纲第三阶固有频率比较
Table 4 The dimensionless third natural frequency with different rotation speed of three discrete methods |
3 结 论
(1)光滑节点插值法通过光滑梯度处理,可降低形函数对连续性的要求. 对于4阶微分方程,使用简单的线性插值即可. 相对有限元,该方法结构更简单,且在同等离散条件下自由度数减少一半.
(2)光滑节点插值法虽使用线性插值,但仍有很高的精度,且能提供应变能的上界值. 假设模态法提供应变能的下界值,进一步研 究发现,通常认为的模态阶数取的越多结果越精确的说法并不成立,当模态阶数大于9时结果将发散. 对于欧拉-伯努利梁取3$\sim $6阶模态即可.
(3)在频率分析中,通过与解析解的对比,发现光滑节点插值法的重要特性:能提供固有频率的下界值,而有限元法和假设模态 法只能提供固有频率的上界值. 在柔性旋转悬臂梁系统中,随着转速的增大,假设模态法有发散的趋势,已不适用. 对于如柔性旋转梁等不能求解析解的问题,有限元法结合光滑节点插值法可以从固有频率的上下界最大程度地逼近真实解,从而达 到提高精度的目的,在柔性多体系统动力学中具有重要的应用价值.
参考文献
| [1] |
洪嘉振,尤超蓝. 刚柔耦合系统动力学研究进展. 动力学与控制学报,2004,2(2):1-6(Hong Jiazhen, You Chaolan. Advances in dynamics of rigid-flexible coupling system. Journal of Dynamics and Control, 2004, 2(2):1-6 (in Chinese))
|
| [2] |
Dwivedy SK, Eberhard P. Dynamic analysis of flexible manipulators, a literature review. Mechanism and Machine Theory , 2006, 41(7): 749-777
|
| [3] |
Yoo HH, Ryan RR, Scott RA. Dynamics of flexible beams undergoing overall motions. Journal of Sound and Vibration, 1995, 181(2): 261-278
|
| [4] |
陈思佳,章定国,洪嘉振. 大变形旋转柔性梁的一种高次刚柔耦合动力学模型. 力学学报,2013, 45(2): 251-256 (Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 251-256 (in Chinese))
|
| [5] |
Yoo HH, Shin SH. Vibration analysis of rotating cantilever beams. Journal of Sound and Vibration, 1998, 212(5): 807-828
|
| [6] |
Chung J, Yoo HH. Dynamic analysis of a rotating cantilever beam by using the finite element method. Journal of Sound and Vibration, 2002, 249(1): 147-164
|
| [7] |
Du H, Lim MK, Liew KM. A nonlinear finite element model for dynamics of flexible manipulators. Mech Mach Theory, 1996, 31(8): 1109-1119
|
| [8] |
张雄,刘岩. 无网格法. 北京:清华大学出版社,2004:1-6 (Zhang Xiong, Liu Yan. Meshless Method. Beijing: Tsinghua University Press, 2004: 1-6 (in Chinese))
|
| [9] |
刘桂荣,顾元通.无网格法理论及程序设计. 济南:山东大学出版社,2007:45-133 (Liu Guirong, Gu Yuantong. An Introduction to Meshfree Methods and Their Programming. Shandong: Shandong University Press, 2007: 45-133 (in Chinese))
|
| [10] |
Sanborn GG, Shanana AA. On the integration of computer aided design and analysis using the finite element absolute nodal coordinate formulation. Multibody Syst Dyn , 2009, 22: 181-197
|
| [11] |
Sanborn GG, Shanana AA. A rational finite element method based on the absolute nodal coordinate formulation. Nonlinear Dyn , 2009, 58: 565-572
|
| [12] |
Sugiyama H, Gerstmayr J, Shabana AA. Deformation modes in the finite element absolute nodal coordinate formulation. Journal of Sound and Vibration, 2006, 298: 1129-1149
|
| [13] |
Lan P, Shabana AA. Integration of B-spline geometry and ANCF finite element analysis. Nonlinear Dyn, 2010, 61: 193-206
|
| [14] |
Liu YN, Sun L, Liu YH, et al. Multi-scale B-spline method for 2-D elastic problems. Applied Mathematical Modelling, 2011, 35: 3685-3697
|
| [15] |
范纪华,章定国. 旋转柔性悬臂梁动力学的 Bezier 插值离散方法研究. 物理学报, 2014, 63(15): 154501 (Fan Jihua, Zhang Dingguo. Bezier interpolation method for the dynamics of rotating flexible cantilever beam. Acta Phys Sin , 2014, 63(15): 154501 (in Chinese))
|
| [16] |
Liu GR, Gu YT. Assessment and applications of point interpolation methods for computational mechanics. International Journal for Numerical Methods in Engineering, 2004, 59: 1373-1397
|
| [17] |
Liu GR, Gu YT. A point interpolation method for two-dimensional solids. Int J Muner Meth Engng, 2001, 50: 937-951
|
| [18] |
Liu GR, Dai KY, Lim KM, et al. A point interpolation mesh free method for static and frequency analysis of two-dimensional piezoelectric structures. Computational Mechanics, 2002, 29(6): 510-519
|
| [19] |
Wang JG, Liu GR. A point interpolation meshless method based on radial basis functions . Int J Numer Meth Eng, 2002, 54(11) : 1623-1648.
|
| [20] |
Belytschko T, Lu YY, Gu L. Element free Galerkin methods. International Journal for Numerical Methods in Engineering , 1994, 37(2): 229-256
|
| [21] |
Cheng RJ, Cheng YM, Ge HX. Element-free Galerkin(EFG) method for a kind of two-dimensional linear hyperbolic equation. Chin Phys B, 2009, 18(10): 4059-4064
|
| [22] |
Atluri SN, Zhu T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Computational Mehcanics, 1998, 22(2): 117-127
|
| [23] |
Chen L, Liew KM. A local Petrov-Galerkin approach with moving Kriging interpolation for solving transient heat conduction problems. Comput Mech, 2011, 47: 455-467
|
| [24] |
Liu WK, Jun S, Zhang YF. Reproducing kernel particle methods. Int J Numer Meth Fluids , 1995, 20: 1081-1106
|
| [25] |
Cheng RJ, Liew KM. The reproducing kernel particle method for two-dimensional unsteady heat conduction problems. Comput Mech, 2009, 45: 1-10
|
| [26] |
Liu GR, Zhang GY, Dai KY. A linearly conforming point interpolation method (LC-PIM) for 2D solid mechanics problems. International Journal of Computational Methods, 2005, 2(4): 645-665
|
| [27] |
Liu GR, Zhang GY. Upper bound solution to elasticity problems: A unique property of the linearly conforming point interpolation method (LC-PIM). Int J Numer Meth Engng, 2008, 74: 1128-1161
|
| [28] |
Cui XY, Liu GR, Li GY, et al. A rotation free formulation for static and free vibration analysis of thin beams using gradient smoothing technique. CMES, 2008, 38(3): 217-229
|
| [29] |
杜超凡, 章定国. 基于无网格点插值法的旋转悬臂梁的动力学分析. 物理学报, 2015, 64(3): 034501 (Du Chaofan, Zhang Dingguo. A meshfree method based on point interpolation for dynamic analysis of rotating cantilever beams. Acta Phys Sin , 2015, 64(3): 034501 (in Chinese))
|
| [30] |
杜超凡, 章定国, 洪嘉振. 径向基点插值法在旋转柔性梁动力学中的应用. 力学学报, 2015, 47(2): 279-288 (Du Chaofan, Zhang Dingguo, Hong Jiazhen. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 279-288 (in Chinese))
|
| [31] |
Liu GR. Meshfree Methods: Moving Beyond the Finite Element Method. USA: CRC Press, 2002: 456-458
|
NODE-BASED SMOOTHED POINT INTERPOLATION METHOD: A NEW METHOD FOR COMPUTING LOWER BOUND OF NATURAL FREQUENCY
Du Chaofan, Zhang Dingguo
School of Sciences, Nanjing University of Science and Technology, Nanjing 210094, China
Fund: The project was supported by the National Natural Science Foundation of China (11272155, 11132007), the 333 Project of Jiangsu Province, China
(BRA2011172), and the Fundamental Research Funds for the Central Universities of China (30920130112009).
Abstract: A meshfree method called node-based smoothed point interpolation method (NS-PIM) is proposed for static analysis of cantilever beam and dynamic analysis of rotating flexible beam for the first time. Gradient smoothing technique is utilized to perform the numerical integration required in the weakened weak (W2) form formulation. The shape functions are approximated using linear interpolation functions, which can be used to solve the 4th order differential equation. In static problems, the cantilever beams with two loading conditions are analyzed, and the results are compared with the analytic solution, which shows a high accuracy of this method even if using linear shape functions. A further study shows that if more than 9 modes were used in the assumed mode method, the result will be divergent. In dynamic problem, the natural frequencies of a rotating flexible beam are analyzed. Simulation results of the NS-PIM are compared with those obtained using finite element method (FEM) and assumed modes method (AMM). It is found that NS-PIM can provide unique lower bounds of natural frequencies, while FEM and AMM can provide upper bounds of natural frequencies. That means we can get more accurate results for the problems by using FEM and NS-PIM in case that exact solution can't be obtained. The NS-PIM has easier shape functions and less independent variable than FEM, and can provide lower bounds of natural frequencies, with a great value of application and dissemination.
Key words:
flexible beam node-based smoothed point interpolation method meshfree method dynamics lower bound of natural frequency


 2015, Vol. 47
2015, Vol. 47