2. 北京应用物理与计算数学研究所, 北京100094
数值模拟中经常需要选择有限的范围作为计算区域,应用无反射边界条件来求解相对无限范围内的力学问题. 在对非稳态问题进行数 值模拟时无法使用周期边界条件,也不能像模拟稳态问题一样引入较强的数值耗散消除边界条件的影响,因而边界条件的处理精度往往 会严重影响到非稳态问题的最终模拟结果,这要求在计算区域边界上产生尽可能小的非物理反射[1].
要精确地建立无反射等类型的边界条件只对某些简单的特定方程是可行的[2],对欧拉方程可以精确构造出保证适定性的边界条 件,在构造纳维-斯托克斯(Navier-Stokes)方程边界条件方法中则要复杂得多. 实际使用中给出的纳维-斯托克斯方程各种边界条件的不同形式都无法完全保证原始纳维-斯托克斯方程 的适定性,并且求解纳维-斯托克斯方程时只有在一些简单算例中才能够评估采用的边界条件的适定性,因此采用数值 方法建立的无反射数值边界一般也无法完全消除非物理反射波,但只要满足一定的需要就仍会得到发展应用[1]. 从1960年代以来,形成了许多形式的边界条件方法[3],其中边界积分法[4]、无限元法[5]、吸收层法[6]和特 征线方法是最常被使用的4种方法,自20世纪90年代中期发展起来的高精度无反射边界条件更是能够得到很高的精度效果[2]. 但好的边界条件方法不仅要精度高,还要计算快、稳定和易实现,即使能达到很高的精度,较苛刻的使用条件、大的计算量、实现的 复杂性以及较窄的使用范围仍会限制方法的广泛应用[7]. 反观非线性一维特征线边界条件方法,虽然在使用中会产生较强的非物理反射波,但凭其简单、健壮的特点,现仍被广泛应用于可压 缩流的数值模拟中[3].
恩奎斯特和马伊达 [8, 9]建立了线性系统特征边界条件的理论基础,赫德斯特伦[10]基于一维非线性特征方法将特征 边界条件应用到一维非线性系统,进而由汤普森[11, 12]将一维无黏假定推广到高维欧拉方程的计算,波因索特和乐乐$^{ [13]又进一步用到纳维-斯托克斯方程中,形成了有名的纳维-斯托克斯特征边界条件并 应用到很多实际计算中[14, 15],马丁等[16]将特征无反射边界条件应用到光滑粒子法计算中,对准一维喷管和二维 圆柱绕流进行了数值模拟.} 还有众多学者对该方法进行了应用和改 进[17, 18, 19, 20, 21, 22, 23, 24],但都无法超出一维无黏假定的内在限 制[3]. 国内有学者在气动声学、水下爆炸以及岩土力学中对无反射边界条件进行了较为广泛的应用研 究[25, 26, 27]. 居鸿宾等[28]运用特征分析和事后修正法对汤普森[11]和贾尔斯[29]无反射边界进行了分析,将无反射边界以统一的形式表达出来,并得到这类边界的事后修正式. 王存诚等[30]在贾尔斯理论[29]的基础上,提出一种与时间推进法相匹配的,适用于多级流场计算的无反射边界条件,并从物理本质上解释了它的含义. 王泽晖等[31]论述了无反射边界条件的发展历程及在气动声学数值计算中的关键作用. 陈荣钱等[32]采用特征无反射边界条件和吸收层技术相结合的边界处理方法,在二维圆柱绕流模拟中得到了很好的模拟结果. 李德波等[33, 34]对面特征无反射边界条件和其中的角点问题进行了细致的研究,提出新的数学处理方法,并在可压缩圆孔射流数值模拟中得到了与实验吻合较好的模拟结果. 王子辉等[27]根据波在传播中的幅值变化规律构造流体饱和多孔介质黏弹性动力人工边界,具有较好的精度和稳定性. 刘晓等[35]根据无反射边界条件的物理思想,利用最小二乘法提出的一种高阶的光滑拟合外推边界格式,可以同时用在内点和边界点上,使边界格式在应用到大气波动传播问题时更为简便并得到了较好的无反射效果.
本文通过传播理论估计波幅值变化,将使用时间插值的特征方法应用到拉氏边界中,形成了一种新型的基于特征线方法的移动边界条件方法,给出了新方法在光滑粒子法无反射边界条件中的应用形式,进行了数值验证.
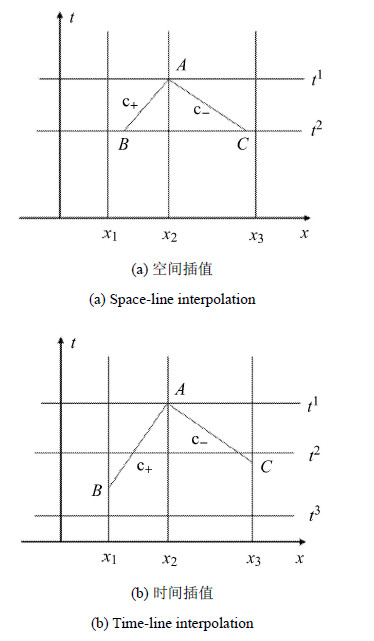
1 边界条件中的特征线方法 1.1 特征线方法在应用特征线方法时一般可以分为两类:图1(a)中的空间插值和图1 (b)的时间插值[35]. 在空间插值方法中,取固定的时 间长度($t^{1}-t^{2})$,则到达$A$点的$c_{ + }$和$c_{-}$特征线与$t^{2}$时间轴的交点$B$和$C$一般并不在已知点上,需要由已知点$x_{1}$,$x_{2}$,$x_{3}$在$t^{2}$时间轴上进行空间插值得到$B$,$C$点的状态. 若取固定的距离($x_{2}-x_{1})$和($x_{3}-x_{2})$,如图1(b)所示,则$c_{ + }$特征线与$x = x_1 $的交点$B$和$c_{ - }$特征线与$x = x_3 $的交点$C$一般也不在已知的时间点上,则需要用$x = x_1 $处已知时刻的数值进行时间插值得到$B$点的状态,用$x = x_3 $处的数值进行时间插值得到$C$点状态.
|
图 1 特征线方法 Fig.1 Characteristics method |
在进行内部计算时,两种方法都是稳定的并各具优缺点,空间插值方法具有天然的数值阻尼和耗散[36],时间插值方法有更 高的精度[37],但实现上相对要复杂一些并需要更多的内存量. 构造边界条件区信息时,空间插值要进行单边外插,精度下降,依靠内部信息的空间插值也无法构造处于边界条件区的拐点以及奇点信息. 而时间插值与进行内部计算时没有区别,因为进行了时间历程记录,具有了天然的高时间精度,能够分辨位于边界条件区的拐点 和奇点,在构造边界条件时比空间插值更加适合.
1.3 边界上的特征线构造欧拉边界条件时,物质会穿过边界,因为计算区域内和边界外物质的计算方法不同,所以要判断流动方向以决定物质是由边 界外进入计算区域的入流条件还是穿过边界离开计算区域的出流条件. 使用特征线方法时,3种特征波的传播速度分别为$u + c$,$u$和$u- c$,则要区分亚声速和超声速的不同以决定边界外区域不同族特征线的取值. 比如对亚声速出流条件,计算区域内的c$_{-}$特征波的传播速度$ u- c < 0$,因而不会影响到边界外,则在无反射边界条件中,边界外区域与c$_{ - }$特征波相对应的特征值应该取0,而对超声速出流条件有$ u-c > 0$,c$_{-}$特征波也能够传播到边界外,则其c$_{ - }$特征值也该由计算区域内的c$_{ - }$特征值朝边界外进行插值得到[38] (见图2).

|
图 2 欧拉场中的特征线 Fig.2 Characteristics lines in Euler flow |
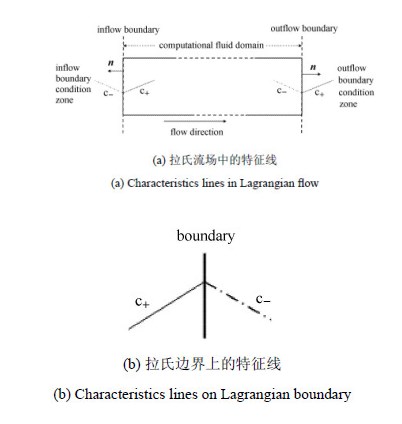
构造拉氏边界则要简单地多,如图3所示,因为边界以物质速度$u$进行移动,特征波的拉氏传播速度为$c$,$0$和$ - c$. 在图3 (b) 拉氏边界上,亚声速和超声速下都没有物质通过界面,到达拉氏边界上特征波的传播速度都分别为$c$和$ - c$,则只需要区分边界外和计算域内的不同,来自边界外的特征线由来流或出流条件决定,来自计算域内的特征线则需要根据 图4的特征线法求得.
|
图 3 拉氏框架下的特征线 Fig.3 Characteristics lines in Lagrangian system of coordinates |
|
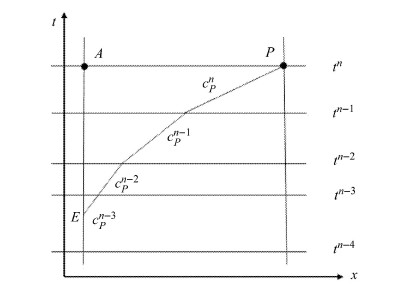
图 4 拉氏边界上的时间插值特征线法 Fig.4 Time-line interpolation method of characteristics on Lagrangian boundary |
如图4所示,从计算区域内位置$A$传出的特征波在每个时间步中都是以当地声速朝边界外传播并在$t^n$时刻到达边界外$P$点,据此计算该特征线与$x = A$空间轴的交点$E$的时刻,再在$x = A$的空间轴上进行时间插值得到$E$点状态.
2 采用特征线法的拉氏边界条件 2.1 拉氏中的特征传播公式假设一维小扰动特征波携带的脉动量$\varepsilon $在传播过程中幅值不变,也就是$\varepsilon $从$E$点沿特征线到达$P$点 时仍为$\varepsilon $,假定$x=A$处在$t_0 - \Delta t'$时刻的扰动经过时间$\Delta t'$到达$P$点,$t - \Delta t$时刻的扰动经过时间$\Delta t$到达$P$点,则在积分情况下有
| $ \int_{{t_0}}^t {{\varepsilon _P}} dt = {\rm{ }}\int_{{t_0} - \Delta t'}^{t - \Delta t} {{\varepsilon _A}} dt = {\rm{ }}\int_{{t_0}}^{t - \Delta t} {{\varepsilon _A}} dt + {\rm{ }}\int_{{t_0} - \Delta t'}^{{t_0}} {{\varepsilon _A}} dt $ | (1) |
数值上有
| $ \psi _P^t - \psi _P^{{t_0}} = {\rm{ }}\int_{{t_0}}^t {{\varepsilon _P}} dt = {\rm{ }}\int_{{t_0} - \Delta t'}^{t - \Delta t} {{\varepsilon _A}} dt = \psi _A^{t - \Delta t} - \psi _A^{{t_0} - \Delta t'} $ | (2) |
| $ \psi _P^t = \psi _A^{t - \Delta t} - \psi _A^{{t_0} - \Delta t'} + \psi _P^{{t_0}}{\rm{ }} $ | (3) |
$\psi _A^{t - \Delta t}$ 和$\psi _A^{t_0 - \Delta t'}$ 分别是 $x = A$空间轴上$t$时刻和$t_0$ 时刻处所对应的状态.
在$(t_0 - \Delta t',t_0 )$时间范围内无脉动也就是$\varepsilon _A = 0$的情况下$\int_{{t_0} - \Delta t'}^{{t_0}} {{\varepsilon _A}{\rm{ }}} dt = 0$,则
| $ \int_{{t_0}}^t {{\varepsilon _P}} dt = {\rm{ }}\int_{{t_0}}^{t - \Delta t} {{\varepsilon _A}} {\rm{d}}t $ | (4) |
| $ \psi _P^t - \psi _P^{{t_0}} = \int_{{t_0}}^t {{\varepsilon _P}} dt = \int_{{t_0}}^{t - \Delta t} {{\varepsilon _A}} dt = \psi _A^{t - \Delta t} - \psi _A^{{t_0}} $ | (5) |
| $ \psi _P^t = \psi _A^{t - \Delta t} + (\psi _P^{{t_0}} - \psi _A^{{t_0}}){\rm{ }} $ | (6) |
记录$A$点状态的时间历程,根据 式(3)和式(6)就得到了边界外$P$点的状态. 并且 式(3)和式(6)对激波也是成立的.
对于激波,假定在欧拉坐标下的传播速度为$D$,则在图4中使用的传播速度应为$D-v$,比如$t^{n - 1}$到$t^n$之间使用的扰动 传播速度数值上不再是$c_P^n $,而是距离使用$P$点对应时刻$ A - P $时的左传速度$- D -v_A^n $或者距离使用$E$点对应时刻$ P-A $时的右传速度$D -v_P^n $.
计算中可以使用物理量的变化比如$\Delta p$作为判据,$p_P^n > \alpha p_P^{n - 1} $时可以认为激波到达了$P$点则采用激波公式,否则则采用小扰动公式,其中$\alpha $为大于0的系数.
2.2 拉氏边界条件在光滑粒子方法中的应用本文使用的光滑粒子 方法详见文献[39],使用的粒子化后的控制方程为
| ${m_j}v_{ij}^\beta $ | (7) |
| $ \$ \frac{{dv_i^\alpha }}{{dt}} = - {\rm{ }}\sum\limits_{j = 1}^N {{m_j}} {\mkern 1mu} (\frac{{{p_i}}}{{\rho _i^2}} + \frac{{{p_j}}}{{\rho _j^2}}{\mkern 1mu} )\frac{{\partial {W_{ij}}}}{{\partial x_i^\alpha }} $ | (8) |
| $ \frac{{d{e_i}}}{{dt}} = \frac{1}{2}\sum\limits_{j = 1}^N {{m_j}} (\frac{{{p_i}}}{{\rho _i^2}} + \frac{{{p_j}}}{{\rho _j^2}}{\mkern 1mu} )v_{ij}^\beta \frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}{\rm{ }} $ | (9) |
式中,$\rho $为密度,$m$为粒子质量,$v$为粒子速度,$p$为静水压,$e$为单位质量的内能,$W$为光滑函数.
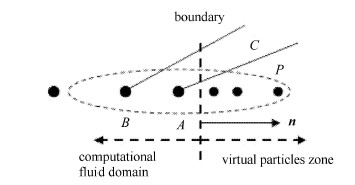
如图5所示,在一维光滑粒子法方法中采用设置虚粒子的方法建立拉氏边界条件时,到达虚粒子$P$的左传特征波来自于粒子右方的 边界条件区域,右传特征波则来自于计算区域内部. 来自边界条件区域的特征波状态由边界条件类型(如出流、入流条件)决定,如果是无波形输入的平稳来流或出流条件则左传特征波 扰动为0,若是其他边界条件类型则需要作相应的处理. 在到达$P$的右传特征波中,所有计算区域粒子中$A$点传出的特征波最先到达,则在构造$P$点状态时只使用$A$点状态,使图中 的$A$和$P$点分别与图4中的$A$和$P$点相对应. 特征传播公式中的脉动量可以简单选择为密度、压力和速度. 虚粒子的位置根据与计算区域粒子相同的公式计算得到,虚粒子光滑长度的更新使用公式$\Big(\dfrac{h}{h_0 }\Big)^d = \dfrac{\rho _0 }{\rho }$,其中$d$为维数.
|
图 5 使用特征线法计算光滑粒子法中的虚粒子状态 Fig.5 Get SPH virtual particles' state by method of characteristics |
本文中对激波管、炸药爆轰和水下爆炸的一维问题进行了数值模拟,计算中对图4的计算过程进行了简化,取$(c_p^n + c_p^{n - i} ) / 2$作为$t^{n - i}\sim t^n$间的平均声速,计算激波公式时同样取平均速度$D - (v_p^n + v_p^{n - i} ) / 2$.
3.1 一维激波管初始状态$(\rho ,u,p)_{\rm L} = (0.25$,0.0,0.179\,5),$(\rho ,u,p)_{\rm R} = (1.0$,0.0,1.0) 的一维激波管问题,精确解包含了一个左传激波、接触间断和右传稀疏波. 在光滑粒子法初始离散中接触间断位 于$x = 0$位置,取相同的粒子间距1.875$\times $10$^{-3}$,计算中使用固定时间步长$ t = 5\times 10^{-4}$
.在两侧设置无反射边界条件时,最靠近右边界的粒子标记为$A$,最靠近左侧边界的粒子为$B$,其初始坐 标$A = 0.5071875 $,$B = - 0.5071875 $,不设置边界条件则取足够大的计算区域.
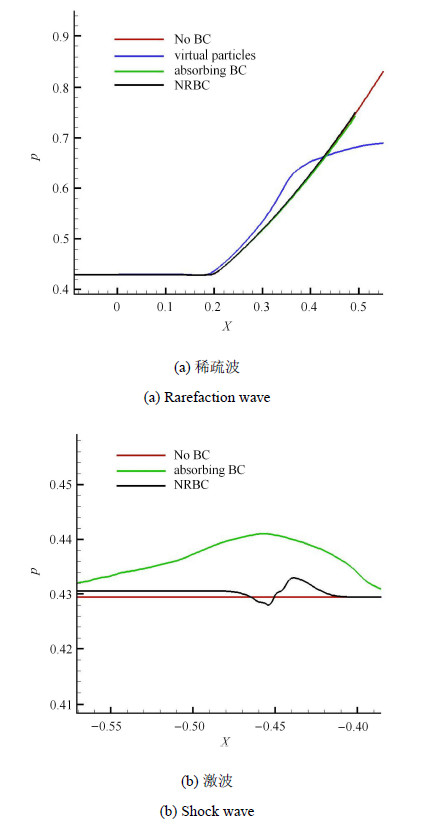
图6中显示了运算1100个时间步时稀疏波区和激波区的压力分布,包括无边界条件、采用虚粒子法、吸收层形式边界 条件[40]和本文的方法,虚粒子法无法在激波状况下使用因而在激波区没有应用. 虚粒子法计算效率高,但从计算结果看精度偏低. 吸收层边界条件法需要空间上较宽的吸收层(本文中使用了30个光滑粒子法粒子宽度),并且吸收层区域也要进行计算,而本 文方法需要记录边界点在计算时刻之前时间序列的状态,并计算特征波的传播历程,因而这两种方法都需要一定的额外存储 空间,计算效率上比较相近且比虚粒子法低,但在稀疏波区都能得到较高的精度. 在激波区的计算中可以看到,本文方法能得到更稳定的波后状态并具有更低的误差. 但本文方法需要较精确的激波速度,而吸收层法则不需要额外的波系信息.
|
图 6 一维激波管问题中的无反射边界条件 Fig.6 Non-reflection boundary conditions of one-dimensional shock wave tube |
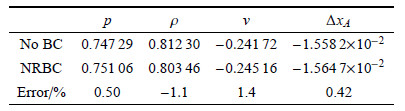
表1和表2中分别给出了边界点$A$和$B$在无边界条件和使用本文方法时的状态和位移比较. 可以看到,稀疏波和激波在通过本文的 拉氏边界时误差都较小. 只是激波在边界上会形成一个非物理反射波,在此算例中,其压力扰动、密度扰动和速度扰动幅值都不到当地状态量的2%,但有大约70个粒子宽度.
| 表 1 边界点$A$的状态和移动距离 Table 1 State and displacement of boundary point $A$ |
| 表 2 边界点$B$的状态和移动距离 Table 2 State and displacement of boundary point $B$ |
图7中时间步长取原来的1/3时非物理反射波的幅值变小了. 时间步长取1/3,同时初始粒子间距取原来的1/3时,结果与只缩小时 间步长相比非物理反射波的幅值基本不变,但宽度减小了,说明方法中非物理反射波的幅值和影响宽度可以通过缩小时间和空 间步长的方法得到控制.

|
图 7 缩小时间步长和空间步长使扰动变小 Fig.7 Amplitude and range of spurious reflection are decreased when time step and space step is reduced |
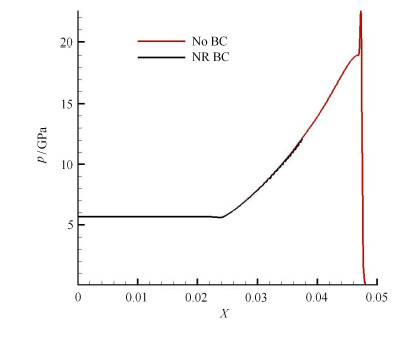
将无反射拉氏边界条件应用到一维``TNT''板条的爆轰计算过程,炸药用``JWL''状态方程,$D_{CJ} = 6\,930$m/s,$p_{CJ} = 21$\,GPa,计算中$t = 0$时从0点开始采用一点起爆,起爆方式使用时间起爆. 初始粒子间距取$10^{ - 4}$m,在$x = 0.035$m处设置无反射边界条件,取固定时间步长$d t = 3.607\,5$\,ns,计算1900步.
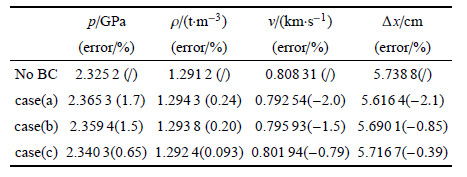
从图8和表3可以看到,爆轰波经过无反射边界条件时产生的误差也较小.
|
图 8 爆轰波通过拉氏无反射边界条件 Fig.8 Detonation wave passes the NRBC in Lagrangian system of coordinates |
| 表 3 边界点的状态和移动距离 Table 3 State and displacement of boundary point |
对宽度为0.1m的一维``TNT''炸药的爆轰波在水中传播过程进行了数值模拟,``TNT''炸药使用与算例3.2中相同的状 态方程,水使用多项式状态方 程[39]. 炸药和水取相同的初始粒子宽度$2.5\times 10^{ - 4}$m,计算中取固定时间步长$d t = 9.018\,8$\,ns.
分别计算了(a)在0.15m处设置边界条件,(b)在0.2m处设置边界条件,(c) 计算时间步$n=0$时不设置边界条件,从$n = 3500$开始在0.15m处设置边界条件3种情况. 在计算8000步时的计算结果与不设置边界条件的结果如图9所示.
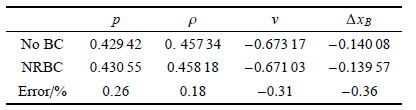
从图中可以看到,直接设置边界条件的方法会产生非物理反射波,计算8000步时,(a)算例的反射波波峰在0.05m附近,(b)算例的反射波波峰在0.115m附近,(c)算例没有明显的非物理反射波,这是因为(c)算例在$n = 3500$时才开始在0.15m设置边界条件,此时水中冲击波已经到达了0.185m附近,0.15m处已经属于波后. 图9中$A$和$B$附近状态的比较如表4和表5所示.

|
图 9 压力曲线 Fig.9 Pressure curve |
| 表 4 爆炸产物中$A$位置状态 Table 4 State and displacement of $A$ in detonation production |
| 表 5 水中$B$位置状态 Table 5 State and displacement of $B$ in water |
从表4、表5的结果可以看到,(a)、(b)算例中在左传非物理反射波波后区域中也能够得到较好的结果,而在激波波后设置边界条 件的(c)算例则不会产生明显的非物理反射波,效果最好.
图10记录了(a)和(b)算例非物理反射波传播过程中压力峰值的变化情况,在向计算区域内部传播的过程中,非物理反射波峰值比 例在当地也是衰减的,因而不会对计算区域内的结果产生颠覆性的影响. 在0.2m处设置无反射边界条件比在0.15m处设置引起的非物理反射的扰动强度要小,这是因为冲击波在水中传播时是衰减的,到达较远的边界时幅值变小,产生了更弱的非物理反射波.

|
图 10 非物理反射波的扰动变化 Fig.10 Evolvement of spurious reflection wave |
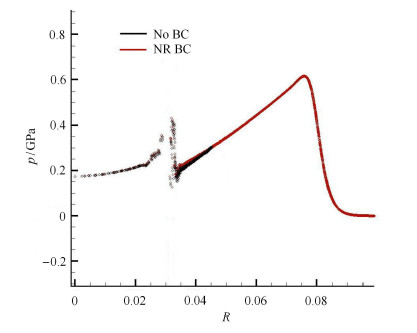
对中心起爆的二维水下爆炸进行了数值模拟,状态方程、粒子间距等都与算例3.3相同,根据传播理论,计算中假定脉动量按照$1 / \sqrt R $ 的规律变化. 无边界条件和采用拉氏边界条件的压力分布如图11所示,在计算结果中,两种状态的压力相差不超过5%.
|
图 11 二维水下爆炸压力分布 Fig.11 Pressure field in 2D underwater explosion |
基于特征线法决定特征波的传播速度,根据传播理论预计扰动的传播规律,在拉氏框架下构造了一种新的边界条件构造方法. 将采用 无反射形式的新方法应用到光滑粒子法中对激波管、炸药爆轰和水下爆炸问题进行了数值模拟,得到如下结论:
(1) 在使用特征线法构造边界条件时,时间插值方法能够保持计算域内和边界格式的一致性,并且能够构造出边界区的奇点信息,因而 比空间插值方法更加适合于在构造边界条件时进行应用.
(2) 在拉氏框架下应用特征线法构造边界条件时,不需要区分亚声速和超声速的不同,在出流和入流的不同条件下有相同的形式,因而比欧拉框架下更加简洁易行.
(3) 本文构造的方法不仅可以应用到稀疏波,在冲击波波和爆轰波的模拟中也能够得到较好的数值结果.
本文进行了采用特征线形式拉氏边界条件构造方法的论述,并将使用无反射边界条件的新方法在光滑粒子法数值模拟中进行了验证,取得的较好结果显示了方法的有效性.
| [1] | Poinsot T, Veynante D. Theoretical and Numerical Combustion. 2nd ed. France: Edwards, 2005: 431-447 |
| [2] | Givoli D. High-order local non-reflecting boundary conditions: a review. Wave Motion, 2004, 39: 319-326 |
| [3] | Liu QL, Vasilyev OV. Nonreflecting boundary conditions based on nonlinear multidimensional characteristics. International Journal for Numerical Methods in Fluids, 2010, 62: 24-55 |
| [4] | Rizzo FJ. The boundary element method - some early history : a personal view. In: Beskos DE, ed. Boundary Elements in Structural Analysis, ASCE, New York, 1989: 1-16 |
| [5] | 李录贤, 国松直, 王爱琴. 无限元方法及其应用. 力学进展, 2007, 37(2): 161-174 (Li Luxian, Guo Songzhi, Wang Aiqin. The infinite element method and its application. Advances in Mechanics, 2007, 37(2): 161-174 (in Chinese)) |
| [6] | Hu FQ. A perfectly matched layer absorbing boundary condition for linearized Euler equations with a non-uniform mean flow. Journal of Computational Physics, 2005, 208: 469-492 |
| [7] | Dea JR. High-order non-reflecting boundary conditions for the linearized Euler equations.[PhD Thesis]. Monterey, California: NAVAL Postgraduate School, 2008: 1-36 |
| [8] | Engquist B, Majda A. Absorbing boundary conditions for numerical simulation of waves. Mathematics of Computation, 1977, 31: 629-651 |
| [9] | Engquist B, Majda A. Radiation boundary conditions for acoustic and elastic wave calculations. Communications on Pure and Applied Mathematics, 1979, 32: 313-357 |
| [10] | Hedstrom GW. Nonreflecting boundary conditions for nonlinear hyperbolic systems. Journal of Computational Physics, 1979, 30: 222-237 |
| [11] | Thompson KW. Time-dependent boundary conditions for hyperbolic systems. Journal of Computational Physics, 1987, 68: 1-24 |
| [12] | Thompson KW. Time-dependent boundary conditions for hyperbolic systems II. Journal of Computational Physics, 1990, 89: 439-461 |
| [13] | Poinsot T, Lele S. Boundary conditions for direct simulations of compressible viscous flows. Journal of Computational Physics, 1992, 101: 104-129 |
| [14] | Moureau V, Lartigue G, Sommerer Y, et al. Numerical methods for unsteady compressible multi-component reacting flows on fixed and moving grids. Journal of Computational Physics, 2005, 202: 710-736 |
| [15] | Okong'o N, Bellan J. Consistent boundary conditions for multicomponent real gas mixtures based on characteristic waves. Journal of Computational Physics, 2002, 176: 330-344 |
| [16] | Lastiwka M, Basa M, Quinlan N J. Permeable and non-reflecting boundary conditions in SPH. International Journal for Numerical Methods in Fluids, 2009, 61(7): 709-724 |
| [17] | Nicoud F. Defining wave amplitude in characteristic boundary conditions. Journal of Computational Physics, 1999, 149: 418-422 |
| [18] | Prosser R. Improved boundary conditions for the direct numerical simulation of turbulent subsonic flows, I, inviscid flows. Journal of Computational Physics, 2005, 207: 736-768 |
| [19] | Prosser R. Toward improved boundary conditions for the dns and les of turbulent subsonic flows . Journal of Computational Physics, 2007, 222: 469-474 |
| [20] | Yoo CS, Wang Y, Trouve A, et al. Characteristic boundary conditions for direct simulations of turbulent counterflow flames. Combustion Theory and Modelling, 2005, 9: 617-646 |
| [21] | Yoo CS, Im HG. Characteristic boundary conditions for simulations of compressible reacting flows with multidimensional, viscous and reaction effects. Combustion Theory and Modelling, 2007, 11: 259-286 |
| [22] | Atassi OV, Galan JM. Implementation of nonreflecting boundary conditions for the nonlinear Euler equations. Journal of Computational Physics, 2008, 227(3): 1643-1662 |
| [23] | Morinigo JA, Salva JJ. Robust non-reflecting boundary conditions for the simulation of rocket nozzle flow. Aerospace Science and Technology, 2010, 4: 429-441 |
| [24] | Dorodnicyn LV. Nonreflecting boundary conditions and numerical simulation of external flows. Computational Mathematics and Mathematical Physics, 2011, 51(1): 143-159 |
| [25] | 王巍, 赵晓路. 使用非定常无反射边界条件模拟上游尾迹/叶片排干扰问题. 工程热物理学报,1997, 18(6): 689-694 (Wang Wei, Zhao Xiaolu. Numerical simulation of interaction between upstream wakes and blade row using unsteady non-reflecting boundary conditions. Journal of Engineering Thermophysics, 1997, 18(6): 689-694 (in Chinese)) |
| [26] | 师华强, 汪玉, 宗智 等. 近水面水下爆炸二维Level-set数值模拟.计算力学学报,2010, 27(3): 409-414 (Shi Huaqiang, Wang Yu, Zong Zhi, et al. 2D numerical simulation of underwater explosion near free surface based on level-set method. Chinese Journal of Computational Mechanics, 2010, 27(3): 409-414 (in Chinese)) |
| [27] | 王子辉, 赵成刚, 董亮. 流体饱和多孔介质黏弹性动力人工边界. 力学学报, 2006, 38(5): 605-611 (Wang Zihui, Zhao Chenggang, Dong Liang. A viscous-spring dynamical artificial boundary for saturated porous media. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 605-611 (in Chinese)) |
| [28] | 居鸿宾, 沈孟育. 气动声学数值模拟中无反射边界处理及声源模型的建立. 上海交通大学学报, 1998, 32(7): 36-39 (Ju Hongbin, Shen Mengyu. Non-reflective boundary conditions and sound source modeling in computational aeroacoustics. Journal of Shanghai Jiaotong University, 1998, 32(7): 36-39 (in Chinese)) |
| [29] | Giles MB. Nonreflecting boundary conditions for Euler equation calculations. AIAA J, 1990, 28(2): 2050-2058 |
| [30] | 王存诚, 胡小仙. 叶轮机械计算中动静叶排间的非定常效应. 清华大学学报(自然科学版), 1998, 38(7): 70-73 (Wang Cuncheng, Hu Xiaoxian. Consideration of unsteady interactions between blading rows in steady turbomachinery flow calculations. Journal of Tsinghua University(Science and Technology), 1998, 38(7): 70-73 (in Chinese)) |
| [31] | 王泽晖, 罗柏华, 刘宇陆. 关于气动声学数值计算的方法与进展. 力学季刊, 2003, 24(2): 219-226 (Wang Zehui, Luo Baihua, Liu Yulu. Numerical methods and advances for aeroacoustics. Chinese Quarterly of Mechanics, 2003, 24(2) : 219-226 (in Chinese)) |
| [32] | 陈荣钱, 伍贻兆, 夏健. 特征无反射边界条件应用于二维圆柱绕流模拟. 航空计算技术, 2012, 42(2): 73-76 (Chen Rongqian, Wu Yizhao, Xia Jian. Characteristic non-reflecting boundary conditions applied in two-dimensional cylinder flow simulation. Aeronautical Computing Technique, 2012, 42(2): 73-76 (in Chinese)) |
| [33] | 李德波, 樊建人, 易富兴 等. 面特征无反射边界条件处理关键问题的直接数值模拟. 燃烧科学与技术, 2012, 18(5): 427-434 (Li Debo, Fan Jianren, Yi Fuxing, et al. Direct numerical simulation of characteristic non-reflecting boundary conditions in treatment of face. Journal of Combustion Science and Technology, 2012, 18(5): 427-434 (in Chinese)) |
| [34] | 李德波, 杨建山, 樊建人 等. 角点处理的特征无反射边界条件中直接数值模拟, 动力工程学报, 2013, 33(1): 31-36 (Li Debo, Yang Jianshan, Fan Jianren, et al. Treatment of corners in characteristic non-reflecting boundary conditions by direct numerical simulation. Chinese Journal of Power Engineering, 2013, 33(1): 31-36 (in Chinese)) |
| [35] | 刘晓, 徐寄遥. 大气波动传播问题的一种无反射数值边界格式. 空间科学学报, 2006, 26(2): 111-117 (Liu Xiao, Xu Jiyao. A kind of non-reflection numerical boundary scheme for the propagation of atmosphere waves. Chinese Journal of Space Science, 2006, 26(2): 111-117 (in Chinese)) |
| [36] | Mao ZY, Zhao XF. Numerical simulation of transient pressured flow by characteristics method using time-line interpolation. Science Technology and Engineering, 2007, 7(8): 1670-1674 |
| [37] | Goldberg DE, Wylie EB. Characteristics method using time-line interpolations. Journal of Hydraulic Engineering, ASCE, 1983, 109(5): 670-683 |
| [38] | Lai C. Multicomponent-flow analysis by multimode method of characteristics. Journal of Hydraulic Engineering, ASCE, 1994, 120(3): 981-987 |
| [39] | Lastiwka M, Basa M, Nathan J, et al. Permeable and non-reflecting boundary conditions in SPH. International Journal of Numerical Methods in Fluids, 2009, 61(7): 709-724 |
| [40] | Liu GR, Liu MB. 光滑粒子流体动力学------一种无网格粒子法. 韩旭, 杨刚, 强洪夫 译. 长沙: 湖南大学出版社, 2005: 104-145 (Liu GR, Liu MB. Smoothed Particle Hydrodynamics: A Meshfree Particle Method. Han Xu, Yang Gang, Qiang Hongfu, Transl. Changsha: Hunan University Press, 2005: 104-145 (in Chinese)) |
| [41] | 张伟, 李晓东. 一种渐变无反射边界条件的建立与验证. 强度与环境, 2009, 36(6): 27-35 (Zhang Wei, Li Xiaodong. Construction and validation of a gradually diminished flux nonreflecting boundary condition. Sturcture & Environment Engineering}, 2009, 36(6): 27-35 (in Chinese)) |
2. Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
 2015, Vol. 47
2015, Vol. 47