2. 中国空气动力研究与发展中心计算空气动力研究所, 绵阳621000;
3. 国防科学技术大学, 长沙410073
当标识流动稀薄程度的努森数较大时,连续性假设失效. 研究者常常通过求解玻尔兹曼模型方程来获得飞行器的气动特性. 在这一过程中,不可避免的需要对相空间进行离散,在高速流动中,相空间需要布置较多的点数才能保证计算结果的精度及可靠性. 为了降低计算量,可以减少相空间网格规模,最直接的方法就是采用网格自适应. Yu[1],Chen等[2],Arslanbekov等[3],Baranger等[4]都完成了此类方法的实现及验证. 但是相空间网格自适应的缺点是网格丧失了结构化特征,因而导致数据存储结构以及程序实现的复杂化.
实际上,对于定常问题来说,目前常用的采用非定常计算逼近定常结果的方法是非常不经济的. 因而有必要借鉴传统CFD (computational fluid dynamics)技术中常用的如LUSGS[5] (lower-upper symmetric-Gauss-Seidel)等隐式方法来加速收敛,以降低计算成本,提高计算效率. Yang等[6]在结构网格上实现了隐式求解玻尔兹曼模型方程,在求解过程中采用了近似LU分解,且对源项的雅可比矩阵进行了近似,不过没有见到隐式方法加速收敛的报道. 毕林[7]采用隐式NND (non-oscillatory and non-free-parameters dissipative)格式对模型方程进行数值离散,构造了求解二维问题的气体运动论格式,并开展了二维内流动问题气体运动论隐式格式应用研究. 王强等[8, 9]采用隐式通量修正二阶迎风总变差减小(total variation diminishing,TVD)格式差分求解模型方程,并通过超声速圆柱算例验证了算法的有效性. Titarev等[10, 11]提出了在非结构网格上的隐式方法,对模型方程源项中的生成项和消失项分别进行显式和半隐式化处理,针对有限长管道流动给出了显式和隐式方法在残差收敛方面的比较,完成了三维复杂再入外形超声速外流常的计算.
以上隐式处理都是基于直接离散求解玻尔兹曼模型方程的方法进行的. 香港科技大学徐昆[2, 12, 13, 14, 15]没有采用传统的CFD技术直接离散求解模型方程,而是采用玻尔兹曼方程的模型演化解,基于离散空间直接建模构造得到了适用于全流域流动的UGKS (unified gas kinetic scheme)方法. 到目前为止,尚未看到隐式UGKS的相关报道.
不过,在连续流域,同样基于模型方程演化解的GKS (gas kinetic scheme)方法[15, 16]的隐式处理方面已经有 研究者做了不少工作. 在超声速/高超声速流动的应用研究中,利用LUSGS方法,毛枚良等[17],Xu等[18]通过引入时间平均的通量函数,构造了隐式GKS方法. Jiang[19]采用隐式GKS方法完成了跨音速翼身组合体外形黏性流场的模拟. Li等[20]在非结构网格上对GKS进行拓展完成了无黏高温平衡流动的模拟. 江定武等[21]对隐式GKS方法中演化时间步长的选取进行了较为仔细的研究.
本文在之前隐式GKS方法研究的基础上,结合UGKS的特点,采用近似LU分解,实现了隐式UGKS算法. 通过不同来流马赫数下的圆柱算例,比较了隐式和显式方法在残差和气动力收敛等方面的表现,考察了隐式加速收敛效果. 并将圆柱和尖楔计算结果与著名的DSMC (direct simulation Monte Carlo)模拟软件DS2V[22]的计算结果进行比对,进一步考察了算法的精度和有效性.
1 UGKS方法及其隐式实现本文研究基于Shakhov模型方程,二维情形下,无量纲化以后可以写为[23]
| $ {f_t} + u{f_x} + v{f_y} = \frac{{{f^ + } - f}}{\tau } $ | (1) |
该方程修正了标准形式的BGK (Bhatnagar--Gross--Krook)方程得不到正确普朗特数的缺陷. 其中$f$为粒子热运动分布函数,它是空间坐标$x$,$y$,时间$t$,粒子速度$u$,$v$以及内自由度$\xi$的函数,碰撞时间$\tau $与黏性和热传导系数有关. $f^ + $可以表示为
| $f^ + = f_{\rm M} + f^{ + + }$ |
式中,$f_{\rm M}$是麦克斯韦平衡态分布函数
| $ {f_{\rm{M}}} = \rho {\left( {\frac{\lambda }{\pi }} \right)^{(K + 2)/2}}\exp \{ - \lambda \left[{{{\left( {u - U} \right)}^2} + {{\left( {v - V} \right)}^2} + {\xi ^2}} \right]\} $ |
其中,$\xi ^2 = \xi _1^2 + \xi _2^2 + \cdots + \xi _K^2 $. 对本文研究的单原子气体而言: 内自由度为0,总自由度$K = 1$ 代表了$z$方向上的粒子运动. $f^{ + + }$的表达式参见文献[23].
单元界面通量可以表示为
| $ \begin{array}{l} {\mathop \iiint \limits}{u_{\rm{n}}}{f_{\rm{p}}}\left( {\begin{array}{*{20}{c}} 1\\ u\\ v\\ {\frac{1}{2}({u^2} + {v^2} + {\xi ^2})} \end{array}} \right)dudvd\xi = \\ {\mathop \iint \limits}g\left( {\begin{array}{*{20}{c}} 1\\ u\\ v\\ {\frac{1}{2}({u^2} + {v^2})} \end{array}} \right){u_{\rm{n}}}du{\rm{d}}v + \\ \frac{1}{2}{\mathop \iint \limits}\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ h \end{array}} \right){u_{\rm{n}}}du{\rm{d}}v \end{array} $ |
其中$u_{\rm n}$和$f_{\rm p} $分别为垂直于单元界面的粒子速度以及单元界面上的粒子分布函数,$f_{\rm p} (t)$ 的具体表达式可以参考文献[12]. $g$和$h$是为了减少计算和存储量而引入的约化分布函数.
以$g$为例说明隐式方法的实现步骤. 网格单元 ($i$,$j$)相空间点$ u_{l,m} = (u_l ,v_m )$上$g$的控制方程
| $ \frac{{\partial g_{i,j,l,m}^n}}{{\partial t}} + {u_l}\frac{{\partial g_{i,j,l,m}^n}}{{\partial x}} + {v_m}\frac{{\partial g_{i,j,l,m}^n}}{{\partial y}} = \frac{{(g_{i,j,l,m}^ + - {g_{i,j,l,m}})}}{{{\tau ^n}}} $ | (2) |
令$\Delta g = g^{n + 1} - g^n$,$\Delta t = t^{n + 1} - t^n$,则隐式推进方法为
| $ \begin{array}{l} (1 + \Delta t/{\tau ^n} + \Delta t \cdot {u_{l,m}}\nabla ){(\Delta g)_{l,m}} = \Delta t \cdot L_{i,j,l,m}^n\\ \;\;\;\;\;\;\;L_{i,j,l,m}^n = - {u_{l,m}}\nabla g_{l,m}^n + J_{l,m}^n = \\ \;\;\;\;\;\; - {u_l}\frac{{\partial g_{l,m}^n}}{{\partial x}} - {v_m}\frac{{\partial g_{l,m}^n}}{{\partial y}} + \frac{{{g^ + } - g}}{{{\tau ^n}}} = \\ \;\;\;\;\; - R + \frac{{{g^ + } - g}}{{{\tau ^n}}} \end{array} $ | (3) |
式中,$R$是对演化时间进行平均得到的单元通量,可以表示为
| $ R = \frac{{\int_0^{\Delta T} {\sum\limits_{ii = 1}^4 {{u_{\rm{n}}}{g_{\rm{p}}}} } (t)dt}}{{\Delta T}} $ | (4) |
其中$u_{\rm n} = u_{l,m} \cdot n_{ii} $,$ n_{ii} $为结构网格第$ii$条边的单位外法向. 演化时间步长$\Delta T$与隐式算法推进时间步长$\Delta t$并不是完全一样的. 经过数值试验之后本文给出了$\Delta T$选取的一个原则
| $ \Delta T < \Delta {t_{\min }}/CFL = \Delta {T_{{\rm{ref}}}} $ | (5) |
其中$\Delta t_{\min } $是由$CFL$确定的全场最小时间步长.
式(3)可以进一步写为
| $ \begin{array}{l} (1 + \Delta t/{\tau ^n}){(\Delta g)_{i,j,l,m}} + \frac{{\Delta t}}{{\left| {{V_{i,j}}} \right|}}\sum\limits_{ii = 1}^4 {({u_{l,m}} \cdot {n_{ii}})} \cdot \left| {{S_{i,j,ii}}} \right| \cdot \\ \;\;\;\;\;\;FF({(\Delta g)_{i,j,l,m}},{(\Delta g)_{i1,j1,l,m}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta t \cdot L_{i,j,l,m}^n \end{array} $ | (6) |
其中下标 ($i1$,$j1$)代表与 ($i,j$)单元共用第$ii$条边的那个网格单元.
| $ \begin{array}{*{20}{l}} {FF({{(\Delta g)}_{i,j,l,m}},{{(\Delta g)}_{i1,j1,l,m}}) = }\\ {\;\;\;\frac{1}{2}({{(\Delta g)}_{i,j,l,m}} + {{(\Delta g)}_{i1,j1,l,m}}) + }\\ {\;\;\;\;\frac{1}{2}{\rm{sign}}({u_{l,m}} \cdot {\rm{ }}{n_{ii}})({{(\Delta g)}_{i,j,l,m}} - {{(\Delta g)}_{i1,j1,l,m}})} \end{array} $ |
上式带入式(6),整理后得到
| $ \begin{array}{l} {(\Delta g)_{i,j,l,m}} + \sum\limits_{ii = 1,2,3,4} {\Delta t \cdot {z_{i,j,l,m}} \cdot {{(\Delta g)}_{i1,j1,l,m}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\Delta t}}{{{\lambda _{i,j,l,m}}}} \cdot L_{i,j,l,m}^n \end{array} $ | (7) |
其中
| $ \begin{array}{*{20}{l}} {{\lambda _{i,j,l,m}} = 1 + \Delta t/{\tau ^n} + \Delta t \cdot {b_{i,j,l,m}},{z_{i,j,j,m}} = \frac{{{c_{i,j,l,m}}}}{{{\lambda _{i,j,l,m}}}}}\\ {{b_{i,j,l,m}} = {\rm{ }}\sum\limits_{ii = 1}^4 ( {u_{l,m}} \cdot {\rm{ }}{n_{ii}}) \cdot (1 + {\rm{sign}}({u_{l,m}} \cdot {\rm{ }}{n_{ii}}))\frac{{\left| {{S_{i,j,ii}}} \right|}}{{2\left| {{V_{i,j}}} \right|}}}\\ {{c_{i,j,l,m}} = ({u_{l,m}} \cdot {\rm{ }}{n_{ii}}) \cdot (1 - {\rm{sign}}({u_{l,m}} \cdot {n_{ii}}))\frac{{\left| {{S_{i,j,ii}}} \right|}}{{2\left| {{V_{i,j}}} \right|}}} \end{array} $ |
式(7)写成矩阵形式
| $ \begin{array}{*{20}{l}} {(I + \Delta t \cdot {Z_{l,m}}) \cdot {{(\Delta g)}_{l,m}} = \Delta t \cdot \Lambda _{l,m}^{ - 1} \cdot {\rm{ }}L_{l,m}^n}\\ {{{(\Delta g)}_{l,m}} = \left( {\begin{array}{*{20}{c}} {{{(\Delta g)}_{1,1,l,m}}}\\ {{{(\Delta g)}_{2,1,l,m}}}\\ \cdots \\ {{{(\Delta g)}_{NI - 1,NJ - 1,l,m}}} \end{array}} \right),{\rm{ }}L_{l,m}^n = \left( {\begin{array}{*{20}{c}} {L_{1,1,l,m}^n}\\ {L_{2,1,l,m}^n}\\ \cdots \\ {L_{NI - 1,NJ - 1,l,m}^n} \end{array}} \right)}\\ {{\Lambda _{l,m}} = \left( {\begin{array}{*{20}{c}} {{\lambda _{1,1,l,m}}}&0& \cdots &0\\ 0&{{\lambda _{2,1,l,m}}}& \cdots &0\\ 0&0& \cdots &0\\ 0&0& \cdots &{{\lambda _{NI - 1,NJ - 1,l,m}}} \end{array}} \right)} \end{array} $ | (8) |
其中,$NI$和$NJ$分别为结构网格$i$和$j$方向上的点数. 对$( I + \Delta t \cdot Z_{l,m} )$进行近似LU分解得到
| $ I + \Delta t \cdot Z_{l,m} = L_{l,m} \cdot U_{l,m} + O(\Delta t^2) $ |
$ L_{l,m}$和$ U_{l,m}$都是标量三对角矩阵
其中
| $ \begin{array}{l} {l_{pq}} = \left\{ {\begin{array}{*{20}{l}} {\Delta t \cdot {z_{pq}},}&{p < q}\\ {0,}&{p > q} \end{array}} \right.\\ {u_{pq}} = \left\{ {\begin{array}{*{20}{l}} {0,}&{p < q}\\ {\Delta t \cdot {z_{pq}},}&{p > q} \end{array}} \right.\\ {l_{pp}} = {u_{pp}} = 1 \end{array} $ |
隐式方法的最终形式为
| $ {L_{l,m}} \cdot {U_{l,m}} \cdot {(\Delta g)_{l,m}} = \Delta t \cdot {\rm{ }}\Lambda _{l,m}^{ - 1} \cdot L_{l,m}^n $ | (9) |
通过在结构网格中进行前后两次扫描迭代,可以得到$(\Delta g)_{l,m} $,进而可以得到$n+1$时刻的$ g_{l,m} $. $ h_{l,m} $可以类似地得到. 有了$n+1$时刻的$ g_{l,m} $和$ h_{l,m} $,即可通过对约化分布函数求积分得到$n+1$时刻的宏观变量.
本文的研究中还对原始的UGKS中采用传统的离散速度坐标法导致的相容性条件得不到严格满足的缺点进行了修正. 具体做法[24]为,假定
| $ f^ + = f^ + ({\rho }',{U}',{V}',{\lambda }',{q}'_x ,{q}'_y ) $ |
采用牛顿迭代法求解式(10)
| $ \begin{array}{l} \sum {{f^ + }\psi _2^{\rm{T}}} - {\left( {\rho ,\rho U,\rho V,\rho E,{q_x},{q_y}} \right)^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\;{\left( {0,0,0,0,- {\mkern 1mu} 2/3{q_x},- {\mkern 1mu} 2/3{q_y}} \right)^{\rm{T}}} \end{array} $ | (10) |
在这一离散形式的$f^ + $下,宏观量的守恒性得到严格满足,此即为守恒型离散速度坐标法.
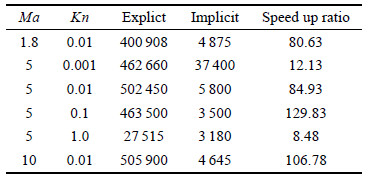
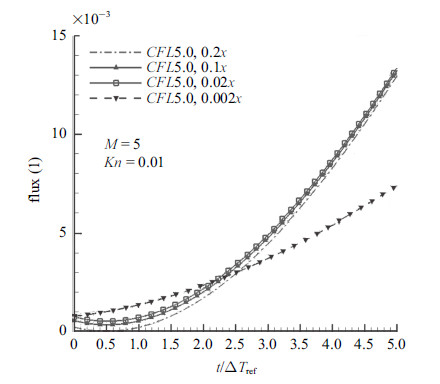
2 数值结果首先给出演化时间选取的相关结果. 来流条件: $M_{\infty}=5.0$,基于圆柱半径的努森数$Kn_{\infty}=0.01$. 数值试验表明,如果演化时间步长大于$\Delta T_{\rm ref} $的话,二阶格式的计算是不稳定的,壁面反射粒子密度极易出现小于0的情况导致计算无法进行. 同时研究了相同的$CFL$条件下,不同的演化时间步长对计算结果的影响,共计完成了4个算例的计算比较. 分别为[$CFL=5.0$,0.2$x$],[$CFL=5.0$,0.1$x$],[$CFL=5.0$,0.02$x$],[$CFL=5.0$,0.002$x$]. 各个算例以[$CFL=a$,$bx$]表示,其中`$b$' 表示演化时间步长取`$b$'倍的全场最小时间步长. 结果显示,4个算例壁面上的压力、热流和应力分布相差不超过0.1%. 图1给出了计算收敛之后驻点线第二层网格界面上密度通量随演化时间的变化. 图2给出了时间平均的密度通量随演化时间的变化. 可以看出,尽管几个算例中界面演化时间不同,导致计算收敛以后密度通量的分布曲线差别较大,但是达到收敛以后指定界面上的时间平均通量是一致的. 而这个时间平均的通量正是我们在做隐式迭代时用到的. 也就是说,UGKS中界面通量分布函数构造中蕴含的动理学机制是合理有效的,只要演化时间满足小于$\Delta T_{\rm ref}$的条件,最终收敛的结果基本不受演化时间步长大小的影响.
|
图 1 计算收敛以后驻点线上第二层网格界面上密度通量随演化时间的变化 Fig.1 The time-dependent flux of density on the secondinterface along the stagnation line |
|
图 2 计算收敛以后驻点线上第二层网格界面上时间平均的密度通量随演化时间的变化 Fig.2 The time-averaged flux of density on the secondinterface along the stagnation line |
第一个测试算例为单原子氩气圆柱绕流,计算条件为: $M_{\infty}=1.8$,5.0,10,基于圆柱半径的努森数 $Kn_{\infty }=0.001$,0.01,0.1,1.0.
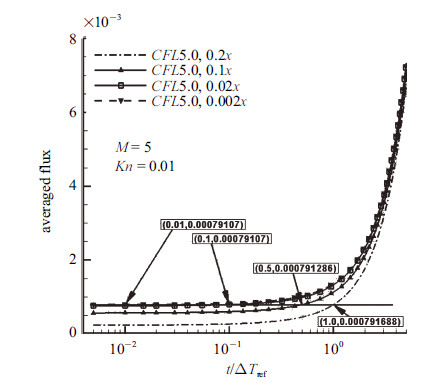
图3和图4分别给出了来流马赫数5,努森数0.1和1.0时不同网格下圆柱表面应力分布. 共计采用了5套网格,图中以网格距离 壁面最小间距进行标识. 可以看出,法向网格间距小到一定程度之后,应力不再变化,即得到了网格收敛解. 热流的变化规律与应力类似,而壁面压力分布对法向网格间距不太敏感 (篇幅所限,没有示出).

|
图 3 不同网格下圆柱表面应力分布 Fig.3 Stress on the solid surface |
|
图 4 不同网格下圆柱表面应力分布 Fig.4 Stress on the solid surface |
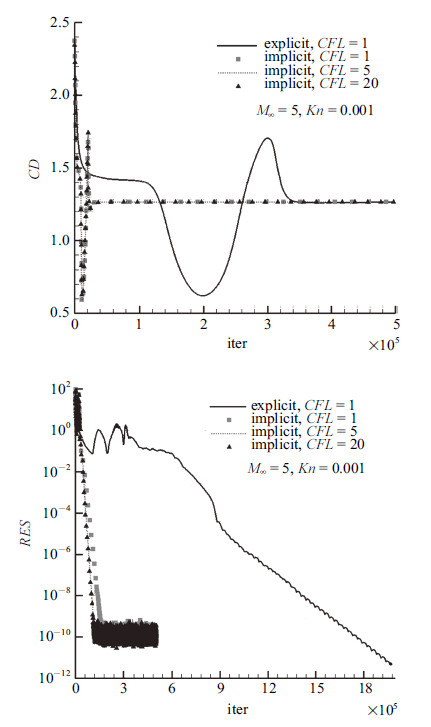
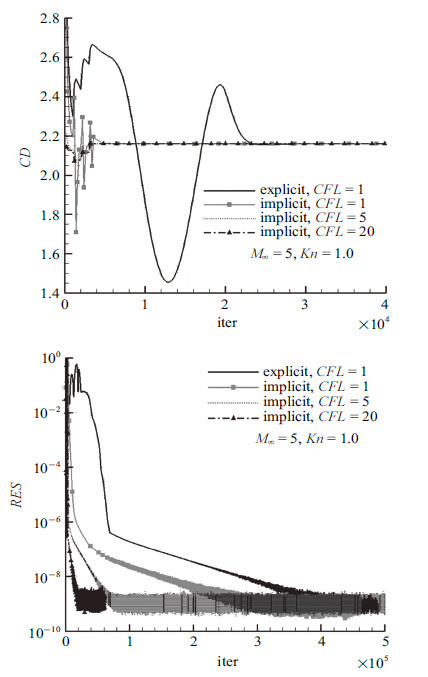
下面研究隐式加速收敛效果时,$Kn=1.0$所用网格壁面最小间距0.0184,$Kn\leqslant 0.1$所用网格壁面最小间距0.001. 图5和图6给出了来流马赫数5时显式和隐式计算得到的圆柱阻力和残差的收敛历程.
|
图 5 阻力和残差收敛历程 Fig.5 Convergent histories of the drag coefficient and residual |
|
图 6 阻力和残差收敛历程 Fig.6 Convergent histories of the drag coefficient and residual |
表1给出了显式和隐式计算收敛所需迭代步数比较. 表中迭代所需步数的选取以最后一次与最终收敛结果相差0.1%时 的步数为准. 实际计算中发现,隐式方法单步计算时间比显式方法的仅多2%左右. 因而隐式计算加速比约为显式迭代步数除以隐式迭代步数再除以1.02. 可以看出,隐式计算加速比介于8$\sim$130, 具体加速多少还与采用网格的最小间距以及来流条件有关. 针对图5和图6两个算例, 如果以残差不再单调下降作为收敛标准的话,对应的加速比分别为15和22.5.
| 表 1 显式和隐式计算收敛所需迭代步数比较 Table 1 Comparison of iteration steps for the explicit and implicit methods |
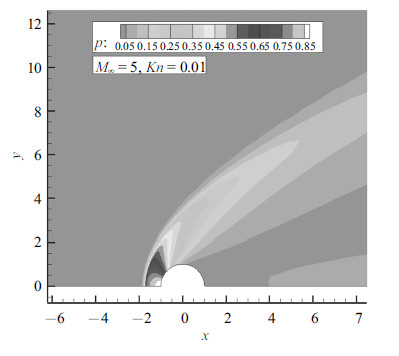
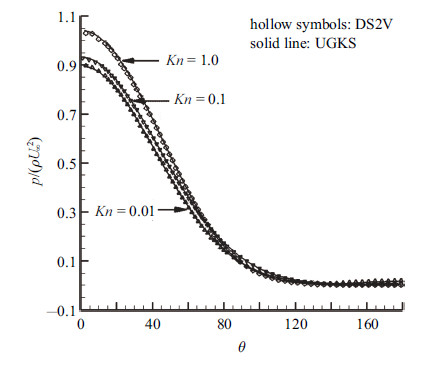
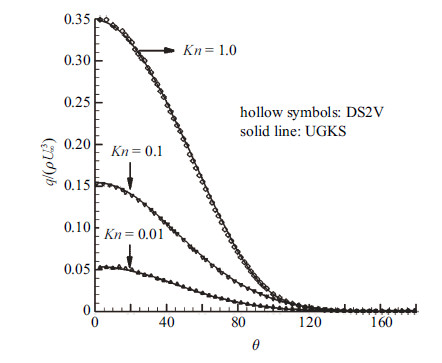
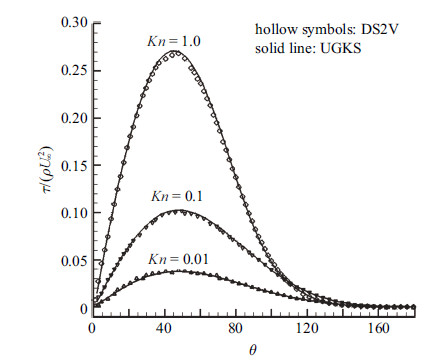
图7给出了努森数0.01时圆柱压力分布. 图8~图10分别是壁面压力、热流以及应力与DS2V对比的结果. 可以看出,二者吻合很好.
|
图 7 圆柱算例, 压力分布 Fig.7 Pressure contour around the cylinder |
|
图 8 圆柱表面压力比较 Fig.8 Pressure distribution on the cylinder wall |
|
图 9 圆柱表面热流比较 Fig.9 Heat flux on the cylinder wall |
|
图 10 圆柱表面应力比较 Fig.10 Stress distribution on the cylinder wall |
另一个算例为尖楔绕流,与Liu[25]考核GRASP (generalized rarefied gas~simulation package)软件时相同, 计算条件为: 氩气,$M_{\infty }=10.0$,基于尖楔底部长度 (0.2\;m)的努森数$Kn_{\infty}=0.05$,攻角10$^\circ$, 来流温度200K,壁面温度300K.
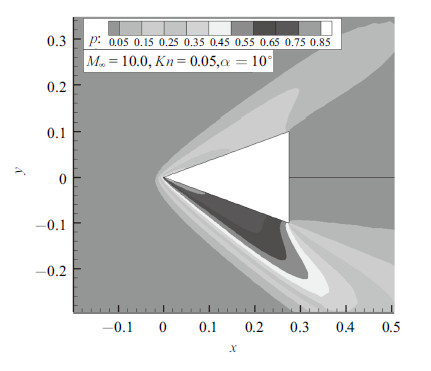
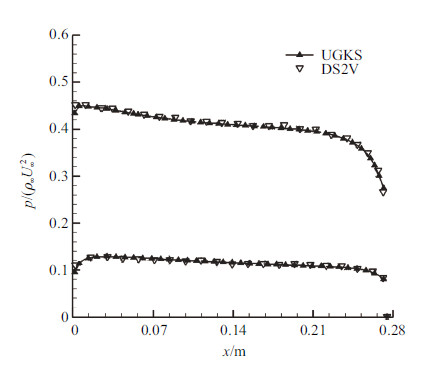
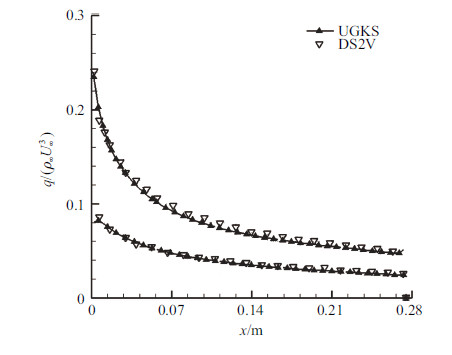
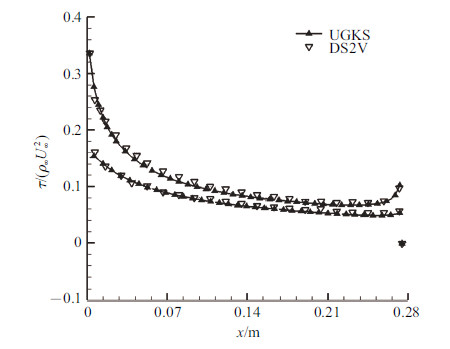
图11给出了空间压力分布. 图12~图14分别是上下壁面压力、热流以及应力与DS2V对比的结果. 可以看出,二者吻合良好. 需要指出的是,此算例中,UGKS在相空间采用了61$\times$61的网格,能够在较小规模的网格上得到合理可信的结果得益于采用了守恒性离散速度坐标法[24].
|
图 11 尖楔算例, 压力分布 Fig.11 Pressure contour around the wedge |
|
图 12 尖楔表面压力比较 Fig.12 Pressure distribution on the wedge wall |
|
图 13 尖楔表面热流比较 Fig.13 Heat flux on the wedge wall |
|
图 14 尖楔表面应力比较 Fig.14 Stress distribution on the wedge wall |
本文采用近似LU分解方法,实现了对结构化网格下UGKS程序的隐式改造,考察了隐式方法的加速收敛效果. 并完成了圆柱和尖楔算例与DS2V计算结果的比较,得到以下结论:
(1)对高速流动定常问题,隐式UGKS具有明显的加速收敛效果,与显式方法相比,计算效率提高1$\sim$2个量级;
(2)UGKS与DS2V在高超声速圆柱和尖楔上的计算结果高度吻合,进一步验证了隐式方法实现的正确性以及UGKS方法在模拟高超声速流动中良好的精度.
在计算中发现当来流努森数较小时,尽管隐式方法较显式方法还具有很好的加速效果,但是收敛速度存在变慢的趋势. 因此,将继续开展隐式处理方法的研究,解决在低努森数下的计算效率下降的问题,为算法在三维复杂外形多流域共存问题上的应用奠定基础.
| [1] | Yu PB. A unied gas kinetic scheme for all knudsen number flows. [PhD Thesis], Hong Kong:The Hong Kong University of Science and Technology,2013. |
| [2] | Chen SZ, Xu K, Lee CB, et al. A unified gas kinetic scheme with moving mesh and velocity space adaptation. Journal of Computational Physics, 2012, 231(20): 6643-6664. |
| [3] | Arslanbekov RR, Kolobov VI, Kolobov AA. Kinetic solvers with adaptive mesh in phase space, In: Abe T, Ed. Rarefied Gas Dynamics, Melville, 2012, Amer Inst Physics, 2012, 294-301. |
| [4] | Baranger C, Claudel J, Claudel N, et al. Locally refined discrete velocity grids for deterministic rarefied flow simulations, In: Abe T, Ed. Rarefied Gas Dynamics, Melville, 2012, Amer Inst Physics, 2012, 389-396. |
| [5] | Yoon S, Jameson A. Lower upper symmetric Gauss Seidel method for the Euler and Navier-Stokes equations. AIAA Journal, 1988, 26(efeq9): 1025-1026. |
| [6] | Yang JY, Huang JC. Rarefied flow computations using nonlinear model Boltzmann equations. Journal of Computational Physics, 1995, 120(efeq2): 323-339. |
| [7] | 毕林. Boltzmann模型方程数值算法在槽道流问题中的应用研究. [硕士论文].四川绵阳: 中国空气动力研究与发展中心, 2007 (Bi Lin. Application and study on numerical algorithm of the Boltzmann model equation in channel flow. [Master Thesis]. Mianyang: China Aerodynamic Research and Development Center, 2007 (in Chinese)) |
| [8] | 王强, 程晓丽, 庄逢甘. 基于简化Boltzmann方程的超声速流稀薄效应分析. 航空学报, 2005. 26(efeq3):281-285 (Wang Qiang, Cheng Xiaoli, Zhuang Fenggan. Rarefaction effect analysis of supersonic flows based on reduced Boltzmann equations. Acta Aeronautica Et Astronautica Sinica, 2005, 26(efeq3): 281-285 (in Chinese)) |
| [9] | 王强, 程晓丽, 庄逢甘. 稀薄流非线性模型方程离散速度坐标法有限差分解. 计算力学学报, 2006, 23(efeq2): 235-241 (Wang Qiang, Cheng Xiaoli, Zhuang Fenggan. Finite difference solution of nonlinear model equations for rarified gas using discrete velocity ordinate method. Chinese Journal of Computational Mechanics, 2006, 23(efeq2): 235-241 (in Chinese)) |
| [10] | Titarev VA. Efficient deterministic modelling of three-dimensional rarefied gas flows. Communications in Computational Physics, 2012, 12(efeq1):162-192. |
| [11] | Titarev VA, Dumbser M, Utyuzhnikov S. Construction and comparison of parallel implicit kinetic solvers in three spatial dimensions. Journal of Computational Physics, 2014, 256: 17-33. |
| [12] | Xu K, Huang JC. A unified gas-kinetic scheme for continuum and rarefied flows. Journal of Computational Physics, 2010, 229(20): 7747-7764. |
| [13] | Huang JC, Xu K, Yu PB. A unified gas-kinetic scheme for continuum and rarefied flows II: multi-dimensional cases. Communications in Computational Physics, 2012, 12(efeq3): 662-690. |
| [14] | Huang JC, Xu K, Yu PB. A unified gas-kinetic scheme for continuum and rarefied flows III: Microflow simulations. Communications in Computational Physics, 2012, 14(efeq5): 1147-1173. |
| [15] | 徐昆, 李启兵, 黎作武. 离散空间直接建模的计算流体力学方法. 中国科学: 物理学 力学 天文学, 2014, 44(efeq5):519-530 (Xu Kun, Li Qibing, Li Zuowu. Direct modeling-based computational fluid dynamics. Scientia Sinica Physica, Mechanica & Astronomica, 2014, 44(efeq5): 519-530 (in Chinese)) |
| [16] | Xu K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method. Journal of Computational Physics, 2001, 171(efeq1): 289-335. |
| [17] | 毛枚良, 徐昆, 邓小刚. 动能BGK算法在近连续流模拟中的应用. 空气动力学学报, 2005, 23(efeq3): 317-321 (Mao Meiliang, Xu Kun, Deng Xiaogang. Application of kinetic BGK algorithm in simulating near continuum flow. Acta Aerodynamica Sinica, 2005, 23(efeq3): 317-321 (in Chinese)) |
| [18] | Xu K, Mao ML, Tang L. A multidimensional gas-kinetic BGK scheme for hypersonic viscous flow. Journal of Computational Physics, 2005, 203(efeq2): 405-421. |
| [19] | Jiang J, Qian YH. Implicit gas-kinetic BGK scheme with multigrid for 3D stationary transonic high-Reynolds number flows. Computers & Fluids, 2012, 66: 21-28. |
| [20] | Li WD, Masayuki K, Kazuhiko S. An implicit gas kinetic BGK scheme for high temperature equilibrium gas flows on unstructured meshes. Computers & Fluids, 2014, 93: 100-106. |
| [21] | Jiang DW, Li J, Mao ML, et al. Implicit implementation of bgk-ns method and its application in complex flows. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30(supp): 87-92. |
| [22] | Bird GA. The DS2V/3V program suite for DSMC calculations, In: Capitelli M, Ed. Rarefied Gas Dynamics, 2005, Amer Inst Physics, 2005, 541-546. |
| [23] | Shakhov E. Generalization of the Krook kinetic equation. Fluid Dynamics, 1968, 3(efeq5): 95-96. |
| [24] | 江定武, 毛枚良, 李锦 等. 气体动理学统一算法中相容性条件不满足引起的数值误差及其影响研究. 力学学报, 2014, 47(efeq1): 163-168 (Jiang Dingwu, Mao Meiliang, Li Jin, et al. Study on the numerical error introduced by dissatisfying the conservation constraint in UGKS and its effects. Chinese Journal of Theoretical and Applied Mechanics, 2014, 47(efeq1): 163-168 (in Chinese)) |
| [25] | Liu HL, Cai CP, Zou C. An object-oriented serial implementation of a DSMC simulation package. Computers & Fluids, 2012, 57: 66-75. |
2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China;
3. National University of Defense Technology, Changsha 410073, China
 2015, Vol. 47
2015, Vol. 47