2. 北京航空航天大学航空科学与工程学院, 北京100191
在机械系统中,物体间普遍存在着接触、碰撞和摩擦等问题,如航天器的对接、空间机构的展开、飞机的着陆、车辆的行驶、步行机器人的行走和夯机压实路面等都存在物体间的碰撞和摩擦问题. 关于碰撞和摩擦问题的研究已取得了很多阶段性成果[1, 2, 3, 4, 5, 6, 7]. 20世纪末和21世纪初,人们研究了多种形式的接触力模型,其中赫兹接触理论考虑了接触点的局部变形,是研究历史最悠久的接触模型[4, 6],但该模型不能反映接触碰撞过程中的能量耗散. 近数十年来基于赫兹模型,学者们提出了若干种考虑能量损耗的接触力模型[6, 8]. 常用的接触力模型是将接触面的法向力表示成嵌入量与嵌入速度的非线性函数[8, 9]. 在实际工程中,常用的摩擦模型有库伦干摩擦模型、修正的库伦摩擦模型、黏性摩擦模型、斯特里贝克(Stribeck)摩擦模型和达尔(Dahl)摩擦模型等[7, 10, 11, 12],其中库伦干摩擦模型能够反映摩擦的动态和静态特性,被认为是最简单使用较广泛的摩擦模型[5, 6]. 但该模型的不连续性给多个摩擦点的黏滞滑移(stick-slip)运动状态切换(非光滑事件)的判断和动力学方程的求解带来困难[3, 5]. 修正的库伦摩擦模型虽然避免了摩擦力的不连续性给数值计算带来的困难,但不能反映摩擦的静动态特性[6, 13].
有人将线性互补问题(LCP)的相关理论引入到具有单边约束非光滑多体系统动力学的研究中[5, 14],有效地解决了非光滑事件的判断. 有人基于接触模型和修正的库伦摩擦模型,给出了考虑铰链间隙的机械多体系统动力学的建模方法与计算方法[6, 13],该方法仅适用于无黏滞滑移运动状态切换的机械系统. 基于线性互补理论,有人给出了考虑滑移铰间隙的平面多刚体系统动力学的建模方法与数值算法[15],应用时间步进算法可有效判断物体间的接触分离和黏滞滑移等非光滑事件,但当间隙充分小时,算法存在违约问题. 将约束稳定化方法嵌入到时间步进法中,有人给出了非光滑多刚体系统动力学数值算法,有效地抑制了约束的漂移[16]. 有人将间隙充分小的滑移铰视为双边约束,基于线性互补理论,结合鲍姆加藤(Baumgarte)约束稳定化方法,给出了滑移铰含库伦干摩擦多刚体系统动力学的建模与计算方法[17, 18],应用事件驱动算法可有效地分析滑移铰的黏滞滑移运动状态的切换,并有效地抑制了约束的漂移. 有人做了进一步的推广,给出的算法既可以判断非光滑事件,又可以求解理想铰链的约束力和非定常约束的驱动力[18, 19],但该方法的互补维数较高,影响了数值求解的计算效率. 有人采用线性互补方法给出了含摩擦多体系统动力学方程的计算方法,既可以求解非光滑铰链的约束力也可以求解理想铰链的约束力或驱动约束力,且理想铰链的约束力或驱动约束力的求解不参与互补运算,可提高计算效率[20, 21]. 但其方法不适用于含碰撞的非光滑多体系统.
本文将研究具有完整理想定常约束(理想铰链约束)和非定常约束(驱动约束)的平面多刚体系统,且考虑非光滑接触面的接触碰撞与摩擦问题. 将非光滑接触面的法向接触力表示成嵌入量与嵌入速度的函数; 摩擦力采用库伦干摩擦模型; 由第一类拉格朗日方程和鲍姆加藤约束稳定化方法导出其动力学方程; 利用事件驱动算法,将物体接触点的黏滞滑移运动状态切换的判断问题以及处于黏滞状态时静摩擦力的计算问题转化成线性互补问题的求解. 该方法与传统方法相比,互补量仅包含了与摩擦有关的量,可降低线性互补方程的维数,提高计算效率. 最后通过数值算例分析了具有偏心转子滑块机构在水平地面上运动的动力学特性,并验证了本文给出方法的有效性.
1 系统的描述及接触力模型设平面多刚体系统由$N$个刚体组成,且具有完整理想定常约束(铰链约束)和非定常约束(电机驱动约束); 考虑物体接触与分离界面的摩擦与碰撞. 设$x_{Ci},y_{Ci} ,\theta _i (i = 1,2,\cdots ,N)$为第$i$个刚体在惯性系中的质心坐标和刚体的转角,则该多体系统的位形坐标可用向量${{ q}} = [x_{C1} ,y_{C1} ,\theta _1 ,\cdots ,x_{CN} ,y_{CN},\theta _N]^{\rm T}$描述.
1.1 法向接触力模型当物体间接触或碰撞时,考虑物体的局部变形,用$\delta $表示物体的法向嵌入量,$\dot{\delta }$为嵌入速度. 其法向接触力$F_N $可表示为[2, 9]
| $ F_N = K\,\delta ^n + c\delta \dot{\delta } $ | (1) |
式中,$K$和$c$分别为广义刚度系数和广义阻尼系数($K$,$c$与接触物体的几何尺寸、材料性质有关),指数$n$通常的取值范围为[1,1.5],由于$\delta $和$\dot{\delta }$可表示为${{ q}},{{\dot{ q}}}$的函数[6, 8],由式(1)可知,法向接触力可以表示为${{ q}},{{\dot{ q}}}$的函数.
1.2 切向接触力模型根据库伦干摩擦模型,作用在物体接触面上的摩擦力在接触面切向上的投影$F_\tau $与法向接触力之间的关系可以表示为[3]
| $ F_\tau = \left\{ {{\begin{array}{ll} - \mu F_N {\rm sgn}(\dot{g}_\tau ),&\dot{g}_\tau \ne 0\\ - \mu _0 F_N \mbox{Sgn}(\ddot{g}_\tau ),&\dot{g}_\tau = 0\\ \end{array} }} \right. $ | (2) |
式中,$\mu ,\mu _0 $分别为物体间的动、静摩擦因数; $\dot{g}_\tau ,\ddot{g}_\tau $分别为接触点的相对速度和相对切向 加速度; ${\rm sgn}(\cdot)$为符号函数,其定义如下
| $ \label{eq1} \mbox{ }(\dot{g}_\tau ) = \left\{ {\begin{array}{ll} + 1,&\dot{g}_\tau > 0 \\ - 1,& \dot{g}_\tau < 0 \\ \end{array}} \right. $ | (3) |
$\mbox{Sgn}(\cdot)$为多值函数[3, 15],其定义如下
| $ \mbox{Sgn}(\ddot{g}_\tau ) = \left\{ {{\begin{array}{ll} + 1,&\ddot{g}_\tau > 0\\{} [- 1,+ 1],&\ddot{g}_\tau = 0\\ - 1,&\ddot{g}_\tau < 0\\ \end{array} }} \right. $ | (4) |
设该系统有$f$个摩擦点,则将所有的$F_{\tau i}$ $(i = 1$,$2,\cdots ,f)$表示成向量形 式${{ F}}_\tau = [F_{\tau 1} ,F_{\tau 2} ,\cdots ,F_{\tau f}]^{\rm T}$.
2 非光滑动力学方程及其算法 2.1 非光滑动力学方程设系统具有$s^*$个完整理想定常约束和$\tilde{s}$个非定常约束,由局部递推法[22]列写相应的约束方程,并可表示为下列矩阵形式
| $ {{ \varPhi }}^\ast ({{ q}}) = {{ 0}}$ | (5) |
| $ {{\tilde{ \varPhi }}}({{ q}},t) = {{ 0}} $ | (6) |
将式(5)和式(6)表达为
| $ {{ \varPhi }}({{ q}},t) = [{{ \varPhi }}^\ast ,{{\tilde{ \varPhi }}}]^{\rm T} = {{ 0}} $ | (7) |
由第一类拉格朗日方程可得到该系统的动力学方程
| $ \left. {\begin{array}{l} {{ M\ddot{ q}}} = {{ \varPhi }}_{{ q}}^{\rm T} {{ \lambda }} + {{ Q}} + {{ Q}}_f \\ {{ \varPhi }}({{ q}},t) = {{ 0}} \\ \end{array}} \right\} $ | (8) |
式中,${{ M}}$为广义质量矩阵; ${{ \varPhi }}_{{ q}}^{\rm T} $为约束方程的雅克比矩阵; ${{ \lambda }} = [\lambda _1^\ast ,\cdots,\lambda _{s\ast }^\ast ,\tilde{\lambda }_1 ,\cdots ,\tilde{\lambda }_{\,\tilde{s}}]$为拉格朗日乘子列向量,其中,$\lambda _i^\ast (i = 1,2,\cdots s^\ast )$为定常约束方程即式(5)对应的约束力(如铰链约束力); $\tilde{\lambda }_{\,i} (i= 1,2,\cdots ,\tilde{s})$ 为非定常约束方程即式(6)对应的约束力(如电机的驱动力偶矩); ${{ Q}}$为系统中主动力的广义力,${{ Q}}_f $ 为系统中摩擦力的广义力.
2.2 库伦摩擦定律的互补关系由于摩擦力的存在,由式(2)可知动力学方程在非光滑点处($\dot{g}_\tau = 0$)是不连续的,这给方程的求解带来了困难,难点主要在于黏滞滑移状态切换(非光滑事件)的判断问题以及处于黏滞状态时摩擦力的计算. 为解决该问题,利用前人工作的基础[3],通过建立库伦摩擦定律的互补关系,将非光滑事件的判断及摩擦力的计算转化为线性互补问题的求解.
设在某时刻,该系统中有$H$个接触点的相对速度为零,即$\dot{g}_{\tau i} = 0\ (i = 1,2,\cdots ,H)$,设接触点的静摩擦因数为$\mu_{0i}$,用矩阵形式可将正向摩擦余量和负向摩擦余量表示为[3]
| $ \left. {\begin{array}{l} {{ F}}_\tau ^ + = {{ \mu }}_0 {{ F}}_N + {{ F}}_\tau ^\ast \\ {{ F}}_\tau ^ - = {{ \mu }}_0 {{ F}}_N - {{ F}}_\tau ^\ast \\ \end{array}} \right\} $ | (9) |
其中${{ \mu }}_0 = \mbox{dig}\left\{ {\mu _{0i} } \right\}$,${{ F}}_N $为$H$个接触点的法向接触力的列向量,${{ F}}_\tau ^\ast $为此时静滑动摩擦力的列向量. 将式(9)中的两式相加可得
| $ {{ F}}_\tau ^ + = 2{{ \mu }}_0 {{ F}}_N - {{ F}}_\tau ^ - $ | (10) |
当$\dot{g}_{{\tau }i} = 0$时,接触点切向的正向加速度和负向加速度分别定义为[18]
| $ \left. \begin{array}{l} \ddot{g}_{\tau i}^ + = \dfrac{1}{2}(\left| {\ddot{g}_{\tau i}} \right| + \ddot{g}_{\tau i} ) \\[2mm] \ddot{g}_{\tau i}^ - = \dfrac{1}{2}(\left| {\ddot{g}_{\tau i}} \right| - \ddot{g}_{\tau i} ) \\ \end{array} \right\} \quad (i = 1,2,\cdots ,H) $ | (11) |
将上式相减并写成向量形式可得
| $ {{\ddot{ g}}}_\tau ^ + - {{\ddot{ g}}}_\tau ^ - = {{\ddot{ g}}}_\tau $ | (12) |
正、负向摩擦余量(${{ F}}_\tau ^ + $,${{ F}}_\tau ^ - $)和正、负向切向加速度(${{\ddot{ g}}}_\tau ^ + $,${{\ddot{ g}}}_\tau ^ - $)存在以下互补关系[3, 18]
| $ \left. {\begin{array}{l} {{\ddot{ g}}}_\tau ^ + \geqslant {\bf 0},\quad {{ F}}_\tau ^ + \geqslant {\bf 0},\quad {{\ddot{ g}}}_\tau ^{\rm +T} {{ F}}_\tau ^ + = {\bf 0} \\ {{\ddot{ g}}}_\tau ^ - \geqslant {\bf 0},\quad {{ F}}_\tau ^ - \geqslant {\bf 0},\quad {{\ddot{ g}}}_\tau ^{ \rm -T} {{ F}}_\tau ^ - = {\bf 0} \\ \end{array}} \right\} $ | (13) |
应用鲍姆加藤约束稳定化方法[6],方程(8)中的第2式改写为
| $ {{\ddot{ \varPhi } + }}\alpha {{\dot{ \varPhi } + }}\beta \varPhi = 0 $ | (14) |
其中,$\alpha ,\beta $为大于零的常数[23, 24],由上式推导可得
| $ {{ \varPhi}}_{{ q}} {{\ddot{ q} + \dot{ \varPhi }}}_{{ q}} \dot{ q} + \alpha {{ \varPhi }}_{{ q}}\dot{ q} + \beta {{ \varPhi }} + \dot{ \varPhi}_t + \alpha {{ \varPhi }}_t = 0 $ | (15) |
其中,${{ \varPhi }}_{{ q}} = {\partial {{ \varPhi }}}/{\partial {{ q}}}$,${{\dot{ \varPhi }}}_{{ q}} = {\mbox{d}{{ \varPhi }}_{{ q}}}/{\mbox{d}t}$,${{ \varPhi }}_t = {\partial {{ \varPhi }}}/{\partial t}$,${{\dot{ \varPhi }}}_t = {\mbox{d}{{ \varPhi}}_t}/{\mbox{d}t}$.
由动力学方程(8)的第1式求出
| $ {{\ddot{ q}}} = {{ M}}^{ - 1}{{ \varPhi }}_{{ q}}^{\rm T} {{ \lambda }} + {{ M}}^{ - 1}{{ Q}} + {{ M}}^{ - 1}{{ Q}}_f $ | (16) |
将其代入式(15)可得
| $ {{ \lambda }} = - {{ D}}^{ - 1}{{ A}} - {{ D}}^{ - 1}{{ \varPhi }}_{{ q}} {{ M}}^{ - 1}{{ Q}}_f $ | (17) |
其中${{ A}} = {{ \varPhi }}_{{ q}} {{ M}}^{ - 1}{{ Q}} + {{\dot{ \varPhi }}}_{{ q}} {{\dot{ q}}} + \alpha {{ \varPhi }}_{{ q}} {{\dot{ q}}} + \beta {{ \varPhi }} + {{\dot{ \varPhi }}}_t + \alpha {{ \varPhi }}_t$,${{ D}} = {{ \varPhi }}_{{ q}} {{ M}}^{ - 1}{{ \varPhi }}_{{ q}}^{\rm T}$. 将式(17)代入式(16),由此可得
| $ {{\ddot{ q}}} = {{ B}}_1 {{+ B}}_2 {{ Q}}_f $ | (18) |
其中${{ B}}_1 = - {{ M}}^{ - 1}{{ \varPhi }}_{{ q}}^{\rm T} {{ D}}^{ - 1}{{ A}} + {{ M}}^{ - 1}{{ Q}}$,${{ B}}_2 = {{ M}}^{ - 1} - {{ M}}^{ - 1}{{ \varPhi }}_{{ q}}^{\rm T} { D}^{-1}{{ \varPhi }}_{{ q}} {{ M}}^{ - 1}$.
将摩擦力的广义力表示成矩阵形式
| $ {{ Q}}_f = {{ G}}_1 {{ F}}_\tau ^s + {{ G}}_2 {{ F}}_\tau ^\ast $ | (19) |
其中${{ G}}_1$和${{ G}}_2 $中的各元素是坐标${{ q}}$的函数. 上式中等式右端的第一项为动滑动摩擦力${{ F}}_\tau ^s $ 的广义力,第二项为静滑动摩擦力${{ F}}_\tau ^\ast $的广义力,则该系统的动力学方程可以写为
| $ {{\ddot{ q}}} = {{ B}}_1 + B_2 {{ G}}_1 {{ F}}_\tau ^s + {{ B}}_2 {{ G}}_2 {{ F}}_\tau ^\ast $ |
将上式改写成
| $ {{\ddot{ q}}} = {{ B}}_3 + {{ B}}_2 {{ G}}_2 {{ F}}_\tau ^\ast $ | (20) |
式中${{ B}}_3 = {{ B}}_1 + B_2 {{ G}}_1 {{ F}}_\tau ^s $.
物体接触点的相对速度可以表示为系统状态变量的函数,即$\dot{g}_{\tau i} = \dot{g}_{\tau i} ({{ q}}, {{\dot{ q}}})$. 当所有接触点的相对速度均不为零时,即$\dot{g}_{\tau i} \ne 0$ $(i = 1,2,\cdots ,f)$, 其动滑动摩擦力$F_{\tau i}^s $为已知量,可由式(2)的第一式计算得到,其中法向接触力$F_{Ni} $由式(1)计算得到. 将摩擦力列向量带入动力学方程(20),可直接应用常微分方程的数值计算方法求解该方程.
若系统中有$H$个接触点的相对速度为零,即$\dot{g}_{\tau i} = 0$ $(i = 1,2,\cdots ,H)$, 此时这些接触点的静滑动摩擦力$F_{\tau i}^\ast $ 为未知量,由式(2)和式(4)可知,该静滑动摩擦力不仅与${{ q}}, {{\dot{ q}}}$有关,还与${{\ddot{ q}}}$有关. 其他相对速度不为零的接触点的动滑动摩擦力仍为已知量.
为计算这$H$个接触点的静滑动摩擦力,将这$H$个点的相对速度表达式表示成列向量${{\dot{ g}}}_\tau $,将其对时间求导后可得
| $ {{\ddot{ g}}}_\tau = {{ W\ddot{q}}} + {{ w}}_H $ | (21) |
式中,${{ W}} = {\partial {{\dot{ g}}}_{{ \tau }} }/{\partial {{\dot{ q}}}}$,${{ w}}_H = {\partial {{\dot{ g}}}_{{ \tau }} }/{\partial {{ q}}}{{\dot{ q}}}$ 是状态变量${{ q}}$和${{\dot{ q}}}$的函数. 将上式代入式(12),有
| $ {{\ddot{ g}}}_\tau ^ + - {{\ddot{ g}}}_\tau ^ - = {{ W\ddot{ q}}} + {{ w}}_H $ | (22) |
将式(20)代入式(22),整理可得
| $ {{\ddot{ g}}}_\tau ^ - = {{\ddot{ g}}}_\tau ^ + - {{ W B}}_3 - {{ W B}}_2 {{ G}}_2 {{ F}}_{\tau }^{\ast } - {{ w}}_H $ | (23) |
再将式(9)的第2式代入式(23),有
| $ \label{eq2} {{\ddot{ g}}}_\tau ^ - = {{ W B}}_2 {{ G}}_2 {{ F}}_\tau ^ - + {{\ddot{ g}}}_\tau ^ + - {{ W B}}_3 - {{ W B}}_2 {{ G}}_2 {{ \mu }}_0 {{ F}}_N - {{ w}}_H $ | (24) |
将式(10)与式(24)联立,可以得到下列线性互补方程
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\ddot g_\tau ^ - }\\ {F_\tau ^ + } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {W{B_2}{G_2}1}\\ { - 10} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {F_\tau ^ - }\\ {\ddot g_\tau ^ + } \end{array}} \right] + \\ \qquad \left[ {\begin{array}{*{20}{c}} { - W{B_3} - W{B_2}{G_2}{\mu _0}{F_N} - {w_H}}\\ {2{\mu _0}{F_N}} \end{array}} \right] \end{array} $ | (25) |
应用线性互补问题的数值算法,由式(25)求解出${{ F}}_{\tau {\kern 1pt} }^ - $,再由式(9)中的第二式求出${{ F}}_\tau ^\ast $,将其代入式(20),应用常微分方程的数值解法求解该方程.
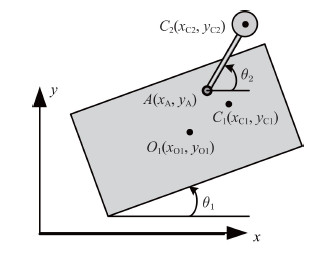
3 算例源于平板夯机的具有偏心转子的机械系统,如图1所示. 设夯机的主体为长为2$a$,高为2$b$的非均质矩形箱体, 其质量为$m_1$,几何中心$O_1 $ 的坐标为$x_{O1} ,y_{O1} $,质心$C_1 $的坐标为$x_{C1} ,y_{C1} $, 夯机底板与地面的夹角为$\theta _1 $; 质量为$m_2 $偏心距为$e$ 的转子通过电机与夯机箱体连接,电机的转轴$A$视为光滑柱铰链,电机驱动转子的相对角速度为$\omega$,偏心转子质心$C_2 $的坐标为$x_{C2} ,y_{C2} $,$C_2 A$与水平面的夹角为$\theta _2 $; 夯机工作时,其箱体与地面发生接触与碰撞, 法向接触力由公式(1)给出,其中$n=1.5$; 设夯机与地面间的静、动摩擦系数分别为$\mu_0 ,\mu $.
|
图 1 具有定常和非定常约束的滑块摆杆机构 Fig. 1 Slider-bar Mechanism with scleronomic and rheonomic constraints |
设铰链$A$和夯机箱体质心$C_1 $相对夯机箱体的几何中心$O_1 $的坐标分别为$(A_x ,A_y )$和$(C_x ,C_y )$,则该铰链$A$的定常约束方程和电机驱动的非定常约束方程可表示为
| $ \left\{ {\begin{array}{l} \phi _1^\ast = x_{C2} - x_{C1} - e\cos \theta _2 - d_1 = 0 \\ \phi _2^\ast = y_{C2} - y_{C1} - e\sin \theta _2 - d_2 = 0\quad \\ \tilde{\phi } = \theta _2 - \theta _1 - \omega {\kern 1pt} {\kern 1pt} t = 0 \\ \end{array}} \right. $ |
其中
| $ \left\{\begin{array}{l} d_1 = (A_x - C_x )\cos \theta _1 - (A_y - C_y )\sin \theta _1 \\ d_2 = (A_x - C_x )\sin \theta _1 + (A_y - C_y )\cos \theta _1 \\ \end{array}\right. $ |
参考HZR-92型平板夯的主要参数,取值如下: $m_1 = 92.0$ kg,$m_2 = 7.0$ kg,$a = 0.2$ m,$b = 0.128$ m,$e = 0.018$ m,$J_{C1} = 0.442\,3$ kg$\cdot$m$^2$,$J_{C2} = 0.002\,47$ kg$\cdot$m$^2$; 箱体质心$C_1 $和电机轴$A$相对箱体几何中心的坐标分别为: $C_x = - 0.033$ m,$C_y = 0.032$ m,$A_x = 0.03$ m,$A_y = 0.124$ m. 取计算步长h = 1 µs,鲍姆加藤违约修正系数为[24]$\alpha = 1\times 10^6$,$\beta = 1.4\times 10^6$.
情况一: 设夯机的电机转速为$\omega = 420$ rad/s,在中等硬度路面作业,其接触面的相关参数[25, 26]: $K = 3.1$ MN/m$^{1.5}$,$c = 23$ kNs/m$^{2}$,摩擦系数为$\mu _0 = 0.6$,$\mu = 0.45$. 用本文给出的方法对其进行数值仿真.
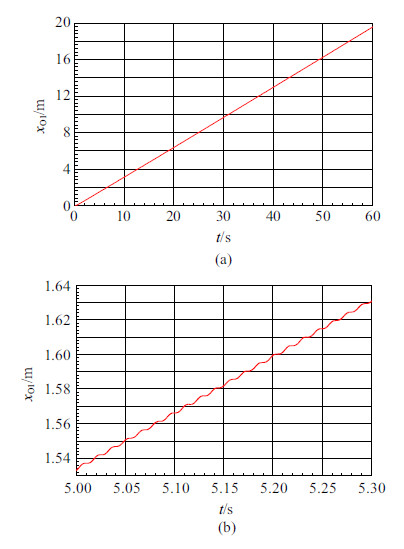
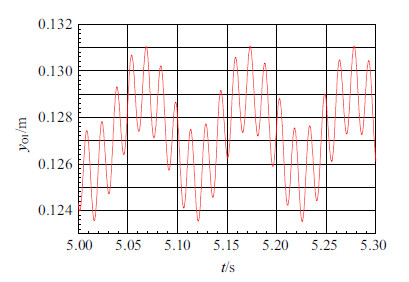
图2$\sim$ 图4分别给出了夯机位形坐标$x_{O1} ,y_{O1} ,\theta _1 $的时间历程图. 由图2(a)可知,夯机移动的平均速度为19.58\;m/min; 由图2(b)$\sim$ 图4可知,夯机的稳态运动为周期运动,夯机箱体上下跳动的同时还伴有俯仰运动.
|
图 2 滑块上O1点水平位移图 Fig. 2 Horizontal displacement of point O1 on slider |
|
图 3 滑块上O1点铅垂位移图 Fig. 3 Vertical displacement of point O1 on slider |

|
图 4 滑块角位移图 Fig. 4 Angular displacement of slider |
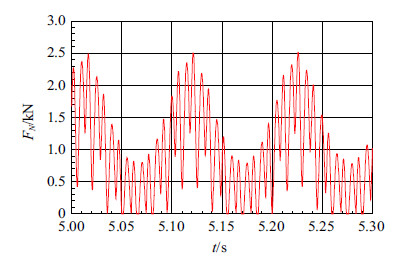
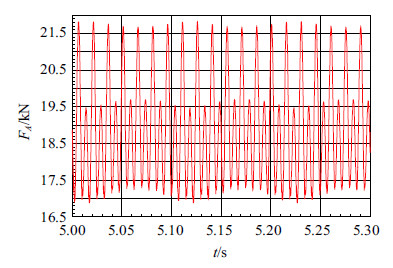
图5给出了地面法向接触力的时间历程图. 由图可知,法向接触力为零时,夯机与地面没有接触,是处于腾空状态. 图6给出了铰链$A$处的约束力$F_A$的时间历程图,该约束力为铰链$A$的定常约束方程对应的约束力. 图7给出了电机驱动力矩$M_e$ 的时间历程图,该驱动力矩为非定常约束方程对应的约束力.
|
图 5 作用在滑块上的法向接触力 Fig. 5 Normal contact force on slider |
|
图 6 铰链A的约束力 Fig. 6 Constraint force of joint A |

|
图 7 驱动摆杆力矩 Fig. 7 Driving bar moment |
图8给出了定常约束$\left\| {{{ \varPhi }}^\ast } \right\| = \sqrt{(\phi _1^\ast )^2 + (\phi _2^\ast )^2} $的时间历程图. 其中红色线为鲍姆加藤约束稳定化方法的计算结果,其值$\left\| {{{ \varPhi }}^\ast } \right\| < 0.075$ mm,并当时间充分大时,该值趋于零; 虚线为无约束稳定化方法的计算结果. 由于该系统存在冲击与碰撞现象, 因此在没有违约修正时,计算仿真结果不满足约束方程,使运动失真. 对于非定常约束$\left\| {{\tilde{ \varPhi }}} \right\| = \left| \tilde{\phi } \right| < 10^{ - 6}$ rad.

|
图 8 $\left\| {{ \varPhi }} \right\|$的时间历程图 Fig. 8 Time history of $\left\| {{ \varPhi }} \right\|$ |
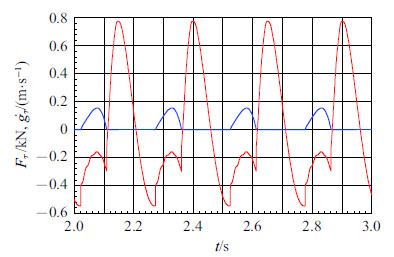
情况二: 为验证本文给出的算法的有效性,设夯机与坚硬路面的接触力参数为$K= 490$ MN/m$^{1.5}$,$c = 33$ MNs/m$^{2}$; 夯机与地面的静、动摩擦因数分别为$\mu _0 = 0.7$,$\mu = 0.52$. 为使得夯机不脱离地面, 设电机的驱动角速度$\omega = 25$ rad/s. 图9和图10分别给出了不同偏心距$e$时,地面作用于夯机上的摩擦力$F_\tau $(红色线)和接触点切向速度$\dot{g}_\tau $ (蓝色线)的时间历程图. 当$e = 0.10$ m时, 夯机始终处于黏滞状态(如图9所示),当$e = 0.15$ m时,夯机有黏滞滑移运动状态的切换(如图10所示). 该计算结果与假设刚性路面且用试算法计算出的结果完全吻合.

|
图 9 当$e = 0.1$ m时$F_\tau , \dot{g}_\tau $的时间历程图 Fig. 9 Time history of $F_\tau $ and $\dot{g}_\tau $ with $e = 0.1$ m |
|
图 10 当$e = 0.15$ m时$F_\tau , \dot{g}_\tau $的时间历程图 Fig. 10 Time history of $F_\tau $ and $\dot{g}_\tau $ with $e = 0.15$ m |
本文基于接触力学与线性互补理论,利用现有的接触力模型,将物体间的法向接触力表示成嵌入量与嵌入速度的非线性函数,因此可根据嵌入量计算接触点的法向力并由此可判断物体间的接触与分离; 接触点的摩擦力采用库伦干摩擦模型,建立了摩擦余量与接触点切向加速度的互补关系式,利用线性互补算法可判断物体接触点间的黏滞滑移运动状态的切换和静滑动摩擦力的计算; 本文给出的方法与传统方法相比,法向接触力不参与互补运算,可降低线性互补方程的维数,提高其计算效率. 应用第一类拉格朗日方程并结合鲍姆加藤约束稳定化方法,建立了具有完整理想定常约束(理想铰链约束)和非定常约束(驱动约束)平面多刚体系统动力学方程,由该动力学方程不仅可以求解系统的运动量、法向接触力、切向摩擦力,还可以求解铰链约束力和驱动约束力,弥补了原有方法的不足,并可有效地抑制约束的漂移. 最后通过算例说明了本文给出算法的有效性.
| [1] | 董富祥, 洪嘉振.多体系统动力学碰撞问题研究综述.力学进展, 2009, 39(3): 352-359 (Dong Fuxiang, Hong Jiazhen. Review of impact problem for dynamics of multibody system. Advances in Mechanics, 2009, 39(3): 352-359 (in Chinese)) |
| [2] | 曹登庆, 初世明, 李郑发, 等. 空间可展机构非光滑力学模型和动力学研究. 力学学报, 2013, 45(1): 4-14 (Cao Dengqing, Chu Shiming, Li Zhengfa, et al. Study on the non-smooth mechanical model and dynamics for space deployable mechanism. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(1): 4-14 (in Chinese)) |
| [3] | 王琪, 庄方方, 郭易圆, 等. 非光滑多体系统动力学数值算法的研究进展. 力学进展, 2013, 43(1): 101-111 (Wang Qi, Zhuang Fangfang, Guo Yiyuan, et al. Advances in the research on numerical methods for non-smooth dynamics of multibody systems. Advances in Mechanics. 2013, 43(1): 101-111 (in Chinese)) |
| [4] | 王庚祥, 刘宏昭. 多体系统动力学中关节效应模型的研究进展. 力学学报, 2015, 47(1): 31-50 (Wang Gengxiang, Liu Hongzhao. Research progress of joint effects model in multibody system dynamics. Journal of Theoretical and Applied Mechanics, 2015, 47(1): 31-50 (in Chinese)) |
| [5] | Pfeiffer F, Glocker C. Multibody Dynamics with Unilateral Contacts. New York: John Wiley & Sons. Inc.1996 |
| [6] | Flores P, mbrosio J. Kinematics and Dynamics of Multibody Systems with Imperfect Joints. Berlin: Springer, 2008 |
| [7] | 刘丽兰, 刘宏昭, 吴子英, 等. 机械系统中摩擦模型的研究进展. 力学进展, 2008, 38(2): 200-213 (Liu Lilan, Liu Hongzhao, Wu Ziying, et al. An overview of friction models in mechanical systems. Advances in Mechanics, 2008, 38(2): 200-213 (in Chinese)) |
| [8] | Machado M, Moreira P, Flores P. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mechanism and Machine Theory, 2012, 53: 99-121 |
| [9] | 刘才山, 陈滨, 王玉玲. 考虑摩擦作用的多柔体系统点面碰撞模型.中国机械工程, 2000, 11(6): 616-619 (Liu Caishan, Chen Bin, Wang Yuling. The point-surface impact model considering the friction effect in flexible multi-body system. China Mechanical Engineering, 2000, 11(6): 616-619 (in Chinese)) |
| [10] | 丁千, 翟红梅. 机械系统摩擦动力学研究进展. 力学进展, 2013, 43(1): 112-131 (Ding Qian, Zhai Hongmei. The advance in researches of friction dynamics in mechanics system. Advances in Mechanics, 2013, 43(1): 112-131 (in Chinese)) |
| [11] | Pennestri E, Valentini P P, Vita L. Multibody dynamics simulation of planar linkages with Dahl friction. Multibody Syst. Dyn., 2007, 17: 321-347 |
| [12] | Dopico D, Luaces A, Gonzalez M, et al. Dealing with multiple contacts in a human-in-the-loop application, Multibody System Dynamics, 2011, 25 (2):167-183 |
| [13] | Flores P, Ambrosio J. Translational joints with clearance in rigid multibody systems. ASME Journal of Computational and Nonlinear Dynamics, 2008, 3: 011007(1-10) |
| [14] | Pfeiffer F, Foerg M. Uibrich H. Numerical aspects of non-smooth multibody dynamics. Computer Methods in Applied Mechanics and Engineering, 2006, 195: 6891-6908 |
| [15] | Flores P, Leine R, Glocker C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody System Dynamics, 2010, 23: 165-190 |
| [16] | Anitescu1 M, Hart G D. A constraint-stabilized time-stepping approach for rigid multibody dynamics with joints, contact and friction. Int J Numer Meth Engng, 2004, 60: 2335-2371 |
| [17] | Wang Q, Peng H L, Zhuang F F. A constraint-stabilized method for multibody dynamics with friction-affected translational joints based on HLCP. Discrete and Continuous Dynamical Systems Series B, 2011, 16(2): 589-605 |
| [18] | Zhuang F F, Wang Q. Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints. Multibody Syst Dyn, 2012, 29: 403-423 |
| [19] | Zhuang F F, Wang Q. Modeling and analysis of rigid multibody systems with driving constraints and frictional translation joints. Acta Mechanica Sinica, 2014, 30(3): 437-446 |
| [20] | 王晓军, 王琪, 庄方方. 含摩擦滑移铰及驱动约束多刚体系统数值算法. 动力学与控制学报, 2014, 12(4): 335-340 (Wang Xiaojun, Wang Qi, Zhuang Fangfang. The numerical method for multibody system with frictional translational joints and driving constraints. Journal of Dynamics and Control, 2014, 12(4): 335-340 (in Chinese)) |
| [21] | 范新秀, 王琪. 车辆纵向非光滑多体动力学建模与数值算法研究. 力学学报, 2015, 47(2): 301-309 (Fan Xinxiu, Wang Qi. Research on modeling and simulation of longitudinal vehicle dynamics based on non-smooth dynamics of multibody systems. Journal of Theoretical and Applied Mechanics, 2015, 47(2): 301-309 (in Chinese)) |
| [22] | 洪嘉振. 多体系统动力学. 北京:高等教育出版社, 1999 (Hong Jiazhen. Computation Dynamics of Multi-body Systems. Beijin: Higher Education Press, 1999 (in Chinese)) |
| [23] | Neto M A, Ambrósio J. Stabilization methods for the integration of DAE in the presence of redundant constraints. Multibody Syst. Dyn., 2003, 10: 81-105 |
| [24] | Flores, P, Machado, M, Seabra, E, et al. A parametric study on the Baumgarte stabilization method for forward dynamics of constrained multibody systems. J. Comput. Nonlinear Dyn., 2011, 6(1): 011019-011027 |
| [25] | 杨孟余, 冯德成, 沙爱民, 等. 公路沥青路面设计规范. 北京: 人民交通出版社, 2006 (Yang Mengyu, Feng Decheng, Sha Aiming, et al. Specification for Design of Highway Asphalt Pavement. Beijing: China Communications Press, 2006 (in Chinese)) |
| [26] | 申爱琴, 张艳红, 郭寅川, 等. 三类沥青路面结构力学响应的对比分析.长安大学学报, 2009, 29(4):1-7 (Shen Aiqin, Zhang Yanhong, Guo Yinchuan, et al. Comparative analysis of mechanical response of three typical asphalt pavement structures. Journal of Chang'an University, 2009, 29(4): 1-7 (in Chinese)) |
2. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China
 2015, Vol. 47
2015, Vol. 47