结构和机械系统常模型化为多自由度振动系统. 由于系统中存在耦合效应,常常会产生内共振[1, 2],从而产生许多显著的 动力学现象,如能量传递、能量采集、饱和现象、振动吸收等[3, 4, 5, 6, 7, 8, 9, 10]. 作为一个简单而直观的物理模型,由一个主振子耦合一个质量$\!$-$\!$-$\!$弹\linebreak 簧$\!$-$\!$-$\!$阻尼系统的模型引起了广泛的关注. 根据系统中耦合项的结构,可能存在不同类型的内共振[11, 12]. 如果耦合项是线性的,系统中只可能存在1$\!\!\!$∶$\!\!\!$1内共振. 如果耦合项是平方非线性的,那么系统中可能存在 1$\!\!\!$∶$\!\!\!$1或者1$\!\!\!$∶$\!\!\!$2内共振. 1$\!\!\!$∶$\!\!\!$2内共振常常用来产生所谓的饱和现象,这种现象可用来吸收注入主系统的多余能量. 如果耦合项是立方非线性的,系统中可能存在3种内共振,即1$\!\!\!$∶$\!\!\!$1, 1$\!\!\!$∶$\!\!\!$2以及3$\!\!\!$∶$\!\!\!$1内共振. 3$\!\!\!$∶$\!\!\!$1内共振已被用于吸收主振子的振动[4].
上述的研究都是针对确定性系统展开的. 普遍认为,随机激励在工程中是无处不在的. 例如大气紊流、地震等[13]. 迄今为止,已有大量关于随机激励下的单自由度线性或非线性系统的随机响应以及随机稳定性的研究文献. 而对于存在内共振的多自由度随机非线性系统,相关的研究较少. 文献[14]的作者得到了多自由度拟线性系统在随机力与谐和力共同激励下稳态响应的平均精确解,讨论了内共振以及外共振的情况. 之后,他们提出了谐和力与高斯白噪声共同激励下多自由度强非线性拟可积哈密顿系统的随机平均法,研究了内共振 与外共振情形平均 系统的稳态响应[15]. 徐伟等[16]应用多尺度法研究了二自由度弱非线性耦合振子在窄带噪声激励下的稳态响应,考虑了1$\!\!\!$∶$\!\!\!$2内共 振情形,Bergman等[17]研究了 随机性对于1$\!\!\!$∶$\!\!\!$1内共振俘获情况下能量定向转移(targeted energy transfer)的影响. 张雷和吴勇军研究了谐和力与宽带噪声联合激励下耦合二自由度达芬$\!$-$\!$-$\!$范德波尔系统在外共振情形的首次穿越问题, 未考虑内共振[18]. 最近,贾万涛和朱位秋提出了高斯白噪声与泊松白噪声联合激励下拟可积哈密顿系统的随机平均法,经过复杂的推导,得到了内共振与非内共 振两种情况下系统的平均随机积分$\!$-$\!$-$\!$微分方程,进而建立了平均广义福克$\!$-$\!$-$\!$普朗克$\!$-$\!$-$\!$柯尔莫 哥洛夫方程(Fokker-$\!$-Planck-$\!$-Kolmogorov,FPK,中文简称:福普柯)方程. 求解退化广义福普柯(FPK)方程得到了稳态响应的概率密度[19, 20].
当研究受随机激励的系统的动态行为时,一个关键的问题是确定系统安全可靠地工作的概率. 一般而言,这个动力学可靠性问题可以 转化为系统的状态停留在安全域内的概率问题. 当响应状态首次离开某个安全域,系统就发生失效,这就是所谓的首次穿越(离出或退出)损坏问题[21]. 显然,内共振对系统可靠性的影响非常大. 迄今为止,对于考虑内共振的可靠性问题,文献中尚未见报道.
本文研究了二自由度耦合机械振子的动力学可靠性问题. 随机激励模型化为高斯白噪声. 推导了\linebreak 1$\!\!\!$∶$\!\!\!$1内共振情况下的平均伊藤随机微 分方程. 建立了后向柯尔莫哥洛夫方程以及庞德辽金方程,给出了相应边界条件和初始条件. 用数值方法求解这两个偏微分方程得到了系统的条件可靠性函数以及平均首次穿越时间. 为了研究内共振对可靠性的影响,建立并求解了无内共振情况的后向柯尔莫哥洛夫方程以及庞德辽金方程. 将内共振情形的结果与无内共振情形的结果进行了比较. 用蒙特卡罗数值模拟对理论结果进行了验证. 最后对结果进行了分析并给出了结论.
1 平均伊藤随机微分方程考虑如下耦合的二自由度达芬$\!$-$\!$-$\!$范德波尔系统
| $ \left.\!\! \ddot {X}_1 + (\beta _{10} + \beta _{11} X_1^2 + \beta _{12} X_2^2 )\dot {X}_1 +\\ \qquad \omega _{01}^2 X_1 + \alpha _1 X_1^3 + \eta _{12} \dot {X}_2 = W_1 (t) \\ \ddot {X}_2 + (\beta _{20} + \beta _{21} X_1^2 + \beta _{22} X_2^2 )\dot {X}_2 +\\ \qquad \omega _{02}^2 X_2 + \alpha _2 X_2^3 + \eta _{21} \dot {X}_1 = W_2 (t) \right \} $ | (1) |
式中,$\beta_{ij}$,$\omega_{0i}$,$\alpha_{i}$和 $\eta_{ij}$均为常数 ($i =1$,2,$j =0$,1,2). 其中 $\beta_{ij}$和 $\eta _{ij}$ 为阻尼系数,$\omega_{0i}$ 为退化线性系统的固有频率,$\alpha_{i}$ 为非线性刚度系数. $W_{i}(t)$是强度为$2 D_{i}$的独立高斯白噪声. 此处假定 $\beta_{ij}$, $\eta_{ij}$及$D_{i}$为小量.
根据文献[18],系统(1)的解可表示为如下的广义谐和函数形式
| $ \left. X_i (t) = A_i \cos \varPhi _i (t) \\ \dot {X}_i (t) = - A_i \nu _i (A_i ,\varPhi _i )\sin \varPhi _i (t) \right\} $ | (2) |
此处的$A_{i}$,$\varPhi_{i}$和 $\nu_{i}$均为随机过程,$A_{i}$和 $\varPhi_{i}$分别为单个振子的振幅与相位. $\nu_{ i}(A_{ i},\varPhi_{ i})$ 是系统(1)中第$i$个振子的瞬时频率,其平均频率$\omega_{i}$是振幅$A_{i}$的函数,可近似为
| $ \left. \omega _i (A_i ) = (\omega _{0i}^2 + {3\alpha _i A_i^2 }/ 4)^{1/2}(1 - {\lambda _i^2 }/{16}) \\ \lambda _i = {\alpha _i A_i^2 } \Big / {\left[{4\left( {\omega _{0i}^2 + 3{\alpha _i A_i^2 }/4} \right)} \right]} \right\} $ | (3) |
下面分两种情况推导系统(1)的平均伊藤随机微分方程.
1.1 内共振情况考虑1$\!\!\!$∶$\!\!\!$1 内共振情形,此时存在如下的频率关系
| $ \dfrac{\omega _1 (A_1 )}{\omega _2 (A_2 )} = 1\pm \varepsilon $ | (4) |
式中,$\varepsilon $为正的小参数. 引入新的慢变量$\Gamma =\varPhi_{1}- \varPhi _{2}$. 应用平均法[21],得到如下关于慢变量$A_{1}$,$A_{2}$及$\Gamma $的平均伊藤随机微分方程
| $\left. \begin{array}{l} {\rm{d}}{A_1} = \bar m_1^{(1)}({A_1},{A_2},\Gamma ){\rm{d}}t + \bar \sigma _{11}^{(1)}{\rm{d}}{B_1}(t) + \bar \sigma _{12}^{(1)}{\rm{d}}{B_2}(t)\\ {\rm{d}}{A_2} = \bar m_2^{(1)}({A_1},{A_2},\Gamma ){\rm{d}}t + \bar \sigma _{21}^{(1)}{\rm{d}}{B_1}(t) + \bar \sigma _{22}^{(1)}{\rm{d}}{B_2}(t)\\ {\rm{d}}\Gamma = \bar m_1^{(2)}({A_1},{A_2},\Gamma ){\rm{d}}t + \bar \sigma _{11}^{(2)}{\rm{d}}{B_1}(t) + \bar \sigma _{12}^{(2)}{\rm{d}}{B_2}(t) \end{array} \right\}$ | (5) |
漂移系数$\bar {m}_i^{(j)} $与扩散系数$\bar {\sigma }_{ij}^{(k)} $ ($i =1$,2 $j =1$,2,$k =1$,2)的表达式较复杂,可用科技数学软件``Mathematica''推导完成(见附录).
1.2 无内共振情况考虑无内共振情形. 此时不存在式(4)的频率关系. 此种情况下系统(1)的平均方程退化为如下仅关于振幅$A_{1}$和 $A_{2}$的伊藤随机微分方程
| $ \left.\!\! {\rm{d}} A_1 = \tilde {m}_1^{(1)} \left( {A_1 ,A_2 } \right) {\rm{d}} t + \tilde {\sigma }_{11}^{(1)} {\rm{d}} B_1 (t) + \tilde {\sigma }_{12}^{(1)} {\rm{d}} B_2 (t) \\ {\rm{d}} A_2 = \tilde {m}_2^{(1)} \left( {A_1 ,A_2 } \right) {\rm{d}} t + \tilde {\sigma }_{21}^{(1)} {\rm{d}} B_1 (t) + \tilde {\sigma }_{22}^{(1)} {\rm{d}} B_2 (t) \!\!\right\} $ | (6) |
此处漂移系数$\tilde {m}_i^{(1)} $只需将内共振情形的漂移系数$\bar {m}_i^{(1)} $中含 $\Gamma $ 的项去掉即可. 扩散系数$\tilde {\sigma }_{ij}^{(1)} $与$\bar {\sigma }_{ij}^{(1)} $相同.
2 后向柯尔莫哥洛夫方程理论上,系统(1)中每个振子的振幅$A_{i}(t)$均可在[0,$\infty )$上变化. 在(0, $t$]时间内,如果每个振子的振幅$A_{i}(t)$都小于阈值$A_{i{\rm c}}$,则可认为系统是完全可靠的(即可靠性函数为1). 相反,只要有一个振子的振幅$A_{i}(t)>A_{i{\rm c}}$,则认为系统发生了首次穿越而损坏. 为得到系统可靠性函数满足的偏微分方程,需区分共振与非共振两种情况.
2.1 内共振情况在1$\!\!\!$∶$\!\!\!$1内共振情形,系统的状态方程由式(5)决定. 条件可靠性函数定义为系统的状态停留在安全域内的概率,即
| $ R(t | A_{10} ,A_{20} ,\Gamma _0 ) = \\ \qquad P\,\Big\{A_1 (s) \in [0,A_{1{\rm c}} ) \cap A_2 (s) \in [0,A_{2{\rm c}} ),s \in (0,t] \\ \qquad | A_{i0} \in [0,A_{i{\rm c}} ),\Gamma _0 \in [0,2\pi]\,,\ i = 1,2\Big\} \hskip 17mm $ | (7) |
显然,条件可靠性函数$R$是系统的初始状态($A_{10}$,$A_{20}$,$\Gamma _{0})$以及时间$t$的函数,满足如下后向柯尔莫哥洛夫方程[21]
| $ \dfrac{\partial R}{\partial t} = \bar {m}_{10}^{(1)} \dfrac{\partial R}{\partial A_{10} } + \bar {m}_{20}^{(1)} \dfrac{\partial R}{\partial A_{20} } + \bar {m}_{10}^{(2)} \dfrac{\partial R}{\partial \Gamma _{10} } +\\ \qquad \dfrac{1}{2}\bar {b}_{110}^{(11)} \dfrac{\partial ^2R}{\partial A_{10}^2 } + \dfrac{1}{2}\bar {b}_{220}^{(11)} \dfrac{\partial ^2R}{\partial A_{20}^2 } + \dfrac{1}{2}\bar {b}_{110}^{(22)} \dfrac{\partial ^2R}{\partial \Gamma _{10}^2 } $ | (8) |
式中,$\bar {m}_{10}^{(1)} $,$\bar {m}_{20}^{(1)} $,$\bar {m}_{10}^{(2)} $,$\bar {b}_{110}^{(11)} $,$\bar {b}_{220}^{(11)} $和 $\bar {b}_{110}^{(22)} $的表达式分别与$\bar {m}_1^{(1)} $,$\bar {m}_2^{(1)} $,$\bar {m}_1^{(2)} $,$\bar {b}_{11}^{(11)} $,$\bar {b}_{22}^{(11)} $和 $\bar {b}_{11}^{(22)} $相同,只是将变量($A_{1},A_{2}$,$\Gamma $)分别代之以($A_{10},A_{20}$,$\Gamma _{0}$).
偏微分方程(8)的初始条件以及边界条件为
| $ \left.\!\! R(0 | A_{10} ,A_{20} ,\Gamma _0 ) = 1 \\ A_{i0} \in [0,A_{i{\rm c}} )\,,\ \ \Gamma _0 \in [0,2\pi] \\ \dfrac{\partial R}{\partial A_{i0} } \Big |_{A_{i0} = 0} = 0 \,,\ \ \dfrac{\partial R}{\partial \Gamma _0 } \Big |_{A_{i0} = 0} = 0 \,,\ \ \dfrac{\partial ^2R}{\partial \Gamma _0^2 } \Big |_{A_{i0} = 0} = 0 \\ R(t | A_{10} ,A_{20} ,\Gamma _0 ) = 0 \,,\ \ A_{i0} = A_{i{\rm c}} \ \ (i = 1,2) \\ R(t | A_{10} ,A_{20} ,0) = R(t | A_{10} ,A_{20} ,2\pi ) \!\!\right\} $ | (9) |
此时,系统的状态方程由式(6)决定. 类似地,系统的条件可靠性函数可定义为
| $ R(t | A_{10} ,A_{20} ) = \\ \qquad P \,\Big \{A_1 (s) \in [0,A_{1{\rm c}} ) \cap A_2 (s) \in [0,A_{2{\rm c}} ),s \in (0,t] \\ \qquad | A_{i0} \in [0,A_{i{\rm c}} ),i = 1,2 \Big\} \hskip 35mm $ | (10) |
与共振情形不同的是,此时系统的条件可靠性函数$R$为系统的初始状态($A_{10}$, $A_{20})$以及时间$t$的函数,满足如下后向柯尔莫哥洛夫方程
| $ \dfrac{\partial R}{\partial t} = \tilde {m}_{10}^{(1)} \dfrac{\partial R}{\partial A_{10} } + \tilde {m}_{20}^{(1)} \dfrac{\partial R}{\partial A_{20} } + \\ \qquad \dfrac{1}{2}\tilde {b}_{110}^{(11)} \dfrac{\partial ^2R}{\partial A_{10}^2 } + \dfrac{1}{2}\tilde {b}_{220}^{(11)} \dfrac{\partial ^2R}{\partial A_{20}^2 } $ | (11) |
此处,$\tilde {b}_{110}^{(11)} =\bar {b}_{110}^{(11)} $,$\tilde {b}_{220}^{(11)} =\bar {b}_{220}^{(11)} $. 偏微分方程(11)的初始条件以及边界条件为
| $\left. \begin{array}{l} R(0|{A_{10}},{A_{20}}) = 1{\mkern 1mu} ,\;\;{A_{i0}} \in [0,{A_{i{\rm{c}}}})\\ {\left. {\frac{{\partial R}}{{\partial {A_{i0}}}}} \right|_{{A_{i0}} = 0}} = 0\\ R(t|{A_{10}},{A_{20}}) = 0{\mkern 1mu} ,\;\;{A_{i0}} = {A_{i{\rm{c}}}}\;\;\;(i = 1,2) \end{array} \right\}$ | (12) |
后向柯尔莫哥洛夫方程(8)与(11)属于高维抛物型偏微分方程,本文采用显式有限差分格式求数值解[22],用蒙特卡罗数值模拟验证得到的结果.
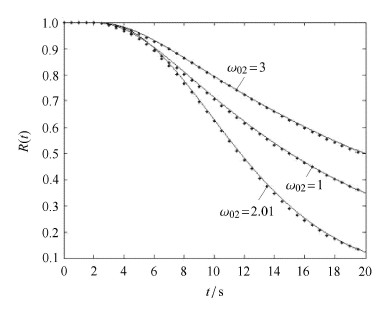
参数选取为:$A_{ic} =0.5$,$\omega_{01} =2$,$\beta_{ij} =0.01$,$\eta_{12} = \eta_{21} =0.3$, $\alpha_{1}=\alpha_{2}=1$,$D_{1} =0.03$,$D_{2} =0.006$. 为了研究内共振对系统可靠性的影响, $\omega_{02}$分别取1.0,2.01以及3,其中2.01属于1$\!\!\!$∶$\!\!\!$1内共振情况. 求解结果如图1,其中实线表示理论结果,黑点表示蒙特卡罗数值模拟结果,可以看到理论结果与数值模拟结果吻合得很好.
|
图 1 内共振情况与无内共振情况的条件可靠性函数 Fig. 1 Conditional reliability function in the case of internal resonance and non-internal resonance ($X_{10} = \dot {X}_{10} = X_{20} = \dot {X}_{20} = 0,\Gamma _0 = 0)$ |
根据定义式(10)可知,条件可靠性函数反映了系统未发生首次穿越损坏的概率,其值越大说明系统越可靠. 随着随机外激不 断地作用,系统必然会发生首次穿越损坏. 从图1可以看出,初始时刻($t=0$)系统的可靠性最大,随着时间的增加其值逐渐趋向于0. 表明时间越长,系统可靠性越低,这是符合实际规律的. 从模型方程(1)中可知,在没有内共振时,增大 $\omega_{02}$提高了第2个弹簧振子的刚度,从而可以提高系统的可靠性,对比$\omega_{02}=1$以及 $\omega_{02}=3$两种情况也能得出这一结论.
然而对于 $\omega_{02}=2.01$的情形,此时系统中存在\linebreak 1$\!\!\!$∶$\!\!\!$1内共振. 尽管提高了第2个振子的刚度,系统的可靠性反而比 $\omega_{02} =1.0$时小. 显然,这是由于内共振的产生降低了系统的可靠性.
3 庞德辽金方程 3.1 内共振情况实际情况中也对系统的平均首次穿越时间(平均寿命)感兴趣. 显然,平均首次穿越时间 $\mu $ 也是初始状态 ($A_{10}, A_{20}$,$\Gamma _{0})$的函数,由如下庞德辽金方程决定
| $ \begin{array}{l} - 1 = \bar m_{10}^{(1)}\frac{{\partial \mu }}{{\partial {A_{10}}}} + \bar m_{20}^{(1)}\frac{{\partial \mu }}{{\partial {A_{20}}}} + \bar m_{10}^{(2)}\frac{{\partial \mu }}{{\partial {\Gamma _0}}} + \\ \;\;\;\;\;\;\;\frac{1}{2}\bar b_{110}^{(11)}\frac{{{\partial ^2}\mu }}{{\partial A_{10}^2}} + \frac{1}{2}\bar b_{220}^{(11)}\frac{{{\partial ^2}\mu }}{{\partial A_{20}^2}} + \frac{1}{2}\bar b_{110}^{(22)}\frac{{{\partial ^2}\mu }}{{\partial \Gamma _0^2}} \end{array} $ | (13) |
相应的边界条件为
| $ \left. \begin{array}{l} \frac{{\partial \mu }}{{\partial {A_{i0}}}}{|_{{A_{i0}} = 0}} = 0{\mkern 1mu} ,\;\;\frac{{\partial \mu }}{{\partial {\Gamma _0}}}{|_{{A_{i0}} = 0}} = 0{\mkern 1mu} ,\;\;\frac{{{\partial ^2}\mu }}{{\partial \Gamma _0^2}}{|_{{A_{i0}} = 0}} = 0\\ \mu ({A_{10}},{A_{20}},{\Gamma _0}) = 0{\mkern 1mu} ,\;\;{A_{i0}} = {A_{i{\rm{c}}}}\;\;\;(i = 1,2)\\ \mu ({A_{10}},{A_{20}},0) = \mu ({A_{10}},{A_{20}},2\pi ) \end{array} \right\} $ | (14) |
与内共振情况类似,无内共振情况下平均首次穿越时间 $\mu $ 是初始状态($A_{10},A_{20})$的函数,由如下庞德辽金方程决定
| $ \begin{array}{l} - 1 = \tilde m_{10}^{(1)}\frac{{\partial \mu }}{{\partial {A_{10}}}} + \tilde m_{20}^{(1)}\frac{{\partial \mu }}{{\partial {A_{20}}}} + \\ \;\;\;\;\;\;\;\frac{1}{2}\tilde b_{110}^{(11)}\frac{{{\partial ^2}\mu }}{{\partial A_{10}^2}} + \frac{1}{2}\tilde b_{220}^{(11)}\frac{{{\partial ^2}\mu }}{{\partial A_{20}^2}} \end{array} $ | (15) |
相应的边界条件为
| $ \left. \begin{array}{l} {\left. {\frac{{\partial \mu }}{{\partial {A_{i0}}}}} \right|_{{A_{i0}} = 0}} = 0\\ \mu ({A_{10}},{A_{20}}) = 0{\mkern 1mu} ,\;\;{A_{i0}} = {A_{i{\rm{c}}}}\;\;\;(i = 1,2) \end{array} \right\} $ | (16) |
庞德辽金方程(13)与(15)同样也是高维偏微分方程,需要数值求解. 利用三点中心差分格式离散,然后利用超松弛迭代法求 解,计算中超松弛迭代因子取为1.75,当相邻两次迭代结果之间的绝对误差小于10$^{-5}$时,迭代结束,此时的解便是庞德辽 金方程的解,用蒙特卡罗数值模拟验证得到的结果.
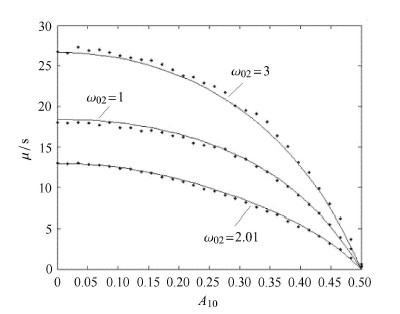
图2给出一组结果. 实线表示数值结果,黑点表示蒙特卡罗数值模拟结果. 可以看到,理论结果与数值模拟结果吻合得很好. 在 $\omega_{02}=2.01$的情形,此时系统中存在1$\!\!\!$∶$\!\!\!$1内共振. 从图1可以看出,1$\!\!\!$∶$\!\!\!$1内共振显著降低了系统的可靠性,即系统越容易发生首次穿越损坏,相应地其平均首次 穿越时间越短. 从图2可以看出,内共振的产生明显地缩短了系统平均首次穿越的时间.
|
图 2 内共振情况与无内共振情况平均首次穿越时间 Fig. 2 Mean first-passage time in the case of internal resonance and non-internal resonance |
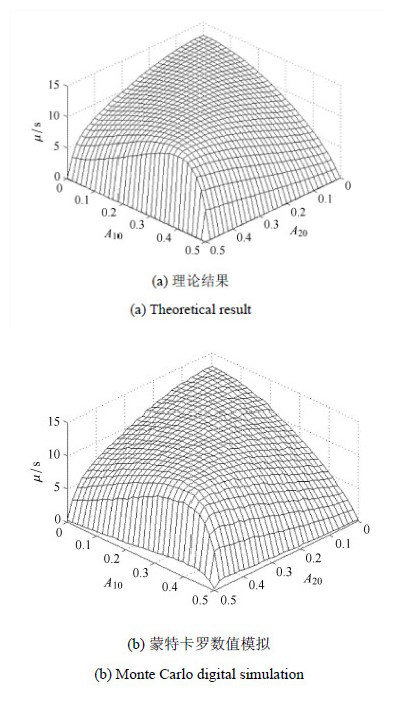
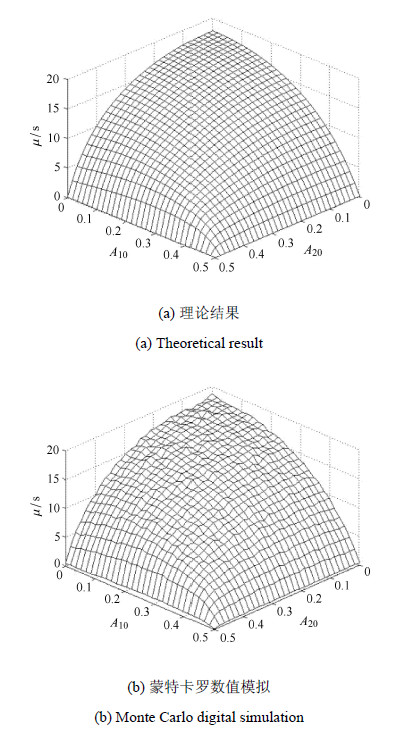
图3和图4给出了内共振情况与无内共振情况平均首次穿越时间与$A_{10}$, $A_{20}$的三维图像,内共振情况下取 $\Gamma _{0}=0$. 可以看到,理论结果与蒙特卡罗数值模拟得到的结果吻合的较好. 在普通计算机上,模拟图3(b)耗时约15小时,图4(b)耗时约20小时. 而求解偏微分方程(13),(15)仅需几分钟. 这也可以看出理论分析方法具有明显的优势.
|
图 3 内共振情况平均首次穿越时间, $\omega_{02}=2.01$ Fig. 3 Mean first-passage time in the case of internal resonance, $\omega_{02}=2.01$ |
|
图 4 无内共振情况平均首次穿越时间, $\omega_{02}=1 $ Fig. 4 Mean first-passage time in the case of non-internal resonance, $\omega_{02}=1 $ |
本文研究了二自由度耦合达芬$\!$-$\!$-$\!$范德波尔振子在高斯白噪声激励下的动力可靠性问题. 以往的文献中未研究内共振的情况. 本文分1$\!\!\!$∶$\!\!\!$1内共振以及无内共振两种情况进行了讨论. 首先将系统运动方程的解表示成广义谐和函数的形式,再利用平均法化为关于慢变量的伊藤随机微分方程,建立了可靠性函 数满足的后向柯尔莫哥洛夫方程及平均首次穿越时间满足的庞德辽金方程,给出了相应的边界条件和初始条件. 用有限差分法求解这两个偏微分方程得到了系统的条件可靠性函数及平均首次穿越时间. 理论结果与蒙特卡罗数值模拟结果吻合得很好,证明了本文的理论方法具有较高的精度.
通过比较3种情况下($\omega_{02}=1$,$\omega_{02}=2.01$, $\omega_{02}=3$)系统的条件可靠性函数及平均首次穿越时间可以看到,当 $\omega_{02}=2.01$时,由于系统中存在1$\!\!\!$∶$\!\!\!$1内共振,可靠性函数、平均首次穿越时间都比无内共振时小. 表明1$\!\!\!$∶$\!\!\!$1内共振能降低系统的可靠性,缩短系统的平均首次穿越时间(平均寿命). 这个现象提示我们,在实际工程中要尽量避免出现1$\!\!\!$∶$\!\!\!$1内共振.
需要说明的是,本文仅讨论了1$\!\!\!$∶$\!\!\!$1内共振对可靠性的影响. 其他形式的内共振(1$\!\!\!$∶$\!\!\!$2或1$\!\!\!$∶$\!\!\!$3内共振)对可靠性有何影响,尚需进一步研究. 此外,本文只讨论了高斯白噪声随机外激励的情况. 工程中常常存在周期性激励力. 如果系统(1)同时受到周期力及高斯白噪声外激作用,则在理论分析中除了讨论内共振,还需讨论外共振. 如果同时存在内外共振,那么后向柯尔莫哥洛夫方程以及庞德辽金方程维数更高,求解将会更困难. 这部分工作将在另外的文章中报道.
附:平均伊藤随机微分方程(5) 的漂移以及扩散系数
| $\begin{array}{l} \bar m_i^{(1)} = \bar m_{i1}^{(1)} + \bar m_{i2}^{(1)}\\ \bar m_{i1}^{(1)} = \left\{ { - 4{A_i}\left[{4{\beta _{i0}} + A_i^2{\beta _{ii}} + } \right.2\left. {{\beta _{ij}}A_j^2} \right]} \right. + \frac{{12A_i^3{D_i}\alpha _i^2}}{{{{\left( {A_i^2{\alpha _i} + \omega _{0i}^2} \right)}^3}}} - \frac{{26{D_i}{A_i}{\alpha _i}}}{{{{\left( {A_i^2{\alpha _i} + \omega _{0i}^2} \right)}^2}}} + \\ \qquad [16{D_i} + A_i^6{\alpha _i}{\beta _{ii}} + 3A_i^4{\alpha _i}\left( {2{\beta _{i0}} + A_j^2{\beta _{ij}}} \right)]/\left. {\left[{{A_i}\left( {A_i^2{\alpha _i} + \omega _{0i}^2} \right)} \right]} \right\}/32\\ \bar m_{i2}^{(1)} = {A_i}A_j^2{\beta _{ij}}\left( {{\alpha _i}A_i^2 + 2\omega _{0i}^2} \right)\cos \left( {2\Gamma } \right)/\left[{16\left( {{\alpha _i}A_i^2 + \omega _{0i}^2} \right)} \right] - \\ \qquad {A_j}\left[{2{b_{10}}\left( {{A_1}} \right) - {b_{12}}\left( {{A_1}} \right)} \right]\left[{2{b_{20}}\left( {{A_2}} \right) - {b_{22}}\left( {{A_2}} \right)} \right]{\eta _{ij}}\cos \Gamma /\left[{8\left( {{\alpha _i}A_i^2 + \omega _{0i}^2} \right)} \right] - \\ \qquad {A_j}\left[{{b_{12}}\left( {{A_1}} \right) - {b_{14}}\left( {{A_1}} \right)} \right]\left[{{b_{22}}\left( {{A_2}} \right) - {b_{24}}\left( {{A_2}} \right)} \right]{\eta _{ij}}\cos 3\Gamma /\left[{8\left( {{\alpha _i}A_i^2 + \omega _{0i}^2} \right)} \right] - \\ \qquad {A_j}\left[{{b_{14}}\left( {{A_1}} \right) - {b_{16}}\left( {{A_1}} \right)} \right]\left[{{b_{24}}\left( {{A_2}} \right) - {b_{26}}\left( {{A_2}} \right)} \right]{\eta _{ij}}\cos 5\Gamma /\left[{8\left( {{\alpha _i}A_i^2 + \omega _{0i}^2} \right)} \right] - \\ \qquad {A_j}{b_{16}}\left( {{A_1}} \right){b_{26}}\left( {{A_2}} \right){\eta _{ij}}\cos 7\Gamma /\left[{8\left( {{\alpha _i}A_i^2 + \omega _{0i}^2} \right)} \right]{\mkern 1mu} ,\\ \qquad \left( {i,j = 1,2{\mkern 1mu} ;\;\;i \ne j{\mkern 1mu} ;\;{\rm{no}}\;{\rm{summation}}\;{\rm{about}}\;i} \right)\\ \bar m_1^{(2)} = {b_{10}}({A_1}) - {b_{20}}({A_2}) - A_2^2{\beta _{12}}\left( {3{\alpha _1}A_1^2 + 4\omega _{01}^2} \right)\left. {\sin \left( {2\Gamma } \right)} \right]/\left[{32\left( {{\alpha _1}A_1^2 + \omega _{01}^2} \right)} \right] - \\ \qquad A_1^2{\beta _{21}}\left( {3{\alpha _2}A_2^2 + 4\omega _{02}^2} \right)\sin \left( {2\Gamma } \right)/\left[{32\left( {{\alpha _2}A_2^2 + \omega _{02}^2} \right)} \right] + \\ \qquad {A_2}\left[{2{b_{10}}\left( {{A_1}} \right) + {b_{12}}\left( {{A_1}} \right)} \right]\left[{2{b_{20}}\left( {{A_2}} \right) - {b_{22}}\left( {{A_2}} \right)} \right]{\eta _{12}}\sin \Gamma /\left[{8{A_1}\left( {{\alpha _1}A_1^2 + \omega _{01}^2} \right)} \right] + \\ \qquad {A_2}\left[{{b_{12}}\left( {{A_1}} \right) + {b_{14}}\left( {{A_1}} \right)} \right]\left[{{b_{22}}\left( {{A_2}} \right) - {b_{24}}\left( {{A_2}} \right)} \right]{\eta _{12}}\sin 3\Gamma /\left[{8{A_1}\left( {{\alpha _1}A_1^2 + \omega _{01}^2} \right)} \right] + \\ \qquad {A_2}\left[{{b_{14}}\left( {{A_1}} \right) + {b_{16}}\left( {{A_1}} \right)} \right]\left[{{b_{24}}\left( {{A_2}} \right) - {b_{26}}\left( {{A_2}} \right)} \right]{\eta _{12}}\sin 5\Gamma /\left[{8{A_1}\left( {{\alpha _1}A_1^2 + \omega _{01}^2} \right)} \right] + \\ \qquad {A_2}{b_{16}}\left( {{A_1}} \right){b_{26}}\left( {{A_2}} \right){\eta _{12}}\sin 7\Gamma /\left[{8{A_1}\left( {{\alpha _1}A_1^2{\rm{ + }}\omega _{01}^2} \right)} \right] + \\ \qquad {A_1}\left[{2{b_{10}}\left( {{A_1}} \right) - {b_{12}}\left( {{A_1}} \right)} \right]\left[{2{b_{20}}\left( {{A_2}} \right) + {b_{22}}\left( {{A_2}} \right)} \right]{\eta _{21}}\sin \Gamma /\left[{8{A_2}\left( {{\alpha _2}A_2^2 + \omega _{02}^2} \right)} \right] + \\ \qquad {A_1}\left[{{b_{12}}\left( {{A_1}} \right) - {b_{14}}\left( {{A_1}} \right)} \right]\left[{{b_{22}}\left( {{A_2}} \right) + {b_{24}}\left( {{A_2}} \right)} \right]{\eta _{21}}\sin 3\Gamma /\left[{8{A_2}\left( {{\alpha _2}A_2^2 + \omega _{02}^2} \right)} \right] + \\ \qquad {A_1}\left[{{b_{14}}\left( {{A_1}} \right) - {b_{16}}\left( {{A_1}} \right)} \right]\left[{{b_{24}}\left( {{A_2}} \right) + {b_{26}}\left( {{A_2}} \right)} \right]{\eta _{21}}\sin 5\Gamma /\left[{8{A_2}\left( {{\alpha _2}A_2^2 + \omega _{02}^2} \right)} \right] + \\ \qquad {A_1}{b_{16}}\left( {{A_1}} \right){b_{26}}\left( {{A_2}} \right){\eta _{21}}\sin 7\Gamma /\left[{8{A_2}\left( {{\alpha _2}A_2^2 + \omega _{02}^2} \right)} \right]\\ {b_{i0}}\left( {{A_i}} \right) = {\left( {\omega _{0i}^2 + 3{\alpha _i}A_i^2/4} \right)^{1/2}}\left( {1 - \lambda _i^2/16} \right)\\ {b_{i2}}\left( {{A_i}} \right) = {\left( {\omega _{0i}^2 + 3{\alpha _i}A_i^2/4} \right)^{1/2}}\left( {{\lambda _i}/2 + \lambda _i^3/64} \right)\\ {b_{i4}}\left( {{A_i}} \right) = {\left( {\omega _{0i}^2 + 3{\alpha _i}A_i^2/4} \right)^{1/2}}\left( { - \lambda _i^2/16} \right)\\ {b_{i6}}\left( {{A_i}} \right) = {\left( {\omega _{0i}^2 + 3{\alpha _i}A_i^2/4} \right)^{1/2}}\left( {\lambda _i^3/64} \right)\\ {\lambda _i} = {\alpha _i}A_i^2/\left[{4\left( {\omega _{0i}^2 + 3{\alpha _i}A_i^2/4} \right)} \right]\\ \bar b_{ii}^{(11)} = \bar \sigma _{i1}^{(1)}\bar \sigma _{i1}^{(1)} + \bar \sigma _{i2}^{(1)}\bar \sigma _{i2}^{(1)} = {D_i}\omega _{0i}^2/{\left( {A_i^2{\alpha _i} + \omega _{0i}^2} \right)^2} + 5A_i^2{D_i}{\alpha _i}/\left[{8{{\left( {A_i^2{\alpha _i} + \omega _{0i}^2} \right)}^2}} \right]{\mkern 1mu} ,\\ \qquad (i = 1,2,\;{\rm{no}}\;{\rm{summation}}\;{\rm{about}}\;i)\\ \bar b_{11}^{(22)} = \bar \sigma _{11}^{(2)}\bar \sigma _{11}^{(2)} + \bar \sigma _{12}^{(2)}\bar \sigma _{12}^{(2)} = {D_1}\left( {7A_1^2{\alpha _1} + 8\omega _{01}^2} \right)/\left[{8{{\left( {A_1^3{\alpha _1} + \omega _{01}^2{A_1}} \right)}^2}} \right] \end{array}$ |
| [1] | 吴志强, 陈世栋, 雷娜等. 三层结构模型的内共振和组合共振. 振动与冲击, 2014, 33(8): 1-3 (Wu Zhiqiang, Chen Shidong, Lei Na, et al. Internal and combinational resonances of a three-story structure. Journal of Vibration and Shock, 2014, 33(8): 1-3 (in Chinese)) |
| [2] | 熊柳杨, 张国策, 丁虎等. 黏弹性屈曲梁非线性内共振稳态周期响应. 应用数学和力学, 2014, 35(11): 1188-1196 (Xiong Liuyang, Zhang Guoce, Ding Hu, et al. Steady state periodic responses of a viscoelastic buckled beam in nonlinear internal resonance. Applied Mathematics and Mechanics, 2014, 35(11): 1188-1196 (in Chinese)) |
| [3] | Karimpour H, Eftekhari M. Exploiting internal resonance for vibration suppression and energy harvesting from structures using an inner mounted oscillator. Nonlinear Dynamics, 2014, 77: 699-727. |
| [4] | Ji JC. Design of a nonlinear vibration absorber using three-to-one internal resonances. Mechanical Systems and Signal Processing , 2014, 42: 236-246. |
| [5] | Plaksiy KY, Mikhlin YV. Dynamics of nonlinear dissipative systems in the vicinity of resonance. Journal of Sound and Vibration , 2015, 334: 319-337. |
| [6] | Zhang YL, Chen LQ. External and internal resonances of the pipe conveying fluid in the supercritical regime. Journal of Sound and Vibration , 2013, 332: 2318-2337. |
| [7] | Sayed M, Kamel M. Non-linear normal forced vibration modes in systems with internal resonance. Applied Mathematical Modelling, 2012, 36: 310-332. |
| [8] | Beltrán-Carbajal F, Silva-Navarro G. Active vibration control in Duffing mechanical systems using dynamic vibration absorbers. Journal of Sound and Vibration, 2014, 333: 3019-3030. |
| [9] | Ji JC, Zhang N. Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber. Journal of Sound and Vibration, 2010, 329: 2044-2056. |
| [10] | Kerschen GT, Michael D. Experimental demonstration of transient resonance capture in a system of two coupled oscillators with essential stiffness nonlinearity. Journal of Sound and Vibration, 2007, 299: 822-838. |
| [11] | 胡海岩. 应用非线性动力学. 北京:航空工业出版社,2000 (Hu Haiyan. Applied Nonlinear Dynamics. Beijing: Aeronautic Industry Press, 2000 (in Chinese)) |
| [12] | 褚亦清, 李翠英. 非线性振动分析. 北京:北京理工大学出版社,1996 (Zhu Yiqing, Li Cuiying. Nonlinear Vibration Analyze. Beijing: Beijing Institute of Technology Press, 1996 (in Chinese)) |
| [13] | 朱位秋. 随机振动. 北京: 科学出版社,1998 (Zhu Weiqiu. Random Vibration. Beijing: Science Press, 1998 (in Chinese)) |
| [14] | Huang ZL, Zhu WQ. Exact stationary solutions of averaged equations of stochastically and harmonically excited MDOF quasi-linear systems with internal and or external resonances. Journal of Sound and Vibration, 1997, 204(2): 249-258. |
| [15] | Huang ZL, Zhu WQ. Stochastic averaging of quasi-integrable Hamiltonian systems under combined harmonic and white noise excitations. International Journal of Non-Linear Mechanics, 2004, 39: 1421-1434. |
| [16] | Xu W, He Q, Rong HW, et al. One-to-two internal resonance in two-degrees-of-freedom nonlinear system with narrow-band excitations. Nonlinear Dynamics, 2002, 27: 385-395. |
| [17] | Sapsis TP, Vakakis AF, Bergman LA. Effect of stochasticity on targeted energy transfer from a linear medium to a strongly nonlinear attachment. Probabilistic Engineering Mechanics, 2011, 26: 119-133. |
| [18] | 张雷,吴勇军. 外共振耦合Duffing-van der Pol系统的首次穿越. 力学学报, 2012, 44(2): 437-446 (Zhang Lei, Wu Yongjun. First-passage of coupled Duffing-Van Der Pol system in the case of external resonance. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(2): 437-446 (in Chinese)) |
| [19] | Jia WT, Zhu WQ. Stochastic averaging of quasi-integrable and non-resonant Hamiltonian systems under combined Gaussian and Poisson white noise excitations. Nonlinear Dynamics , 2014, 76(2): 1271-1289. |
| [20] | Jia WT, Zhu WQ. Stochastic averaging of quasi-integrable and resonant hamiltonian systems under combined gaussian and poisson white noise excitations. Journal of Applied Mechanics- ASME, 2014, 81(4): 041009-13 |
| [21] | 朱位秋. 非线性随机动力学与控制---Hamilton理论体系框架. 北京: 科学出版社,2003 (Zhu Weiqiu. Nonlinear Stochastic Dynamics and Control--Hamiltonian Theoretical Framework. Beijing: Science Press, 2003 (in Chinese)) |
| [22] | 陆金甫, 关治. 偏微分方程数值解法. 北京:清华大学出版社,2004 (Lu Jinfu, Guan Zhi. Numerical Methods for Partial Differential Equations. Beijing: Tsinghua University Press, 2004 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47