2. 航天飞行动力学技术重点实验室, 西安710072
航天器集群编队,从编队飞行的概念演化而来,随着现代小卫星的迅速发展而出现的一种新的航天器空间运行模式. 集群编队是 指多个航天器在无特定任务需求时利用自然力维持松散构形,而在执行任务时稍加控制,保持一定的构形,协同飞行,完成单个 大型航天器无法完成的任务. 在轨飞行过程中,各航天器彼此密切联系,通过星间通信链路实现信息共享,统一规划各航天器的运动状态,协同完成特定的空 间任务,在空间操作和对地观测等领域均有重要应用. 集群编队不同于传统意义编队飞行之处主要在于,其不需要实时保持特定构形,仅仅保证相对运动的有界约束,编队航天器之间 做周期或者准周期相对运动. 这样可以减小相对运动状态到达约束边界的机会,从而减少控制系统的启动次数,节省星上有限燃料.
由于一些编队任务周期较长,需要几个月甚至几年进行观测,如果利用航天器自身携带的推进剂进行长时间保持航天器的相对轨 道,则需要消耗大量的燃料. 另外,对于一些集群编队微小卫星来说,不仅星上能源有限,机动能力更加受到限制. 所以,如何充分利用自然力进行周期性相对轨道设计成为了近些年一些学者的研究重点[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]. 大量的研究结果表明,合理地选择初始条件可以大大减小燃料消耗. 然而,空间环境特别复杂,各种摄动力,例如地球非球形摄动力、太阳光压力、大气阻力作用显著,推力发动机也存在偏差, 这些因素都会导致相对构形的初始化误差. 因此,如何利用较少的机动次数,并充分结合自然力来实现多航天器集群编队的周期性相对运动,是十分具有理论及现实意义的.
构形初始化方面,有学者利用小参数摄动级数展开法求解非线性相对运动方程得到二阶解析解,进而给出考虑二阶引力项时的 周期性初始条件,用来修正基于线性解的误差[1]. 有人基于能量匹配原理,推导出在引力非线性和无摄动条件下任意时刻需要满足的周期性约束方程[2]. 更多人给出了在考虑非球形摄动时产生准周期相对运动的算法[3- 11]. 如果初始化出现误差,则需要进行修正. 还有人利用脉冲对平均轨道要素进行反馈控制,但是由于编队航天器相对导航输出参数为相对状态,因此利用平均轨道要素 进行控制时,需要进行相应的转换,会导致控制精度降低[12]. 有学者提出了集群编队的循环控制算法[13, 14, 15],还有一些学者基于一致性理论进行多航天器协同控 制[16, 17]. 文献[2]仅仅针对主从式航天器,给出了最优单脉冲修正策略,而对于无实际领导者模式的集群甚至蜂拥空间分布式系统,则需 要做出改进,这正是本文研究的重点.
综上所述,一个问题亟待解决:当集群航天器只有虚拟主航天器(无实际领导者),并存在初始化误差时,如何通过尽可能 少的机动次数,来保证各成员围绕虚拟主航天器做周期性相对运动,并且燃料最省?或者说,是否存在一个最优参考长半 轴以及最优机动时刻,使得各航天器在这些时刻只进行一次脉冲机动,就能维持周期性相对运动,并最省燃料?为此, 本文提出了一种航天器集群编队飞行最优单脉冲机动策略,对传统主从式编队的最优性条件进行了扩展. 针对不同的任务需求,对机动时刻给定和机动时刻未定情况下的最优性问题进行探讨. 并将它们分别转化为对一元二次方程求极值或单零点方程求根,以及多零点方程求根,极大地简化了问题. 另外,由于每个航天器携带的燃料有差异,即机动能力不同,本文在推导中考虑了权值.
1 动力学模型首先定义相关坐标系.
赤道惯性坐标系$\mathcal{I}$:原点$O$为地心,单位矢量$\hat{\pmb X}$指向春分点,$\hat{\pmb Z}$指向地球北极, $\hat{\pmb Y}$在赤道平面内,构成右手坐标系.
轨道坐标系$\mathcal{L}$ (LVLH坐标系):原点$o$为航天器的质心,单位矢量$ \hat {\pmb x}$由地心指向航天器,$\hat{\pmb z}$与航天器瞬时角动量方向一致,$\hat{\pmb y}$由右手法则确定.
速度坐标系$\mathcal{T}$:原点$o$为航天器的质心,单位矢量$\hat{\pmb t}$沿速度方向,$\hat{\pmb h }$沿航天器轨道角动量方向,$ \hat {\pmb n}$由右手法则确定.
文中约定以下标$C$和$i$分别代表虚拟主航天器和第$i$个(从)航天器,其中,$i = 1,2,\cdots$. 令$\left[{ {\pmb\rho}_i } \right]_{\mathcal{L}_{\rm C} } = \left[{ {\pmb r}_i } \right]_{\mathcal{L}_{\rm C} } - \left[ { {\pmb r}_{\rm C} } \right]_{\mathcal{L}_{\rm C} } \triangleq \left[{x_i},\ \ {y_i},\ \ {z_i } \right]^{\rm T}$,则在轨道坐标系$\mathcal{L}_{\rm C} $中建立相对运动方程为
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} {{\ddot x}_i} - 2{{\dot f}_{\rm{C}}}{{\dot y}_i} - \dot f_{\rm{C}}^2{x_i} - {{\ddot f}_{\rm{C}}}{y_i} = \frac{\mu }{{r_{\rm{C}}^2}} - \frac{{\mu \left( {{r_{\rm{C}}} + {x_i}} \right)}}{{{{\left[ {{{\left( {{r_{\rm{C}}} + {x_i}} \right)}^2} + y_i^2 + z_i^2} \right]}^{{\textstyle{3 \over 2}}}}}}\\ {{\ddot y}_i} + 2{{\dot f}_{\rm{C}}}{{\dot x}_i} + {{\ddot f}_{\rm{C}}}{x_i} - \dot f_{\rm{C}}^2{y_i} = - \frac{{\mu {y_i}}}{{{{\left[ {{{\left( {{r_{\rm{C}}} + {x_i}} \right)}^2} + y_i^2 + z_i^2} \right]}^{{\textstyle{3 \over 2}}}}}}\\ {{\ddot z}_i} = - \frac{{\mu {z_i}}}{{{{\left[ {{{\left( {{r_{\rm{C}}} + {x_i}} \right)}^2} + y_i^2 + z_i^2} \right]}^{{\textstyle{3 \over 2}}}}}} \end{array} \end{array}} \right\}$ | (1) |
其中,$\mu $为引力常数,$f_{\rm C} $为虚拟主航天器的真近点角. 虚拟主航天器的向径
| $ r_{\rm C} = \left\| { {\pmb r}_{\rm C} } \right\|_2 = \dfrac{a_{\rm C} \left( {1 - e_{\rm C}^2 } \right)}{1 + e_{\rm C} \cos f_{\rm C} } $ | (2) |
虚拟主航天器角速度为
| $ \dot {f}_{\rm C} = \dfrac{n_{\rm C} \left( {1 + e_{\rm C} \cos f_{\rm C} } \right)^2}{\left( {1 - e_{\rm C}^2 } \right)^{\tfrac{3}{2}}} $ | (3) |
式中,$n_{\rm C} = \sqrt {\mu / a_{\rm C}^3 } $为主航天器轨道平均角速度.
虚拟主航天器角加速度
| $ \ddot {f}_{\rm C} = \dfrac{ - 2e_{\rm C} n_{\rm C}^2 \left( {1 + e_{\rm C} \cos f_{\rm C} } \right)^2\sin f_{\rm C} }{\left( {1 - e_{\rm C}^2 } \right)^3} $ | (4) |
联立方程(1)$\sim$(4)即为在集群中各航天器在虚拟主航天器坐标系$\mathcal{L}_{\rm C}$中的相对运动模型.
2 最优单脉冲机动假设由于初始化误差的影响,各航天器$S_i $的机械能或长半轴不能精确匹配,使得周期性条件被破坏 [2],导致相对轨道在短时间内发生发散现象,因此需要进行修正. 假设坐标系$\mathcal{T}$中,摄动或控制加速${\pmb d}$具有如下形式
| $ {\pmb d} = d_n \hat{\pmb n } + d_t \hat{\pmb t } + d_h \hat{\pmb h } = \left[{d_n },\ \ {d_t },\ \ {d_h } \right]^{\rm T} $ | (5) |
其中,$d_n $,$d_t $,$d_h $分别为${\pmb d}$在$\hat{\pmb n}$,$\hat{\pmb t}$,$\hat{\pmb h}$方向的分量. 由于在二体问题中,长半轴唯一地决定了轨道的周期,因此只给出关于长半轴的高斯变分方程
| $ \dfrac{{\rm{d}} a}{{\rm{d}} t} = \dfrac{2a^2v}{\mu }d_t $ | (6) |
其中,$a$为长半轴,$v = \left\| {\pmb v} \right\|_2 = \sqrt {\mu / p\left( {1 + 2e\cos f + e^2} \right)} $,为航天器的速度大小,$p = a\left( {1 - e^2} \right)$为半通径.
这里假定速度脉冲是在瞬时施加的,则在无限小的时间区间内,有
| $ \mathop {\lim }\limits_{ \Delta t \to 0} \dfrac{{\rm{d}} a}{{\rm{d}} t} \cdot {\Delta }t = {\Delta }a\,,\ \ \mathop {\lim }\limits_{ \Delta t \to 0} d_t \cdot \Delta t = \Delta v_t $ | (7) |
其中,$ \Delta v_t $为施加的切向速度. 因此,长半轴修正量与所施加的切向速度脉冲之间的关系为
| $ \Delta a = \dfrac{2a^2v}{\mu } \Delta v_t $ | (8) |
本文假设脉冲施加的方向是可变的,因而选取施加速度脉冲的二范数作为性能指标. 接下来对机动时刻给定和未定两种情况分别展开讨论.
这里对性能指标的选取做下说明:如果仅从燃料消耗的角度,选择所有航天器燃料消耗的一范数之和为性能指标更具工程意义. 但是,这会造成一些航天器燃料消耗过大,而另一些几乎无消耗的情况,降低编队任务的整体寿命. 因此,为了弱化此问题,本文基于燃料消耗均衡的考虑,选择所有航天器燃料消耗的二范数之和为性能指标,寻求二范数意义下的最优解.
2.1 机动时刻给定对于由$n$个航天器形成的集群编队,假设在$t = \tilde {t}$时所有编队航天器需要执行任务,即在给定的$t_1 = t_2 = \cdots = t_n = \tilde {t}$时刻同时进行脉冲机动,所以机动前编队航天器的状态矢量已知. 因此,可以基于式(8)推导最优速度脉冲. 于是,该问题可以描述为:在$t_i = \tilde {t}$时刻,集群中各航天器施加一次脉冲,使得机动后各航天器的长半轴达到一致,均为$\tilde {a}^ * $(称为最优参考长半轴),从而满足周期性约束条件,同时达到能量最省
| $ J^2\left( {\tilde {a}^ * } \right) = \min \sum {} _{i = 1}^n {\tilde {k}_i \left\| {\left[{ \Delta {\pmb v}_i } \right]_{{\cal T}_i } } \right\|_2^2 } $ | (9) |
其中,$\tilde {k}_i $为权值,代表第$i$个航天器机动能力的大小,$\tilde {k}_i $越大表示机动能力越强.
由高斯变分方程可知,要改变长半轴,最佳的施加脉冲方向为沿着航天器运动速度方向. 因此,在坐标系$\mathcal{T}_i $中,有$\left[{ \Delta {\pmb v}_i } \right]_{\mathcal{T}_i } = \left[0,\ \ \Delta v_i ,\ \ 0 \right]^{\rm T}$. 联立方程(8)和(9)得到
| $ J^2\left( \tilde {a} \right) = \sum {} _{i = 1}^n {\tilde {k}_i \dfrac{\mu ^2}{4a_i^4 v_i^2 }\left( {\tilde {a} - a_i } \right)^2} $ | (10) |
因此,最优性问题被转化为对一个一元二次方程求极值. 令
| $ \dfrac{\partial J^2\left( \tilde {a} \right)}{\partial \tilde {a}} = 0 $ | (11) |
并进行化简,得到
| $ \tilde {a}^ * = \dfrac{\sum {} _{i = 1}^n {\left( {\tilde {k}_i a_i \cdot \prod\limits_{j = 1,j \ne i}^n {a_j^4 v_j^2 } } \right)} }{\sum {} _{i = 1}^n {\left( {\tilde {k}_i \cdot \prod\limits_{j = 1,j \ne i}^n {a_j^4 v_j^2 } } \right)} } $ | (12) |
此问题同样可以通过能量匹配原理来求解. 在考虑引力非线性时,要维持周期性相对运动,集群编队航天器的机械能应该严格相等. 文献[2]基于能量匹配原理,给出了考虑非线性引力项时,周期性相对运动的充要条件
| $ \varepsilon _i = \dfrac{1}{2}\left\| { {\pmb v }_i } \right\|_2^2 - \dfrac{\mu }{r_i } = - \dfrac{\mu }{2a_{\rm C} } = \varepsilon _{\rm C} $ | (13) |
其中,$\varepsilon $表示单个航天器的机械能. 在坐标系$\mathcal{L}_{\rm C} $中,第$i$个航天器的速度和位置矢量
| $\left[{{\pmb v}_i } \right]_{\mathcal{L}_C } = \left[\dot {x}_i + \dot {r}_{\rm C} - \dot {f}_{\rm C} y_i ,\ \ \dot {y}_i + \dot {f}_{\rm C} x_i + \dot {f}_{\rm C} r_{\rm C} ,\ \ \dot {z}_i \right]^{\rm T} $ | (14) |
| $\left[{{\pmb r}_i } \right]_{\mathcal{L}_{\rm C} } = \left[{ r_{\rm C} + x_i ,\ \ y_i ,\ \ z_i } \right]^{\rm T} $ | (15) |
将式(13)视为等式约束,基于拉格朗日乘子法,构造函数
| $ {\varPhi } = \sum {} _{i = 1}^n {\tilde {k}_i \left\| {\left[ { \Delta {\pmb v}_i } \right]_{\mathcal{L}_C } } \right\|_2^2 } + \sum {} _{i = 1}^n {\lambda _i \left( {\varepsilon _i^ + + \dfrac{\mu }{2\tilde {a}}} \right)} $ | (16) |
其中,$\left[{ \Delta {\pmb v}_i } \right]_{\mathcal{L}_C } = \left[\Delta v_{xi} ,\ \ \Delta v_{yi} ,\ \ \Delta v_{zi} \right]^{\rm T}$,代表坐标系$\mathcal{L}_C $中所施加的速度脉冲,$\lambda _i $为拉格朗日乘子,$\varepsilon _i^ + $为施加脉冲后每个航天器的机械能.
在主从模式的编队飞行中,主航天器的长半轴为已知量,而对于本文探讨的无主航天器集群编队问题,则$\tilde {a}$必须视为待定量,因此需要满足
| $ \dfrac{\partial {\varPhi }}{\partial \tilde {a}} = 0 $ | (17) |
通过化简,式(17)等价于
| $ \sum {} _{i = 1}^n {\lambda _i } = 0 $ | (18) |
最优性条件的确定还需要以下各式成立
| $ {\dfrac{\partial {\varPhi }}{\partial \lambda _i } = 0,} \ \ {\dfrac{\partial {\varPhi }}{\partial \left[{ {\Delta }{\pmb v}_i } \right]_{\mathcal{L}_C } } = {\bf 0 }_{3\times 1} ,} \ \ {\dfrac{\partial ^2 {\varPhi }}{\partial \left[{ {\Delta }{\pmb v }_i } \right]_{\mathcal{L}_C }^2 } > {\bf 0 }_{3\times 3} } $ | (19) |
联立式(17)和(19),得到一个含有$4n+1$个未知量的方程组,可以唯一求解. 经过一系列数学运算,得到最优参考长半轴$\tilde {a}^ * $满足
| $ \sum {} _{i = 1}^n {\sqrt {\dfrac{\left( {2a_i - r_i } \right)\tilde {a}^ * }{\left( {2\tilde {a}^ * - r_i } \right)a_i }} = } \sum {} _{i = 1}^n {\tilde {k}_i } $ | (20) |
式(12)与式(20)虽然是基于不同的思路得到的最优解$ {\Delta }{\pmb v}_i^ * $,但都是基于周期性约束条件,因此它们是等价的. 在航天器速度坐标系$\mathcal{T}_i $与轨道坐标系$\mathcal{L}_i $中所施加的速度脉冲,有如下转换关系
| $ {\left[ {\Delta {v_i}} \right]_{{\Gamma _i}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\gamma _i}}&{\sin {\gamma _i}}&0\\ { - \sin {\gamma _i}}&{\cos {\gamma _i}}&0\\ 0&0&1 \end{array}} \right]{\left[ {\Delta {v_i}} \right]_{{\Gamma _i}}} $ | (21) |
其中,$\gamma _i $为飞行路径角,满足关系式
| $ \cos \gamma _i = \dfrac{1 + e_i \cos f_i }{\sqrt {1 + 2e_i \cos f_i + e_i^2 } } $ | (22) |
另外,$\left[{ {\Delta }{\pmb v}_i } \right]_{\mathcal{L}_i } $与$\left[{ {\Delta }{\pmb v}_i } \right]_{\mathcal{L}_{\rm C} } $的转换也可通过坐标转换得到[18],这里不再赘述.
2.2 机动时刻未定如果集群编队航天器机动时刻未定,可依任务需求进行自由选择,则待优化变量不仅包含参考长半轴$\bar {a}$,还有公共的机动时刻$t_1 = t_2 = \cdots = t_n = \bar {t}$. 于是该问题可描述为:选取公共的最优机动时刻$t_i = \bar {t}^ * $,各集群航天器在最优机动时刻分别施加一次速度脉冲,机动后各航天器的长半轴达到一致,均为$\bar {a}^ * $,满足周期性约束条件,同时达到能量最省
| $ J^2\left( {\bar {a}^ * ,\bar {t}^ * } \right) = \min \sum {} _{i = 1}^n {\bar {k}_i \left\| {\left[{ {\Delta }{\pmb v}_i } \right]_{\mathcal{T}_i } } \right\|_2^2 } $ | (23) |
第2.1节探讨的问题只含有一个待优化变量$\tilde {a}$,因此利用式(11)或(17)便可直接求得$\tilde {a}^ * $. 而如果机动时刻不定,则式(10)中各航天器的速度大小必须视为变量,随各自的真近点角$f_i $变化. 因此,为了降低待优化变量的数目,可考虑借助$f_i \mapsto \bar {t}$的映射,将式(23)转化为只含有变量$\bar {a}$和$\bar {t}$的函数,以减小计算量. 对于在开普勒轨道上运行的各航天器,有
| $\sin E_i = \dfrac{\sqrt {1 - e_i^2 } \sin f_i }{1 + e_i \cos f_i } $ | (24) |
| $M_i = E_i - e_i \sin E_i = n_i \left( {\bar {t} - \bar {t}_{0_i } } \right) $ | (25) |
其中$\bar {t}_{0_i } $表示第$i$个航天器经过其近地点的时刻.
将式(24)和式(25)代入式(23),得到关于时间$\bar {t}$的一元函数,由于式(25)为超越方程,无法直接解析求解最优速度脉冲$ {\Delta }{\pmb v}_i^ * $,需要迭代计算. 为了减小数值积分计算量,并得到显含时间$\bar {t}$的表达式,可通过傅里叶$\!$-$\!$-$\!$贝塞尔级数将$f_i $按照$\bar {t}$进行展开[19]
| $ f_i = M_i + 2\sum {} _{\kappa = 1}^\infty {\dfrac{1}{\kappa }} \left[ {\sum {} _{\eta = - \infty }^{ + \infty } { {\rm J}_\nu \left( { - \kappa e_i } \right)\beta _i^{\left| {\kappa + \eta } \right|} } } \right]\sin \left( {\kappa M_i } \right) $ | (26) |
其中,${\rm J}_\nu \left( { - \kappa e_i } \right)$代表第1类$\eta $阶贝塞尔函数
| $ {\rm J}_\eta \left( \nu \right) = \sum {} _{j = 0}^\infty {\dfrac{\left( { - 1} \right)^j\left( \nu \right)^{\eta + 2j}}{2^{\eta + 2j}{ j}!\left( {\eta + j} \right)!}} $ | (27) |
并且
| $ \beta _i = \dfrac{1 - \sqrt {1 - e_i^2 } }{e_i } $ | (28) |
同样,通过傅里叶$\!$-$\!$-$\!$贝塞尔级数展开,得到
| $ \cos f_i = - e_i + \dfrac{2\left( {1 - e_i^2 } \right)}{e_i }\sum {} _{\kappa = 1}^\infty {{\rm J}_\kappa \left( {\kappa e_i } \right)\cos \left( {\kappa M_i } \right)} $ | (29) |
在式(26)和式(29)中保留至二阶项$e_i^2 $,有
| $f_i \approx M_i + 2e_i \sin M_i + \dfrac{5}{4}e_i^2 \sin 2M_i $ | (30) |
| $\cos f_i \approx - e_i + \left( {1 - \dfrac{9}{8}e_i^2 } \right)\cos M_i + e_i \cos 2M_i + \dfrac{9}{8}e_i^2 \cos 3M_i $ | (31) |
将式(30)和式(31)代入式(23),并令
| $ \dfrac{\partial J^2\left( {\bar {a},\bar {t}} \right)}{\partial \bar {a}} = 0 $ | (32) |
得到最优参考长半轴$\bar {a}^ * $显含最优时刻$\bar {t}^ * $的表达式
| $\begin{array}{l} {{\bar a}^*} = \sum {_{i = 1}^n} {{\bar k}_i}n_i^2\left( {1 - e_i^2} \right){a_i}\prod\limits_{j = 1,j \ne i}^n {[1 - e_j^2 + } \\ \;\;\;\;\;\;\;2{e_j}\cos \left( {{n_j}{{\bar t}^*} - {{\tilde M}_{j0}}} \right) + \\ \;\;\;\;\;\;\;2e_j^2\cos (2{n_j}{{\bar t}^*} - 2{{\tilde M}_{j0}})]/\\ \;\;\;\;\;\;\;\{ \sum {_{i = 1}^n} {{\bar k}_i}n_i^2(1 - e_i^2)\prod\limits_{j = 1,j \ne i}^n {[1 - e_j^2 + } \\ \;\;\;\;\;\;\;2{e_j}\cos \left( {{n_j}{{\bar t}^*} - {{\tilde M}_{j0}}} \right) + \\ \;\;\;\;\;\;\;2e_j^2\cos \left( {2{n_j}{{\bar t}^*} - 2{{\tilde M}_{j0}}} \right)]\} \end{array}$ | (33) |
其中,$\tilde {M}_{j0} \triangleq n_j \bar {t}_0 - M_{j0} $.
如果机动时刻$\bar {t}$给定,则式(33)退化为机动时刻给定情况下,最优参考长半轴$\bar {a}^ * $关于机动时刻$\bar {t}$的显式二阶偏心率意义下的近似解. 如果机动时刻$\bar {t}$未定,则需要择优选取,即
| $ \dfrac{\partial J^2\left( {\bar {a},\bar {t}} \right)}{\partial \bar {t}} = 0 $ | (34) |
得到
| $ \sum {} _{i = 1}^n \bar {k}_i n_i^3 e_i \left( {1 - e_i^2 } \right)\left( {\bar {a}^ * - a_i } \right)^2\Big [\sin \left( {n_i \bar {t}^ * - \tilde {M}_{i0} } \right) +\\ \qquad 2e_i \sin \left( {2n_i \bar {t}^ * - 2\tilde {M}_{i0} } \right) \Big] \Bigg / \\ \qquad \Big [ \left( {1 - e_i^2 } \right) + 2e_i \cos \left( {n_i \bar {t}^ * - \tilde {M}_{i0} } \right) + \\ \qquad 2e_i^2 \cos \left( {2n_i \bar {t}^ * - 2\tilde {M}_{i0} } \right) \Big]^2 = 0 $ | (35) |
将式(33)代入式(35),得到关于最优机动时刻$\bar {t}^ * $,且含周期项$\cos \left( {n_j \bar {t}^ * - \tilde {M}_{j0} } \right)$,$\cos \left( {2n_j \bar {t}^ * - 2\tilde {M}_{j0} } \right)$,$\sin \left( {n_j \bar {t}^ * - \tilde {M}_{j0} } \right)$和$\sin \left( {2n_j \bar {t}^ * - 2\tilde {M}_{j0} } \right)$的一元方程,因此具有无穷多的解,并表现出周期性. 下文的仿真表明,在计算软件 Matlab 中给定机动时刻区间,并提供一个良好的初始猜想,很快可以得到最优解$\bar {a}^ * $和$\bar {t}^ * $.
3 数值仿真本文针对以上讨论的两种情况分别进行仿真. 假定虚拟主航天器在半径为8 000\ km的无摄圆轨道飞行,有3颗航天器围绕 其进行集群编队. 由于初始化误差的影响,3颗航天器长半轴并不精确匹配,存在一定的误差. 坐标系$\mathcal{L}_{\rm C} $中,3颗航天器相对于虚拟主航天器的初始状态如表1所示:
| 表 1 编队航天器初始状态 Table 1 Initial conditions for each spacecraft in cluster flight |
选取方程(1)$\sim$(4)为积分模型,则可求得3颗航天器的长半轴分别为$a_1 = 8\,011.38$\ km,$a_2 = 8\,000.03$\ km,$a_3 = 8\,022.78$\ km. 这里假设权值相等,即$\tilde {k}_i = \bar {k}_i = 1 \ \left( {i = 1,2,3} \right)$.
3.1 机动时刻给定假设集群航天器在$t_1 = t_2 = t_3 = \tilde {t} = 500$\,s施加脉冲. 联立式(14) $\sim $式(20),解得
| $ \begin{array}{l} {\left[ {\Delta v_1^*} \right]_{{\mathcal{L}_{\rm{C}}}}} = {\left[ { - 0.000{\mkern 1mu} 21,\;\;0.892{\mkern 1mu} 28,\;\;0.001{\mkern 1mu} 01} \right]^{\rm{T}}}{\mkern 1mu} {\rm{mm/s}}\\ {\left[ {\Delta v_2^*} \right]_{{\mathcal{L}_{\rm{C}}}}} = {\left[ { - 0.002{\mkern 1mu} 82,\;\;5.002{\mkern 1mu} 22,\;\;0.005{\mkern 1mu} 66} \right]^{\rm{T}}}{\mkern 1mu} {\rm{m/s}}\\ {\left[ {\Delta v_3^*} \right]_{{\mathcal{L}_{\rm{C}}}}} = {\left[ { - 0.000{\mkern 1mu} 51,\;\; - 5.001{\mkern 1mu} 79,\;\; - 0.005{\mkern 1mu} 65} \right]^{\rm{T}}}{\mkern 1mu} {\rm{m/s}} \end{array} $ |
进而得到二范数意义下最优的总速度脉冲增量
| $ J\left( {\tilde {a}^ * } \right) = \sqrt {\left\| {\left[{ {\Delta }{\pmb v}_1^ * } \right]_{\mathcal{L}_{\rm C} } } \right\|_2^2 + \left\| {\left[{ {\Delta }{\pmb v}_2^ * } \right]_{\mathcal{L}_{\rm C} } } \right\|_2^2 + \left\| {\left[{ {\Delta }{\pmb v}_3^ * } \right]_{\mathcal{L}_{\rm C} } } \right\|_2^2 } =\\ \qquad 7.073\,91\,{\rm m/s} $ |
编队航天器机动以后,长半轴趋于一致,等于最优参考长半轴,为$\tilde {a}^ * = 8\,011.383\,9$\ km.
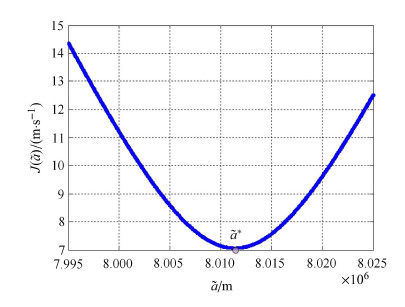
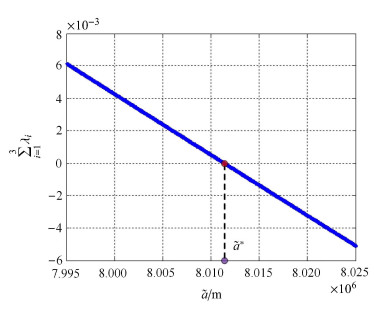
图1给出了在满足周期性约束条件(13)的前提下当参考长半轴取不同值时所对应的总速度脉冲消耗. 图2为式(18)中约束 拉格朗日乘子之和为零,以保证$a_i = \tilde {a}^ * $. 显而易见,图1和图2都从数值的角度验证了本文所求最优解的正确性.
|
图 1 不同参考长半轴取对应的总的速度脉冲增量 Fig. 1 The overall velocity impulse varying with different semimajor axes |
|
图 2 拉格朗日乘子之和随参考长半轴的变化 Fig. 2 The sum of Lagrange multipliers varying with different semimajor axes |
为了直观地描述航天器之间的相对距离,本文选取集群编队航天器两两距离之和,即所构成动态三角形的周长作为衡量标准. 将3颗集群航天器视作质点,则它们在空间构成的动态三角形周长为
| $ L \triangleq \sum {} _{i,j = 1,i \ne j}^3 {\left\| { {\pmb r}_i-{\pmb r}_j } \right\|_2 } $ | (36) |
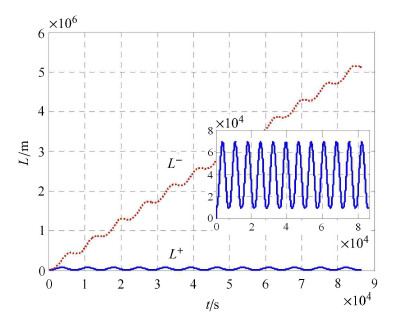
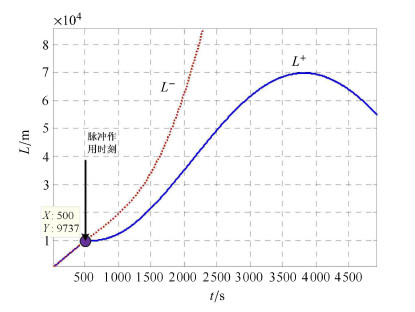
以$L^ - $和$L^ + $分别表示在时刻$\tilde {t} = 500$\,s施加速度脉冲与不施加速度脉冲动态三角形的周长. 图3中的 虚线代表一天内$L^ - $的变化,实线代表$L^ + $的变化. 图4给出了施加速度脉冲时刻的局部放大图.
|
图 3 $L^ + $与$L^ - $的比较 Fig. 3 The comparison between $L^ + $ and $L^ - $ |
|
图 4 $L^ + $ 和$L^ - $的放大图 Fig. 4 The magnified view of $L^ + $ and $L^ - $ |
由图3和图4可知,若不施加脉冲,则集群航天器的相对距离在相当长的时间内会呈现出发散现象,这是由初始长半轴 未精确匹配导致的,即$a_1 = 8\,011.38$\ km,$a_2 = 8\,000.03$\ km,$a_3 = 8\,022.78$\ km. 而在给定时刻$\tilde {t} = 500$\,s施加速度脉冲$\left[{ {\Delta }{\pmb v}_i^ * } \right]_{\mathcal{L}_{\rm C} } $进行修正之后,集群航天器的长半轴精确匹配,即$\tilde {a}^ * = 8\,011.38$\ km. 因此,相对距离呈现出周期性变化规律,并且与施加速度脉冲后集群编队中任一航天器的轨道周期相等.
3.2 机动时刻未定为了求解式(33)和(34),可以使用计算软件 Matlab 中的"fsolve"函数. 由于含有多个周期解,因此不妨限 定求解范围为$\bar {t}^ * \in \left[0,\ \ 8\,000\,{\rm s} \right]$,并给定$\hat {a} = 1 /n\sum {} _{i = 1}^n {\bar {a}_i } $为初始猜想. 经过几次迭代便可得到最优参考长半轴$\bar {a}^ * = 8\,011.385\,46$\ km,$\bar {t}^ * = 6\,874$\,s. 进而得到二范数意义下总的最优速度脉冲$J\left( {\bar {a}^ * ,\bar {t}^ * } \right) = 7.070\,184$\ m/s.
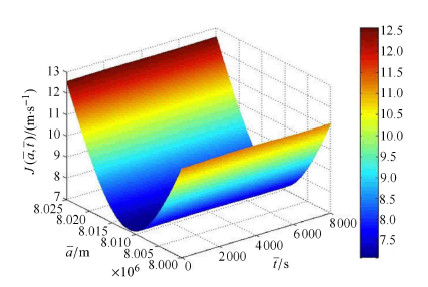
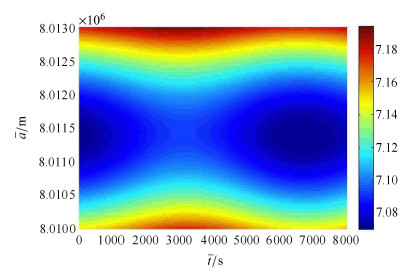
图5为参考长半轴与脉冲施加时刻分别取不同值时总速度脉冲消耗,图6为$J\left( {\bar {a},\bar {t}} \right)$在$\left( {\bar {t}\sim \bar {a}} \right)$平面的投影.
|
图 5 $J\left( {\bar {a},\bar {t}} \right)$随参考长半轴以及机动时刻的变化曲线 Fig. 5 The contour lines of $J\left( {\bar {a},\bar {t}} \right)$ |
|
图 6 $J\left( {\bar {a},\bar {t}} \right)$在$\left( {\bar {t}\sim \bar {a}} \right)$平面的投影 Fig. 6 The projected contour lines of total velocity impulse consumption in $\left( {\bar {t}\sim \bar {a}} \right)$ plane |
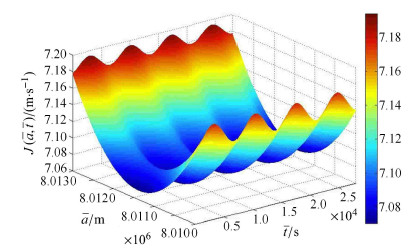
如前文所述,最优参考长半轴$\bar {a}^ * $只有一个,而最优机动时刻$\bar {t}^ * $有无限多个解,并呈现出周期性特征. 图7给出了7.78小时内,不同机动时刻和参考长半轴所对应的总速度脉冲消耗.
|
图 7 在7.78小时内$J\left( {\bar {a},\bar {t}} \right)$随参考长半轴和机动时刻的变化曲线 Fig. 7 Contour lines of $J\left( {\bar {a},\bar {t}} \right)$ within 7.78 hours |
文献[13]断定最优参考长半轴大小为机动前各航天器长半轴的平均值,但根据本文作者的研究,发现其只不过为粗略的近似,即$\tilde {a}^ * \approx \bar {a}^ * \approx 1 / n\sum {} _{i = 1}^n {a_i } $,精确值由式(20)和式(33)给出. 进一步的研究发现,如果各航天器的偏心率$e_i \to 1$且差别较大,则使用初始长半轴的平均值进行近似,误差会显著增大. 由于篇幅所限,这里不再赘述.
4 结 论本文研究了航天器集群编队最优单脉冲机动问题. 在周期性相对运动条件约束下,分别探讨了机动时刻给定和机动时刻未定情 况下的能量最省问题. 如果机动时刻未定,从高斯变分方程和基于能量匹配条件的拉格朗日乘子法两个角度分别进行了探讨,将问题转化为对一元 二次方程求极值或对一个单零点非线性方程求根;对于机动时刻未定的情况,将问题转化为对一个多零点非线性方程求根, 通过傅里叶$\!$-$\!$-$\!$贝塞尔级数展开可以得到任意高阶近似解. 由于第一种情况限定了机动时刻,约束较强,因此消耗的速度脉冲大于第二种情况. 数值仿真验证了本文的方法.
本文所得结论可用于航天器集群编队飞行,特别是对于一些携带燃料少,机动能力有限的微小卫星,更具参考价值. 为了 更加贴近工程实际,未来将对更多摄动影响和约束条件下的最优机动问题展开研究,例如考虑非球形和大气阻力摄动影响、空间碎片规避等.
| [1] | Vaddi SS, Vadali SR, Alfriend KT. Formation flying: accommodating nonlinearity and eccentricity perturbations. Journal of Guidance, Control, and Dynamics, 2003, 26(2): 214-223. |
| [2] | Gurfil P. Relative motion between elliptic orbits: generalized boundedness conditions and optimal formation-keeping. Journal of Guidance, Control, and Dynamics, 2005, 28(4): 761-767. |
| [3] | Kasdin NJ, Gurfil P, Kolemen E. Canonical modeling of relative spacecraft motion via epicyclic orbital elements. Celestial Mechanics and Dynamical Astronomy, 2005, 92(4): 337-370. |
| [4] | Schaub H, Alfriend KT. J2 Invariant relative orbits for spacecraft formations. Celestial Mechanics and Dynamical Astronomy, 2001, 79(2): 77-95. |
| [5] | Xu M, Wang Y, Xu SJ. On the existence of J2 invariant relative orbits from the dynamical system point of view. Celestial Mechanics and Dynamical Astronomy, 2012, 112(4): 427-444. |
| [6] | Damaren CJ. Almost periodic relative orbits under J2 perturbations. Proceedings of the Institution of Mechanical Engineers. Part G, Journal of Aerospace Engineering, 2007, 221(5): 767-774. |
| [7] | Guibout VM, Scheeres DJ. Spacecraft formation dynamics and design. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 121-133. |
| [8] | Sabatini M, Izzo D, Bevilacqua R. Special inclinations allowing minimal drift orbits for formation flying satellites. Journal of Guidance, Control, and Dynamics, 2008, 31(1): 94-100. |
| [9] | Vadali SR, Sengupta P, Yan Hui, et al. Fundamental frequencies of satellite relative motion and control of formations. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1239-1248. |
| [10] | Lara M, Gurfil P. Integrable approximation of J2-perturbed relative orbits. Celestial Mechanics and Dynamical Astronomy, 2012, 114(3): 229-254. |
| [11] | Martinusi V, Gurfil P. Solutions and periodicity of satellite relative motion under even zonal harmonics perturbations. Celestial Mechanics and Dynamical Astronomy, 2011, 111(4): 387-414. |
| [12] | Vadali SR, Yan Hui, Alfriend KT. Formation maintenance and reconfiguration using impulsive control. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, August 2008, Honolulu, Hawaii. AIAA 2008-7359 |
| [13] | Beigelman I, Gurfil P. Optimal fuel-balanced impulsive formation-keeping for perturbed spacecraft orbits. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1266-1283. |
| [14] | Mazal L, Mingotti G, Gurfil P. Optimal on-off cooperative maneuvers for long-term satellite cluster flight. Journal of Guidance, Control, and Dynamics, 2014, 37(2): 391-402. |
| [15] | Marshal JA, Broucke ME. Formation of vehicles in cyclic pursuit. IEEE Transactions on Automatic Control, 2004, 49(11): 1963-1974. |
| [16] | 毕鹏,罗建军,张博. 一种基于一致性理论的航天器编队飞行协同控制方法. 宇航学报,2010,31(1):70-74 (Bi Peng, Luo Jianjun, Zhang Bo. Cooperated control algorithm for spacecraft formation flying. Journal of Astronautics, 2010, 31(1): 70-74 (in Chinese)) |
| [17] | 马广富,梅杰. 多星系统相对轨道的自适应协同控制. 控制理论与应用,2011,28(6):781-787 (Ma Guangfu, Mei Jie. Adaptive cooperative control for relative orbits of multi-satellite systems. Control Theory and Applications, 2011, 28(6): 781-787 (in Chinese)) |
| [18] | Alfriend KT, Vadali SR, Gurfil P, et al. Spacecraft Formation Flying: Dynamics, Control and Navigation. Oxford: Butterworth-Heinemann Press, 2010. 124-126 |
| [19] | Battin RH. An Introduction to the Mathematics and Methods of Astrodynamics. Broadway, New York: American Institute of Aeronautics and Astronautics, Inc., 1999. 206-212 |
2. National Key Laboratory of Aerospace Flight Dynamics, Xi'an 710072, China
 2015, Vol. 47
2015, Vol. 47
